小学奥数中的涂色问题
六年级奥数题及答案-涂颜色

六年级奥数题及答案-涂颜色
导语:六年级是学习的冲刺阶段,也是拓展思维的好时机,有效的进行习题训练有助于同学们奥数能力的提升。
圆周上有12个点,其中一个点涂红,还有一个点涂了蓝色,其余10个点没有涂色,以这些点为顶点的凸多边形中,其顶点包含了红点及蓝点的多边形称为双色多边形;只包含红点(蓝点)的多边形称为红色(蓝色)多边形.不包含红点及蓝点的称无色多边形.试问,以这12个点为顶点的所有凸多边形(边数可以从三角形到12边形)中,双色多边形的个数与无色多边形的个数,哪一种较多?多多少个?。
小学奥数杂题染色问题【三篇】

小学奥数杂题染色问题【三篇】
解析:对房间染色,使最下面的两个房间染成黑色,与黑色相邻的
房染成白色,
则图中有7个黑色房间和5个白色房间.
如果要想不重复地走过每一个房间,黑色与白色房间数应该相等.故题中的想法是不能实现的.
点评:完成本题也可根据要求据图中的房间实际找下路线,看是
否能够找到.
【第二篇】
展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入
口进去,不重复地参观完全部展室后,从出口出来呢?
答案:
不能.对展室实行染色,使相邻两房间分别是黑色和白色的.此时入
口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个
展室,入口与出口展室的颜色应该不相同.
【第三篇】
染色问题基本解法:
三面涂色和顶点相关 8个顶点。
两面染色和棱长相关。
即新棱长(棱长-2)×12
一面染色和表面积相关。
同样用新棱长计算表面积公式(棱长-2)×(棱长-2)*6
0面染色和体积相关。
用新棱长计算体积公式(棱长-2)×(棱长-2)×(棱长-2)
长方体的解法和立方体同理,即计算各种公式前长、宽、高都要先减2再利用公式计算。
涂色问题练习题

涂色问题练习题涂色问题是数学中的一个常见的应用题,主要用于培养逻辑思维和分析问题的能力。
本文将为读者提供一些关于涂色问题的练习题,帮助读者巩固对涂色问题的理解和应用。
一、题目一在一个方形的纸上,每一边都有8个小正方形,如下所示:```1 2 3 4 5 6 7 89 10 11 12 13 14 15 1617 18 19 20 21 22 23 2425 26 27 28 29 30 31 3233 34 35 36 37 38 39 4041 42 43 44 45 46 47 4849 50 51 52 53 54 55 5657 58 59 60 61 62 63 64```我们要使用三种颜色(红、绿、蓝),对这些小正方形进行涂色,要求相邻的小正方形不能使用相同的颜色。
请问有多少种涂色方案?解析:对于每个小正方形,它的上、下、左、右四个方向都有相邻的小正方形,因此我们可以通过逐个尝试的方法来找到合适的涂色方案。
首先,我们从第一个小正方形开始涂色,假设我们将第一个小正方形涂成红色,那么第二个小正方形可以选择绿色或蓝色,第三个小正方形可以选择红色或蓝色,以此类推。
通过不断尝试,直到涂到最后一个小正方形,就可以统计出所有的涂色方案。
二、题目二在一张圆形的纸上,有六个小扇形区域,如下图所示:```1___6 / \ 2/ \5 \ / 3\___4```我们要使用四种颜色(红、黄、蓝、绿),对这六个小扇形区域进行涂色,要求相邻的小扇形区域不能使用相同的颜色。
请问有多少种涂色方案?解析:对于每个小扇形区域,它的上、下、左、右、左上和右下六个方向都有相邻的小扇形区域,因此我们同样可以通过逐个尝试的方法来找到合适的涂色方案。
首先,我们从第一个小扇形区域开始涂色,假设我们将第一个小扇形区域涂成红色,那么第二个小扇形区域可以选择黄色、蓝色或绿色,第三个小扇形区域可以选择红色、蓝色或绿色,以此类推。
通过不断尝试,直到涂到最后一个小扇形区域,就可以统计出所有的涂色方案。
小学奥数中的涂色问题

涂色问题的常见方法与涂色问题有关的试题新颖有趣,其中包含着丰富的数学思想。
解决涂色问题方法技巧性强且灵活多变,故这类问题的利于培养学生的创新思维能力、分析问题与观察问题的能力,有利于开发学生的智力。
本文拟总结涂色问题的常见类型及求解方法。
一、区域涂色问题1、 根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
例1、 用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?分析:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有3种,由于④号与①、②不相邻,因此④号有4种涂法,根据分步计数原理,不同的涂色方法有5434240⨯⨯⨯=2、 根据共用了多少种颜色讨论,分别计算出各种出各种情形的种数,再用加法原理求出不同的涂色方法种数。
例2、(2003江苏卷)四种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
分析:依题意只能选用4种颜色,要分四类:(1)②与⑤同色、④与⑥同色,则有44A ;(2)③与⑤同色、④与⑥同色,则有44A ;(3)②与⑤同色、③与⑥同色,则有44A ;(4)③与⑤同色、② 与④同色,则有44A ;(5)②与④同色、③与⑥同色,则有44A ;所以根据加法原理得涂色方法总数为544A =120例3、(2003年全国高考题)如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有多少种? 分析:依题意至少要用3种颜色1) 当先用三种颜色时,区域2与4必须同色,2) 区域3与5必须同色,故有34A 种;① ②③ ④ ⑤ ⑥3) 当用四种颜色时,若区域2与4同色,4) 则区域3与5不同色,有44A 种;若区域3与5同色,则区域2与4不同色,有44A 种,故用四种颜色时共有244A 种。
由加法原理可知满足题意的着色方法共有34A +244A =24+2⨯24=723、 根据某两个不相邻区域是否同色分类讨论,从某两个不相邻区域同色与不同色入手,分别计算出两种情形的种数,再用加法原理求出不同涂色方法总数。
小学奥数专题15:染色问题
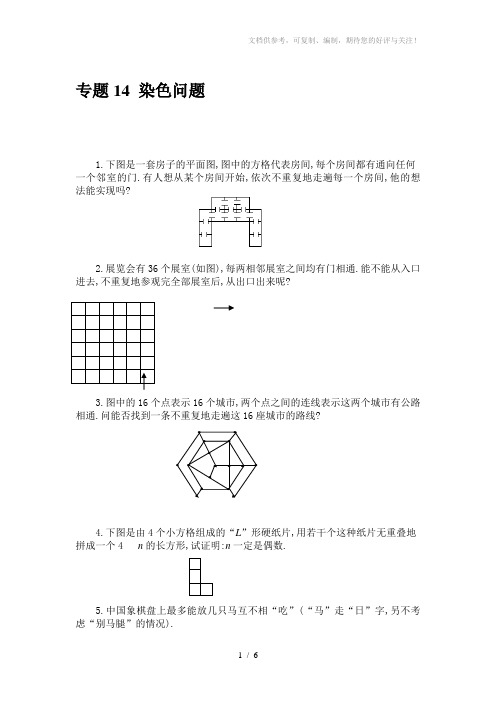
专题14 染色问题1.下图是一套房子的平面图,图中的方格代表房间,每个房间都有通向任何 一个邻室的门.有人想从某个房间开始,依次不重复地走遍每一个房间,他的想法能实现吗?2.展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入口 进去,不重复地参观完全部展室后,从出口出来呢?3.图中的16个点表示16个城市,两个点之间的连线表示这两个城市有公路 相通.问能否找到一条不重复地走遍这16座城市的路线?4.下图是由4个小方格组成的“L ”形硬纸片,用若干个这种纸片无重叠地 拼成一个4n 的长方形,试证明:n 一定是偶数.5.中国象棋盘上最多能放几只马互不相“吃”(“马”走“日”字,另不考虑“别马腿”的情况).6.能否用一个田字和15个41矩形覆盖88棋盘?7.能否用1个田字和15个T 字纸片,拼成一个88的正方形棋盘?8.在88棋盘上,马能否从左下角的方格出发,不重地走遍棋盘,最后回到起点?若能请找出一条路,若不能,请说明理由.9.下面三个图形都是从44的正方形分别剪去两个11的小方格得到的,问可否把它们分别剪成12的七个小矩形? (1) (2) (3)10.把三行七列的21个小格组成的矩形染色,每个小格染上红、蓝两种色中的一种.求证:总可以找到4个同色小方格,处于某个矩形的4个角上(如图)红 红 红 红11.17个科学家互相通信,在他们的通信中共讨论3个问题,而任意两个科学家之间仅讨论1个问题.证明:至少有3个科学家,他们彼此通信讨论的是同一个问题.12.用一批124的长方体木块,能不能把一个容积为666的正方体木箱充塞填满?说明理由.13.在平面上有一个2727的方格棋盘,在棋盘的正中间摆好81枚棋子,它们被罢成一个99的正方形.按下面的规则进行游戏:每一枚棋子都可沿水平方向或竖直方向越过相邻的棋子,放进紧挨着这枚棋子的空格中,并把越过的这格棋子取出来.问:是否存在一种走法,使棋盘上最后恰好剩下一枚棋子?14.1212的超极棋盘上,一匹超级马每步跳至34矩形的另一角(如图).问能否从任一点出发遍历每一格恰一次,再回到出发点(这种情况又称马有“回 O12 3O———————————————答案——————————————————————1. 不能.对房间染色,使最下面的两个房间染成黑色,与黑色相邻的房染成白色,则图中有7个黑色房间和5个白色房间.如果要想不重复地走过每一个房间,黑色与白色房间数应该相等.故题中的想法是不能实现的.2. 不能.对展室进行染色,使相邻两房间分别是黑色和白色的.此时入口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个展室,入口与出口展室的颜色应该不相同.3. 不能.对这16个城市进行黑白相间的染色,一种颜色有9个,另一种颜色有7个.而要不重复地走遍这16个城市,黑色与白色的个数应该相等.4. 如图,对4n长方形的各列分别染上黑色和白色.任一L形纸片所占的方格只有两类:第一类占3黑1白,第二类占3白1黑.n个设第一类有a个,第二类有b个,因为涂有两种颜色的方格数相等,故有3b+a=3a+b,即a=b,也就是说第一类与第二类相等,因此各种颜色的方格数都是4的倍数,总数是8的倍数,从而n是偶然.5. 将棋盘黑白相间染色,由“马”的走法可知,放在黑点上的“马”,只能吃放在某些白点上的马.整个棋盘上黑、白点的个数均为45,故可在45个黑点放上马,它们是不能互吃的.6. 如图的方式对棋盘染色.那么一个田字形盖住1个或3个白格,而一个41的矩形盖住2个白格.这样一来一个田字和15个41的矩形能盖住的白格数是一个奇数,但上图中的白格数是一个偶数,因此一个田字形和15个41.7. 将棋盘里黑白相间涂色.一个田字形盖住2个白格,一个T字形盖住3个或1个白格.故1个田字和15个T字盖住的白格数是一个奇数,但棋盘上的白格数是一个偶数.因此一个田字形和15个T字形不能盖住88的棋盘.8. 将棋盘黑白相间地染色后,马的走法是从一种颜色的格子跳到另一种颜色.棋盘上有32个白格与32个黑格,故马可能跳遍整个棋盘.图中给出了一种走法.56 41 58 35 50 39 60 3347 44 55 40 59 34 51 3842 57 46 49 36 53 32 6145 48 43 54 31 62 37 5220 5 30 63 22 11 16 1329 64 21 4 17 14 25 106 19 2 278 23 12 151 28 7 18 3 26 9 249. 先对44的棋盘黑白相间的涂色(如图),这道题的实际问题是问7个12矩形能否分别复盖剪去A、B;剪去A、C;剪去A、D的三个棋盘.若7个12矩形可以复盖剪残的棋盘,因为每个12矩形均可盖住一个白格和一个黑格,所以棋盘的白格与黑格数目应该相等.都是7个.而剪去A格和C格的棋盘(2)有5个白格8个黑格,剪去A、D的棋盘(3)有5个白格8个黑格,因此这两个剪损的棋盘均不能被7个12矩形复盖,也就不能剪成7个12的矩形. ABCD棋盘(1)可以被7个12的矩形所复盖.下面给出一种剪法:A 1 1 27 7 B 26 5 4 36 5 4 310. 在第一行的7格中必有4格同色,不妨设这4格位于前4个位置,且均为红色.然后考虑前4列构成的34矩形.若第二行和第3行中出现2个或2个以上的红色格子.则该行的两个红色格子与第一行的红色格子就组成一个4角同为红色格子的矩形.若不然,则第2、3行中都至少有3个蓝格在前4列中,不妨设第2行前3格为蓝色,显然第三行中的前3格中至少有2个蓝格,故在二、三行的前4列中必存在四角都是蓝色的矩形.11. 将17个科学家用17个点代表,两点之间连结的线段表示两个科学家之间讨论的问题.用三种颜色给这些线段染色,表示三个问题,于是问题就变成:给17个点之间的所有连结线段用三种颜色染色,必有同色三角形.从任意一点,不妨设从A 向其他16点A 1,A 2,…A 16共可连成16条线段,用三种颜色染色,由抽屉原则可知,必有6条线段同色.设这6条线段为AA 1,AA 2,…AA 6且同为红色.考虑A 1,A 2,A 3,A 4,A 5,A 6这六点之间的连线,若有一条为红色,(如A 1A 2为红色) ,则三角形AA 1A 2为红色的同色三角形.若这六点之间的连线中,没有一条是红色的,则它们之间只能涂两种颜色.考虑从A 1引出的五条线段A 1A 2 A 1A 3 A 1A 4 A 1A 5 A 1A 6,由抽屉原理知,其中必有三条是同色的.不妨设这三条为A 1A 2 A 1A 3 A 1A 4,且同为蓝色.若三角形A 2A 3A 4的三边中有一条为蓝色的,则有一个蓝色的三角形存在;若三角形A 2A 3A 4三边都不是蓝色的,则它的三边是同为第三色的同色三角形.12. 把正方体木箱分成27个小正方体,每个小正方体的体积为222=8.将这些正方体如右图黑白相间染上色.显然黑色222的正方体有14个,白色222小正方体有13个.每一个这样的正方体相当于8个111的小正方体.将124的长方体放入木箱,无论怎么放,每个长方体木块盖住8个边长为1的单位正方体,其中有4个黑色的,4个白色的.木箱共含666=216个单位正方体,26个长方体木块共盖住826=208个单位正方体,其中黑白各占104个,余下216-208=8个单位正方体是黑色的.但是第27个124长方体木块不管怎样放,也无法盖住这8个黑色单位正方体.13. 如图,将整个棋盘的每一格都分别染上红、白、黑三种颜色,这种染色方式将棋盘分成了三个部分.按照游戏规则,每走一步,有两种颜色方格中的棋子数分别减少了1个,而第三种颜色的棋子数增加了一个.这表明每走一步,每个部分的棋子的奇偶性要发生改变.AA 1 A 2A 3A 4A 5 A 6 A 1A 2 A 3 A 4因为一开始时,81枚棋子摆成一个99的正方形,显然三个部分的棋子数是相同的,从而每走一步,三部分中的棋子数的奇偶性是相同的.如果走了若干步以后,棋盘上恰好剩下一枚棋子,则两部分上的棋子数为偶数,而另一部分上的棋子数为奇数.这种结果是不可能出现的.14. 用两种方法对超级棋盘染色.首先,将棋盘黑白相间染色,则马每跳一步,它所在的方格就要改变一次颜色.不妨设第奇数步跳入白格.其次,将棋盘的第3,4,5及8,9,10这六行染成黑色,其余六行染成白色.在此种染色方式下,马从白格一定跳入黑格.又因黑白格总数相同,马要遍历每一格恰一次又回到出发点,因此,马从黑格只能跳入白格而不能跳入黑格.不妨设马第奇数步跳入白格.但是对于一种满足要求跳法,在两种染色方式下第奇数步跳入的格子的全体是不同的,这显然是不可能的,故题目要求的跳法是不存在的.。
小学奥数中的涂色问题

涂色问题的常见方法 与涂色问题有关的试题新颖有趣,其中包含着丰富的数学思想。
解决涂色问题方法技巧性强且灵活多变,故这类问题的利于培养学生的创新思维能力、分析问题与观察问题的能力,有利于开发学生的智力。
本文拟总结涂色问题的常见类型及求解方法。
一、 区域涂色问题1、 根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
例1、 用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?分析:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有3种,由于④号与①、②不相邻,因此④号有4种涂法,根据分步计数原理,不同的涂色方法有5434240⨯⨯⨯=2、 根据共用了多少种颜色讨论,分别计算出各种出各种情形的种数,再用加法原理求出不同的涂色方法种数。
例2、(2003江苏卷)四种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
分析:依题意只能选用4种颜色,要分四类:(1)②与⑤同色、④与⑥同色,则有44A ;(2)③与⑤同色、④与⑥同色,则有44A ;(3)②与⑤同色、③与⑥同色,则有44A ;(4)③与⑤同色、② 与④同色,则有44A ;(5)②与④同色、③与⑥同色,则有44A ; 所以根据加法原理得涂色方法总数为544A =120例3、(2003年全国高考题)如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有多少种? 分析:依题意至少要用3种颜色1) 当先用三种颜色时,区域2与4必须同色,2) 区域3与5必须同色,故有34A 种;3) 当用四种颜色时,若区域2与4同色,4) 则区域3与5不同色,有44A 种;若区域3与5同色,则区域2与4不同色,有② ① ③ ④ 2 4 3 1 5 ① ②③ ④ ⑤ ⑥44A 种,故用四种颜色时共有244A 种。
小学奥数杂题染色问题【三篇】

小学奥数杂题染色问题【三篇】
导读:本文小学奥数杂题染色问题【三篇】,仅供参考,如果觉得很不错,欢迎点评和分享。
【第一篇】 1.如图是一套房子的平面图,图中的方格代表房间,每个房间都有通向任何一个邻室的门.有人想从某个房间开始,依次不重复地走遍每一个房间,他的想法能实现吗?
解析:对房间染色,使最下面的两个房间染成黑色,与黑色相邻的房染成白色,
则图中有7个黑色房间和5个白色房间.
如果要想不重复地走过每一个房间,黑色与白色房间数应该相等.故题中的想法是不能实现的.
点评:完成本题也可根据要求据图中的房间实际找下路线,看是否能够找到.【第二篇】展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入口进去,不重复地参观完全部展室后,从出口出来呢? 答案:不能.对展室进行染色,使相邻两房间分别是黑色和白色的.此时入口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个展室,入口与出口展室的颜色应该不相同. 【第三篇】染色问题基本解法:三面涂色和顶点有关8个顶点。
两面染色和棱长有关。
即新棱长(棱长-2)×12一面染色和表面积有关。
同样用新棱长计算表面积公式(棱长-2)×(棱长-2)*6 0面染色和体积有关。
用新棱长计算体积公式(棱
长-2)×(棱长-2)×(棱长-2)长方体的解法和立方体同理,即计算各种公式前长、宽、高都要先减2再利用公式计算。
小学奥数中的涂色问题(课堂参照)

涂色问题的常见方法与涂色问题有关的试题新颖有趣,其中包含着丰富的数学思想。
解决涂色问题方法技巧性强且灵活多变,故这类问题的利于培养学生的创新思维能力、分析问题与观察问题的能力,有利于开发学生的智力。
本文拟总结涂色问题的常见类型及求解方法。
一、区域涂色问题1、 根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
例1、 用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?分析:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有3种,由于④号与①、②不相邻,因此④号有4种涂法,根据分步计数原理,不同的涂色方法有5434240⨯⨯⨯=2、 根据共用了多少种颜色讨论,分别计算出各种出各种情形的种数,再用加法原理求出不同的涂色方法种数。
例2、(2003江苏卷)四种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
分析:依题意只能选用4种颜色,要分四类:(1)②与⑤同色、④与⑥同色,则有44A ;(2)③与⑤同色、④与⑥同色,则有44A ;(3)②与⑤同色、③与⑥同色,则有44A ;(4)③与⑤同色、② 与④同色,则有44A ;(5)②与④同色、③与⑥同色,则有44A ;所以根据加法原理得涂色方法总数为544A =120例3、(2003年全国高考题)如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有多少种? 分析:依题意至少要用3种颜色1) 当先用三种颜色时,区域2与4必须同色,2) 区域3与5必须同色,故有34A 种;② ① ③ ④ 2 3 1 5 ① ②③ ④ ⑤ ⑥3) 当用四种颜色时,若区域2与4同色,4) 则区域3与5不同色,有44A 种;若区域3与5同色,则区域2与4不同色,有44A 种,故用四种颜色时共有244A 种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
涂色问题的常见方法
与涂色问题有关的试题新颖有趣,其中包含着丰富的数学思想。
解决涂色问题方法技巧性强且灵活多变,故这类问题的利于培养学生的创新思维能力、分析问题与观察问题的能力,有利于开发学生的智力。
本文拟总结涂色问题的常见类型及求解方法。
一、区域涂色问题
1、 根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
例1、 用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种
颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种
4种方法,接着给③号涂色方法有3涂色方法有543
4⨯⨯⨯=2、 求出不同的涂色方法种数。
例2、(2003江苏卷)四种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
分析:依题意只能选用4种颜色,要分四类:
(1)②与⑤同色、④与⑥同色,则有44A ; (2)③与⑤同色、④与⑥同色,则有44
A ;
(3)②与⑤同色、③与⑥同色,则有4
4A ; (4)③与⑤同色、② 与④同色,则有44A ;(5)②与④同色、③与⑥同色,则有44A ;
所以根据加法原理得涂色方法总数为544A =120
例3、(2003年全国高考题)如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有多少种 分析:依题意至少要用3种颜色
1) 当先用三种颜色时,区域2与4必须同色,
2) 区域3与5必须同色,故有34A 种;
3) 当用四种颜色时,若区域2与4同色,
4) 则区域3与5不同色,有44A 种;若区域3与5同色,则区域2与4不同色,
有44A 种,故用四种颜色时共有244A 种。
由加法原理可知满足题意的着色方
① ②③ ④ ⑤
⑥
法共有34A +244A =24+2⨯24=72
3、 根据某两个不相邻区域是否同色分类讨论,从某两个不相邻区域同色与不同色入
手,分别计算出两种情形的种数,再用加法原理求出不同涂色方法总数。
例4用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一
种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,共有多少种不同
的涂色方法
分析:可把问题分为三类: (1) 四格涂不同的颜色,方法种数为45A ;
(2) 有且仅两个区域相同的颜色,即只
1254
2C A ; 5)
两组对角小方格分别涂相同的颜色,涂法种数为25A ,
因此,所求的涂法种数为212255452260A C A A ++=
4、 根据相间区使用颜色的种类分类
例5如图, 6个扇形区域A 、B 、C 、D 、E 、F ,现给这6个区域着色,要求同一
区域涂同一种颜色,相邻的两个区域不得使用同一种颜色,现有4种不同的颜色
可1A 解(1)当相间区域A 、C 、E 着同一种颜色时,
有4种着色方法,此时,B 、D 、F 各有3种着色方法,
此时,B 、D 、F 各有3种着色方法故有4333108⨯⨯⨯=
种方法。
(2)当相间区域A 、C 、E 着色两不同的颜色时,有2234C A 种着色方法,此时B 、
D 、F 有322⨯⨯种着色方法,故共有2234322432C A ⨯⨯⨯=种着色方法。
(3)当相间区域A 、C 、E 着三种不同的颜色时有34A 种着色方法,此时B 、D 、
F 各有2种着色方法。
此时共有34222192A ⨯⨯⨯=种方法。
故总计有108+432+192=732种方法。
说明:关于扇形区域区域涂色问题还可以用数列中的递推公来解决。
如:如图,把一个圆分成(2)n n ≥个扇形,每个扇形用红、白、蓝、黑四
色之一染色,要求相邻扇形不同色,有多少种染色方法
解:设分成n 个扇形时染色方法为n a 种
(1) 当n=2时1A 、2A 有2
4A =12种,即2a =12 (2) 当分成n 个扇形,如图,1A 与2A 不同色,2A 与3A 不同色,L ,1n A -
与n A 不同色,共有143n -⨯种染色方法, 但由于n A 与1A 邻,所以应排除n A 与1
A 同色的情形;n A 与1A 同色时,可把n A 、 1A 看成一个扇形,与前2n -个扇形加在一起为1n -个扇形,此时有1n a -种染色法,故有如下递推关系:
二、点的涂色问题
方法有:(1)可根据共用了多少种颜色分类讨论,(2)根据相对顶点是否同色分类讨论,(3)将空间问题平面化,转化成区域涂色问题。
例6、将一个四棱锥S ABCD -的每个顶点染上一种颜色,并使同一条棱的两端点异色,如果只有5种颜色可供使用,那么不同的染色方法的总数是多少
解法一:满足题设条件的染色至少要用三种颜色。
(1) 若恰用三种颜色,可先从五种颜色中任选一种染顶点S ,再从余下的
四种颜色中任选两种涂A 、B 、C 、D 四点,此时只能A 与C 、B 与D
分别同色,故有125460C A =种方法。
(2) 若恰用四种颜色染色,可以先从五种颜色中任选一种颜色染顶点S ,
再从余下的四种颜色中任选两种染A 与B ,由于A 、B 颜色可以交换,
故有24A 种染法;再从余下的两种颜色中任选一种染D 或C ,而D 与
C ,而
D 与C 中另一个只需染与其相对顶点同色即可,故有
12115422240C A C C =种方法。
(3) 若恰用五种颜色染色,有55120A =种染色法
综上所知,满足题意的染色方法数为60+240+120=420种。
解法二:设想染色按S —A —B —C —D 的顺序进行,对S 、A 、B 染色,有54360⨯⨯=种染色方法。
由于C 点的颜色可能与A 同色或不同色,这影响到D 点颜色的选取方法数,故分类讨论:
C 与A 同色时(此时C 对颜色的选取方法唯一),
D 应与A (C )、S 不同色,有3种选择;C 与A 不同色时,C 有2种选择的颜色,D 也有2种颜色可供选择,从而对C 、D 染色有13227⨯+⨯=种染色方法。
3
A
由乘法原理,总的染色方法是607420
⨯=
解法三:可把这个问题转化成相邻区域不同色问题:如图,
对这五个区域用5种颜色涂色,有多少种不同的涂色方法
解答略。
三、线段涂色问题
1)根据共用了多少颜色分类讨论
2)根据相对线段是否同色分类讨论。
例7、用红、黄、蓝、白四种颜色涂矩形ABCD的四条边,每条边只涂一种颜色,
且使相邻两边涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方
法
解法一:(1)使用四颜色共有4
4
A种
(2)使用三种颜色涂色,则必须将一组对边染成同色,故有112
423
C C A种,
(3)使用二种颜色时,则两组对边必须分别同色,有2
4
A种
因此,所求的染色方法数为41122
4423484
A C C A A
++=种
解法二:涂色按AB-BC-CD-DA的顺序进行,对AB、BC涂色有4312
⨯=种涂色方法。
由于CD的颜色可能与AB同色或不同色,这影响到DA颜色的选取方法数,故
分类讨论:
当CD与AB同色时,这时CD对颜色的选取方法唯一,则DA有3种颜色可供选择CD与AB不同色时,CD有两种可供选择的颜色,DA也有两种
可供选择的颜色,从而对CD、DA涂色有13227
⨯+⨯=种涂色方法。
由乘法原理,总的涂色方法数为12784
⨯=种
例8、用六种颜色给正四面体A BCD
-的每条棱染色,要求每条棱只染一种颜色且共顶点的棱涂不同的颜色,问有多少种不同的涂色方法
解:(1)若恰用三种颜色涂色,则每组对棱必须涂同一颜色,而这三组间的颜色不同,
故有3
6
A种方法。
(2)若恰用四种颜色涂色,则三组对棱中有二组对棱的组内对棱涂同色,但组
与组之间不同色,故有34
66
C A种方法。
(3)若恰用五种颜色涂色,则三组对棱中有一组对棱涂同一种颜色,故有15
36
C A 种方法。
(4)若恰用六种颜色涂色,则有66A 种不同的方法。
综上,满足题意的总的染色方法数为4080665613462336=+++A A C A C A 种。
四、面涂色问题
例9、从给定的六种不同颜色中选用若干种颜色,将一个正方体的6个面涂色,每两个具有公共棱的面涂成不同的颜色,则不同的涂色方案共有多少种
分析:显然,至少需要3三种颜色,由于有多种不同情况,仍应考虑利用加法原理分类、乘法原理分步进行讨论
解:根据共用多少种不同的颜色分类讨论
(1)用了六种颜色,确定某种颜色所涂面为下底面,则上底颜色可有5种选择,在上、下底已涂好后,再确定其余4种颜色中的某一种所涂面为左侧面,则其余3个面有3!种涂色方案,根据乘法原理30!351=⨯=n
(2)共用五种颜色,选定五种颜色有656=C 种方法,必有两面同色(必为相对面),
确定为上、下底面,其颜色可有5种选择,再确定一种颜色为左侧面,此时的方法数取决于右侧面的颜色,有3种选择(前后面可通过翻转交换)
(3)共用四种颜色,仿上分析可得
(4)共用三种颜色,20364==C n
例10、四棱锥P ABCD -,用4种不同的颜色涂在四棱锥的各个面上,要求相邻不
同色,有多少种涂法
4相当于四个 1与3同色、2种; 3同色、2与41424C A ; 31442472A C A += B C。
