晶体的定向和晶面符号
合集下载
3.晶体定向及晶面符号概述

面 -----单面 1、平行双面1、反映双面及轴双面1 。
柱 ----(单柱 4 、复柱3) 锥 ----(单锥7、双锥 7) 体 ------ 23
低级晶族的单形
平行双面
轴双面
斜方单锥
斜方四面体
斜方双锥
斜方柱
中级晶族的单形
三方单锥
六方单锥
四方单锥
复三方单锥复六方单锥复四方Fra bibliotek锥三方双锥
六方双锥
四方双锥
晶面符号举例!
1. 等轴晶系:立方体、八面体 2. 四方晶系:四方柱、四方双锥 3. 六方晶系:六方柱 4. 三方晶系:菱面体 5. 斜方晶系:斜方双锥 6. 单斜晶系:石膏单晶
3、简整指数定律: 晶面在晶轴上的截距系数之比,往往为简单的整数比。 (1)简单?见P.38 图4-8 网面密度:a1b1 > a1b2 > a1b3 > a1b4 > ……a1bx 晶面在x、y、轴上的截距系数之比: b1 b2 b3 b4 b5 b6 bx a1b1 = 1:1 Z Y a1b2 = 1:2 a1b3 = 1:3 a1 a1b4 = 1:4 …… a2 a1bx= 1: x 网面密度越大、晶面在 X 晶轴上的截距系数之比 网面密度与截距系数比的关系 越简单。布拉维法则: 实际晶体往往被网面密度较大的晶面所包围。
(2)整数?(见P.38 图4-7 ) 把平行于晶胞的三个行列 作为晶轴,用该行列上的结 点间距作为轴单位。晶轴相 应于行列,晶面相应于面网, 晶面截晶轴于结点(a1b2), 或者晶面平移后截晶轴于结 点(kb5→a2b4),故晶面在 晶轴上的截距系数之比必为 一整数比。
(a1b2:x=1a ,y= 2b :即1: 2) (a2b4:x=2a ,y= 4b :即2: 4)
第四章 晶体定向和晶面符号
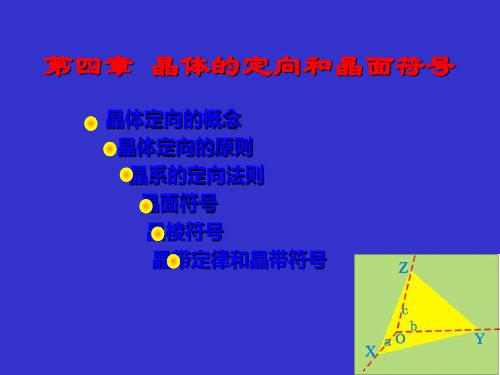
r = 0×0-1×0 =0,s = 0×0-1×0 =0,t = 1×1-0×0 =1,即此晶带
的符号为(001)。
35
⒉ 求位于晶带[rst]和晶带[uvw]交点的晶面(hkl)。 因为: hr +ks +lt =0 hu +kv +lw =0 则与例(1)类比,可用下列行列式计算:
27
整数定律
晶面在晶轴上的截距 系数之比为简单的整数比
b0
b1
b2
(010)
晶面指数为简单整数.
ao
为什么?
因为指数越简单的 晶面对应到内部结构是
a1
面网密度大的面网,而面
网密度大的面网容易形
成晶面,所以实际晶体上
的晶面就是晶面指数简
单的晶面。
b3
y
28
五、晶棱符号、晶带与晶带定律
1、晶棱符号:表征晶棱方向的 符号,所有平行的晶棱具有 同一个晶棱符号。
• 晶棱符号只涉及方向, 不涉及 具体位置。
• 截距系数比:表达为[rst]
r:s:t = MR/a : MK/b : MF/c
• [r s t] = [r s t]
此例:[rst] = [123]
29
四轴定向时的晶棱符号 • 以[u v m w]的形式表达 • 也有三指数形式: [u v w] • 四指数和三指数
c 直立,b 左右, a 前后
a=bc ===90
11
斜方晶系
3L2 a b c 轴 1L2 c轴 2P法线 a b 轴
c 直立,b 左右, a 前后
abc == =90
12
单斜晶系
1L2/1P法线 b轴, 2晶棱 a c轴
c 直立,b 左右 a 前后但向前下方倾斜 使>90
晶体定向和晶面符号

3L2为三轴,(3L2;3L23PC) L2为Z轴,2个P的法线为X、Y轴(L22P) L2为Y轴(L2;L2PC) P之法线为Y轴(P) 2个均垂直与b轴的适当晶棱方向为X、Z轴 三个适当的晶棱方向为Z、X、Y轴
三、晶面符号
晶体定向后,表示晶面在空间相对位置的符号,又 叫米氏符号。
即晶面在三个晶轴(X,Y,Z)上截距系数的倒数比h:k:l; 通常表示为(hkl)
3、同一米氏符号中,如有两个指数的绝对值相等,而且 与它们相对应的那两个结晶轴的轴单位也相等时,则晶面 与此二结晶轴以等角度相交;
4、在同一个晶体中,如有两个晶面的三组米氏指数的绝 对值全都相等,而且正、负号恰好全都相反,则此二晶面 平行。
四、单形符号
1、因为单形是一组由对称要素联系起来的相同晶面, 故可以用一个面来表示整个单形。
晶体定向和晶面符号
一、晶体定向的概念
晶体定向:就是在晶体上选定坐标系统,从而确 定晶面、晶棱的空间方位
二、建立坐标系统
1、晶体是多面体
三维坐标系统
三个方向即晶轴 量度单位轴单位
2、选择方法
微观上: 选择平行六面体中交于一点的三个行列的方向
宏观体现: 选择对称轴、对称面的法线、晶棱 的方向
摆法:
X轴:前后,前为 +,后为 - Y轴:左右,右为+ Z轴:上下,上为+
a=b≠c α=β=γ=90°
a≠b≠c α=γ=90° β>90°
a≠b≠c
α≠β ≠ γ a≠b≠c
选轴原则(按晶体几何常数特征)
以三个相互垂直的L4(Li4,L2)为X、Y、Z三 轴
唯一的高次轴为Z轴; 两个相互垂直的L2(P 之法线,晶棱)为X、Y轴
唯一的高次轴为Z轴 三个互成60°交角的L2(P之法线,适当晶 棱)为X、Y、U轴
三、晶面符号
晶体定向后,表示晶面在空间相对位置的符号,又 叫米氏符号。
即晶面在三个晶轴(X,Y,Z)上截距系数的倒数比h:k:l; 通常表示为(hkl)
3、同一米氏符号中,如有两个指数的绝对值相等,而且 与它们相对应的那两个结晶轴的轴单位也相等时,则晶面 与此二结晶轴以等角度相交;
4、在同一个晶体中,如有两个晶面的三组米氏指数的绝 对值全都相等,而且正、负号恰好全都相反,则此二晶面 平行。
四、单形符号
1、因为单形是一组由对称要素联系起来的相同晶面, 故可以用一个面来表示整个单形。
晶体定向和晶面符号
一、晶体定向的概念
晶体定向:就是在晶体上选定坐标系统,从而确 定晶面、晶棱的空间方位
二、建立坐标系统
1、晶体是多面体
三维坐标系统
三个方向即晶轴 量度单位轴单位
2、选择方法
微观上: 选择平行六面体中交于一点的三个行列的方向
宏观体现: 选择对称轴、对称面的法线、晶棱 的方向
摆法:
X轴:前后,前为 +,后为 - Y轴:左右,右为+ Z轴:上下,上为+
a=b≠c α=β=γ=90°
a≠b≠c α=γ=90° β>90°
a≠b≠c
α≠β ≠ γ a≠b≠c
选轴原则(按晶体几何常数特征)
以三个相互垂直的L4(Li4,L2)为X、Y、Z三 轴
唯一的高次轴为Z轴; 两个相互垂直的L2(P 之法线,晶棱)为X、Y轴
唯一的高次轴为Z轴 三个互成60°交角的L2(P之法线,适当晶 棱)为X、Y、U轴
第三章晶体的定向和晶面符号知识讲解

晶面指数-米氏符号中小括号内的三个数字称晶面指数。
整数定律
晶面在晶轴上的截距 系数之比为简单的整数比
面网密度越大 越简单 简单的
晶面截晶轴于结点 整数比
在确定晶体上晶面的米氏符号时,并不需要知道a, b,c的大小。可以首先选择一个晶面作单位面。单位面 应该是晶体上发育很好、与三个晶轴都相截,而且截距 尽可能相等或相近的晶面。将单位面的符号定为(111 ),即认为该晶面的截距系数p=q=r,截距之比为a:b :c。确定了单位面之后,其它晶面的符号可通过与单 位面的比较而求得。
第三章晶体的定向和晶面符号
三、如何为晶体定向
1、选择晶轴的原则
(1)晶轴平行行列方向。
优先
其次
晶轴平行 对称轴
对称面的法线
Z +_
_ +Y
+
X_ 再次
平行晶棱
(2)晶轴要尽可能的互相垂直或近于
垂直,即尽可能使 ===90,
具a体=步b=骤c
高次轴 L2 P 法线 显著晶棱
三、如何为晶体定向
(3)等轴、四方、斜方、单斜及 三斜等五个晶系选三个晶轴(X、 Y、Z),其中
同一单形的各个晶面的指 数的绝对值不变,而只有 正负号的区别
知道了单形的一个晶面 的符号,则该单形的其 它晶面的符号即可导出
用单形一个代表晶 面的符号来代表整 个单形
定义:单形符号简称形号,它是指在单形中选择一 个代 表面,把该晶面的晶面指数用“{ }”括 起来,用以表征组成该单形的一组晶面的 结晶学取向的符号
矿物的规则连生体的形态
1、平行连生
同种晶体彼此平行的连生在一起,连生 着的每一个晶体的相对应的晶面和晶棱 都是相互平行的
平行连生从外形来看是多晶体的连生,但它们 的内部格子构造是平行、连续的
第五章晶体定向和晶面符号

聚形的概念
❖ 两个以上的单形的聚合称为聚形。下图分别 表示了四方柱和四方双锥、立方体和菱形十 二面体的 聚合,用粗线勾划出了它们的聚形 的形态。显然,有多少种单形相聚,其聚形 上就会出现多少种不同的晶面,它们的性质 各异;对于理想形态而言,同一单形的晶面 同形等大。
第五章 晶体的定向和晶面符号
晶体定向:设置坐标系 晶面符号:用数学符号表示方位 1 晶体定向 选择坐标轴和确定各轴上轴单位的比值。 1.1 晶轴和晶体几何常数 晶轴:于晶体上所设置的坐标轴。 轴角:每两个晶轴正端之间的夹角。 =Y∧Z =Z∧X =X∧Y
晶体定向的作用:
❖ 晶体定向后就可以对晶体上所有的面、线等 进行标定,给出这些面、线的晶体学方向性 符号;
关系式 :
θx、θy、θz
h:k:l=a Cosθx :b Cosθy : c Cosθz 可直接求出晶面指数
❖ 零表示与晶轴的 ❖ 平行关系,负数 ❖ 表示与晶轴负端 ❖ 相交。
四轴:形式(hkil)且h+k+i=0
h+
(三)单形符号
4 几个概念:
❖ 4.1 晶带
❖
晶面彼此相交的晶棱相互平行的一组晶面的组合。形
式 为〔rst〕
❖ 4.2 晶带定律
❖
晶体上任一晶面至少同时属于两个晶带;而一个晶带
❖ 有对称中心; ❖ 但没有对称面
斜方四面体
❖ 注意:三条边不等长, 所以没有对称面,只有 3个L2,单斜晶系,低级 晶族。
❖ L33L23P ❖ 晶系: ❖ 晶族:
复三方柱
❖ L66L27PC ❖ 晶族: ❖ 晶系:
六方柱
❖ L33P ❖ 晶族: ❖ 晶系:
复三方单锥
三方双锥
晶体定向和晶面符号《结晶学》
一、晶体定向的概念
晶体定向就是在晶体上选择坐标系统。即选择
坐标轴(或称为结晶轴)和确定各坐标轴上的 单位长(轴单位)之比(轴率)。
Z
Z
U Y X Y
X
1、晶轴:交于晶体中心的三条轴,它们分别称为x、y、z
轴,晶轴之间的夹角称为轴角,分别表示为:(yz)、 (zx)、(xy)。 注意:三方晶系及六方晶系为四轴定向,在水平方向 上为x、y、u三条互成120度夹角的坐标。
B、在上述前提下,应尽可能使晶轴垂直,轴单位
近乎相等。
§3.2各晶系晶体定向的具体原则
三轴定向
等轴、四方、斜方、单斜、三斜
四轴定向
三方、六方
1、等轴晶系
选轴原则:相互垂直的L4或Li4或L2为x、y、z轴
Z
Y
X
晶体常数:a=b=c,α =β =γ =900
2、四方晶系
选轴原则:以L4或Li4为z轴,以垂直z轴并相 互垂直的L2或P的法线或晶棱方向为x、y轴。
:
OC2
= e:f:g
C2
O
A1 A2
B2
B1
X
Y
1、截距系数之比为整数比
因为晶面是面网,晶轴是行列,晶面与晶轴之交点 为结点,或平移相交于结点。因此,若以晶轴之结 点间距为度量单位,则晶面在晶轴上的截距系数之 比为整数比
c
a
b
2、为简单整数比
晶体面网密度越大,则晶面在晶轴上的截距系数之 比越简单。又依布拉维法则,晶体总是为面网密度 较大的面网所包围,所以为简单整数比。
数为0表示晶棱垂直于相应晶轴。
(4)对于三方、六方晶系的四轴定向,相应晶棱 符号的一般式写作 [u v · w].
晶体定向和晶面符号

二、晶体定向原则
• 结晶轴的选择应当符合晶体固有的对称性
–首先选择对称轴和对称面的法线方向 –不存在对称轴和对称面,则平行晶棱方向选取
• 尽量使得晶轴之间夹角为90
每个晶系的对称特点不同,因此每个晶系的选择晶轴 的具体方法也不同,见表5-1(此表非常重要,要熟记).
等轴晶系的定向:
晶体几何常数为: a = b = g = 90°, a = b = c – 三个互相垂直的L4, Li4或L2为 x, y, z 轴 – z 轴直立,y 轴左右水平,x 轴前后水平
只写出对称型中的三类对称要素 只写出对称轴,对称面,旋转反伸轴,其它对称要素 可根据组合定理推导出来 国际符号中对称要素的表示法 对称面:m 对称轴:以轴次的数字表示,如1、2、3,4和6; 旋转反伸轴:轴次数字上面加“-”号,如1、2、3、 4和6。 由于1=Li1=C,2=Li2=P=m,习惯用1代表对称中心.m代 表2。
r:s:t = MR/a : MK/b : MF/c
• [r s t] = [r s t]
此例:[r v w] = [1 2 3]
2、晶带: (zone) 彼此间的交棱均相互平行的一组晶面之组合。 晶带轴(zone axis) 通过晶体中心的一根直线,它平行于该晶带中的所有晶 面,也就是平行于该晶带中各个晶面的公共交棱,用以 表示晶带方向。
卤钠石(sulphohalite )的平行连生体
赤铜矿的连生晶体
明矾八面体的平行连生
萤石立方体的平行连生
自然铜立方体的树枝状平行连生
内 部 的 晶 体 格 子 是 连 续 的
2、双晶(孪晶) twin
定义:互不平行的同种单体,彼此间按一定的 对称关系相互取向而组成的规则连生晶体。
第四章 晶体定向和晶面符号
晶
体
的
定
向
方
法
10
四方晶系
1L4 c轴 2L2 /2P法线/2晶棱 a b轴
c 直立,b 左右, a 前后
a=bc ===90
11
斜方晶系
3L2 a b c 轴 1L2 c轴 2P法线 a b 轴
c 直立,b 左右, a 前后
abc == =90
12
单斜晶系
1L2/1P法线 b轴, 2晶棱 a c轴
交可决定一可能晶带(晶棱).
33
3、晶带方程应用
即:任一属于[u v w]晶带的晶面(h k l),必定有: h u + k v + l w = 0 晶带方程
简单的证明: 三维空间的一般平面方程为 Ax + By + Cz + D = 0 系数A、B、C决定该平面的方向,常数项D决定距原点 的距离。 那么过坐标原点且平行于(h k l)的平面方程则可以表达 为
23
考察晶体模型晶面的晶面符号:
Cube
(001) (100) (010)
Octahedron
(111) (111)
Dodecahedron
(111)
(111)
101
011
_
110
110
_
_
101
011
24
All three combined:
001
_
101
111
011 111
_ 110
100
010 110
c 直立,b 左右 a 前后但向前下方倾斜 使>90
abc ==90 >90
13
三斜晶系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 结晶轴的选择应当符合晶体固有的对称性
–首先选择对称轴和对称面的法线方向 –不存在对称轴和对称面,则平行晶棱方向选取
• 尽量使得晶轴之间夹角为90
晶轴选择遵循的(优选性)原则:
1、优选对称轴 2、其次选对称面的法线,如L22P 3、最后选择平行于发育晶棱的方向 4、使三个坐标轴尽可能互相垂直
每个晶系的对称特点不同,因此每个晶系的选择晶轴的具体方法 也 不 同 , 见 教 材 表 5-1( 此 表 非 常 重 要 , 要 熟 记 ).
三方和六方晶系的四轴定向:
– 选择唯一的高次轴作为直立结晶轴z轴,在垂直 z 轴 的平面内选择三个相同的、即互成60°交角的L2或 P的法线,或适当的显著晶棱方向作为水平结晶轴, 即x 轴、 y 轴以及 u 轴
– 晶体几何常数: a = b = 90°, g =120°, a = b < > c
– z 轴直立, y 轴左右水平, x 轴前后水平偏左30°
a、b、c和α、β、γ称之为晶体几何常数
•晶体的三轴定向:
–选择三个不共面的坐标轴 x, y, z安置晶体。
摆法:
X轴:前后,前为 +,后为 - Y轴:左右,右为+ Z轴:上下,上为+
晶体常数:轴率、轴角
Z
c
a
bY
X
•晶体的四轴定向:
–适用于六方和三方晶系 –一个直立轴,三个水平轴
二、晶体定向原则
晶体的定向和晶面符号
• 晶体定向的概念 • 晶体定向的原则 • 晶系的定向法则(重点) • 对称型的国际符号 • 晶面符号 • 晶棱符号 • 晶带符号
一、晶体定向的概念
晶体定向:就是在晶体上选定坐标系统,从而确 定晶面、晶棱的空间方位。
首选建立坐标系统
1、晶体是多面体
三维坐标系统
三个方向即晶轴 量度单位轴单位
等轴晶系的定向:
晶体几何常数为: a = b = g = 90°, a = b = c
– 三个互相垂直的L4, Li4或L2为 x, y, z 轴 – z 轴直立,y 轴左右水平,x 轴前后水平
四方晶系的定向:
晶体几何常数:
a = b = g = 90°, a = b < > c
– 唯一的L4或Li4为 z 轴; 相互 垂直的L2, 或相互垂直的对 称面法线, 或适当的晶棱为 x, y 轴 。
2、定向方法(三轴定向) 在晶体上确定坐标系统,即选坐标轴和确
定各轴上的轴单位长度之比。 (1) 晶轴:是交于晶体中心的三条直线。为x、y、
z。 (2) 轴角:α、β、γ (3) 轴长和轴率:晶轴 是晶体中格子构造中 的行列,轴单位是该 行列上的结点间距。 分别以 a、b、c表示, a:b:c为轴率。
– z 轴直立, y 轴左右水平, x 轴前后水平。
斜方晶系的定向:
晶体几何常数: a = b = g = 90°, a < > b < > c
三个相互垂直的 L2为 z, x, y 轴; 或L2 为z轴, 相互垂直的 对称面法线为 x, y 轴。 z 轴直立, y 轴左 右水平,x 轴前后 水平。
各晶系的晶体几何常数特点
等轴晶系:a = b = c,a = b = g = 90; 四方晶系:a = b ≠ c,a = b = g = 90; 三方和六方晶系:a = b ≠ c,a = b = 90,g =
120;
三方晶系菱面体格子:a = b = c,a = b = g
60 90 10928’16’’
斜方晶系:a ≠ b ≠ c,a = b = g = 90; 单斜晶系:a ≠ b ≠ c,a = g = 90,b > 90; 三斜晶系:a ≠ b ≠ c,a ≠ b ≠ g ≠ 90 ;
晶系
选轴原则
晶体常数特点
等轴晶系 四方晶系
以互相垂直的L4或Li4为X、Y、Z轴 L4或Li4为Z轴,以垂直Z轴,并互相垂 直的L2或P的法线为X、Y轴
a=b=c
a = b = g = 90
a=b≠c
a = b = g = 90
在三个行列上有晶胞参数(a,b,c; α ,β ,γ ), 这些参数就构成了三个晶轴上的轴单位和 晶轴之间的夹角.
晶体外形不可能知道轴单位,但根据对 称性可以知道轴单位之间的比值关系,即: a:b:c
例如, 等轴晶系的 a:b:c =? 四方晶系的 a:b:c =?
我们将a:b:c (轴率), α,β,γ(轴角), 轴率与轴角统称晶体常数.见下表.表中 列出的是晶体常数特点.因为根据晶体的 宏观形态只能定出晶体常数特点,不能定 出晶体常数.
请注意:
在晶体的宏观形态上根据对称特点选出 的三根晶轴,与晶体内部结构的空间格子 的三个不共面的行列方向是一致的.
为什么?
因为空间格子中三个不共面的行列也是 根据晶体的对称性,人为地画出来的.而晶 轴也是根据晶体的对称性,人为地选出来 的.晶体的内部对称与晶体的宏观对称是 一致的,所以 晶轴与三个行列就是一致的.
单斜晶系的定向:
晶体几何常数:
a = g = 90°, b > 90°
a<>b<>c L2为 y 轴; 或对称面法线为 y 轴,z 轴起立, y 轴左右 水平, x 轴前后向前下倾斜。
三斜晶系的定向:
晶体几何常数:
a < > b < > g < > 90 °
a<>b<>c 适当的晶棱为 x, y, z 轴。 大致上 z 轴直立, y 轴 左右, x 轴前后。
晶系
晶体常数特点
选轴原则(按晶体几何常数特征)
等轴 四方 三、六 方
斜方 单斜
α=β=γ=90° a=b=c
α=β=γ=90° a=b≠c
α=β=90° γ=120° a=b≠c
α=β=γ=90° a≠b≠c
α=γ=90° β>90°
aHale Waihona Puke b≠c以三个相互垂直的L4(Li4,L2)为X、Y、Z三轴
唯一的高次轴为Z轴; 两个相互垂直的L2(P之 法线,晶棱)为X、Y轴
唯一的高次轴为Z轴 三个互成120°交角的L2(P之法线,适当晶棱) 为X、Y、U轴
3L2为三轴,(3L2;3L23PC) L2为Z轴,2个P的法线为X、Y轴(L22P) L2为Y轴(L2;L2PC) P之法线为Y轴(P) 2个均垂直与b轴的适当晶棱方向为X、Z轴
三斜
α≠β ≠ γ a≠b≠c
三个适当的晶棱方向为Z、X、Y轴
–首先选择对称轴和对称面的法线方向 –不存在对称轴和对称面,则平行晶棱方向选取
• 尽量使得晶轴之间夹角为90
晶轴选择遵循的(优选性)原则:
1、优选对称轴 2、其次选对称面的法线,如L22P 3、最后选择平行于发育晶棱的方向 4、使三个坐标轴尽可能互相垂直
每个晶系的对称特点不同,因此每个晶系的选择晶轴的具体方法 也 不 同 , 见 教 材 表 5-1( 此 表 非 常 重 要 , 要 熟 记 ).
三方和六方晶系的四轴定向:
– 选择唯一的高次轴作为直立结晶轴z轴,在垂直 z 轴 的平面内选择三个相同的、即互成60°交角的L2或 P的法线,或适当的显著晶棱方向作为水平结晶轴, 即x 轴、 y 轴以及 u 轴
– 晶体几何常数: a = b = 90°, g =120°, a = b < > c
– z 轴直立, y 轴左右水平, x 轴前后水平偏左30°
a、b、c和α、β、γ称之为晶体几何常数
•晶体的三轴定向:
–选择三个不共面的坐标轴 x, y, z安置晶体。
摆法:
X轴:前后,前为 +,后为 - Y轴:左右,右为+ Z轴:上下,上为+
晶体常数:轴率、轴角
Z
c
a
bY
X
•晶体的四轴定向:
–适用于六方和三方晶系 –一个直立轴,三个水平轴
二、晶体定向原则
晶体的定向和晶面符号
• 晶体定向的概念 • 晶体定向的原则 • 晶系的定向法则(重点) • 对称型的国际符号 • 晶面符号 • 晶棱符号 • 晶带符号
一、晶体定向的概念
晶体定向:就是在晶体上选定坐标系统,从而确 定晶面、晶棱的空间方位。
首选建立坐标系统
1、晶体是多面体
三维坐标系统
三个方向即晶轴 量度单位轴单位
等轴晶系的定向:
晶体几何常数为: a = b = g = 90°, a = b = c
– 三个互相垂直的L4, Li4或L2为 x, y, z 轴 – z 轴直立,y 轴左右水平,x 轴前后水平
四方晶系的定向:
晶体几何常数:
a = b = g = 90°, a = b < > c
– 唯一的L4或Li4为 z 轴; 相互 垂直的L2, 或相互垂直的对 称面法线, 或适当的晶棱为 x, y 轴 。
2、定向方法(三轴定向) 在晶体上确定坐标系统,即选坐标轴和确
定各轴上的轴单位长度之比。 (1) 晶轴:是交于晶体中心的三条直线。为x、y、
z。 (2) 轴角:α、β、γ (3) 轴长和轴率:晶轴 是晶体中格子构造中 的行列,轴单位是该 行列上的结点间距。 分别以 a、b、c表示, a:b:c为轴率。
– z 轴直立, y 轴左右水平, x 轴前后水平。
斜方晶系的定向:
晶体几何常数: a = b = g = 90°, a < > b < > c
三个相互垂直的 L2为 z, x, y 轴; 或L2 为z轴, 相互垂直的 对称面法线为 x, y 轴。 z 轴直立, y 轴左 右水平,x 轴前后 水平。
各晶系的晶体几何常数特点
等轴晶系:a = b = c,a = b = g = 90; 四方晶系:a = b ≠ c,a = b = g = 90; 三方和六方晶系:a = b ≠ c,a = b = 90,g =
120;
三方晶系菱面体格子:a = b = c,a = b = g
60 90 10928’16’’
斜方晶系:a ≠ b ≠ c,a = b = g = 90; 单斜晶系:a ≠ b ≠ c,a = g = 90,b > 90; 三斜晶系:a ≠ b ≠ c,a ≠ b ≠ g ≠ 90 ;
晶系
选轴原则
晶体常数特点
等轴晶系 四方晶系
以互相垂直的L4或Li4为X、Y、Z轴 L4或Li4为Z轴,以垂直Z轴,并互相垂 直的L2或P的法线为X、Y轴
a=b=c
a = b = g = 90
a=b≠c
a = b = g = 90
在三个行列上有晶胞参数(a,b,c; α ,β ,γ ), 这些参数就构成了三个晶轴上的轴单位和 晶轴之间的夹角.
晶体外形不可能知道轴单位,但根据对 称性可以知道轴单位之间的比值关系,即: a:b:c
例如, 等轴晶系的 a:b:c =? 四方晶系的 a:b:c =?
我们将a:b:c (轴率), α,β,γ(轴角), 轴率与轴角统称晶体常数.见下表.表中 列出的是晶体常数特点.因为根据晶体的 宏观形态只能定出晶体常数特点,不能定 出晶体常数.
请注意:
在晶体的宏观形态上根据对称特点选出 的三根晶轴,与晶体内部结构的空间格子 的三个不共面的行列方向是一致的.
为什么?
因为空间格子中三个不共面的行列也是 根据晶体的对称性,人为地画出来的.而晶 轴也是根据晶体的对称性,人为地选出来 的.晶体的内部对称与晶体的宏观对称是 一致的,所以 晶轴与三个行列就是一致的.
单斜晶系的定向:
晶体几何常数:
a = g = 90°, b > 90°
a<>b<>c L2为 y 轴; 或对称面法线为 y 轴,z 轴起立, y 轴左右 水平, x 轴前后向前下倾斜。
三斜晶系的定向:
晶体几何常数:
a < > b < > g < > 90 °
a<>b<>c 适当的晶棱为 x, y, z 轴。 大致上 z 轴直立, y 轴 左右, x 轴前后。
晶系
晶体常数特点
选轴原则(按晶体几何常数特征)
等轴 四方 三、六 方
斜方 单斜
α=β=γ=90° a=b=c
α=β=γ=90° a=b≠c
α=β=90° γ=120° a=b≠c
α=β=γ=90° a≠b≠c
α=γ=90° β>90°
aHale Waihona Puke b≠c以三个相互垂直的L4(Li4,L2)为X、Y、Z三轴
唯一的高次轴为Z轴; 两个相互垂直的L2(P之 法线,晶棱)为X、Y轴
唯一的高次轴为Z轴 三个互成120°交角的L2(P之法线,适当晶棱) 为X、Y、U轴
3L2为三轴,(3L2;3L23PC) L2为Z轴,2个P的法线为X、Y轴(L22P) L2为Y轴(L2;L2PC) P之法线为Y轴(P) 2个均垂直与b轴的适当晶棱方向为X、Z轴
三斜
α≠β ≠ γ a≠b≠c
三个适当的晶棱方向为Z、X、Y轴
