第4章 晶体定向和晶体学符号
合集下载
第4章晶体定向与结晶符号
不同晶系中，这三个序号位所代表的方向完全 不同，所以，不同晶系的国际符号写法也不同（每 个晶系的国际符号写法见表4-3）
Company Logo
晶系
等轴
序号位
1 2 3 1 2 3
代表方向
X或Y或Z方向 三次轴方向 X、Y或X、Z或Y、Z轴之间 四次轴方向，即Z轴方向 与四次轴垂直，在X或Y轴方向 与四次轴垂直，与X或Y成45°角方向
Z Z
X
立方体 Y X Y 八面体
Company Logo
四方晶系（唯一的L4或Li4）
晶体几何常数为: = = = 90°, a = b ≠ c ●唯一的L4或Li4为 z 轴; 相互垂直的L2, 或相互垂 直的对称面法线, 或适当的晶棱为x, y 轴 z 轴直立，y 轴左右水平，x 轴前后水平
四方
三、六
1 2 3
1 2 3 1
三、六次轴方向，即Z轴方向 与三或六次轴垂直，在X或Y轴方向 与三或六次轴垂直，与X或Y成45°角方向
X轴方向 Y轴方向 Z轴方向 Y方向
斜方
单斜
三斜
1
任意方向
Company Logo
等轴晶系：
晶系 序号位 代表方向
等轴
1 2 3
（2）在上述前提下，应尽可能使晶轴垂直，并使 轴单位相等，即尽可能使===90, a=b=c
Company Logo
具体地 ① 优先选Ln或Lin为晶轴； ② 若Ln的数量不足时，则由P的法线方向来补 充作晶轴； ③ 若无足够的Ln和P，则选平行于晶棱的方向 作晶轴； ④ 在以上前提下，选择晶轴尽量使得 α=β=γ=900, a=b=c。
第四章 晶体定向与结晶符号
三个结晶轴之轴单位的比率 a:b:c 。
5 ． 晶体常数 （ crystal constants ）： 轴角 、、 和 轴率 a:b:c 之合称。
是表征 晶体座标系统的一组基本 参数，同时可表征晶胞形状。
•6．晶胞参数（cell
parameters）：
• 、、 和 a0、b0、 c0 之合称。
各晶系选轴原则及晶体常数特点
选 择 原 则
以互垂的 3L4 或 3L2或 3Li4为X、Y、Z轴。 以 L4 或Li4 为 Z轴，以 ⊥Z 轴 且互垂的 2个L2 或 P的法线或晶棱的方向为X、Y轴。 以 L3 或 L6 或 Li6 为 Z 轴， 以 ⊥Z 轴 且彼此交于 120° 的 3个 L2 或 P 的法线或 晶棱的方向为 X、Y、U 轴。 以互垂的 3L2为 X、Y、Z轴；在L22P中， 以L2为Z轴，以2P的法线方向为为X、Y轴。 以 且 近于互垂的 2个主要晶棱方向为 Z、X轴。 以 不在 同一平面内、且 近于 互垂的 3个主要晶棱方向为 X、Y、Z 轴。 L2或P的法线方向为Y轴，以⊥Y轴 晶体常数特点
对称型
晶 系
晶 族
国际符号
1、平行Z轴有L4 ,垂直Z有P 4 /m 2、平行X、Y有L2，垂直X、Y有 P 2/m 3、平行于X、Y角平分线方向有L2 , 垂直于该方向有P 2/m 4 /m 2/m 2/m 或 4/m m m 1、平行于XYZ有L4，垂直于XYZ 有P 4/m 2、平行于a+b+c方向有L3 3 3、平行于XY或XZ或YZ角平分线 方向有L2，垂直方向有P 2/m 4/m 3 2/m 或 m 3 m
——
L ；
3 i
—— L
4 i
5 ． 晶体常数 （ crystal constants ）： 轴角 、、 和 轴率 a:b:c 之合称。
是表征 晶体座标系统的一组基本 参数，同时可表征晶胞形状。
•6．晶胞参数（cell
parameters）：
• 、、 和 a0、b0、 c0 之合称。
各晶系选轴原则及晶体常数特点
选 择 原 则
以互垂的 3L4 或 3L2或 3Li4为X、Y、Z轴。 以 L4 或Li4 为 Z轴，以 ⊥Z 轴 且互垂的 2个L2 或 P的法线或晶棱的方向为X、Y轴。 以 L3 或 L6 或 Li6 为 Z 轴， 以 ⊥Z 轴 且彼此交于 120° 的 3个 L2 或 P 的法线或 晶棱的方向为 X、Y、U 轴。 以互垂的 3L2为 X、Y、Z轴；在L22P中， 以L2为Z轴，以2P的法线方向为为X、Y轴。 以 且 近于互垂的 2个主要晶棱方向为 Z、X轴。 以 不在 同一平面内、且 近于 互垂的 3个主要晶棱方向为 X、Y、Z 轴。 L2或P的法线方向为Y轴，以⊥Y轴 晶体常数特点
对称型
晶 系
晶 族
国际符号
1、平行Z轴有L4 ,垂直Z有P 4 /m 2、平行X、Y有L2，垂直X、Y有 P 2/m 3、平行于X、Y角平分线方向有L2 , 垂直于该方向有P 2/m 4 /m 2/m 2/m 或 4/m m m 1、平行于XYZ有L4，垂直于XYZ 有P 4/m 2、平行于a+b+c方向有L3 3 3、平行于XY或XZ或YZ角平分线 方向有L2，垂直方向有P 2/m 4/m 3 2/m 或 m 3 m
——
L ；
3 i
—— L
4 i
第04章 晶体定向和晶体符号
米氏符号用晶面在结晶轴上的截距系数的倒数 比来表示。
第四章
晶体定向和晶体符号
一、为何要进行晶体定向
二、何谓要进行晶体定向
要了解晶体的具体形态，只知道对称型是不够的 晶体的具体形态取决于晶体的晶面与对称要素之 间的关系 为了准确描述晶体的形态，确定晶体的空间分布 特点，就必须……
三、如何为晶体定向
（3）等轴、四方、斜方、单斜及 三斜等五个晶系选三个晶轴（X、 Y、Z），其中 Z轴—直立方向，上正、下负；
X轴—对着观察者，前正、后负；
Y轴—置于左右方向，右正、左负
三、如何为晶体定向
（4）三方、六方晶系选四个晶 轴（X、Y、U、Z），其中
Z轴—直立方向，上正、下负； X轴、Y轴、U轴均在一个水平面 上，其正端的夹角为1200，其 正负如右图所示，它们都与Z轴 垂直。
3L24L3、 3L24L33PC、3Li44L36P、 3L44L36L2、 3L44L36L29PC
L4、L44L2、 L4PC、 L44P、 L44L25PC、 Li4、Li44L22P
四、晶面符号
晶面符号—代表晶面在空间的方位的符号 晶体定向后，晶面的空间方位可以借晶面与晶 轴的截交关系来确定。 晶面符号的表达方式—米氏符号
结晶学课件 第4章 晶体的定向与结晶符号
选晶轴的原则:
1）与晶体的对称特点相符合(既一般都以对称要 素作晶轴，要么对称轴，要么对称面法线);
2）在遵循上述原则的基础上尽量使晶轴夹角为 90度.
每个晶系的对称特点不同,因此每个晶系的选择 晶轴的具体方法也不同,见表4-1(此表非常重要， 要熟记).
表4-1
定向举例: (示范模型: 等轴、四方、六方、斜方)
z
x 宏观形态
y 微观结构
在三个行列上有晶胞参数(a,b,c; α,β,γ), 这些参数就构成了三个晶轴上的轴单位和 晶轴之间的夹角.
晶体外形不可能知道轴单位,但根据对称性可以 知道轴单位之间的比值关系,即： a:b:c
例如, 等轴晶系的 a:b:c =? 四方晶系的 a:b:c =?
我们将a:b:c 称为轴率, α,β,γ称轴角,轴率 与轴角统称晶体常数.见表4－1.表中列出的是晶 体常数特点.因为根据晶体的宏观形态只能定出 晶体常数特点,不能定出晶体常数.
不同晶系中,这三个序号位所代表的方向完全 不同,所以,不同晶系的国际符号的写法也就完全 不同,一定不要弄混淆!!
每个晶系的国际符号写法见表4－3(此表很重 要，要熟记！).
表4-3: 国际符号举例: (示范模型: 等轴、四方、六方、斜方)
三、 晶面符号与晶棱符号
1. 晶面符号:
晶体定向后, 晶面在空间的相对位置就可以根 据它与晶轴的关系来确定, 表示晶面空间方位 的符号就叫晶面符号,常用的是米氏符号:
四、 整数定律与晶带定律
1. 整数定律
晶面指数为简单整数. 为什么?
因为指数越简单的晶面 对应到内部结构是面 网密度大的面网,而面 网密度大的面网容易 形成晶面（因为能量 低容易形成晶面）,所 实际晶体上的晶面就 是晶面指数简单的晶 面.
4章 晶体定向与结晶符号
第四章晶体定向与结晶符号晶体定向(crystal orientation)就是在晶体中建立一个坐标系，这样晶体中各个晶面、晶棱以及对称要素就可以在其中标定方向，这种表示晶面、晶棱及对称要素等的方位的符号统称结晶符号(crystal indices)。
由于晶体的各种特性(形态、物性、结构等)都与晶体的方向有关，所以晶体定向是研究晶体的最基本的工作。
一、晶体定向晶体定向就是在晶体中以晶体中心为原点建立一个坐标系，这个坐标系一般由三根晶轴 X、Y、Z轴(也可用a、b、c轴表示)组成。
三根晶轴正端之间的夹角分别表示为α(Y∧Z)、β(Z∧X)、γ(X∧Y)。
对于三、六方晶系的晶体，通常要用四轴定向法，即要选出四根晶轴。
那么，究竟选择晶体中哪些方向上的直线作为晶轴呢?选择的原则有两点：① 与晶体的对称特点相符合（即一般都以对称要素作晶轴）；② 在遵循上述原则的基础上尽量使晶轴夹角=90°。
各晶系对称特点不同，具体选择晶轴的方法也不同，具体选择原则见表3－1。
表3－1 各晶系选择晶轴的具体方法及晶体常数特点请注意，这里在晶体宏观形态中按对称特点选出的晶轴，实际上与晶体内部结构中空间格子的三个不共面的行列方向一致。
二、晶胞参数及晶面符号、晶棱符号1 晶胞参数X、Y、Z三根晶轴方向上的行列上的结点间距分别表示为a0、b0、c0，称为轴长；三根晶轴正端之间的夹角α、β、γ称为轴角，轴长和轴角统称晶胞参数（cell parameter）。
在第一章我们就已知，a0、b0、c0以及α、β、γ决定空间格子中平行六面体的大小和形状。
但是，在晶体宏观形态上是定不出轴长的，只能根据对称特点定出a0∶b0∶c0（或表示为a∶b∶c），这一比例称为轴率。
轴率与轴角统称晶体常数 (crystal constants)，晶体常数特点是可以在晶体宏观形态上体现出来的，例如：等轴晶系晶体对称程度高，晶轴X、Y、Z为彼此对称的行列，它们通过对称要素的作用可以相互重合，因此它们的轴长是相同的，即a=b=c，轴率a∶b∶c=1∶1∶1；中级晶族（四方、三方和六方晶系）晶体中只有一个高次轴，以高次轴为Z轴，通过高次轴的作用可使X轴与Y轴重合（在三方与六方晶系中可使X轴、Y轴、U轴重合），因此轴长a=b，但与c不等，轴率a∶c因晶体的种别而异；低级晶族（斜方、单斜和三斜晶系）晶体对称程度低，X、Y、Z轴不能通过对称要素的作用而重合，所以a≠b≠c，晶体的种类不同，轴率a∶b∶c数据不同。
第四章 晶体定向和晶面符号
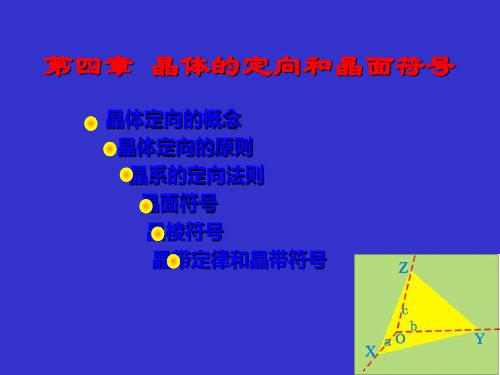
r = 0×0-1×0 =0，s = 0×0-1×0 =0，t = 1×1-0×0 =1，即此晶带
的符号为(001)。
35
⒉ 求位于晶带[rst]和晶带[uvw]交点的晶面（hkl）。 因为： hr +ks +lt =0 hu +kv +lw =0 则与例（1）类比，可用下列行列式计算：
27
整数定律
晶面在晶轴上的截距 系数之比为简单的整数比
b0
b1
b2
(010)
晶面指数为简单整数.
ao
为什么?
因为指数越简单的 晶面对应到内部结构是
a1
面网密度大的面网,而面
网密度大的面网容易形
成晶面,所以实际晶体上
的晶面就是晶面指数简
单的晶面。
b3
y
28
五、晶棱符号、晶带与晶带定律
1、晶棱符号：表征晶棱方向的 符号，所有平行的晶棱具有 同一个晶棱符号。
• 晶棱符号只涉及方向, 不涉及 具体位置。
• 截距系数比：表达为[rst]
r:s:t = MR/a : MK/b : MF/c
• [r s t] = [r s t]
此例：[rst] = [123]
29
四轴定向时的晶棱符号 • 以[u v m w]的形式表达 • 也有三指数形式: [u v w] • 四指数和三指数
c 直立，b 左右， a 前后
a=bc ===90
11
斜方晶系
3L2 a b c 轴 1L2 c轴 2P法线 a b 轴
c 直立，b 左右， a 前后
abc == =90
12
单斜晶系
1L2/1P法线 b轴, 2晶棱 a c轴
c 直立，b 左右 a 前后但向前下方倾斜 使>90
第四章晶体定向和晶面符号
§4.5
对称型的国际符号
对称面：m
一、国际符号中对称要素的表示法
对称轴：以轴次的数字表示， 如 1、2、3、4 和 6 旋转反伸轴：轴次数字上面加“-”号， 如 1 、 、 和 。 、 2 3 4 6 注意:由于1 L1i C ，习惯用 1 代表对称中心。
6、三方、六方晶系
对称特点：有且只有一个L3或L6或Li6。 选轴原则：以L6、Li6、L3为z轴，以垂直z轴并彼此相 交为1200的3个L2或P的法线或晶棱方向为x、y、u轴
z
u
y x
晶体常数特点 a＝b≠c，α＝β＝９０°γ＝１２０°
总结－晶体定向方法
1、根据晶体对称型，确定晶体属于何种晶系
整数比, 此时的h, k, l就称为晶面指数;
晶面符号写作（ h k l ）
注意：若晶面交于晶轴负端，则在相应指数上方加“－”号
Z
C
已知晶面ABC在X、Y、 Z轴上的截距为： OA=2a， OB=3b， OC=6c； 求晶面的米氏符号。
Oc a b A X
B
Y
截距系数的倒数比： 1/2∶1/3∶1/6 化整→ 3∶2∶1 去比例号，加小括号→(321)。
2、对应各晶系定向原则，确定相应的x轴、y轴、z轴
注意：七大晶系中，单斜晶系先确定y轴，其它 晶系均先确定z轴
§4.3晶面符号
一、 晶面符号
–所谓晶面符号就是根据晶面(或晶体中平行于 晶面的其他平面)与晶轴的空间关系，用简单 的数字符号形式来表达它们在晶体上方位的的 一种晶体学符号; –目前国际上通用的都是米氏符号(Miller’s symbol)，亦称米勒符号。
等轴晶系
2 3 1
四方晶系
2 3 1 2 3 1 2 3
第4章 晶体定向与结晶符号(修改)
第四章 晶体定向与结晶符号
晶体定向——在晶体中建立一个坐标系，对晶 体中各晶面、晶棱以及对称要素标定方向。 结晶符号——表示晶面、晶棱及对称要素等的 方位的符号。
因晶体的各种特 本章内容——晶体定向的方法 性（形态、物性、 ——32种对称型各对称要素空间分布 结构等）都与晶体 ——国际符号，圣弗利斯符号 的方向有关，故晶 体定向是研究晶体 ——晶面符号及晶棱符号等 的最基本的工作。
我们并不知道晶面截晶轴的截距系数, 但我 们可以知道截距大小相对关系。 例如: 八面体（111）、立方体（100）
（晶面与某晶轴平行，该晶轴 上的晶面指数为0）
27
17
注意事项：
晶面符号的书写有一定的规定：
括号内第一个位置写晶面在X轴上的指数，中间写晶面在Y轴上的指 数，最后位置写晶面在Z轴上的指数。这个顺序不可任意颠倒。
国际符号中： 1,2,3,4,6——对称轴； 1, 2 , 3 , 4 , 6 ——旋转反伸轴，m——对称面。 2 若对称面与对称轴垂直，以斜线或横线隔开，如L2PC——2／m(或 ）
m
(可见，对称中心C不必再表示出来了，因为偶次轴垂直 对称面定会产生一个C)。
27 10
具体写法
设置三个位序（最多只有三个）,每个位序规定了写什么 方向上的对称要素。 位序与方向对应，是国际符号最主要特色 对称意义完全相同方向上的对称要素,不管有多少,只写 一个即可，即在对称型的国际符号中凡是可以通过其它对 称要素可以派生出来的对称要素都省略了。 简化，是国际符号的另一特色
晶带
27
24
晶带定律
晶带——交棱相互平行的一组晶面的组合。 晶带轴——表示晶带方向的直线，即过晶体中心该晶带 各晶面交棱方向直线。晶带轴的符号就是晶棱符号。 通常以晶带轴符号来表示晶带符号，如晶带[001]，表示 以[001]直线为晶带轴的那一组交棱相互平行的晶带。
晶体定向——在晶体中建立一个坐标系，对晶 体中各晶面、晶棱以及对称要素标定方向。 结晶符号——表示晶面、晶棱及对称要素等的 方位的符号。
因晶体的各种特 本章内容——晶体定向的方法 性（形态、物性、 ——32种对称型各对称要素空间分布 结构等）都与晶体 ——国际符号，圣弗利斯符号 的方向有关，故晶 体定向是研究晶体 ——晶面符号及晶棱符号等 的最基本的工作。
我们并不知道晶面截晶轴的截距系数, 但我 们可以知道截距大小相对关系。 例如: 八面体（111）、立方体（100）
（晶面与某晶轴平行，该晶轴 上的晶面指数为0）
27
17
注意事项：
晶面符号的书写有一定的规定：
括号内第一个位置写晶面在X轴上的指数，中间写晶面在Y轴上的指 数，最后位置写晶面在Z轴上的指数。这个顺序不可任意颠倒。
国际符号中： 1,2,3,4,6——对称轴； 1, 2 , 3 , 4 , 6 ——旋转反伸轴，m——对称面。 2 若对称面与对称轴垂直，以斜线或横线隔开，如L2PC——2／m(或 ）
m
(可见，对称中心C不必再表示出来了，因为偶次轴垂直 对称面定会产生一个C)。
27 10
具体写法
设置三个位序（最多只有三个）,每个位序规定了写什么 方向上的对称要素。 位序与方向对应，是国际符号最主要特色 对称意义完全相同方向上的对称要素,不管有多少,只写 一个即可，即在对称型的国际符号中凡是可以通过其它对 称要素可以派生出来的对称要素都省略了。 简化，是国际符号的另一特色
晶带
27
24
晶带定律
晶带——交棱相互平行的一组晶面的组合。 晶带轴——表示晶带方向的直线，即过晶体中心该晶带 各晶面交棱方向直线。晶带轴的符号就是晶棱符号。 通常以晶带轴符号来表示晶带符号，如晶带[001]，表示 以[001]直线为晶带轴的那一组交棱相互平行的晶带。
晶体定向和晶面符号
二、晶体定向原则
• 结晶轴的选择应当符合晶体固有的对称性
–首先选择对称轴和对称面的法线方向 –不存在对称轴和对称面，则平行晶棱方向选取
• 尽量使得晶轴之间夹角为90
每个晶系的对称特点不同,因此每个晶系的选择晶轴 的具体方法也不同,见表5-1(此表非常重要，要熟记).
等轴晶系的定向:
晶体几何常数为: a = b = g = 90°, a = b = c – 三个互相垂直的L4, Li4或L2为 x, y, z 轴 – z 轴直立，y 轴左右水平，x 轴前后水平
只写出对称型中的三类对称要素 只写出对称轴，对称面，旋转反伸轴，其它对称要素 可根据组合定理推导出来 国际符号中对称要素的表示法 对称面：m 对称轴：以轴次的数字表示，如1、2、3，4和6； 旋转反伸轴：轴次数字上面加“-”号，如1、2、3、 4和6。 由于1=Li1=C,2=Li2=P=m，习惯用1代表对称中心．m代 表2。
r:s:t = MR/a : MK/b : MF/c
• [r s t] = [r s t]
此例：[r v w] = [1 2 3]
2、晶带: (zone) 彼此间的交棱均相互平行的一组晶面之组合。 晶带轴(zone axis) 通过晶体中心的一根直线，它平行于该晶带中的所有晶 面，也就是平行于该晶带中各个晶面的公共交棱，用以 表示晶带方向。
卤钠石(sulphohalite )的平行连生体
赤铜矿的连生晶体
明矾八面体的平行连生
萤石立方体的平行连生
自然铜立方体的树枝状平行连生
内 部 的 晶 体 格 子 是 连 续 的
2、双晶（孪晶） twin
定义：互不平行的同种单体，彼此间按一定的 对称关系相互取向而组成的规则连生晶体。
第四章 晶体定向和晶面符号
晶
体
的
定
向
方
法
10
四方晶系
1L4 c轴 2L2 /2P法线/2晶棱 a b轴
c 直立，b 左右， a 前后
a=bc ===90
11
斜方晶系
3L2 a b c 轴 1L2 c轴 2P法线 a b 轴
c 直立，b 左右， a 前后
abc == =90
12
单斜晶系
1L2/1P法线 b轴, 2晶棱 a c轴
交可决定一可能晶带(晶棱).
33
3、晶带方程应用
即：任一属于[u v w]晶带的晶面(h k l)，必定有： h u + k v + l w = 0 晶带方程
简单的证明： 三维空间的一般平面方程为 Ax + By + Cz + D = 0 系数A、B、C决定该平面的方向，常数项D决定距原点 的距离。 那么过坐标原点且平行于(h k l)的平面方程则可以表达 为
23
考察晶体模型晶面的晶面符号：
Cube
(001) (100) (010)
Octahedron
(111) (111)
Dodecahedron
(111)
(111)
101
011
_
110
110
_
_
101
011
24
All three combined:
001
_
101
111
011 111
_ 110
100
010 110
c 直立，b 左右 a 前后但向前下方倾斜 使>90
abc ==90 >90
13
三斜晶系
第四章 晶体定向和晶面符号
几何结晶学基础
第四章 晶体定向和晶面符号
五、各晶系晶体定向及常见单形符号
5.单斜晶系
（4） 常 见 聚 形
几何结晶学基础
第四章 晶体定向和晶面符号
五、各晶系晶体定向及常见单形符号
6.三斜晶系
⑴ 对称特点
无对称轴和对称面，共有2个对称型， 常见晶体多为C对称型。
⑵ 晶体定向
选三个近于相互垂直的晶棱方向为XYZ 轴。晶体常数特点为a≠b≠c， α≠β≠γ≠90°。
几何结晶学基础
第四章
一、晶体定向
4.晶体常数
晶体定向和晶面符号
各晶系的对称特点不同，因而选择晶轴 的方法及晶体常数的特点也不同。由于确定 晶轴和轴单位的方法和在晶体构造中划晶胞 的原则或确定平行六面体的原则一致，所以 各晶系晶体常数和格子参数完全吻合。
几何结晶学基础
第四章 晶体定向和晶面符号
二、晶面符号
晶带定律（zone law）
任意两晶棱（晶带）相交必可决定一可能 晶面，而任意两晶面相交必可决定一可 能晶棱（晶带）
几何结晶学基础
第四章 晶体定向和晶面符号
四、晶带及晶带符号
2.晶带的表示方法—晶带符号 表示晶带的空间方位的符号称为晶带符号。 晶带符号是以晶带轴的符号来代表的，而 晶带轴的符号又与该晶带中晶棱的符号相 同，故晶带符号可以用晶棱符号代替。
几何结晶学基础
第四章
一、晶体定向
3.晶轴的摆法
晶体定向和晶面符号
x轴：前后放置，前端为正；
y轴：左右放置，右端为正；
z轴：上下放置，上端为正；
三方、六方晶系还要层增加u轴， u轴的前端为负，后端为正，x、y、 u的正端之间的交角为120定向
4.晶体常数
四 晶体定向与晶面符号
二 、晶 面 符 号
1． 晶面符号的概念
晶体定向后，晶面在空间的相对位置即可根 据它与晶轴的关系予以确定。这种相对位置可 以用一定的符号来表征。表征晶面空间方位的 号称为晶面符号(参看图1一5一1)
米氏符号
米氏符号：用晶面在三个晶轴上的截距系数 的倒数比来表示。现举例说明如下。 如图I一5—3所示，设有一个晶面HKL在X、Y、 Z轴上的截距分别为2a、3b、6c 。 2、3、6称为 截距系数，其倒数比为1／2：1／3：1／6＝3：2： 1，去其比例符号，以小括号括之，写作(321)， 即为该晶面的米氏符号。小括号内的数字称为晶 面指数。晶面指数是按照X、Y、Z轴顺序排列的， 一般式写作(hkl)；对于三方、六方晶系晶面指数 按X、Y、U、Z轴顺序排列，一般式写作(hkil)。 若晶面平行于某晶轴，则晶面在晶轴上的截距系 数为∞，截距系数的倒数应为0。
(3)轴长与轴率 晶轴系格子构造中的行列， 该行列上的结点间距称为轴长。 X、Y、Z 轴上的轴长分别以“a。、b。、c。表示。 由于结点间距极小(以nm计)，需藉X射线分 析方能测定。根据晶体外形的宏观研究不 能定出轴长，但应用几何结晶学的方法可 以求出它们的比率a：b：c，这一比率称为 轴率。
不同物质的晶体结构不同，结点间距不同，轴长各异。 如图I一5—1a闪锌矿的“a。＝0．540nm，方铅矿的a。 ＝0．594nm。 等轴晶系晶体对称程度高，品轴X、Y、Z为彼此对称 的行列，它们通过对称要素的作用可以相互重合，因此 它们的轴长是相同的，即a＝b＝c，轴率a：b：c＝1：1： 1(图I一5—1a)。 中级晶族(四方、三方和六方晶系)晶体中只有一个高 次铀，以高次轴为Z轴，通过高次轴的作用可以使X轴与 Y轴重合，因此轴长a＝b,但与c不等，轴率a：c因晶体的 种别而异(图I一5—1b、c、d)。 低级晶族(斜方、单斜和三斜晶系)晶体对称程度低， X、Y、Z轴不能通过对称要素的作用而重合，所以α≠β≠γ， 晶体的种别不同．轴率a：b：c数值不同(图I一5一1e、f)
第四章 晶体定向和晶体学符号
点群
3和3 选择三次轴的方向作为z轴，另外三个合
适晶棱的方向作为x，y，u轴。 均有三条L2垂直于三次轴，且互相夹角为
32和3m
120o（或相邻夹角为60o）的三条，分别选作x，
y，u轴。
六方晶系的特点：有唯一的高次轴，包含7个点群
6 ，选择六次轴的方向作为z轴，另外三个合 6、和 6
3.斜方晶系晶体定向
斜方晶系包含三个点群。 222和mmm有三条互相垂直的L2 ，分别作为x轴、y轴 和z轴;
mm2选L2作为z轴，两个互相垂直的对称面它们的法线 也互相垂直，分别作为x轴和y轴。
其几何参数为
a b c, 90o
4.单斜晶系的晶体定向
=
四方底心
四方简单格子
为 什 么 没 有 四 方 面 心
=
四方面心
四方体心
六方晶系（h)
六方简单格子 （hP）
三方晶系 (r)
三方简单格子 （rP）
六方R心格子 （hR）
单斜晶系包含三个点群，其对称特点是含有或P，且它
们的数目均不多于一个。
对于2和2/m，m的法线和L2平行，选L2作为y轴，x轴和 z轴选择适当晶棱的方向。
对于m，选m的法线作为y轴，x轴和z轴选择适当晶棱 的方向
其晶体几何常参数为
a b c, 90 , 90
o
o
条L2互相垂直，我们选它们分别作为x轴和y轴；
4mm没有L2 ，但是有两个互相垂直的平面，它们的法线 也互相垂直，将两个平面的法线分别作为x轴和y轴。
4，4/m和 4 ，它们既没有L2也没有P，选两条垂直于L4 ， 且互相垂直的适当的晶棱分别作为x轴和y轴。
3和3 选择三次轴的方向作为z轴，另外三个合
适晶棱的方向作为x，y，u轴。 均有三条L2垂直于三次轴，且互相夹角为
32和3m
120o（或相邻夹角为60o）的三条，分别选作x，
y，u轴。
六方晶系的特点：有唯一的高次轴，包含7个点群
6 ，选择六次轴的方向作为z轴，另外三个合 6、和 6
3.斜方晶系晶体定向
斜方晶系包含三个点群。 222和mmm有三条互相垂直的L2 ，分别作为x轴、y轴 和z轴;
mm2选L2作为z轴，两个互相垂直的对称面它们的法线 也互相垂直，分别作为x轴和y轴。
其几何参数为
a b c, 90o
4.单斜晶系的晶体定向
=
四方底心
四方简单格子
为 什 么 没 有 四 方 面 心
=
四方面心
四方体心
六方晶系（h)
六方简单格子 （hP）
三方晶系 (r)
三方简单格子 （rP）
六方R心格子 （hR）
单斜晶系包含三个点群，其对称特点是含有或P，且它
们的数目均不多于一个。
对于2和2/m，m的法线和L2平行，选L2作为y轴，x轴和 z轴选择适当晶棱的方向。
对于m，选m的法线作为y轴，x轴和z轴选择适当晶棱 的方向
其晶体几何常参数为
a b c, 90 , 90
o
o
条L2互相垂直，我们选它们分别作为x轴和y轴；
4mm没有L2 ，但是有两个互相垂直的平面，它们的法线 也互相垂直，将两个平面的法线分别作为x轴和y轴。
4，4/m和 4 ，它们既没有L2也没有P，选两条垂直于L4 ， 且互相垂直的适当的晶棱分别作为x轴和y轴。
晶体定向与结晶符号
β X
L2 2P
α γ Y
4.2 各晶系晶轴的选择及晶体几何常数特点
L2 PC ⑷单斜晶系 对称特点 L2或P的个数不多于1个。 选轴原则 L2 → Y 2 以L 或P的法线为Y轴， 以两根均垂直Y轴的合适晶 棱方向为X、Z轴。 晶轴安置 晶体几何常数 Z轴直立， a≠b≠c， Y轴左右水平， α=γ=90°， X轴前后并向前下倾斜。 β＞90°
α
Y
4.2 各晶系晶轴的选择及晶体几何常数特点
⑹三方和六方晶系 对称特点 有且只有一个L3或L6或Li6。 选轴原则 3 6 6 以L 或L 或Li 为Z轴， 2 以3L 或3P法线或3晶棱方向 为X、Y、U轴。 晶体几何常数： a=b≠c， o α=β=90 ， o γ=120 。 L6 6L2 7PC
Z(+)
β
α
Y(+) γ
X(+)
晶轴的名称、安置和轴角
四轴定向 Z轴直立，上端正。 Y轴左右，右端正； X轴左前，前端正； U轴右前，后端正。
Z(+)
U(+)
β
α
Y(+)
轴角：
X(+)
α：Z∧Y＝90° β：Z∧X＝90° γ：X∧Y＝120°
γ
四轴定向时，三根水平晶轴正端之间的夹角为120 °
4.1结晶轴和晶体几何常数
晶体中的坐标轴称为结晶轴(crystallographic axis) 晶轴是与晶体对称有关的几根假想直线 原点在晶体中心
晶轴的名称、安置和轴角 三轴定向 Z轴直立，上端为正； Y轴左右，右端为正。 X轴前后，前端为正； 轴角(interaxial angle) 晶轴正端之间的夹角。 α ：Z∧Y； β：Z∧X； γ：X∧Y
L2 2P
α γ Y
4.2 各晶系晶轴的选择及晶体几何常数特点
L2 PC ⑷单斜晶系 对称特点 L2或P的个数不多于1个。 选轴原则 L2 → Y 2 以L 或P的法线为Y轴， 以两根均垂直Y轴的合适晶 棱方向为X、Z轴。 晶轴安置 晶体几何常数 Z轴直立， a≠b≠c， Y轴左右水平， α=γ=90°， X轴前后并向前下倾斜。 β＞90°
α
Y
4.2 各晶系晶轴的选择及晶体几何常数特点
⑹三方和六方晶系 对称特点 有且只有一个L3或L6或Li6。 选轴原则 3 6 6 以L 或L 或Li 为Z轴， 2 以3L 或3P法线或3晶棱方向 为X、Y、U轴。 晶体几何常数： a=b≠c， o α=β=90 ， o γ=120 。 L6 6L2 7PC
Z(+)
β
α
Y(+) γ
X(+)
晶轴的名称、安置和轴角
四轴定向 Z轴直立，上端正。 Y轴左右，右端正； X轴左前，前端正； U轴右前，后端正。
Z(+)
U(+)
β
α
Y(+)
轴角：
X(+)
α：Z∧Y＝90° β：Z∧X＝90° γ：X∧Y＝120°
γ
四轴定向时，三根水平晶轴正端之间的夹角为120 °
4.1结晶轴和晶体几何常数
晶体中的坐标轴称为结晶轴(crystallographic axis) 晶轴是与晶体对称有关的几根假想直线 原点在晶体中心
晶轴的名称、安置和轴角 三轴定向 Z轴直立，上端为正； Y轴左右，右端为正。 X轴前后，前端为正； 轴角(interaxial angle) 晶轴正端之间的夹角。 α ：Z∧Y； β：Z∧X； γ：X∧Y
第四章：晶体定向与结晶符号
(1).晶面指数——在米氏符号中小 括号内数字称为晶面指数。如晶面符 号（321）中 的321即为晶面指数。 注意：晶面指数是一组无公约数的 整数。
(2).晶面指数特点——均为简单整 数（整数定律或有理数定律）。
4.晶面指数写法 ⑴.三轴定向的晶系 对三轴定向的晶系而言：晶面 指数按X、Y、Z轴的顺序排列。 如果能确定具体数字时，用阿 拉伯数字表示，如果不能确定具 体数字时，用h、k、l表示。 如:（110）（hkl）（hko）
即尽可能使： α=β=γ= 90° a=b=c。
（2）确定晶体常数
晶体常数 轴角 轴角是指晶轴 正端的夹角。通 常用α、β、γ表 示。
α（y∧z） γ（x∧y） β（z∧x）
β x
z α γ y
晶体常数 轴长
晶轴与空间格子中的行列相 对应，行列上结点的间距称为轴 单位（轴长）。 轴单位是结晶轴长度计量的 单位。即：a、b、c。
3.各晶系晶轴选择的原则及 晶体常数特征
（1）等轴晶系
（2）四方晶系
（3）三方晶系及六方晶系
（4）斜方晶系
（5）单斜晶系
（6）三斜晶系
二 结晶符号
1.晶面符号的概念
晶面符号——表征晶面空间方位 的符号。
晶面符号有多种形式，通常采用的是米 氏符号（英国的米勒于1839年创立） 。
2.米氏符号的表示方法 晶面在三个（或四个）结 晶轴上的截距系数的倒数比， 并去掉比例符号，用小括号括 之来表示。
⑵四轴定向的晶系
对四轴定向的晶体而言： 晶面指数按X、Y、U、Z轴顺
序排列，一般写作（hkil）。
注意:
①米氏符号中某个数为0时，表 示该晶面与相应的晶轴平行。 ②同一米氏符号中，晶面指数越 大，表示晶面在相应结晶轴上的截 距系数越小。
(2).晶面指数特点——均为简单整 数（整数定律或有理数定律）。
4.晶面指数写法 ⑴.三轴定向的晶系 对三轴定向的晶系而言：晶面 指数按X、Y、Z轴的顺序排列。 如果能确定具体数字时，用阿 拉伯数字表示，如果不能确定具 体数字时，用h、k、l表示。 如:（110）（hkl）（hko）
即尽可能使： α=β=γ= 90° a=b=c。
（2）确定晶体常数
晶体常数 轴角 轴角是指晶轴 正端的夹角。通 常用α、β、γ表 示。
α（y∧z） γ（x∧y） β（z∧x）
β x
z α γ y
晶体常数 轴长
晶轴与空间格子中的行列相 对应，行列上结点的间距称为轴 单位（轴长）。 轴单位是结晶轴长度计量的 单位。即：a、b、c。
3.各晶系晶轴选择的原则及 晶体常数特征
（1）等轴晶系
（2）四方晶系
（3）三方晶系及六方晶系
（4）斜方晶系
（5）单斜晶系
（6）三斜晶系
二 结晶符号
1.晶面符号的概念
晶面符号——表征晶面空间方位 的符号。
晶面符号有多种形式，通常采用的是米 氏符号（英国的米勒于1839年创立） 。
2.米氏符号的表示方法 晶面在三个（或四个）结 晶轴上的截距系数的倒数比， 并去掉比例符号，用小括号括 之来表示。
⑵四轴定向的晶系
对四轴定向的晶体而言： 晶面指数按X、Y、U、Z轴顺
序排列，一般写作（hkil）。
注意:
①米氏符号中某个数为0时，表 示该晶面与相应的晶轴平行。 ②同一米氏符号中，晶面指数越 大，表示晶面在相应结晶轴上的截 距系数越小。
第四章-晶体定向和结晶符号
4.1. 晶体定向的概念
晶体定向(crystal orientating):
–
在晶体中选定一个三维的坐标系，并将晶体按相应的空间取向 关系作好安置
几个基本术语:
– – – – –
结晶轴(crystallographic axis): X、Y、Z, 或a、b、c 轴角(interaxial angle):α=b^c，β=c^a，γ=a^b 轴单位(axial unit distance) 轴率(axial ratios): a:b:c 晶体几何常数(crystal constants): a:b:c, α,β,γ
– – – –
1 已知两个晶面，求包含此二晶面的晶带之符号 2 求同时属于某二已知晶带的该晶面之晶面符号 3 判断某一已知晶面是否属于某个已知的晶带 4 由四个互不平行的已知晶面, 或四个已知晶带, 求出晶体上一切可能 的晶面与晶带(即晶棱)
如, 求含晶面(h1 k1 l1)和(h2 k2 l2)的晶带[u v w]
3
结晶学与矿物学
4.3. 晶体定向的原则
选择适宜的晶棱方向作为结晶轴 选择适宜的对称要素作为结晶轴 轴率应当与相应行列上的结点间距一致
4
结晶学与矿物学
4.4. 各晶系的定向法则
晶体的三轴定向和四轴定向 等轴晶系的定向 四方晶系的定向 斜方晶系的定向 单斜晶系的定向 三斜晶系的定向 三方和六方晶系的四轴定向
h1u+k1v+1lw=0 h2u+k2v+l2w=0
22
三斜晶系的定向:
–
– –
–
共有2个点群: 1, -1 晶格常数为: α< >β< >γ< > 90 °, a < > b < > c 适当的晶棱为a, b, c轴 大致上c轴直立，b轴左右，a轴前后
5-第四章晶体定向和晶体符号
5-第四章晶体定向和晶体符号第四章晶体定向和晶体符号[内容介绍] 本章介绍晶体定向、晶面符号、单形符号、晶带符号的概念、各晶系晶体的定向原则及各种晶体符号的确定方法。
[学习目的] 理解和掌握晶体定向、晶体符号的概念及其确定原则和方法，系统地掌握结晶学的基本知识，为学习矿物学和晶体光学打下良好基础。
图4-1所示的两个晶体，都是由四方柱和四方双锥组成的聚形，均属L 44L 25PC 对称型，但其形态明显不同。
这种形态的差异，是由于四方柱和四方双锥的相对位置不同造成的。
由此可见，在研究晶体时，仅确定其对称型和由哪些单形所组成，仍不能获得晶体形态的完整概念，必须进一步确定各单形在空间的相对位置，因而需要在晶体上选定一个坐标系统，这就是晶体定向。
还必须进一步研究晶面、晶棱（晶带）以及单形等在晶体上的方向，并用一定的符号表示它们，这就是所谓的晶面符号、晶棱符号与单形符号。
这些符号统称为晶体符号。
晶体定向和晶体符号不仅在研究晶体形态时需要，在确切地描述晶体的异向性、对称性以及矿物鉴定、矿物内部结构和物理性质的研究工作中都具有重要的意义。
第一节晶体定向一、晶体定向的概念晶体定向就是在晶体中确定坐标系统。
具体说来，就是要选定坐标轴（晶轴）和确定各晶轴上单位长度（轴长）及其比值（轴率）。
（一）晶轴如图4-2所示，晶轴系交于晶体中心的三条直线，它们分别为a 轴（或称x 轴）前端为“+”，后端为“-”、b 轴（或称y 轴）右端为“+”，左端为“-”和c 轴（或称z 轴）上端为“+”，下端为“-”；对于三方和六方晶系要增加一个d 轴或称u 轴，前端为“-”，后端为“+”（图4-3）。
晶轴的选择：晶体中晶轴的选择应与空间格子类型的特征相吻合。
三个晶轴的方向应当平行晶胞中三个棱的方向。
图4-1 由四方柱和四方锥组成的二种聚形由于对称轴、对称面法线及晶棱的方向与空间格子的行列方向相平行。
因此，晶轴的选择，首先应选对称称轴作为晶轴，在无对称轴及对称轴数量不足时，可选对称面法线作为晶轴，若两者均缺乏时，则可选择平行主要晶棱的方向线作为晶轴。
第四章晶体的定向和晶面符号
第四章 晶体的定向和晶面符号
• • • • • 晶体定向的概念 晶体定向的原则 各晶系的定向法则 晶面符号与单形符号 晶带及晶带符号
一、晶体的定向（三轴定向）
在晶体上确定坐标系统，即选坐标轴和确 定各轴上的轴单位长度之比。 (1) 晶轴：是交于晶体中心的三条直线。为x、y、 z（或a、b、c）。 (2) 轴角:α、β、γ (3) 轴长和轴率：晶轴 是晶体中格子构造中 的行列，轴长（轴单位） 是该行列上的结点间距。 分别以 a、b、c表示， a:b:c为轴率。 （4）晶体常数： 轴率a：b：c和轴角α、β、γ
三方和六方晶系的四轴定向：
– 选择唯一的高次轴作为直立结晶轴Z轴，在垂直Z 轴的平面内选择三个相同的、即互成60°交角的L2 或P的法线，或适当的显著晶棱方向作为水平结晶 轴，即x 轴、 y 轴以及 d 轴(U轴) – 晶体几何常数: a = b = 90°, g =120°, a = b ≠ c – z 轴直立， y 轴左右水平， x 轴前后水平偏左30°
斜方晶系 单斜晶系
a = b = g = 90
a≠b≠c a = g = 90 b > 90 a≠b≠c a≠b≠g
以L2或P的法线为Y轴，以垂直于Y轴 的主要晶棱方向为X、Z轴 以不在同一平面的三个主要的晶棱方 向为X、Y、Z轴
三斜晶系
四、晶面符号与单形符号
1.整数定律
• 任何晶面截距系数之比，都是简单的整数比。
a=b≠c a = b = 90 g = 120
a≠b≠c
三方晶系 及六方晶系
以L3或 L6 或Li6 为Z轴，以垂直Z轴并彼 此交角120°（正端）的3个L2或P法线或 晶棱方向为 X 、 Y 、 U ， 在 L i 6 3L 2 3P 对称
1.4晶体的定向及晶面符号
晶体定向
5. 六方晶系：具有一个六次轴（包括六次反轴）的点群。首先 选择六次轴或六次反轴作为C轴，然后将垂直于六次轴的两个 二次轴或晶面法线作为a、b晶轴。为了满足六次轴的对称，a、 b轴必须满足：①单位轴长必须相等，即a0=b0；②交角为120º
晶体定向
6. 三方晶系：具有一个三次轴的点群。有2种取向方式：①六方晶
①由晶面（h1 k1 l1）和（h2 k2 l2）求晶带符号 根据晶带定律建立方程组：
h1u＋k1v＋l1w = 0 h2u＋k2v＋l2w = 0 解出：
u:v:wk1l1:l1h1:h1k1 k2l2 l2h2 h2k2
解法：①将每一个晶面的面指数在一 列上连续写2次，其指数按次序一一对 应； ②将最右及最左的纵行删去，如 右式； ③用交叉相乘方法，并依次取 出乘积差数即可。
晶面间距好像晶体的指纹，是进行物相鉴别 的重要依据。
1 晶体的定向和晶体的分类 2 晶面指数和晶棱指数 3 晶带定律 4 晶面间距
晶体定向
晶体的定向就是以晶体中心为原点建立一个坐标系,由X,Y,Z三轴 组成,也可由X,Y,U,Z四轴组成(对三方晶系与六方晶系).
c 大拇指
Z
β
α
O
食指
γ
a
=bc
β= a c
γ=ab
中指
b
U
Y
X
120º
坐标轴符合右手定则
晶带定律
②由晶向[u1 v1 w1]和[u2 v2 w2]求晶面符号 建立方程组：
得：
hu1＋kv1＋lw1 = 0 hu2＋kv2＋lw2 = 0
h:k:lv1w1:w1u1:u1v1 v2w2 w2u2 u2v2
晶带定律
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5
结晶学与矿物学
晶体定向方法
• 各晶系的晶体几何常数特点
– – – – – – 等轴晶系：a = b = c，a = b = g = 90； 四方晶系：a = b ≠ c，a = b = g = 90； 三方和六方晶系：a = b ≠ c，a = b = 90，g = 120； 斜方晶系：a ≠ b ≠ c，a = b = g = 90； 单斜晶系：a ≠ b ≠ c，a = g = 90，b > 90； 三斜晶系：a ≠ b ≠ c，a ≠ b ≠ g；
符号统称结晶符号
由于晶体的各种特性(形态、物性、结构等)都与晶 体的方向有关，所以晶体定向是研究晶体的最基本 的工作
2
一、晶体定向方法
晶体定向就是在晶体中以晶 体中心为原点建立一个坐标 系，这个坐标系一般由三根 晶轴X、Y、Z轴(也可用a、b、 c轴表示)组成。三根晶轴正 端之 间的夹角分别表示为 α(Y∧Z)、β(Z∧X)、 γ(X∧Y)。对于三、六方晶 系的晶体，通常要用四轴定 向法，即要选出四根晶轴
25
结晶学与矿物学
实际晶体之晶面
26
结晶学与矿物学
晶带符号
• 晶带(zone)
– 交棱相互平行的一组晶面的组合
• 晶带轴(zone axis)
– 表示晶带方向的一根直线，即该晶带中各晶面交棱方 向直线，并移至过晶体中心
• 晶带符号(zone symbol)
– 晶带轴的符号就是晶棱符号。通常以晶带轴符号来表 示晶带符号
• 晶面可与晶轴垂直, 平行或斜交
19
结晶学与矿物学
晶面符号
– 举例（3D）
c
C Z
x = (h k l) = ? y = (h k l) = ?
A
O Y
B
X
a
20
b
结晶学与矿物学
晶面符号
四轴定向时的晶面 符号:
– 定义同三轴定向 – 用(h k i l)的形式表达 – 指数依次与X、Y、U 和Z轴相对应 – 存在 h + k + i = 0
四、晶面符号、晶棱符号
• 晶面符号(面号):
– 它是根据晶面(或晶体中平行于晶面的其他平面) 与各结晶轴的交截关系，用简单的数字符号形
式来表达它们在晶体上方位的一种晶体学符号;
– 目前国际上通用的都是米氏符号，亦称米勒符
号：晶面在三根晶轴上的截距系数的倒数比
17
结晶学与矿物学
晶面符号
• 晶面符号的确定:
– 以[u v p w]的形式表达 – 也有三指数形式: [r s t] • 四指数和三指数之间的比较
• r : s : t =(u-p):(v-p):w
23
结晶学与矿物学
五、整数定律及晶带定律
整数定律或有理指
数定律：晶面指数
为简单整数
24
结晶学与矿物学
布拉维法则
实际晶面为面网密 度大 的面网所包围
晶体宏观形态中按对称特点选出的晶轴，实际上与晶体内部 结构中空间格子的三个不共面的行列方向一致 6
结晶学与矿物学
晶胞参数及晶体常数特点
X、Y、Z三根晶轴方向上的行列上的结点间距分别 表示为a0、b0、c0，称为轴长；三根晶轴正端之间的
夹角α、β、γ称为轴角，轴长和轴角统称晶胞参数
在晶体宏观形态上是定不出轴长的，只能根据对称
3
结晶学与矿物学
晶体定向原则
• 与晶体的对称特点相符合
–适宜的对称元素作为结晶轴
–适宜的晶棱方向作为结晶轴
• 尽量使得晶轴之间夹角为90
4
结晶学与矿物学
晶体定向原则
• 晶体的三轴定向:
– 选择三个不共面的坐标轴 x, y, z安置晶体
• 晶体的四轴定向:
– 适用于六方和三方晶系 – 一个直立轴，三个水平轴
18
结晶学与矿物学
晶面符号
– 米氏指数(Miller indices)是指：用来表达晶面在晶体 上之方向的一组无公约数的整数，它们的具体数值 等于该晶面在结晶轴上所截截距系数的倒数比。 – 如果将米氏指数按顺序连写，并置于园括号内, 表达
为(h k l), 便构成了晶面的米氏符号。
• 按X、Y、Z轴顺序，不得颠倒！ • 晶轴有正负方向，指数的负号写在上面
– 任意两晶棱（晶带）相交必可决定一可能晶面，而任 意两晶面相交必可决定一可能晶棱（晶带） 任一属于[u v w]晶带的晶面(h k l)，必定有： h u + k v + l w = 0---晶带方程
29
结晶学与矿物学
晶带定律的应用
• • • • 已知两个晶面，求包含此二晶面的晶带之符号 求同时属于某二已知晶带的该晶面之晶面符号 判断某一已知晶面是否属于某个已知的晶带 由四个互不平行的已知晶面, 或四个已知晶带, 求出晶体 上一切可能 的晶面与晶带(即晶棱)
10
结晶学与矿物学
各晶系的定向法则
• 斜方晶系的定向:
– 晶体常数为: a = b = g = 90°, a < > b < > c – 三个相互垂直的L2为 z, x, y 轴; 或L2为z轴, 相互垂直的 对称面法线为 x, y 轴 – z 轴直立， y 轴左右水平，x 轴前后水平
11
结晶学与矿物学
特点定出a0∶b0∶c0（或 表示为a∶b∶c），这一比
例称为轴率。轴率与轴角统称晶体常数。晶体常数 特点是可以在晶体宏观形态上体现出来的
7
结晶学与矿物学
各晶系的定向法则
• 等轴晶系的定向:
– 晶体常数为: a = b = g = 90°, a = b = c – 三个互相垂直的L4, Li4或L2为 x, y, z 轴 – z 轴直立，y 轴左右水平，x 轴前后水平
各晶系的定向法则
• 三方和六方晶系的四轴定向
选择唯一的高次轴作为直立结晶轴c轴，在垂直 z 轴的平面内 选择三个相同的、即互成60°交角的L2或P的法线，或适当的 显著晶棱方向作为水平结晶轴，即x 轴、 y 轴以及 d 轴(U轴) – 晶格常数为: a = b = 90°, g =120°, a = b < > c – z 轴直立， y 轴左右水平， x 轴前后水平偏左30°
– 晶体上任意一个晶面，若它在三 个结晶轴 X 轴、 Y 轴、 Z 轴上的截 距依次为 OA、OB、OC, 已知轴 率为a∶b∶c，则该晶面在晶轴上 的截距系数p, q, r分别为: p = OX/a, q = OY/b, r = OZ/c 其倒数比 1/p:1/q:1/r = h : k : l – 晶面指数( 米氏指数): 取h:k:l的最 简单整数比, 此时的h, k, l就称为 晶面指数;
各晶系的定向法则
• 单斜晶系的定向:
– 晶格常数为: a = b = 90°, g > 90°, a < > b < > c – L2为 y 轴; 或对称面法线为 y 轴 – z 轴起立， y 轴左右水平， x 轴前后向前下倾斜
12
结晶学与矿物学
各晶系的定向法则
• 三斜晶系的定向:
– 晶体常数为: a < > b < > g < > 90 °, a < > b < > c
8
结晶学与矿物学
各晶系的定向法则
• 四方晶系的定向:
– 晶体常数为: a = b = g = 90°, a = b < > c – 唯一的L4或Li4为 z 轴; 相互垂直的L2, 或相互 垂直的对称面法线, 或 适当的晶棱为 x, y 轴 – z 轴直立， y 轴左右水 平，x 轴前后水平
9
结晶学与矿物学
27
结晶学与矿物学
晶带符号
• 例如 – (1-10), (100), (110), (010)… 的交棱相互平行，组成一个 晶带; 直线CC’即可表达为 此晶带的晶带轴 –此组晶棱的符号,即该晶带 轴的符号，为[001]（或者 [00-1]）晶带
28
结晶学与矿物学
晶带定律
• 晶带定律(zone law)
15
对称型的国际符号：
在国际符号中有1～3个序位，每一序位中的一个
对称要素符号可代表一定方向的、可以互相派生
（ 或复制）的多个对称要素，即在对称型的国 际符号中凡是可以通过其它对称要素可以派生出 来的对称要素都省略了
2、对称型的圣弗利斯符号：
见课本P64~P65及表3-4（P40~P41）
16
结晶学与矿物学
h1 k1 h2 k 2
l1 l2
h1 h2
k1 l1 k 2 l2
31
[uvw] u : v : w (k1l 2 k 2 l1 ) : (l1 h2 l 2 h1 ) : (h1 k 2 h2 k1 )
作业
课后习题：第1、5、6、7题
32
30
结晶学与矿物学
晶带定律的应用
• 举例：若已知属于同一晶带的两晶面为(h1 k1 l1)和(h2 k2 l2)，求 晶带符号。
– 根据晶带方程hu + kv + lw = 0，可以得出： • h1u + k1v + l1w = 0 (1) • h2u + k2v + l2w = 0 (2) – 解联立式(1)和式(2)的方程组，可得 [u v w] = u : v : w = (k1l2 - k2l1) : (l1h2 - l2h1) : (h1k2 - h2k1)
结晶学与矿物学
晶体定向和结晶符号
• • • • • 晶体定向方法 各对称型中对称要素的空间分布 对称型的国际符号及圣弗利斯符号 晶面符号、晶棱符号 整数定律、晶带定律
1