晶体学符号
晶体学符号与倒格子

例题:在立方晶系中画出(210)与 晶面 ( 121)
画晶面时,标注出面与晶轴交点离原点的距离(以晶轴长度为单位)
晶面指数说明
• 1,坐标系建立:晶体中坐标系x,y,z不一定是正交系,但满足右手 关系,其中晶轴a,b,c分别对应x,y,z轴。 • 2,当晶面交于晶轴的负方向是,对应的指数就是负值,并将负号标 注在数字的上面。 • 3,晶面指数中的1,2,3位数字分别代表与a,b,c轴的截距倒数。 • 4,一个晶面指数代表某一方向(晶面法向)的一组晶面,而不是一 个面。 • 5,晶面对应某晶轴的指数为零时,晶面平行于该晶轴。 • 6,与晶向指数类似,晶体中存在一组等价晶面,即晶面族,用{hkl} 表示。 • 7,设基矢a,b,c ,末端分别落在离原点距离为hd,kd,ld 的晶面 上,h,k,l 为整数,d为晶面间距,h,k,l是互质的整数。用结晶学 原胞(惯用晶胞)基矢坐标系表示的晶面指数称为密勒指数。
指数为负数的情况
A 轴截距为1 B轴截距为1/2 C轴截距为-1/3
(123)
例:在一个面心立方晶胞中画出(012)和(122)晶面。
c b
a
b
a
b
晶面指数等于0,则平行该轴!存在附加面!
晶面指数标注:
1/2
晶面指数确定时选择离原点最近的晶面。 判断方法:过原点做已知晶面的平行面,看两平行晶面间是否有格点不在晶面上?
z [100] 2
[100]
[100] x
o
y
x
z
[011]
晶向指数实际上代表所有相互平行、
1
o [011] x 2 y
方向一致的晶向。
平行反向有“—”号
例题:立方晶胞中,已知晶向指数[231] ,画出[231]晶向?
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系
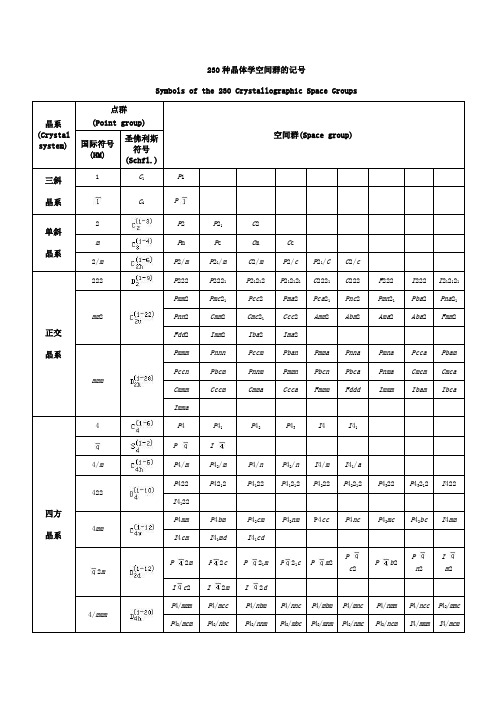
230种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups2m 2P P 2m bI c22m 11m P R m c m2m c23m 33I P3Im m n Pm Pn Fm Fm Fd mFdm d空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个,它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群。
菱方是不标准的说法,应该是三方,菱面体是三方的R点阵中的一种,7个晶系分别是立方cubic(a=b=c,α=β=γ=90o,只有一个晶胞参数a)四方tetragonal(a=b≠c,α=β=γ=90o,有2个晶胞参数a和b)六方hexagonal(a=b≠c,α=β=90o,γ=120o,有2个晶胞参数a和c)正交orthorhombic(a≠b≠c,α=γ=90o,有3个晶胞参数a,b和c)单斜monoclinic(a≠b≠c,α=γ= 90o,β≠90o,有4个晶胞参数a,b,c和β)三斜triclinic(a≠b≠c,α≠β≠γ,有6个晶胞参数a,b,c,α,β和γ)三方(a=b≠c,α=β=90o,γ=120o,有2个晶胞参数a和c) rhombohedral对于三方这个问题,很多书上都是错误的,三方跟六方绝对不能混为一谈F is face-centered;P is Primitive; I is body-centered;不同晶系的晶格类型32种晶体学点群的记号2mm mm2m(4)3m 3(3)mm (4)点群不存在平移操作,所有的对称要素都集中在一个共同的点上。
对称要素包括旋转、反映、反伸(对称中心)与旋转反伸。
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系
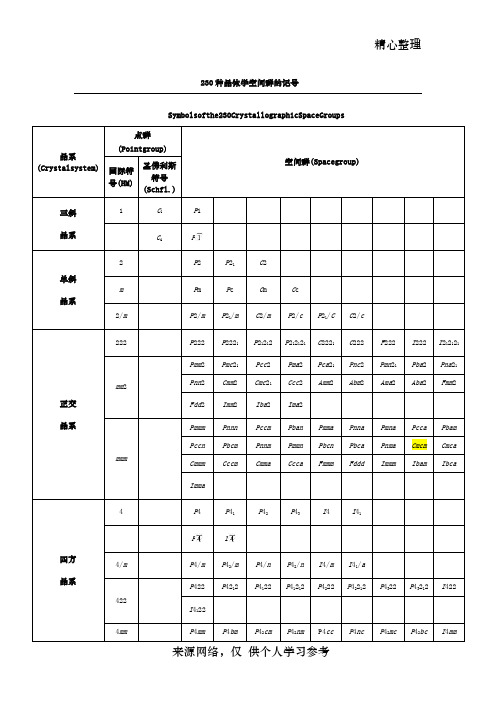
Symbolsofthe230CrystallographicSpaceGroups
晶系(Crystalsystem)
点群
(Pointgroup)
空间群(Spacegroup)
国际符号(HM)
圣佛利斯符号(Schfl.)
三斜
晶系
1
C1
P1
Ci
P
单斜
晶系
2
P2
P21
C2
m
Pm
刚玉
Al2O3
三方
正长石
KAlSi3O8
单斜
3·2莫来石
3Al2O3·2SiO2
正交
钾石膏
K2Ca(SO4)2·2H2O
单斜
2·1莫来石
2Al2O3·SiO2
正交
钾盐
KCl
立方
勃姆石
AlO(OH)
正交
羟铁云母
KFe3[AlSi3O10](OH)2
单斜
水铝石
AlO(OH)
正交
铁羟铁云母
KFe3[FeSi3O10](OH)2
m
D3d
6
六方晶系
c
a
[210]
6
C6
6
6/m
C3h
6/m
C6h
622
D6
6
2(3)
2(3)
6/mmm
6mm
C6v
6
m(3)
m(3)
m2
D3h
m(3)
2(3)
6/mmm
D6h
7
立方晶系
c
[111]
[110]
23
T
2(3)
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系

(Nameofregularpolyhedron)
正四面体(Regulartetrahedron)
正六面体(Regularhexahedron)
正八面体(Regularoctahedron)
正十二面体
(Regulardodecahedron)
正二十面体
(Regularicosahedron)
11.3662a2
外接球体积V外接球
1.2410a3
2.7205a3
1.4809a3
11.7496a3
3.6033a3
中心原子半径r
0.0443a
0.3660a
0.2071a
0.9103a
0.45105a
配位原子半径R
0.5a
0.5a
0.5a
0.5a
0.5a
r/R
0.0886
0.7320
0.4142
立方
钡钠长石
BaNaAl4Si4O16
正交
氟镁石
MgF2
四方
重晶石
BaSO4
正交
方镁石
MgO
立方
金绿宝石
BeAl2O4
正交
水镁石
Mg(OH)2
六方
铍石
BeO
六方
泻盐矿
MgSO4·7H2O
正交
铋华
α-Bi2O3
单斜
无水钠镁矾
MgSO4·3Na2SO4
单斜
辉铋矿
Bi2S3
正交
斜顽火石
MgSiO3
单斜
碲铋矿
4
P4
P41
P42
P43
I4
I41
P
I
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系
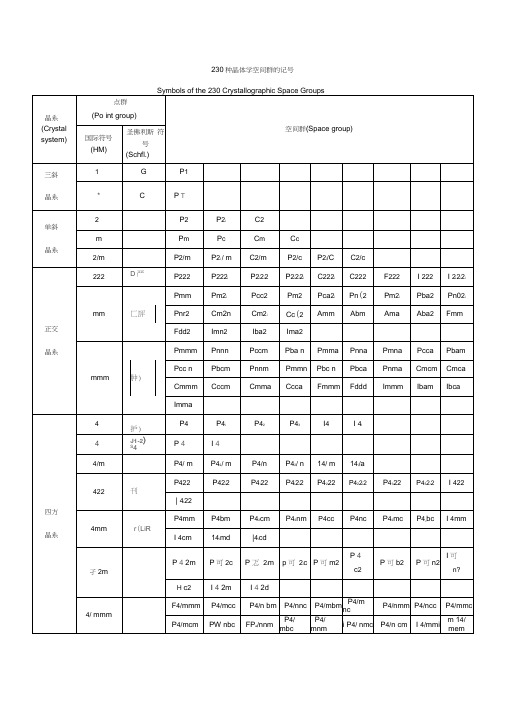
四方
晶系
4
护)
P4
P4i
P42
P43
I4
I4i
4
J1-2)
S4
P4
I4
4/m
P4/m
P42/m
P4/n
P42/n
14/m
14i/a
422
刊
P422
P42i2
P4i22
P4i2i2
P4222
P422i2
P4322
P432i2
I422
|4i22
4mm
r(LiR
P4mm
P4bm
P42cm
P42nm
Th
-(H賈
頁⑷
432
O
4(3)
3⑷
2(6)
m吾m
兀3m
Td
忑3(3)
3⑷
%6)
m3m
O
-G)
頁⑷
%
科
点群不存在平移操作,所有的对称要素都集中在一个共同的点上。对称要素包括旋转、反 映、反伸(对称中心)与旋转反伸。有这4个对称要素组合岀32个点群。
下表中“轴向对称要素的方向和数目”的圆括号内数据代表该对称要素的数目
P2i
C2
m
Pm
Pc
Cm
Cc
2/m
P2/m
P2i/m
C2/m
P2/c
P2i/C
C2/c
正交
晶系
222
D严
P222
P222i
P2i2i2
P2i2i2i
C222i
C222
F222
I222
I2i2i2i
mm
Pmm
Pm2i
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系
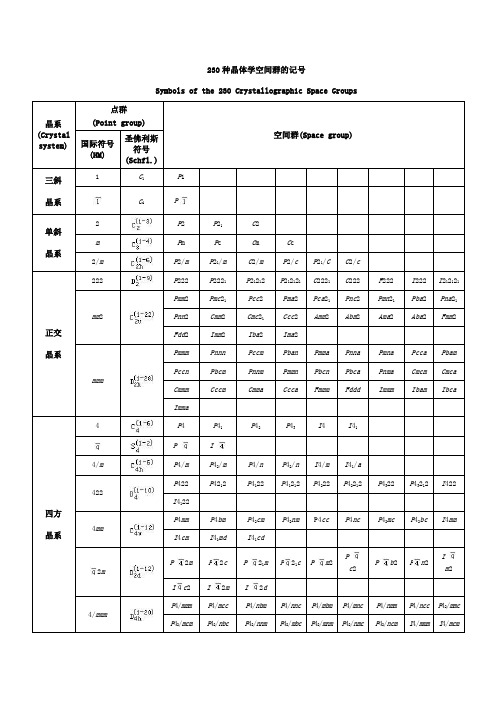
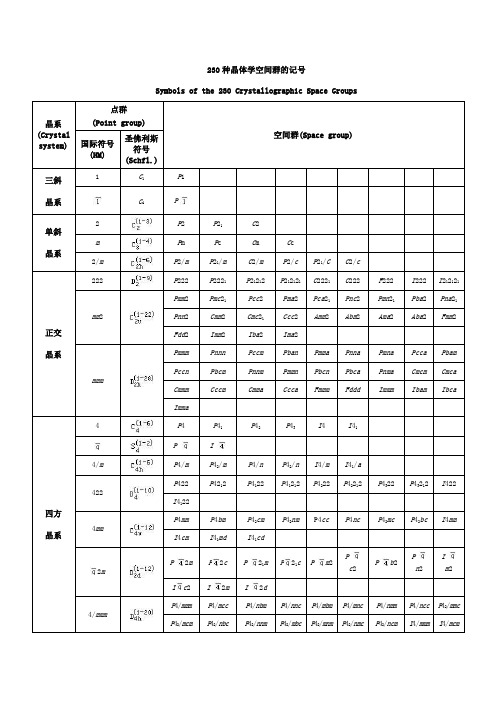
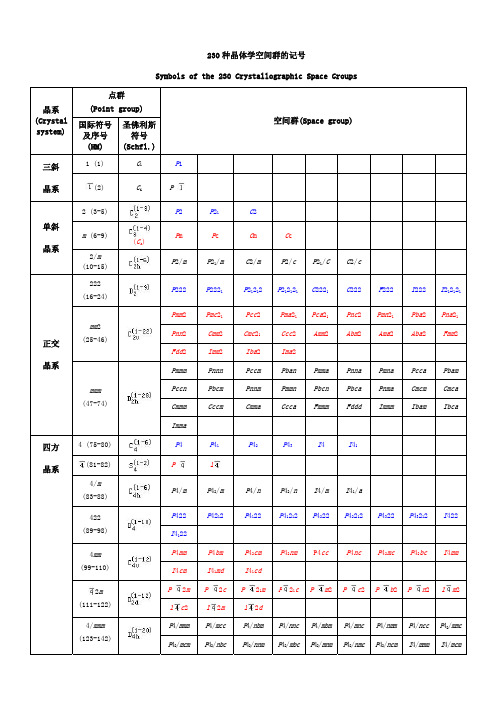
230种晶体学空间群的记号
Symbols of the 230 Crystallographic Space Groups
2m 2P P 2m b n
I c22
m 11m P R c m2
m c2
3m 33I P3
I
m m n Pm Pn Fm Fm Fd m
Fd
m d
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个,它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群。
不同晶系的晶格类型
32种晶体学点群的记号
2m
m m
m2
m
(4)
3m 3(3)
m
m (4)
点群不存在平移操作,所有的对称要素都集中在一个共同的点上。
对称要素包括旋转、反映、反伸(对称中心)与旋转反伸。
有这4个对称要素组合出32个点群。
下表中“轴向对称要素的方向和数目”的圆括号内数据代表该对称要素的数目。
正多面体的数学和结晶学参数
Mathematic and Crystallographic Parameters of Regular Polyhedrons
常见单质的所属晶系
常见矿石的名称、分子式与所属晶系
Names, Molecular Formulas and Crystal Systems of Common Ores。
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系(DOC)
230种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups2m 2P P 2m bI c22m 11m P R m c m2m c23m 33I P3Im m n Pm Pn Fm Fm Fd mFdm d空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个,它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群。
菱方是不标准的说法,应该是三方,菱面体是三方的R点阵中的一种,7个晶系分别是立方cubic(a=b=c,α=β=γ=90o,只有一个晶胞参数a)四方tetragonal(a=b≠c,α=β=γ=90o,有2个晶胞参数a和b)六方hexagonal(a=b≠c,α=β=90o,γ=120o,有2个晶胞参数a和c)正交orthorhombic(a≠b≠c,α=γ=90o,有3个晶胞参数a,b和c)单斜monoclinic(a≠b≠c,α=γ= 90o,β≠90o,有4个晶胞参数a,b,c和β)三斜triclinic(a≠b≠c,α≠β≠γ,有6个晶胞参数a,b,c,α,β和γ)三方(a=b≠c,α=β=90o,γ=120o,有2个晶胞参数a和c) rhombohedral对于三方这个问题,很多书上都是错误的,三方跟六方绝对不能混为一谈F is face-centered;P is Primitive; I is body-centered;不同晶系的晶格类型32种晶体学点群的记号2mm mm2m(4)3m 3(3)mm (4)点群不存在平移操作,所有的对称要素都集中在一个共同的点上。
对称要素包括旋转、反映、反伸(对称中心)与旋转反伸。
230种晶体学空间群的记号
晶系
(2)
Ci
P
2 (3-5)
P2
P21
C2
单斜
m (6-9)
Pm
Pc
Cm
Cc
(Cs)
晶系
2/m (10-15)
P2/m
P21/m
C2/m
P2/c P21/C C2/c
222 (16-24)
P222
P2221
P21212 P212121 C2221
C222
F222
I222 I212121
正交 晶系
mm2 (25-46)
m (200-206)
432 (207-214)
3m (215-220)
mm (221-230)
(C6h)
I41/amd I41/acd
P3
P31
P32
R3
P
R
P312
P321
P3112
P3121 P3212 P3221
R32
P3m1
P31m
P3c1
P31c
R3m
R3c
P 1m P 1c P m1 P c1 R m R c
Pmm2
Pmc21
Pcc2
Pma21 Pca21 Pnc2 Pmn21 Pba2 Pna21
Pnn2
Cmm2
Cmc21
Ccc2 Amm2 Abm2 Ama2 Aba2 Fmm2
Fdd2
Imm2
Iba2
Ima2
Pmmm
Pnnn
Pccm
Pban Pmma Pnna Pmna Pcca Pbam
mmm (47-74)
P6
P61
P65
