第七周自测《旋转之求线段最值》
一道与旋转有关的动点最值问题的探究

试题研究2023年10月下半月㊀㊀㊀一道与旋转有关的动点最值问题的探究◉湖北省武汉市吴家山第二中学㊀李幽兰㊀㊀初中平面几何中,由图形运动而产生的最值问题历来是学生解题的难点,究其原因是图形一直在变化,学生无法捕捉到运动变化背后 不变 的元素,难以分析出取最值时变化元素的位置,也就无法根据具体图形分析求解[1].其中,与旋转有关的动点求最值问题,热度一直高居不下,近几年常 驻 各地中考选填题和几何综合题的压轴位置,令莘莘学子头疼畏惧.下面笔者分享一道题目的解法和变式的深入探究,希望给读者一点启发.图1题目㊀(武汉蔡甸2021 第10题)如图1,在平面直角坐标系中,Q 是直线y =-12x +2上的一个动点,将Q 绕点P (1,0)顺时针旋转90ʎ,得到点Q ᶄ,连接O Q ᶄ,则O Q ᶄ的最小值为(㊀㊀).A.455㊀㊀㊀B .5㊀㊀㊀C .523㊀㊀㊀D.655图2解法1:(坐标法)分别过点Q和Q ᶄ作x 轴的垂线,垂足分别为点M 和N ,如图2.于是øQ M P =øP N Q ᶄ=90ʎ,则øP Q ᶄN +øN P Q ᶄ=90ʎ.因为øQ P Q ᶄ=øQ P M +øN P Q ᶄ=90ʎ,则øP Q ᶄN =øQ P M .又P Q =Q ᶄP ,所以әP M Q ɸәQ ᶄN P (A A S ).故P M =Q ᶄN ,Q M =P N .设Q (a ,-12a +2).因为P (1,0),所以P M =Q ᶄN =a -1,Q M =P N =-12a +2.于是O N =O P +P N =3-12a .所以Q ᶄ(3-12a ,1-a ).所以O Q ᶄ=O N 2+Q ᶄN 2=(3-12a)2+(1-a )2=54(a -2)2+5ȡ5.故选答案:B .点评:解法1抓住平面直角坐标系中的有利条件,构造了 一线三垂直 模型证三角形全等.首先设未知数表示出动点Q 的坐标,用坐标来表示线段长度进行转化,然后由勾股定理表示两点之间的距离,用含x 的式子将O Q ᶄ表示出来,最后运用二次函数的知识求出最值.这种方法虽然很巧妙㊁简便,但是有一定的局限性,只能用于有坐标系且旋转角度特殊的题目.图3解法2:(轨迹法)如图3,将әA O B 绕点P 顺时针旋转90ʎ得到әA ᶄO ᶄB ᶄ,则Q ᶄ为直线A ᶄB ᶄ上一动点,根据垂线段最短,O Q ᶄ的最小值为点O 到直线A ᶄB ᶄ的垂线段的长度d .由直线A B 的解析式为y =-12x +2,得A (0,2),B (4,0),所以O A =2,O B =4.由题意,得O ᶄ(1,1),A ᶄ(3,1),B ᶄ(1,-3).设直线A ᶄB ᶄ的解析式为y =k x +b ,则有3k +b =1,k +b =-3,{解得k =2,b =-5.{于是直线A ᶄB ᶄ的解析式为y =2x -5,则E (52,0),F (0,-5),故O E =52,O F =5.所以E F =O E 2+O F 2=(52)2+52=552.由S әO E F =12O E O F =12E F d ,得O Q ᶄ的最小值为O E O F E F =52ˑ5552=5.点评:解法2由旋转的本质出发,直线A B 绕点P顺时针旋转90ʎ所得直线A ᶄB ᶄ即为动点Q ᶄ的轨迹,但直接求直线A ᶄB ᶄ的解析式不方便,因此旋转整个әA O B ,先求出点A ᶄ和B ᶄ的坐标,再求直线A ᶄB ᶄ的解析式,最后用面积法求出点O 到直线A ᶄB ᶄ的距离.85Copyright ©博看网. All Rights Reserved.2023年10月下半月㊀试题研究㊀㊀㊀㊀当然,在求出了直线A ᶄB ᶄ的解析式后,也可以由此设Q ᶄ的坐标,用解法1中的坐标法,运用勾股定理和二次函数来求最值.解法2适用于大部分的动点旋转求最值问题,即先确定动点轨迹.图4解法3:(逆向轨迹法)O Q ᶄ的最小值其实是定点O 到直线y =-12x +2绕点P 顺时针旋转90ʎ所得到直线的距离,问题可转化为O ᶄ(1,-1)(由点O 绕点P 逆时针旋转90ʎ得到)到直线y =-12x +2的距离d .如图4,过点O ᶄ(1,-1)作O ᶄA 垂直于x 轴交直线y =-12x +2于点A ,O ᶄB 垂直于y 轴交直线y =-12x +2于点B .于是A (1,32),B (6,-1),所以O ᶄA =52,O ᶄB =5.故A B =O ᶄA 2+O ᶄB 2=(52)2+52=552.由S әA O ᶄB =12O ᶄA O ᶄB =12A B d ,得O ᶄQ 的最小值为O ᶄA O ᶄBA B=5,即为O Q ᶄ的最小值.点评:解法3在求O ᶄQ 的最小值时同样可以用解法1的坐标法来求,在本质上它与解法2是一样的,都是将所求最值转化成定点到定直线的距离,但是解法3对解法2进行了简化,免去了求直线y =-12x +2旋转后的直线解析式,直接旋转定点O ,思路新颖巧妙.变式1㊀在R t әA O B 中,O A =2,A B =4,P 是O B 上一点,O P =1,Q 是边A B 上的一个动点,将Q 绕点P 逆时针旋转30ʎ得到点Q ᶄ,连接O Q ᶄ,则O Q ᶄ的最小值为.图5解析:点Q 在A B 上运动,即点Q 的轨迹为A B ,那么将A B 绕点P 旋转就能得到点Q ᶄ的轨迹.于是,将әA O B 绕点P 逆时针旋转30ʎ得到әA ᶄO ᶄB ᶄ,如图5,则点O 到A ᶄB ᶄ的距离即为O Q ᶄ的最小值.由旋转,得øB P B ᶄ=30ʎ.在R t әA O B 中,O A =2,A B =4,所以øB =øB ᶄ=øB P B ᶄ=30ʎ,于是A ᶄB ᶄʊO B ,则øA E B ᶄ=øA O B =90ʎ.所以点O 到A ᶄB ᶄ的距离为O E 的长度.如图5,过点B ᶄ作B ᶄF ʅO B 于点F ,则øB ᶄF P =90ʎ,于是四边形O E B ᶄF 是矩形.由O B =A B 2-O A 2=42-22=23,O P =1,得B P =B ᶄP =23-1.øB ᶄF P =90ʎ,øB P B ᶄ=30ʎ,所以B ᶄF =12B ᶄP =23-12.故O Q ᶄ的最小值为O E =23-12.变式1没有坐标系背景,显然解法1不适用,而运用解法3,将点O 绕点P 顺时针旋转30ʎ以后再求O ᶄ到A B 的距离较为麻烦,经对比发现,此题解法2是最简便的.类似地,还可以变化图形形状和旋转角度,解法一样.图6变式2㊀如图6,在等腰三角形A B C 中,øB A C =120ʎ,A B =A C ,D 是AB 上一点,A D =2,B D =4,E 是边BC 上的动点,若点E 绕点D 逆时针旋转30ʎ的对应点是F ,连C F ,则C F 的最小值是.基于以上分析,我们可以总结:解决这类绕定点旋转的最值问题有三种方法,分别为坐标法㊁轨迹法㊁逆向轨迹法,根据不同的题目来选择合适的方法,最常用的是轨迹法.若是动点所在的直线绕定点旋转,则先确定动点旋转后的轨迹,再根据垂线段最短求点到直线的距离,最后解直角三角形得到所求最值.动态问题解题的关键是在 动 中寻找 定 的量,再由这些定量探寻出动点形成的轨迹,从而根据轨迹分析出最值位置,即 由动寻定,由定定轨,由轨求最 [2].题目只是知识方法的一个素材,解题的过程能让学生理解知识的原理,提炼方法的本质,注重解法的策略,总结问题的归类,从而达到利用有限的题目实现无限的再创造.由解一道题变成会解一类题,乃至通解一种体系的题,这也是解题教学的方向[1].参考文献:[1]郭源源.旋转位似 似 成双定点定形 轨 一致[J ].教学月刊 中学版(教学参考),2020(10):11G15.[2]郭源源. 定量 构建动点轨迹 隐圆 巧解最值问题[J ].中学数学杂志,2018(10):42G44.Z95Copyright ©博看网. All Rights Reserved.。
中考数学复习:旋转之求线段最值
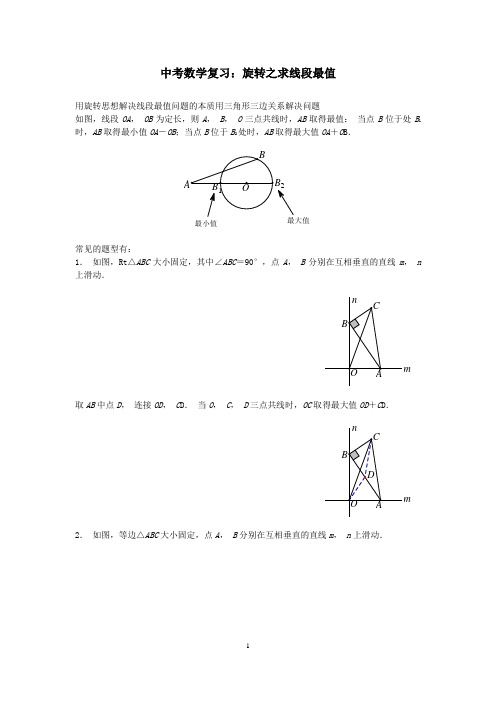
中考数学复习:旋转之求线段最值用旋转思想解决线段最值问题的本质用三角形三边关系解决问题如图,线段OA,OB为定长,则A,B,O三点共线时,AB取得最值:当点B位于处B1时,AB取得最小值OA-OB;当点B位于B2处时,AB取得最大值OA+O B.最小值常见的题型有:1.如图,Rt△ABC大小固定,其中∠ABC=90°,点A,B分别在互相垂直的直线m,n 上滑动.m取AB中点D,连接OD,C D.当O,C,D三点共线时,OC取得最大值OD+C D.Arraym2.如图,等边△ABC大小固定,点A,B分别在互相垂直的直线m,n上滑动.m取AB中点D,连接OD,C D.当O,C,D三点共线时,OC取得最大值OD+C D.m3.如图,Rt△ABC大小固定,其中∠ABC=90°,点A,B分别在互相垂直的直线m,n 上滑动.取AB中点D,连接OD,C D.当O,C,D三点共线时,OC取得最小值|CD –OD|.m例题讲解例1.已知Rt△ABC中,∠ACB=90°,tan∠BAC=12.若BC=6,点D在边AC的三等分点处,将线段AD绕A点旋转,E始终为BD的中点,求线段CE长度的最大值.解:在Rt△ABC中,AC=tan BCBAC=12,AB=①如图1,当AD=13AC时,取AB的中点F,连接EF和CF,则CF=12AB=,EF=12AD=2.所以当且仅当C,E,F三点共线且点F在线段CE上时,CE最大,此时CE=CF+EF=2+图1②如图2,当AD=23AC时,同理可得CE的最大值为4+.综上可得,当点D在靠近点C的三等分点处时,线段CE的长度的最大值为4+图2例2 以平面上一点O 为直角顶点,分别画出两个直角三角形,记作△AOB 和△COD ,其中∠ABO =30°.如图,若BO=N 在线段OD 上,且NO =2,P 是线段AB 上的一个动点,在将△AOB 绕点O 旋转的过程中,线段PN 长度的最小值为________,最大值为________.BCDPNO A-2;2. 过点O 作OE ⊥AB 于点E ,则OE =12OB.故当点P 在点E 处时,OP;当点P 在点B 处时,OP长度取最大值A O NPDBCE①当△AOB 绕点O 旋转到O ,E ,D 三点共线,且点E 在线段OD 上时,PN 取最小值,即OE -ON-2;D②当△AOB 绕点O 旋转到O ,B ,D 三点共线,且点B 在线段DO的延长线上时,PN 取最大值,OB +ON =2.所以线段PN 长度的最小值为-2,最大值为2.D进阶训练1. 已知△AOB 和△COD 是等腰三角形,其中BA =BO =2,CD =CO =3,∠ABO =∠DCO .连结AD ,BC ,M ,N 分别为OA ,BC 的中点.若固定△AOB ,将△COD 绕点O 旋转,求MN 的最大值.NMABCDO【答案】52. 【提示】如图,取OB 的中点E ,连结EM ,EN ,则EM ,EN 为定值,当点E 在线段MN 上时,MN 取最大值.EODCBAM N2. 已知:在Rt △ABC 中,∠BAC =90°,AC =AB =4,D ,E 分别是AB ,AC 的中点.若等腰Rt △ADE 绕点A 旋转,得到等腰Rt △AD 1E 1,记直线BD 1与CE 1的交点为P . (1)设BC 的中点为M ,求线段PM 的长; (2)求点P 到AB 所在直线的距离的最大值.E 1D 1A BC DEP【答案】(1)2)1【提示】(1)易证△E 1AC ≌△D 1AB ,所以∠E 1CA =∠D 1BA ,从而可得∠BPC =∠BAC =90°,所以PM =12BC=MPEDC BA D 1E 1(2)由题意知,点D1,E1在以A为圆心、AD为半径的圆上,而点P在直线BD1上,所以当直线BD1与⊙A相切时,点P到AB的距离最大.此时四边形AD1PE1是正方形,即PD1=AD1=2.如图,作PG⊥AB于点G,解Rt△PGB即可.B3.已知:正方形ABCD的边长为1,P为正方形内的一个动点,若点M在AB延长线上,且满足△PBC∽△PAM,延长BP交AD的延长线于点N,连结CM,是否存在满足条件的点P,使得PC=12?请说明理由.ACDPN【答案】不存在满足条件的点P,使得PC=12.【提示】因为△PBC∽△PAM,可得∠ABP+∠PAM=∠ABP+∠PBC=90°,所以AP⊥BN.以AB为直径,作半圆O,连结OC,OP,则OP+PC≥OC,从而PC件的点P,使得PC=12.ONPD CA。
旋转中的最值问题

旋转中的最值问题 Revised at 2 pm on December 25, 2020.
A
旋转中的最值问题
1.已知,线段AB=6,线段AC=4,将线段AC 绕A 旋转,则线段BC 的最大值为 10 最小值为 2 。
2. 如图,在△ABC 中,∠C=90°,AC=4,BC=2,点A 、C 分别在x 轴、y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动,在运动过程中,求点离是。
找AC 中点D,O 、B 、D 三点共线时,OB 最长 3.如图,已知△ABC 中,∠ACB=90°,P 满足CP 绕C 顺时针旋转90°得到线段CD ,连DA 、DB 、PB 。
求BD 的最大值最小值。
最大:根号
最小:根号10 4.如图,已知△ABC 中,∠ACB=90°,BC=6,AC=12,点D 在,将线段AD 绕点A 旋转,D 点对应点为'D ,连接'BD ,点F 为,线段CF 的最大值为多少?
5.如图,PA=2,PB=4,以AB 为一边作正方形ABCD ,使P 、AB 的两侧,当∠APB 变化时,求PD 的最大值。
6.如图,在Rt △POQ 中,OP=OQ=4,M 是PQ M
处,以M 为旋转中心,旋转三角尺,三角尺的两直角边与△点A 、B 。
(1)求证:MA=MB ; (2)连接AB ,探究:在旋转三角尺的过程中,求△AOB。
初中数学几何旋转最值最短路径问题专题训练

初中数学几何旋转最值最短路径问题专题训练专练3 最短路径模型——旋转最值类基本模型图:【典例1】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连结B′D,则B′D的最小值是().A. B.6 C. D.4【思路探究】根据E为AB中点,BE=B′E可知,点A、B、B′在以点E为圆心,AE长为半径的圆上,D、E为定点,B′是动点,当E、B′、D三点共线时,B′D的长最小,此时B′D=DE-EB′,问题得解.【解析】∵AE=BE,BE=B′E,由圆的定义可知,A、B、B′在以点E为圆心,AB长为直径的圆上,如图所示. B′D的长最小值= DE-EB′.故选A.22-=-【启示】此题属于动点(B′)到一定点(E )的距离为定值(“定点定长”),联想到以E 为圆心,EB′为半径的定圆,当点D 到圆上的最小距离为点D 到圆心的距离-圆的半径.当然此题也可借助三角形三边关系解决,如,当且仅当点E 、B′、D 三点共线B D DE B E ''≤-时,等号成立.【典例2】如图,E 、F 是正方形ABCD 的边AD 上两个动点,满足AE =DF ,连接CF 交BD 于点G ,连结BE 交AG 于点H ,若正方形的边长是2,则线段DH 长度的最小值是.【思路探究】根据正方形的轴对称性易得∠AHB =90°,故点H 在以AB 为直径的圆上.取AB 中点O ,当D 、H 、O 三点共线时,DH 的值最小,此时DH =OD -OH ,问题得解.【解析】由△ABE ≌△DCF ,得∠ABE =∠DCF ,根据正方形的轴对称性,可得∠DCF =∠DAG ,∠ABE =∠DAG ,所以∠AHB =90°,故点H 在以AB 为直径的圆弧上.取AB 中点O ,OD 交⊙O 于点H ,此时DH 最小,∵OH =,OD =,∴DH 的最小值为112AB=OD -OH .1【启示】此题属于动点是斜边为定值的直角三角形的直角顶点,联想到直径所对圆周角为直角(定弦定角),故点H 在以AB 为直径的圆上,点D 在圆外,DH 的最小值为DO -OH .当然此题也可利用的基本模型解决.DH OD OH ≤-【针对训练 】1. 如图,在△ABC 中,∠ACB =90°,AC =2,BC =1,点A ,C 分别在x 轴,y 轴上,当点A 在轴正半轴上运动时,点C 随之在轴上运动,在运动过程中,点B 到原点O 的最大x y 距离为( ).ABC .D .312.如图,在矩形ABCD 中,AB =4,BC =6,E 是矩形内部的一个动点,且AE ⊥BE ,则线段CE 的最小值为().A . B. C. D.4323. 如图,在△ABC 中,AB =10,AC =8,BC =6,以边AB 的中点O 为圆心,作半圆与AC 相切,点P 、Q 分别是边BC 和半圆上的运点,连接PQ ,则PQ 长的最大值与最小值的和是( ).A.6B.C.9D.1+3224.如图,AC =3,BC =5,且∠BAC =90°,D 为AC 上一动点,以AD 为直径作圆,连接BD 交圆于E 点,连CE ,则CE 的最小值为().A. B. C.5 D.213-213+9165.如图,已知正方形ABCD 的边长为2,E 是BC 边上的动点,BF ⊥AE 交CD 于点F ,垂足为G ,连结CG ,则CG 的最小值为().A B 11-1-1+6.如图,△ABC 、△EFG 是边长为2的等边三角形,点D 是边BC 、EF 的中点,直线AG 、FG 相交于点M ,当△EFG 绕点D 旋转时,线段BM 长的最小值是A . B21+1-7.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是.8.如图,△ABC为等边三角形,AB=2,若点P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为.。
九年级上学期数学旋转中的最值问题

九年级数学——旋转中的最值问题
1、如图,已知PA=2,PB=4,以AB为边作正方形ABCD,连PD,
且P、D在直线AB的两侧,当∠APB变化时,求PD的最大值。
2、如图△ABC中,AB=5,AC=3,以BC为边作等腰Rt△BCD,且∠BDC=90°,当BC的长度发生变化时,求出线段AD的取值范围。
3、在△PAB
中,,PB=1,以AB为边作正方形ABCD,
则PD的最小值是,PC的最大值是。
4、如图,点M是正方形ABCD对角线上的一点,当AM+BM+CM 的最小值为时,求正方形的边长。
5、Rt△ACB中,∠ACB=90°,,BC=4,P在△ACB的内部,且∠APC=120°,求的最小值。
6、如图,已知线段AB=4,C为AB的中点,CM=1,CM在
平面内绕C点逆时针旋转角(),以BM为边作
等腰直角三角形,使得PM=BM,∠PMB=90°,求AP的最
小值。
A B。
中考数学模型--旋转综合之线段最值问题

旋转综合之线段最值问题初三中考复习在即,在数学中考中,几何变换往往是中考中最令人头痛的题型,其辅助线的添加非常灵活,和其他几何知识的综合性也非常强。
在几何变换中,旋转是最为常见、也是最为重要的变换,本周我们集中讲解旋转综合中常见的模型、题型,这部分是本期内容的第五讲:旋转综合之利用旋转求线段最值,希望各位同学能从中收益。
利用旋转求线段最值的解题方法1. 使目标线段与定长线段放在三角形中,根据三角形三边关系,当三点共线时,取得最值;如图所示,当点 B 位于 B 1 时, AB 取得最小值| OA - OB | ;当点 B 位于 B 2 时, AB 取得最大值OA + OB .2. 把线段或线段和差放到同一条直线上,根据两点之间,线段最短来求最值.如图所示,定线段 OA = a , Rt △BOC 中直角边 OB = b ,锐角∠B = θ ,点 P 是斜边 BC 上的一个动点,Rt △BOC 在绕点O 旋转的过程中, AP 的最值如下:①如图,当OP ⊥ BC ,且O , A , P 三点共线时, AP 取得最小值| OB ⋅ sin θ - OA |;②如图,当 B , P 重合,且O , A , P 三点共线时, AP 取得最大值| OB + OA |例1 如图,在△ABC 中,∠C = 90︒,AC = 4 ,BC = 2 ,点A , C 分别在x 轴、y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动,在运动过程中,点B 到原点的最大距离是.答案 2 2 + 2 .解析作AC 的中点M ,连接OM , BM .由OB… OM +BM ,可得当O ,M ,B 三点共线且点M 在线段OB 上时,OB 取得最大值.此时OB =OM +BM = 2 + 2 2.例 2 已知,△A OB和△COD 是等腰三角形,其中BA=B O=2,CD =CO = 3 ,∠ABO=∠DCO.连接AD , BC,点M, N分别为OA, BC的中点.若固定△AOB,将△C O D绕点O 旋转,求MN 的最大值.解 取OB 的中点 E ,连接 EM , EN .则ME= 1 AB = 1,NE = 1 CO = 3.2 2 2当 M , E , N 三点共线,且点 E 在线段 MN 上时, MN 取最大值,最大值为 ME + NE = 5.2例 3 在Rt △ABC 中, ∠ACB = 90︒ , tan ∠BAC = 1.若2BC = 6 ,点 D 在边 AC 的三等分点处,将线段 AD 绕点 A 旋转,点 E 始终为 BD 中点,求线段CE 长度的最大值.解 在Rt △ABC 中,AC =BCtan ∠BAC= 12, AB = 6 5.①如图,当 AD = 1AC 时,取 AB 的中点 F ,连接 EF 和CF .3则CF =1AB = 3 5, EF =1AD = 2.2 2所以当且仅当C , E , F 三点共线且F 在线段CE 上时CE 最大,此时CE =CF +EF = 2 + 3 5.②如图,当时,同理可得CE 的最大值为4 + 3AD =2AC3.综合可得,当点D 在靠近点C 的三等分点时,线段CE 的长度取得最大值为4 + 3 .旋转变换是中考中非常重要的题型,本节课我们重点讲解了旋转中求线段最值问题,到此为止,本周我们共讲解了有关旋转的五种常见考题,希望各位同学多加体会、总结,平时遇到类似题目注意应用和练习。
2020重庆中考复习利用旋转法解几何最值问题应用举例

利用旋转法解几何最值问题应用举例例1、在平面直角坐标系中,已知点A (4,0),点B 为y 轴正半轴上一个动点,连接AB ,以AB 为一边向下作等边△ABC ,连结OC ,则OC 的最小值为 .M解:如图,将△ABO 绕点A 逆时针旋转60°得△AACM ,并延长MC 交x 轴于点N .则点C 在直线MN 上运动,当OC ⊥MN 时,OC 最小,∴OC =AM =2,则OC 的最小值为2.例2、如图,PA =2,PB =4,将线段PA 绕P 点旋转一周,以AB 为边作正方形ABCD ,则PD 的最大值为 .解:将△PAD 绕点A 顺时针旋转90°得到△P 'AB ,PD 的最大值即为P 'B 的最大值,∴PA =PA ',∠PAP '=90°∴PP '=PA =2 ∵△P 'PB 中,P 'B <PP '+PB ,PP ′=PA =2,PB =4,且P 、D 两点落在直线AB 的两侧,∴当P '、P 、B 三点共线时,P 'B 取得最大值(如图)此时P 'B =PP '+PB =2+4,即P 'B 的最大值为2+4. 例3、(2019•马鞍山二模)如图,在等腰直角△ABC 中,∠BAC =90°,点D 是△ABC 所在平面上一点,且满足DB =3,DA =5,则CD 的最小值为( )A . B. C .2 D .1解:将△ADC绕点A顺时针旋转90°,得到△ABE.则CD=BE,△ADE是等腰直角三角形,ED=5.∵AE、AD、BD都是定值,∴当E、B、D三点共线时,BE最小,即CD最小.此时BE最小值为DE﹣BD=5﹣3.故选:A.例4、如图,平行四边形ABCD中,∠B=60°,BC=12,AB=10,点E在AD上,且AE=4,点F是AB上一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为 .解:将线段AE绕点E逆时针旋转120°得到EH,连接HG,过点H作HM⊥AD, ∵四边形ABCD是平行四边形,∴∠A+∠B=180°,∴∠A=120°,∵将线段AE绕点E逆时针旋转120°得到EH,将线段EF绕点E逆时针旋转120°得到EG, ∴EF=EG=4,AE=EH,∠AEH=∠FEG=120°,∴∠DEH=60°,∠AEF=∠HEG,且EF=EG,AE=EH,∴△AEF≌△HEG(SAS)∴∠A=∠EHG=120°=∠AEH,∴AD∥HG,∴点G的轨迹是过点H且平行于AD的直线, ∴当DG⊥HG时,线段GD长度有最小值,∵∠HEM=60°,EH=4,HM⊥AD,∴EM=2,MH=EM=2,∴线段GD长度的最小值为2,例5、(2019•宿迁)如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .解:由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动 将△EFB绕点E旋转60°,使EF与EG重合,得到△EFB≌△EHG,从而可知△EBH为等边三角形,点G在垂直于HE的直线HN上,作CM⊥HN,则CM即为CG的最小值,作EP⊥CM,可知四边形HEPM为矩形,则CM=MP+CP=HE+EC=1+=,故答案为.例6、如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边AB上的一个动点将线段EF 绕着点E逆时针旋转60°得到EG,连接BG、CG,则BG+CG的最小值为( )A.3 B.2 C.4 D.2+2解:如图,取AB的中点N.连接EN,EC,GN,作EH⊥CD交CD的延长线于H. ∵四边形ABCD是菱形,∴AD=BD,∵AE=ED,AN=NB,∴AE=AN,∵∠A=60°,∴△AEN是等边三角形,∴∠AEN=∠FEG=60°,∴∠AEF=∠NEG,∵EA=EN,EF=EG,∴△AEF≌△NEG(SAS),∴∠ENG=∠A=60°,∵∠ANE=60°,∴∠GNB=180°﹣60°﹣60°=60°,∴点G的运动轨迹是射线NG,易知B,E关于射线NG对称, ∴GB=GE,∴GB+GC=GE+GC≥EC,在Rt△DEH中,∵∠H=90°,DE=2,∠EDH=60°,∴DH=DE=1,EH=,在Rt△ECH中,EC==2,∴GB+GC≥2,∴GB+GC的最小值为2.故选:B.例7、如图,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,则线段AN的最大值为 .解:如图,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP, 则△APM是等腰直角三角形,∴MA=MP=2,BP=AN,∴PA=2,∵AB=6,∴线段AN长的最大值=线段BP长的最大值,∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=6+2.例8、(2019•龙岩一模)如图,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA,PB,PC,则PA+PB+PC的最小值为 .解:如图,将△ABP绕着点B逆时针旋转60°,得到△DBE,连接EP,CD,∴△ABP≌△DBE∴∠ABP=∠DBE,BD=AB=4,∠PBE=60°,BE=PE,AP=DE,∴△BPE是等边三角形∴EP=BP∴AP+BP+PC=PC+EP+DE,∴当点D,点E,点P,点C共线时,PA+PB+PC有最小值CD ∵∠ABC=30°=∠ABP+∠PBC,∴∠DBE+∠PBC=30°,∴∠DBC=90°,∴CD==, 练习1、(2019•常熟市二模)已知x轴上一点A(1,0),B为y轴上的一动点,连接AB,以AB为边作等边△ABC如图所示,已知点C随着点B的运动形成的图形是一条直线,连接OC,则AC+OC的最小值是 .解:将△ABO绕点A逆时针旋转60°得△ACD,并作直线CD,延长AD交y轴于点A'.∵等边△ABC、等边△AOD,∴AB=AC,AO=AD,∠BAC=∠OAD=60°∴∠BAC﹣∠OAC=∠OAD﹣∠OAC,∴∠BAO=∠CAD在△BAO和△CAD中,∴△BAO≌△CAD(SAS),∴∠AOB=∠ADC∵∠AOB=90° ∴∠ADC=90°,∴CD⊥AD,∴点C随着点B的运动形成的图形是直线CD∵∠AOA'=90°,∠OAD=60°∴∠AA'O=30°∴OA=AA' ∴AD=OA=AA'∴点D是AA'的中点,∵CD⊥AD,∴CD是AA'的中垂线 ∴AC=A'C,∴AC+OC=A'C+OC又∵点C在直线CD上运动,所以点O、C、A'三点共线时,A'C+OC的值最小,最小值为OA'的长.在R△AOA'中,∠AOA'=90°,∠OAD=60°,OA=1,O A'=OA=,∴AC+OC的最小值为.2、已知:AD=2,BD=4,以AB为一边作等边三角形ABC.使C、D两点落在直线AB的两侧.当∠ADB变化时,则CD的最大值 .解:把△ADC绕点A顺时针旋转60°得到△AEB,则AE=AD,BE=DC,∠EAD=60°, ∴△ADE为等边三角形,∴DE=DA=2,∠ADE=60°,当E点在直线BD上时,BE最大,最大值为2+4=6,∴CD的最大值为6.3、如图,在等腰直角△ABC中,∠BAC=90°,点D是△ABC所在平面上一点,且满足DB=6,DA=10,则CD的最小值为解:将△ADC绕点A顺时针旋转90°,得到△ABE.则CD=BE,△ADE是等腰直角三角形,ED=10.∵AE、AD、BD都是定值,∴当E、B、D三点共线时,BE最小,即CD最小.此时BE最小值为DE﹣BD=10﹣5.故选:A.4、如图,平行四边形ABCD中,∠B=60°,BC=6,AB=5,点E在AD上,且AE=2,点F是AB上一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为 .解:将线段AE 绕点E 逆时针旋转120°得到EH ,连接HG ,过点H 作HM ⊥AD ,∵四边形ABCD 是平行四边形,∴∠A +∠B =180°,∴∠A =120°,∵将线段AE 绕点E 逆时针旋转120°得到EH ,将线段EF 绕点E 逆时针旋转120°得到EG , ∴EF =EG ,AE =EH ,∠AEH =∠FEG =120°,∴∠DEH =60°,∠AEF =∠HEG ,且EF =EG ,AE =EH ,∴△AEF ≌△HEG (SAS )∴∠A =∠EHG =120°=∠AEH ,∴AD ∥HG ,∴点G 的轨迹是过点H 且平行于AD 的直线, ∴当DG ⊥HG 时,线段GD 长度有最小值,∵∠HEM =60°,EH =2,HM ⊥AD ,∴EM =1,MH =,∴线段GD 长度的最小值为,5、如图,长方形 ABCD 中,AB=3,BC=4,E 为 BC 上一点,且 BE =2,F 为 AB 边上的一个动点,连接 EF ,将 EF 绕着点 E 顺时针旋转 45˚到 EG 的位置,连接 FG 和 CG ,则 CG 的最小值为 .F解:由题意可知,点F 是主动点,点G 是从动点,点F 在线段上运动,点G 也一定在直线轨迹上运动,将△EFB 绕点E 旋转45°,使EF 与EG 重合,得到△EFB ≌△EHG ,从而可知△EBH 为等腰直角三角形,点G 在垂直于HE 的直线HG上,作CM ⊥HG ,则CM即为CG 的最小值,作EN ⊥CM ,可知四边形HENM 为矩形,则CM =MN +CN =HE =12 6、(2019秋•海曙区校级月考)如图,菱形ABCD 的边长是6,∠A =60°,E 是AD 的中点,F 是AB 边上一个动点,EG =EF 且∠GEF =60°,则GB +GC 的最小值是AA解:取AB的中点H,连接HG、HE、HG、BE、CE,则△AEF≌△HEG∴∠GHE=∠A=60°,∴HG∥AD,可知△BHG≌△EHG,∴BG=GE,∴CE的长就是GB+GC的最小值;在Rt△EBC中,EB=3,BC=6,∴EC=3,∴GB+GC的最小值3.7、如图,AB=8,点M为线段AB外一个动点,且AM=4,MB=MN,∠BMN=90°,则线段AN的最大值为.解:如图,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP, 则△APM是等腰直角三角形,∴MA=MP=4,BP=AN,∴PA=4,∵AB=8,∴线段AN长的最大值=线段BP长的最大值,∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=8+4.8、(2019秋•蔡甸区期中)如图,在△ABC中,∠ABC=60°,AB<AC,点P是△ABC内一点,AB=6,BC=8,则PA+PB+PC的最小值是 .解:如图,将△PBF绕点B逆时针旋转60°得到△BFE,作EH⊥CB交CB的延长线于H. ∵∠ABC=60°,∠PBF=60°,∵∠ABP=∠EBF,∴∠EBF+∠BC=60°,∴∠EBC=120°, ∵PB=BF,∠PBF=60°,∴△PBF是等边三角形,∴PB=PF,∵PA=EF,∴PA+PB+PC=CP+PF+EF,根据两点之间线段最短可知,当E,F,P,C共线时,PA+PB+PC的值最小,最小值=EC的长, 在Rt△EBH中,∵∠EBH=60°,EB=6,∴BH=BE•cos60°=3,EH=EB•sin60°=3,∴CH=BH+CB=3+8=11,∴EC===2.。
中考数学压轴题专项汇编专题旋转之求线段最值

专题7 旋转之求线段最值破解策略用旋转思想解决线段最值问题的本质用三角形三边关系解决问题如图,线段OA , OB 为定长,则A , B , O 三点共线时,AB 取得最值: 当点B 位于处B 1时,AB 取得最小值OA -OB ;当点B 位于B 2处时,AB 取得最大值OA +O B .最大值最小值B 1OB 2AB常见的题型有:1. 如图,Rt △ABC 大小固定,其中∠ABC =90°,点A , B 分别在互相垂直的直线m , n 上滑 动.n mO BAC取AB 中点D , 连接OD , C D . 当O , C , D 三点共线时,OC 取得最大值OD +C D .mn D OBAC2. 如图,等边△ABC 大小固定,点A , B 分别在互相垂直的直线m , n 上滑动.mn CO BA取AB 中点D , 连接OD , C D . 当O , C , D 三点共线时,OC 取得最大值OD +C D .n mD CO B A3. 如图,Rt △ABC 大小固定,其中∠ABC =90°,点A , B 分别在互相垂直的直线m , n 上滑动.n OB AC取AB 中点D , 连接OD , C D . 当O , C , D 三点共线时,OC 取得最小值|CD –OD |.mn D OB AC例题讲解例1.已知Rt△ABC中,∠ACB=90°,tan∠BAC=12.若BC=6,点D在边AC的三等分点处,将线段AD绕A点旋转,E始终为BD的中点,求线段CE长度的最大值.解:在Rt△ABC中,AC=tan BCBAC=12,AB=①如图1,当AD=13AC时,取AB的中点F,连接EF和CF,则CF=12AB=,EF=12AD=2.所以当且仅当C,E,F三点共线且点F在线段CE上时,CE最大,此时CE=CF+EF=2+图1②如图2,当AD=23AC时,同理可得CE的最大值为4+.综上可得,当点D在靠近点C的三等分点处时,线段CE的长度的最大值为4+图2例2 以平面上一点O 为直角顶点,分别画出两个直角三角形,记作△AOB 和△COD ,其中∠ABO =30°.如图,若BO =33,点N 在线段OD 上,且NO =2,P 是线段AB 上的一个动点,在将△AOB 绕点O 旋转的过程中,线段PN 长度的最小值为________,最大值为________.BCDPNO A解:332-2;33+2. 过点O 作OE ⊥AB 于点E ,则OE =12OB =332.故当点P 在点E 处时,OP 长度取最小值332;当点P 在点B 处时,OP 长度取最大值33.A O NPDBCE①当△AOB 绕点O 旋转到O ,E ,D 三点共线,且点E 在线段OD 上时,PN 取最小值,即OE -ON =332-2; E (P )CDO A BN②当△AOB 绕点O 旋转到O ,B ,D 三点共线,且点B 在线段DO 的延长线上时,PN 取最大值,OB +ON =332.所以线段PN 长度的最小值为33-2,最大值为332.B (P )ODC AN进阶训练1. 已知△AOB 和△COD 是等腰三角形,其中BA =BO =2,CD =CO =3,∠ABO =∠DCO .连结AD ,BC ,M ,N 分别为OA ,BC 的中点.若固定△AOB ,将△COD 绕点O 旋转,求MN 的最大值.NMABCDO【答案】52. 【提示】如图,取OB 的中点E ,连结EM ,EN ,则EM ,EN 为定值,当点E 在线段MN 上时,MN 取最大值.EODCBAM N2. 已知:在R t △ABC 中,∠BAC =90°,AC =AB =4,D ,E 分别是AB ,AC 的中点.若等腰Rt △ADE 绕点A 旋转,得到等腰Rt △AD 1E 1,记直线BD 1与CE 1的交点为P . (1)设BC 的中点为M ,求线段PM 的长; (2)求点P 到AB 所在直线的距离的最大值.E 1D 1A BC DEP【答案】(1)22;(2)13【提示】(1)易证△E 1AC ≌△D 1AB ,所以∠E 1CA =∠D 1BA ,从而可得∠BPC =∠BAC =90°,所以PM =12BC =22. MPEDC BA D 1E 1(2)由题意知,点D 1,E 1在以A 为圆心、AD 为半径的圆上,而点P 在直线BD 1上,所以当直线BD 1与⊙A 相切时,点P 到AB 的距离最大.此时四边形AD 1PE 1是正方形,即PD 1=AD 1=2.如图,作PG ⊥AB 于点G ,解Rt △PGB 即可.G P EDC BA D 1E 13. 已知:正方形ABCD 的边长为1,P 为正方形内的一个动点,若点M 在AB 延长线上,且满足△PBC ∽△PAM ,延长BP 交AD 的延长线于点N ,连结CM ,是否存在满足条件的点P ,使得PC =12?请说明理由. A B CDPMN【答案】不存在满足条件的点P ,使得PC =12. 【提示】因为△PBC ∽△PAM ,可得∠ABP +∠PAM =∠ABP +∠PBC =90°,所以AP ⊥BN .以AB 为直径,作半圆O ,连结OC ,OP ,则OP +PC ≥OC ,从而PC ≥512,所以不存在满足条件的点P ,使得PC =12.O N MPDCB A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
P O
B N
C
D
解: 3 3 -2; 3 3 +2. 2
过点 O 作 OE⊥AB 于点 E,则 OE= 1 OB= 3 3 .
2
2
故当点 P 在点 E 处时,OP 长度取最小值 3 3 ;当点 P 在点 B 处时,OP 长度取最大值 2
3 3.
A E P
O
B N
C
D
①当△AOB 绕点 O 旋转到 O,E,D 三点共线,且点 E 在线段 OD 上时,PN 取最小值,即 OE- ON= 3 3 -2;
B N
MA O
C
D
【答案】 5 . 2
【提示】如图,取 OB 的中点 E,连结 EM,EN,则 EM,EN 为定值,当点 E 在线段 MN 上时,MN 取最大值.
B N
E
A
M O
C
D
2. 已知:在 Rt△ABC 中,∠BAC=90°,AC=AB=4,D,E 分别是 AB,AC 的中点.若等腰 Rt△ADE 绕点 A 旋转,得到等腰 Rt△AD1E1,记直线 BD1 与 CE1 的交点为 P. (1)设 BC 的中点为 M,求线段 PM 的长; (2)求点 P 到 AB 所在直线的距离的最大值.
专题 7《旋转之求线段最值》
破解策略 用旋转思想解决线段最值问题的本质用三角形三边关系解决问题 如图,线段 OA, OB 为定长,则 A, B, O 三点共线时,AB 取得最值: 当点 B 位于处 B1 时, AB 取得最小值 OA-OB;当点 B 位于 B2 处时,AB 取得最大值 OA+OB.
B
n B
O Am
C
取 AB 中点 D, 连接 OD, CD. 当 O, C, D 三点共线时,OC 取得最小值|CD –OD|. n
B D
O
m A
C
2
例题讲解
1 例 1.已知 Rt△ABC 中,∠ACB=90°,tan∠BAC= . 若 BC=6, 点 D 在边 AC 的三等分
2 点处,将线段 AD 绕 A 点旋转,E 始终为 BD 的中点,求线段 CE 长度的最大值.
C
P
E1
E
D1
GA D
B
3. 已知:正方形 ABCD 的边长为 1,P 为正方形内的一个动点,若点 M 在 AB 延长线上,且 满足△PBC∽△PAM,延长 BP 交 AD 的延长线于点 N,连结 CM,是否存在满足条件的点 P,使 得 PC= 1 ?请说明理由.
2
N
D
C】不存在满足条件的点 P,使得 PC= 1 . 2
2. 如图,等边△ABC 大小固定,点 A, B 分别在互相垂直的直线 m, n 上滑动.
1
n B
C
OA
m
取 AB 中点 D, 连接 OD, CD. 当 O, C, D 三点共线时,OC 取得最大值 OD+CD.
n
B C
D
OA
m
3. 如图,Rt△ABC 大小固定,其中∠ABC=90°,点 A, B 分别在互相垂直的直线 m, n 上 滑动.
C
E D1 P
A
D
B
E1
【答案】(1) 2 2 ;(2)1+ 3 . 【提示】(1)易证△E1AC≌△D1AB,所以∠E1CA=∠D1BA,从而可得∠BPC=∠BAC=90°,
5
所以 PM= 1 BC= 2 2 . 2
C
E
M
D1 P
A
D
B
E1
(2)由题意知,点 D1,E1 在以 A 为圆心、AD 为半径的圆上,而点 P 在直线 BD1 上,所以当 直线 BD1 与⊙A 相切时,点 P 到 AB 的距离最大.此时四边形 AD1PE1 是正方形,即 PD1=AD1= 2.如图,作 PG⊥AB 于点 G,解 Rt△PGB 即可.
【提示】因为△PBC∽△PAM,可得∠ABP+∠PAM=∠ABP+∠PBC=90°,所以 AP⊥BN.以 AB 为直径,作半圆 O,连结 OC,OP,则 OP+PC≥OC,从而 PC≥ 5 1 ,所以不存在满足条件
2 的点 P,使得 PC= 1 .
2
6
N
D
C
P
A
O
BM
7
A B1 O
B2
值值值
值值值
常见的题型有: 1. 如图,Rt△ABC 大小固定,其中∠ABC=90°,点 A, B 分别在互相垂直的直线 m, n 上 滑动.
nC B
OA m
取 AB 中点 D, 连接 OD, CD. 当 O, C, D 三点共线时,OC 取得最大值 OD+CD. n C
B D
OA m
A
D
E
C
B
解:在 Rt△ABC 中,AC= BC =12,AB=6 5 . tan BAC
①
1 如图 1,当 AD= AC 时,取 AB 的中点 F,连接 EF 和 CF,
1 则 CF=
AB= 3
5,
3
2
1 EF= AD=2. 所以当且仅当 C, E, F 三点共线且点 F 在线段 CE 上时,CE 最大,
2
O A
N E(P)
B
C
D
②当△AOB 绕点 O 旋转到 O,B,D 三点共线,且点 B 在线段 DO 的延长线上时,PN 取最大值,
OB+ON= 3 3 +2.
所以线段 PN 长度的最小值为 3 3 -2,最大值为 3 3 +2. 2
4
B(P)
O
A
N
C
D
进阶训练 1. 已知△AOB 和△COD 是等腰三角形,其中 BA=BO=2,CD=CO=3,∠ABO=∠DCO.连结 AD,BC,M,N 分别为 OA,BC 的中点.若固定△AOB,将△COD 绕点 O 旋转,求 MN 的最大 值.
2
此时 CE=CF+EF=2+3 5 .
A
D
FE
C
B
图1
2 ② 如图 2,当 AD= AC 时,同理可得 CE 的最大值为 4+3 5 .
3
综上可得,当点 D 在靠近点 C 的三等分点处时,线段 CE 的长度的最大值为 4+3 5 .
A
D
F
E
C
B
图2
3
例 2 以平面上一点 O 为直角顶点,分别画出两个直角三角形,记作△AOB 和△COD,其中∠ ABO=30°.如图,若 BO= 3 3 ,点 N 在线段 OD 上,且 NO=2,P 是线段 AB 上的一个动点, 在将△AOB 绕点 O 旋转的过程中,线段 PN 长度的最小值为________,最大值为________.
