信号与系统第3章作业解答
信号与系统第1-3章习题

卷积 y(t) u (t 2) et u( t 1) 等于________________。 信号 x(n) cos(3 n / 5) 2sin(2 n / 3) 的基波周期为_______________。
sin 2t 2 ( t )dt _________。 t
(1) 确定该系统的单位冲激响应; (2) 画出系统方框图。 56、已知信号 f (t ) t[u(t) u(t 2)] ,试确定该信号的奇分量和偶分量。 57、已知系统的冲激响应 h(t ) u(t 1) u(t 2) ,激励 f(t ) u(t 1) u(t 2) ,求系统的零 状态响应 y(t)。 58、已知 f 1 2t 的波形如题图 58 所示,画出 f t 的波形,并写出 f t 的表达式。
d x1 (t ) 作 dt
6
54、什么叫稳定系统?一个因果稳定的离散时间 LTI 系统应满足什么条件? 55、考虑一因果的 LTI 系统,y(t)为系统输出,x(t)为系统输入,其微分方程为:
d 2 y (t ) dy (t ) 3dx(t ) 4 3 y (t) x(t ) 2 dt dt dt
j / 4
的直角坐标式为_____________________。
信号 x(t ) 2 cos(10t 1) sin( 4t 1) 的基波周期为_____________________。
4
25、 26、 27、
t
e ( )d _________。
(2t ) __________________。
B
1
-4 -3 -2 -1 0
t
北理工-信号与系统-第三版-第三章-作业参考答案
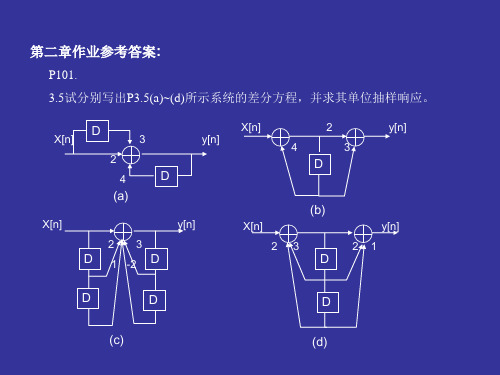
k
| u[k ] | ,有界
是非稳定系统
(e) 显然n<0时,h[n]=0,所以是因果系统;
k
| h[k ] | | u[k ] / n | ,无界
k
是非稳定系统
(f) 显然n<0时,h[n]=0,所以是因果系统;
| h[k ] |
(d)
y[n] x[n] h[n]
k
[k n ] [n k n ]
1 2
[n n1 n2 ]
3.11在LTI离散时间系统中 已知x[n]=u[n]时的零状态响应(单位阶跃响应)为s[n],求单位抽样响应h[n]; 已知h[n],求s[n].
y[n] - 4y[n-1] =2x[n]+3x[n-1];
令x[n]=δ[n],则有 h[n] – 4h[n-1] =2 δ[n]+3 δ[n-1];当n<0时,h[n]=0,得h[0]=2,h[1]=11,
特征方程为 λ-4=0, 得λ=4,
h[n]=c(4)nu[n],由h[1]=4c=11,c=11/4得 h[n]=(11/4)(4)nu[n-1]=11 (4)n-1u[n-1],考虑h[0]=2=2 δ[n],得 h[n]=2 δ[n]+11 (4)n-1u[n-1]。(n>0的解) (b).据图有同(a)一样的结果…。 (c).据图 y[n]=3y[n-1]- 2y[n-2]+ x[n]+2x[n-1]+x[n-2] ,即差分方程为 y[n] -3y[n-1]+2y[n-2] = x[n]+2x[n-1]+x[n-2], 先求
哈工大信号与系统第三章术后作业答案张晔

fltnzlults因为是bniif.c EJ.siunwndttjErsincnwtsdt品奇这是咋求的求锯⻮信号ftkocnejnmtcniiffme则⼴哻f则fits品蕊ei哔世这是利⽤指数表示求三⻆函数形式下的⽐⼆ffctldt.FI ff aniiffmcoscnwtgdtiifl ttEjcoscnwtydttf奇㷒依然为奇则为0⼆if Ewscnwtdt2元ㄨ103kHz 6.128X 2X106t1间隔ME巺⼆㗟s不4112X1066.28106带亮13乺烈烈6nfzxi14三次诮波11批t 10⽐红__2.12Et E 4i 1lCniÈffme atdtfcne atdttffze.at dt其中ain⼆弦表ǏF试⻦扣与fun的傅⽴叶变换Fifn Filmfit Alum ut沙井控ult.int坷同样将fun表示⼀下⼆是cult ultt t Al ul ti Ultt则Fl funk Ftw ejwto詏们对于la 来说原因为三⻆以及余弦之积inn则n 01wtionjtoiw zuScilE 2对于⼼来说原⼆Sin 5元右侧的相当于则Sachi ii nl ócw 5元-01W 5到vivre怎么看出来的ht利⽤时域积分把原函看成积分原⽐⽐出⼀吐动deno 个吢砟⼼ólug201W e iwi nameÍjmjw⼆⽆以costing tisinihgznwilosciugtisin int器nomaunt jw求的傅⾥叶变换利⽤傅⾥叶变换的定义式求FlwkfofneiTltftltgeiwtdt.ttcu.int Fxi Eij w W2t恐器加⼀兜圜篮圝噬部⼆品ceiwte Mtice2N.ie可以应leine全部转化为⼼sin之形成三吉xzcoswth.zwszwtfw.zsinz.ru为了求得⽴叶级则要利⽤原tniiFocwilninw.F4从⽽cnet.to cnn.in代⼊上式中则代⼊到了覃⽴叶级数的公式中funÍcneimt⼀H求⼼的傅⾥叶交换则Rcntawhn HIM⼆舙⽅站1jhntl 然后求输⼊信号的得主叶交换在⼀个周期内P fltsejwtdt in哭⼏⼆T T teiwtdtiwlteiwt jeiwtsiEijiMn D 求fun的傅⽴叶级数90i hits dtf.li灬i1第⼀次分布积分⼜弄错了duty卡twsnwitdt ijtwscnw ndt lnwdwscnwnliw.co scnwtsi ǜǐ⼆声n.dz cost 哔_sinc 哔⼆前211叮n华⼆则no 时IAN则An 有加上n 为偶iq ⼥终900则⼈品㹷n 为奇彘流iiwiwiwj.ws对fun 进⾏傉⽴叶交他fun为奇函数外an sc.no求dni ǐǕsincnwmdt.lu 笇d n ⾔Ǖs in2巺七d t ⾔ǜ则所求即为flat fun 不⽤合求iii nt1111111iinnnniiii。
第三章作业答案_1-7

a2 N =
1 1 T 1 T − j (4 N π / T ) t 2 x t e dt = x(t )e− j (4 Nπ / T )t dt + ∫T x(t )e− j (4 Nπ / T )t dt ( ) ∫ ∫ T T T 0 T 2 =
T 1 T T ( ∫ 2 x(t )e − j (4 Nπ / T )t dt + ∫T − x(t − )e− j (4 Nπ / T )t dt ) T 0 2 2 T 1 T ( ∫ 2 x(t )e − j (4 Nπ / T ) t dt + ∫ 2 − x(t )e− j (4 Nπ / T )t dt ) = 0 0 T 0
+∞
e − j 2ω (答案) 2 + jω
+∞ +∞ −∞
X ( jϖ ) = ∫ x(t )e − jωt dt = ∫ e −2 ( t − 2) u (t − 2)e − jωt dt = ∫ e −2 ( t − 2) e − jωt dt
−∞ 2
= ∫ e −( 2+ jω )t + 4 dt =
jkπt
,由已知条件 k ≤ 4 时,H(jw)不为零,而 k ≥ 5 ,H(jw)=0
jkπt
故响应为: y k (t ) = H ( jkπ ) a k e 当 k > 5 时,激励 x k (t ) = a k e 此有 y (t ) =
= (1 −
k 5
)a k e jkπt , k ≤ 4
(2) 由于系统的单位冲激响应 h(t)已知,可以据此而求出其频谱。因为 h(t)是方波脉冲,直 接由典型信号的频谱得:
FT h(t ) ←→ H ( jω ) =
信号与系统课后习题与解答第三章
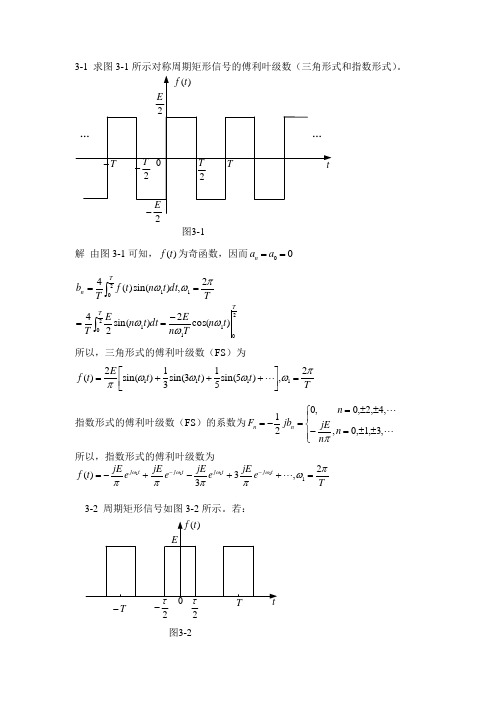
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
奥本海姆 信号与系统 习题参考答案

.第三章作业解答3.1解:420ππω==T , j a a 4*33-==- 则:t j t j t j t j k tjk ke a e a e a e a ea t x 00000333311)(ωωωωω----∞-∞=+++==∑-)243cos(84cos 443sin 84cos 4)](21[8)(2144422434344434344πππππππππππππ++=-=--⨯++⨯=-++=------t t tt e e je e jejeeet j t j t j t j t jt jt j t j3.3解:)35sin(4)32cos(2)(t t t x ππ++= 则3)32cos(1=→T t π 56)35s i n (2=→T t π故:6],[21==T T lcm T 320ππω==T )(214)(21235353232t j t j t j t j e e je e ππππ---⨯+++=则:20=a 2122==-a a 25j a -= 25j a =- 3.9x[n]波形如下图所示:0 1 4 5 n…- 4 -3则:N=4,220ππω==N ]84[41]}1[8][4{41][41][122302300πππωδδjk n jk n n jk n n jk N n k e e n n e n x e n x N a --=-=->=<+=-+===∑∑∑即:2112133210j a a j a a +=-=-==3.15解:6π=T ,1220==Tπω )(ωj H 如下图所示:则:⎩⎨⎧>≤=9||08||1)(0k k jk H ωtjk k kea t x 0)(ω∑∞-∞==tjk k ktjk k k ea ea jk H t y 00880)()(ωωω∑∑-=∞-∞===而:)()(t y t x =,即:t jk k k tjk k k e a t y ea t x 0088)()(ωω∑∑-=∞-∞====故:当9||≥k 时,0=k a3.22解:(a )2=T ,ππω==T20 ]|[12121)(11111110dt e te jk dt te dt e t x T a tjk t jk t jk T t jk k ⎰⎰⎰---------===πππωπkjk t jk t jk k j k j k k je k j e jk te k j )1(k ]02[21]|1|[211111-=⎪⎪⎩⎪⎪⎨⎧-=--=---=-----πππππππππ为奇数为偶数021110==⎰-dt t a(注意:与性质验证,由于x(t)是实奇函数,则a k 为纯虚的奇函数,满足: *k k k a a a -=-=- 且:00=a ) (d) 2=T ,ππω==T20 ])1(21[21]21[21)]1(2)([21)(1200k jk t jk T tjk k e dt e t t dt e t x T a --=-=--==---⎰⎰--ππωδδ21)]1(2)([21200-=--=⎰--dt t t a δδ3.28(b )解:)(21)(21)2cos()32sin(][223232nj n j n jnje e eejn n n x ππππππ--++== )(416/76/6/6/7n j n j n j n j e e e e j ππππ----+=12/2.712/2.12/2.12/2..7(41ππππn j jn jn n j e e e e j----+=⎪⎪⎪⎩⎪⎪⎪⎨⎧++=-++==othersrN rN k j rN rN k j a k 05,11417,141 则:⎪⎩⎪⎨⎧++++==othersrN rN rN rN k a k 05,11,7,141||⎪⎪⎪⎩⎪⎪⎪⎨⎧++=++=-=∠othersrN rN k rN rN k a k 05,1127,12ππ 3.34解:(b)∑∞-∞=--=n nn t t x )()1()(δ其波形如下图所示:其周期T=2,基波频率为:ππω==T20 ⎩⎨⎧=--=-=--==---⎰⎰--是偶数是奇数k 01])1(1[21]1[21)]1()([21)(1200k e dt e t t dt e t x T a k jk t jk T tjk k ππωδδ而:⎪⎩⎪⎨⎧<>==--00)(44||4t et e et h t tt则:240401684141)()(s s s dte e dt e e dt e t h s H st t st t st -=++-=+==--∞-∞--∞∞-⎰⎰⎰故:2)(168)(ππjk jk H -=故:⎪⎩⎪⎨⎧-==∑∞-∞=为偶数为奇数(k k e jk ea jk H t y tjk tjk k k 0)168)()(200πωπω3.357π=T ,1420==Tπω 解:)(ωj H 如下图所示:则:⎩⎨⎧<>=17||017||1)(0k k jk H ωtjk k kea t x 0)(ω∑∞-∞==tjk k k tjk k k ea ea jk H t y 0018||0)()(ωωω∑∑∞=∞-∞===而:)()(t y t x =,即:tjk k ktjk k kea t y ea t x 0018||)()(ωω∑∑∞=∞-∞====故:当18||<k 时,0=k a3.44解:(1)*k k a a =- (2)6=T ,320ππω==T (3)⎩⎨⎧===其他,不为02||1||0k k a k(4)k jk k k a e b t x a t x π--=→--→)3()(k jk k a ea π--= 则:当为偶数k a k 0=结合(3)则:⎩⎨⎧==其他不为01||0k a k(5)帕斯瓦尔关系式:21||21||||12121=⇒=+-a a a (6)211=a 211=-a 则t e e ea e a t x t j t j t j tj 3cos )(21)(333131πππππ=+=+=--- 故:03,1===C B A π。
信号与线性系统题解第三章
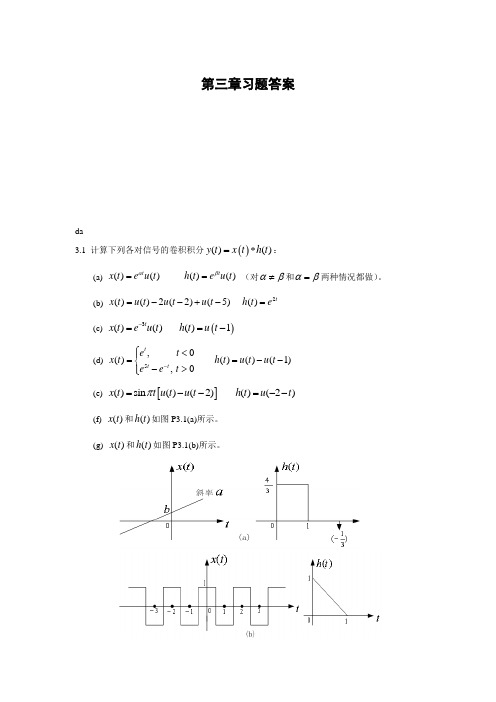
第三章习题答案da3.1 计算下列各对信号的卷积积分()()()y t x t h t =*:(a) ()()()()t tx t e u t h t e u t αβ==(对αβ≠和αβ=两种情况都做)。
(b) 2()()2(2)(5)()tx t u t u t u t h t e =--+-=(c) ()3()()()1tx t eu t h t u t -==-(d) 5,0()()()(1),0tt t e t x t h t u t u t e e t -⎧<⎪==--⎨->⎪⎩(e) []()sin ()(2)()(2)x t t u t u t h t u t π=--=--(f) ()x t 和()h t 如图P3.1(a)所示。
(g) ()x t 和()h t 如图P3.1(b)所示。
图P3.1 解:(a) ()()0()()()(0)t ttty t x t h t eed eed t βτατβαβτττ------=*==>⎰⎰当αβ≠时,()1()()ttey t e u t αβββα----=-当αβ=时,()()t y t te u t α-=(b) 由图PS3.1(a)知, 当1t ≤时,252()2()22(2)2(5)021()22t t t t t y t ed ed e e e ττττ----⎡⎤=-=-+⎣⎦⎰⎰ 当13t ≤≤时,252()2()22(2)2(5)121()22t t t t t y t ed ed e e e ττττ-----⎡⎤=-=-+⎣⎦⎰⎰ 当36t ≤≤时,52()2(5)211()2t t t y t ed e e ττ---⎡⎤=-=-⎣⎦⎰ 当6t >时,()0y t =(c) 由图PS3.1(b)知,当1t ≤时,()0y t = 当1t >时,133(1)01()13t t y t ed e ττ----⎡⎤==-⎣⎦⎰3(1)1()1(1)3t y t e u t --⎡⎤∴=--⎣⎦(d) 由图PS3.1(d)知: 当0t ≤时,11()tt t t y t e d e eττ--==-⎰当01t <≤时,055(1)1014()(2)255t ttt t y t e d e e d e eeτττττ-----=+-=+--⎰⎰当1t >时,555(1)(1)111()(2)2255t tt tt t y t e ed eeeeτττ------=-=-+-⎰(e) 如下图所示:(f) 令()11()(2)3h t h t t δ⎡⎤=+--⎢⎥⎣⎦,则11()()()(2)3y t x t h t x t =*-- 由图PS3.1(h)知,11424()()()()(21)333t t y t x t h t a b d a t b ττ-=*=+=-+⎰2411()(21)(2)()3333a y t tb a t b a t b x t ∴=-+---=+= (g) ()x t 是周期信号,由此可推知()()()y t x t h t =*也是周期的,且周期也为2。
信号与系统第三章习题部分参考答案

(w)
(14) f (t)u(t) ↔ 1 F ( jw) *[ 1 + πδ (w)]
2π
jw
(15) df (1 − t) ↔ jwF (−w)e− jw
dt t df (1 − t) ↔ jwF (−w)e− jw − F (−w)e− jw − wF ′(−w)e− jw
dt
(16) (t − 2) f (t)e j2(t−3) ↔ e− j6[F ′(w − 2) − 2F (w − 2)]
−τ τ
w
方法二 利用时域微分性质
对 f(t)求一阶导数得到
f
′(t)
=
1 τ
G2τ
(t)
−
δ
(t
+
τ
)
−
δ
(t
−
δ
)
F1 (w) = 2sa(wτ ) − 2 cos(wτ )
F1 (0) = 0
F (w) =
F1 (w) jw
+
πF1
(0)δ
(w)
=
j
2 [cos(wτ ) − sa(wτ )] w
1
− F(
jw )]
−∞
−∞
j2w 2
(12) df (t) ↔ jwF (w)
dt
df (t) + f (3t − 2)e− jt ↔ jwF (w) + 1 F ( w + 1)e j2(w+1) / 3
dt
33
(13) sa(t) ↔ πG4 (w) / 2
f
(t)
*
sa(t)
↔
π 2
F (w)G4
↔ 2π e−a⎜−ω⎜
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P94 3.26
解: 先求零输入响应:
y(n) 0.7 y(n 1) 0.1y(n 2) 2x(n) 3x(n 2)
D() ( 0.2)( 0.5) 0 1 0.2 2 0.5
y0 (n) c1(0.2)n c2 (0.5)n n 0
u(n) *u(n) *(t 1) u(n) *(n 1) (1)n u(n) *u(n) * (n 1)
n
[(n 1)u(n)]*(t 1) u(n 1) [((1)k )u(n)]* (n 1) k 0
第三章 连续时间系统的时域分析 7/9
nu(n 1) u(n 1) [1 1 (1)n1]u(n) * (n 1) 22
第三章 连续时间系统的时域分析——作业参考答案
P59 2.20 (1) 解: y(t) 3y (t) 2y (t ) 0
3 32 2 0
( 2)( 1) 0 1 0 , 2 2 , 3 1
P61 2.28
yx (t) k1et k2e2t k3
y(0) y (0)
yx (0) k1 yx (0) k1
3 t)
t 0
2
2
因
i(0 ) 0, i(0 ) 10
解得: A 0, B 20 3
i(t)
20
-1t
e2
sin
3 tu(t)
3
2
即:
20
31 t
3
i(t )
e 2 s i n tu t ( )
3
2
P62 2.34
解:
由方程解得特征根为: 1 2, 2 1
设单位冲激响应为 h(t) ( Ae2t Bet )u(t)
(2)
第三章 连续时间系统的时域分析 6/9
x(n 2) a(n 3) a(n 1)
(3)
y(n 3) a(n 3) a(n 1)
(4)
由(1)(2)(3)(4)式整理化简得
y(n 3) y(n 1) x(n 2) x(n)
(2) 由
y(n 3) y(n 1) x(n 2) x(n)
u(n )u n( ) ( n2u)n ( u) n 3 ( )n u( n 2 ) ( )
1 u(n) [u(n) (2)n1u(n)] 3 1 [u(n) (2)n1u(n)]
3
3
1 n u( n) 4 u( n) 1 4 ( n2 ) u (n )
3
9
9
y(n)
y0 (n)
yx (n)
第三章 连续时间系统的时域分析 4/9
y(n) 2 y(n 1) x(n) D() 2 0 2
y0 (n) c(2)n 由方程 y( n) 2 y (n 1) n( 2u) n( )
y(0) 2 y(1) (2) y(1) 3 / 2
y0 (1)
y(1)
c(2)1
3 2
c3
yx (t) y(t) y f (t) (4et 3e2t )u(t)
自然响应: 强迫响应: 稳态响应:
[1 4et 7e2t ]u t( ) 32
1 e4tu(t) 6
0
瞬态响应: [14 et 7 e2t 1 e4t ]u(t) 326
P93 3.11
解
dy(t) lim y[(n 1)T ] y(nT )
k2
k3 1
2k2
1
kk12
3 1
y (0) yx (0) k1 4k2 1
k3 3
yx (t) 3et e2t 3 , t 0
证明: ∵ y(t) f (t) h(t)
又 ∵ 线性时不变系统
y(t) [ f (t) h(t)] f (t) h(t)
故该系统对于 f (t) 的响应为 y(t) P61 2.29
将上式及其一阶导、二阶导代入方程: h(t) 3h(t) 2 y(t) (t) 3 (t)
解得 A 1 B 2
故有 h(t) (e2t 2et )u(t)
第三章 连续时间系统的时域分析 2/9
y f (t) f (t) h(t) (e4t )u(t) (e2t 2et )u(t) ( 2 et 1 e2t 1 e4t )u(t) 32 6
故有
h(0) C A B 0
h(1) D A B 1
h(2) A B 0
h(3) A B 2
A 1 B 1 C 0 D 1
h(n) (n 1) [1 (1)n ]u(n)
或 h(n) [1 (1)n1]u(n 1) (n 1)
(3) s(n) yx (n) h(n) *u(n) [u(n 1) (n 1) (1)n1u(n 1)]*u(n)
(b)
第三章 连续时间系统的时域分析 5/9
y(n) x(n) * h1(n) * h3(n) x(n) * h1(n) * h3(n) * h2 (n) x(n) *[h1(n) * h3(n) h1(n) * h2 (n) * h3(n)]
h(n) h1(n) * h3 (n) h1(n) * h2 (n) * h3(n)
整理得 y( n 2 ) 3y (n 1) y5 n( ) x n( )
(b) y(n) 4 y(n 1) 5y(n 2) 3x(n) 2x(n 1)
整理得 y(n) 4 y(n 1) 5y(n 2) 3x(n) 2x(n 1)
P93 3.14
(2)
y(n) 2 y(n 1) 0 D() 1 2 1 0 y0 (n) 2n c1
(6)
(10)
y(n) 2 y(n 1) y(n 2) 0 y(0) y(1) 1
D() 2 2 1 0 1(二阶)
y0 (n) (c1 c2n)(1)n
y0 y0
(0) y(0) c1 (1) y(1)
1 (c1
c2
)(1)
1
cc12
1 2
y0 (n) (1 2n)(1)n u(n)
y0 (1) y(1) 2c1 1
(4)
yo (n) 2n1u(n) y(n) 1 y(n 1) 0
3
y(1) 1 2
c1
1 2
y(1) 1
y0
(n)
c1
(
1 3
)
n
1 3
y0 (1) y(1) c1(3) 1
c1
1 3
y0 (n)
1 ( 3
1)n 3
( 1)n1u(n) 3
整理得: y( n 2 ) 1 . y7 n( 1) 0 .y7 n2 ( ) x0 .n0 2 ( ) y( 0 ) 0 y ( 0 ) 3y( 1 ) y ( 0 ) y ( 1 ) 0 . 3 0.1
第三章 连续时间系统的时域分析 3/9
P93 3.12
解:(a)
y(n 2) 3y(n 1) 5y(n) x(n)
Σ
E-1 a(n)
E-1 b(n) E-1
Σ
y(n)
由图可得:b(n) a(n 1)
y(n) a(n) b(n 1) a(n) a(n 2)
a(n 1) x(n) b(n) x(n) a(n 1)
整理可得: y(n 1) a(n 1) a(n 1)
(1)
x(n) a(n 1) a(n 1)
dt T 0
T
T 足够小时 d y( t) y[ (n 1 )T] y (nT )
dt
T
同理可得 :
y( n 1 ) y (n ) T
d 2 y(t) dt 2
y[(n 2)T ] 2 y[(n 1)T ] T2
y(nT )
y(n 2) 2 y(n 1) y(n)
T2
对输入 x(t)也做间隔时间 T 取样,t=nT 处取值为 x(nT)
y0 (n) 3(2)n n 0
设 h(n) A(2)n u(n) 代入方程 h(n) 2h(n 1) (n) 得 A 1
故有 h(n) (2)n u(n) yx (n) x(n) h(n) (n 2)u(n) (2)nu(n)
(n 1 3)u(n) (2)n u(n) [(n 1)u(n)](2)nu(n) 3u(n) (2)nu(n)
y0 y0
(1) (2)
c1 c1
10 2
c2
10 5
26
(10 ) 2 2
c2
(10 5
)2
202
cc12
10 12
y0 (n) 10(0.2)n 12(0.5)n
第二步求单位样值响应
n0
h(n) 0.7h(n 1) 0.1h(n 2) 2 (n) 3 (n 2)
由 h(n) 0.7h(n 1) 0.1h(n 2) 2 (n) 3 (n 2)
d 2 y( t) d (y )t
d t2 3
2y (t ) x2 t( ) dt
y(n 2) 2 y(n 1) y(n) 3 y(n 1) y(n) 2 y(n) 2x(n)
T2
T
T=0.1
y(n 2) 2 y(n 1) y(n) 3T[ y(n 1) y(n)] 2T 2 y(n) 2T 2x(n)
1 3
nu(n)
4 9
u(n)
13 9
(2)n u(n)
P94 3.17
解:(a)
y(n) h3 (n) *[x(n) * h1(n) x(n) * h1(n) * h2 (n)] x(n) *[h1(n) * h3 (n) h1(n) * h2 (n) * h3(n)]
h(n) h1(n) * h3 (n) h1(n) * h2 (n) * h3(n)
