《电磁场与电磁波基础》刘岚_课后习题解答(第五章)
《电磁场与电磁波》-习题及详细题解

$! $" $# !)( ")#) ! ( # $% !''$!$&&$"$(($#
, ' #4
)"标量场 & !!# ""# "#!",计算其梯度。 Nhomakorabea
解::106( &) 7! &
7!(#!"#") $!"(#""#!) $" $"求曲面 #!!# ""# 在点((,(,#) 处的法线方向。
···
689"!("#"
$! $" $#
)"! · ·!
· ·"
· ·#
!$#( #!$()
!"" !# ""# 4
&"(() 求标量函数 "!!# "#的梯度。 (#) "在一个指定方向的方向导数,此方向由单位矢量
槡 槡 槡 % $!" & $"" ' $#定出,求其在(#,%,() 点的方向导数值。 '4 '4 '4
预备知识:矢量分析习题及题解
!"给定三个矢量 !、"和 #如下:
!!$!"#$"$%$# "!$&$""$# #!'$!$#$#
求:(() $$。 (#) !$" 。 (%) !·"。 (&) )$%。 (') !在 "上的分量。 (。) !)#。
电磁场课后答案5

k1 sin θ B = k 2 sin θ 2
案
ε 2 k1 cosθ B = ε 1k 2 cosθ 2
cos θ 2 =
网
= 0, k z2 ε 1 − k z1 ε 2 = 0
ww w
Z 2 − Z 1 ωε 2 = k z2 Z 2 + Z1
− +
ωε 2
.k hd
k z1
对于 TM 模
ωε 1
所以
ε 1 ε 1 μ1 − ε 2 μ 2 2 μ1 ε 12 − ε 2
θ B = arccos
ε 1 ε 1 μ1 − ε 2 μ 2 2 μ1 ε 12 − ε 2
co
m
μ1 μ1ε 1 − μ 2ε 2 2 ε 1 μ12 − μ 2
当
μ1 = μ 2 ,θ B = arccos
ε1 + ε 2
2 2 μ2 k1 k 2 1 − cos θ B = 1 − 2 12 cos 2 θ B k2 μ1 k 2
两边平方,均整理后得到
cos 2 θ B =
所以
μ1 μ1ε 1 − μ 2ε 2 2 ε 1 μ12 − μ 2
θ B = arccos
k z2 ΓTM =
要使 ΓTM 即 由相位匹配条件: 由(1)
ρs
y =d
=0
案
网
ww w
(2) ∇ × E ≠ 0 ,是有旋场,不能用标量函数的负梯度表示
.k hd
aw .
co
⎞ ⎟ ⎟ ⎠
解: (1) ∇ ⋅ E =
∂E x ∂E y ∂E z + + =0 ∂x ∂y ∂z ⎛ ∂E y ∂E x ⎛ ∂E z ∂E y ⎞ ⎛ ∂E x ∂E z ⎞ ∇ × E = x0 ⎜ ⎜ ∂x − ∂y ⎜ ∂y − ∂z ⎟ ⎟ + y 0 ⎜ ∂z − ∂x ⎟ + z 0 ⎜ ⎝ ⎠ ⎝ ⎝ ⎠ π ⎛π ⎞ ⎛π ⎞ = −y 0 jkA sin⎜ y ⎟e j (ωt − kz ) − z 0 A cos⎜ y ⎟e j (ωt −kz ) d ⎝d ⎠ ⎝d ⎠
电磁场与电磁波课后习题及答案

电磁场与电磁波课后习题及答案习题解答如题图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为U0,求槽内的电位函数。
解根据题意,电位?(x,y)满足的边界条件为y?)?a(y,?) 0①?(0,) 0②?(x,0?③?(x,b)?U0 根据条件①和②,电位?(x,y)的通解应取为y ?(x,y)??Ansinh(n?1?n?yn?x)sin()aa b o U0 条件③,有 a 题图U0??Ansinh(? ax n?1n?bn?x)sin()aa sin(两边同乘以n?x)a,并从0到a对x积分,得到a2U0n?xAn?sin()dx?asinh(n?ba)?a04U0?,n?1,3,5,?n?sinh(n?ba)2U0?(1?cosn?) ??n?2,4,6,n?sinh(n?ba)?0,?(x,y)?故得到槽内的电位分布4U01?,sinh?n?1,3,5nn?(ban?ysinh()a?nx)sin(a ) 两平行无限大导体平面,距离为b,其间有一极薄的导体片y?d到y?b(???x??)。
上板和薄片保持电位U0,下板保持零电位,求板间电位的解。
设在薄片平面上,从y?0到y?d,电位线性变化,?(0,y)?U0yd。
y U0解应用叠加原理,设板间的电位为?(x,y)??1(x,y)??2(x,y) 其中,boxydxy oxy 题图?1(x,y)为不存在薄片的平行无限大导体平面间的电位,即?1(x,y)?U0yb;?2(x,y)是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:①?2(x,0)??2(x,b)?0②?2(x,y)?0(x??) U0?U?y??0b?2(0,y)??(0,y)??1(0,y)???U0y ?U0y?b?d③(0?y?d)(d?y?b) ??xn?y?nb?2(x,y)?? Ansin()e?(x,y)的通解为bn?1根据条件①和②,可设 2 U0?U?y?n?y??0bAnsin()???bn?1?U0y?U0 y?b?d条件③有sin(两边同乘以d(0?y?d)(d?y?b) n?y)b,并从0到b 对y积分,得到b2U2Uyn?y11n?yAn?0?(1?)sin()dy?0?(?) ysin()dy?2U02bsin(n?d)b0bbbddbb(n?)db ?xU02bU0?1n?dn?y?nby?sin()sin()e 2?2?(x,y)?bd?bbn?1n故得到求在上题的解中,除开定出边缘电容。
电磁场与电磁波_部分课后习题解答

电磁场与电磁波部分课后习题解答CH11.2给定三个矢量A ,B ,C:A =x a+2y a -3z a B= -4y a +z aC =5x a-2z a求:⑴矢量A的单位矢量A a ;⑵矢量A 和B的夹角AB θ; ⑶A ·B 和A ⨯B⑷A ·(B ⨯C )和(A ⨯B)·C ;⑸A ⨯(B ⨯C )和(A ⨯B )⨯C解:⑴A a =A A=(x a +2y a -3z a )⑵cos ABθ=A ·B /A BAB θ=135.5o⑶A ·B =-11, A ⨯B=-10x a -y a -4z a⑷A ·(B ⨯C )=-42(A ⨯B)·C =-42⑸A ⨯(B ⨯C)=55x a -44y a -11z a(A ⨯B)⨯C =2x a -40y a +5z a1.3有一个二维矢量场F(r) =x a(-y )+y a (x),求其矢量线方程,并定性画出该矢量场图形。
解:由dx/(-y)=dy/x,得2x +2y =c1.6求数量场ψ=ln (2x +2y +2z )通过点P (1,2,3)的等值面方程。
解:等值面方程为ln (2x +2y +2z )=c 则c=ln(1+4+9)=ln14 那么2x +2y +2z =141.9求标量场ψ(x,y,z )=62x 3y +ze 在点P (2,-1,0)的梯度。
解:由ψ∇=x a x ψ∂∂+y a y ψ∂∂+z a zψ∂∂=12x 3y x a +182x 2y y a +z e z a 得ψ∇=-24x a +72y a +z a1.10 在圆柱体2x +2y =9和平面x=0,y=0,z=0及z=2所包围的区域,设此区域的表面为S: ⑴求矢量场A沿闭合曲面S 的通量,其中矢量场的表达式为A =x a32x +y a (3y+z )+z a (3z -x)⑵验证散度定理。
电磁场与电磁波课后习题及答案

电磁场与电磁波课后习题解答1.1 给定三个矢量A 、B 和C 如下: 23x y z =+-A e e e4y z =-+B e e52x z =-C e e求:(1)A a ;(2)-A B ;(3)A B ;(4)AB θ;(5)A 在B 上的分量;(6)⨯A C ;(7)()⨯A B C 和()⨯A B C ;(8)()⨯⨯A B C 和()⨯⨯A B C 。
解 (1)23A x y z+-===-e e e A a e e e A (2)-=A B (23)(4)x y z y z +---+=e e e ee 64x y z +-=e e e (3)=A B (23)x y z +-e e e (4)y z -+=e e -11(4)由 c o s AB θ=8==A B A B ,得 1c o s AB θ-=(135.5= (5)A 在B 上的分量 B A =A c o s AB θ==A B B (6)⨯=A C 123502xy z-=-e e e 41310x y z ---e e e (7)由于⨯=B C 041502x yz-=-e e e 8520x y z ++e e e ⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C (23)x y z +-e e e (8520)42x y z ++=-e e e ()⨯=A B C (1014)x y z ---e e e (52)42x z -=-e e(8)()⨯⨯=A B C 1014502x y z---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520xy z -=e e e 554411x y z --e e e1.2 三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。
(1)判断123PP P ∆是否为一直角三角形;(2)求三角形的面积。
电磁场课后习题第五章
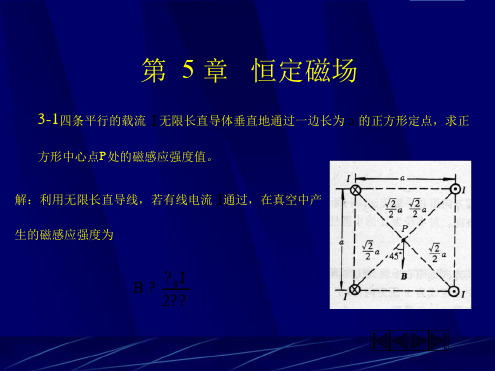
B1=
?
0
J0 2
?
1
其方向用右手螺旋法则判断,它以大圆柱轴线为中心,? 1为半径圆环的切线方
向。对半径为 a 的小圆柱,在空洞内P点所产生的磁感应强度大小为
B2=
?
0
J0 2
?
2
uvu 其方向也由右手螺旋法则判断,只是电流沿 (? e z ) 方向。若设大圆柱与小圆柱中
心连线为x的正方向,则P点的磁感应强度应为两圆柱各自在 P点产生的磁感应强
面上的磁化电流线密度为
uuuv uuv uuv uuv K m ??e?z e? M0 e?
uuuv uuv 由此可见,要求永久磁化圆柱沿轴线的磁场,就是求磁化电流线密度 K m ? M0 e?
在空间沿轴各处的磁感应强度。圆柱面上的磁化电流可以视为若干个小圆环电
流,每个小圆环电流为
dI m= Kmd z?=M 0 dz ?
uv uvu Z ? 0 处的 B 和H 。
解: 利用媒质分界面上的衔接条件,因为B1 ? 1Wb / m2 ,则
? B2 ? B1 cos
? 0.5WB / m2,Bt ? B1 sin? ?
3 Wb / m2 。利用 2
B2n ? B1n ? 0.5 Wb/ m2
H2t
?
H1t
?
B1t
? r1? 0
? ? 12cm 处,作以圆环中心为圆心的安培环路,则
uuv v
?l H gdl ? 0
所以环的截面以外各处 B ? 0 ,H ? 0。在环的截面内可认为磁场分布均匀,选
? ? 12 ? 10 ? 11cm 为半径,作一安培环路
2
uuv v
?l Hlgd ? NI
电磁场与电磁波 第五章答案

第五章 恒定磁场重点和难点该章重点及处理方法与静电场类似。
但是磁感应强度的定义需要详细介绍,尤其要强调磁场与运动电荷之间没有能量交换,电流元受到的磁场力垂直于电流的流动方向。
说明磁导率与介电常数不同,磁导率可以小于1,而且大多数媒质的磁导率接近1。
讲解恒定磁场时,应与静电场进行对比。
例如,静电场是无散场,而恒定磁场是无旋场。
在任何边界上电场强度的切向分量是连续的,而磁感应强度的法向分量是连续的。
重要公式磁感应强度定义:根据运动电荷受力: B v F ⨯=q根据电流元受力: B l F ⨯=d I 根据电流环受力: B m T ⨯=真空中恒定磁场方程: 积分形式: I ⎰=⋅ll B 0d μ⎰=⋅SS B 0d微分形式:J B 0 μ=⨯∇0=⋅∇B已知电流分布求解电场强度:1,A B ⨯∇=V V ''-'=⎰'d )(4)( 0 r r r J r A πμ2,V V ''-'-⨯'=⎰'d )()( 4)(30 r r r r r J r B πμ 毕奥─萨伐定律。
3,I ⎰=⋅ll B 0d μ安培环路定律。
面电流产生的矢量磁位及磁感应强度分别为S ''-'=⎰'d )(4)(0 r r r J r A S S πμS ''-'-⨯'=⎰'d )()(4)( 30 r r r r r J r B S S πμ 线电流产生的矢量磁位及磁感应强度分别为⎰''-'=l r r l r A d 4)(0I πμ⎰''-'-⨯'=l r r r r l r B 30 )(d 4)(I πμ矢量磁位满足的微分方程:J A 0 2μ-=∇无源区中标量磁位满足的微分方程: 0 2=∇m ϕ 媒质中恒定磁场方程: 积分形式: I l =⋅⎰l H d⎰=⋅SS B 0d微分形式:J H =⨯∇ 0=⋅∇B磁性能均匀线性各向同性的媒质:场方程积分形式:⎰=⋅lI d μl B⎰=⋅BS H 0d场方程微分形式: J B μ=⨯∇ 0=⋅∇H矢量磁位微分方程:J A 2μ-=∇矢量磁位微分方程的解: V V ''-'=⎰'d )(4)(r r r J r A πμ 恒定磁场边界条件:1,t t H H 21=。
电磁场与电磁波课后答案

第一章 矢量场1.1 z y x C z y x B z y xA ˆˆˆ3;ˆ2ˆˆ;ˆˆ3ˆ2+-=-+=-+=ρρρ 求:(a) A ; (b) ∃b ; (c) ρρA B ⋅ ; (d) ρρB C ⨯ ; (e) ()ρρρA B C ⨯⨯ (f)()ρρρA B C ⨯⋅ 解:(a) 14132222222=++=++=z y x A A A A ; (b) )ˆ2ˆˆ(61ˆz y x BB b -+==ρρ( c) 7=⋅B A ρρ; (d) z y xC B ˆ4ˆ7ˆ---=⨯ρρ (e)z y x C B A ˆ4ˆ2ˆ2)(-+=⨯⨯ρρρ (f)19)(-=⋅⨯C B A ρρρ 1.2 ρA z =++2∃∃∃ρπϕ; ρB z =-+-∃∃∃ρϕ32 求:(a) A ; (b) ∃b ; (c) ρρA B ⋅ ; (d) ρρB A ⨯ ; (e) B A ρρ+解:(a) 25π+=A ;(b) )ˆ2ˆ3ˆ(141ˆz b -+-=ϕρ;(c) 43-=⋅πB A ρρ (d) z A B ˆ)6(ˆ3ˆ)23(+--+=⨯πϕρπρρ (e) z B A ˆˆ)3(ˆ-++=+ϕπρρρ 1.3 ρA r=+-22∃∃∃πθπϕ; ρB r =-∃∃πθ 求:(a) A ; (b) ∃b ; (c) ρρA B ⋅ ; (d) ρρB A ⨯ ; (e) ρρA B +解:(a) 254π+=A ; (b) )ˆˆ(11ˆ2θππ-+=r b ; (c) 22π-=⋅B A ρρ ; (d) ϕπθππˆ3ˆ2ˆ22++=⨯rA B ρρ ; (e) ϕπˆ2ˆ3-=+r B A ρρ 1.4 ρA x y z =+-∃∃∃2; ρB x y z =+-α∃∃∃3 当ρρA B ⊥时,求α。
解:当ρρA B ⊥时,ρρA B ⋅=0, 由此得 5-=α1.5 将直角坐标系中的矢量场ρρF x y z xF x y z y 12(,,)∃,(,,)∃==分别用圆柱和圆球坐标系中的坐标分量表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题及参考答案5.1 一个点电荷 Q 与无穷大导体平面相距为d ,如果把它移动到无穷远处,需要作多少功?解:用镜像法计算。
导体面上的感应电荷的影响用镜像电荷来代替,镜像电荷的大小为-Q ,位于和原电荷对称的位置。
当电荷Q 离导体板的距离为x 时,电荷Q 受到的静电力为2)2(042x Q F επ-=静电力为引力,要将其移动到无穷远处,必须加一个和静电力相反的外力2)2(042x Q f επ=在移动过程中,外力f 所作的功为d Q d dx dx Q dx f 016220162επεπ=⎰∞⎰∞= 当用外力将电荷Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以,在整个过程中,外力作的总功为dq8/2επ。
也可以用静电能计算。
在移动以前,系统的静电能等于两个点电荷之间的相互作用能:d Q d Q Q d Q Q q q W 082)2(04)(21)2(042122211121επεπεπϕϕ-=-+-=+= 移动点电荷Q 到无穷远处以后,系统的静电能为零。
因此,在这个过程中,外力作功等于系统静电能的增量,即外力作功为dq8/2επ。
5.2 一个点电荷放在直角导体内部(如图5-1),求出所有镜像电荷的位置和大小。
解:需要加三个镜像电荷代替 导体面上的感应电荷。
在(-a ,d )处,镜像电荷为-q ,在(错误!链接无效。
镜像电荷为q ,在(a ,-d )处,镜像电荷为-q 。
5.3 证明:一个点电荷q 和一个带有电 荷Q 、半径为R 的导体球之间的作用力为]2)22(2[04R D DRq D D qR Q q F --+=επ其中D 是q 到球心的距离(D >R )。
证明:使用镜像法分析。
由于导体球不接地,本身又带电Q ,必须在导体球内加上两个镜像电荷来等效导体球对球外的影响。
在距离球心b=R 2/D 处,镜像电荷为q '= -Rq/D ;在球心处,镜像电荷为D Rq Q q Q q /2+='-=。
点电荷q 受导体球的作用力就等于球内两个镜像电荷对q 的作用力,即]2)2(2[04]2)(22[04DR D D q R D D q R Q q b D q D qq F --++=-'+=επεπ]2)22(2[04R D D R qD D q R Q q--+=επ 5.4 两个点电荷+Q 和-Q 位于一个半径为a 的接地导体球的直径的延长线上,分别距离球心D 和-D 。
(1)证明:镜像电荷构成一电偶极子,位于球心,偶极矩为2a 3Q/D 2。
(2)令Q 和D 分别趋于无穷,同时保持Q/D 2不变,计算球外的电场。
解:(1)使用导体球面的镜像法叠加原理分析。
在球内应该加上两个镜像电荷:一个是Q 在球面上的镜像电荷,q 1 = -aQ/D ,距离球心b=a 2/D ;第二个是-Q 在球面上的镜像电荷,q 2 = aQ/D ,距离球心b 1=-a 2/D 。
当距离较大时,镜像电荷间的距离很小,等效为一个电偶极子,电偶极矩为232)1(1DQa b b q p --= (2)球外任意点的电场等于四个点电荷产生的电场的叠加。
设+Q 和-Q 位于坐标z 轴上,当Q 和D 分别趋于无穷,同时保持Q/D 2不变时,由+Q 和-Q 在空间产生的电场相当于均匀平板电容器的电场,是一个均匀场。
均匀场的大小为204/2D Q επ,方向在-e z 。
由镜像电荷产生的电场可以由电偶极子的公式计算:)θθθεπsin cos 2(34e r e r P E +=)θθθεπsin cos 2(230432e r e D r Qa +-=5.5 接地无限大导体平板上有一个半径为a 的半球形突起,在点(0,0,d )处有一个点电荷q (如图5-5),求导体上方的电位。
解:计算导体上方的电位时,要保持 导体平板部分和半球部分的电位都为 零。
先找平面导体的镜像电荷q 1 = -q , 位于(0,0,-d )处。
再找球面镜像 电荷q 2 = -aq/d ,位于(0,0,b )处, b= a 2/d 。
当叠加这两个镜像电荷和原电荷共同产生的电位时,在导体平面上和 图5-5球面上都不为零,应当在球内再加上一个镜像电荷q 3 =aq/d ,位于(0,0,-b )处。
这时,三个镜像电荷和原电荷共同产生的电位在导体平面和球面上都为零。
而且三个镜像电荷在要计算的区域以外。
导体上方的电位为四个点电荷的叠加,即)(332211041rq r qr q R q+++=επϕ其中21]2)(22[d z y x R -++=21]2)(22[1d z y x r +++= 21]2)(22[2b z y x r -++= 21]2)(22[3b z y x r +++= 5.6 求截面为矩形的无限长区域(0<x<a ,0<y<b )的电位,其 四壁的电位为0,0,==)()(b x x ϕϕ0,0=)(y ϕ⎪⎩⎪⎨⎧<<-≤<=by b by U b y b yUy a 2),1(020,0,)(ϕ解:由边界条件0,0,==)()(b x x ϕϕ知,方程的基本解在y 方向应该为周期函数,且仅仅取正弦函数,即 )(sin b n nkynk nY π==在x 方向,考虑到是有限区域,选取双曲正弦和双曲余弦函数,使用边界条件0,0=)(y ϕ,得出仅仅选取双曲正弦函数,即 x b n shnX π=将基本解进行线性组合,得bxn n b x n sh nC ππϕ∑∞==1sin待定常数由x=a 处的边界条件确定,即bxn n b xn sh n C y a ππϕ∑∞==1sin),( 使用正弦函数的正交归一性质,有dy by n b y a b an sh n C bπϕπ⎰=0sin ),(22]cos sin 2)[(0sin 020b b y n y n b b y n n b b U dy b y n b y U b πππππ-=⎰]2cos 222sin 2)[(0ππππn n b n n b b U-=2]cos sin 2)[(02cos 0sin )21(0b b b y n y n b b y n n b b U b b b y n n bU dy b yn b yb b U πππππππ---=⎰- πππππππn b n b b Un n b b Un n n bU cos 02sin 2)(0)2cos cos 0++--=(2c o s20ππn bn b b U -化简以后得dy b y n b y a b a n sh n C bπϕπ⎰=0sin ),(2=2sin2202ππn n b U 求出系数,代入电位表达式,得b x n shb y n ban n n U n πππππϕsin sin 2sin 22041∑∞== 5.7一个截面如图5-7所示的长槽,向y 方向无限延伸,两则的电位是零,槽内y →∞,φ→0,底部的电位为0,U x =)(ϕ求槽内的电位。
解:由于在x=0和x=a 两个边界的 电位为零,故在x 方向选取周期解,且仅仅取正弦函数,即)(sin a n nk xnk n Xπ== 图5-7在y 方向,区域包含无穷远处,故选取指数函数,在y →∞时,电位趋于零,所以选取由基本解的叠加构成电位的表示式为yy n k e nY -= 由基本解的叠加构成电位的表示式为ay n ea x n n n ππϕ-∑∞==sin 1C待定系数由y=0的边界条件确定。
在电位表示式中,令y=0,得a xn n nU πsin 1C 0∑∞==)cos 1(00sin 02πππn n aUdx a xn a U a n C-=⎰= 当n 为奇数时,πn UnC 04=,当n 为偶数时,00=C 。
最后,电位的解为ay n e ax n n U n πππϕ-∑∞==sin45,3,15.7 若上题的底部的电位为00,U x =)(ϕaxπ3sin重新求槽内的电位。
解:同上题,在x 方向选取正弦函数,即)(sin an nk x nk nX π==,在y方向选取yn k e nY -=。
由基本解的叠加构成电位的表示式为ay n ea x n n n ππϕ-∑∞==sin 1C将y=0的电位代入,得0U a xπ3sin a xn n nπsin1C ∑∞==应用正弦级数展开的唯一性,可以得到n=3时,03C C =,其余系数00=C ,所以a y eax ππϕ33sin 0U -=5.9 一个矩形导体槽由两部分构成,如图5-9所示,两个导体板的电位分别是U 0和零,求槽内的电位。
解:将原问题的电位看成是两个电 位的叠加。
一个电位与平行板电容 器的电位相同(上板电位为U 0,下 板电位为零),另一个电位为U ,即U y a+=Uϕ 图5-9其中,U 满足拉普拉斯方程,其边界条件为y=0 , U=0y=a , U=0 x=0时,⎪⎪⎩⎪⎪⎨⎧<<-<<-=-=20,02,000,0U a y ay U ay a a y U U ay U y )(ϕx →∞时,电位U 应该趋于零。
U 的形式解为ayφ=U 0a x n e a yn n nU ππ-∑∞==sin 1C待定系数用x=0的条件确定。
=)(y ,0U ay n n n U πsin1C ∑∞==dy ay n a y U n C aπ⎰=0sin ),0(22]cos sin 2)[(0sin 020a a y n y n a a y n n a a Udy a y n a y U aπππππ--=-⎰ ]2cos 222sin 2)([0ππππn n a n n a a U+-=2]c o s s i n 2)[(02cos 0sin )21(0a a a y n y n a a y n n a a U a a a y n n aU dy a yn a ya a U πππππππ---=⎰- πππππππn a n a a Un n a a Un n n aU cos 02sin 2)(0)2cos cos 0++--=(2c o s20ππn an a a U -化简以后,得到dy a y n a y U n C aπ⎰=0sin ),0(2=2cos 0ππn n a U只有偶数项的系数不为零。
将系数求出,代入电位的表达式,得a x n ea y n n n U n y a Uππππϕ-∑∞=+=sin 2cos 02,4,20 5.10 将一个半径为a 的无限长导体管平分成两半,两部分之间互相绝缘,上半(0<Ф<π)接电压U 0,下半(π<Ф<2π)电位为零,如图5-10,求管内的电位。
