4-1.7三角函数小结和复习(2)--高一上学期必修四【文教案】
4-1.7三角函数小结和复习(2)
高一数学必修模块4第一章三角函数单元测试卷
一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．集合A={|,}2n n Z π
αα=
∈2{|2,}3n n Z ααππ=±∈，B={2|,}3n n Z πββ=∈1
{|,}2
n n Z ββππ=+∈， 则A 、B 之间关系为
（ ）
A ．A
B ⊂
B ．B A ⊂
C ．B A
A B 2．函数)4
2sin(log 2
1π
+
=x y 的单调减区间为
）
A ．(,]()4k k k Z π
ππ-
∈
B ．(k π
C ．3
(,]
()k k k Z π
πππ-+∈
D ．(8
k π
3的值等于（ ）
A D ．－3 4α= （ ）
D ．2
π－3 5
（ ）
6．下列函数中同时具有①最小正周期是π；②图象关于点（
6
π
,0）对称这两个性质的是（ ） A. y ＝cos （2x ＋6π） B ．y ＝sin （2x ＋6π） Ｃ．y ＝sin （2x ＋6π）Ｄ．y ＝tan （x ＋6
π
）
7．已知cos (02)y x x π=≤≤的图象和直线y=1围成一个封闭的平面图形，该图形的面积
是
（ ）
A ．4π
B ．2π
C ．8
D ．4
8．与正弦曲线x y sin =关于直线34
x π=对称的曲线是（ ）
A ．x y sin =
B ．x y cos =
C ．x y sin -=
D ．x y cos -=
9. 若方程1cos +=ax x 恰有两个解，则实数a 的取值集合为 （ ）
A. 2222,,33ππππ-
-⎛⎫⎛⎫ ⎪ ⎪
⎝⎭⎝⎭ B.
22,00,ππ-⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭}
2π 10．已知函数)sin(ϕω+=x A y 在同一周期内，9
π
=x 小值－
2
1
，则该函数解析式为 （ ） A ．)63sin(2π-=x y B ．)63sin(21π+=x y C =y )6
3π
-x
11．.4π，则)4
(π
f 的
值是 （ ）
12],[)cos()(b a x M x g 在ϕω+=上
D ．可以取得最小值－M
131415．设)co s()sin ()(21απαπ
+++=x n x m x f ，其中m 、n 、1α、2α都是非零实数，若 (2001)1,f =则(2005)f = .
16．设函数()sin()(0,)2
2
f x x π
π
ωϕωϕ=+>-<<
，给出以下四个论断：
①它的图象关于直线12
x π
=
对称； ②它的图象关于点(
,0)3
π
对称；
③它的周期是π； ④在区间[,0)6
π
-
上是增函数。
以其中两个论断作为条件，余下论断作为结论，写出你认为正确的两个命题： （1）_________________ ； （2）__________________.（用序号表示） 三、解答题：本大题共6小题，解答应写出文字说明、证明过程或演算步骤． 17．若x
x x x x tan 2
cos 1cos 1cos 1cos 1-
=+---+, 求角x 的取值范围.
18tan x 的图像经过怎样的变换得到。
19．已知4
3tan -=θ，求θθθ2
cos cos sin 2-+的值。
20．设)(x f 满足(sin )3(sin )4sin cos (||)2
f x f x x x x π
-+=⋅≤
,
（１）求)(x f 的表达式； （２）求)(x f 的最大值．
21
22R 上的偶函数，其图象关于点)0,4
3(πM
参考答案
1.C
2. B
3.C
4.C
5.C
6. A
7.B 8 D 9.D 10.B 11.A 12.A 13.
1
8
14. 5 15.－1 16.(1) ①③⇒②④ (2) ②③⇒①④ 17．左|
sin |cos 2|sin ||cos 1||sin ||cos 1|x x x x x x =--+==右，
).(222,0sin ,sin cos 2|sin |cos 2Z k k x k x x
x x x ∈+<<+<-=∴
ππππ
18．可先把tan y x =
tan()6
y x π
=-
，从而得到
1tan()26
y x π
=-的图像。
19．θθθ2
cos cos sin 2=-+
20．得f 由３21x x -．
()f x ==＝x =时，max 1.f =
21．
1sin sin 3x y +=1
sin sin 3
x y ∴=-代入μ中，得
21sin (1sin )3y y μ=---222111sin sin (sin )3212
y y y =--=--
1sin 1x -≤≤214
sin 333
x ∴-≤-≤
又1sin sin ,1sin 13y x y =--≤≤且2
sin 13y ∴-≤≤
min max 11124
(),()21239
μμμμ∴==-=-=
22．解：由f (x )是偶函数，得f (－x )= f (－x ).
即： ).sin()sin(ϕωϕω+=+-x x 所以－x x ωϕωϕsin cos sin cos =
对任意x 都成立，且,0>ω所以得ϕcos =0.
，
由f (x )的图象关于点M 对称，得)43(f x f -=-π
)4
3(π
f ，所以)4
3(
π
f =0. .;
;
.
.3cos )3sin()3(
∴∴=+=ωωππωππ所以当当当k k k f。
数学北师大版高中必修4三角函数 本章复习与小结
三角函数本章复习与小结彭泽一中谷中庆教学目标：1、知识与技能（1）了解本章的知识结构体系，在整体上有一个初步的认识；（2）加深对任意角、弧度及三角函数的理解；（3）掌握三角函数的图像与性质，能利用性质进行解题；（4）掌握一定的解题方法，形成较好的能力。
2、过程与方法三角函数是一种重要的函数，通过整理本章的各知识点以及它们之间的联系，帮助学生系统地认识本章内容，从而对本章内容有全面的认识，上升到更高一个水平；启发学生将本章内容与数学1、数学2的横向联系，形成知识的网络化。
3、情感态度与价值观通过本节的复习，使同学们对三角函数有一个全面的认识；以辩证唯物主义的观点看待任何事，养成一种科学的态度；帮助学生树立正确的世界观和人生观，树立远大理想，立志为国争光，为洋浦的开发建设贡献力量。
二、教学重、难点重点: 三角函数定义，以及三角函数的图像与性质难点: 本章内容的系统掌握与灵活运用三、学法与教学用具师生共同整理本章的知识结构体系，从角到角的度量，从三角函数的定义到它们之间的关系，再到三角函数的图像与性质；整理本章出现的各种题目，从中理顺它们的关系，将它们适当归类，提炼其中的方法，争取做到举一反三、触类旁通。
教学用具：投影仪、三角板四、教学思路【知识的初步整合】【知识的概括与引申】1．角是由射线的旋转所产生的，那么就有旋转量与旋转方向的问题，所以必须推广到任意正角、负角和零角。
为了使弧长公式在形式上变得简单，引进了弧度制，这一度量单位不仅使弧长公式、扇形面积公式得以简化，也为定义任意角的三角函数作好了准备。
2．同角三角函数的基本关系的作用是：已知某任意角的一种三角函数值，就能求出另一种三角函数值。
3．诱导公式的作用是：把求任意角的三角函数值转化为求锐角三角函数值。
4．三角函数的图像和性质是本章的重要内容，是三角函数应用的基础。
【例题选讲】例1．求图中公路弯道处弧AB 的长l （精确到1m ）图中长度单位为：m解： ∵ 360π=∴ )(471514.3453m R l ≈⨯≈⨯=⋅=πα例2． 已知θ是第三象限角且02cos <ϑ，问2ϑ解：∵2)12()12(ππϑπ++<<+k k )(Z k ∈ ∴4322ππθππ+<<+k k )(Z k ∈ 则2ϑ是第二或第四象限角 又∵02cos<ϑ 则2ϑ是第二或第三象限角 ∴2ϑ必为第二象限角 例3．已知α=αcos 2sin ，求的值。
新人教版高中数学 第1章 三角函数复习与小结教案必修四
高中数学 第1章 三角函数复习与小结教案 新人教版必修4 教学目标：1．进一步巩固三角函数的图象、性质；2．应用三角函数解决实际问题；3．渗透数形结合与转化思想．教学重点：让学生掌握三角函数的图象；熟练运用三角公式．教学难点：图象变换．教学过程：一、问题情景问题：本章有哪些知识点？1．任意角的概念；2．角度制与弧度制；3．任意角的三角函数；4．三角函数的图象与性质；二、学生活动1．sin390°＋cos120°＋sin225°的值是 ．2．︒-︒︒-︒23cos 37cos 23sin 37sin ＝ ． 3．已知sin θ＋cos θ＝51-，(0,),πθ∈ tan θ的值是 ． 4．关于函数f (x )＝4sin(2x ＋π3)(x ∈R)，有下列命题： （1）y ＝f (x )的表达式可改写为y ＝4·cos(2x －π6)； （2）y ＝f (x )是以2π为最小正周期的周期函数；（3）y ＝f (x )的图象关于点（－π6，0）对称； （4）y ＝f (x )的图象关于直线x ＝－π6对称．其中正确的命题序号是 （注：把你认为正确的命题序号都填上）．三、数学应用1．例题：例1 已知角α终边上一点0),3,4(≠-a a a P ，求)29sin()211cos()sin()2cos(απαπαπαπ+---+的值． 分析 利用三角函数的定义，以及诱导公式．例2 已知函数cos 2(0)6y a b x b π=-+>⎛⎫ ⎪⎝⎭的最大值为23，最小值为21-. （1）求b a ,的值；（2）求函数)3sin(4)(π--=bx a x g 的最小值并求出对应x 的集合.分析：（1）利用三角函数的性质，]1,1[)62cos(-∈+πx （2）利用三角函数的性质，]1,1[)3sin(-∈-πbx 2．练习：（1）函数)22cos(π+=x y 的图象的对称轴方程是 ；（2）要得到函数y ＝sin(2x -3π)的图象，只要将函数y ＝sin2x 的图象 ； （3）已知()sin()cos()4f x a x b x παπβ=++++（,,,a b αβ为非零实数），(2007)5f =，则(2008)f = ；（4）函数)32cos(π--=x y 的单调递增区间是 ． 四、要点归纳与方法小结1．进一步巩固、熟悉了三角函数的图象、性质并加以灵活应用；2．初步学会了如何应用三角函数解决实际问题；3．进一步渗透了数形结合与转化思想．。
高中数学必修四《三角函数章节复习与小结》优秀教学设计
三角函数章节复习与小结学习目标：1、对本章知识系统化，网络化。
2、通过本章学习，感受三角函数与实际生活的紧密联系，感受数学的价值. 学习重点：三角函数的图象与性质. 学习难点：三角函数知识的综合运用. 学习过程：一、背景设置1、三角函数章节有关知识点：⑴三角函数的定义，符号，任意角三角函数 ⑵三角函数线，弧长公式，弧度与角度的互化 ⑶同角三角函数关系式 ⑷诱导公式⑸三角函数的性质，定义域，值域，周期性，奇偶性，最值，对称轴，对称中心二、探究研究1 .一个半径为R 的扇形，它的周长为4R ，则这个扇形所含弓形的面积是：A ． ))1sin(cos 2(212R - B ．)1sin(cos 212RＣ．221R Ｄ．221cos 1sin R R -２.设θ是第二象限角，则必有： Ａ.2cot2tanθθ>；Ｂ.2cot2tanθθ<；Ｃ.2cos2sinθθ>；Ｄ.2cos2sinθθ<3. 已知Ｐ（-4k,3k ）(0≠k )是角α终边上一点，则ααcos sin 2+ 的值等于： Ａ.52±Ｂ. 52 Ｃ. 52- Ｄ.51±４.将函数()x f y =的图象沿x 轴向左平移6π个单位，再使图象上所有点的纵坐标不变，横坐标变为原来的２倍，得到x y cos =的图象，则)(x f 可能是：Ａ.)62cos()(π+=x x f Ｂ. )62cos()(π-=x x fＣ. )32cos()(π+=x x f Ｄ. )32cos()(π-=x x f5 .在ABC ∆中，若)sin()sin(C B A C B A +-=-+，则ABC ∆形状是 A 、等腰∆ B 、∆Rt C 、等腰∆Rt D 、等腰或∆Rt6 .比较大小：.47cos ,101sin ,23cos -____________________. 7 .已知,21cos sin 1-=+x x 则=-xx sin 1cos ____________.8 .已知)(x f 为奇函数，且)()4(x f x f =+，则____________)2006(=f .三、教学精讲例1 已知,57cos sin =+αα且1tan >α，求αcos 的值。
高中数学 第四章 三角函数小结与复习(3)教案
三角函数小结与复习（3）知识目标：1任意角的三角函数、任意角的概念、弧度制、任意角的三角函数的概念、同角三角函数间的关系、诱导公式；2两角和与差的三角函数、二倍角的三角函数； 3三角函数的图象和性质、已知三角函数值求角 教学目的：1理解任意角的概念、弧度的意义；能正确地进行弧度与角度的换算； 2掌握任意角的正弦、余弦、正切的定义，并会利用与单位圆有关的三角函数线表示正弦、余弦和正切；了解任意角的余切、正割、余割的定义；掌握同角三角函数的基本关系式；掌握正弦、余弦的诱导公式；3掌握两角和与两角差的正弦、余弦、正切公式；掌握二倍角的正弦、余弦、正切公式；4能正确运用三角公式，进行三角函数式的化简、求值及恒等式证明； 5会用与单位圆有关的三角函数线画出正弦函数、正切函数的图象，并在此基础上由诱导公式画出余弦函数的图象；理解周期函数与最小正周期的意义；并通过它们的图象理解正弦函数、余弦函数、正切函数的性质；会用“五点法”画正弦函数、余弦函数和函数y ＝A sin(ωx ＋ϕ)的简图，理解A 、ω、ϕ的物理意义；6会用已知三角函数值求角，并会用符号arcsin x 、arccos x 、arctan x 表示教学重点：三角函数的知识网络结构及各部分知识教学难点：熟练掌握各部分知识，并能灵活应用其解决相关问题 德育目标：1渗透“变换”思想、“化归”思想； 2培养逻辑推理能力； 3培养学生探求精神 教学方法：讲练结合法通过讲解强化训练题目，加深对三角函数知识的理解，提高对三角函数知识的应用能力授课类型：复习课 课时安排：1课时教 具：多媒体、实物投影仪 教学过程： 一、讲解范例：例1化简：8cos 228sin 12+++解：原式)14cos 2(224cos 4sin 2122-+++=4cos 2)4cos 4(sin 222++== 2|sin4 + cos4| +2|cos4|∵)23,(4ππ∈ ∴sin4 + cos4 < 0 cos4 < 0 ∴原式= -2(sin4 + cos4) -2cos4 = -2sin4 - 4cos4例2已知),2(,61)4sin()4sin(ππ∈α=α-πα+π，求sin4α的值 解：∵61)4sin()4sin(=α-πα+π ∴31)4cos()4sin(2=α+πα+π∴31)]4(2sin[=α+π ∴cos2α =31又∵),2(ππ∈α ∴2α∈ (π, 2π)∴sin2α = 322)31(12cos 122-=--=α-- ∴sin4α = 2sin2αcos2α = 92431)322(2-=⨯-⨯ 例3已知3sin 2α + 2sin 2β = 1，3sin2α - 2sin2β = 0，且α、β都是锐角，求α+2β的值解：由3sin 2α + 2sin 2β = 1 得1 - 2sin 2β = 3sin 2α ∴cos2β = 3sin 2α 由3sin2α - 2sin2β = 0 得sin2β =23sin2α = 3sin αcos α ∴cos(α+2β) = cos αcos2β -sin αsin2β = cos α3sin 2α - sin α3sin αcos α = 0∵0︒<α<90︒, 0︒<β<90︒ ∴0︒< α+2β <270︒ ∴α+2β = 90︒例4已知sin α是sin θ与cos θ的等差中项，sin β是sin θ、cos θ的等比中项，求证：α=θ+π=β2cos 2)4(cos 22cos 2证：由题意： 2sin α = sin θ + cos θ ①sin β2= sin θcos θ ② ①2-2②：4sin 2α - 2sin 2β = 1∴1 - 2sin 2β = 2 - 4sin 2α ∴cos2β = 2cos2α由②：1 - 2sin β2= 1 - 2sin θcos θ∴cos2β = (sin θ - cos θ)2= )4(cos 2)]4cos(2[22θ+π=θ+π ∴α=θ+π=β2cos 2)4(cos 22cos 2原命题成立 例5奇函数f (x )在其定义域)2,2(ππ-上是减函数， 并且f (1-sin α) + f(1-sin 2α) < 0，求角α的取值范围解：∵f (1-sin α) < f (sin 2α -1) ∴ ⎪⎪⎪⎩⎪⎪⎪⎨⎧<-<-<-<--<-211sin 2121sin 1211sin sin 122αααα解之得：α∈(2k π+4π, 2k π+2π)∪(2k π+2π, 2k π+43π) (k ∈Z)例6已知sin α = a sin(α+β) (a >1)，求证：a-ββ=β+αcos sin )tan(证：∵sin α = sin[(α+β)-β] = sin(α+β)cos β-cos(α+β)sin β = a sin(α+β)∴sin(α+β)(cos β - a ) = cos(α+β)sin β∴a-ββ=β+αcos sin )tan(例7如图半⊙O 的直径为2，A 为直径MN 延长线上一点，且OA=2，B 为半圆周上任一点，以AB 为边作等边△ABC (A 、B 、C 按顺时针方向排列)问∠AOB 为多少时，四边形OACB 的面积最大？这个最大面积是多少？ 解：设∠AOB=θ 则S △AOB =sin θ S △ABC =243AB 作BD ⊥AM, 垂足为D, 则BD=sin θ OD=-cos θAD=2-cos θ∴22222)cos 2(sin ϑϑ-+=+=AD BD AB=1+4-4cos θ=5-4cos θ ∴S △ABC =43(5-4cos θ)=ϑcos 3435- 于是S 四边形OACB =sin θ-3cos θ+435=2sin(θ-3π)+4A∴当θ=∠AOB=65π时四边形OACB 的面积最大，最大值面积为2+435例8 求函数y=3tan(x 6π+3π)的定义域、最小正周期、单调区间 解：x 6π+3π≠k π+2π得x ≠6k+1 (k ∈Z) 定义域为{x|x ≠6k+1, k ∈Z }由T=ωπ得T=6 即函数的最小正周期为6 由k π+2π<x 6π+3π< k π+2π (k ∈Z)得：6k -5<x<6k+1 (k+1) 单调区间为：(6k -1,6k+1) (k ∈Z) 例9 比较大小：1︒tan(-59π)与tan 512π解：tan(-59π)=tan 5π tan 512π= tan 52π∵-2π<5π<52π<2π且y=tanx 在此区间内单调递增 2︒若α, β为锐角且cot α>tan β，比较α+β与2π的大小 解：cot α= tan(2π-α) ∵cot α>tan β ∴tan(2π-α)>tan β ∵0<2π-α<2π 0<β<2π且y=tanx 在此区间内递增 ∴2π-α>β ∴α+β<2π 例10 求函数f (x )=xx cot tan 1-的最小正周期解：f (x )=)sin (cos 2cos sin 2cos sin cos sin 1sin cos cos sin 12222x x xx xx x x xxx x --=-=-x x x 2tan 212cos 22sin -=-=∴最小正周期T=2π二、小结三、课后作业：1． 如果函数y=sin2x+acos2x 的图象关于直线x=-8π对称，那么a 等于……（D ） (A)2(B)1(C)- 2(D)-1解一：（特殊值法） 点(0,0)与点(-4π,0)关于直线x=-8π对称 ∴f (0)=f (-4π) 即sin0+acos0=sin(-2π)+acos(-2π) ∴a=-1 解二：（定义法）∵函数图象关于直线x=-8π对称 ∴sin2(-8π+x)+acos2(-8π+x)= sin2(-8π-x)+acos2(-8π-x) ∴2cos4πsin2x=-2asin 4πsin2x ∴a=-1 解三：（反推检验法） 当a=2时y=sin2x+2cos2x ∴y max =3 y min =-3而当x=-8π时 y=1-22≠±3 可排除A ，同理可排除B 、C2． 函数f (x )=Msin(ωx+φ) (ω>0)在区间[a,b]上是增函数，且f (a )=M ，f (b )=-M 则函数g (x )= Mcos(ωx+φ))在区间[a,b]上……………（C ） (A)是增函数 (B)是减函数 (C)可取得最大值M (D)可取得最小值-M解一：由已知M>0 -2π+2k π≤ωx+φ≤2π+ (k ∈Z) ∴有g (x )在[a,b]上不是增函数也不是减函数，且 当ωx+φ=2k π时 g (x )可取得最大值M解二：令ω=1, φ=0 区间[a,b]为[-2π,2π] M=1 则g (x )为cosx ，由余弦函数g (x )=cosx 的性质得最小值为-M3．直线y=a （a 为常数）与正切曲线y=tan ωx (ω为常数且ω>0)相交的相邻两点间的距离是………………………………（C ） (A)π (B)ωπ2 (C)ωπ(D)与a 有关 解：由正切函数的图象可知“距离”即为周期 四、板书设计（略）五、课后记：。
高中数学必修四教案：第一章+三角函数复习与小结
格一课堂教学方案精美句子1、善思则能“从无字句处读书”。
读沙漠，读出了它坦荡豪放的胸怀；读太阳，读出了它普照万物的无私；读春雨，读出了它润物无声的柔情。
读大海，读出了它气势磅礴的豪情。
读石灰，读出了它粉身碎骨不变色的清白。
2、幸福幸福是“临行密密缝，意恐迟迟归”的牵挂；幸福是“春种一粒粟，秋收千颗子”的收获. 幸福是“采菊东篱下，悠然见南山”的闲适；幸福是“奇闻共欣赏，疑义相与析”的愉悦。
幸福是“随风潜入夜，润物细无声”的奉献；幸福是“夜来风雨声，花落知多少”的恬淡。
幸福是“零落成泥碾作尘，只有香如故”的圣洁。
幸福是“壮志饥餐胡虏肉，笑谈渴饮匈奴血”的豪壮。
幸福是“先天下之忧而忧，后天下之乐而乐”的胸怀。
幸福是“人生自古谁无死，留取丹心照汗青”的气节。
3、大自然的语言丰富多彩：从秋叶的飘零中，我们读出了季节的变换；从归雁的行列中，我读出了集体的力量；从冰雪的消融中，我们读出了春天的脚步；从穿石的滴水中，我们读出了坚持的可贵；从蜂蜜的浓香中，我们读出了勤劳的甜美。
4、成功与失败种子，如果害怕埋没，那它永远不能发芽。
鲜花，如果害怕凋谢，那它永远不能开放。
矿石，如果害怕焚烧（熔炉），那它永远不能成钢（炼成金子）。
蜡烛，如果害怕熄灭（燃烧），那它永远不能发光。
航船，如果害怕风浪，那它永远不能到达彼岸。
5、墙角的花，当你孤芳自赏时，天地便小了。
井底的蛙，当你自我欢唱时，视野便窄了。
笼中的鸟，当你安于供养时，自由便没了。
山中的石！当你背靠群峰时，意志就坚了。
水中的萍！当你随波逐流后，根基就没了。
空中的鸟！当你展翅蓝天中，宇宙就大了。
空中的雁！当你离开队伍时，危险就大了。
地下的煤！你燃烧自己后，贡献就大了6、朋友是什么？朋友是快乐日子里的一把吉它，尽情地为你弹奏生活的愉悦；朋友是忧伤日子里的一股春风，轻轻地为你拂去心中的愁云。
朋友是成功道路上的一位良师，热情的将你引向阳光的地带；朋友是失败苦闷中的一盏明灯，默默地为你驱赶心灵的阴霾。
数学必修4教学设计(第一章小结复习2)
课题：高中数学北师大版必修4
第一章《三角函数》小结复习（2）
主备人：刘克忠 时间： 班级：高一（ 、 ）
（数学必修4第66页）
1．了解任意角的概念和弧度制，能进行弧度与角度的互化；
2．理解任意角的三角函数的定义；
3．能正确画出函数sin y x =，cos y x =，tan y x =的图像，会利用单位圆或三角函数的图像推导出诱导公式，并能借助图像理解正弦函数、余弦函数在区间
[0,2]π，正切函数在区间(0,2)π上的性质；
4．理解函数sin()y A x ωϕ=+的实际意义；会画函数sin()y A x ωϕ=+的图像，体会参数A ，ω，ϕ对函数图像的影响.
阅读北师大版数学必修4课本6869P P -内容，自主完成下列问题：
1．课本68P 复习参考题A 组第1题.
2．课本68P 复习参考题A 组第2题.
3．课本68P 复习参考题A 组第6题.
阅读北师大版数学必修4课本6869P P -内容，小组交流完成下列问题：
1．课本68P 复习参考题A 组第8题.
2．课本68P 复习参考题A 组第9题.
3．课本68P 复习参考题A 组第13题.
阅读北师大版数学必修4课本6869P P -内容，小组交流、教师指导完成下列问题：
1．课本68P 复习参考题A 组第11题.
P复习参考题A组第12题.
2．课本
68
P复习参考题B组第2，5题. 1．课后作业：北师大版数学必修4课本
69
P复习参考题B组第1，3，4题. 2．课后练习：北师大版数学必修4课本
69
【教学反思与评价】。
高一数学三角函数复习教案
必修4 第一章 三角函数 复习（一）一、 基本知识1、任意角：（1）正角：按逆时针旋转所形成的角 （2）负角：按顺时间旋转所形成的角（3）零角：没有旋转（始边和终边重合） 2、象限角：终边所在象限3、与角α终边相同的角：360 n n Z βα=+⋅∈4、弧度制和角度制的转化：180 rad π=5、弧长公式：12l R α=扇形面积公式：212S R lR α== 6、特殊角三角函数值：（1）同角三角函数基本关系：22sin cos 1αα+= sin tan cos ααα=（2）三角函数诱导公式：公式一：角度制：sin()sin 360k αα+⋅︒= 弧度制： sin(2)sin k απα+=ααcos )360cos(=︒⋅+k cos(2)cos k απα+= ααtan )360tan(=︒⋅+k tan(2)tan k απα+=公式二：角度制：sin(180sin αα︒+=-）弧度制：sin(sin παα+=-） cos(180cos αα︒+=-） cos(cos παα+=-） ααtan 180tan(=+︒） ααπtan tan(=+）公式三： sin()sin αα-=- cos()cos αα-= tan()tan αα-=- 公式四：角度制：ααsin 180sin(=-︒）弧度制：ααπsin sin(=-） cos(180cos αα︒-=-） cos(cos παα-=-） ααtan 180tan(-=-︒） ααπtan tan(-=-）公式五：角度制：sin(90)cos αα-= 弧度制： sin()cos 2παα-=cos(90)sin αα-= cos()sin 2παα-=公式六：角度制：sin(90)cos αα+= 弧度制： sin()cos 2παα+=cos(90)sin αα+=- cos()sin 2παα+=-8、周期函数：一般地，对于函数f (x )，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有f (x ＋T )＝f (x )，那么函数f (x )就叫做周期函数，非零常数T 叫做这个函数的周期9、正弦函数：y=sinx（1）定义域：R 值域：[-1,1]（2）图象：五点法画图正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是：(0,0) (2π,1) (,0) (23π,-1) (2,0)（3）周期性：2k π(k ∈Z 且k ≠0)都是它的周期，最小正周期是2π （4）奇偶性：正弦函数在定义域R 内为奇函数，图象关于原点对称（5）单调性：在［－2π＋2k π，2π＋2k π］(k ∈Z )上都是增函数；在［2π＋2k π，23π＋2k π］(k ∈Z )上都是减函数。
高中数学必修四第一章《三角函数》学案 三角函数章节复习与小结(教师版)
三角函数章节复习与小结 总第 16课时学习目标：1、对本章知识系统化，网络化。
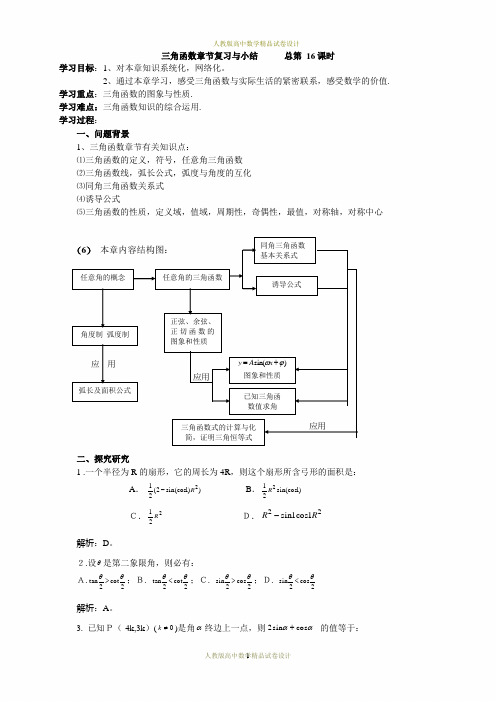
2、通过本章学习，感受三角函数与实际生活的紧密联系，感受数学的价值. 学习重点：三角函数的图象与性质. 学习难点：三角函数知识的综合运用. 学习过程：一、问题背景1、三角函数章节有关知识点：⑴三角函数的定义，符号，任意角三角函数 ⑵三角函数线，弧长公式，弧度与角度的互化 ⑶同角三角函数关系式 ⑷诱导公式⑸三角函数的性质，定义域，值域，周期性，奇偶性，最值，对称轴，对称中心（6） 本章内容结构图：二、探究研究1 .一个半径为R 的扇形，它的周长为4R ，则这个扇形所含弓形的面积是：A ． ))1sin(cos 2(212R - B ．)1sin(cos 212RＣ．221R Ｄ．221cos 1sin R R -解析：D 。
２.设θ是第二象限角，则必有： Ａ.2cot2tanθθ>；Ｂ.2cot2tanθθ<；Ｃ.2cos2sinθθ>；Ｄ.2cos2sinθθ<解析：A 。
3. 已知Ｐ（-4k,3k ）(0≠k )是角α终边上一点，则ααcos sin 2+ 的值等于：同角三角函数 基本关系式诱导公式任意角的三角函数任意角的概念 )sin(ϕω+=x A y 图象和性质 正弦、余弦、正切函数的图象和性质 已知三角函数值求角 三角函数式的计算与化简，证明三角恒等式 角度制 弧度制弧长及面积公式 应用应用应用Ａ.52±Ｂ. 52 Ｃ. 52- Ｄ.51±解析：A 。
４.将函数()x f y =的图象沿x 轴向左平移6π个单位，再使图象上所有点的纵坐标不变，横坐标变为原来的２倍，得到x y cos =的图象，则)(x f 可能是：Ａ.)62cos()(π+=x x f Ｂ. )62cos()(π-=x x fＣ. )32cos()(π+=x x f Ｄ. )32cos()(π-=x x f解析：D 。
高中数学必修四章三角函数章末小结导学案
高中数学必修四章三角函数章末小结导学案三角函数章末小结【学习目标】理解任意角的概念、弧度的意义；能正确地进行弧度与角度的换算；掌握任意角的正弦、余弦、正切的定义，并会利用三角函数线表示正弦、余弦和正切；掌握同角三角函数的基本关系式；掌握正弦、余弦的诱导公式；并能应用它们进行简单的求值、化简、证明；能画出正弦函数、余弦函数、正切函数的图象；理解周期函数与最小正周期的意义；并通过它们的图象理解正弦函数、余弦函数、正切函数的性质；会用“五点法”画出正弦函数、余弦函数及的图象，理解的物理意义；复习中渗透“变换”、“化归”思想；体会数形结合思想，学会用数形结合来思考和解决数学问题。
【新知自学】知识回顾：图表一：知识网络结构图理解本章知识结构体系，了解本章知识之间的内在联系。
图表二：三角函数定义、同角三角函数基本关系式、三角函数值的正负．．．“象限全为正，”图表三：诱导公式函数角图表四：三角函数的图像和性质函数正弦函数余弦函数正切函数图像定义域值域最大值为1，最小值为-1最大值为1，最小值为-1无最值周期性最小正周期最小正周期最小正周期奇偶性奇函数偶函数奇函数单调性在上是增函数；在上是减函数在上是增函数；在上是减函数在上是增函数；对点练习：若角的终边落在直线上，求和的值。
利用图像变换讨论由得图像怎样得到的图像判断下列函数的奇偶性①y=-3sin2x②y=-2cos3x-1③y=-3sin2x+1④y=sinx+cosx⑤y=1-cos【合作探究】典例精析：例1、已知，求下列各式的值：变式练习1：计算：证明：例2.已知函数试确定该函数的值域、单调增区间、最大值及取得最大值时x的集合。
变式练习2：观察正弦函数的图像，写出使的的集合。
求适合的集合。
例3、求函数y=-3cos的最大值，并求此时角x的值。
例4、求函数的定义域。
【课堂小结】【当堂达标】．已知cos240约等于0.92,则sin660约等于A．0.92B．0.85c．0.88D．0.95．已知tanx=2，则的值是。
必修4第一章 《三角函数》期末复习教案
第一章《三角函数》期末复习教案一、网络构建二、要点归纳1．任意角三角函数的定义在平面直角坐标系中，设α是一个任意角，它的终边与单位圆交于点P (x ，y )，那么： (1)y 叫做α的正弦，记作sin α，即sin α＝y . (2)x 叫做α的余弦，记作cos α，即cos α＝x . (3)y x 叫做α的正切，记作tan α，即tan α＝yx (x ≠0)． 2．同角三角函数的基本关系式 (1)平方关系：sin 2α＋cos 2α＝1.(2)商数关系：tan α＝sin αcos α ⎝⎛⎭⎫α≠k π＋π2，k ∈Z . 3．诱导公式六组诱导公式可以统一概括为“k ·π2±α(k ∈Z )”的诱导公式．当k 为偶数时，函数名不改变；当k 为奇数时，函数名改变，然后前面加一个把α视为锐角时原函数值的符号．记忆口诀为“奇变偶不变，符号看象限”．4．正弦函数、余弦函数和正切函数的性质函数y ＝sin xy ＝cos xy ＝tan x图象定义域 R R ⎩⎨⎧⎭⎬⎫x |x ∈R 且x ≠k π＋π2，k ∈Z值域[－1,1][－1,1]R对称性对称轴：x ＝k π＋π2(k ∈Z )；对称中心：(k π，0)(k ∈Z ) 对称轴：x ＝k π(k ∈Z )；对称中心：⎝⎛⎭⎫k π＋π2，0(k ∈Z )对称中心：⎝⎛⎭⎫k π2，0(k ∈Z )， 无对称轴奇偶性 奇函数 偶函数 奇函数 周期性最小正周期：2π 最小正周期：2π 最小正周期：π 单调性在⎣⎡⎦⎤－π2＋2k π，π2＋2k π(k ∈Z )上单调递增；在[－π＋2k π，2k π] (k ∈Z )上单调递增；在[2k π，π＋2k π]在开区间⎝⎛⎭⎫k π－π2，k π＋π2 (k ∈Z )上单调递增在⎣⎡⎦⎤π2＋2k π，3π2＋2k π(k ∈Z )上单调递减(k ∈Z )上单调递减最值当x ＝π2＋2k π(k ∈Z )时，y max ＝1；当x ＝－π2＋2k π(k ∈Z )时，y min ＝－1当x ＝2k π(k ∈Z )时，y max ＝1；当x ＝π＋2k π(k ∈Z )时，y min ＝－1无最值题型一 三角函数的化简与求值例1 已知f (α)＝sin 2(π－α)·cos (2π－α)·tan (－π＋α)sin (－π＋α)·tan (－α＋3π).(1)化简f (α)；(2)若f (α)＝18，且π4<α<π2，求cos α－sin α的值；(3)若α＝－47π4，求f (α)的值．考点 综合运用诱导公式化简、求值 题点 综合运用诱导公式化简、求值 解 (1)f (α)＝sin α·cos α·tan α(－sin α)(－tan α)＝sin α·cos α.(2)由f (α)＝sin α·cos α＝18可知，(cos α－sin α)2＝cos 2α－2sin α·cos α＋sin 2α ＝1－2sin α·cos α＝1－2×18＝34.又∵π4<α<π2，∴cos α<sin α，即cos α－sin α<0，∴cos α－sin α＝－32. (3)∵α＝－47π4＝－6×2π＋π4，∴f ⎝⎛⎭⎫－47π4＝cos ⎝⎛⎭⎫－47π4·sin ⎝⎛⎭⎫－47π4 ＝cos ⎝⎛⎭⎫－6×2π＋π4·sin ⎝⎛⎭⎫－6×2π＋π4 cos π4·sin π4＝22×22＝12.反思感悟 解决三角函数的化简与求值问题一般先化简再求值．在应用中，要注意掌握解题的技巧．比如：已知sin α±cos α的值，可求cos αsin α，注意应用(cos α±sin α)2＝1±2sin αcos α. 跟踪训练1 已知α是三角形的内角，且sin α＋cos α＝15.(1)求tan α的值； (2)把1cos 2α－sin 2α用tan α表示出来，并求其值．考点 运用基本关系式求三角函数值 题点 运用基本关系式求三角函数值 解 (1)由sin α＋cos α＝15，得1＋2sin αcos α＝125，所以sin αcos α＝－1225，因为α是三角形的内角，所以sin α>0，cos α<0， 所以sin α－cos α＝(sin α－cos α)2 ＝(sin α＋cos α)2－4sin αcos α ＝⎝⎛⎭⎫152＋4825＝75， 故得sin α＝45，cos α＝－35，所以tan α＝－43.(2)1cos 2α－sin 2α＝cos 2α＋sin 2αcos 2α－sin 2α＝1＋tan 2α1－tan 2α， 又tan α＝－43，所以1cos 2α－sin 2α＝1＋tan 2α1－tan 2α＝－257. 题型二 三角函数的图象与性质例2 函数f (x )＝3sin ⎝⎛⎭⎫2x ＋π6的部分图象如图所示．(1)写出f (x )的最小正周期及图中x 0，y 0的值； (2)求f (x )在区间⎣⎡⎦⎤－π2，－π12上的最大值和最小值． 考点 正弦、余弦函数的最大(小)值 题点 正弦、余弦函数的最大(小)值 解 (1)f (x )的最小正周期为π，x 0＝7π6，y 0＝3.(2)因为x ∈⎣⎡⎦⎤－π2，－π12，所以2x ＋π6∈⎣⎡⎦⎤－5π6，0， 于是，当2x ＋π6＝0，即x ＝－π12时，f (x )取得最大值0；当2x ＋π6＝－π2，即x ＝－π3时，f (x )取得最小值－3.反思感悟 研究y ＝A sin(ωx ＋φ)的单调性、最值问题，把ωx ＋φ看作一个整体来解决．跟踪训练2 已知函数f (x )＝2sin(ωx ＋φ)(ω>0，|φ|<π)的部分图象如图所示，且A ⎝⎛⎭⎫π2，1，B (π，－1)，则φ的值为 ．考点 求三角函数解析式 题点 根据三角函数图象求解析式 答案 －5π6解析 根据函数f (x )＝2sin(ωx ＋φ)(ω>0，|φ|<π)的图象，且A ⎝⎛⎭⎫π2，1，B (π，－1)，可得从点A 到点B 正好经过了半个周期，即12·2πω＝π－π2，所以ω＝2.再把点A ，B 的坐标代入可得2sin ⎝⎛⎭⎫2×π2＋φ＝－2sin φ＝1,2sin(2×π＋φ)＝2sin φ＝－1， 所以sin φ＝－12，所以φ＝2k π－π6，或φ＝2k π－5π6，k ∈Z .又|φ|<π，所以φ＝－π6或－5π6.当φ＝－π6时不合题意，所以φ＝－5π6.题型三 三角函数的最值或值域命题角度1 可化为y ＝A sin(ωx ＋φ)＋k 型例3 求函数y ＝－2sin ⎝⎛⎭⎫x ＋π6＋3，x ∈[0，π]的最大值和最小值． 考点 正弦、余弦函数的最大(小)值 题点 正弦、余弦函数的最大(小)值 解 ∵x ∈[0，π]，∴x ＋π6∈⎣⎡⎦⎤π6，7π6， ∴－12≤sin ⎝⎛⎭⎫x ＋π6≤1.当sin ⎝⎛⎭⎫x ＋π6＝1，即x ＝π3时，y 取得最小值1. 当sin ⎝⎛⎭⎫x ＋π6＝－12，即x ＝π时，y 取得最大值4. ∴函数y ＝－2sin ⎝⎛⎭⎫x ＋π6＋3，x ∈[0，π]的最大值为4，最小值为1. 反思感悟 利用y ＝A sin(ωx ＋φ)＋k 求值域时要注意角的取值范围对函数式取值的影响． 跟踪训练3 (2017·全国Ⅲ)函数f (x )＝15sin ⎝⎛⎭⎫x ＋π3＋cos ⎝⎛⎭⎫x －π6的最大值为( ) A.65 B ．1 C.35 D.15考点 正弦、余弦函数的最大(小)值 题点 正弦、余弦函数的最大(小)值 答案 A解析 ∵⎝⎛⎭⎫x ＋π3＋⎝⎛⎭⎫π6－x ＝π2， ∴f (x )＝15sin ⎝⎛⎭⎫x ＋π3＋cos ⎝⎛⎭⎫x －π6 ＝15sin ⎝⎛⎭⎫x ＋π3＋cos ⎝⎛⎭⎫π6－x ＝15sin ⎝⎛⎭⎫x ＋π3＋sin ⎝⎛⎭⎫x ＋π3 ＝65sin ⎝⎛⎭⎫x ＋π3≤65. ∴f (x )max ＝65.故选A.命题角度2 可化为二次函数型例4 函数y ＝－tan 2x ＋4tan x ＋1，x ∈⎣⎡⎦⎤－π4，π4的值域为 ． 考点 正切函数的定义域、值域 题点 正切函数的值域 答案 [－4,4]解析 ∵－π4≤x ≤π4，∴－1≤tan x ≤1.令tan x ＝t ，则t ∈[－1,1]， ∴y ＝－t 2＋4t ＋1＝－(t －2)2＋5. ∴当t ＝－1，即x ＝－π4时，y min ＝－4，当t ＝1，即x ＝π4时，y max ＝4.故所求函数的值域为[－4,4]．反思感悟 在换元时要立刻写出新元的范围，否则极易出错．跟踪训练4 (2017·全国Ⅱ)函数f (x )＝sin 2x ＋3cos x －34⎝⎛⎭⎫x ∈⎣⎡⎦⎤0，π2的最大值是 ． 考点 正弦、余弦函数的最大(小)值 题点 余弦函数的最大(小)值 答案 1解析 f (x )＝1－cos 2x ＋3cos x －34＝－⎝⎛⎭⎫cos x －322＋1. ∵x ∈⎣⎡⎦⎤0，π2，∴cos x ∈[0,1]， ∴当cos x ＝32时，f (x )取得最大值，最大值为1. 题型四 数形结合思想在三角函数中的应用例5 如果关于x 的方程sin 2x －(2＋a )sin x ＋2a ＝0在x ∈⎣⎡⎦⎤－π6，5π6上有两个实数根，求实数a 的取值范围．考点 三角函数中的数学思想 题点 三角函数中的数形结合思想 解 sin 2x －(2＋a )sin x ＋2a ＝0， 即(sin x －2)(sin x －a )＝0. ∵sin x －2≠0，∴sin x ＝a ，∴此题转化为求在x ∈⎣⎡⎦⎤－π6，5π6上，sin x ＝a 有两个实数根时a 的取值范围． 由y ＝sin x ，x ∈⎣⎡⎦⎤－π6，5π6与y ＝a 的图象(图略)知12≤a <1. 故实数a 的取值范围是⎣⎡⎭⎫12，1.反思感悟 数形结合思想贯穿了三角函数的始终，对于与方程解有关的问题以及在研究y ＝A sin(ωx ＋φ)(A >0，ω>0)的性质和由性质研究图象时，常利用数形结合思想． 跟踪训练5 方程lg|x |＝sin ⎝⎛⎭⎫x ＋π3的实数根的个数为( ) A ．4 B ．5 C ．6 D ．7 考点 三角函数的数学思想 题点 三角函数中的数形结合思想 答案 C解析 由⎪⎪⎪⎪sin ⎝⎛⎭⎫x ＋π3≤1得－1≤lg|x |≤1，即110≤|x |≤10， 方程lg|x |＝sin ⎝⎛⎭⎫x ＋π3实根的个数就是函数y ＝lg|x |与y ＝sin ⎝⎛⎭⎫x ＋π3图象公共点的个数， 当x >0时，两函数图象如图所示，两图象有3个公共点，同理，当x <0时，两图象也有3个公共点， 故两图象共有6个公共点，从而方程有6个实数根， 故选C.1．已知sin ⎝⎛⎭⎫α－π4＝13，则cos ⎝⎛⎭⎫π4＋α等于( ) A.223 B ．－223 C.13 D ．－13答案 D解析 cos ⎝⎛⎭⎫π4＋α＝sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫π4＋α＝sin ⎝⎛⎭⎫π4－α＝－sin ⎝⎛⎭⎫α－π4＝－13. 2．函数f (x )＝2sin(ωx ＋φ)⎝⎛⎭⎫ω>0，－π2<φ<π2的部分图象如图所示，则ω，φ的值分别是( )A ．2，－π3B ．2，－π6C ．4，－π6D ．4，π3考点 求三角函数的解析式 题点 根据三角函数的图象求解析式 答案 A解析 从图象可得34T ＝5π12－⎝⎛⎭⎫－π3＝3π4， ∴T ＝π＝2πω，∴ω＝2.又∵f ⎝⎛⎭⎫5π12＝2sin ⎝⎛⎭⎫2×5π12＋φ＝2sin ⎝⎛⎭⎫5π6＋φ＝2， 且－π2<φ<π2，∴φ＝－π3.3．函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位长度后，得到一个偶函数的图象，则φ的一个可能的值为( )A ．－π4B ．0 C.π4 D.3π4考点 三角函数图象的平移、伸缩变换 题点 三角函数图象的平移变换 答案 C解析 平移后的图象对应的函数为y ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π8＋φ＝sin ⎝⎛⎭⎫2x ＋π4＋φ. 因为此函数为偶函数，中小学教育资源及组卷应用平台21世纪教育网() 所以π4＋φ＝π2＋k π(k ∈Z )， 所以φ的一个可能值为π4. 4．y ＝2sin x sin x ＋2的最小值是( ) A ．2 B ．－2 C ．1 D ．－1考点 正弦、余弦函数的最大(小)值 题点 正弦函数的最大(小)值答案 B解析 由y ＝2sin x sin x ＋2＝2－4sin x ＋2， 当sin x ＝－1时，y ＝2sin x sin x ＋2取得最小值－2. 5．已知函数f (x )＝2sin ⎝⎛⎭⎫2x －π6＋a ，a 为常数． (1)求函数f (x )的最小正周期；(2)求函数f (x )的单调递增区间；(3)若x ∈⎣⎡⎦⎤0，π2时，f (x )的最小值为－2，求a 的值． 考点 正弦、余弦函数性质的综合应用 题点 正弦、余弦函数性质的综合应用解 (1)f (x )＝2sin ⎝⎛⎭⎫2x －π6＋a ， 所以f (x )的最小正周期T ＝2π2＝π. (2)由2k π－π2≤2x －π6≤2k π＋π2(k ∈Z )， 得k π－π6≤x ≤k π＋π3(k ∈Z )， 所以f (x )的单调递增区间为⎣⎡⎦⎤k π－π6，k π＋π3(k ∈Z )． (3)当x ∈⎣⎡⎦⎤0，π2时，2x －π6∈⎣⎡⎦⎤－π6，5π6， 所以当x ＝0时，f (x )取得最小值，即2sin ⎝⎛⎭⎫－π6＋a ＝－2，故a ＝－1.。