典型例题6:静定结构弯矩图(复杂刚架不求支座反力)
结构力学弯矩图练习

设 有 静 定 与 超 静 定 杆 件 结 构 , 二 者 除 了 支 承 情 况 不 同 外 , 其 余 情 况 完 全 相 同 , 则 在 同 样 的 荷 载 作 用 下 超 静 定 的 比 静 定 的 变 形 要 大 。
( )图 a 与 图 b 的 内 力 除 E 、F 点 附 近 截 面 外 , 其 它 截 面 相 同 。
( )(a llhh(b ll图 示 桁 架 , 当 杆 C D 截 面 积 A 增 加 一 倍( 其 它 杆 截 面 积 不 变 ), 则 其 应 力 就 减 小 一 倍 。
( )PCD超 静 定 结 构 中 如 果 要 降 低 某 些 杆 截 面 弯 矩 10 %, 可 把 该 杆 惯 性 矩 增 大 10 % 。
( )若 不 考 虑 轴 向 变 形 , 则 欲 求 图 示 结 构 D 点 有 单 位 水 平 位 移 时 产 生 的 弯 矩 图 , 可 以 采 用 力 矩 分 配 法 。
( )A BCD图 示 结 构 中 ,E I = 常 数 , EI 1=∞ , 全 长 受 均 布 荷 载 q ,则 : A . M ql AB =-212/ ;B . M AB =0 ;C. M ql AB =-28/ ;D . M ql AB =-131082/ 。
( )EI ABEI 1l /3l /3l /3EI 1图 示 结 构 中 ,梁 式 杆 EI = 常 数 ,链 杆 C D 截 面 积 为 A ,且 I Aa =2, 则 轴 力 N CD 等 于 :A . -P;B. -P /2 ; C . 0 ;D . -P /4 。
( )a a图 a 和 b 图 结 构 的 基 本 频 率 分 别 为 ωa 和ωb , 则 :A . ωωa b > , 但 不 等 于 2ωb ;B . ωωb a > , 但 不 等 于 2ωa ;C . ωωa b = ;D . ωωb a =2 。
第三章3静定结构受力分析(平面刚架)

四.刚架的内力分析及内力图的绘制
①分段:根据荷载不连续点、结点分段。 ②定形:根据每段内的荷载情况,定出内力图的形状。 ③求值:由截面法或内力算式,求出各控制截面的内力值。
④画图:画M图时,将两端弯矩竖标画在受拉侧,连以直 线,再叠加上横向荷载产生的简支梁的弯矩图。Q,N 图要标
方法:切断两个刚片之间的约束,取一个刚片为隔离体,假定 约束力的方向,由隔离体的平衡建立三个平衡方程.
例1: 求图示刚架的支座反力
C
B
C
B
l
2
YB
P
lP
A
l
2
A X A YA
解:
Fx 0, X A P 0, X A P()
MA
0, P
l 2
YB
l
0,YB
P 2
()
Fy
0,YA
YB
0,YA
另外,根据这些关系,常可不经计算直观检查 M 图的轮廓是否正确。 ①M图与荷载情况不符。 ②M图与结点性质、约束情况不符。 ③作用在结点上的各杆端弯矩及结点集中力偶不满足平衡条件。
内力图形状特征
Q图 M图
1.无何载区段 2.均布荷载区段 3.集中力作用处
平行轴线
↓↓↓↓↓↓
+ -
发生突变
+P -
斜直线
2m
8kN
B24kN.m
6kN
4m
6kN
0
-6kN
∑X = 8-8 = 0
8kN
∑Y = -6-(-6) = 0
16kN.m 6kN
∑M = 24-8 - 16 = 0
作内力图
8kN
QDA=8kN NDA=0 MDA=8kN.m(左拉)
结构力学--超静定问题典型习题解析

3
代入变形协调方程 wB = wC + ∆BC ,得
3 F a3 F a q(2a )4 FN (2a ) − = N + N 8EI 3EI 3EI EA
解得 FN =
2 qa 2 qa 3 A = 2 1 3a A + I 3+ 2 Aa
4
图示梁的右端为弹性转动约束,设弹簧常量为 k。AB 段可视为刚性,并与梁刚性连接。
()
3 结构如图示,设梁 AB 和 CD 的弯曲刚度 EI 相同。拉杆 BC 的拉压刚度 EA 已知,求拉杆 BC 的轴力。
C
a q A 2a B FN FN B FN C a FN a D a D
解题分析:将杆 CB 移除,则 AB、CD 均为静 定结构。杆 CB 的未知轴力 FN 作用在 AB,CD 梁上。为一度静不定问题。 解: 1、写出变形协调方程
2⎡
2
=
FR 3 EI
⎛ 3π 2 − 8 π − 4 ⎞ ⎜ ⎟ ⎜ ⎟ 8π ⎝ ⎠
6 结构如图 a 所示, AC = AD = BC = BD = a ,已知各杆弯曲刚度 EI 相同。A、B 点为刚 性连接,C、D 点为铰连接。将 C、D 点用一弹簧相连,弹簧常数为 2k。但由于弹簧短了 ∆ , 强行相连后,在 A、B 点加力 F。试问:当 F 为多大时,弹簧回复到其原长?
C
D
A
B
A
B
(c-1) 题 1 图(c)
1
(c-2)
大家论坛
(d) 解:图示结构为一封闭的圆圈,在任意截面截开后,有三个未知内力分量,故为三 度静不定。沿对称轴将圆环截开,由于对称性,轴力等于
F ,剪力等于零,只剩 2
结构力学 静定梁与静定刚架习题

M BC 2kNm
3、取AB为研究对象
MBA
或 取B节点为研究对象
2 kNm 2 kNm MBA
MBA=0
-4 kN
练习题
2
M
2
B
A 2m 1m
D
2m L P L L L L L
P
练习题
L
P L
P
L
P L
练习题
C
1kN/m
VC A VA 4m D
3、取AD为研究对象 B 4m
4m
VA
MDA VDA
3 kNm
3、取BCD为研究对象
2 kN
B
A 2m
C
D
1m
1m
MBC
1m
MBC= -1 kNm,上侧 1
MBA
1、取整体为研究对象
VC=4 kN
HA=2 kN 2、取AB为研究对象 MBA= - 2 kNm ,右侧受拉
B
2 A
C
D
练习题 2kN/m
C
8kN
20kNm 2m
3、BC为悬臂部分 MBC= 4 kNm,左侧
20 kN/m
4m
VB
MCB
MCD=90
MCF=135
VF
3.基本部分的计算,为悬臂杆。
VB=135
ME=135×3=405 kNm,左侧受拉
4. 作出弯矩图。
90 90
405
135
45
[习题3] 作弯矩图,剪力图,轴力图。
1.取整体为研究对象, ∑MA=0 ,VC×94×5-2×5×2.5=0 , 解得VC= 5 kN , ∑Y=0,VA=5 kN ∑X=0,HA=8 kN 8 kN 4 kN 2 kN/m HA VA VC
地质大学远程网络继续教育结构力学习题集以及答案解读

1、杆系结构中梁、刚架、桁架及拱的分类,是根据结构计算简图来划分的。
(正确)2、定向支座总是存在—个约束反力矩(正确)和一个竖向约束反力。
(错误)3静力和动力荷载的区别,主要是取决于它随时间变化规律、加载速度的快慢。
其定性指标由结构的自振周期来确定。
(正确)4、铰结点的特性是被连杆件在连接处既不能相对移动,(正确)又不能相对转动。
(错误)5、线弹性结构是指其平衡方程是线性的,(正确)变形微小,(正确)且应力与应变之间服从虎克定律。
(正确)1、学习本课程的主要任务是:研究结构在各种外因作用下结构内力与()计算,荷载作用下的结构反应;研究结构的()规则和()形式等问题。
正确答案:位移,动,组成,合理2、支座计算简图可分为刚性支座与弹性支座,其中刚性支座又可分为()、()、()和()。
正确答案:链杆,固定铰支座,固定支座,滑动支座3、永远作用在结构上的荷载称为固定荷载,暂时作用在结构上的荷载称为()它包括()、()、()、()和()等正确答案:活载,风,雪,人群,车辆,吊车4、刚节点的特性是被连接的杆件载连接处既无()又不能相对();既可传递(),也可传递()正确答案:移动,转动,力,力矩第二章平面体系的几何构成分析1、图中链杆1和2的交点O可视为虚铰。
()O正确答案:正确2、两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必须满足的条件。
()正确答案:正确3、在图示体系中,去掉1-5,3-5,4-5,2-5,四根链杆后,的简支梁12,故该体系具有四个多余约束的几何不变体系。
()12345正确答案:错误4、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
()正确答案:错误5、图示体系是几何不变体系。
()正确答案:错误2-2几何组成分析1.正确答案:几何不变,且无多余联系。
2.(图中未编号的点为交叉点。
)A B CDEF正确答案:铰接三角形BCD视为刚片I,AE视为刚片II,基础视为刚片III;I、II间用链杆AB、EC构成的虚铰(在C点)相连,I、III间用链杆FB和D处支杆构成的虚铰(在B点)相联,II、III 间由链杆AF和E处支杆构成的虚铰相联3.(图中未画圈的点为交叉点。
结构力学计算题经典(有答案)
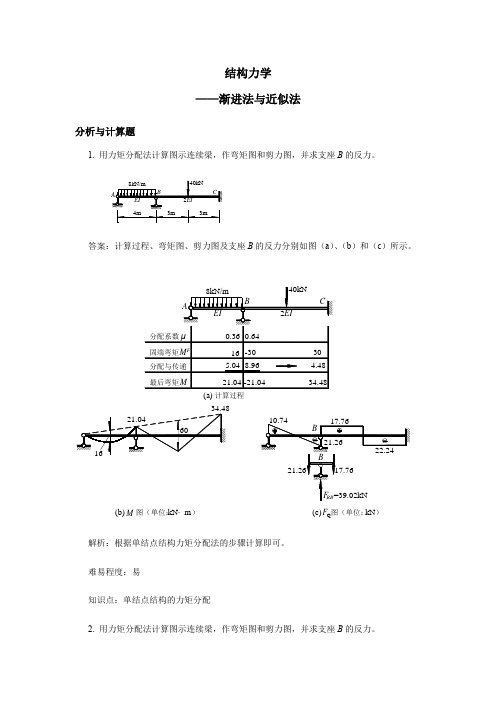
结构力学 ——渐进法与近似法分析与计算题1. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:计算过程、弯矩图、剪力图及支座B 的反力分别如图(a )、(b )和(c )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:易知识点:单结点结构的力矩分配2. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
A60kN 40kN·m EIEI B C4m4m6m(b)M 图(单位: )kN·m 图(单位: )(c)kNQ F (a)计算过程答案:图(a )为求解结点B 约束力矩的受力分析图。
计算过程、弯矩图、剪力图及支座B 的反力分别如图(b )、(c )和(d )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:中知识点:单结点结构的力矩分配3. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:CD 段为静定悬臂梁,将其截开并暴露出截面C 的弯矩,用力矩分配法计算如图(a )所示结构。
弯矩图和剪力图如图(b )、(c )所示。
BCEIN/m2EI m3m3m40kN(b)计算过程F BM (a)图(单位: )(c)M kN·m图(单位: )Q F (d)kN10kN20kN12kN/m ABCDEI 2EI 2m 4m4m解析:根据单结点结构力矩分配法的步骤计算即可。
本题中悬臂段CD 若不切除,则可按B 、C 两个刚结点的结构进行计算。
难易程度:中知识点:单结点结构的力矩分配4. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:AB 段为静定悬臂梁,将其截开并暴露出截面B 的弯矩,用力矩分配法计算过程如图(a )所示。
弯矩图和剪力图图(b )、(c )所示。
kNQ F (c)图(单位: )m M 图(单位: )(b)RB F =63.02kN ( )计算过程(a)mkN·10kN/m 60kN EI 2IB CD2m6m2m解析:根据单结点结构力矩分配法的步骤计算即可。
结构力学 第三章 静定结构

MBC=1kN· m
B
MBE= 4kN· m
MBA=5kN· m
FP1=1kN FP2=4kN
• 用计算中未使 用过的隔离体平衡 条件校核结构内力 计算是否正确。
5kN· m
1kN
3kN
FP3=1kN
2、简支刚架
• 解: • (1)、求支座 反力 • ∑y=0 • FCy =80kN(↑) • ∑m0=0 • FAx=120kN(←) •∑x=0 •FBx=80kN(→)
§3-2 静定多跨梁
•
由中间铰将若干根梁(简单梁) 联结在一起而构成的静定梁,称为静 定多跨梁。
1、几何组成:
• 基本部分+附属部分。 • (1)、基本部分:不依赖其它部分, 本身能独立承受荷载并维持平衡。 • (2)、附属部分:依赖于其它部分而 存在。
2、层叠图和传力关系
(1)、附属部分荷载 传 基本部分或 支撑它的附属部分。 • (2)、基本部分的荷载对附属部分无 影响,从层叠图上可清楚的看出来。 •
练习: 分段叠加法作弯矩图
q
A B
C
1 2 ql 4
l
q
1 ql 2
ql
l l l
例题
4kN· m
4kN
3m
3m
(1)集中荷载作用下
6kN· m
(2)集中力偶作用下
4kN· m 2kN· m
(3)叠加得弯矩图
4kN· m
4kN· m
例题
3m
8kN· m
2kN/m
3m
2m
(1)悬臂段分布荷载作用下
FP2=4kN
q=0.4kN/m
结构力学第2章习题及参考答案
解悬臂刚架,梁部分先求杆端控制弯矩,再区段叠加。柱剪力为零,弯矩图为常数。
2-21(b)
解两刚片三支杆组成单体刚架,先求支座反力,再作弯矩图。注意二杆结点有外力偶作用时,杆端弯矩将产生突变,突变值等于力偶值。
2-21(c)
解(1)铰附近截面作用有集中力偶时,弯矩值等于力偶值,据此,可知顶铰左右两侧截面的弯矩为M,上侧受拉。又因为横梁上没有竖向集中力作用,弯矩图应是一条直线。考虑本题结构对称,荷载也对称,则横梁上的弯矩图为一条水平线。
2-14试作图示多跨静定梁内力图。
解:(1)确定求解顺序:EF→CDE→ABC
(2)求支座反力及各部分之间的相互作用力。结果如图(b)所示。
(3)分别画出每一部分的内力图,组合在一起就是原结构的内力图,如图(c)和(d)所示。
2-15试作图示多跨静定梁弯矩图。
解:(1)确定求解顺序。DEF→DCB→AB。
(2)二杆刚结点上,若无集中力偶作用时,则两个杆的杆端弯矩应该相等,且同时外侧受拉。这样就可以画出两个柱子的弯矩图了。
2-21(d)
解本题为基——附型结构,先算上部、后算下部。两个部分均三铰刚架,分别求解即可。
2-21(e)
2-22试作图示组合结构的弯矩图和轴力图。
FN12= -75kN,FN34=75kN
100kn100kn50kn2520251875knm202550kn截面内力5mcos3025sincos187525295kncossin5050188knsincos5050683kn5m305m5m213求图示三铰拱结构的支座反力链杆轴力并求指定截面k1求支座反力10kn10kn取ceb部分为隔离体截面的弯矩取kad部分为隔离体40knayed20kn4m4m4m4m214试作图示多跨静定梁内力图
