河北省曲周县2017届高三数学下学期第一次模拟考试试题 理 精
【全国百强校】2017届河北省曲周县第一中学高三下学期第一次模拟考试文数试卷(带解析)

绝密★启用前【全国百强校】2017届河北省曲周县第一中学高三下学期第一次模拟考试文数试卷(带解析)试卷副标题考试范围:xxx ;考试时间:69分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、甲、乙等人在微信群中每人抢到一个红包,金额为三个元,一个元,则甲、乙的红包金额不相等的概率为( )A .B .C .D .2、若函数,则( )A .4B .0C .D .13、一个几何体的三视图如图所示,则其体积为()A. B. C. D.4、设等差数列的前项和为,若,则()A.0 B.C.4 D.15、已知双曲线:的右顶点为,过右焦点的直线与的一条渐近线平行,交另一条渐近线于点,则()A. B. C. D.6、已知为单位向量,则的最大值为()A. B.3 C. D.7、已知函数为锐角,且,则()A. B. C. D.8、下列命题正确的是()A.若一直线与两个平面所成角相等,则这两个平面平行B.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行C.若两个平面垂直于同一个平面,则这两个平面平行D.若两条直线和同一个平面平行,则这两条直线平行9、一种在实数域和复数域上近似求解方程的方法可以设计如下图所示的程序框图,若输入的,则输出的结果( )A .B .C .D .410、已知集合,,则( ) A .B .C .D .11、若复数满足,则是实部为( ) A .B .4C .D .312、已知函数,若,则( )A .B .C .D .第II卷(非选择题)二、填空题(题型注释)13、将函数的图象向右平移个单位后得到函数的图象,则正数的最小值等于.14、设数列的前项和为,且,若,则.15、若变量满足约束条件,则的最小值是__________.16、已知抛物线:的焦点为,,抛物线上的点满足,且,则__________.17、已知的内角的对边分别为,.(1)若,求;(2)若,求.三、解答题(题型注释)18、选修4-4:坐标系与参数方程已知直线的参数方程为(为参数,),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为,与交于不同的两点.(1)求的取值范围; (2)以为参数,求线段中点轨迹的参数方程.19、如图,三棱柱中,平面,,,是的中点.(1)求证:平面平面;(2)求点到平面的距离.20、某市春节期间7家超市的广告费支出(万元)和销售额(万元)数据如下: 广告费支出销售额(1)若用线性回归模型拟合与的关系,求关于的线性回归方程; (2)用二次函数回归模型拟合与的关系,可得回归方程:,经计算二次函数回归模型和线性回归模型的分别约为和,请用说明选择哪个回归模型更合适,并用此模型预测超市广告费支出为3万元时的销售额. 参数数据及公式:,,.已知,(1)求的最小值;(2)是否存在,满足?并说明理由.22、已知函数.(1)若曲线与轴相切于原点,求的值;(2)若时,成立,求的取值范围.23、已知椭圆的离心率,左顶点为.(1)求椭圆的方程;(2)已知为坐标原点,是椭圆上的两点,连接的直线平行交轴于点,证明:成等比数列.参考答案1、C2、D3、D4、A5、D6、C7、A8、B9、B10、A11、C12、D13、14、15、16、2或617、(Ⅰ),;(Ⅱ).18、(1);(2)(为参数,).19、(1)详见解析;(2).20、(1);(2)二次函数回归模型更好,预测值为万元.21、(Ⅰ)2;(Ⅱ)不存在.22、(Ⅰ);(Ⅱ).23、(1);(2)详见解析.【解析】1、甲乙等四人在微信中每人抢到一个红包金额为三个一元,一个五元,基本事件总数为,甲乙的红包金额不相等包含的基本事件有:甲乙的红包金额分别为。
河北省曲周县高三数学下学期第一次模拟考试试题文(扫描版)

河北省曲周县2017届高三数学下学期第一次模拟考试试题文(扫描版)文科数学参考答案一、选择题:CADBD ABDBA CD 二、填空题:(13)-2 (14) 12(15) 3 2(16)2或6三、解答题: (17)解:(Ⅰ)由已知B =π 6,a 2-ab -2b 2=0结合正弦定理得: 2sin 2A -sin A -1=0,于是sin A =1或sin A =- 1 2(舍).…4分因为0<A <π,所以,A = π 2,C = π3.…6分(Ⅱ)由题意及余弦定理可知a 2+b 2+ab =196,由(Ⅰ)a 2-ab -2b 2=0得(a +b )(a -2b )=0即a =2b , …8分联立解得b =27,a =47.所以,S △ABC = 12ab sin C =14 3.…12分(18)解:(Ⅰ)b ˆ=ni =1∑x i y i -n ·x -y-n i =1∑x 2i -nx-2=2794-7×8×42708-7×82=1.7 …3分a ˆ=y --b ˆx -=28.4所以,y 关于x 的线性回归方程是yˆ=1.7x +28.4…6分 (Ⅱ)∵0.75<0.93,∴二次函数回归模型更合适. …9分 当x =3万元时,预测A 超市销售额为33.47万元. …12分(19)解:(Ⅰ)由A 1A ⊥平面ABC ,CM ⊂平面ABC ,则A 1A ⊥CM . 由AC =CB ,M 是AB 的中点,则AB ⊥CM . 又A 1A ∩AB =A ,则CM ⊥平面ABB 1A 1,又CM ⊂平面A 1CM ,所以平面A 1CM ⊥平面ABB 1A 1.…6分(Ⅱ)设点M 到平面A 1CB 1的距离为h , 由题意可知A 1C =CB 1=A 1B 1=2MC =22, S △A 1CB 1=23,S △A 1MB 1=22.由(Ⅰ)可知CM ⊥平面ABB 1A 1,得,V C -A 1MB 1= 13MC ·S △A 1MB 1=V M -A 1CB 1= 13h ·S △A 1CB 1,所以,点M 到平面A 1CB 1的距离h =MC ·S △A 1MB 1S △A 1CB 1=233.…12分(20)解: (Ⅰ)由e =ca =22,a =2得c =b =2, 故椭圆C 的方程为x 24+y 22=1.…4分(Ⅱ)设B (x 1,y 1),C (x 2,y 2),OC :y =kx ,则AB :y =k (x +2), 将y =k (x +2)代入x 24+y 22=1,整理得(1+2k 2)x 2+8k 2x +8k 2-4=0,…5分 -2x 1=8k 2-41+2k 2,得x 1=2-4k21+2k 2,…6分|AB |=1+k 2|x 1+2|=41+k21+2k2,|AD |=1+k 2|0+2|=21+k 2,|AB |·|AD |=8(1+k 2)1+2k2.…9分将y =kx 代入x 24+y 22=1,整理得(1+2k 2)x 2-4=0,得x 22=41+2k 2,|OC |2=(1+k 2)x 22=4(1+k 2)1+2k2.故|AB |·|AD |=2|OC |2,所以,|AB |,2|OC |,|AD |成等比数列. …12分 (21)解:(Ⅰ)f '(x )=2cos x +1cos 2x-a ,…3分由f '(0)=0得a =3.…4分(Ⅱ)x ∈[0, π2),cos x ∈(0,1].令t =cos x ,则f '(x )=g (t )=2t + 1t2-a ,t ∈(0,1],g '(t )=2-2t3≤0,当且仅当t =1时取等号,故t ∈(0,1]时,g (t )单调递减,g (t )≥g (1)=3-a . …7分 (ⅰ)若a ≤3,则f '(x )≥0,仅当x =0时取等号, f (x )单调递增,f (x )≥f (0)=0.…8分(ⅱ)若a >3,令h (x )=3tan x -ax ,A C 11CBMA 1h '(x )=3cos 2x -a ,存在x 0∈[0,π2),使得h '(x 0)=0, 且当x ∈(0,x 0)时,h '(x )<0,h (x )单调递减, h (x )<h (0)=0,因为x ∈[0, π2),sin x ≤tan x ,所以f (x )≤3tan x -ax ,故存在β∈(0,x 0),f (β)<0,即f (x )≥0不能恒成立,所以a >3不合题意. 综上所述,a 的取值范围是(-∞,3]. …12分 (22)解:(Ⅰ)曲线C 的直角坐标方程为x 2+y 2=1,将⎩⎨⎧x =t cos φ,y =-2+t sin φ代入x 2+y 2=1得t 2-4t sin φ+3=0(*) 由16sin 2φ-12>0,得|sin φ|>32,又0≤φ<π,所以,φ的取值范围是( π 3,2π3); …5分(Ⅱ)由(*)可知,t 1+t 22=2sin φ,代入⎩⎨⎧x =t cos φ,y =-2+t sin φ中,整理得P 1P 2的中点的轨迹方程为⎩⎨⎧x =sin 2φ,y =-1-cos 2φ(φ为参数, π 3<φ<2π3) …10分(23)解:(Ⅰ) 1 x + 1y =x +y xy =x 2+y 2xy ≥2xy xy=2,当且仅当x =y =1时,等号成立.所以 1 x + 1y的最小值为2.…5分(Ⅱ)不存在.因为x 2+y 2≥2xy ,所以(x +y )2≤2(x 2+y 2)=2(x +y ), 又x ,y ∈(0,+∞),所以x +y ≤2.从而有(x +1)(y +1)≤[(x +1)+(y +1) 2]2=4,因此不存在x ,y ,满足(x +1)(y +1)=5. …10分。
河北省邯郸市曲周县第一中学2017届高三下学期2月模拟考试数学(理)

2017届2月模拟考试 数学试卷(理)第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、已知集合2{|16},{}A x x B m =≥=,若A B A = ,则实数m 的取值范围是 A .(,4)-∞- B .[4,)+∞ C .[4,4]- D .(,4][4,)-∞-+∞2、下列函数中,周期为π 的奇函数是A .2sin y x =B .tan 2y x =C .sin 2cos 2y x x =+D .sin cos y x x = 3、“1a = ”是“10ax y ++=与直线(2)320a x y +--=垂直”的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件 4、已知i 为虚数单位,复数()1a i z a R i -=∈-,若01(sin )z x dx ππ=-⎰,则a =A .1±B .1C .1-D .12±5、设,m n 为两条不同的直线,,αβ为两个不同的平面,给出下列命题: ①若,m m αβ⊥⊥,则//αβ ②若//,//m m αβ,则//αβ ③若//,//m n αα,则//m n ④若,m n αα⊥⊥,则//m n 上述命题中,所有真命题的序号是A .①④B .②③C .①③D .②④6、已知235xyz==,且,,x y z 均为正数,则2,3,5x y z 的大小关系为A .235x y z <<B .325y x z <<C .532z y x <<D .523z x y << 7、ABC ∆的角,,A B C 所对的边分别是,,a b c ,若7cos ,2,38A c a b =-==,则a = A .2B .52 C .3 D .728、已知直线y =和椭圆22221(0)x y a b a b +=>>交于不同的两点,M N ,若,M N 在x 轴上的射影恰好为椭圆的两个焦点,则椭圆的离心率为 A.2 B.39、函数()sin cos f x a x b x =-的一条对称轴为4x π=,则直线0ax by c -+=的倾斜角为A .45B .60C .120D .13510、已知,x y 为正实数,且115x y x y+++=,则x y +的最大值是 A .3 B .72 C .4 D .9211、过双曲线22115y x -=的右支上一点P ,分别向圆221:(4)4C x y ++= 和圆222:(4)4C x y -+=作切线,切点分别为,M N ,则22PM PN -的最小值为A .10B .13C .16D .1912、已知函数()2ln(1)f x a x x =+-,在区间(0,1)内任取两个不相等的实数,p q ,若不等式()()111f p f q p q+-+>-恒成立,则实数a 的取值范围是A .[15,)+∞B .[6,)+∞C .(,15]-∞D .(,6]-∞第Ⅱ卷本卷包括必考题和选考两部分,第13题-第21题为必考题,每个试题考生都必须作答,第22题-第23题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分, 13、抛物线24y x =-的准线方程是14、如图为某几何体的三视图,则该几何体的体积为15、已知,x y 满足2420x x y x y m ≥⎧⎪+≤⎨⎪--≤⎩,若目标函数3z x y =+的最大值为10,则m 的值为16、已知等腰OAB ∆中,2OA OB ==且OA OB +≥ ,那么OA OB ⋅ 的取值范围是三、解答题:本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤 17、(本小题满分12分)在ABC ∆中,,,a b c 分别为内角,,A B C 的对边,且ssin sin()3a Bb A π=-+.(1)求A 的值;(2)若ABC ∆的面积为2S =,求sin C 的值.18、(本小题满分12分)已知等差数列{}n a 的前n 项和为n S ,非常数等比数列{}n b 的公比是q , 且满足1122232,1,3,a b S b a b ====(1)求n a 与n b ;(2)设223na n n cb λ=-⋅,若数列{}nc 是递减数列,求实数λ的取值范围.19、(本小题满分12分)已知在边长为4的等边ABC ∆(如图1所示)中,//,MN BC E 为BC 的中点,连接AE 交MN 于点F ,现将AMN ∆沿MN 折起,使得平面AMN ⊥平面MNCB (如图2所示). (1)求证:平面ABC ⊥平面AEF ;(2)若3BCNM AMN S S ∆=,求直线AB 与平面ANC 所成角的正弦值.20、(本小题满分12分)在平面直角坐标系xOy 中,已知椭圆22122:1(0)x y C a b a b +=>>的离心率e =1C 的短轴长为2,.(1)求椭圆1C 的方程; (2)设1(0,),16A N 为抛物线22:C y x -上一动点,过点N 作抛物线2C 的切线交椭圆1C 于,BC 两点,求ABC ∆面积的最大值.21、(本小题满分12分) 已知函数()ln xx kf x e+=(其中, 2.71828k R e ∈=是自然对数的底数),()f x '为()f x 的导函数.(1)当2k =时,求曲线()y f x =在点(1,(1))f 处的切线方程; (2)若(0,1]x ∈时,()0f x '=都有解,求k 的取值范围;(3)若()10f '=,试证明:对于任意()2210,e x f x x x-+'><+恒成立.请考生在第(22)、(23)两题中任选一题作答,如果多做,则按所做的第一题记分,作答时请写清题号.22、(本小题满分10分) 选修4-4 坐标系与参数方程在极坐标系中,已知圆C 的圆心)4C π,半径r =(1)求圆C 的极坐标方程; (2)若[0,)4a π∈,直线l 的参数方程2cos (2sin x t t y t αα=+⎧⎨=+⎩为为参数),直线l 交圆C 于,A B 两点,求弦长AB 的取值范围.23、(本小题满分10分)选修4-5 不等式选讲 设函数()212f x x x =--+.(1)解不等式()0f x >;(2)若0x R ∃∈,使得20()24f x m m +<,求实数m 的取值范围.数学(理科)参考答案13.161=y 14.π 15.5 16.[)42,- 17.(12分)【解】(1))3sin(sin π+-=A b B a , ∴由正弦定理,得)34sin(sin π+-=A ,即A A A cos 23sin 21sin ---=,化简得33tan -=A ,),(π0∈A ,65π=∴A (2)21sin 65=∴=A A ,π ,由c b bc A bc c S 3,41sin 21432====得, 2227cos 2c A b c b a =-+=∴,则c a 7=,由正弦定理,得147sin sin ==a A c C . 18.(12分)【解】(1)由已知可得⎩⎨⎧==+,,32222q a q a 所以0232=+-q q ,解得)(12舍或==q q ,从而42=a ,所以12,2-==n n n b n a .(2)由(1)知,λλn n nn n a b c 32232-=⋅-=,由题意,n n c c <+1对任意的*∈N n 恒成立,即λλn n n n 323211-<-++恒成立,亦即nn 232>λ恒成立,即n⎪⎭⎫ ⎝⎛⋅>3221λ恒成立.由于函数xy ⎪⎭⎫ ⎝⎛⋅=3221在R 上是减函数,所以当1=n 时,n⎪⎭⎫⎝⎛⋅3221有最大值,且最大值为313221=⨯.因此n⎪⎭⎫ ⎝⎛⋅>3221λ恒成立,所以实数λ的取值范围是⎪⎭⎫⎝⎛∞+,3120. [解](1)因为43222222=-==ab a ac e ,所以b a 42=.又1=b 所以椭圆1C 的方程是1422=+y x。
2017高考模拟试卷理数及答案
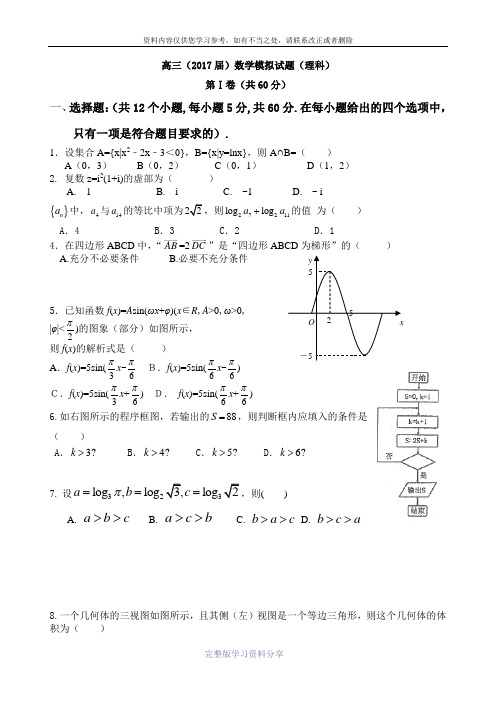
高三(2017届)数学模拟试题(理科)第Ⅰ卷(共60分)一、选择题:(共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.设集合A={x|x 2﹣2x ﹣3<0},B={x|y=lnx},则A ∩B=( )A (0,3)B (0,2)C (0,1)D (1,2) 2. 复数z=i 2(1+i)的虚部为( )A. 1B. iC. -1D. - i{}n a 中,4a 与14a 的等比中项为22,则27211log log a a +的值 为( )A .4B .3C .2D .1 4.在四边形ABCD 中,“AB =2DC ”是“四边形ABCD 为梯形”的( ) A.充分不必要条件 B.必要不充分条件 5.已知函数f (x )=A sin(ωx +φ)(x ∈R ,A >0,ω>0, |φ|<2π)的图象(部分)如图所示,则f (x )的解析式是( )A .f (x )=5sin(3πx -6π B.f (x )=5sin(6πx -6π)C.f (x )=5sin(3πx +6π) D. f (x )=5sin(6πx +6π)6.如右图所示的程序框图,若输出的88S =,则判断框内应填入的条件是( )A .3?k >B .4?k >C .5?k >D .6?k >7. 设323log ,log 3,log 2a b c π===,则( )A.a b c >>B.a cb >>C.b ac >> D. b c a >>8.一个几何体的三视图如图所示,且其侧(左)视图是一个等边三角形,则这个几何体的体积为( )x -5y O 5 2 5A .433 B .533 C .23 D .833x y 、满足121y y x x y m ≥⎧⎪≤-⎨⎪+≤⎩,如果目标函数z x y =-的最小值为-1,则实数m =( )A .6B .5C .4D .3 10.函数()2sin f x x x =+的部分图象可能是( )11. 已知双曲线()222210,0x y C a b a b-=>>:的右焦点为F ,过F 且斜率为3的直线交C 于A B 、两点,若4AF FB =,则C 的离心率为A .95 B. 75 C. 58 D. 6512、已知定义在R 上的可导函数f(x)的导函数为/()f x ,满足/()f x <()f x ,且()(2)f x f x -=+,(2)1f =,则不等式()x f x e <的解集为( )A. ()2,-+∞B. (0,+∞)C.(1, +∞)D.(2, +∞)第Ⅱ卷(非选择题 共90分)二、填空题:(本大题共4个小题,每小题5分,共20分). 13. (4y x 的展开式中33x y 的系数为 。
高三理综下学期第一次模拟考试试题(扫描版)(2021年整理)

河北省曲周县2017届高三理综下学期第一次模拟考试试题(扫描版)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(河北省曲周县2017届高三理综下学期第一次模拟考试试题(扫描版))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为河北省曲周县2017届高三理综下学期第一次模拟考试试题(扫描版)的全部内容。
河北省曲周县2017届高三理综下学期第一次模拟考试试题(扫描版)理科综合能力测试参考答案及评分参考生物部分(共90分)1.A 2.C 3.C 4.B 5.D 6.A29.(共10分,每空2分)(1)协助扩散基质(2)弱光(3)酶的活性和含量(及载体蛋白X含量)光反应和暗反应(答不全不给分)30。
(共11分,除特殊标注外,每空2分)(1)体液特异性受体(2)药物Ⅰ和生理盐水 A组>C组>B组(3)防止因甲状腺激素含量变化引起促甲状腺激素释放激素分泌量的不同,进而影响垂体的分泌。
(其他合理答案也可给分)(3分)31.(共8分,每空2分)(1)三、四(答不全不给分)(2)100只·km-2 (3)b和c、d和e(答不全不给分) (4)小于32。
(共10分,每空2分)(1)不能因为显性亲本为杂合子时,后代的表现型为绿色和黄色,因此无法判断显隐性(2)①绿色②全部为绿色全部为黄色或黄色:绿色=1:137.(共15分,除特殊标注外,每空2分)(1)葡萄糖蛋白质(2)琼脂稀释涂布平板法(3)a 快速增加目的菌的种群数量(扩大培养)(4)大幅度降低发酵液中其他酶的活性(3分)38. (共15分,除特殊标注外,每空2分)(1)基因重组(2)必需是安全的(不会对受体细胞有害,或不能进入到除受体细胞外的其他生物细胞中去)分子大小应适合(以便提取和在体外进行操作)宿主范围广对靶细胞具有较高的转化效率在宿主细胞中不会引起免疫排斥(或免疫排斥较低)(3)GATCC—………………—GG—………………—CCTAG (或—G GATCC——CCTAG G—)(3分)否(4)抗原-抗体杂交(5)基因与基因78910111213A B A B C B D26.(14分)(1)关闭旋塞E,装置C中加水没过导管口,给A装置微热,装置C中导管口有气泡冒出,撤去热源后,导管内有倒吸产生的液柱,且高度保持不变。
河北省曲周县高三数学下学期第一次模拟考试试题 理(扫描版)

河北省曲周县2017届高三数学下学期第一次模拟考试试题理(扫描版)理科数学参考答案一.选择题:DADBD ADBAD CB二.填空题: (13)-2 (14) 1 2(15)2或6 (16)(3,41)三.解答题: (17)解:(Ⅰ)由已知B =5π6,a 2+b 2=6ab 结合正弦定理得:4sin 2A -26sin A +1=0,于是sin A =6±24. …4分 因为0<A <π 6,所以sin A < 12,取sin A =6-24…6分(Ⅱ)由题意可知S △ABC = 1 2ab sin C =312c 2,得:1 2ab sin C =312(a 2+b 2-2ab cos C )=312(4ab -2ab cos C ). 从而有:3sin C +cos C =2,即sin (C + π 6)=1又 π 6<C + π 6<7π6,所以,C = π 3.…12分(18)解:(Ⅰ)b ˆ=ni =1∑x i y i -n ·x -y-n i =1∑x 2i -nx-2=2794-7×8×42708-7×82=1.7 …3分a ˆ=y --b ˆx -=28.4所以,y 关于x 的线性回归方程是y ˆ=1.7x +28.4…6分 (Ⅱ)∵0.75<0.97,∴对数回归模型更合适. …9分当x =8万元时,预测A 超市销售额为47.2万元.…12分(19)解:(Ⅰ)连接AC 1,BC 1,则N ∈AC 1且N 为AC 1的中点,又∵M 为AB 的中点,∴MN ∥BC 1, 又BC 1⊂平面BB 1C 1C ,MN ⊄平面BB 1C 1C ,故MN ∥平面BB 1C 1C . …4分 (Ⅱ)由A 1A ⊥平面ABC ,得AC ⊥CC 1,BC ⊥CC 1. 以C 为原点,分别以CB ,CC 1,CA 所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,设CC 1=2λ(λ>0), 则M (1,0,1),N (0,λ,1),B 1(2,2λ,0),CM →=(1,0,1),MN →=(-1,λ,0),NB 1→=(2,λ,-1). 取平面CMN 的一个法向量为m =(x ,y ,z ), 由CM →·m =0,MN →·m =0得:⎩⎨⎧x +z =0,-x +λy =0,令y =1,得m =(λ,1,-λ) 同理可得平面B 1MN 的一个法向量为n =(λ,1,3λ) …8分∵平面CMN ⊥平面B 1MN ,∴ m ·n =λ2+1-3λ2=0解得λ=22,得n =(22,1,322),又AB →=(2,0,-2), 设直线AB 与平面B 1MN 所成角为θ,则 sin θ=|cos 〈n ,AB →〉|=|n ·AB →||n ||AB →|=66. 所以,直线AB 与平面B 1MN 所成角的正弦值是66. …12分(20)解:(Ⅰ)由e 2=c 2 a 2= 1 2,得 b 2a 2= 1 2,将Q 代入椭圆C 的方程可得b 2=4,所以a 2=8,故椭圆C 的方程为x 28+y 24=1.…4分(Ⅱ)当直线PN 的斜率k 不存在时,PN 方程为:x =2或x =-2, 从而有|PN |=23,所以S = 1 2|PN |·|OM |= 12×23×22=26.…5分当直线PN 的斜率k 存在时,设直线PN 方程为:y =kx +m (m ≠0),P (x 1,y 1),N (x 2,y 2).将PN 的方程代入C 整理得:(1+2k 2)x 2+4kmx +2m 2-8=0, 所以x 1+x 2=-4km 1+2k 2,x 1·x 2=2m 2-81+2k2,…6分y 1+y 2=k (x 1+x 2)+2m =2m1+2k2, 由OM →=OP →+ON →得:M (-4km 1+2k 2,2m1+2k 2),将M 点坐标代入椭圆C 方程得:m 2=1+2k 2.…8分点O 到直线PN 的距离d =|m |1+k2, |PN |=1+k 2|x 1-x 2|,S =d ·|PN |=|m |·|x 1-x 2|=1+2k 2·|x 1-x 2|=16k 2-8m 2+32=26.综上,平行四边形OPMN 的面积S 为定值26. …12分 (21)解:(Ⅰ)f '(x )=cos x +1cos 2x-2 …2分因为x ∈(-π 2, π2),所以cos x ∈(0,1],于是 f '(x )=cos x +1cos 2x -2≥cos 2x +1cos 2x -2≥0(等号当且仅当x =0时成立).故函数f (x )在(-π 2, π2)上单调递增. …4分(Ⅱ)由(Ⅰ)得f (x )在(0,π2)上单调递增,又f (0)=0,所以f (x )>0, (ⅰ)当m ≤0时,f (x )>0≥mx 2成立. …5分 (ⅱ)当m >0时,令p (x )=sin x -x ,则p '(x )=cos x -1, 当x ∈(0,π2)时,p '(x )<0,p (x )单调递减,又p (0)=0,所以p (x )<0, 故x ∈(0,π2)时,sin x <x .(*)…7分由(*)式可得f (x )-mx 2=sin x +tan x -2x -mx 2<tan x -x -mx 2,令g (x )=tan x -x -mx 2,则g '(x )=tan 2x -2mx由(*)式可得g '(x )<x 2cos 2x -2mx =xcos 2x(x -2m cos 2x ),…9分令h (x )=x -2m cos 2x ,得h (x )在(0,π2)上单调递增, 又h (0)<0,h (π 2)>0,所以存在t ∈(0, π2)使得h (t )=0,即x ∈(0,t )时,h (x )<0, 所以x ∈(0,t )时,g '(x )<0,g (x )单调递减,又g (0)=0,所以g (x )<0,即x ∈(0,t )时,f (x )-mx 2<0,与f (x )>mx 2矛盾.综上,满足条件的m 的取值范围是(-∞,0]. …12分 (22)解:(Ⅰ)曲线C 的直角坐标方程为x 2+y 2=1,将⎩⎨⎧x =t cos φ,y =-2+t sin φ代入x 2+y 2=1得t 2-4t sin φ+3=0(*)由16sin 2φ-12>0,得|sin φ|>32,又0≤φ<π, 所以,φ的取值范围是( π 3,2π3); …5分(Ⅱ)由(*)可知,t 1+t 22=2sin φ,代入⎩⎨⎧x =t cos φ,y =-2+t sin φ中,整理得P 1P 2的中点的轨迹方程为⎩⎨⎧x =sin 2φ,y =-1-cos 2φ (φ为参数, π 3<φ<2π3) …10分(23)解:(Ⅰ) 1 x + 1y =x +y xy =x 2+y 2xy ≥2xy xy=2,当且仅当x =y =1时,等号成立.所以 1 x + 1y的最小值为2.…5分(Ⅱ)不存在.因为x 2+y 2≥2xy ,所以(x +y )2≤2(x 2+y 2)=2(x +y ), 又x ,y ∈(0,+∞),所以x +y ≤2.从而有(x +1)(y +1)≤[(x +1)+(y +1) 2]2=4,因此不存在x ,y ,满足(x +1)(y +1)=5.。
河北省曲周县第一中学2017届高三下学期第一次模拟考试数学(理)试题含答案

2017届高三三月第一次模拟理科数学 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数z 满足25)43(=+z i ,则复平面内表示z 的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.已知集合}0|{2>-=x xx A ,}33|{<<-=x x B ,则( )A .RB A = B .A B ⊆C .B A ⊆D .∅=B A 3.若函数⎪⎩⎪⎨⎧>-≤=-1,51,)(21x x x e x f x ,则=))2((f f ( )A .4B .0C .25e - D .1 4。
一个几何体的三视图如图所示,则其体积为( )A .42+πB .4+πC 。
22+π D .2+π5。
在ABC ∆中,90=∠B ,)2,1(-=AB ,),3(λ=AC ,则=λ( )A .1B .23C 。
4D .1-6.设等差数列}{na 的前n 项和为nS ,若6,464=-=S S,则=5S ( )A .0B .2-C 。
4D .1 7。
已知双曲线C :1322=-y x 的右顶点为A ,过右焦点F的直线l 与C 的一条渐近线平行,交另一条渐近线于点B ,则=∆ABFS ()A .3B .433 C.833 D .23 8。
二项式7)(a x -的展开式中,含4x 项的系数为280-,则=⎰e edx x21( )A .12ln +B .1C 。
2241e e - D .2ln9。
一种在实数域和复数域上近似求解方程的方法可以设计如下图所示的程序框图,若输入的n 为6时,输出结果为2。
45,则m 可以是( )A .0。
1B .0。
01C 。
0.05D .0。
6 10.已知0>ω,将函数x x f ωcos )(=的图象向右平移2π个单位后得到函数)4sin()(πω-=x x g 的图象,则ω的最小值是( )A .3B .34C 。
河北省邯郸市曲周县第一中学高三数学2月模拟考试试题

河北省邯郸市曲周县第一中学2017届高三数学2月模拟考试试题文(扫描版)DCBAS数学(文科)参考答案一、选择题:本大题共12小题,每小题5分,共60分. 题号13. 6 14. 0 15.206 16. 3612 17.(Ⅰ)由222b c a bc +=+得222b c a bc+-=,故 2221cos 22b c a A bc +-== ---- 3 分又∵0A π<< ∴60A =︒ ---------- 5分 (Ⅱ)由2sin aA=得2sin a A == -------------- 8分 由余弦定理得2222cos a b c bc A =+- 即22212cos 603422b c bc bc =+-︒=-⨯,即∴1bc = 10分∴11sin 1sin 6022ABC S bc A ∆==⨯⨯︒=分 18. 【答案】:(Ⅰ)n a =2n (Ⅱ)6k =【解析】::(Ⅰ)设数列{}n a 的公差为d,由题意知112282412a d a d +=⎧⎨+=⎩ 解得12,2a d ==所以1(1)22(1)2n a a n d n n =+-=+-= (Ⅱ)由(Ⅰ)可得1()(22)(1)22n n a a n n nS n n ++===+ 因12,,k k a a S + 成等比数列,所以212k k a a S += 从而2(2)2(2)(3)k k k =++ ,即 2560k k --=解得6k = 或1k =-(舍去),因此6k = 。
19.解:(Ⅰ)设O 为AC 的中点,连接,OS OD ,----------------1分,SA SC OS AC =∴⊥------------------------2分,,DA DC DO AC =∴⊥--------------------------------3分又,OS OD ⊂平面SOD ,且OS DO O =,AC ⊥平面SOD ,------------------------4分又SD ⊂平面SODAC SD ∴⊥--------------------------------5分(Ⅱ)连接BD ,在ASC ∆中,,SA SC =060ASC ∠=,O 为AC 的中点,ASC ∴∆为正三角形,且2,AC OS =,----------------------------------------6分在ADC ∆中,2224DA DC AC +==,O 为AC 的中点,---------------------7分090ADC ∴∠=,且1OD =,-------------8分在SOD ∆中,222OS OD SD +=---------------------9分SOD ∴∆为直角三角形,且090SOD ∠=SO OD ∴⊥又OS AC ⊥,且AC DO O = SO ∴⊥平面ABCD ---------------------10分13B SAD S BAD BAD V V S SO --∆∴==⋅⋅------------------------11分111132323AD CD SO =⨯⋅⋅⋅=⨯= ------- 12分 20. 解: (1) 设椭圆C 的方程为22221(0)x y a b a b+=>>, 半焦距为c .依题意12c e a ==, 由椭圆C 上的点到右焦点的最大距离3, 得3=+c a , 解得1,2c a ==, 所以 2223b a c =-=, 所以椭圆C 的标准方程是22143x y +=. (2) 设直线l 的方程为m kx y +=, 由22143y kx mx y =+⎧⎪⎨+=⎪⎩, 得222(34)84120k x kmx m +++-=,222(8)4(34)(412)0,km k m ∆=-+-> 化简得2234k m +>.设11(,)A x y , 22(,)B x y , 则21212228412,3434km m x x x x k k -+=-=++.以AB 为直径的圆过原点等价于0OA OB ⋅=,所以12120x x y y +=, 即1212()()0x x kx m kx m +++=,则221212(1)()0k x x km x x m ++++=,222224128(1)03434m kmk km m k k-+⋅-⋅+=++, 化简得2271212m k =+.将227112k m =-代入2234k m +>中, 22734(1)12m m +->, 解得234m >. 又由227121212m k =+≥,从而212,7m m ≥≥或m ≤所以实数m 的取值范围是2(,[21,)7-∞+∞.21解:(1)函数的定义域为(0,)+∞,2211ln ln ()x xf x x x --'==-. 令()0f x '=,得1x =;当(0,1)x ∈时,()0f x '>,()f x 单调递增; 当(1,)x ∈+∞时,()0f x '<,()f x 单调递减. 所以,1x =为极大值点, 所以112a a <<+,故112a <<,即实数a 的取值范围为1(,1)2. (6分)(2)当1x ≥时,(1)(1ln )x x k x ++≤,令(1)(1ln )()x x g x x++=,则221[1ln 1](1)(1ln )ln ()x x x x x x x g x x x+++-++-'==.再令()ln h x x x =-, 则1()10h x x'=-≥,所以()(1)1h x h ≥=,所以()0g x '>, 所以()g x 为单调增函数,所以()(1)2g x g ≥=,故2k ≤.(12分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北省曲周县2017届高三数学下学期第一次模拟考试试题理(扫描版)
理科数学参考答案
一.选择题:
DADBD ADBAD CB
二.填空题: (13)-2 (14) 1 2
(15)2或6 (16)(3,41)
三.解答题: (17)解:
(Ⅰ)由已知B =5π6,a 2+b 2
=6ab 结合正弦定理得:
4sin 2
A -26sin A +1=0,于是sin A =6±2
4
. …4分 因为0<A <
π 6,所以sin A < 1
2,取sin A =6-24
…6分
(Ⅱ)由题意可知S △ABC = 1 2ab sin C =312
c 2
,得:
1 2ab sin C =312(a 2+b 2-2ab cos C )=3
12(4ab -2ab cos C ). 从而有:3sin C +cos C =2,即sin (C + π 6)=1
又 π 6<C + π 6<7π6,所以,C = π 3.
…12分
(18)解:
(Ⅰ)b ˆ=n
i =1
∑x i y i -n ·x -y
-n i =1
∑x 2i -nx
-2=2794-7×8×42708-7×82
=1.7 …3分
a ˆ=y --
b ˆx -=28.4
所以,y 关于x 的线性回归方程是y ˆ=1.7x +28.4
…6分 (Ⅱ)∵0.75<0.97,∴对数回归模型更合适. …9分
当x =8万元时,预测A 超市销售额为47.2万元.
…12分
(19)解:
(Ⅰ)连接AC 1,BC 1,则N ∈AC 1且N 为AC 1的中
点,
又∵M 为AB 的中点,∴MN ∥BC 1, 又BC 1⊂平面BB 1C 1C ,MN ⊄平面BB 1C 1C ,
故MN ∥平面BB 1C 1C . …4分 (Ⅱ)由A 1A ⊥平面ABC ,得AC ⊥CC 1,BC ⊥CC 1. 以C 为原点,分别以CB ,CC 1,CA 所在直线为x 轴,
y 轴,z 轴
建立如图所示的空间直角坐标系,
设CC 1=2λ(λ>0), 则M (1,0,1),N (0,λ,1),B 1(2,2λ,0),
CM →=(1,0,1),MN →=(-1,λ,0),NB 1→=(2,λ,-1). 取平面CMN 的一个法向量为m =(x ,y ,z ), 由CM →·m =0,MN →·m =0得:
⎩⎨⎧x +z =0,
-x +λy =0,
令y =1,得m =(λ,1,-λ) 同理可得平面B 1MN 的一个法向量为n =(λ,1,3λ) …8分
∵平面CMN ⊥平面B 1MN ,∴ m ·n =λ2
+1-3λ2
=0
解得λ=
22,得n =(22,1,32
2
),又AB →=(2,0,-2), 设直线AB 与平面B 1MN 所成角为θ,则 sin θ=|cos 〈n ,AB →〉|=|n ·AB →||n ||AB →|=66
. 所以,直线AB 与平面B 1MN 所成角的正弦值是66
. …12分
(20)解:
(Ⅰ)由e 2
=
c 2 a 2= 1 2,得 b 2
a 2= 1 2
,
将Q 代入椭圆C 的方程可得b 2=4,所以a 2
=8,
故椭圆C 的方程为x 28+y 2
4
=1.
…4分
(Ⅱ)当直线PN 的斜率k 不存在时,PN 方程为:x =2或x =-2, 从而有|PN |=23,
所以S = 1 2|PN |·|OM |= 1
2
×23×22=26.
…5分
当直线PN 的斜率k 存在时,
设直线PN 方程为:y =kx +m (m ≠0),P (x 1,y 1),N (x 2,y 2).
将PN 的方程代入C 整理得:(1+2k 2)x 2+4kmx +2m 2
-8=0, 所以x 1+x 2=-4km 1+2k 2,x 1·x 2=2m 2
-8
1+2k
2,
…6分
y 1+y 2=k (x 1+x 2)+2m =
2m
1+2k
2, 由OM →=OP →+ON →得:M (-4km 1+2k 2,2m
1+2k 2),
将M 点坐标代入椭圆C 方程得:m 2
=1+2k 2
.
…8分
点O 到直线PN 的距离d =|m |
1+k
2
, |PN |=1+k 2
|x 1-x 2|,
S =d ·|PN |=|m |·|x 1-x 2|=1+2k 2·|x 1-x 2|=16k 2-8m 2+32=26.
综上,平行四边形OPMN 的面积S 为定值26. …12分 (21)解:
(Ⅰ)f '(x )=cos x +1
cos 2x
-2 …2分
因为x ∈(-
π 2, π
2
),所以cos x ∈(0,1],于是 f '(x )=cos x +1cos 2x -2≥cos 2x +1
cos 2x -2≥0(等号当且仅当x =0时成立).
故函数f (x )在(-
π 2, π
2
)上单调递增. …4分
(Ⅱ)由(Ⅰ)得f (x )在(0,
π
2)上单调递增,又f (0)=0,所以f (x )>0, (ⅰ)当m ≤0时,f (x )>0≥mx 2
成立. …5分 (ⅱ)当m >0时,
令p (x )=sin x -x ,则p '(x )=cos x -1, 当x ∈(0,
π
2
)时,p '(x )<0,p (x )单调递减,又p (0)=0,所以p (x )<0, 故x ∈(0,
π
2
)时,sin x <x .(*)
…7分
由(*)式可得f (x )-mx 2
=sin x +tan x -2x -mx 2
<tan x -x -mx 2
,
令g (x )=tan x -x -mx 2,则g '(x )=tan 2
x -2mx
由(*)式可得g '(x )<x 2cos 2x -2mx =x
cos 2x
(x -2m cos 2
x ),
…9分
令h (x )=x -2m cos 2
x ,得h (x )在(0,
π
2
)上单调递增, 又h (0)<0,h (
π 2)>0,所以存在t ∈(0, π
2
)使得h (t )=0,即x ∈(0,t )时,h (x )<0, 所以x ∈(0,t )时,g '(x )<0,g (x )单调递减,又g (0)=0,所以g (x )<0,
即x ∈(0,t )时,f (x )-mx 2<0,与f (x )>mx 2
矛盾.
综上,满足条件的m 的取值范围是(-∞,0]. …12分 (22)解:
(Ⅰ)曲线C 的直角坐标方程为x 2
+y 2
=1,将⎩⎨
⎧x =t cos φ,y =-2+t sin φ
代入x 2+y 2
=1得
t 2-4t sin φ+3=0(*)
由16sin 2
φ-12>0,得|sin φ|>
3
2
,又0≤φ<π, 所以,φ的取值范围是( π 3,2π
3
); …5分
(Ⅱ)由(*)可知,t 1+t 2
2=2sin φ,代入⎩⎨⎧x =t cos φ,y =-2+t sin φ
中,
整理得P 1P 2的中点的轨迹方程为
⎩⎨⎧x =sin 2φ,y =-1-cos 2φ (φ为参数, π 3<φ<2π3) …10分
(23)解:
(Ⅰ) 1 x + 1
y =x +y xy =x 2+y 2xy ≥2xy xy
=2,
当且仅当x =y =1时,等号成立.
所以 1 x + 1
y
的最小值为2.
…5分
(Ⅱ)不存在.
因为x 2+y 2
≥2xy ,
所以(x +y )2≤2(x 2+y 2
)=2(x +y ), 又x ,y ∈(0,+∞),所以x +y ≤2.
从而有(x +1)(y +1)≤[(x +1)+(y +1) 2]2
=4,
因此不存在x ,y ,满足(x +1)(y +1)=5.。
