中考数学经典难题

初三数学重点难点几何题及答案

压轴题经典难题（1）1、已知：如图，P 是正方形ABCD 点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）2、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）D 2 C 2B 2 A 2 D 1C 1 B 1 C B DA A 1A FG CE B O D A P C D BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难 1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC 求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难1、已知：△ABC 是正三角形，P求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．FP DE CBAA PC BAC BPDEDA ACBPD经典难题（一）1.如下图做GH⊥AB,连接EO。

超难的中考数学试题及答案

超难的中考数学试题及答案一、选择题1. 已知等差数列{an}的公差为5，首项为3，若a1+a2+a3+a4=150，求a5的值。

A. -10B. 10C. 15D. 20答案：A. -10解析：根据已知条件，可以列出等差数列的通项公式an = a1 + (n-1)d，其中d为公差。

a1+a2+a3+a4 = 4a1 + 6d = 150由a1 = 3和d = 5，代入得到：12 + 30 = 15042 = 150解得d=-10。

因此，a5 = a1 + (5-1)d = 3 + 4(-10) = -37.2. 已知函数y = ax^2 + bx + c的图像经过点(1, 4)，(2, 9)，(3, 16)，求a, b, c的值。

A. a=1, b=2, c=2B. a=1, b=2, c=3C. a=2, b=3, c=4D. a=2, b=2, c=1答案：A. a=1, b=2, c=2解析：将给定的三个点分别代入函数，可以得到以下三个方程：a(1)^2 + b(1) + c = 4a(2)^2 + b(2) + c = 9a(3)^2 + b(3) + c = 16化简并解方程可得：a +b +c = 44a + 2b + c = 99a + 3b + c = 16求解该方程组，得到a=1，b=2，c=2。

二、填空题1. 设正整数a、b、c满足a<b<c，且满足c的立方减去b的立方等于a的立方减去b的立方，求a、b、c的最小值。

答案：a=6，b=7，c=8解析：根据题意，可以列出方程c^3 - b^3 = a^3 - b^3。

根据立方差公式(a^3 - b^3 = (a-b)(a^2 + ab + b^2))，可以得到：(a-b)(a^2 + ab + b^2) = (c-b)(c^2 + cb + b^2)由于a<b<c，令a-b=1和c-b=2，代入方程得到：(1)(a^2 + ab + b^2) = (2)(c^2 + cb + b^2)化简并整理得：a^2 - 2b + b^2 = 4c + 2ba^2 + b^2 = 4c + 4b根据a<b<c，我们可以假设最小的三个数分别为6、7和8，代入方程验证：6^2 + 7^2 = 4(8) + 4(7)36 + 49 = 32 + 28因此，a=6，b=7，c=8是满足条件的最小值。

中考数学几何经典难题(标准答案)

中考数学几何经典难题(标准答案)中考数学几何经典难题（标准答案）
题目一
已知直角三角形ABC，∠B=90°，AB=3cm，BC=4cm。

求三角形ABC的斜边AC的长度。

解答一
根据勾股定理，直角三角形的斜边的平方等于两直角边的平方和。

所以，斜边AC的长度可以通过计算得到：
AC² = AB² + BC²
AC² = 3² + 4²
AC² = 9 + 16
AC² = 25
根据开方运算，可以得到AC的长度为5cm。

题目二
已知等腰梯形ABCD，AB∥CD，AB=10cm，CD=16cm，AD=BC=6cm，求梯形ABCD的面积。

解答二
等腰梯形的面积可以通过以下公式计算：
其中，a和b分别表示上底和下底的长度，h表示梯形的高。

根据已知条件可以得到：
上底a = AB = 10cm
下底b = CD = 16cm
高h = AD = BC = 6cm
将这些值代入公式进行计算：
面积 = ((a + b) * h) / 2
面积 = ((10 + 16) * 6) / 2
面积 = (26 * 6) / 2
面积 = 156 / 2
面积 = 78
所以，梯形ABCD的面积为78平方厘米。

以上就是中考数学几何的两个经典难题的标准答案。

希望对你有帮助！。

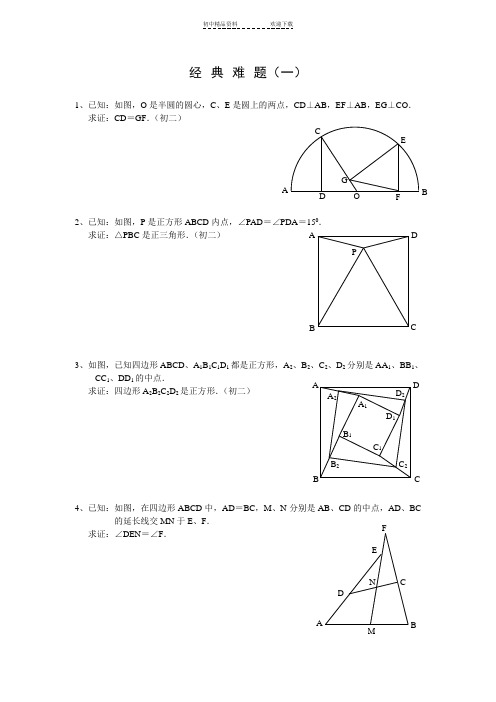
1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、Ptolemy （托勒密）定理：设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，l ＝PA ＋PB ＋PC ，求证：≤l ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．。

九年级上册数学难题及其解答

九年级上册数学难题及其解答一、一元二次方程相关（5题）1. 已知关于x的一元二次方程x^2-(2k + 1)x + k^2+k = 0。

- 求证：方程有两个不相等的实数根。

- 若ABC的两边AB、AC的长是这个方程的两个实数根，第三边BC的长为5。

当ABC是等腰三角形时，求k的值。

- 解答：- 对于一元二次方程ax^2+bx + c = 0(a≠0)，判别式Δ=b^2-4ac。

在方程x^2-(2k + 1)x + k^2+k = 0中，a = 1，b=-(2k + 1)，c=k^2+k。

- Δ=(2k + 1)^2-4(k^2+k)- =4k^2+4k + 1-4k^2-4k- =1>0，所以方程有两个不相等的实数根。

- 由一元二次方程x^2-(2k + 1)x + k^2+k = 0，根据韦达定理x_1+x_2=-(b)/(a)，x_1x_2=(c)/(a)，可得x_1+x_2=2k + 1，x_1x_2=k^2+k。

- 因为ABC是等腰三角形，BC = 5，设AB=x_1，AC = x_2。

- 当AB=BC = 5或AC = BC = 5时，把x = 5代入方程x^2-(2k + 1)x +k^2+k = 0得：- 25-5(2k + 1)+k^2+k = 0- 25-10k - 5+k^2+k = 0- k^2-9k + 20 = 0- (k - 4)(k - 5)=0- 解得k = 4或k = 5。

- 当k = 4时，原方程为x^2-9x+20 = 0，解得x_1=5，x_2=4，三角形三边为5，5，4，满足三角形三边关系。

- 当k = 5时，原方程为x^2-11x + 30 = 0，解得x_1=5，x_2=6，三角形三边为5，5，6，满足三角形三边关系。

2. 若关于x的一元二次方程mx^2-(3m - 1)x+2m - 1 = 0，其根的判别式的值为1，求m的值及该方程的根。

- 解答：- 对于一元二次方程ax^2+bx + c = 0(a≠0)，判别式Δ=b^2-4ac。

九年级数学难题压轴题

九年级数学难题压轴题题目：如图，在平面直角坐标系中，抛物线公式与公式轴的一个交点为公式，与公式轴的交点为公式，对称轴是公式，对称轴与公式轴交于点公式。

（1）求抛物线的函数表达式；（2）经过公式的直线公式平移后与抛物线交于点公式，与公式轴交于点公式，当以公式为顶点的四边形是平行四边形时，求出点公式的坐标。

解析：（1）1. 对于抛物线公式（本题公式），已知抛物线对称轴公式公式，对称轴是公式，所以公式，即公式。

2. 因为抛物线公式过点公式，把公式代入抛物线方程可得：公式。

3. 将公式代入上式得：公式，公式，解得公式。

4. 再把公式代入公式，得公式。

5. 所以抛物线的函数表达式为公式。

（2）1. 首先求公式点坐标，当公式时，公式，所以公式。

2. 由对称轴公式可得公式。

3. 设直线公式的解析式为公式，把公式，公式代入可得公式，解得公式，所以直线公式的解析式为公式。

4. 因为直线公式平移后与抛物线交于点公式，与公式轴交于点公式，设平移后的直线公式的解析式为公式。

5. 设公式，联立直线公式与抛物线方程公式，消去公式得：公式，整理得公式。

6. 即公式，根据韦达定理公式（设方程的另一个根为公式）。

7. 当以公式为顶点的四边形是平行四边形时，分两种情况：当公式为平行四边形的边时：因为公式平行公式，公式。

设公式，则公式。

由直线公式，当公式时，公式，即公式。

根据两点间距离公式公式。

又因为公式，联立方程求解。

由公式，公式，将其代入距离公式求解公式的值，进而得到公式的坐标。

当公式为平行四边形的对角线时：公式，设公式，公式。

根据中点坐标公式，公式中点坐标为公式，公式中点坐标公式，则公式，公式，即公式。

把公式代入抛物线公式，解得公式或公式。

当公式时，公式与公式重合，舍去。

当公式时，公式。

中考数学经典难题集锦

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．经典难题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、Ptolemy （托勒密）定理：设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：1≤L ＜中考数学经典难题集锦2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a4、如图，△ABC 中，∠ABC＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠EBA ＝200，求∠BED 的度数．。

九年级数学难题精选(有答案)

一、如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N，其顶点为D．（1）抛物线及直线AC的函数关系式；（2）设点M（3，m），求使MN+MD的值最小时m的值；（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF ∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E 的坐标；若不能，请说明理由；（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．解：（1）由抛物线y=﹣x2+bx+c过点A（﹣1，0）及C（2，3）得，，解得，故抛物线为y=﹣x2+2x+3又设直线为y=kx+n过点A（﹣1，0）及C（2，3）得，解得故直线AC为y=x+1；（2）作N点关于直线x=3的对称点N'，则N'（6，3），由（1）得D（1，4），故直线DN'的函数关系式为y=﹣x+，当M（3，m）在直线DN'上时，MN+MD的值最小，则m=﹣×=；（3）由（1）、（2）得D（1，4），B（1，2）∵点E在直线AC上，设E（x，x+1），①当点E在线段AC上时，点F在点E上方，则F（x，x+3），∵F在抛物线上，∴x+3=﹣x2+2x+3，解得，x=0或x=1（舍去）∴E（0，1）；②当点E在线段AC（或CA）延长线上时，点F在点E下方，则F（x，x﹣1）由F在抛物线上∴x﹣1=﹣x2+2x+3解得x=或x=∴E（，）或（，）综上，满足条件的点E为E（0，1）、（，）或（，）；（4）方法一：过点P作PQ⊥x轴交AC于点Q；过点C作CG⊥x轴于点G，如图1设Q（x，x+1），则P（x，-x2+2x+3）∴PQ=（-x2+2x+3）-（x﹣1）=-x2+x+2又∵S△APC=S△APQ+S△CPQ=PQ·AG=（-x2+x+2）×3=-（x﹣）2+∴面积的最大值为．二、已知：直角梯形OABC中，BC∥OA，∠AOC=90°，以AB为直径的圆M交OC于D、E，连结AD、BD、BE。

中考数学试卷超难含答案

一、选择题（每题3分，共30分）1. 已知函数f(x) = 2x - 3，若f(x+1) = 2f(x)，则x的值为（）A. 1B. 2C. 3D. 4答案：B解析：由题意得，2(x+1) - 3 = 2(2x - 3)，解得x = 2。

2. 在△ABC中，AB = 5，AC = 6，BC = 7，若点D、E分别在AB、AC上，且AD = 2，AE = 3，则DE的长度为（）A. 2√3B. 3√2C. 4D. 5答案：A解析：由余弦定理可得cos∠BAC = (25 + 36 - 49) / (2×5×6) = 1/5。

由正弦定理可得sin∠BAC = 2√6/5。

在△ADE中，由正弦定理可得DE/ sin∠BAC = AD/ sin∠DAE，即DE = AD × sin∠BAC / sin∠DAE = 2 × 2√6/5 = 2√3。

3. 若方程x^2 - 2(k+1)x + k = 0的解为x1和x2，且x1 + x2 = 2(k+1)，则k 的值为（）A. -1B. 0C. 1D. 2答案：A解析：由韦达定理可得x1 + x2 = 2(k+1) = 2k + 2，又因为x1 + x2 = 2(k+1)，所以2k + 2 = 2k + 2，即k = -1。

4. 在直角坐标系中，点P(2,3)关于直线y=x的对称点为（）A. (3,2)B. (2,3)C. (1,4)D. (4,1)答案：A解析：点P(2,3)关于直线y=x的对称点坐标为(3,2)。

5. 若等差数列{an}的前n项和为Sn，且a1 = 3，S10 = 165，则第15项an的值为（）A. 18B. 19C. 20D. 21答案：C解析：由等差数列的前n项和公式可得Sn = n(a1 + an)/2，代入已知条件得165 = 10(3 + an)/2，解得an = 20。

6. 在△ABC中，AB = AC，∠B = 30°，BC = 4，则△ABC的面积S为（）A. 2√3B. 4√3C. 6D. 8答案：A解析：由勾股定理可得AB = AC = 2√3，由正弦定理可得S = 1/2 × AB × AC × sin∠B = 1/2 × 2√3 × 2√3 × sin30° = 2√3。

初三数学难题精选答案及讲解

1、如果将点P 绕定点M 旋转180°后与点Q 重合，那么称点P 与点Q 关于点M 对称，定点M 叫做对称中心。

此时，M 是线段PQ 的中点。

如图，在平面直角坐标系中，△ABO 的顶点A ，B ，O 的坐标分别为（1，0），（0，1），（0，0）。

点列P 1，P 2，P 3，…中的相邻两点都关于△ABO 的一个顶点对称：点P 1与点P 2关于点A 对称，点P 2与点P 3关于点B 对称，点P 3与点P 4关于点O 对称，点P 4与点P 5关于点A 对称，点P 5与点P 6关于点B 对称，点P 6与点P 7关于点O 对称…对称中心分别是A ，B ，O ，A ，B ，O ，…，且这些对称中心依次循环。

已知点P 1的坐标是（1，1），则点P 2017的坐标为。

解：P 2的坐标是（1，-1），P 2017的坐标是（1，-1）。

理由：作P 1关于A 点的对称点，即可得到P 2（1，-1），P 3（-1，3），P 4（1，-3），P 5（1，3），P 6（-1，-1），又回到原来P 1的坐标，P 7（-1，-1）；由此可知，每6个点为一个周期，作一次循环，2017÷6＝336…1，循环了336次后又回到了原来P 1的坐标，故P 2017的坐标与P 1的坐标一样为（1，1）。

点评：此题主要考查了平面直角坐标系中中心对称的性质，以及找规律问题，根据已知得出点P 的坐标每6个一循环是解题关键．2、如图①，已知△ABC 是等边三角形，点E 在线段AB 上，点D 在直线BC 上，且DE=EC ，将△BCE 绕点C 顺时针旋转60°至△ACF ，连接EF 。

试证明：AB=DB+AF 。

【类比探究】（1）如图②，如果点E 在线段AB 的延长线上，其它条件不变，线段AB 、DB 、AF 之间又有怎样的数量关系？请说明理由。

（2）如果点E 在线段BA 的延长线上，其他条件不变，请在图③的基础上将图形补充完整，并写出AB ，DB ，AF 之间数量关系，不必说明理由。

初中数学中考数学经典难题

初中数学中考数学经典难题1. 引言中考是初中学生在数学学科中的重要考试，具有很高的挑战性。

在中考数学中，经典难题是考生必须要面对的。

这些难题既考察了学生的思维逻辑能力，又考察了他们对数学知识的掌握程度。

本文将介绍一些中考数学的经典难题，并提供答案和解析，帮助学生更好地应对这些难题。

2. 题目1：直角三角形的性质题目：已知直角三角形ABC，∠B=90°，AC=5cm，BC=12cm，求∠A和∠C的大小。

解析：根据直角三角形的性质，∠A + ∠C = 90°。

我们可以通过三角形的正弦定理求解此题。

根据正弦定理，我们有：sin(∠A) = AC / BC = 5 / 12所以，∠A = arcsin(5 / 12) ≈ 23.6°根据∠A + ∠C = 90°，我们可以得出，∠C = 90° - ∠A ≈ 66.4°所以，∠A ≈ 23.6°，∠C ≈ 66.4°3. 题目2：解线性方程组题目：解方程组： 2x + 3y = 8 3x - 2y = 5解析：我们可以使用消元法或代入法来解决此题。

让我们使用代入法来解决它。

我们可以将第一个方程写为x = (8 - 3y) / 2，并将其代入第二个方程中。

3(8 - 3y) / 2 - 2y = 5解方程得到：24 - 9y - 4y = 10-13y = -14y = 14 / 13 ≈ 1.08将y的值代入第一个方程中，解出x：2x = 8 - 3(1.08)2x ≈ 4.76x ≈ 2.38所以，方程组的解为x ≈ 2.38，y ≈ 1.08。

4. 题目3：三角形的面积计算题目：已知三角形ABC，AB = 5cm，BC = 8cm，∠B = 60°，求三角形ABC的面积。

解析：我们可以使用正弦定理来求解三角形的面积。

根据正弦定理，我们有：sin(∠A) / AB = sin(∠B) / BCsin(∠A) / 5 = sin(60°) / 8sin(∠A) = 5 * sin(60°) / 8sin(∠A) ≈ 0.72由此，我们可以解出∠A ≈ arcsin(0.72) ≈ 46.3°所以，三角形ABC的面积为(1 / 2) * AB * BC * sin(∠B) = (1 / 2) * 5 * 8 * sin(60°) ≈ 17.32cm²5. 题目4：平方根的求解题目：求解方程x² + 5x + 4 = 0的解。

初中数学经典难题(含答案)

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）E1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、Ptolemy （托勒密）定理：设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）1、设P 是边长为1的正△ABC 内任一点，l ＝PA ＋PB ＋PC ，求证：3≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．经典难题（一）1、2、3、4、经典难题（二）1、2、4、经典难题（三）1、3、4、1、2、3、4、证明：过D 作DQ ⊥AE ，DG ⊥CF,并连接DF 和DE ，如右图所示则S △ADE =21S ABCD =S △DFC ∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线，∴∠DPA=∠DPC1、2、3、3、4、。

中考巨难数学试卷及答案

一、选择题（每题5分，共50分）1. 已知函数f(x) = 2x^3 - 3x^2 + 4x + 1，若f(x)在x=1处的切线斜率为k，则k的值为：A. 1B. 2C. 3D. 4答案：B解析：由导数的定义，f'(x) = 6x^2 - 6x + 4，代入x=1得f'(1) = 6 - 6 + 4= 4，所以切线斜率k=4。

2. 在等差数列{an}中，a1=1，公差d=2，则第10项an的值为：A. 19B. 20C. 21D. 22答案：A解析：由等差数列的通项公式an = a1 + (n-1)d，代入a1=1，d=2，n=10，得an= 1 + (10-1)×2 = 1 + 18 = 19。

3. 已知三角形ABC中，AB=AC，BC=4，则角A的正弦值为：A. 1/2B. √2/2C. √3/2D. 1答案：C解析：由勾股定理，AB=AC=√(BC^2/4) = √(4^2/4) = √4 = 2。

在直角三角形ABC中，sinA = 对边/斜边 = BC/AB = 4/2 = 2。

4. 若复数z满足|z-1|+|z+1|=4，则复数z对应的点在复平面上的轨迹是：A. 矩形B. 等腰梯形C. 矩形D. 等腰梯形答案：B解析：由复数的几何意义，|z-1|表示点z到点(1,0)的距离，|z+1|表示点z到点(-1,0)的距离。

因为|z-1|+|z+1|=4，所以点z到这两个点的距离之和为4，对应的轨迹是一个等腰梯形。

5. 已知函数f(x) = ax^2 + bx + c，若f(1) = 2，f'(2) = 6，则a+b+c的值为：A. 2B. 3C. 4D. 5答案：B解析：由导数的定义，f'(x) = 2ax + b，代入x=2得f'(2) = 4a + b = 6。

又因为f(1) = a + b + c = 2，解得a+b+c=3。

二、填空题（每题5分，共25分）6. 已知函数f(x) = x^2 - 4x + 3，则f(x)的图像与x轴的交点坐标为______。

中考数学难题集锦

中考数学难题集锦难题一：甲、乙两个机器同时开始工作。

甲每分钟可以工作4件产品，乙每分钟可以工作6件产品。

请问，甲、乙两个机器同时工作10分钟，能生产多少件产品？解析：甲每分钟可以生产4件产品，那么在10分钟内甲可以生产4x10=40件产品。

同样地，乙每分钟可以生产6件产品，所以在10分钟内乙可以生产6x10=60件产品。

因此，甲、乙两个机器同时工作10分钟，总共可以生产40+60=100件产品。

难题二：若一个角的余弦值等于0.6，那么这个角的弧度值是多少？解析：根据三角函数的定义，余弦值等于邻边长度与斜边长度的比例。

假设该角对应的直角边长为x，斜边长为1。

根据勾股定理，可得到x2+12=1，即x^2=0，所以x=0。

因此，该角的弧度值为0。

难题三：一个立方体的边长为a，体积为V，若将该立方体的体积增加到原来的8倍，边长变为原来的一半，求增加后的体积。

解析：原立方体的体积为V，边长为a。

增加后的立方体边长为a/2，体积为8V。

我们可以通过体积的公式得到方程：(a/2)3=8V。

将等式两边同时开立方，得到a3/8=8V，化简为a^3=64V。

所以，增加后的体积为64V。

难题四：某商场原价为100元的商品打六折促销，然后进行满减活动，满200元减20元。

问若购买者购买该商品2件，实际需要支付的金额是多少？解析：首先，打六折，原价100元的商品会有60元的折扣，所以每件商品的价格为100-60=40元。

购买2件商品的总价为2x40=80元。

然后，根据满减活动，若满200元减20元，则购买者需要支付的金额为总价80元-20元=60元。

难题五：若正方形的边长为x，那么它的对角线长度是多少？解析：正方形的对角线可以看作是直角三角形的斜边。

直角三角形的两条直角边分别为正方形的边长，假设为x。

根据勾股定理，可得对角线的长度为√(x2+x2)=√(2x^2)=x√2。

以上是一些中考数学的难题集锦及其解析。

这些题目涵盖了各个考点，帮助学生通过解题训练提高数学思维和解题能力。

初三中考数学压轴难题有答案

1．矩形纸片ABCD中，AB＝5，AD＝4．（1）如图1，四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形．你能否在该矩形中裁剪出一个面积最大的正方形，最大面积是多少？说明理由；（2）请用矩形纸片ABCD剪拼成一个面积最大的正方形．要求：在图2的矩形ABCD中画出裁剪线，并在网格中画出用裁剪出的纸片拼成的正方形示意图（使正方形的顶点都在网格的格点上）．2．在平面直角坐标系xOy中，点P的坐标为（x1，y1），点Q的坐标为（x2，y2），且x1≠x2，y1≠y2，若P，Q为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”，如图为点P，Q的“相关矩形”示意图．（1）已知点A的坐标为（1，0），①若点B的坐标为（3，1），求点A，B的“相关矩形”的面积；②点C在直线x＝3上，若点A，C的“相关矩形”为正方形，求直线AC的表达式；（2）⊙O的半径为 2 ，点M的坐标为（m，3），若在⊙O上存在一点N，使得点M，N 的“相关矩形”为正方形，求m的取值范围．3．问题背景：如图①，在四边形ADBC中，∠ACB＝∠ADB＝90°，AD＝BD，探究线段AC，BC，CD 之间的数量关系．小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C 分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE＝ 2 CD，从而得出结论：AC＋BC＝ 2 C D．简单应用：（1）在图①中，若AC＝ 2 ，BC＝2 2 ，则CD＝___________．（2）如图③，AB是⊙O的直径，点C、D在⊙上，⌒AD＝⌒BD，若AB＝13，BC＝12，求CD的长．拓展规律：（3）如图④，∠ACB＝∠ADB＝90°，AD＝BD，若AC＝m，BC＝n（m＜n），求CD的长（用含m，n的代数式表示）（4）如图⑤，∠ACB＝90°，AC＝BC，点P为AB的中点，若点E满足AE＝13AC，CE＝CA，点Q为AE的中点，则线段PQ与AC的数量关系是_______________________．4．爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC＝a，AC ＝b，AB＝c．【特例探究】（1）如图1，当tan∠P AB＝1，c＝4 2 时，a＝_________，b＝_________；如图2，当∠P AB＝30°，c＝2时，a＝_________，b＝_________；【归纳证明】（2）请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．【拓展证明】（3）如图4，□ABCD中，E、F分别是AD、BC的三等分点，且AD＝3AE，BC＝3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD＝3 5 ，AB＝3，求AF的长．1．如图，抛物线y＝x2－2x－3交x轴于A（－1，0）、B（3，0），交y轴于C（0，－3），M是抛物线的顶点，现将抛物线沿平行于y轴的方向向上平移三个单位，则曲线CMB在平移过程中扫过的面积为___________（面积单位）．2．如图，点A为函数y＝9x（x＞0）图象上一点，连结OA，交函数y＝1x（x＞0）的图象于点B，点C是x轴上一点，且AO＝AC，则△ABC的面积为_____________．3．书店举行购书优惠活动：①一次性购书不超过100元，不享受打折优惠；②一次性购书超过100元但不超过200元一律打九折；③一次性购书超过200元一律打七折．小丽在这次活动中，两次购书总共付款229.4元，第二次购书原价是第一次购书原价的3倍，那么小丽这两次购书原价的总和是_____________．4．已知抛物线y＝ax2－4ax＋c经过点A（0，2），顶点B的纵坐标为3．将直线AB向下平移，与x轴、y轴分别交于点C、D，与抛物线的一个交点为P，若D是线段CP的中点，则点P的坐标为_________________．5．在平面直角坐标系中，点O 为坐标原点，A 、B 、C 三点的坐标为（ 3 ，0）、（3 3 ，0）、（0，5），点D 在第一象限，且∠ADB ＝60°，则线段CD 的长的最小值为____________．6．若直线y ＝m （m 为常数）与函数y ＝ ⎩⎨⎧x 22(x ≤2)4x (x ＞2) 的图象恒有三个不同的交点，则常数m 的取值范围是_____________．7．如图，在正方形ABCD 外侧作直线DE ，点C 关于直线DE 的对称点为M ，连接CM ，AM ．其中AM 交直线DE 于点N ．若45°＜∠CDE ＜90°，则当MN ＝4，AN ＝3时，正方形ABCD 的边长为_____________．8．如图1，在平面直角坐标系中，将▱ABCD 放置在第一象限，且AB ∥x 轴．直线y ＝－x 从原点出发沿x 轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l 与直线在x 轴上平移的距离m 的函数图象如图2所示，那么AD 的长为 ______________．9．如图，已知A 、C 是半径为2的⊙O 上的两动点，以AC 为直角边在⊙O 内作等腰Rt △ABC ，∠C ＝90°，连接OB ，则OB 的最小值为__________．10．如图，在Rt △ABC 中，∠B ＝60°，BC ＝3，D 为BC 边上的三等分点，BD ＝2CD ，E 为AB 边上一动点，将△DBE 沿DE 折叠到△DB ′E 的位置，连接AB ′，则线段AB ′的最小值为：_________．11．如图，在Rt △ABC 中，∠C ＝90°，AC ＝6，BC ＝8，点F 在边AC 上，并且CF ＝2，点E 为边BC 上的动点，将△CEF 沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是_________．12．如图，矩形ABCD 中，点E ，F ，G ，H 分别在边AB ，BC ，CD ，DA 上，点P 在矩形ABCD 内．若AB ＝4cm ，BC ＝6cm ，AE ＝CG ＝3cm ，BF ＝DH ＝4cm ，四边形AEPH 的面积为5cm 2，则四边形PFCG 的面积为___________________．OCBA14．在面积为15的平行四边形ABCD 中，过点A 作AE 垂直于直线BC 于点E ，作AF 垂直于直线CD 于点F ，若AB ＝5，BC ＝6，则CE ＋CF 的值为_____________．15．已知：直线y ＝－ n n ＋1x ＋ 2n ＋1 （n 为整数）与两坐标轴围成的三角形面积为s n ，则s 1＋s 2＋s 3＋…s n ＝___________________．16．如图，矩形ABCD 中，AB ＝8，BC ＝6，P 为AD 上一点，将△ABP 沿BP 翻折至△EBP ，PE 与CD 相交于点O ，且OE ＝OD ，则AP 的长为___________．18．如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y ＝x 的图象上，从左向右第3个正方形中的一个顶点A 的坐标为（8，4），阴影三角形部分的面积从左向右依次记为S 1 、S2、S 3 、…、S n ，则S n 的值为________．（用含n 的代数式表示，n 为正整数）AB CD19．如图，E 是正方形ABCD 内一点，E 到点A 、D 、B 的距离EA 、ED 、EB 分别为1、3 2 、2 5 ，延长AE 交CD 于点F ，则四边形BCFE 的面积为________________．20．如图，矩形OABC 的边OA 、OC 分别在x 轴、y 轴上，点B 的坐标为（7，3），点E 在边AB 上，且AE ＝1，已知点P 为y 轴上一动点，连接EP ，过点O 作直线EP 的垂线段，垂足为点H ，在点P 从点F （0，254）运动到原点O 的过程中，点H 的运动路径长为____________．21．如图，在等腰直角三角形ABC 中，∠ABC =90°，AB =BC =2，P 是△ABC 所在平面内一点，且满足P A ⊥PB ，则PC 的取值范围为．22．已知一次函数y =－43x +4与x 轴、y 轴分别交于点A 、B ，现有点M （m ，－m ），N （m ＋3，－m －4）则当四边形MNAB 周长最小时，m ＝____________．23．如图，四边形ABCD 的顶点都在坐标轴上，若AD ∥BC ，△ACD 与△BCD 的面积分别为10和20，若双曲线y ＝k x恰好经过边AB 的四等分点E （BE ＜AE ），则k 的值为____________．1.（1）16 设AM=x，则MD=4-x，得S=2(x-2)2+8,故当x=0或4时面积最大。

初中数学中考常见重难点题大全

以下是初中数学中考常见的重难点题目：
1. 初一下数学：
- 平方差公式的运用；
- 两点间距离公式的运用；
- 正比例、反比例的运用；
- 简单统计：平均数、中位数、众数、极差等。

2. 初一上数学：
- 一元一次方程式的解法：解方程、解不等式问题；
- 合并同类项、开平方问题以及它们的运算；
- 面积知识：基本平面图形面积以及环的面积；
- 相交线与平行线性质问题。

3. 初一下数学：
- 二元一次方程组与不等式组的求解；
- 三角形（等腰三角形、直角三角形、角平分线问题）面积计算；
- 勾股定理的运用；
- 正方体的表面积、体积计算。

4. 初二上数学：
- 一元二次方程式的求解：解方程组、解不等式问题；
- 计算容斥、组合、排列；
- 立体图形的表面积、体积计算；
- 二次函数的解析式、图像以及相关变换问题。

5. 初二下数学：
- 斜率、二直线问题；
- 数列等差、等比问题及求和问题；
- 概率与统计相关问题；
- 初中三角题基本应用。

以上是初中数学中考常见的重难点题目，建议在复习中注重以上重点题目的练习和掌握，同时也应注意整体的知识综合及应用能力的培养。

中考数学经典难题

1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、Ptolemy （托勒密）定理：设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，l ＝PA ＋PB ＋PC ，求证：≤l ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．。

初中数学经典几何难题及答案

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·4、平行四边形ABCD 中，设E、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）1、设P 是边长为1的正△ABC内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC0，∠EBA ＝200，求∠BED 的度数．经典难题（一）1.如下图做GH ⊥AB,连接EO 。

初三数学中考难题

A BCDPE第2题图第3题图ABCBOAC O A C B 一、选择题1．如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是（）Ａ．74 Ｂ．73 Ｃ．72 Ｄ．71解：∵空白部分的小正方形共有7个，其中在最下面一行中取任意一个均能够成这个正方体的表面展开图，最下面一行共有4个空格，∴任取一个涂上阴影，能构成这个正方体的表面展开图的概率是：．故选A ．2．如图所示，矩形ABCD 中，AB =4，BC =43，点E 是折线段A －D －C 上的一个动点（点E 与点A 不重合），点P 是点A 关于BE 的对称点．在点E 运动的过程中，使△PCB 为等腰三角形的点E 的位置共有 A ．2个 B ．3个 C ．4个 D ．5个根据题意，结合图形，分情况讨论：①BP 为底边；②BP 为等腰三角形一腰长．解答：解：①BP 为底边时，符合点E 的位置有2个；②BP 为等腰三角形一腰长时，符合点E 的位置有2个； ③以PC 为底边，B 为顶点时，这样的等腰三角形不存在．故选C ．3．如图，在△ABC 中，AB = AC ，AB = 8，BC = 12，分别以 AB 、AC 为直径作半圆，则图中阴影部分的面积是（）A ．64127π-B ．1632π-C ．16247π-D ．16127π-设3个阴影部分的交点为D ，连线AD ，将上部阴影分为左、右，设为阴影1、2，设左下阴影为3，右下为4,面积分为S1 S2 S3 S4则：S 圆ABD=S 三角ABD+S3+S2······1式 S 圆ACD=S 三角ACD+S4+S1······2式联立式1、2得阴影部分面积=S1+S2+S3+S4=S 圆ABD+S 圆ACD-S 三角ABD-S 三角ACD（1题图）俯视图左视图主视图第5题图4．如图是一个几何体的三视图，其中主视图、左视图都是腰为13cm ，底为10cm 的等腰三角形，则这个几何的侧面积是 ( )A ．60πcm 2B ．75πcm 2C ．70πcm 2D ．65πcm 2 5．如图，在⊙O 中，OA ＝AB ，OC ⊥AB ，则下列结论错误的是 A ．弦AB 的长等于圆内接正六边形的边长 B ．弦AC 的长等于圆内接正十二边形的边长C ．AC BC = D ．∠BAC=30°6.如图，一种电子游戏，电子屏幕上有一正六边形ABCDEF ，点P 沿直线AB 从右向左移动，当出现点P 与正六边形六个顶点中的至少两个顶点距离相等时，就会发出警报，则直线AB 上会发出警报的点P 有( )A ．3个B ．4个C ．5个D ．6个7．多项式21xy xy -+的次数及最高次数的系数是（） A ．2,1 B ．2，-1 C ．3,-1 D ．5，-18．如图5是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x ，y 表示直角三角形的两直角边（x y >），下列四个说法：①2249x y +=，②2x y -=，③2449xy +=，④9x y +=.其中说法正确的是（）A ．①②B . ①②③ C. ①②④ D. ①②③④ ９．如图，两条抛物线12121+-=x y 、12122--=x y 与分别经过点()0,2-,()0,2且平第6题E A BCDFPyx第8题ABOCH行于y 轴的两条平行线围成的阴影部分的面积为（）Ａ．8 Ｂ．6 Ｃ．10 Ｄ．410．已知：如图，在梯形ABCD 中，AD ∥BC ，∠DCB = 90°，E 是AD 的中点，点P 是BC 边上的动点（不与点B 重合），EP 与BD 相交于点O.当P 点在BC 边上运动时，△BOP ∽△DOE ；若相似比为2，且AD ︰BC = 2︰3.则四边形ABPE 是（）A ．平行四边形 B. 直角梯形 C.等腰梯形 D.矩形11．已知二次函数2y ax bx c =++（a ≠0）的图象如图所示，则下列结论： ① ac >0； ② a –b +c <0； ③当x <0时，y <0； ④方程20ax bx c ++=（a ≠0）有两个大于－1的实数根．其中错误的结论有（）A ．② ③B ．② ④C ．① ③D ．① ④12．如图，矩形纸片ABCD 中，AB =4，AD =3，折叠纸片使AD边与对角线BD 重合，折痕为DG ，记与点A 重合点A ′,则△A ′BG 的面积与该矩形面积的比为（）A.112B.19C.18D. 1613．某种气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P （kPa ）是气球体积V （m 3）的反比例函数，其图像如图所示，当气球内的气压大于120kPa 时，气球将爆炸，为了安全，气球的体积应该（）A. 不小于45m 3 B ．小于54m 3 C. 不大于54m 3 D ．小于45m 314．如图，AB 为O 的直径，CD 为弦，且CD AB ⊥。

中考数学试卷超难题

1. 已知函数f(x) = x^3 - 3x + 2，若存在实数a，使得f(a) = 0，则a的取值范围是（）A. a ≥ 0B. a ≤ 0C. a > 0D. a < 02. 若等差数列{an}的公差d=2，且前n项和S_n = 2n^2 + n，则数列{an}的通项公式是（）A. an = n + 1B. an = n + 2C. an = 2n + 1D. an = 2n3. 在平面直角坐标系中，若点A(2,3)，B(-1,1)，C(m,2m)共线，则m的值为（）A. -1B. 0C. 1D. 24. 已知等比数列{an}的公比q=2，且前n项和S_n = 2^n - 1，则数列{an}的通项公式是（）A. an = 2^n - 1B. an = 2^(n-1) - 1C. an = 2^n + 1D. an = 2^(n-1) + 1二、填空题（每题4分，共16分）5. 若函数f(x) = ax^2 + bx + c在x=-1时取得最小值，则a，b，c的关系是______。

6. 若等差数列{an}的首项a_1 = 3，公差d = 2，则第10项a_10 = ______。

7. 已知点P(1,2)，Q(x,y)在直线y=2x-1上，且PQ的中点坐标为(3,2)，则x=______。

8. 若函数f(x) = x^3 - 3x + 2在x=1处取得极值，则该极值为______。

三、解答题（每题12分，共36分）9. （12分）已知函数f(x) = ax^3 + bx^2 + cx + d（a≠0）的图像如图所示，且f(-1) = 0，f(1) = 0。

（1）求a，b，c，d的值。

（2）若函数g(x) = f(x) + x^2 - 2x，求g(x)的极值。

10. （12分）已知等差数列{an}的首项a_1 = 1，公差d = 2，等比数列{bn}的首项b_1 = 1，公比q = 2。

中考数学经典难题

初三数学重点难点几何题及答案

超难的中考数学试题及答案

中考数学几何经典难题(标准答案)

中考数学经典难题

九年级上册数学难题及其解答

九年级数学难题压轴题

中考数学经典难题集锦

九年级数学难题精选(有答案)

中考数学试卷超难含答案

初三数学难题精选答案及讲解

初中数学 中考数学经典难题

初中数学经典难题(含答案)

中考巨难数学试卷及答案

中考数学难题集锦

初三中考数学压轴难题有答案

初中数学中考常见重难点题大全

中考数学经典难题

初中数学经典几何难题及答案

初三数学中考难题

中考数学试卷超难题

初中数学中考数学经典难题