CRC 校验码编码实验
crc校验码编程

crc校验码编程
CRC校验码是一种常用的差错检测方法,广泛应用于数据通信和数据存储领域。
它通过对数据进行一系列运算,生成一个校验码,用于检测数据传输过程中是否发生了错误。
CRC校验码的生成过程相对简单,但其原理却非常巧妙。
首先,需要选择一个预定的生成多项式,通常是一个固定的二进制位数。
然后,将待校验的数据与一个初始值进行异或运算,得到一个结果。
接下来,将这个结果不断地与生成多项式进行异或运算,直到所有数据都被处理完毕。
最后,将最终的结果作为校验码附加在原始数据后面。
CRC校验码的优点在于,它可以快速检测出错误,且具有很高的检测概率。
通过对数据的每一个位进行计算,CRC校验码可以有效地检测出单个或多个位的错误。
而且,CRC校验码的生成过程是不可逆的,即无法通过校验码推导出原始数据,从而保证了数据的安全性。
在实际应用中,CRC校验码被广泛用于网络通信、存储设备和传感器等领域。
例如,在网络传输中,发送方会将数据进行分组,并计算每个分组的CRC校验码。
接收方在接收到数据后,同样计算CRC 校验码,并与接收到的校验码进行比对。
如果两者一致,说明数据传输无误;如果不一致,则意味着数据可能发生了错误,需要进行重新传输或纠错处理。
总的来说,CRC校验码作为一种差错检测方法,具有简单、高效、可靠的特点。
它在保障数据传输的准确性和可靠性方面起到了重要的作用。
通过合理应用CRC校验码,我们可以提高数据传输的质量,确保信息的完整性和可靠性。
CRC校验算法详解及代码实现

CRC校验算法详解及代码实现CRC校验算法的原理是利用生成多项式来计算数据的校验值。
在发送端,将数据和生成多项式进行计算得到一个校验值,然后将这个校验值附加到发送的数据后面一起传输。
在接收端,接收到数据后再次进行计算,并与接收到的校验值进行比较,如果相同则说明数据传输过程中没有错误,否则说明数据传输过程中出现错误。
下面是CRC校验算法的具体步骤:1.选择一个生成多项式,通常用一个二进制数表示。
生成多项式的位数称为CRC位数,常见的有CRC-8,CRC-16,CRC-32等。
2.将生成多项式的最高位与数据的最高位对齐,然后进行异或运算。
异或运算的结果作为下一次异或运算的输入,直到将所有数据都计算完毕。
3.将计算得到的结果作为校验值附加到数据后面一起传输。
下面是一个简单的CRC校验算法的代码实现:```pythondef crc(data, generator):crc_value = 0generator_length = len(generator)for bit in data:crc_value ^= bitif crc_value & 0x1:crc_value = (crc_value >> 1) ^ int(generator, 2)else:crc_value = crc_value >> 1return crc_value#测试数据data = [1, 0, 1, 1]generator = "1011"#进行CRC校验residue = crc(data, generator)print(residue)```在上面的代码中,`data`表示要进行校验的数据,以列表的形式表示,每个元素是一个二进制位。
`generator`表示生成多项式,以字符串的形式表示,每个字符是一个二进制位。
程序输出的结果为校验值。
总结:本文详细介绍了CRC校验算法的原理和步骤,并给出了一个简单的代码实现。
CRC检验码实验报告
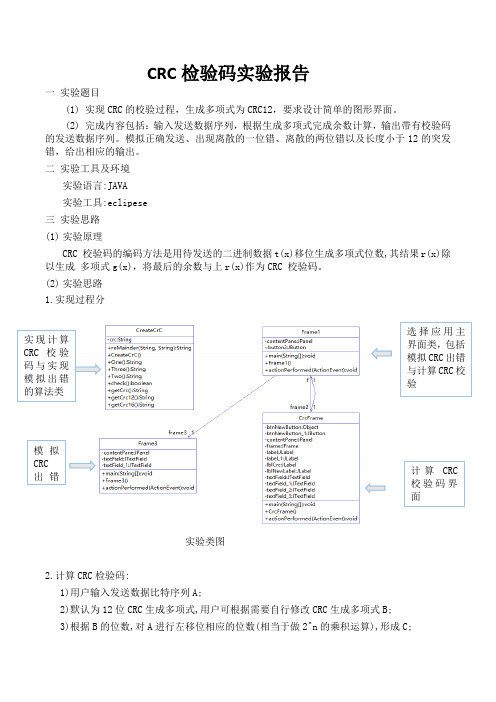
CRC 检验码实验报告一 实验题目(1) 实现CRC 的校验过程,生成多项式为CRC12,要求设计简单的图形界面。
(2) 完成内容包括:输入发送数据序列,根据生成多项式完成余数计算,输出带有校验码的发送数据序列。
模拟正确发送、出现离散的一位错、离散的两位错以及长度小于12的突发错,给出相应的输出。
二 实验工具及环境实验语言:JAVA 实验工具:eclipese 三 实验思路 (1) 实验原理CRC 校验码的编码方法是用待发送的二进制数据t(x)移位生成多项式位数,其结果r(x)除以生成 多项式g(x),将最后的余数与上r(x)作为CRC 校验码。
(2) 实验思路 1.实现过程分实验类图2.计算CRC 检验码:1)用户输入发送数据比特序列A;2)默认为12位CRC 生成多项式,用户可根据需要自行修改CRC 生成多项式B; 3)根据B 的位数,对A 进行左移位相应的位数(相当于做2^n 的乘积运算),形成C;实现计算CRC 校验码与实现模拟出错的算法类选择应用主界面类,包括模拟CRC 出错与计算CRC 校验计算CRC 校验码界面模拟CRC 出错4)对生成多项式和发送数据流进行异或运算,计算余数D;5)余数D+C就形成了带有CRC检验码的数据比特序列。
3. CRC检验码出错模拟:用户输入原CRC检验码的数据比特序列A,选择待模拟的错误类型;程序给出相应模拟出错结果。
四实验结论1.优点1)实现了多种生成多项式CRC检验码的生成与检验2)检验与计算分开,功能明确3)可对用户输入数据进行检查,动态交互2.缺点1)在检验CRC校验码时,只能有用户手动输入数据,不能粘贴复制,比较麻烦2)页面布局与外观有待提高。
CRC编码实验实验报告

11001———————除数
————
11110
1001
————
11111
11001
————
000100——————余数
2)
input=[1 0 1 1 0 0 1 1];crc_no=4;
k = size(input,2);
generator = zeros(1,crc_no+1);
output = zeros(1,k+crc_no);
end
output = [input output(1:crc_no)];
n = size(input,2);
output = input(1:n-crc_no);
forii = 1:n-crc_no
if(input(1) == 1)
input(1:crc_no+1) = mod((input(1:crc_no+1)+generator),2);
而发送信息位 1111,可转换为数据多项式为C(x)=x^3+x^2+x+1。
2)、生成多项式
是接受方和发送方的一个约定,也就是一个二进制数,在整个传输过程中,这个数始终保持不变。
在发送方,利用生成多项式对信息多项式做模2除生成校验码。在接受方利用生成多项式对收到的编码多项式做模2除检测和确定错误位置。
循环冗余校验编解码电路设计实验报告

循环冗余校验编解码电路设计实验报告一、引言循环冗余校验(CRC)是一种常用于检测和校正数据传输错误的技术。
在通信领域,CRC编解码电路是一种重要的硬件设计,用于验证数据传输的准确性。
本实验旨在通过设计循环冗余校验编解码电路,探索其工作原理和实际应用。
二、背景知识1.循环冗余校验原理循环冗余校验利用多项式除法的性质来实现数据校验。
发送端将数据和校验值进行运算得到余数,并将余数附加到数据后一起发送。
接收端通过对接收到的数据进行除法运算,得到的余数判断数据是否正确。
2.CRC编码过程–发送端:将数据进行扩展,加上用于校验的位数,并使用预定的生成多项式进行除法运算得到余数,将余数附加在数据后面发送出去。
–接收端:接收到数据后,再次进行除法运算,得到的余数为0则说明数据传输正确,否则说明存在错误。
3.CRC解码过程–发送端:发送数据和余数。
–接收端:接收数据和余数,使用与发送端一样的生成多项式进行除法运算,得到的余数判断数据是否正确。
三、实验设计与实现1. 实验目的了解循环冗余校验的原理,并通过设计和实现循环冗余校验编解码电路加深对其理解。
2. 实验器材与材料•FPGA开发板:用于搭建实验电路•Vivado软件:用于设计和验证电路•扁平电缆:用于连接FPGA开发板和外部设备3. 实验步骤1.了解所用的生成多项式,确定校验位数和除法运算方式。
2.使用Vivado软件创建工程,选择适合的FPGA开发板型号。
3.设计循环冗余校验编码模块,并使用Verilog语言进行描述。
4.设计循环冗余校验解码模块,并使用Verilog语言进行描述。
5.设计测试模块,用于生成测试数据和验证结果。
6.进行RTL级仿真,验证电路设计的正确性。
7.将设计文件综合、实现和下载到FPGA开发板。
8.在FPGA开发板上测试编解码电路的功能和性能。
9.分析实验结果,总结经验和教训。
四、实验结果与分析1. RTL级仿真结果在RTL级仿真中,我们生成了不同的输入数据,并通过编解码电路计算得到校验值和余数。
crc校验原理及代码

crc校验原理及代码CRC(循环冗余校验)是一种错误检测技术,通过对数据进行计算和比较,来确定数据是否被改变或破坏。
它主要用于数据通信中,确保数据的完整性。
CRC校验的原理是通过生成多项式来计算发送数据的校验码,并将校验码附加到数据末尾,接收方通过再次计算校验码来验证数据的完整性。
CRC采用二进制多项式除法的方式实现。
以下是一种常见的CRC校验算法,称为CRC-32算法,它使用32位的校验码:```pythondef crc32(data):crc = 0xFFFFFFFFfor byte in data:crc ^= bytefor _ in range(8):if crc & 1:else:crc >>= 1crc ^= 0xFFFFFFFFreturn crc```利用以上的代码,可以计算给定数据的CRC-32校验码。
下面是代码的解释:1. `crc32`函数的输入参数是字符串类型的数据。
2. `crc`变量初始值为0xFFFFFFFF,是32位全1的二进制数。
3.循环遍历输入数据中的每个字节,并进行计算。
4. `crc ^= byte`将校验码与当前字节进行异或操作。
5.在每个字节的8位中,循环判断最低位是否为17.若最低位为0,则直接右移一个位置。
8.在全部字节处理完成后,将校验码与0xFFFFFFFF进行异或操作,得到最终的校验码。
CRC校验在数据通信中非常常见,特别是在网络传输和存储媒介上。
它可以帮助检测传输过程中发生的位错误,提高数据的可靠性和完整性。
需要注意的是,CRC校验是一种错误检测机制,而不是错误纠正机制。
它只能告诉我们数据是否出现错误,而无法纠正错误。
若数据被改变或破坏,则接收方可以要求重新发送数据。
CRC校验的算法实现

CRC校验的算法实现一、CRC简介CRC基于多项式的编码技术。
在多项式编码中,将信息位串看成阶次为从X^k-1到X^0的信息多项式M(x)的系数序列,在计算CRC码时,发送方和接收方必须采用同一个生成多项式G(x),G(x)的阶次应该低于M(x),且最高和最低阶的系数为1。
根据发送端要传送的k位二进制码序列,可以以一定的规则产生一个r位检验码(就是CRC码),附在信息后面,构成一个新的二进制码序列数共(k+r)位,为传送多项式T(x),最后将其发送出去。
产生CRC码的方法是:以16位CRC码产生规则为例:先将要发送的二进制序列数左移16位(即乘以2的16 次方后)后,再除以生成多项式(这里采用的是模2运算法则,即多项式除法中采用不带借位的减法运算,运算等同于异或运算。
),最后所得到的余数就是CRC码。
任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。
例如:代码1010111对应的多项式为x6+x4+x2+x+1,而多项式为x5+x3+x2+x+1对应的代码101111。
二、检验原理因为接收端接收到的传送多项式T(x)一定能被生成多项式G(x)模2整除,所以可用来判断传输过程是否出现错码。
接收端有两种处理方式:1、计算k位序列的CRC码,与接收到的CRC比较,一致则接收正确。
2、计算整个k+r 位的CRC码,若为0,则接收正确。
三、算法实现这里采用 CRC-CCITT 多项式G(X) = X16 + X12 + X5 + 1,多项式为0x11021,因为第一位固定位1可省略,故C语言编程时,参与计算的为0x1021。
当按位计算CRC时,例如计算二进制序列为1001 1010 1010 1111时,将二进制序列数左移16位,即为1001 1010 1010 1111 (0000 0000 0000 0000),实际上该二进制序列可拆分为1000 0000 0000 0000 (0000 0000 0000 0000) + 000 0000 0000 0000 (0000 0000 0000 0000) + 00 0000 0000 0000 (0000 0000 0000 0000) + 1 0000 0000 0000 (0000 0000 0000 0000) + ……共16个二进制分序列。
实验三 循环冗余码效验(CRC)
实验三循环冗余码效验(CRC)
一、实验目的
熟悉和学习ISO/IEC18000-3,ISO15693标准规范第三部分协议,其中贯串所有指令部分CRC的内容,特别是AnnexD的内容。
理解它的原理、流程和软件实验办法。
二、实验内容
通过使用带CRC处理过程的指令和不带CRC过程的指令读取单个标签,比较其指令的读取结果。
分析实验数据,了解CRC的作用,掌握指令的应该取得的结果。
三、实验原理
ISO15693标准规范第三部分下的AnnexD部分。
四、所需仪器
供电电源、单张电子标签。
五、实验步骤
1、设置
加电运行系统,在系统的天线内放置多个标签,打开软件Tag-reader.exe.正确设置串门、操作如图
2、操作
2.1 带CRC命令操作
在系统软件下,“寻卡”处,选择“单卡识别”,确定“寻卡”动作。
操作如图所示:
清空数据,在系统软件下,“测试命令”处,选择运行“测试循环冗余校验码”,选择“发送带循环冗余校验的寻卡命令”,操作如图:
2.2不带CRC命令操作
清空数据,选择“发送不带循环冗余校验的寻卡命令”,操作如图:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
crc_no = CRC_Number(crc_index) output = crc_add(input, crc_no) [output_after_check, indicate] =crc_check(output,crc_no) end function [ output, indicate] = crc_check( input, crc_no ) % the function is proposed for deleting crc bits from the input sequence n = size(input,2); generator = zeros(1,crc_no+1); output = zeros(1,n-crc_no); switch crc_no case 3 generator = [1 0 1 1]; case 8 generator = [1 1 0 0 1 1 0 1 1]; %D^8+D^7+D^4+D^3+D+1 case 12 generator = [1 1 0 0 0 0 0 0 0 1 1 1 1]; %D^12+D^11+D^3+D^2+D+1 case 16 generator = [1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1]; %D^16+D^12+D^5+1 case 24 generator = [1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1]; %D^24+D^23+d^6+D^5+D+1 otherwise fprintf('\nPlease the number of crc bits should be 8 12 16 24\n'); end output = input(1:n-crc_no); for ii = 1:n-crc_no if(input(1) == 1) input(1:crc_no+1) = mod((input(1:crc_no+1)+generator),2); end input = [input(2:end) input(1)]; end if sum(input) == 0 indicate = 0; else indicate = 1; end function [ output ] = crc_add( input, crc_no ) % the function is proposed for adding crc bits to the input sequence k = size(input,2); generator = zeros(1,crc_no+1); output = zeros(1,k+crc_no); switch crc_no case 3 generator = [1 0 1 1]; case 8 generator = [1 1 0 0 1 1 0 1 1]; %D^8+D^7+D^4+D^3+D+1 case 12 generator = [1 1 0 0 0 0 0 0 0 1 1 1 1]; %D^12+D^11+D^3+D^2+D+1 case 16 generator = [1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1]; %D^16+D^12+D^5+1 case 24 generator = [1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1]; %D^24+D^23+d^6+D^5+D+1 otherwise fprintf('\nPlease the number of crc bits should be 8 12 16 24\n'); end output(1:k)=input; for ii = 1:k if(output(1) == 1) output(1:crc_no+1) = mod((output(1:crc_no+1)+generator),2); end output = [output(2:end) output(1)]; end output = [input output(1:crc_no)];
该字符串CRC 校验编码结果。 步骤4:如果要解码,首先确认编码多项式,然后将接收字符串除以编码多项式。如果能
够整除,说明字符串在传输或存储中没有发生错误;否则,表明字符串在传输或 存储中产生错误,导致CRC 校验失败。 六、实验结果
修改内存 65 该为 06,如下:
3
结果:出错了
七、思考题 1.掌握按字节编码的过程,试着写出CRC 校验编码的Matlab 程序?
实验四 CRC 校验码编码实验
班级:
姓名: 学号:
一、实验目的
1.学习CRC 编码基本流程, 学会调试循环冗余校验码编码程序。
2.掌握CRC 校验码的编码原理,重点掌握按字节根据实验原理掌握CRC 校验码编码/解码基本流程。
2.在C++编译器下能够调试编码算法每一个步骤,重点掌握按字节编码的过程。
以一个多项式,最后所得到的余数既是CRC 码。求CRC 码所采用模2 加减运算法则,既是不
带进位和借位的按位加减,这种加减运算实际上就是逻辑上的异或运算,加法和减法等价,
乘法和除法运算与普通代数式的乘除法运算是一样,符合同样的规律。接收方将接收到的二
进制序列数(包括信息码和CRC 码)除以多项式,如果余数为0,则说明传输中无错误发生,
其中Qn(X) 为整数, Rn(X) 为16位二进制余数,将上式代入前式得:
由于:
其中RnH8(X) 是Rn(X)的高八位, RnL8(X)是Rn(X)的低八位,代入前式得到: 再设: 其中Qn-1(X ) 为整数, Rn-1(X ) 为16位二进制余数,继续代入前式,多次迭代得到:
2
显然,十六位二进制数R0(X)即是要求的CRC码。 五、实验步骤
SIGNAL D: STD_LOGIC_VECTOR (31 DOWNTO 0) ; SIGNAL R, crc_temp: STD_LOGIC_VECTOR (15 DOWNTO 0) ; BEGIN D < = sdata; PROCESS( clk, crc_in) BEGIN IF crc_in =‘1’THEN R < = (OTHERS = >‘0’) ; ELSIF rising_edge ( clk) THEN crc_temp (0) < =D (31) XOR D (30) XOR D (27) XOR D (26) XOR D ( 25) XOR D ( 24) XOR D ( 23) XOR D (22) XOR D (21) XOR D (20) XOR D (19) XOR D (18) XOR D ( 17) XOR D ( 16) XOR D (15) XOR D (13) XOR D ( 12) XOR D ( 11) XOR D ( 10 ) XOR D ( 9) XOR D ( 8) XOR D (7) XOR D (6) XOR D (5) XOR D (4) XOR D (3) XOR D (2) XOR D (1) XOR D (0) XOR R (0) XOR R (1) XOR R (2) XOR R (3) XOR R (4) XOR R (5) XOR R (6) XOR R (7) XOR R (8) XOR R (9) XOR R (10) XOR R (11) XOR R (14) XOR R (15) ; crc_temp (1) < =D (31) XOR D (28) XOR D (27) XOR D ( 26) XOR D ( 25) XOR D ( 24) XOR D ( 23) XOR D (22) XOR D (21) XOR D (20) XOR D (19) XOR D (18) XOR D ( 17) XOR D ( 16) XOR D (14) XOR D (13) XOR D ( 12) XOR D ( 11) XOR D ( 10 ) XOR D ( 9) XOR D ( 8) XOR D (7) XOR D (6) XOR D (5) XOR D (4) XOR D (3) XOR D (2) XOR D (1) XOR R (0) XOR R (1) XOR R (2) XOR R (3) XOR R (4) XOR R (5) XOR R (6) XOR R (7) XOR R (8) XOR R (9) XOR R (10) XOR R (11) XOR R (12) XOR R (15) ; crc_temp (2) < =D (31) XOR D ( 30) XOR D ( 29) XOR D ( 28) XOR D ( 16) XOR D ( 14) XOR D ( 1) XOR D (0) XOR R (0) XOR R (12) XOR R (13) XOR R (14) XOR R (15) ; crc_temp (3) < =D (31) XOR D ( 30) XOR D ( 29) XOR D (17) XOR D (15) XOR D ( 2) XOR D (1) XOR R (1) XOR R (13) XOR R (14) XOR R (15) ; crc_temp (4) < =D (31) XOR D (30) XOR D (18) XOR D (16) XOR D (3) XOR D (2) XOR R (0) XOR R (2) XOR R (14) XOR R (15) ; crc_temp (5) < = D ( 31) XOR D ( 19) XOR D ( 17 ) XOR D ( 4 ) XOR D ( 3 ) XOR R ( 1 ) XOR R ( 3 ) XOR R (15) ; crc_temp (6) < =D (20) XOR D (18) XOR D (5) XOR D (4) XOR R (2) XOR R (4) ; crc_temp (7) < =D (21) XOR D (19) XOR D (6) XOR D (5) XOR R (3) XOR R (5) ; crc_temp (8) < =D (22) XOR D (20) XOR D (7) XOR D (6) XOR R (4) XOR R (6) ; crc_temp (9) < =D (23) XOR D (21) XOR D (8) XOR D (7) XOR R (5) XOR R (7) ;
