长方体和正方体基础知识与练习题专项练习汇编
苏教版六年级上册《长方体和正方体》专项练习

六上《长方体和正方体》专项练习(一)题型一:长方体展开图求面积解法点拨:步骤1.确定“前面”,2.描出长、宽、高(三条交于一点),3.找出已知长度再求其余长度。
例1:一个长方体的平面展开图如右图所示(长度:dm),求它的表面积和体积。
【反馈练习】1.一个长方体的平面展开图如右图所示(长度:c m),求它的表面积。
2. 一个长方体的平面展开图如右图所示(长度:c m),求它的表面积。
★3.右图是一个无盖长方体纸盒的展开图,请算出这个长方体纸盒的表面积和体积。
题型二:长方体和正方体展开图的判断解法点拨:1.正方体:“141”“231”“222”“33”四种模型共11种。
2.长方体:符合正方体的基础模型,同时根据对应面相等(一个隔一个)判断。
例2:下面图形中,能沿虚线折成正方体的是()。
例3:下面的图形沿虚线折叠,哪些能折成一个长方体?在括号里画“√”,不能的画“×”。
【反馈练习】1. 下面的图形沿虚线折叠,哪些能折成一个长方体?在括号里画“√”,不能的画“×”。
2.下面是一个正方体的展开图,将它折叠成正方体后,与数字6相对的数字是()。
A. 1B. 2C. 3D. 4★3.下面这个正方体的展开图可能是()。
★4.下面是同一个正方形从三个不同角度拍到的照片,这个正方体的展开图是()。
六上《长方体和正方体》专项练习(二)题型一:表面积和体积扩大倍数问题解法点拨:看“单位即可”,棱长(单位:m)扩大a倍,则棱长和(单位:m)扩大a倍,表面积(单位:m2)扩大a2倍,体积(单位:m3)扩大a3倍。
例1:一个正方体的棱长扩大为原来的2倍,则棱长和扩大为原来的()倍,底面积扩大为原来的()倍,表面积扩大为原来的()倍,体积扩大为原来的()倍。
A . 2 B. 4 C. 12 D. 8【反馈练习】1.一个正方体的棱长扩大为原来的3倍,则棱长和扩大为原来的()倍,底面积扩大为原来的()倍,表面积扩大为原来的()倍,体积扩大为原来的()倍。
长方体和正方体单元全套练习题

长方体和正方体单元全套练习题第二单元:长方体(一)全套练练一:长方体的认识1.填空1) 长方体有6个面,它们一般都是矩形形,也可能有2个面是正方形。
2) 长方体的上面和下面、前面和后面、左面和右面都叫做面,它们的面积不同。
3) 长方体的12条棱,每相对的4条棱算作一组,12条棱可以分成3组。
4) 正方体有6个面,每个面都是正方形,面积都相等。
5) 一个正方体的棱长是6厘米,它的棱长总和是24厘米。
6) 一个长方体的长是1.5分米,宽是1.2分米,高是1分米,它的棱长和是4.8分米。
7) 一个长方体的棱长总和是80厘米,其中长是10厘米,宽是7厘米,高是33厘米。
8) 把两个棱长1厘米的正方体拼成一个长方体,这个长方体的棱长总和是8厘米。
2.判断题1) 长方体和正方体都有6个面,12条棱,8个顶点。
(正确)2) 长方体的6个面不可能有正方形。
(错误)3) 长方体的12条棱中,长、宽、高各有4条。
(正确)4) 正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
(正确)5) 长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
(正确)6) 一个长方体长12厘米,宽8厘米,高7厘米,把它切成一个尽可能大的正方体,这个正方体的棱长是8厘米。
(错误)3.选择题1) 下列物体中,形状不是长方体的是:茶杯。
2) 长方体的12条棱中,高有8条。
3) 下列三个图形中,能拼成正方体的是:以上答案都不对。
练二:长方体的棱长和、表面积1.计算题1) 一根长52厘米的铁丝,恰好可以焊接成一个长6厘米,宽4厘米,高7厘米的长方体。
2) 一个长方体的水池,长20厘米,宽10厘米,深2米,占地0.2平方米。
3) 用96厘米长的铁丝焊接成一个正方体的框架,然后用纸给它的表面包裹起来,至少需要120平方厘米的纸。
4) 一个长方体,长12厘米,宽和高都是8厘米,这个长方体的表面积是320平方厘米。
5) 用两个棱长为5厘米的正方体拼成一个长方体,这个长方体的表面积是94平方厘米。
长方体和正方体经典题目

长方体和正方体经典题目正方体和长方体的表面积练题1、正方体是由六个完全相同的正方形围成的立体图形,正方体有12条棱,它们的长度都相等,正方体有8个顶点。
2、因为正方体是长、宽、高都相等的长方体,所以正方体是立方体。
3、一个正方体的棱长为A,棱长之和是12A,当A=6厘米时,这个正方体的棱长总和是72厘米。
4、相交于一个顶点的三条棱,分别叫做长方体的长、宽、高。
5、一根长96厘米的铁丝围成一个正方体,这个正方体的棱长是24厘米。
6、一个长方体的棱长总和是80厘米,长10厘米,宽是7厘米。
高是3厘米。
7、至少需要24厘米长的铁丝,才能做一个底面周长是18厘米,高3厘米的长方体框架。
8、一个长方体的长、宽、高都扩大2倍,它的表面积就扩大4倍。
9、一个长方体最多可以有三个面是正方形,最多可以有六条棱长度相等。
10、一个长方体的长是25厘米,宽是20厘米,高是18厘米,最大的面的长是25厘米,宽是18厘米,一个这样的面的面积是450平方厘米;最小的面长是18厘米,宽是20厘米,一个这样的面的面积是360平方厘米。
11、3个棱长都是4厘米的正方体拼成一个长方体,表面积减少了24平方厘米,它的体积是64立方厘米。
12、正方体的底面积是25平方分米,它的表面积是150平方分米,它的体积是125立方分米。
13、一个长124厘米,宽10厘米,高10厘米的长方体锯成最大的正方体,最多可以锯成5个。
14、3个棱长4分米的正方体粘合成一个长方体,长方体的表面积比3个正方体的表面积少24平方分米.15、长8cm,宽6cm,高4cm的长方体木块可锯成体积是1立方厘米的小正方体15块。
16、长方体的体积是96立方分米,底面积是16平方分米,它的高是6分米.17、一个长方体的棱长总和是48cm,宽是2cm,长是宽的2倍,它的表面积是184平方厘米。
18、长方体方木,长2m,宽和厚都是30cm,把它的长截成2段,表面积增加2400平方厘米。
长方体和正方体每周练习
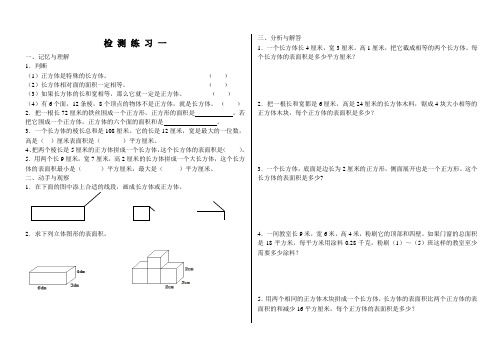
检 测 练 习 一一、记忆与理解 1.判断(1)正方体是特殊的长方体。
﹙ ﹚ (2)长方体相对面的面积一定相等。
﹙ ﹚ (3)如果长方体的长和宽相等,那么它就一定是正方体。
﹙ ﹚ (4)有6个面,12条棱,8个顶点的物体不是正方体,就是长方体。
﹙ ﹚ 2.把一根长72厘米的铁丝围成一个正方形,正方形的面积是 。
若把它围成一个正方体,正方体的六个面的面积和是 。
3.一个长方体的棱长总和是108厘米。
它的长是12厘米,宽是最大的一位数,高是( )厘米表面积是( )平方厘米。
4、把两个棱长是5厘米的正方体拼成一个长方体,这个长方体的表面积是( )。
5.用两个长9厘米,宽7厘米,高2厘米的长方体拼成一个大长方体,这个长方体的表面积最小是( )平方厘米,最大是( )平方厘米。
二、动手与观察12.求下列立体图形的表面积。
三、分析与解答1.一个长方体长4厘米,宽3厘米,高1厘米,把它截成相等的两个长方体。
每个长方体的表面积是多少平方厘米?2.把一根长和宽都是6厘米,高是24厘米的长方体木料,锯成4块大小相等的正方体木块,每个正方体的表面积是多少?3.一个长方体,底面是边长为2厘米的正方形,侧面展开也是一个正方形。
这个长方体的表面积是多少?4.一间教室长9米,宽6米,高4米,粉刷它的顶部和四壁。
如果门窗的总面积是18平方米,每平方米用涂料0.28千克,粉刷(1)~(5)班这样的教室至少需要多少涂料? 5.用两个相同的正方体木块拼成一个长方体,长方体的表面积比两个正方体的表面积的和减少16平方厘米,每个正方体的表面积是多少?检测练习二一、理解与记忆1、判断:(1)两个长方体的表面积相等,它们的体积也相等。
()(2)棱长为6厘米的正方体,它的表面积与体积相等。
()(3)一个正方体棱长之和是24分米,它的体积是8立方分米。
()2、常用的体积单位从高到低分别是、、。
3、棱长为1厘米的正方体的体积是,有一个物体含有X个这样的体积单位,那么这个物体的体积是。
长方体和正方体认识练习题

10、一个长方体的底面积是0.2平方分米,高是8分米,它的体积是()立方分米。
11、表面积是54平方厘米的正方体,它的体积是()立方厘米。
12、一个长方体的棱长总和是120厘米,长是5厘米,宽3厘米,高是2厘米,这个长方体的体积是()立方厘米。
13、长方体的长、宽各扩大2倍,高不变,体积将扩大()倍。
2、一个水箱从里面量,长是60厘米、宽是40厘米、深是20厘米,这个水箱注入2/3的水大约有多少升?列式:_______________________()答:这个水箱注入2/3的水大约有()升。
3、一段长方体钢材,长为1.6米,横截面是边长为4厘米的正方形。
每立方厘米钢重7.8克,这段长方体钢材重多少克?列式:_______________________()答:这段长方体钢材重()克。
4、一个正方体鱼缸,棱长为4分米。
如果把满缸水倒入另一个长为8分米,宽为2.5分米的长方体空水槽里,求槽中水面的高。
列式:_______________________()答:槽中水面高()分米。
5、有一种无盖的玻璃鱼缸,长20厘米、宽15厘米、高10厘米,做这样一个鱼缸需要多少平方厘米的玻璃?这个玻璃鱼缸能装水多少升?列式:_______________________()答:做这样一个鱼缸需要()平方厘米的玻璃;这个玻璃鱼缸能装水升。
45000cm³=()dm³1、65l=()cm³9、填上适当的单位一台立式空调的体积约是2();一个火柴盒的体积约是8();运货集装箱的容积约是70();一个墨水瓶的容积约是60()。
10、一个正方体的棱长扩大2倍,表面积扩大()倍,体积扩大()倍。
二、判断1、540dm³=540ml ()2、用4个同样大小的正方体可以拼成一个大正方体。
()3、把体积是1dm³的正方体纸盒放在桌面上,纸盒所占桌面的面积是1d㎡。
()4、体积相等的两个正方体,表面积也相等。
第9讲-长方体和正方体(讲义)小升初数学精讲精练专题汇编讲义(解析版)

小升初数学长方体和正方体专项训练(解析版)一、填空题1.将一个正方体纸盒展开(如图),现有三个正方形分别填着3、6、8,如果要使相对面上两个数的和都为10。
那么A=( ),B=( )。
答案: 4 7解析:找出正方体展开图中三个数字的相对面,找相对面时,先找同行,同行中间隔一个正方形的两个面是相对面,再找异行,异行中间隔两个正方形的两个面是相对面,最后求出A、B 代表的数字,据此解答。
分析可知,B和“3”是相对面,C和“8”是相对面,A和“6”是相对面,则A=10-6=4,B =10-3=7。
2.李爷爷用厚0.5厘米的玻璃板自制了一个无盖的鱼缸。
鱼缸从外面量长32厘米,宽24厘米,高12.5厘米,这个鱼缸的容积是( )升。
答案:8.556解析:鱼缸的容积需要从里面进行测量,从里面量得鱼缸的长是32-0.5×2=31厘米,宽是24-0.5×2=23厘米,高是12.5-0.5=12厘米,根据长方体的容积公式:V=abh,据此进行计算即可。
(32-0.5×2)×(24-0.5×2)×(12.5-0.5)=31×23×12=713×12=8556(立方厘米)=8.556(升)则这个鱼缸的容积是8.556升。
3.在学习圆柱的体积计算公式时,我们把一个圆柱体切拼成一个近似的长方体,这个过程中变的是形状,不变的是体积。
假设:圆柱的底面半径是5cm,高是10cm,观察图形,它的体积还可以从另外一个角度观察,分三步推导计算:第一步:3.14×5=15.7(cm),表示图中长方体的( )是15.7cm。
第二步:15.7×10=157(cm2),表示图中长方体的( )是157cm2。
第三步计算出圆柱的体积,算式和结果是:( )。
有了这样等积变形的学习,如果把底面积是4cm2,高是6cm的圆柱形的橡皮泥捏成一个长方体,那么可能是长( )cm、宽( )cm、高( )cm的长方体。
苏教版小学数学六年级上册第一单元 长方体和正方体 必考知识点重难点习题汇编(单元测试)【含答案】

苏教版小学数学六年级上册第一单元长方体和正方体必考知识点重难点习题汇编(单元测试)(,完成)一、选择题(满分16分)1.把一个长、宽、高分别是6分米、2分米、2分米的长方体锯成三个大小完全相等的小正方体,表面积比原来增加了()A.16平方分米B.8平方分米C.4平方分米D.24平方分米2.下面三个水果,哪一个占的空间最大?()A.B.C.3.一个圆柱形水桶,求这只水桶能装多少水是求()。
A.水桶的容积B.水桶的体积C.水桶的表面积4.下面的物体都是用1立方厘米的正方体摆成的,()的体积最大.A.B.C.5.做20个棱长为30厘米的小正方体纸箱,至少需要()平方米硬纸.A.9平方米B.54平方米C.10.8平方米6.一个正方体的棱长是0.5分米,它的表面积是()平方分米.A.1平方分米B.1.5平方分米C.2平方分米7.做一个长方体纸盒,需要多少硬纸板,是求长方体的().①体积②容积③表面积A.体积B.容积C.表面积8.用8个棱长是2厘米的小正方体摆成一个大正方体,这个正方体的表面积是()平方厘米。
A.32B.64C.96二、填空题(满分16分)9.一个长方体的长、宽、高分别是10厘米、2厘米、2厘米。
这个长方体的表面积是( )平方厘米,体积是( )立方厘米。
10.从前面、右面和上面分别观察同一个长方体,看到的形状如图。
这个长方体的表面积是( )平方厘米,体积是( )立方厘米。
11.在括号里填上合适的单位名称。
一个热水瓶的容积约是2( );一个梨的体积约是200( );一台空调的高约是1.8( ),占地约0.5( )。
12.把如图所示的长方体沿虚线切开,表面积比原来增加( )平方厘米。
13.至少( )个体积是1立方厘米的小正方体才能拼成一个大正方体,拼成的这个大正方体的表面积是( )平方厘米。
14.从一个正方体上锯下一个角(一个四面体)后,剩下的部分(一个多面体)最少有( )条棱,最多有( )条棱。
人教版五年级下册《长方体与正方体》专项练习试题(10套)

人教版五年级下册《长方体与正方体》专项练习试题(10套)人教版五年级下册《长方体与正方体》专项练试题(10套)长方体和正方体的认识一、填空:(38%)1、长方体和正方体都有6个面,12条棱,8个顶点。
2、长方体的每个面都是矩形形或有一组对面是平行四边形。
它有12条棱,平行的4条棱都相等。
3、相交于长方体一个顶点的三条棱的长度分别叫做它的长、宽和高。
4、长方体有6个面,从不同的角度观察一个长方体,最多能看到3个面。
5、一个长方体的长是5分米,宽是4分米,高是3分米,6个面中最小的一个面的面积是12平方分米,最大的一个面的面积是20平方分米。
6、一个长方体,长4米,宽3米,高2米,它的占地面积最大是24平方米。
7、一个长方体模型,从前面看是12平方厘米,从上面看是12平方厘米,右面的面积是6平方厘米。
8、长方体的右侧面面积是12平方厘米,前面面积是8平方厘米,上面面积是6平方厘米,这个长方体的长、宽、高分别是3厘米、2厘米、2厘米。
二、选择(8%):1、一个长方体水池,长20米,宽10米,深2米,这个水池占地400平方米。
2、下面的图形中,能按虚线折成正方体的是C。
3、从一个体积是30立方厘米的长方体木块中,挖掉一小块后(如下图),它的表面积比原来小。
4、用一根52厘米长的铅丝,正好可以焊成长6厘米,宽4厘米,高3厘米的长方体教具。
三、计算下面每个形体的棱长和(6%)。
四、下面各题,列式计算,不写答。
(40%)1、一个长方体,长5分米,宽3分米,高4分米,求它的所有棱长的和:20分米+14分米+12分米=46分米。
2、用钢筋做一个长和宽都是3.5分米,高是10厘米的长方体,需多少分米的钢筋。
2(3.5+3.5+10)厘米=49厘米。
3、棱长是4分米的正方体,棱长总和是多少分米。
4×12=48分米。
4、一个长方体的棱长和是36厘米,从一个顶点出发的三条棱的长度总和是多少厘米。
36×3-2×(长+宽+高)=48厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体和正方体的表面积
我们已经学习过了长方体和正方体的表面积计算公式
长方体的表面积:
若长方体的长、宽、高分别用字母a、b、c表示,则长方体的表面积
可表示为:
正方体的表面积:
若正方体的棱长用字母a表示,则正方体的表面积可表示为:
我们必须熟悉长方体和正方体的特点
1、长方体有()个顶点,有()条棱,有()个面。
2、相交于长方体一个顶点的三条棱分别叫做长方体的()、()和(),它们各有()条。
那么长方体的棱长和可表示为()
3、长方体的相对的两个面都();若长方体有一个面是正方形,则长方体有()个面是一样的长方形。
把一个长方体平均分开,正好成为两个相等的正方体(长比宽长),想一想这样的长方体的长是宽的()倍,长是高的()倍。
1、正方体有()顶点,有()条棱,有()面;()都相等的长方体叫正方体,正方体是()长方体,6个面都是
(),6个面的面积(),12条棱的长度都()。
(1)长方体的体积=(),用字母表示为()正方体的体积=(),用字母表示为()思考下列问题
①若已知长方体的体积为V,长为a,宽为b,则如何表示高c:()
②若已知长方体的体积为V,长为a,高为c,则如何表示宽b:()
③若已知长方体的体积为V,宽为b,高为c,则如何表示长a:()
④若已知正方体的棱长和为L,则正方体棱长为(),则体积
更多精品文档
表示为:
(2)单位换算
54厘米=()分米 3.6平方米=()平方分米 3.083
cm
dm=()3 4600平方厘米=()平方分米 2.5L=()3
cm=()
cm36003
mL
(3)判断正误
①体积单位比面积单位要大()
②体积单位之间的进率都是1000 ()
③一个长方体底面积不变,高越大,体积越大()
④油箱的体积就是油箱的容积;()
⑤计算容积,只能用升和毫升作单位。
()
例1、做一种横截面是边长为4分米的正方形,高是 2.5米的长方体
烟囱管,20节这样的烟囱管至少要用铁皮多少平方米?
例2、一个长方体的表面积是40平方厘米,把它平均分开,正好成为
两个相等的正方体,每个正方体的表面积是多少平方厘米?
例3、用一根长84厘米的铁丝做成一个长为9厘米、宽为6厘米的长方体框架,然后糊上一层彩纸,彩纸的面积至少有多大?
例4、一个正方体木块,表面积是50平方米,如果把它截成8个体积相等的正方体小木块,每个小木块的表面积是多少?
更多精品文档
一、“认真细致”填一填:
1、长方体和正方体都有()个面、()条棱、()个顶点,每个顶点都有()
条棱相交。
2、物体所占()叫做物体的体积。
3、2.1 m3=()dm32040 cm3=()dm3
4.5 L =()ml 0.5 L =()dm3
4、一个正方体的棱长为4cm,它的表面积是(),体积是()。
5、一个长方体长5dm、宽 4 dm、高 2 dm,它的表面积是(),
体积是()。
6、1dm3的正方体可以分成()个1cm3的小正方体。
如果把这些小正方体排成一
行,一共长()。
7、焊接一个长7cm、宽2cm、高1cm的长方体框架,至少要用()cm的铁丝。
8、挖一个长和宽都是5m的长方体菜窖,要使菜窖的容积是50m3,应该挖()m深。
9、一个正方体木箱的表面积是72dm2,这个木箱占地面积是()dm2。
10、用三个棱长都是2cm的正方体拼成一个长方体,这个长方体的表面积是
()。
体积是()。
二、“对号入座”选一选:(选择正确答案的序号填在括号里)
1、一本数学书的体积大约是220()。
【① m3②dm3③cm3】
2、加工一个长方体油箱要用多少铁皮,是求这个油箱的()。
【①表面积②体积③容积】
3、一个正方体的棱长扩大3倍,它的体积扩大()倍。
【① 27 ② 9 ③ 3 】
4、下面正确的是()。
【①一个物体的表面积有可能与体积一样大。
②32.0=0.06
③一个正方体的棱长之和是12 cm,它的体积是 1 cm3。
】
5、至少()个棱长 2 cm的小正方体可以拼成一个大正方体。
【① 4 ② 8 ③ 12 】
三、求下面各立方体的表面积和体积:
四、走进生活,解决问题:
1、一个长方体木箱,长10 dm,宽8 dm,
高6 dm,做这个木箱至少需要木板
多少dm2?2、一块正方体木料,它的棱长是4dm,
如
果1dm3的石料重 2.7kg,这块石料重多
少kg?
更多精品文档
更多精品文档。
