椭圆的特殊性质
数学知识点:椭圆的性质(顶点、范围、对称性、离心率)_知识点总结

数学知识点:椭圆的性质(顶点、范围、对称性、离心率)_知识点总结
椭圆的焦距与长轴长之比叫做椭圆的离心率。
椭圆的性质:
1、顶点:A(a,0),B(-a,0),C(0,b)和D(0,-b)。
2、轴:对称轴:x轴,y轴;长轴长|AB|=2a,短轴长|CD|=2b,a为长半轴长,b为短半轴长。
3、焦点:F1(-c,0),F2(c,0)。
4、焦距:。
5、离心率:;
离心率对椭圆形状的影响:e越接近1,c就越接近a,从而b就越小,椭圆就越扁;e越接近0,c就越接近0,从而b就越大,椭圆就越圆;
6、椭圆的范围和对称性:(a>b>0)中-a≤x≤a,-b≤y≤b,对称中心是原点,对称轴是坐标轴。
利用椭圆的几何性质解题:
利用椭圆的几何性质可以求离心率及椭圆的标准方程.要熟练掌握将椭圆中的某些线段长用a,b,c表示出来,例如焦点与各顶点所连线段的长,过焦点与长轴垂直的弦长等,这将有利于提高解题能力。
椭圆中求最值的方法:
求最值有两种方法:
(1)利用函数最值的探求方法利用函数最值的探求方法,将其转化为函数的最值问题来处理.此时应充分注意椭圆中x,y的范围,常常是化为闭区间上的二次函数的最值来求解。
(2)数形结合的方法求最值解决解析几何问题要注意数学式子的几何意义,寻找图形中的几何元素、几何量之间的关系.
椭圆中离心率的求法:
在求离心率时关键是从题目条件中找到关于a,b,c的两个方程或从题目中得到的图形中找到a,b,c的关系式,高考物理,从而求离心率或离心率的取值范围.。
椭圆的简单几何性质

椭圆的简单几何性质
1. 椭圆是一个由平面上所有离两个固定点(称为焦点)距离之和等于常数的点构成的几何图形。
2. 椭圆的长轴和短轴分别为椭圆的两条相互垂直的轴,长轴的长度是椭圆的两个焦点之间的距离,而短轴的长度是椭圆的两个焦点到中心点的距离。
3. 任意一条椭圆轴与椭圆相交的点称为端点,一个椭圆有四个端点。
4. 椭圆上任意一点到两个焦点距离之和等于常数,这个常数称为椭圆的长轴的长度。
5. 椭圆的离心率是一个非负实数,等于椭圆的长轴与短轴之差的一半除以椭圆长轴的长度。
6. 椭圆的面积等于长轴和短轴所围成矩形的面积的1/4乘以π。
高中椭圆性质大全(92条含证明)

椭圆1.122PF PF a +=2.标准方程22221x y a b += 3.111PF e d =< 4.点P 处的切线PT 平分△PF 1F 2在点P 处的外角.5.PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点. 6.以焦点弦PQ 为直径的圆必与对应准线相离. 7.以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.8.设A 1、A 2为椭圆的左、右顶点,则△PF 1F 2在边PF 2(或PF 1)上的旁切圆,必与A 1A 2所在的直线切于A 2(或A 1).9.椭圆22221x y a b+=(a >b >0)的两个顶点为1(,0)A a -,2(,0)A a ,与y 轴平行的直线交椭圆于P 1、P 2时A 1P 1与A 2P 2交点的轨迹方程是22221x y a b-=.10.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b +=.11.若000(,)P x y 在椭圆22221x y a b +=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.12.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M 为AB 的中点,则22OM AB b k k a⋅=-.13.若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+. 14.若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y y x y a b a b+=+. 15.若PQ 是椭圆22221x y a b+=(a >b >0)上对中心张直角的弦,则122222121111(||,||)r OP r OQ r r a b +=+==. 16.若椭圆22221x y a b +=(a >b >0)上中心张直角的弦L 所在直线方程为1Ax By +=(0)AB ≠,则(1) 222211A B a b+=+;(2) L =17.给定椭圆1C :222222b x a y a b +=(a >b >0), 2C :222222222()a b b x a y ab a b-+=+,则(i)对1C 上任意给定的点00(,)P x y ,它的任一直角弦必须经过2C 上一定点M 222202222(,)a b a b x y a b a b---++. (ii)对2C 上任一点'''00(,)P x y 在1C 上存在唯一的点'M ,使得'M 的任一直角弦都经过'P 点. 18.设00(,)P x y 为椭圆(或圆)C:22221x y a b+= (a >0,. b >0)上一点,P 1P 2为曲线C 的动弦,且弦PP 1, PP 2斜率存在,记为k 1, k 2, 则直线P 1P 2通过定点00(,)M mx my -(1)m ≠的充要条件是212211m b k k m a+⋅=-⋅-. 19.过椭圆22221x y a b+= (a >0, b >0)上任一点00(,)A x y 任意作两条倾斜角互补的直线交椭圆于B,C 两点,则直线BC 有定向且2020BC b x k a y =(常数).20.椭圆22221x y a b += (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点三角形的面积为122tan2F PF S b γ∆=,2(tan )2b Pc γ± . 21.若P 为椭圆22221x y a b+=(a >b >0)上异于长轴端点的任一点,F 1, F 2是焦点,12PF F α∠=, 21PF F β∠=,则tan tan 22a c a c αβ-=+.22.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c ,00(,)M x y ).23.若椭圆22221x y a b+=(a >b >0)的左、右焦点分别为F 1、F 2,左准线为L ,则当11e ≤<时,可在椭圆上求一点P ,使得PF 1是P 到对应准线距离d 与PF 2的比例中项.24.P 为椭圆22221x y a b+=(a >b >0)上任一点,F 1,F 2为二焦点,A 为椭圆内一定点,则2122||||||2||a AF PA PF a AF -≤+≤+,当且仅当2,,A F P 三点共线时,等号成立. 25.椭圆22221x y a b +=(a >b >0)上存在两点关于直线l :0()y k x x =-对称的充要条件是22220222()a b x a b k -≤+.26.过椭圆焦半径的端点作椭圆的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.27.过椭圆焦半径的端点作椭圆的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.28.P 是椭圆cos sin x a y b ϕϕ=⎧⎨=⎩(a >b >0)上一点,则点P 对椭圆两焦点张直角的充要条件是2211sin e ϕ=+. 29.设A,B 为椭圆2222(0,1)x y k k k a b +=>≠上两点,其直线AB 与椭圆22221x y a b+=相交于,P Q ,则AP BQ =.30.在椭圆22221x y a b+=中,定长为2m (o <m ≤a )的弦中点轨迹方程为()2222222221()cos sin x y m a b a b αα⎡⎤=-++⎢⎥⎣⎦,其中tan bx ay α=-,当0y =时, 90α=.31.设S 为椭圆22221x y a b+=(a >b >0)的通径,定长线段L 的两端点A,B 在椭圆上移动,记|AB|=l ,00(,)M x y 是AB 中点,则当l S ≥Φ时,有20max ()2a l x c e =-222(c a b =-,ce a=);当l S <Φ时,有0max ()x =0min ()0x =.32.椭圆22221x y a b+=与直线0Ax By C ++=有公共点的充要条件是22222A aB bC +≥.33.椭圆220022()()1x x y y a b --+=与直线0Ax By C ++=有公共点的充要条件是2222200()A a B b Ax By C +≥++.34.设椭圆22221x y a b+=(a >b >0)的两个焦点为F 1、F 2,P (异于长轴端点)为椭圆上任意一点,在△PF 1F 2中,记12F PF α∠=, 12PF F β∠=,12F F P γ∠=,则有sin sin sin ce aαβγ==+.35.经过椭圆222222b x a y a b +=(a >b >0)的长轴的两端点A 1和A 2的切线,与椭圆上任一点的切线相交于P 1和P 2,则21122||||P A P A b ⋅=.36.已知椭圆22221x y a b+=(a >b >0),O 为坐标原点,P 、Q 为椭圆上两动点,且OP OQ ⊥.(1)22221111||||OP OQ a b +=+;(2)|OP|2+|OQ|2的最小值为22224a b a b +;(3)OPQ S ∆的最小值是2222a b a b +.37.MN 是经过椭圆222222b x a y a b +=(a >b >0)焦点的任一弦,若AB 是经过椭圆中心O 且平行于MN 的弦,则2||2||AB a MN =.38.MN 是经过椭圆222222b x a y a b +=(a >b >0)焦点的任一弦,若过椭圆中心O 的半弦OP MN ⊥,则2222111||||a MN OP a b +=+.39.设椭圆22221x y a b+=(a >b >0),M(m,o) 或(o, m)为其对称轴上除中心,顶点外的任一点,过M 引一条直线与椭圆相交于P 、Q 两点,则直线A 1P 、A 2Q(A 1 ,A 2为对称轴上的两顶点)的交点N 在直线l :2a x m =(或2b y m=)上.40.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.41.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.42.设椭圆方程22221x y a b+=,则斜率为k(k ≠0)的平行弦的中点必在直线l :y kx =的共轭直线'y k x =上,而且2'2b kk a=-.43.设A 、B 、C 、D 为椭圆22221x y a b+=上四点,AB 、CD 所在直线的倾斜角分别为,αβ,直线AB 与CD 相交于P ,且P 不在椭圆上,则22222222cos sin cos sin PA PB b a PC PD b a ββαα⋅+=⋅+. 44.已知椭圆22221x y a b+=(a >b >0),点P 为其上一点F 1, F 2为椭圆的焦点,12F PF ∠的外(内)角平分线为l ,作F 1、F 2分别垂直l 于R 、S ,当P 跑遍整个椭圆时,R 、S 形成的轨迹方程是222x y a +=(()()2222222222a y b x x c c y a y b x c ⎡⎤+±⎣⎦=+±). 45.设△ABC 内接于椭圆Γ,且AB 为Γ的直径,l 为AB 的共轭直径所在的直线,l 分别交直线AC 、BC 于E 和F ,又D 为l 上一点,则CD 与椭圆Γ相切的充要条件是D 为EF 的中点.46.过椭圆22221x y a b+=(a >b >0)的右焦点F 作直线交该椭圆右支于M,N 两点,弦MN的垂直平分线交x 轴于P ,则||||2PF eMN =. 47.设A (x 1 ,y 1)是椭圆22221x y a b +=(a >b >0)上任一点,过A 作一条斜率为2121b x a y -的直线L ,又设d 是原点到直线 L 的距离, 12,r r 分别是A 到椭圆两焦点的距离,ab =.48.已知椭圆22221x y a b +=( a >b >0)和2222x y a bλ+=(01λ<< ),一直线顺次与它们相交于A 、B 、C 、D 四点,则│AB │=|CD │.49.已知椭圆22221x y a b+=( a >b >0) ,A 、B 、是椭圆上的两点,线段AB 的垂直平分线与x 轴相交于点0(,0)P x , 则22220a b a b x a a---<<.50.设P 点是椭圆22221x y a b+=( a >b >0)上异于长轴端点的任一点,F 1、F 2为其焦点记12F PF θ∠=,则(1)2122||||1cos b PF PF θ=+.(2) 122tan 2PF F S b θ∆=.51.设过椭圆的长轴上一点B (m,o )作直线与椭圆相交于P 、Q 两点,A 为椭圆长轴的左顶点,连结AP 和AQ 分别交相应于过H 点的直线MN :x n =于M ,N 两点,则()222290()a n m a m MBN a m b n a --∠=⇔=++. 52.L 是经过椭圆22221x y a b+=( a >b >0)长轴顶点A 且与长轴垂直的直线,E 、F 是椭圆两个焦点,e 是离心率,点P L ∈,若EPF α∠=,则α是锐角且sin e α≤或sin arc e α≤(当且仅当||PH b =时取等号).53.L 是椭圆22221x y a b+=( a >b >0)的准线,A 、B 是椭圆的长轴两顶点,点P L ∈,e是离心率,EPF α∠=,H 是L 与X 轴的交点c 是半焦距,则α是锐角且sin e α≤或sin arc e α≤(当且仅当||abPH c=时取等号).54.L 是椭圆22221x y a b+=( a >b >0)的准线,E 、F 是两个焦点,H 是L 与x 轴的交点,点P L ∈,EPF α∠=,离心率为e ,半焦距为c ,则α为锐角且2sin e α≤或2sin arc eα≤(当且仅当||PH =.55.已知椭圆22221x y a b+=( a >b >0),直线L 通过其右焦点F 2,且与椭圆相交于A 、B两点,将A 、B 与椭圆左焦点F 1连结起来,则2222112(2)||||a b b F A F B a -≤⋅≤(当且仅当AB ⊥x 轴时右边不等式取等号,当且仅当A 、F 1、B 三点共线时左边不等式取等号).56.设A 、B 是椭圆22221x y a b+=( a >b >0)的长轴两端点,P 是椭圆上的一点,PAB α∠=,PBA β∠=,BPA γ∠=,c 、e 分别是椭圆的半焦距离心率,则有(1)22222|cos |||s ab PA a c co αα=-.(2) 2tan tan 1e αβ=-.(3) 22222cot PAB a b S b a γ∆=-.57.设A 、B 是椭圆22221x y a b+=( a >b >0)长轴上分别位于椭圆内(异于原点)、外部的两点,且A x 、B x 的横坐标2A B x x a ⋅=,(1)若过A 点引直线与这椭圆相交于P 、Q 两点,则PBA QBA ∠=∠;(2)若过B 引直线与这椭圆相交于P 、Q 两点,则180PAB QAB ∠+∠=.58.设A 、B 是椭圆22221x y a b+=( a >b >0)长轴上分别位于椭圆内(异于原点),外部的两点,(1)若过A 点引直线与这椭圆相交于P 、Q 两点,(若B P 交椭圆于两点,则P 、Q 不关于x 轴对称),且PBA QBA ∠=∠,则点A 、B 的横坐标A x 、B x 满足2A B x x a ⋅=;(2)若过B 点引直线与这椭圆相交于P 、Q 两点,且180PAB QAB ∠+∠=,则点A 、B的横坐标满足2A B x x a ⋅=.59.设',A A 是椭圆22221x y a b+=的长轴的两个端点,'QQ 是与'AA 垂直的弦,则直线AQ 与''AQ 的交点P 的轨迹是双曲线22221x y a b-=.60.过椭圆22221x y a b+=( a >b >0)的左焦点F 作互相垂直的两条弦AB 、CD 则2222282()||||ab a b AB CD a b a+≤+≤+.61.到椭圆22221x y a b +=( a >b >0)两焦点的距离之比等于a cb-(c 为半焦距)的动点M 的轨迹是姊妹圆222()x a y b ±+=.62.到椭圆22221x y a b +=( a >b >0)的长轴两端点的距离之比等于a cb-(c 为半焦距)的动点M 的轨迹是姊妹圆222()()a b x y e e±+=.63.到椭圆22221x y a b +=( a >b >0)的两准线和x 轴的交点的距离之比为a cb-(c 为半焦距)的动点的轨迹是姊妹圆22222()()a b x y e e±+=(e 为离心率).64.已知P 是椭圆22221x y a b+=( a >b >0)上一个动点,',A A 是它长轴的两个端点,且AQ AP ⊥,''AQ A P ⊥,则Q 点的轨迹方程是222241x b y a a+=.65.椭圆的一条直径(过中心的弦)的长,为通过一个焦点且与此直径平行的弦长和长轴之长的比例中项.66.设椭圆22221x y a b +=( a >b >0)长轴的端点为',A A ,11(,)P x y 是椭圆上的点过P 作斜率为2121b x a y -的直线l ,过',A A 分别作垂直于长轴的直线交l 于',M M ,则(1)''2||||AM A M b =.(2)四边形''MAA M 面积的最小值是2ab .67.已知椭圆22221x y a b+=( a >b >0)的右准线l 与x 轴相交于点E ,过椭圆右焦点F 的直线与椭圆相交于A 、B 两点,点C 在右准线l 上,且//BC x 轴,则直线AC 经过线段EF 的中点.68.OA 、OB 是椭圆2222()1x a y a b-+=( a >0,b >0)的两条互相垂直的弦,O 为坐标原点,则(1)直线AB 必经过一个定点2222(,0)ab a b+.(2) 以O A 、O B 为直径的两圆的另一个交点Q 的轨迹方程是222222222()()ab ab x y a b a b -+=++(0)x ≠.69.(,)P m n 是椭圆2222()1x a y a b-+=(a >b >0)上一个定点,P A 、P B 是互相垂直的弦,则(1)直线AB 必经过一个定点2222222222()()(,)ab m a b n b a a b a b+--++.(2)以P A 、P B 为直径的两圆的另一个交点Q 的轨迹方程是22224222222222222[()]()()()ab a m b n a b n a b x y a b a b a b ++--+-=+++(x m ≠且y n ≠). 70.如果一个椭圆短半轴长为b ,焦点F 1、F 2到直线L 的距离分别为d 1、d 2,那么(1)212d d b =,且F 1、F 2在L 同侧⇔直线L 和椭圆相切.(2)212d d b >,且F 1、F 2在L 同侧⇔直线L 和椭圆相离,(3)212d d b <,或F 1、F 2在L 异侧⇔直线L 和椭圆相交.71.AB 是椭圆22221x y a b+=(a >b >0)的长轴,N 是椭圆上的动点,过N 的切线与过A 、B 的切线交于C 、D 两点,则梯形ABDC 的对角线的交点M 的轨迹方程是222241(0)x y y a b +=≠. 72.设点00(,)P x y 为椭圆22221x y a b +=( a >b >0)的内部一定点,AB 是椭圆22221x y a b+=过定点00(,)P x y 的任一弦,当弦AB 平行(或重合)于椭圆长轴所在直线时22222200max 2()(||||)a b a y b x PA PB b -+⋅=.当弦AB 垂直于长轴所在直线时,22222200min 2()(||||)a b a y b x PA PB a -+⋅=.73.椭圆焦三角形中,以焦半径为直径的圆必与以椭圆长轴为直径的圆相内切. 74.椭圆焦三角形的旁切圆必切长轴于非焦顶点同侧的长轴端点. 75.椭圆两焦点到椭圆焦三角形旁切圆的切线长为定值a+c 与a-c. 76.椭圆焦三角形的非焦顶点到其内切圆的切线长为定值a-c.77.椭圆焦三角形中,内点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率). (注:在椭圆焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.) 78.椭圆焦三角形中,内心将内点与非焦顶点连线段分成定比e. 79.椭圆焦三角形中,半焦距必为内、外点到椭圆中心的比例中项.80.椭圆焦三角形中,椭圆中心到内点的距离、内点到同侧焦点的距离、半焦距及外点到同侧焦点的距离成比例.81.椭圆焦三角形中,半焦距、外点与椭圆中心连线段、内点与同侧焦点连线段、外点与同侧焦点连线段成比例.82.椭圆焦三角形中,过任一焦点向非焦顶点的外角平分线引垂线,则椭圆中心与垂足连线必与另一焦半径所在直线平行.83.椭圆焦三角形中,过任一焦点向非焦顶点的外角平分线引垂线,则椭圆中心与垂足的距离为椭圆长半轴的长.84.椭圆焦三角形中,过任一焦点向非焦顶点的外角平分线引垂线,垂足就是垂足同侧焦半径为直径的圆和椭圆长轴为直径的圆的切点.85.椭圆焦三角形中,非焦顶点的外角平分线与焦半径、长轴所在直线的夹角的余弦的比为定值e.86.椭圆焦三角形中,非焦顶点的法线即为该顶角的内角平分线. 87.椭圆焦三角形中,非焦顶点的切线即为该顶角的外角平分线.88.椭圆焦三角形中,过非焦顶点的切线与椭圆长轴两端点处的切线相交,则以两交点为直径的圆必过两焦点.89. 已知椭圆22221(0,0)x y a b a b+=>>(包括圆在内)上有一点P ,过点P 分别作直线b y x a =及by x a=-的平行线,与x 轴于,M N ,与y 轴交于,R Q .,O 为原点,则:(1)222||||2OM ON a +=;(2)222||||2OQ OR b +=.90. 过平面上的P 点作直线1:b l y x a =及2:bl y x a=-的平行线,分别交x 轴于,M N ,交y 轴于,R Q .(1)若222||||2OM ON a +=,则P 的轨迹方程是22221(0,0)x y a b a b+=>>.(2)若222||||2OQ OR b +=,则P 的轨迹方程是22221(0,0)x y a b a b+=>>.91. 点P 为椭圆22221(0,0)x y a b a b+=>>(包括圆在内)在第一象限的弧上任意一点,过P引x 轴、y 轴的平行线,交y 轴、x 轴于,M N ,交直线by x a=-于,Q R ,记 OMQ ∆与ONR ∆的面积为12,S S ,则:122ab S S +=. 92. 点P 为第一象限内一点,过P 引x 轴、y 轴的平行线,交y 轴、x 轴于,M N ,交直线b y x a =-于,Q R ,记 OMQ ∆与ONR ∆的面积为12,S S ,已知122abS S +=,则P 的轨迹方程是22221(0,0)x y a b a b+=>>.椭圆性质92条证明1.椭圆第一定义。
椭圆的几何性质
解 : 把已知方程化成标准方 程
2 2
x y 2 1.所以, a 5, b 4, c 25 16 2 5 4 3.因此, 长轴2a 10, 短轴2b 8, 离心率e c 3 0.6, 两焦点分别是 F1 3,0 、F2 a 5 3, 0 .椭圆的四个顶点是 A1 5,0 、A2 5,0 、 B1 0, 4 、B2 0, 4 .
4 2 将已知方程变形为 y 25 x . 5 首先, 画出第一象限的图形 . 4 2 取y 25 x .列表如下: 5
x y 0 1 2 3 4 5 4 3.9 3.7 3.2 2.4 0
Y •• • • • •
OHale Waihona Puke X例2 求适合下列条件的椭 圆的标准方程:
(1)经过点P(3,0),Q(0,2); (2)长轴的长等于20,离心 率等于3/5
2 2
a l :x c
/
2
y
椭圆的准 线 M(x,y) d O F
a l:x c
N
2
F
x
椭圆的准线定义:
动点与一个定点的距离 和它到 一条定直线的距离的比 是常数 c e ( e 1), 此动点的轨迹是椭圆 . a 定点是椭圆的焦点 , 定直线是椭圆 的准线.常数e是椭圆的离心率 .
2001.3
椭圆的几何性质
1
练习1、如果椭圆的 两个焦点将长轴三等 分,那么这个椭圆的 两条准线间的距离是 焦距长的( 9 ) 倍。
2001.3
椭圆的几何性质
1
2、椭圆
上一点P到左准线的 距离是5/2,那么P 点到右焦点的距离 是( 8 )
2001.3
椭圆的几何性质
x y 25 9
椭圆的方程所有知识点总结

椭圆的方程所有知识点总结第一部分:椭圆的基本概念1.1 椭圆的定义椭圆是平面上到两个定点F1和F2的距离之和等于常数2a的点P的轨迹。
这两个定点称为焦点,常数2a称为椭圆的主轴长度。
椭圆还具有第三个重要的参数b,b称为次轴长度,椭圆的离心率e和焦点之间的距离c与主轴长度和次轴长度有关。
1.2 椭圆的几何性质椭圆有许多重要的几何性质,例如椭圆的中心、焦点、顶点、边界等。
椭圆还具有许多特殊的对称性质,以及与其他图形的关系,如与圆的关系和与双曲线的关系等。
第二部分:椭圆的方程2.1 椭圆的一般方程椭圆的一般方程是x²/a² + y²/b² = 1,其中a和b分别是椭圆的主轴长度和次轴长度。
这个方程描述了椭圆的形状和位置,可以用来解决各种与椭圆相关的数学问题。
2.2 标准方程和一般方程的相互转换标准方程是描述椭圆的一种特殊形式的方程,可以使用平移和旋转变换将一般方程转换为标准方程。
这样做可以简化椭圆的分析和计算过程,使问题的求解更加方便和直观。
2.3 椭圆的参数方程椭圆还可以通过参数方程进行描述,参数方程可以更加直观地描述椭圆的形状和位置,同时也方便进行相关计算和分析。
第三部分:椭圆的性质和应用3.1 椭圆的焦点和离心率椭圆的焦点是描述椭圆形状的一个重要参数,可以通过椭圆的方程确定焦点的位置。
离心率是描述椭圆形状的另一个重要参数,可以用来衡量椭圆形状的扁平程度。
3.2 椭圆的面积和周长椭圆的面积和周长是椭圆的重要特征,可以通过椭圆的参数方程和一般方程计算得到。
对于不同类型的椭圆,面积和周长的计算方法也有所不同。
3.3 椭圆的应用椭圆在许多领域中都有广泛的应用,如天文学、工程学、几何光学、计算机图形学等。
椭圆方程可以用来描述行星运动、天体轨迹、光学成像等现象,对于解决相关问题具有重要的作用。
第四部分:椭圆的相关证明和推导4.1 椭圆的焦点和离心率的证明椭圆的焦点和离心率是椭圆的重要性质,可以通过椭圆的方程和参数方程进行证明。
椭圆的定义及性质

椭圆的一个顶点,则椭圆的方程为
.
解析:设椭圆的方程为
x2 a2
y2 b2
c
a
3 5
=1(a>b>0),则已知 b 4,
a2 b2
c2,
a 5, 解得 b 4,
c 3,
所以椭圆方程为 x2 y2 =1. 25 16
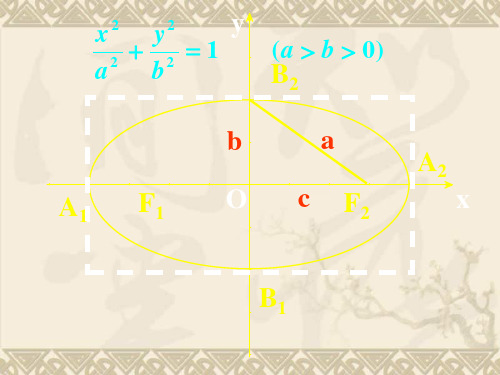
小结:椭圆的标准方程及其简单几何性质
x2
y2
a 2 b2 1(a b 0)
y2 x2 a2 b2 1(a b 0)
图形
对称性 顶点
范围
焦点 焦距
离心率
曲线关于x轴、 y轴、原点对称 长轴顶点(±a,0) 短轴顶点(0,±b)
a x a, b y b
(-c,0)和(c,0)
曲线关于x轴、 y轴、原点对称 长轴顶点(0,±a) 短轴顶点(±b,0)
椭圆关于x轴、y轴、原点对称.
yy B2
AA11
AA2 2
O O
x
在
x2 a2
y2 b2
BB11
1中令y=0, 可得x= a
从而:A1(-a,0),A2(a,0)
同理:B1(0, -b),B2(0, b)
y
B2
A1
A2
O
x
B1
线段A1A2叫椭圆的长轴: 长为2a 线段B1B2叫椭圆的短轴: 长为2b
2.当2a=2c时,轨迹是一条线段, 是以 F1、F2为端点的线段. 3.当2a<2c时,无轨迹,图形不存在. 4.当c=0时,轨迹为圆.
二.椭圆的标准方程
(1)焦点在x轴
x2 a2
椭圆的性质及公式

椭圆的性质及公式
椭圆公式是(x-h)/a+(y-k)/b=1。
椭圆公式是(x-h)/a+(y-k)/b=1。
公式中a,b分别为长短轴长,中心点为(h,k),主轴平行于x轴。
椭圆是平面内到定点F1、F2的距离之和等于常数(大于|F1F2|)的动点P的轨迹,F1、F2称为椭圆的两个焦点。
公人人网面积公式nabS=Tab(其中a,b分别是椭圆的长半轴、短半轴的长),或S= (其中a,b分别是椭圆的长轴短椭圆周长计算公式
L=T(r+R)T为椭圆系数。
可以由r/R的值,查表找出系数T值r为椭圆短半径R为椭圆长半径。
椭圆周长定理椭圆的周长等于该椭圆短半径与长半径之和与该椭圆系数的积(包括正圆)。
S=π(圆周率)×a×b(其中a,b分别是椭圆的长半轴,短半轴的长).或
S=π(圆周率)×A×B/4(其中A,B分别是椭圆的长轴,短轴的长).如果一条固定直线被甲乙两个封闭图形所截得的线段比都为k,那么甲面积是乙面积的k倍。
椭圆(Ellipse)是平面内到定点F1、F2的距离之和等于常数(大于|F1F2|)的动点P的轨迹,F1、F2称为椭圆的两个焦点。
其数学表达式为:|PF1|+|PF2|=2a(2a>|F1F2|)。
高中椭圆的知识点总结

高中椭圆的知识点总结椭圆是数学中的一个重要概念,具有很多应用。
在高中数学中,椭圆也是一个必修的内容,考试中经常会涉及到相关的知识点。
在本文中,我们将对高中椭圆的知识点进行总结和归纳。
一、椭圆的定义椭圆是平面上到两个定点F1和F2距离之和等于定长2a的点P的轨迹。
这两个定点F1和F2被称作椭圆的焦点,定长2a被称为椭圆的长轴,长轴的中点O被称为椭圆的中心,距离中心最远的两点A和B被称为椭圆的顶点,椭圆的离心率为e=(F1F2)/2a。
二、椭圆的方程椭圆的标准方程为 (x^2/a^2)+(y^2/b^2)=1, 其中a>b>0,a为长轴长度,b为短轴长度。
当椭圆的中心不在坐标原点时,可通过平移变换将其移到原点,然后再求解方程。
三、椭圆的性质1. 椭圆的中心位于坐标原点或者与坐标轴的交点上。
2. 椭圆的长轴是平行于x或y轴的直线,短轴是垂直于长轴的直线。
3. 椭圆的离心率e=(F1F2)/2a, e<1。
4. 椭圆的焦点与顶点之间的距离F1A、F2B互相相等,且等于椭圆的长轴长度2a。
5. 椭圆上任意一点到两焦点的距离之和等于定长2a。
6. 椭圆的面积为πab。
7. 椭圆的周长无法用初等函数表示,通常用级数来表示。
四、椭圆的几何意义椭圆的几何意义可以简单地用两条绳子相互交错吊起一个重物来表现。
在两条绳子构成的平面上,可以画出一个椭圆形的轨迹,此时重物到两条绳子的距离之和为定值2a,而椭圆的顶点即为两条绳子的交点。
五、椭圆的应用椭圆具有很多应用,在物理、工程、天文学、生物学等领域中经常会涉及到。
1. 通讯卫星轨道:通讯卫星通常被放置在椭圆轨道上,使得其在地球上的可见度更广,信号传输距离更长。
2. 医学图像:医学图像中的组织轮廓通常是椭圆形的,因此椭圆形适用于医学图像处理。
3. 自动打标机:自动打标机通常采用椭圆形的摆线轮廓来控制字母和数字的运动轨迹。
4. 椭圆滤波器:椭圆滤波器是一种常用的数字信号处理技术,用于高通、低通、带通、带阻等滤波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、椭圆的几何性质(以22a x +22
b
y =1(a ﹥b ﹥0)为例)
1、焦点⊿PF 1F 2中: (1)S ⊿PF1F2=2
tan 2θ•b
(2)(S ⊿PF1F2)max = bc
(3)当P 在短轴上时,∠F 1PF 2最大
2、 过点F 1作⊿PF 1F 2的∠P 的外角平分线的垂线,垂足为M ,则M 的轨迹是x 2+y 2=a 2 证明:延长1F M 交2F P 于F , 连接OM 由已知有1PF FP =,
M 为1F F 中点
∴212OM FF ==()121
2
PF PF +=a
所以M 的轨迹方程为 222x y a +=。
3、以椭圆的任意焦半径为直径的圆,都与圆x 2+y 2=a 2内切
4、过焦点F 的弦AB ,
)(2112定值b
a
BF AF =+ 5、AB 是椭圆的任意一弦,P 是AB 中点,则22
a
b K K OP AB -=•(定值) 证明:令()()1122,,,A x y B x y ,()00,P x y 则
()120
2
x x x +=
()120
2
y y y
+=
x
x
22
1122
22
222211x y a b x y a b ⎫+=⎪⎪⎬⎪+=⎪⎭
()()()()1212121222
..0x x x x y y y y a b +-+-⇒+= ∵ ()()
1212AB y y k x x -=-,0
OP y k x =
, ∴ 2
2AB OP
b k k a
⋅=-。
6、椭圆的长轴端点为A 1、A 2,P 是椭圆上任一点,连结A 1P 、A 2P 并延长,交一准线于N 、M 两点,则M 、N 与对应准线的焦点张角为900
证明:令()221200,,,,,a a M y N y P x y c c ⎛⎫⎛⎫
⎪ ⎪⎝⎭⎝⎭,()1,0A a -,()2,0A a
∴()()100200,,,,A P x a y A P x a y =+=-221122,,,a a A M a y A N a y c c ⎛⎫⎛⎫
=+=- ⎪ ⎪⎝⎭⎝⎭
∵ 由于1A 、P 、M 共线 ,∴ 2
0001210()
a y a x a y c y a y x a a c
⋅++=⇒=++ ∵ 由于2,,A P N 共线 ,∴ 2
0002220()
a y a x a y c y a y x a a c
⋅--=⇒=-- ∴ 22
242200012222
000()()
a a y a y a y a a c c c y y x a x a x a c ⋅-⋅+-==⋅-+-,
∵ 2222
0002222201x y y b a b x a a
+=⇒=-- ∴ 24221222
b a a
c y y a c -=-⋅42b c =-, ∵ 2122,,a FM c y c a FN c y c ⎫
⎛⎫=-⎪
⎪⎝⎭⎪
⎬⎛⎫
⎪=- ⎪⎪
⎝⎭⎭
4122b FM FN y y c ⇒⋅=+ ∴ 0FM FN ⋅=,
∴ M 、N 与对应准线的焦点张角为900
7、圆锥曲线如椭圆上任意一点P 做相互垂直的直线交圆锥曲线于AB ,则AB 必过定
x
点))(,)((2
222022220b a b a y b a b a x +-+-
8、P 为椭圆一定点,PB PA k k =-,当B 变动时,AB k 为一定值。
9、已知点00(,)P x y ,椭圆C :22a x +22
b
y =1(a ﹥b ﹥0。
(1)若P 在C 上,则直线
00221x x
y y
a b +=是椭圆在P 处的切线; (2)若P 在C 外,则直线00221x x
y y
a b +
=是椭圆过P 的切线的切点弦; (3)若P 在C 内,则直线0022
1x x
y y
a
b +
=与椭圆相离; 10、已知圆锥曲线的一个焦点是F ,过F 的焦点弦两端点为A 、B ,分别过A 、B 作圆锥曲线的切线,其交点为C ,则点C 的轨迹是相应于焦点F 的准线,且
CF ⊥AB 。
11、过椭圆)0(122
2
2>>=+b a b y a x 上位于第一象限内的
一点T 作椭圆的切线,与x 轴、y 轴分别交于点A 、
B ,21,F F 分别为椭圆的左右焦点,则∠AB 2F =∠A 1F T.
即B 、1F 、2F 、T 四点共圆.
12、椭圆的光学性质:过一焦点的光线经椭圆反射后必过另一焦点。
13、已知椭圆22
221(0)x y a b a b +=>>内一定点M (,0)(0)m m ≠,过M 的弦的两端点为A 、B ,
过点A 作直线
2a x m =的垂线,垂足为D ,过点B 作直线2a x m =
的垂线,垂足为C ,直线2
a x m =与x 轴交点为K ,则;BC BM AD AM = ∠AKM=∠BKM.。
