第四节-特定要素模型-(1).doc
特定要素模型

特定要素模型
图 3-2: 劳动的边际产量
MPLM
MPLM LM
特定要素模型
图3-3: 特定要素模型中的PPF
食品的生产函数 Output of food, QF (increasing 1'
F
)
PPF
QF =QF(K, LF)
Q2
2' 3'
Labor input in food, LF (increasing ) 劳动资源配置
PF X MPLF (粮食部门的劳动 需求曲线) PM X MPLM (制造品部门的 劳动需求曲线)
制造品部门使用 的劳动, LM L1M 劳动总供给, L L1F
粮食部门使用的劳动 , LF
特定要素模型
MPLMPM=PF MPLF =w -MPLF/MPLM = -PM/PF (3-7)
左边是生产可能性边界在某一特定生产点上的斜率, 右边是负的制造品的相对价格
引言
贸易对国家内部的收入分配有显著影响 原因如下:
资源不可能马上也不可能无成本地在部门间转移 各部门对生产要素的需求有所不同
特定要素模型引入了收入分配问题。 特定要素模型
特定要素模型
假设 生产两种产品:制造品和粮食 三种生产要素: 劳动 (L), 资本 (K) 和土地 (T). 生产制造品需要投入劳动和资本 生产粮食需要投入劳动和土地
特定要素模型中的国际贸易
图 3-11: 贸易和相对价格
制造品的相对价格, 制造品的相对价格 PM /PF RSA RSWORLD (PM /PF )A (PM /PF )W (PM /PF )J RDWORLD 制造品的相对产量, 制造品的相对产量 QM/QF RSJ
国际经济学ch__国际贸易的短期分析—特定要素模型

当Y部门流出部分劳动之后,特定数量的资本与越来越少的 劳动相结合,资本的边际生产力MPKY将下降,根据rY=VMPKY =MPKY·PY可知,相对于Y商品而言,Y部门的资本实际收入下 降了。由于Y商品的价格不变,所以Y部门资本的名义报酬也肯 定下降了。此时,相对于X部门资本所有者的实际报酬上升而言, Y部门资本所有者的实际购买力更是下降了。
(一)国际贸易对非特定要素实际报酬的影响
—在短期内它只能调整原材料及工人的数量,而不能调整固定设备和管理人员的数量。
当两个部门的劳动报酬相同时,其在两部门间的分配便达到均衡,两部门的生产也随之确定。
—长期条件下生产要素在不同部门间可以完全自由流动。
2、特定要素(Specific Factor )
指一种仅限于某一部门需要、而不适合于其它部门 需要的生产要素。在短期内,资本在不同部门之间的流 动性就很小,甚至为零,资本就是特定要素,而劳动则 是非特定要素,即劳动属于流动要素。
(二)边际产出与边际产品价值
“短期”定义:假设有一个生产要素是固定不变的,即 不能加以调整,通常,资本在短期内是不能变动的,即 在不同部门间不能自由流动。 而另一个生产要素(劳 动)则可自由变动。
—在短期内它只能调整原材料及工人的数量,而不能调 整固定设备和管理人员的数量。
“长期”定义:厂商可以根据它所要达到的产量来调整 其全部生产要素。
当X部门由于商品价格上升导致劳动流入时,特定数量的资本与越来越多的劳动相结合,其特定要素—资本的边际生产力MPKX将上升
,根据rX=VMPKX=MPKX·PX可知,X部门资本报酬的增加幅度超过了X商品价格的上升幅度。
根据边际收益递减规律,当其他要素不变时,一种要素连续增加所增加的收益是递减的,因此,各种要素的边际生产力是递减的。
特定要素模型

二、特定要素模型
• 保罗 萨缪尔森和罗纳德·琼斯创建发展的, 保罗·萨缪尔森和罗纳德 琼斯创建发展的 萨缪尔森和罗纳德 琼斯创建发展的, 主要用于解释短期内, 主要用于解释短期内,国际贸易对收入分 配的影响。 配的影响。
(一)模型的基本假设
• • • • • 两种产品生产都使用资本和劳动; X、Y两种产品生产都使用资本和劳动; 规模收益不变( 规模收益不变(Constant Return to Scale); 劳动是同质的,可在两个部门间自由流动; 劳动是同质的,可在两个部门间自由流动; 劳动总量是固定的,并且充分就业; 劳动总量是固定的,并且充分就业; 资本是特定生产要素, 资本是特定生产要素,即两个部门的资本不能互相 使用; 使用; • 每个部门的资本投入都是固定不变的; 每个部门的资本投入都是固定不变的; • 所有商品市场和要素市场都是完全竞争的。 所有商品市场和要素市场都是完全竞争的。
三、国际贸易对要素实际报酬的影响
国际贸易对非特定要素实际报酬 非特定要素实际报酬的影响 (一)国际贸易对非特定要素实际报酬的影响
消 费 结 构 入 水 平 是 否 提 高 , 取 决 于
OX L* L
图4-2 在短期内国际贸易对收入分配的影响
实 际 收
wX
重新达到均衡时: 重新达到均衡时:w/Px 下降, 下降,w/Py上升 上升
VMP’LX F
wY
VMP LY E’ w
**
假设该国依据 比较优势原则, 比较优势原则, 出口X商品,进 商品, 口Y商品 假设PY不变, 不变, 只是PX上升
w
**
w*
VMP LX
E
w*
L**
OY
该国工资水 平将上升, 平将上升, 但提高的幅 度小于X 度小于X商 品价格的上 涨幅度
特定要素模型范文

特定要素模型范文特定要素模型,也被称为特定要素分析模型,是一种由美国军方开发的分析工具,用于帮助决策者或管理者更好地理解问题,并制定相应的解决方案。
特定要素模型的核心思想是将问题分解成一系列关键因素,并分析它们之间的相互关系,以便更好地进行决策。
首先,确定问题是特定要素模型的第一步。
在这一步骤中,决策者或管理者需要明确问题的本质和目标,以便能够明确分析和解决。
接下来,决策者或管理者需要确定问题的要素。
要素是指影响问题的因素,可以是内部因素,如资源,技术和人力等,也可以是外部因素,如政治,经济和环境等。
通过识别关键要素,决策者或管理者可以更好地理解问题,并为制定解决方案提供指导。
在确定问题的要素后,分析这些要素之间的关系是特定要素模型的另一个重要步骤。
通过分析要素之间的相互关系,可以了解不同要素之间的相互影响和依赖关系。
这有助于决策者或管理者确切确定问题的根本原因,并帮助他们制定解决方案。
最后一步是制定解决方案。
通过了解问题的要素和它们之间的关系,决策者或管理者可以制定相应的解决方案。
在制定解决方案时,决策者或管理者需要考虑各个要素的重要性,并找到一种平衡的解决方案。
特定要素模型的优势在于它能够帮助决策者或管理者更全面地理解问题,并从整体上进行分析和解决。
它提供了一个结构化的方法,将决策过程分解成一系列关键因素,以便更好地理解它们之间的相互关系。
这有助于决策者或管理者做出更明智的决策,并采取合适的行动。
然而,特定要素模型也有一些限制。
首先,它假设影响问题的要素和它们之间的关系是静态的。
然而,实际上,这些要素和关系可能会随着时间的推移而变化。
其次,特定要素模型并不能提供具体的数据和解决方案,而只是为决策者或管理者提供了一种分析问题的方法。
总之,特定要素模型是一种管理工具,通过分析问题的关键要素之间的关系,帮助决策者或管理者更好地理解问题,并制定解决方案。
它提供了一个结构化的方法,使决策过程更加系统化和完整。
第四节 特定要素模型 (1)
特定要素模型特定要素模型是由保尔·萨缪尔森和罗纳德·琼斯创建发展的.像简单的李嘉图模型一样,特定要素模型假定一个国家生产两种产品,劳动供给可以在两个部门间进行配置。
与李嘉图模型不同的是,特定根本模型中存在劳动以外的生产要素。
劳动可以在部门间流动,是一种流动要素。
其他要素则是特定的,它们只能被用于生产某些特定产品。
一、模型的假设设想一个国家能够生产两种产品—- 制造品和粮食。
这个国家有三种生产要素:劳动(L) 、资本(K) 和土地(T) 。
生产制造品需要投入劳动和资本,不需要土地。
生产粮食需要投入劳动和土地,不需要资本。
因此劳动是一种流动要素,每个部门都需要使用劳动。
同时,土地和资本都是特定要素,各自只用于一种产品的生产。
如何确定每种产品的产量呢? 制造品的产出取决于在制造业部门中投入的资本和劳动的多少。
产出和投入之间的关系可以用生产函数来归纳.生产函数表明在劳动和资本的投人量一定时制造品的产出量.制造品的生产函数的代数形式为:Q M =Q M (K ,L M )式中, Q M 表示制造品的产出,K 表示资本存量,L M 表示在制造品生产中投入的劳动.同样地,粮食的生产函数可以表示为:Q F =Q F(T ,L F)式中,Q F 表示粮食的产出,T 表示土地的供给量,L F 表示在粮食生产中投入的劳动。
从国家整体上来说,各部门投入的劳动之和等于总的劳动供给量L :L M +L F =L二、生产可能性特定要素模型假设每一种特定要素只能被用于一个生产部门:资本只能用来生产制造品,土地只能用来生产粮食,只有劳动可以用于各部门的生产。
因此,要分析一国的生产可能性,我们只需知道当劳动从一个部门转移到另一个部门时,制造品和粮食的产出组合是怎样变化的。
这个问题可能用画图的方法解决。
首先画出生产函数( 图2-14 和图2—15) ,然后将这两条曲线且合起来导出生产可能性边界。
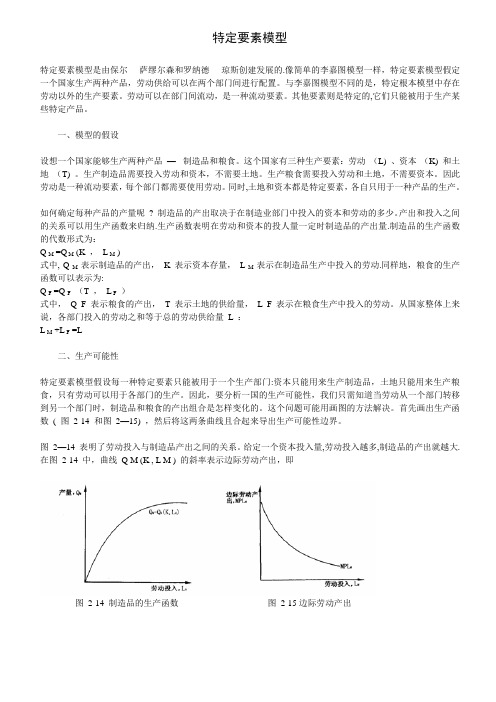
图2—14 表明了劳动投入与制造品产出之间的关系。
4第四讲 特定要素模型

19
第三节 修改版的罗伯金斯基定理
20
第三节 修改版的罗伯金斯基定理
• 食品和电脑的产量都会增加。因此,共同要素禀赋的增加 会导致两种产品产量都增加,罗伯金斯基定理不适用。出 现这种现象的原因在于,劳动力供给的增加使得均衡工资 下降,这导致两个部门都会使用更多的劳动,因此两个部 门的产量均上升。
5
一、模型设定
• 特定要素模型下生产 两种产品:食品和电 脑。食品生产需要土 地和劳动力,电脑的 生产需要资本和劳动 力。右图画出了食品 和电脑的生产函数以 及PPF。I象限是两种 产品的PPF,II象限和 IV象限是生产食物和 电脑不同产量对应的 劳动投入,III象限是 要素投入的预算线。
6
一、模型设定
• 考虑有一部分劳动力从食品产业转移到电脑产业,即从 PPF上的N点转移到N’点。更多劳动力进入电脑产业, 使得电脑产业的劳动生产率下降,而食品产业的劳动生 产率上升,生产电脑的相对成本上升。 • 根据W=P1*MPL1、W=P2*MPL2以及生产函数是递增和凹的, 我们可以知道,L1上升会导致MPL1下降;而K1上升会导 致MPL1上升。
3
一、模型设定
• 特定要素模型是一个2*2*3模型,两个国家与两种商品的 假设与H-O模型完全一样。 • 不同的是,现在有3种要素:劳动力、资本以及土地。 • 生产商品1(食品)使用劳动力以及土地,而生产商品2 (电脑)使用劳动力以及资本。 • 对技术的假设是规模报酬不变; • 市场结构为完全竞争; • 生产两种商品的生产函数分别为 Y1=f(K1, L1); Y2=f(K2, L2); 规模报酬不变意味着两个生产函数都是一次齐次。
• 小结一下:在特定要素模型中,罗伯金斯基定理对于特定 要素仍然成立,但对于共用要素不成立。
4.特定要素模型

4.3.1 贸易的影响
贸易对短期和长期影响的不同: 贸易对短期和长期影响的不同:
短期内国际贸易对收入分配的影响是按部门划分的, 短期内国际贸易对收入分配的影响是按部门划分的, 长期内国际贸易对收入分配的影响是按要素所有者区分的 短期内国际贸易对收入分配的影响之所以不同,原因在于长、 长、短期内国际贸易对收入分配的影响之所以不同,原因在于长、短 期内, 期内,国际贸易对商品要素使用比例的影响是不同的 在长期情况下,国际贸易通过商品价格变化, 在长期情况下,国际贸易通过商品价格变化,使两个部门所使用的资 劳动比例朝着相同的比例变化。 本—劳动比例朝着相同的比例变化。即对资本丰富国,国际贸易会同时 劳动比例朝着相同的比例变化 即对资本丰富国, 降低出口部门、与进口部门相争部门的资本—劳动比例 劳动比例, 降低出口部门、与进口部门相争部门的资本 劳动比例,致使两部门的 相同要素的实际报酬也会按相同方向变化 在短期情况下,由于资本是特定要素, 在短期情况下,由于资本是特定要素,两个部门使用的资本量都无法 调整,国际贸易导致两个部门的资本—劳动比例朝相反方向变化 劳动比例朝相反方向变化, 调整,国际贸易导致两个部门的资本 劳动比例朝相反方向变化,于是 两个部门特定要素的实际收入变化也是相反的
4.2 特定要素模型
基础知识 模型的假设 模型分析
4.2.1 基础知识
(一)厂商利润最大化 在其他要素固定的情况下,厂商选择劳动雇用量L 在其他要素固定的情况下,厂商选择劳动雇用量L进行利润 最大化(假设其他要素是资本): 最大化(假设其他要素是资本):max P • f ( L, K ) − wL 一阶条件为: 一阶条件为: P • f '( L, K ) − w = 0 或者P MPL=w 或者P·MPL=w (二)劳动需求曲线 根据边际收益递减原理,随着雇佣劳动量增加,MPL下降 下降( 根据边际收益递减原理,随着雇佣劳动量增加,MPL下降(边 际产量递减性质),在该商品价格P固定的情况下,边际产 际产量递减性质),在该商品价格P固定的情况下, ),在该商品价格 品价值P MPL MPL如图 品价值P·MPL如图
第4章 特定要素模型

二、均衡
• 劳动力在两个部门间自由流动,因此均衡时,两个部门的 工资必定相等。由于工资等于劳动的边际产值,我们得到 以下劳动力市场均衡条件:
w p1MPL1 p2 MPL2
• 其中 w 为工资,p1、p2分别为两种商品价格,MPL1与 MPL2分别为两种商品的劳动边际产出;
8
• 下图表示劳动市场均衡,在均衡时,有的劳力在电脑部门 工作,而的劳力在食品部门工作。
第四章
特定要素模型 余淼杰
Mar.2014
本章概述
• • • •
2
模型设定 均衡 修改版的S-S定理 修改版的罗伯金斯基定理
第一节
引入:
模型内容
• 在H-O模型中,每个国家都有两种要素,并且生产每种产 品都是使用劳动和资本,要素可以在行业间充分流动。
3
• 在现实中,生产不同产品可能需要不同的要素,并且一些 要素不能够在行业间实现充分转移。特定要素模型为分析 这一类型的问题提供了框架。
第三节
20
修改版的罗伯金斯基定理
第三节
修改版的罗伯金斯基定理
• 食品和电脑的产量都会增加。因此,共同要素禀赋的增加 会导致两种产品产量都增加,罗伯金斯基定理不适用。出 现这种现象的原因在于,劳动力供给的增加使得均衡工资 下降,这导致两个部门都会使用更多的劳动,因此两个部 门的产量均上升。
21
• 小结一下:在特定要素模型中,罗伯金斯基定理对于特定 要素仍然成立,但对于共用要素不成立。
• 考虑有一部分劳动力从食品产业转移到电脑产业,即从 PPF上的N点转移到N’点。更多劳动力进入电脑产业, 使得电脑产业的劳动生产率下降,而食品产业的劳动生 产率上升,生产电脑的相对成本上升。 • 7 根据W=P1*MPL1、W=P2*MPL2以及生产函数是递增和凹的, 我们可以知道,L1上升会导致MPL1下降;而K1上升会导 致MPL1上升。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特定要素模型特定要素模型是由保尔·萨缪尔森和罗纳德·琼斯创建发展的。
像简单的李嘉图模型一样,特定要素模型假定一个国家生产两种产品,劳动供给可以在两个部门间进行配置。
与李嘉图模型不同的是,特定根本模型中存在劳动以外的生产要素。
劳动可以在部门间流动,是一种流动要素。
其他要素则是特定的,它们只能被用于生产某些特定产品。
一、模型的假设设想一个国家能够生产两种产品——制造品和粮食。
这个国家有三种生产要素:劳动(L) 、资本(K) 和土地(T) 。
生产制造品需要投入劳动和资本,不需要土地。
生产粮食需要投入劳动和土地,不需要资本。
因此劳动是一种流动要素,每个部门都需要使用劳动。
同时,土地和资本都是特定要素,各自只用于一种产品的生产。
如何确定每种产品的产量呢? 制造品的产出取决于在制造业部门中投入的资本和劳动的多少。
产出和投入之间的关系可以用生产函数来归纳。
生产函数表明在劳动和资本的投人量一定时制造品的产出量。
制造品的生产函数的代数形式为:Q M =Q M (K ,L M )式中,Q M 表示制造品的产出,K 表示资本存量,L M 表示在制造品生产中投入的劳动。
同样地,粮食的生产函数可以表示为:Q F =Q F (T ,L F )式中,Q F 表示粮食的产出,T 表示土地的供给量,L F 表示在粮食生产中投入的劳动。
从国家整体上来说,各部门投入的劳动之和等于总的劳动供给量L :L M +L F =L二、生产可能性特定要素模型假设每一种特定要素只能被用于一个生产部门:资本只能用来生产制造品,土地只能用来生产粮食,只有劳动可以用于各部门的生产。
因此,要分析一国的生产可能性,我们只需知道当劳动从一个部门转移到另一个部门时,制造品和粮食的产出组合是怎样变化的。
这个问题可能用画图的方法解决。
首先画出生产函数( 图2-14 和图2-15) ,然后将这两条曲线且合起来导出生产可能性边界。
图2-14 表明了劳动投入与制造品产出之间的关系。
给定一个资本投入量,劳动投入越多,制造品的产出就越大。
在图2-14 中,曲线Q M (K ,L M ) 的斜率表示边际劳动产出,即图2-14 制造品的生产函数图2-15边际劳动产出多投人1 人小时的劳动所增加的制造品的产出。
但是,如果只增加劳动投入而不增加资本投入,会产生边际报酬递减效应。
增加一个工人意味着每个工人操作的资本量减少,因此每单位相继增加的劳动所带来的产出增加都比上一个要少。
边际报酬递减可以从生产函数的形状上反映出来。
随着劳动增加,曲线Q 。
(K ,LM) 变得逐渐平缓,即投入的劳动越多,边际劳动产出就越小。
图2-15 以不同的方式体现了上述内容:在图中,我们直接将边际劳动产出表示为劳动投入量的函数。
类似的一对图可以表示粮食的生产函数。
将这向幅图结合起来:则可以导出一国的生产可能性边界( 见图2-16) 。
在图2-16 中,生产可能性边界说明在给定制造部门产出的情况下能生产多少粮食,反之亦然。
图2-16 特定要素模型中的生产可能性边界图2-16 是一张四象限图。
第四象限中的曲线就是前面图2-14 中的制造品的生产函数曲线。
但是在这里,我们将图2-14 颠倒了:沿竖轴向下表示在制造品生产中投入的劳动增加,沿横轴向右表示制造品产出的增加。
第二象限中是相应的粮食的生产函数曲线,这张图也是倒转的。
沿横轴向左表示在粮食中投入的劳动增加,沿竖轴向上表示粮食产出的增加。
第三象限表示一国的劳动配置情况。
劳动投入的衡量与平常的方向相反:沿竖轴向下表示在制造品生产中投入的劳动增加,沿横轴向左表示在粮食生产部门投入的劳动增加。
一个部门的劳动投入增加意味着另一部门的劳动投入减少,因此劳动配置的可能情况可以用一条向下斜倾的直线来表示。
这条直线,即直线AA ,与两轴成45 度角向下倾斜。
也就是说这条直线的斜率为-1 。
为什么这条直线代表了所有可能的劳动配置情况呢? 我们注意到如果所有的劳动都用于生产粮食,L F 就等于L ,L M 等于0 。
如果将劳动逐渐地向制造品部门转移,每转移1 人小时的劳动将使L M 增加一个单位,同时使L F 减少一个单位。
这亲一直到所有的劳动都转移到制造品部门,转移所形成的点(L F ,L M ) 的轨迹是一条斜率为-1 的直线。
因此任何一种特定的劳动配置情况,都可以用直线AA 上的一点来表示,如点 2 。
现在让我们来看一下在劳动配置情况一定时,如何确定各产品的产出。
假定第三象限的点 2 表示过去的配置情况,即有K 单位的劳动用于制造品生产,单位的劳动用于粮食生产。
然后我们采用各部门的生产函数曲线来确定产出:制造品的产出为,粮食的产出为。
和所确定的第一象限的点2' 就表明了制造品和粮食的最后产出情况。
要描画出整条生产可能性边界,只需在不同劳动配置情况下重复上述过程。
我们可以从在粮食生产中投入劳动最多的那一点开始,即第三象限的点1 ,然后逐渐增加在制造品生产中投入的劳动,直到用于生产粮食的劳动变得非常少,如点 3 所示。
第一象限据此得出相应的点,从点1' 点到3' 勾画出了一条曲线。
因此第一象限的曲线PP 表明在给定土地、劳动和资本总量时,一个国家的生产可能性。
在李嘉图模型中,劳动是唯一的生产要素,生产可能性边界是一条直线,即用粮食衡量的制造品机会成本是不变的。
然而在特定要素模型中,其他生产要素的加入使生产可能性边界PP 变为一条曲线。
曲线PP 的弯曲反映了各部门劳动的边际报酬递减规律。
边际报酬递减是特定要素模型和李嘉图模型的关键区别。
在绘制曲线PP 线,我们假定劳动从粮食部门转向制造品部门。
如果将1 人小时的劳动从粮食部门转向制造部门,这一额外投入会使制造品的产出增加,增加的量就是制造品部门的劳动边际产量MPLM 人小时的劳动。
同时,从粮食生产中每转移出l 单位的劳动,将使粮食的和出减少,减少的量等于粮食部门的劳动边际产量MPLF 。
因此要增加l 单位制造品的产出,就必须减少MPL F /MPL M 单位的粮食产出。
所以曲线PP 的斜率也是用粮食的衡量的制造品的机会成本,也就是为增加1 单位制造品的产出所必须牺牲的粮食产量:生产可能性曲线斜率= -MPL F /MPL M现在我们明白了为什么曲线PP 是弓形的。
当我们从点l 移动到点3 时,L M 增加而L F 减少。
然而如图2-15 所示,当LM 增加时,制造品部门的边际劳动产出减小。
相应地,当L F 减少时,粮食部门的边际劳动产出增大。
所以曲线PP 从左向右变得越来越陡。
三、价格、工资和劳动配置各部门分别会投入多少劳动呢? 要回答这一问题就必须来看一下劳动市场的供求状况。
每个部门对劳动的需求取决于本部门产品的价格和工资率,而工资率又取决于制造品和粮食两个部门对劳动的总需求。
在制造品和粮食的价格以及工资率给定时,我们就能确定各个部门的劳动投入量和产出。
首先,我们来看一看劳动的需求。
各部门都要追求利润最大化,因此当增加的1 人小时的劳动所生产的价值等于雇佣1 人小时所需的费用时,对应的劳动投入量就是各部门对劳动的需求。
例如,在制造品部门,增加的 1 人小时的劳动所生产的价值等于制造品部门边际劳动产出乘经制造品的单位价格:MPL M ×P M ,劳动的工资率为W 。
各部门雇佣劳动,直到边际劳动产值等于工资率为止,即:MPL M ×P M =W由于边际报酬递减,制造品部门的边际劳动产出,是一条向下倾斜的曲线( 如图2-15 所示) 。
对应于任何给定的制造品价格,边际劳动产品的价值,即MPL M ×P M ,也应该是一条向下倾斜的曲线。
因此,我们可以用等式上式来定义制造品部门的劳动需求曲线。
如果工资率下降,其他条件不变,制造品部门会雇佣更多的劳动。
同样地,在粮食部门,增加1 人小时的劳动所生产的价值是MPL F ×P F 。
那么粮食部门的劳动需求曲线可以表示为:MPL F ×P F =W因为模型假定劳动力可以在部门问自由流动,所以两个部门的工资率W 是相等的。
也就是说,由于劳动是流动要素,它将从低工资部门向高工资部门转移,直到两个部门的工资率相等为止。
这样,工资率就可以由劳动总需求等于总供给这一条件来确定。
劳动的总供给为:L M +L F =L我们可以用图来表示上述三个等式,图2-17 有助于我们理解在给定的制造和粮食价格下,.工资率和各部门的劳动雇佣量是如何确定的。
图2-17 的横轴表示劳动总供给L 。
图左端的竖轴表示制造品部门的劳动边际产品价值,即图2-15 中的MPL M 曲线和制造品价格P M 的乘积。
曲线MPL M ×P M 也就是制造品部门的劳动需求曲线。
图右端的竖轴表示粮食部门边际劳动产品价值,曲线MPL F ×P F 也就是粮食部门的劳动需求曲线。
点 1 表示均衡时的工资率和劳动在两部门之间的配置情况。
在工资率为w 时,制造品部门的劳动需求(L M ) 和粮食部门的劳动需求(L F ) 之和正好等于劳动总供给L 。
图2-17 劳动的配置从对劳动配置的分析中,我们可以清楚地看到相对价格和产出之间的关系。
这一关系可广泛地应用于特定要素模型以外的情况。
上两式表示:MPL M ×P M = MPL F ×P F =W或改写为:-MPL F /MPL M = -P M /P F上等式的左边是生产可能性边界在某一特定生产点上的斜率,等式的右边是负的制造品的相对价格。
这一结果告诉我们,在生产点上,生产可能性边界一定和一条斜率等于负的制造品价格除以粮食价格的直线相切。
图2-18 表明,如果制造品的相对伶格为(P M /P F ) ,该国就在点1 上进行生产。
图2-18 特定要素模型中的生产当粮食和制造品的价格发生变化时,劳动的配置和收入的分配又会怎样呢? 我们注意到,任何一种价格变化都可以归结为下面两者之一:P M 和P F 变化的比率相同或者P M 和P F 中只有一者发生了变化。
例如,假定制造品的价格上升了17% ,粮食的价格上升了10% ,我们来分析一下这些变化带来的影响。
首先要考虑的是,如果制造品的价格和粮食的价格都上升了10% ,会有什么影响。
然后分析如果制造品的价格单独上升了7% 会有什么影响。
这样,我们就能将总价格的变化带来的影响和相对价格变化带来的影响区分开来。
1 .价格同比率变化。
图2-19 说明P M 和P F 同比率上升所产生的影响。
P M 从上升到;P F 从上升到。
如两种产品价格都上升10% ,两条劳动需求曲线也都相应地上移10% 。
如图2-19 所示,这一移动使工资率也上升了10% ,从w 1 ( 点1) 上升到w2 ( 点2) 。
