欧氏距离类间距离最短距离
利用欧氏距离进行类别数据的分类计算
利用欧氏距离进行类别数据的分类计算欧氏距离是一种用于计算数据相似性的度量方法。
它常用于类别数据的分类计算，可以将样本点归入最接近它的类别中。
在本文中，我们将介绍欧氏距离的概念、计算方法以及在类别数据分类中的应用。
欧氏距离是欧几里得空间中两点之间的直线距离。
对于二维空间中的两个点P(x1,y1)和Q(x2,y2)，欧氏距离可以表示为：d(P,Q)=√((x2-x1)²+(y2-y1)²)。
对于具有多个特征的类别数据，可以通过将每个特征的差值平方相加，再开平方根来计算欧氏距离。
例如，对于包含n个特征的数据集中的两个样本点P(x1, x2, ..., xn)和Q(y1, y2, ..., yn)，欧氏距离可以表示为：d(P,Q) = √(∑(xi-yi)²)。
欧氏距离可用于分类计算，基本思想是将测试样本点与训练样本集中的每个样本点计算欧氏距离，然后将测试样本点归入距离最近的类别中。
具体步骤如下：1.准备训练样本集和测试样本点。
2.对于测试样本点中的每个特征，计算与训练样本集中每个样本点对应特征的差值。
3.平方每个差值，并将它们相加得到总和。
4.对总和取平方根得到欧氏距离。
5.将测试样本点归入距离最近的类别中。
例如，假设我们有一个特征为体重和身高的训练样本集，以及一个测试样本点。
我们可以计算测试样本点与训练样本集中每个样本点的欧氏距离，然后将测试样本点归入距离最近的类别中，例如“正常”或“肥胖”。
欧氏距离的优点是简单易懂、计算简便。
然而，它也存在一些限制。
首先，在计算欧氏距离之前，需要对数据进行标准化，以确保每个特征具有相同的权重。
其次，欧氏距离在处理高维数据时可能会受到维度灾难的影响，因为在高维空间中，数据点之间的距离可能变得非常大，导致欧氏距离不再准确。
为了解决这些限制，可以使用其他度量方法，如曼哈顿距离、闵可夫斯基距离等。
此外，还可以使用特征选择和降维技术来减少数据集的维度，以减轻维度灾难的影响。
多元统计期末复习题
多元数据分析练习题第二章多元正态的参数估计一.判断题（1）若S S =),,(~),,,(21m pT p N X X X X 是对角矩阵，则p X X X ,,,21 相互独立。
（）（2）多元正态分布的任何边缘分布为正态分布，反之也成立。
（）（3）对任意的随机向量Tp X X X X ),,,(21 =来说，其协方差矩阵S 是对称矩阵，并且总是半正定的。
（）（4）对标准化的随机向量来说，它的协方差矩阵与原来变量的相关系数阵相同。
（）（5）若),,(~),,,(21S =m p Tp N X X X X S X ,分别为样本均值和样本协差阵，则S nX 1,分别为S ,m 的无偏估计。
（）二.计算题1.假设随机向量TX X X X ),,(321=的协方差矩阵为úúúûùêêêëé---=S 9232443416，试求相关系数矩阵R 。
úúúúúúúûùêêêêêêêëé----=131413112141211R 2.假设随机向量Tx x x ),(21=的协方差矩阵为úûùêëé=S 20119，令212211,2x x y x x y -=+=，试求Ty y y ),(21=的协方差矩阵。
úûùêëé--=S 2733603.假设úûùêëé---=S 5.005.05.015.0),,(~3A N X m ，其中T)1,2,1(-=m ，úúúûùêêêëé--=S 411121112，试求Ax y =的分布。
模式识别导论习题参考答案-齐敏
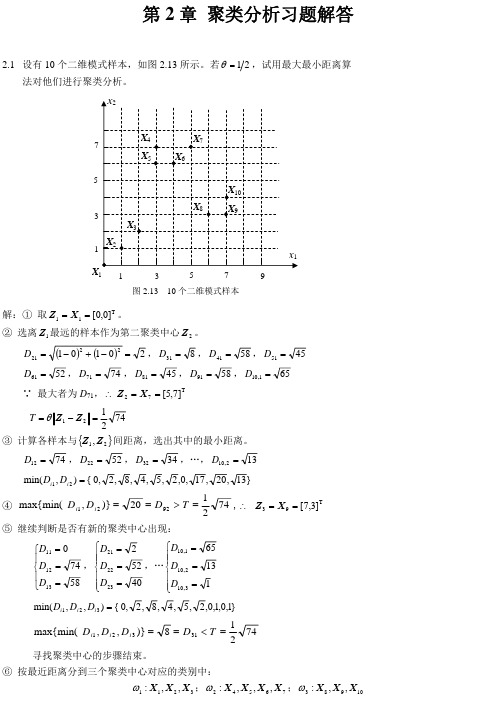
④ max{min( D i1 , D i 2 )}
20 D 92 T
1 74 , Z 3 X 9 [7,3]T 2
⑤ 继续判断是否有新的聚类中心出现：
D10,1 65 D21 2 D11 0 74 52 D D ， ，… 12 22 D10, 2 13 D13 58 D23 40 D10,3 1
G2 (0)
G 3 ( 0)
G4 ( 0 )
G5 (0)
0 1 2 18 32 0 5 13
25
G3 (0)
G4 (0)
0 10 20 0
2
G5 (0)
0
(2) 将最小距离 1 对应的类 G1 (0) 和 G2 (0) 合并为一类，得到新的分类
G12 (1) G1 (0), G2 (0) ， G3 (1) G3 (0)， G4 (1) G4 (0) ， G5 (1) G5 (0)
2
X3 X 6 ) 3.2, 2.8
T
④ 判断： Z j ( 2) Z j (1) ， j 1,2 ，故返回第②步。 ⑤ 由新的聚类中心得：
X1 ： X2 ：
D1 || X 1 Z 1 ( 2) || X 1 S1 ( 2 ) D2 || X 1 Z 2 ( 2) || D1 || X 2 Z1 ( 2) || X 2 S1 ( 2 ) D2 || X 2 Z 2 ( 2) ||
T
(1)第一步：任意预选 NC =1， Z1 X 1 0,0 ，K=3， N 1 ， S 2 ， C 4 ，L=0，I=5。 (2)第二步：按最近邻规则聚类。目前只有一类， S1 { X 1 , X 2 , , X 10 }，N 1 10 。 (3)第三步：因 N 1 N ，无聚类删除。 (4)第四步：修改聚类中心
第二章距离分类器和聚类分析
第二章 距离分类器和聚类分析2.1 距离分类器一、模式的距离度量通过特征抽取，我们以特征空间中的一个点来表示输入的模式，属于同一个类别的样本所对应的点在模式空间中聚集在一定的区域，而其它类别的样本点则聚集在其它区域，则就启发我们利用点与点之间距离远近作为设计分类器的基准。
这种思路就是我们这一章所要介绍的距离分类器的基础。
下面先看一个简单的距离分类器的例子。
例2.1作为度量两点之间相似性的距离，欧式距离只是其中的一种，当类别的样本分布情况不同时，应该采用不同的距离定义来度量。
设,X Y 为空间中的两个点，两点之间的距离(),d X Y ，更一般的称为是范数X Y -，一个矢量自身的范数X 为矢量的长度。
作为距离函数应该满足下述三个条件： a) 对称性：()(),,d d =X Y Y X ；b) 非负性：(),0d ≥X Y ，(),0d =X Y 当且仅当=X Y ； c) 三角不等式：()()(),,,d d d ≤+X Y X Z Y Z 。
满足上述条件的距离函数很多，下面介绍几种常用的距离定义： 设()12,,,Tn x x x =X ，()12,,,Tn y y y =Y 为n 维空间中的两点1、 欧几里德距离：(Eucidean Distance)()()1221,ni i i d x y =⎡⎤=-⎢⎥⎣⎦∑X Y2、 街市距离：(Manhattan Distance)()1,ni i i d x y ==-∑X Y3、 明氏距离：(Minkowski Distance)()11,mnm i i i d x y =⎡⎤=-⎢⎥⎣⎦∑X Y当2m =时为欧氏距离，当1m =时为街市距离。
4、 角度相似函数：(Angle Distance)(),T d ⋅=X YX Y X Y1nTi i i x y =⋅=∑X Y 为矢量X 和Y 之间的内积，(),d X Y 为矢量X 与Y 之间夹角的余弦。
各种几何距离的定义
i 类与 j 类之间的距离可以表示为：
1 d i , j Ni N j
d X , X
Ni k 1 l 1 i k j l
Nj
பைடு நூலகம்
（平均距离法）
当取欧氏距离时，可定义两类之间的均方距离为类别之间的距离：
d 2 i , j
1 Ni N j
X X X X
Ni k 1 l 1 i k j T l i k j l
Nj
有了距离度量之后，我们就可以在此基础上定义可分性判据。一般来讲，当各个类别的 类内距离越小，而类间距离越大时，可分性越强。 对于多类问题，我们可以用各类样本之间的平均距离作为判据：
各种几何距离的定义
1. 点与点的距离 这是一种常见的距离，可以有多种形式，如欧氏距离、马氏距离等，特征矢量 X 和 Y 之间的距离可以表示为：
d X, Y X Y
2. 点与类别之间的距离
T
X Y
（欧氏距离）
常用的有：平均样本法、平均距离法、最近距离法， K -近邻法等。 特征矢量 X 与 i 类别之间距离的平方可以表示为：
i
i
i
i
1 d i Ni Ni
2
d X , X
Ni Ni 2 k 1 l 1 i k i l i k i T i k i
当取欧氏距离时有：
d 2 i
4. 类别之间的距离
1 Ni
X m X m
d 2 X, i
i i i
1 Ni
d X, X （平均距离法）
数学建模-聚类分析
满足输出；不满足循环；
（7）重复；
初始聚类中心的选择
初始聚类中心的选取决定着计算的迭代 次数，甚至决定着最终的解是否为全局最优， 所以选择一个好的初始聚类中心是很有必要 的。
（1）方法一：选取前k个样品作为初始凝聚点。
(2)方法二： 选择第一个样本点作为第一个聚类 中心。然后选取距离第一个点最远的点作为第二个 聚 类中心。……
数据变换：进行[0,1]规格化得到
初始类个数的选择； 初始类中心的选择；
设k=3，即将这15支球队分成三个集团。现抽取日 本、巴林和泰国的值作为三个类的种子，即初始化三 个类的中心为 A：{0.3, 0, 0.19}； B：{0.7, 0.76, 0.5}； C：{1, 1, 0.5}；
样品到类中心的距离； 归类；
计算所有球队分别对三个中心点的欧氏 距离。下面是用程序求取的结果：
第一次聚类结果： A：日本，韩国，伊朗，沙特； B：乌兹别克斯坦，巴林，朝鲜； C：中国，伊拉克，卡塔尔，阿联酋，泰 国，越南，阿曼，印尼。
重新计算类中心；
下面根据第一次聚类结果，采用k-均值法调整各个类的 中心点。
A类的新中心点为：{(0.3+0+0.24+0.3)/4=0.21,
数据变换
（5）极差正规化变换:
x*ij
=
xij
min 1t n
xij
Rj
i 1,，2，...，,n; j 1,..., m
（6）对数变换x*:ij = log xij
i 1,，2，...，,n; j 1,..., m
k
样品间的距离
（1）绝对值距离：
m
dij
xit x jt
t 1
聚类分析
聚类分析是一种建立分类的多元统计分析方法，它能够将一批样本（或变量）数据根据其诸多特征，按照在性质上的亲疏程度在没有先验知识的情况下进行自动分类，产生多个分类结果，类内部个体特征具有相似性，不同类间个体特征的差异性较大。
没有先验知识是指没有事先指定分类标准。
亲疏程度是指各变量取之上的总体差异程度。
对亲疏程度的测量一般有两个角度：第一，个体间的相似程度；第二，个体间的差异程度。
相似程度通常用简单相关系数或等级相关系数。
差异程度通常计算某种距离来测度。
距离公式：①欧氏距离（Euclidean distance ）(),EUCLID x y =②平方欧氏距离（Squared Euclidean distance ）()()21,ki i i SEUCLID x y x y ==-∑③切比雪夫（Chebychev ）距离(),max i i CHEBYCHEV x y x y =-④布洛克（Block ）距离()1,ki i i BLOCK x y x y ==-∑⑤明考斯基（Minkowski ）距离(),MINKOWSKI x y =⑥夹角余弦定理（Cosine ）距离()()2,ki i x y COSINE x y =∑⑦用户自定义（Customized ）距离(),CUSTOMIZED x y =在数据类型不同的情况下，个体间的距离计算也有相应的不同。
主要有： 定距型（Interval ）计数变量（Count ） 二值变量（Binary ）在计数变量时，有卡方距离和Phi 方距离 ①卡方距离（Chi-Square measure ）(),CHISQ x y =②Phi 方距离（Phi-Square measure ）(),PHISQ x y =二值变量时，有简单匹配系数和雅科比系数 ①简单匹配系数（Simple Matching ）(),S x y a b c d =+++②雅科比系数（Jaccard ）(),b cJ x y a b c+=++聚类分析的应注意的几点：1．变量的选择：所选择的变量应符合聚类的要求（即指标体系要符合要求）2．数量级的问题：变量之间不应该有数量级上的差异。
各种距离（欧氏距离、曼哈顿距离、切比雪夫距离、马氏距离等）
各种距离（欧⽒距离、曼哈顿距离、切⽐雪夫距离、马⽒距离等）在做分类时常常需要估算不同样本之间的相似性度量(SimilarityMeasurement)，这时通常采⽤的⽅法就是计算样本间的“距离”(Distance)。
采⽤什么样的⽅法计算距离是很讲究，甚⾄关系到分类的正确与否。
本⽂的⽬的就是对常⽤的相似性度量作⼀个总结。
本⽂⽬录：1.欧⽒距离2.曼哈顿距离3. 切⽐雪夫距离4. 闵可夫斯基距离5.标准化欧⽒距离6.马⽒距离7.夹⾓余弦8.汉明距离9.杰卡德距离& 杰卡德相似系数10.相关系数& 相关距离11.信息熵1. 欧⽒距离(EuclideanDistance)欧⽒距离是最易于理解的⼀种距离计算⽅法，源⾃欧⽒空间中两点间的距离公式。
(1)⼆维平⾯上两点a(x1,y1)与b(x2,y2)间的欧⽒距离：(2)三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧⽒距离：(3)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧⽒距离： 也可以⽤表⽰成向量运算的形式：(4)Matlab计算欧⽒距离Matlab计算距离主要使⽤pdist函数。
若X是⼀个M×N的矩阵，则pdist(X)将X矩阵M⾏的每⼀⾏作为⼀个N维向量，然后计算这M个向量两两间的距离。
例⼦：计算向量(0,0)、(1,0)、(0,2)两两间的欧式距离X= [0 0 ; 1 0 ; 0 2]D= pdist(X,'euclidean')结果：D=1.00002.0000 2.23612. 曼哈顿距离(ManhattanDistance)从名字就可以猜出这种距离的计算⽅法了。
想象你在曼哈顿要从⼀个⼗字路⼝开车到另外⼀个⼗字路⼝，驾驶距离是两点间的直线距离吗？显然不是，除⾮你能穿越⼤楼。
实际驾驶距离就是这个“曼哈顿距离”。
⽽这也是曼哈顿距离名称的来源，曼哈顿距离也称为城市街区距离(CityBlock distance)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
– Log变换 – 线性回归 – 伸缩+平移
Detection of differentially expressed genes
• 两类样本
– t test – Wilcoxon test – ……
• 多类样本 – anova – ……
• 多重检验校正
– Bonferoni – FDR
软件-SAM
• Significance Analysis of Microarrays (Tusher et al. 2001)
• 需要R软件包 • Excel嵌入式函数
Clustering
Clustering三要素
• 相似性度量
– Pearson’s correlation – Spearman’s correlation – Euclidian distance – City block distance
Introduction
• 我只强调一点，基 因芯片数值反应的 是mRNA的丰度 （abundancy）， 因此，可以在一定 程度上反应基因的 表达水平。
Data Analysis & Modelling
Microarray总流程
Biological Question
Sample Preparation
Databases-三大基因表达数据库
• 美国斯坦福大学的SMD数据库 ()
数据预处理
• 数据缺失
– 原因
• 图像受到污染 • 图像分辨率不足 • 片上灰尘或刮痕
– 缺失数据的处理方法
• 舍弃该数据（同时丢掉了有用信息！） • 再做一次实验 （太昂贵了！） • 用某个数取代，比如样本均值 • K-nearest neighbors估计 • 奇异值分解（SVD） 估计
D(2)
X(3)
X(4)
X(5)
C(4)
X(3)
0
1.5
3.5
2.5
X(4)
• 呼吸系统：肺癌、支气管哮喘、原发性 肺动脉高压、肺间质纤维化、结节病等；
• 消化系统：肿瘤，肠炎等 • 其他：造血系统疾病、传染性疾病、生
殖系统疾病以及泌尿系统疾病等
s1 s2 s3• • • • • • • • sj • • • • • sM g1
ቤተ መጻሕፍቲ ባይዱg2
•
•
•
•
gene profile
gi
•
Gi
D(1)
X(1)
X(2)
X(3)
X(4)
X(5)
X(1)
0
X(2)
X(3)
X(4)
X(5)
1
3.5
5
7
0
2.5
4
6
0
1.5
3.5
0
2
0
步骤2
由D(1)知，合并X(1)和X(2)为一新类C(4)={X(1), X(2)}，有：
新的G (2)={X(3) , X(4) , X(5) , C(4)} 新的类别数目m=4 新的类间距离矩阵D(2)
Microarray Detection
Taken from Schena & Davis
Microarray Reaction
应用
• 差异表达基因检测（不同组织、不同时 间、不同条件等）
• 基因联合调控 • 疾病诊断 • 基因功能鉴定 • 药物筛选和新药开发
应用：以人类疾病为例
• 神经系统：肿瘤、aging, CNS炎症、多发 性硬化、老年痴呆、精神分裂症、癫痫、 帕金森病等；
– 打开软件 – 装入数据（格式解释） – 选择聚类办法 – 设置参数 – 运行
层次聚类法的基本步骤
层次聚类法的基本步骤
对数据进行变换； 定义样本间的距离（如欧氏距离）、类别之间的距离 （如最短距离）； 首先将t个样本各自视为一类：得到初始的分类G(1) （含有t类），计算t个样本两两之间的距离，它们等价于 初始的类间距离，得到初始的距离矩阵D(1) ； 将距离最近的两类合并为一新类，得到新的分类G(2) （含有t-1类），并计算新类与其它类的类间距离，得到新 的类间距离矩阵D(2) ，再按照最小距离准则并类，得到G(3) （含有t-2类）、D(3),… 。直到所有样本都并成一类 ； 画出谱系聚类图，决定分类的个数及各类的成员。
X6
X1
X2
X4
X4
X5
X2
X3
X3
X1
X5
X6
层次聚类法举例
已知：根据5种灵长类动物朊粒蛋白的氨基酸序列比较，得到它们之 间的距离矩阵（经过数据变换处理）。 X(1)：Gibbon（长臂猿）； X(2)：Symphalangus； X(3) ：Human（人）； X(4) ：Gorilla（大猩猩）； X(5) ：Chimpanzee（黑猩猩）
Mi,j
array profile
Aj
•
•
•
•
gN
Microarray data matrix
Databases-三大基因表达数据库
• 美国国立生物信息中心NCBI的Gene Expression Omnibus数据库 (GEO, )
Databases-三大基因表达数据库
• 欧洲生物信息学研究所EBI的 ArrayExpress数据库 ()
Analysis of microarray data
Cui Qinghua 2009-03-06
Outline
• Introduction • Databases • Detection of differentially expressed genes • Clustering • Classification • Principal component analysis (PCA) • Pathway and Ontology analysis • Survival analysis
• 聚类准则 • 聚类算法
聚类算法
• 层次聚类：假设有N个样本，第一级，每 个样本为1类，即有N类，依次合并，直 到样本只有一类。
• 非层次聚类
– K-means – Fuzzy c-means – 自组织映射 – 。。。。。。
Clustering软件-Cluster
• Michael Eisen et al. • 步骤：
构造： 样本间距离——欧氏距离； 类间距离——最短距离；
X(1)
X(2)
X(3)
X(4)
X(5)
X(1)
0
X(2)
X(3)
X(4)
X(5)
1
3.5
5
7
0
2.5
4
6
0
1.5
3.5
0
2
0
步骤 1
5个物种各自构成1类，得到5类，有：
初始分类G (1)={X(i)}(i=1, 2, 3, 4, 5) 初始类别数目m=5 初始类间距离矩阵D(1)