高中物理模型组合27讲Word先加速后减速模型
专题01 常见的匀变速直线运动模型-2024届新课标高中物理模型与方法(解析版)

2024版新课标高中物理模型与方法专题01常见的匀变速直线运动模型目录【模型一】刹车模型 (1)【模型二】“0—v—0”运动模型 (5)【模型三】反应时间与限速模型 (13)1.先匀速,后减速运动模型---反应时间问题 (13)2.先加速后匀速运动模型----限速问题 (16)3.先加速后匀速在减速运动模型----最短时间问题 (17)4.多过程运动之“耽误时间(先减后加)”模型 (21)【模型四】双向可逆类运动模型 (24)【模型五】等位移折返模型 (25)【模型六】等时间折返模型 (31)刹车问题在实际生活中,汽车刹车停止后,不会做反向加速运动,而是保持静止。
题目给出的时间比刹车时间长还是短8m/s;(2【答案】(1)28m/s,2【详解】(1)汽车第1s内的中间时刻速度由于无法确定第4s内汽车是否停止,设第联立代数整理得解得做2t时刻汽车的速度大小【答案】(1)0.025;(2)27.38m【详解】(1)假设冰壶速度减到0后冰壶可以反向退回,则冰壶的加速度大小23.2m s 0.08m s 156m s 14.52s 625a -==-若冰壶以加速度2156m s 625a =减速,则冰壶在最后1s 通过的位移1578m 625s x =>所以冰壶在第15s 内的某瞬间已经停止运动,令1s t ∆=,设冰壶运动15x 21512x at =推导可得:A .在t t =0时,油滴刚好穿过A 板的小孔B .在03t t =时,油滴刚好返回到O 点C .油滴受到的重力与电场力之比为2∶3D .O 点到下极板B 的距离为202gt 【答案】ACA.运动员离开飞机10s后打开降落伞B.运动员在空中下落过程用时9s C.运动员距离地面247.5m时打开降落伞D.飞机距离地面375mA.质量m的乘客制动过程对座舱的压力为C.加速过程的时间为2(Hg-【答案】CD【详解】A.制动过程有(1)求门开启时做加速和减速运动的加速度大小;(2)若人以v 0的速度沿图中虚线s 走向感应门,要求人到达门框时左右门同时各自移动传感器水平感应距离l 应为多少?(3)若以(2)的感应距离设计感应门,欲搬运宽为7d4的物体该门,如图(c)所示,物体的移动速度不能超过多少?【答案】:(1)v 02d(2)d(3)23v 0【解析】:(1)依题意每扇门开启过程中的速度图像如图所示:设门全部开启所用的时间为t 0,由图可得d =12v 0t 0由速度公式得:v =a ·12t 0联立解得:a =v 0d(2)要使单扇门打开人只要在t 时间内到达门框处即可符合要求,所以人到门的距离为(3)宽为74d 的物体运动到门框过程中,每扇门至少要运动以加速度a 运动又运动了s 2=78d -A.小轿车刹车的加速度大小为B.小轿车的刹车距离为7mC.绿灯开始闪烁到红灯刚亮的时间为D.绿灯开始闪烁到红灯刚亮的时间为【答案】C【详解】AB.由题意可知小轿车在整个过程的位移所以轿车刹车过程的位移刹车过程根据速度位移关系有A.30.25m B.36.85m【答案】C【详解】为充分保证安全距离,取反应时间最大为反应时间中行驶距离为A.加速与减速的时间不一定相等A.电梯匀速运行的时间为B.电梯匀速运行的时间为C.电梯运行的最大速度为D.电梯运行的最大速度为【答案】C耽误距离,耽误时间a 2t 2t 耽误距离,耽误时间【模型演练1】(2022·全国·统考高考真题)长为l 的高速列车在平直轨道上正常行驶,速率为L 的隧道,当列车的任一部分处于隧道内时,列车速率都不允许超过减速时加速度的大小分别为a 和,则列车从减速开始至回到正常行驶速率v L lv ++B .0v v L a -+)v L lav-++D .()03v v a-+A.通过的最短距离为60m B C.所用的最短时间为4s D 【答案】B【详解】CD.汽车通过ETC通道,减速时间1vt=匀速时间2t 加速时间3vt=从开始减速到恢复正常行驶过程中的时间t 故CD错误;A.加速阶段与减速阶段的加速度大小之比为B.加速阶段与减速阶段的位移大小之比为C.加速阶段与匀速阶段的位移大小之比为D.小汽车从0v开始减速直至再恢复到【答案】D【详解】A.v-t图像中图线斜率表示加速度,加速阶段与减速阶段的加速度大小之比为BCD.v-t图像中图线与时间轴所围的面积在数值上等于位移大小,由题图知减速阶段位移大小为匀速阶段位移大小为加速阶段位移大小为A.8s【答案】C.【解析】:设物体运动的加速度为线运动,则有:最后5因为s∶s=11∶5,解得得,由初速度为v减速到零所通过的路程③;A.物块质量为0.7kgB.物块所受摩擦力大小为0.4NC.0~20m过程中,物块克服摩擦力做功为40JD.0~10m过程中与10m~20m过程中物块所受合力之比为3∶4【答案】A【详解】AB.0~10m内物块上滑,由动能定理得1 5g B.25A.A.重力加速度大小C.斜面的倾角A.物体在斜面上运动的过程机械能减小了B.斜面与物体间的摩擦力大小C.物体的质量为m=2kg如图所示,设物体由即以大小为2a的加速度做匀减速直线运动,从A点运动到B点的时间等于由取向右为正方向:物体从A到B,由运动学公式得:A.物体回到斜面底端的动能小于B.恒力F=2mgsinθC.撤去力F时,物体的重力势能是D.动能与势能相等的时刻一定出现在撤去力mgθ的比应该为3比7 A.F与sinA .小球所受的电场力大小等于重力大小B .板间电压2U qmgd =C .2Tt =时,小球速度大小为54v 0D .t T =时,小球速度大小为v 0【答案】CA.小物块返回A点时速度大小为C.电场强度的大小关系是E【答案】ACA .油滴带负电C .油滴回到出发点的速度为【答案】ABD【解析】充电后,油滴受到向上的电场力,而电容器上极板带正电,电场方向竖直向下,故油滴带负电,A 正确;闭合前,油滴向下运动的过程,解得a =3g ,对第二个过程由牛顿第二定律可得的速度为m at v v 2-=-=机械能减小,故向下运动的过程中,机械能先不变后减小,【模型演练6】物体静止在光滑水平面上,去F 1,立即再对它施一水平向左的水平恒力从A到B则有若C点在A点右侧,从B到C,则有-(1)PQ两板电势差;(2)欲使小球不与下板(3)当t取(2)最大值,为使小球不与差U′满足的条件.【答案】见解析【解析】(1)静止释放,小球做自由落体运动,t时间内下落的高度:t时刻的速度:v1若加上电场后,假设小球的加速度为a1(2tx=-v12t+12根据题意可知:x5。
高中物理模型组合27讲(Word) 运动学

模型组合讲解——运动学【模型概述】在近年的高考中对各类运动的整合度有所加强,如直线运动之间整合,曲线运动与直线运动整合等,不管如何整合,我们都可以看到共性的东西,就是围绕着运动的同时性、独立性而进行。
【模型回顾】 一、两种直线运动模型匀速直线运动:两种方法(公式法与图象法) 匀变速直线运动:20021at t v s at v v t +=+=,,几个推论、比值、两个中点速度和一个v-t 图象。
特例1:自由落体运动为初速度为0的匀加速直线运动,a=g ;机械能守恒。
特例2:竖直上抛运动为有一个竖直向上的初速度v 0;运动过程中只受重力作用,加速度为竖直向下的重力加速度g 。
特点:时间对称(下上t t =)、速率对称(下上v v =);机械能守恒。
二、两种曲线运动模型平抛运动:水平匀速、竖直方向自由落体 匀速圆周运动:ωωmv mr rmv ma F F =====22向向法【模型讲解】一、匀速直线运动与匀速直线运动组合例1. (04年广东高考)一路灯距地面的高度为h ,身高为l 的人以速度v 匀速行走,如图1所示。
(1)试证明人的头顶的影子作匀速运动; (2)求人影的长度随时间的变化率。
图1解法1:(1)设t=0时刻,人位于路灯的正下方O 处,在时刻t ,人走到S 处,根据题意有OS=vt ,过路灯P 和人头顶的直线与地面的交点M 为t 时刻人头顶影子的位置,如图2所示。
OM 为人头顶影子到O 点的距离。
图2由几何关系,有OS OM l OM h -= 联立解得t lh hvOM -=因OM 与时间t 成正比,故人头顶的影子作匀速运动。
(2)由图2可知,在时刻t ,人影的长度为SM ,由几何关系,有SM=OM-OS ,由以上各式得t lh lv SM -=可见影长SM 与时间t 成正比,所以影长随时间的变化率lh lvk -=。
解法2:本题也可采用“微元法”。
设某一时间人经过AB 处,再经过一微小过程)0(→∆∆t t ,则人由AB 到达A ’B ’,人影顶端C 点到达C ’点,由于t v S AA ∆=∆'则人影顶端的移动速度:图3hH Hv t S h H HtS v AA t CC t C -=∆∆-=∆∆=→∆→∆'0'0lim lim可见C v 与所取时间t ∆的长短无关,所以人影的顶端C 点做匀速直线运动。
先加速后减速模型

模型组合讲解——先加速后减速模型汪华【模型概述】物体先加速后减速的问题是运动学中典型的综合问题,也是近几年的高考热点,同学在求解这类问题时一定要注意前一过程的末速度是下一过程的初速度,如能画出速度图象就更明确过程了。
【模型讲解】例. (2004年全国高考)一小圆盘静止在桌面上,位于一方桌的水平桌面的中央。
桌布的一边与桌的AB 边重合,如图1所示。
已知盘与桌布间的动摩擦因数为1μ,盘与桌面间的动摩擦因数为2μ。
现突然以恒定加速度a 将桌布抽离桌面,加速度方向是水平的且垂直于AB 边。
若圆盘最后未从桌面掉下,则加速度a 满足的条件是什么?(以g 表示重力加速度)图1解析:根据题意可作出物块的速度图象如图2所示。
设圆盘的质量为m ,桌边长为L ,在桌布从圆盘下抽出的过程中,盘的加速度为1a ,有11ma mg =μ图2桌布抽出后,盘在桌面上做匀减速运动,以2a 表示加速度的大小,有22ma mg =μ 设盘刚离开桌布时的速度为1v ,移动的距离为1x ,离开桌布后在桌面上再运动距离2x 后便停下,由匀变速直线运动的规律可得:11212x a v = ① 22212x a v =② 盘没有从桌面上掉下的条件是:221L x x ≤+ ③ 设桌布从盘下抽出所经历时间为t ,在这段时间内桌布移动的距离为x ,有:21122121t a x at x ==,,而21L x x =-,求得: 1a a L t -=,及1111a a L a t a v -== 联立解得2121)2(μμμμg a +≥【模型特征】“先加速后减速”模型的v-t 图象中速度为临界点,斜率为加速度、面积为位移。
处理“物体先加速后减速”问题的方法很多,我们可以根据已知条件采用三大定理处理,也可以根据图象快捷处理,借助图象法为我们更加清晰准确的采用全过程法提供了保证。
【热点图象】直线运动的s-t 图;直线运动的v-t 图;平抛运动的y-x 图;机车启动的P-t 图;简谐运动的x-t 图;简谐波的y-x 图;受迫振动的共振曲线;电场线;磁感线;闭合电路的U-I 图;闭合电路的P 出-R 图;部分电路的U-I 图;分子力随距离变化的F 分-r 图;分子势能随距离变化的E P -r 图;电磁感应中的Φ-t 图;电磁感应中的I-t 图;光电效应中的E km -γ图。
模型组合讲解——先加速后减速模型

模型组合讲解一一先加速后减速模型汪华【模型概述】物体先加速后减速的问题是运动学中典型的综合问题,也是近几年的高考热点,同学在求解这类问题时一定要注意前一过程的末速度是下一过程的初速度,如能画出速度图象就更明确过程了。
【模型讲解】例.(2004年全国高考)一小圆盘静止在桌面上,位于一方桌的水平桌面的中央。
桌布的一边与桌的AB边重合,如图1所示。
已知盘与桌布间的动摩擦因数为1,盘与桌面间的动摩擦因数为2。
现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边。
若圆盘最近未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)解析:根据题意可作出物块的速度图象如图2所示。
设圆盘的质量为m,桌边长为L,2mg ma2设盘刚离开桌布时的速度为v i,移动的距离为便停下,由匀变速直线运动的规律可得:X i,离开桌布后在桌面上再运动距离X2后2 小v i2a i x i 2V i 2a2X2盘没有从桌面上掉下的条件是: X iLX22桌布抽出后,盘在桌面上做匀减速运动,以a2表示加速度的大小,有设桌布从盘下抽出所经历时间为t,在这段时间内桌布移动的距离为X,有:联立解得( 12 2)ig2【模型特征】“先加速后减速”模型的 v-t 图象中速度为临界点,斜率为加速度、面积为位移。
处理“物体先加速后减速”问题的方法很多,我们可以根据已知条件采用三大定理处理, 也可以根据图象快捷处理,借助图象法为我们更加清晰准确的采用全过程法提供了保证。
【热点图象】直线运动的s-t 图;直线运动的 v-t 图;平抛运动的y-x 图;机车启动的 P-t 图;简谐运 动的x-t 图;简谐波的y-x 图;受迫振动的共振曲线;电场线;磁感线;闭合电路的 U-I 图;闭合电路的P 出-R 图;部分电路的 U-I 图;分子力随距离变化的F 分-r 图;分子势能随距离变化的E p -r 图;电磁感应中的①-t 图;电磁感应中的l-t 图;光电效应中的 E km -丫图。
“先加速后减速”模型(高一、高三)

“先加速后减速”模型(高一、高三)
徐高本
【期刊名称】《数理天地:高中版》
【年(卷),期】2005(000)012
【摘要】近年的高考题频繁出现质点先加速后减速的运动模型.它注重对过程分析的考查,为纠正当前中学生“重结论,轻过程”的学习习惯起到了很好的导向作用. 1.先做匀加速运动,后做匀减速运动一般用力的观点求解.先分析不同阶段物体的受力情况,再由牛顿运动定律和运动学公式列方程.前一阶段的末速度等于后一阶段的【总页数】2页(P)
【作者】徐高本
【作者单位】湖北省大悟县第一中学
【正文语种】中文
【中图分类】G63
【相关文献】
1.先思后评、寻规变练——高三化学习题课变式教学策略
2.从加速跑的角度分析我国男子百米运动员后程减速的原因
3.中国经济\"结构性加速\"转向\"结构性减速\"源于产业结构吗?——基于一个随机前沿模型的研究
4.“先加速后减速”运动模型命题趋向分析
5.先思后评寻规变练——基于“五环”教学模式下的高三语文讲评课
因版权原因,仅展示原文概要,查看原文内容请购买。
动力学——先加速后减速高中物理

2.先加速后减速(加速再加速、减速再减速):利用好中间速度对于初末速度都为0,先加后减有:2211t a t a v m ==;2211222x a x a v m ==【例1】(2005全国卷1)原地起跳时,先屈腿下蹲,然后突然蹬地。
从开始蹬地到离地是加速过程(视为匀加速),加速过程中重心上升的距离称为“加速距离”。
离地后重心继续上升,在此过程中重心上升的最大距离称为“竖直高度”。
现有下列数据:人原地上跳的“加速距离”m d 50.01=,“竖直高度”m h 0.11=;跳蚤原地上跳的“加速距离”m d 00080.02=,“竖直高度”m h 10.02=。
假想人具有与跳蚤相等的起跳加速度,而“加速距离”仍为0.50m ,则人上跳的“竖直高度”是多少?【答案】63m【解析】用a 表示跳蚤起跳的加速度,v 表示离地时的速度,则对加速过程和离地后上升过程分别有:v 2=2ad 2 v 2=2gh 2若假想人具有和跳蚤相同的加速度a ,令V 表示在这种假想下人离地时的速度,H 表示与此相应的竖直高度,则对加速过程和离地后上升过程分别有V 2=2ad 1 V 2=2gH由以上各式可得:H =h 2d 1d 2代人数值,得:H =63m (62.5m )【例2】跳伞运动员做低空跳伞表演,当飞机在离地面224m 高处水平飞行时,运动员离开飞机在竖直方向做自由落体运动。
运动一段时间后,立即打开降落伞,展伞后运动员以12.5m/s 2的平均加速度匀减速下降。
为了运动员的安全,要求运动员落地速度最大不得超过5m/s 。
g =10m/s 2,求:(1)运动员展伞时离地的高度至少为多少?着地时相当于从多高处自由落下?(2)运动员在空中的最短时间为多少?【答案】(1)99m ,1.25m (2)8.6s 。
【解析】设展伞时跳伞员的速度为v 0,距地面的高度为h ,到达地面速度为v ,据题意有:224m -h =v 202g① v 2-v 20=-2ah ②联立①②得:h =99m ,v 0=50m/s.设实际相当于h ′高度跳下则2gh ′=v 2 ③ 解h ′=1.25m当跳伞员恰好以5m/s 的速度落地时间最短,设时间为t ,自由下落时间为t 1,减速运动时间为t 2,据题意:t =t 1+t 2④ v 0=gt 1⑤ 20at v v +=或者h t v v =+202 ⑥ 联立第(1)问和④⑤⑥式得:t =8.6s【例3】(2011新课标卷第24题)甲乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变。
高中物理模型组合27讲(Word下载)速度分解渡河模型

高中物理模型组合27讲(Word 下载)速度分解渡河模型【模型概述】在运动的合成与分解中,如何判定物体的合运动和分运动是首要咨询题,判定合运动的有效方法是看见的运动确实是合运动。
合运动的分解从理论上讲能够是任意的,但一样按运动的实际成效进行分解。
小船渡河和斜拉船等咨询题是常见的运动的合成与分解的典型咨询题【模型讲解】一、速度的分解要从实际情形动身例1. 如图1所示,人用绳子通过定滑轮以不变的速度0v 拉水平面上的物体A ,当绳与水平方向成θ角时,求物体A 的速度。
图1解法一〔分解法〕:此题的关键是正确地确定物体A 的两个分运动。
物体A 的运动〔即绳的末端的运动〕可看作两个分运动的合成:一是沿绳的方向被牵引,绳长缩短。
绳长缩短的速度即等于01v v =;二是随着绳以定滑轮为圆心的摆动,它不改变绳长,只改变角度θ的值。
如此就能够将A v 按图示方向进行分解。
因此1v 及2v 实际上确实是A v 的两个分速度,如图1所示,由此可得θθcos cos 01v v v A ==。
解法二〔微元法〕:要求船在该位置的速率即为瞬时速率,需从该时刻起取一小段时刻来求它的平均速率,当这一小段时刻趋于零时,该平均速率就为所求速率。
设船在θ角位置经△t 时刻向左行驶△x 距离,滑轮右侧的绳长缩短△L ,如图2所示,当绳与水平方向的角度变化专门小时,△ABC 可近似看做是一直角三角形,因而有θcos x L ∆=∆,两边同除以△t 得:θcos txt L ∆∆=∆∆ 即收绳速率θcos 0A v v =,因此船的速率为:θcos 0v v A =图2总结:〝微元法〞。
可设想物体发生一个微小位移,分析由此而引起的牵连物体运动的位移是如何样的,得出位移分解的图示,再从中找到对应的速度分解的图示,进而求出牵连物体间速度大小的关系。
解法三〔能量转化法〕:由题意可知:人对绳子做功等于绳子对物体所做的功。
人对绳子的拉力为F ,那么对绳子做功的功率为01Fv P =;绳子对物体的拉力,由定滑轮的特点可知,拉力大小也为F ,那么绳子对物体做功的功率为θcos 2A Fv P =,因为21P P =因此θcos 0v v A =。
2024届高考物理复习讲义:专题强化四 动力学中两种典型物理模型
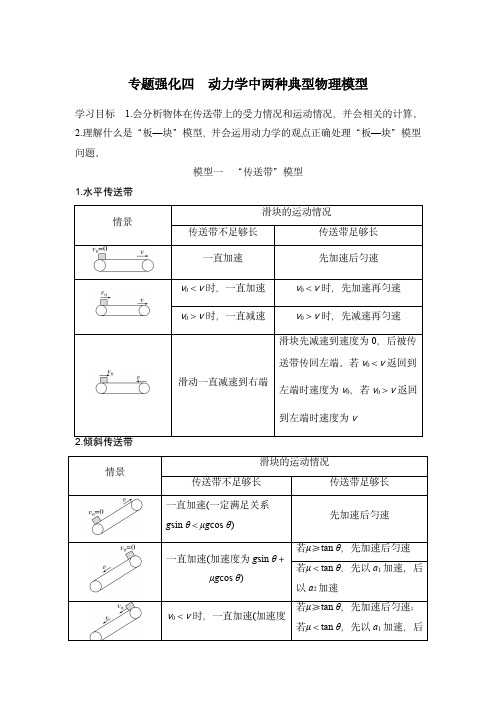
专题强化四动力学中两种典型物理模型学习目标1.会分析物体在传送带上的受力情况和运动情况,并会相关的计算。
2.理解什么是“板—块”模型,并会运用动力学的观点正确处理“板—块”模型问题。
模型一“传送带”模型1.水平传送带情景滑块的运动情况传送带不足够长传送带足够长一直加速先加速后匀速v 0<v 时,一直加速v 0<v 时,先加速再匀速v 0>v 时,一直减速v 0>v 时,先减速再匀速滑动一直减速到右端滑块先减速到速度为0,后被传送带传回左端。
若v 0<v 返回到左端时速度为v 0,若v 0>v 返回到左端时速度为v2.倾斜传送带情景滑块的运动情况传送带不足够长传送带足够长一直加速(一定满足关系g sin θ<μg cos θ)先加速后匀速一直加速(加速度为g sin θ+μg cos θ)若μ≥tan θ,先加速后匀速若μ<tan θ,先以a 1加速,后以a 2加速v 0<v 时,一直加速(加速度若μ≥tan θ,先加速后匀速;若μ<tan θ,先以a 1加速,后为g sin θ+μg cos θ)以a 2加速v 0>v 时,一直加速或减速(加速度大小为g sin θ-μg cos θ)或μg cos θ-g sin θ若μ≥tan θ,先减速后匀速;若μ<tan θ,一直加速(摩擦力方向一定沿斜面向上)g sin θ>μg cos θ,一直加速;g sin θ=μg cos θ,一直匀速g sin θ<μg cos θ,一直减速先减速到速度为0后反向加速:若v 0<v ,到原位置时速度大小为v 0(类竖直上抛运动);若v 0>v ,先反向加速后匀速,反回原位置时速度大小为v角度水平传送带模型例1(2023·山东济宁高三月考)如图1所示,水平固定放置的传送带在电机的作用下一直保持速度v =4m/s 顺时针转动,两轮轴心间距L =10m 。
一个物块(视为质点)以速度v 0=8m/s 从左轮的正上方水平向右滑上传送带,经过t =2s 物块离开传送带,重力加速度g 取10m/s 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模型组合讲解——先加速后减速模型
【模型概述】
物体先加速后减速的问题是运动学中典型的综合问题,也是近几年的高考热点,同学在求解这类问题时一定要注意前一过程的末速度是下一过程的初速度,如能画出速度图象就更明确过程了。
【模型讲解】
例. (2004年全国高考)一小圆盘静止在桌面上,位于一方桌的水平桌面的中央。
桌布的一边与桌的AB 边重合,如图1所示。
已知盘与桌布间的动摩擦因数为1μ,盘与桌面间的动摩擦因数为2μ。
现突然以恒定加速度a 将桌布抽离桌面,加速度方向是水平的且垂直于AB 边。
若圆盘最近未从桌面掉下,则加速度a 满足的条件是什么?(以g 表示重力加速度)
图1
解析:根据题意可作出物块的速度图象如图2所示。
设圆盘的质量为m ,桌边长为L ,在桌布从圆盘下抽出的过程中,盘的加速度为1a ,有11ma mg =μ
图2
桌布抽出后,盘在桌面上做匀减速运动,以2a 表示加速度的大小,有22ma mg =μ 设盘刚离开桌布时的速度为1v ,移动的距离为1x ,离开桌布后在桌面上再运动距离2x 后便停下,由匀变速直线运动的规律可得:
11212x a v = ① 22212x a v = ② 盘没有从桌面上掉下的条件是:2
21L x x ≤+ ③ 设桌布从盘下抽出所经历时间为t ,在这段时间内桌布移动的距离为x ,有:
21122121t a x at x ==,,而2
1L x x =-,求得: 1a a L t -=,及1
111a a L a t a v -== 联立解得2121)2(μμμμg a +≥
【模型特征】
“先加速后减速”模型的v-t 图象中速度为临界点,斜率为加速度、面积为位移。
处理“物体先加速后减速”问题的方法很多,我们可以根据已知条件采用三大定理处理,也可以根据图象快捷处理,借助图象法为我们更加清晰准确的采用全过程法提供了保证。
【热点图象】
直线运动的s-t 图;直线运动的v-t 图;平抛运动的y-x 图;机车启动的P-t 图;简谐运动的x-t 图;简谐波的y-x 图;受迫振动的共振曲线;电场线;磁感线;闭合电路的U-I 图;闭合电路的P 出-R 图;部分电路的U-I 图;分子力随距离变化的F 分-r 图;分子势能随距离变化的E P -r 图;电磁感应中的Φ-t 图;电磁感应中的I-t 图;光电效应中的E km -γ图。
识图要点:
①运用图象首先要搞清楚纵横轴所代表的物理量,明确要描述的是哪两个物理量之间的关系。
如s-t 图象与v-t 图象在纵轴上的区别;简谐运动图象与简谐波的图象在横轴上的差异等。
②图线并不表示物体实际运动的轨迹。
如匀速直线运动的s-t 图象是一条斜向上的直线,但实际运动的轨迹可以是任意方向的。
③了解图象的物理意义。
从图象的形状看出物理过程,在很多情况下,写出物理量的解析式与图象对照,更有助于理解图象物理意义。
④要特别关注图象中的“点”、“线”、“面”、“斜率”、“截距”等及其对应物理意义。
“点”代表状态,描述物体在该状态下所具有的特征;“线”代表过程,描述物体在一段过程中随着横轴所代表的物理量的变化,纵轴代表物理量的变化情况;“面”指的是图线与横轴所围成的面积,表示纵轴所代表的物理量对横轴所代表的物理量的积累;“斜率”指的是x y x ∆∆→∆0lim ,当横轴为时间轴时,斜率表示纵轴所示物理量对时间的变化率;“截距”指的是图线与纵轴的交点,当横轴为时间轴时截距描述初态特征。
【模型演练】
(昆明市高中三年级统一检测)一个质量为m=0.2kg 的物体静止在水平面上,用一水平恒力F 作用在物体上10s ,然后撤去水平力F ,再经20s 物体静止,该物体的速度图象如图3所示,则下面说法中正确的是( )
A. 物体通过的总位移为150m
B. 物体的最大动能为20J
C. 物体前10s内和后10s内加速度大小之比为2:1
D. 物体所受水平恒力和摩擦力大小之比为3:1
答案:ACD
图3。
