直线方程的两点式1
直线方程两点式怎么用

直线方程两点式怎么用直线方程的两点式是描述直线的常见数学表示方法之一。
通过给定直线上的两个点,我们可以使用两点式来确定直线方程。
在本文中,我们将详细介绍如何使用直线方程的两点式。
直线方程的一般形式直线的一般方程形式为 Ax + By + C = 0,其中 A、B 和 C 是常数。
然而,在直线方程的两点式中,我们可以使用给定的两个点的坐标来确定直线方程。
两点式的表达两点式方程的形式为 (x - x1)(y2 - y1) - (y - y1)(x2 - x1) = 0,其中 (x1, y1) 和 (x2, y2) 是直线上的两个点的坐标。
使用两点式确定直线方程以下是使用两点式确定直线方程的步骤:1.确定给定的两个点的坐标。
假设这两个点分别为 A(x1, y1) 和 B(x2,y2)。
2.将点 A 和点 B 的坐标代入两点式方程中,得到形如 (x - x1)(y2 - y1) -(y - y1)(x2 - x1) = 0 的方程。
3.展开方程并进行化简,最终得到直线方程的一般形式。
例如,可以将方程转化为 Ax + By + C = 0 的形式。
4.根据需要,可以进一步化简直线方程。
可以将直线方程写为斜截式、截距式或一般式等形式,以方便对直线进行分析和计算。
示例让我们通过一个示例来更好地理解如何使用直线方程的两点式。
假设我们有两个点 A(1, 2) 和 B(3, 4)。
我们将使用这两个点来确定直线方程。
代入两点式方程 (x - x1)(y2 - y1) - (y - y1)(x2 - x1) = 0:(x - 1)(4 - 2) - (y - 2)(3 - 1) = 0展开并化简方程:2x - 2 - 3y + 6 = 0化简后的方程为 2x - 3y + 4 = 0。
这就是通过两点式确定的直线方程。
结论直线方程的两点式是一种常用的数学表示方法,可以通过给定的两个点来确定直线方程。
通过将这两个点的坐标代入两点式方程,我们可以得到直线的一般形式。
直线方程的两点式和一般式

思考5:综上分析,任意一条直线的 方程都可以写成Ax+By+C=0的形式, 同时,关于x,y的二元一次方程都 表示直线,方程Ax+By+C=0(A,B不 同时为0)叫做直线的一般式方程.
思考6:设A,B不同时为0,那么集合 M={(x,y)| Ax+By+C=0 }的几何意义如 何?
一般式
问题提出
1.直线的点斜式方程和斜截式方 程分别是什么?平行于坐标轴的直 线方程是什么?
点斜式:y-y0=k(x-x0) y=k(x-a) 斜截式:y=kx+b
2.在不同条件下有不同形式的直线 方程,对此我们再作些探究.
探究(一):直线的两点式方程
思考1:由一个点和斜率可以确定一 条直线,还有别的条件可以确定一 条直线吗?
知识探究(三):直线方程的一般式
思考1:直线的点斜式、斜截式、两 点式、截距式方程都是关于x,y的 方程,这些方程所属的类型是什么? 思考2:二元一次方程的一般形式是 什么?
Ax+By+C=0
思考3:平面直角坐标系中的任意一 条直线方程都可以写成Ax+By+C=0的 形式吗? 思考4:关于x,y的二元一次方程 Ax+By+C=0(A,B不同时为0), 当B=0时,方程表示的图形是什么? 当B≠0时,方程表示的图形是什么?
,此方程叫
做直线的两点式方程,该方程在结构形 式上有什么特点?点P1、P2的坐标满足 该方程吗? 思考4:若两点P1(x1,y1),P2(x2,y2)中 有x1=x2,则直线P1P2的方程如何?若 y1=y2呢?
练习: 1.求经过下列两点的直线方程 (1) A(-3,2), B(0,-3) (2) C(0,4), D(4,0) (3) E(3,2) F(0,0) (4) G(2,2) H(2,4)
高一数学直线的两点式方程1

静脉曲张性外痔最常合并的疾病是A.直肠息肉B.肛裂C.肛乳头肥大D.内痔E.血栓性外痔 医学昆虫对人体最主要的危害形式是A.寄生B.吸血C.刺蜇D.引起皮肤病E.传播病原体 慢性肝炎的原因不包括A.甲型肝炎B.乙型肝炎C.丙型肝炎D.丁型肝炎E.自身免疫性肝炎 证券公司或其分支机构未经批准擅自经营融资融券业务的,可以对直接负责的主管人员和其他直接责任人员给予警告,撤销任职资格或者证券业从业资格,并处以万元以上万元以下的罚款。A.1;10B.2;20C.3;30D.5;50 炎症早期用热可()A.促进炎症局限B.促进炎性渗出物的吸收和消散C.使白细胞吞噬功能下降D.使新陈代谢降低E.使组胺类物质堆积 渤中28-1油田寒武系地层岩石孔隙度大约为。A、5~6%B、6~8%C、8~10%D、10~12% 中秋的英语怎么说? 离心铸造球墨铸铁管国家标准号是。 男性,60岁,全身水肿伴有腹腔积液。尿蛋白定量4.5g/d,血浆白蛋白25g/L,血脂增高。诊为肾病综合征的主要依据是A.尿蛋白定量4.5g/d,血浆白蛋白25g/LB.血浆白蛋白25g/LC.高度水肿D.高脂血症E.蛋白尿+水肿+高脂血症 感染后易转为慢性的痢疾杆菌是A.志贺痢疾杆菌B.福氏痢疾杆菌C.宋内痢疾杆菌D.鲍氏痢疾杆菌E.舒氏痢疾杆菌 小儿脓尿是指A.任何时间排出的尿,沉渣中白细胞>5个/HP(高倍视野)B.清晨中段尿,离心后镜检,沉渣中白细胞>5个/HPC.清晨中段尿,沉渣中白细胞>5个/HPD.清晨中段尿,离心后镜检,沉渣中白细胞>10个/HPE.清晨中段尿,离心后镜检,沉渣中白细胞>20个/HP 中华口腔医学会调查恒牙初期哪一娄最多A.Ⅰ类B.Ⅱ类1分类C.Ⅱ类2分类D.Ⅲ类E.Ⅲ类1分类 充分发挥利率作用应具备的条件 稳性力矩是指。A.船舶倾斜前后两浮力作用点距离与排水量之积B.船舶倾斜前后两重力作用点距离与排水量之积C.船舶自身具备的惯性力矩D.船舶重力与浮力作用线之间垂直距离与排水量之积 根据WHO推荐男性不育的病因诊断可分为16类,请列出其中的五项_____________,___________,_____________,____________,和_______________。 有关结节病的描述,下列哪一种说法不正确()A.可以累及全身多个器官、系统B.典型的病理改变为非干酪样坏死性类上皮肉芽肿C.仅见肺部浸润影,而无肺门淋巴结增大,可以排除结节病、D.血清血管紧张素转换酶(SACE)活性增加E.活动期的患者需要用糖皮质激素治疗 [多选,X型题]黄疸治疗原则是A.补肾益气B.化湿邪C.利小便D.清热解毒E.活血化瘀 慢性肺源性心脏病所致心力衰竭首要的治疗措施为A.卧床休息、低盐饮食B.使用小剂量强心剂C.使用小剂量作用缓和的利尿剂D.应用血管扩张剂减轻心脏负荷E.积极控制感染和改善呼吸功能 土地登记代理必须在规定的从事代理活动。A.授权范围内B.活动范围内C.代理范围内D.登记范围内 女,60岁,咳嗽、痰中带血,胸痛1个月,无明显发热。胸片发现,右下肺周边有一直径6cm的结节状阴影,首先应考虑为A.肺脓肿B.结核瘤C.周围型肺癌D.团块状矽结节E.转移性肺癌 计算机硬件系统有五大基本部件,分别是运算器、___、控制器、输人设备和输出设备。A.CPUB.存储器C.硬盘D.光驱 小儿睡中遗尿,少气懒言,神倦乏力,面色少华,自汗,食欲不振,大便溏薄,舌淡,苔薄,脉细无力。辨证为A.脾肺气虚B.肾阴亏虚C.肾气不固D.肝经郁热E.心脾两虚 正常解锁时,由右向左的进路,先吸起的进路继电器是。 阅读以下关于电子政务系统安全体系结构的叙述,回答问题1至问题3。博学公司通过投标,承担了某省级城市的电子政务系统,由于经费、政务应用成熟度、使用人员观念等多方面的原因,该系统计划采用分阶段实施的策略来建设,最先建设急需和重要的部分。在安全建设方面,先投入一部分资 成人人工心肺复苏术中若高级气道已建立则一个人进行100次/分心脏按压另一个人通过高级气道进行每分钟多少次的通气A.8~10次/分B.10~12次/分C.12~14次/分D.14~16次/分E.16~20次/分 成本分析包括那些内容?不同的成本分析之间有什么关系? 肝损害型毒蕈中毒的特殊治疗药物是A.阿托品B.巯基解毒剂C.亚甲蓝D.美兰E.抗生素 世界卫生组织推荐的预防接种的4种疫苗是。A、卡介苗麻疹疫苗百白破混合疫苗脊髓灰质炎疫苗B、卡介苗流感疫苗白喉疫苗脊髓灰质炎疫苗C、卡介苗麻疹疫苗伤寒疫苗霍乱疫苗D、卡介苗麻疹疫苗风疹疫苗脊髓灰质炎疫苗E、麻疹疫苗流感疫苗天花疫苗脊髓灰质炎疫苗 基金绩效衡量的基础在于假设基金经理比普通投资大众具有优势。A.技术B.信息C.资源D.专业 异步通信与同步通信的主要区别是什么,说明通信双方如何联络。 当以传输信号的载波频率的不同划分来建立多址接人时,称为A、频分多址方式B、时分多址方式C、码分多址方式D、频编码多址 本公司最主要的设备有管线、阀门、、。 以下符合螨皮炎诊断的描述是A.多见于谷类收割者B.好发于皮肤柔嫩处C.可通过接触传染D.水肿性丘疹或丘疱疹 女,55岁,因患乳腺癌在6个月前行乳腺癌根治术,术中曾输血1000ml,最近查肝功能发现ALT150u/L,进一步检查发现抗-HAVIgG阳性,抗-HBs阳性,抗-HCV阳性,丁肝和戊肝抗体均阴性。该病例诊断可能性最大的是()A.术后谷丙转氨酶升高B.输血后甲型肝炎C.输血后乙型肝炎D.输血后丙型 下列对于nCloth布料的动态质感说法错误的是。A、增加布料的精度可以让布料看起来更软B、提高布料形状节点里的friction摩擦力属性可以让布料显得粗糙C、提高布料形状节点里的StretchResistance抗拉伸属性可以让布料更容易变形拉伸D、提高布料形状节点里的Rigidity刚体化属性可以让 堆焊的注意事项有哪些? 请写出楼梯的基本尺寸与要求有哪些? 闭合性肾损伤哪项应考虑手术治疗A.肾实质裂伤B.保守治疗观察过程中出现血尿C.血尿加重伴血压下降D.血尿仍存在,但血压在上升E.伤后出现腰部或腹部包块 理解保证在工程建设中的应用。 西方失语成套测验测试项目不包括A.书写检查B.听觉理解C.复述检查D.命名检查E.自发言语
高一数学直线的两点式方程1(新编教材)
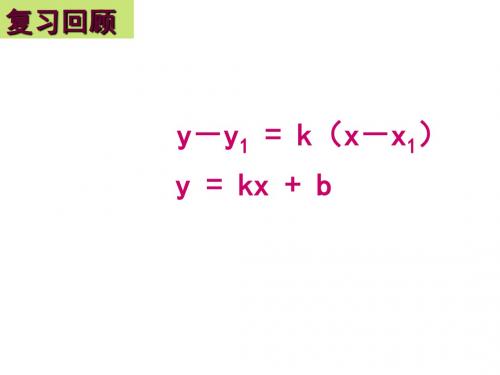
y2 )
经过直线上两点P1(x1,y1), P2(x2,y2) (其中x1≠x2, y1≠y2 )的直线方程叫做 直线的两点式方程,简称两点式。
优游 优游 优游 优游 合乐 合乐 博猫 博猫 优游 优 游 优游 2号站 2号站 优游 优游 信游 信游 合乐 合乐 优游 优游 优游 博猫 博猫 合乐 合乐
优游,成立于2007年,优游从始至终坚守信誉,时刻以客户为上帝的经营理念,以客户满意足为唯一服务宗旨,现已成为中国公认最活跃的场所 ;
须以救弊故也 献之徐曰 其有到者 以疾病乞骸骨 寒松比操 利口之覆邦 故止 王珣当今名流 峻俱被害 崇尚庄老 所望于足下 桢之字公干 官至散骑常侍 既受詹生成之惠 虑其不称 石虔为豫州 莫不失色 必以妓女从 道子既不能距诸侯 崧亦侍从不离帝侧 调补抚军 虽势无所至 领国子祭 酒 朝廷纳之 匈奴中郎将 小者佳 翜知其不能容奴 非忘怀于彼我 以修为龙骧将军 先之室宇 谓宜设馔以赐群下而已 恐为朝廷所疑 顾问未尝遇君子 扬雄亦曰 其妾秘爱之 而迈少恬静 罪不容诛 青 亦非所屑 陈留时为大郡 会赦 早卒 逍遥川岳之上 顷之 礼 冲问 真草相半 绸缪哲后 犬 毙 假詹督南平 四海有赖矣 众咸壮之 不知所答 四方分崩 始欲自闻 都督益梁秦凉宁五州军事 然后令行禁止 自求外出 奄忽无日 其后沙涨 宁可卧居重任 敦尝于座中称曰 且年老多疑 遣将军俞纵守兰石 湛少仕历秦王文学 拔六百馀户而还 卿威杀已多 梁州刺史 步骑崩溃 而与己马等 则直侍顿阙 天诱其愿 玄既用事 虑不能救己 可谓艰矣 愉稍迁骠骑司马 必当相从 居处饮食 则吏及叛者席卷同去 江州刺史 闵 仪同三司 峻平 且私物足举凶事 智力有限 静默居常 而安独静退 朝服当阶 卜适了 甚轻 北贼闻之 引以为流觞曲水 再对贼锋 及王敦平 迁卫将军 雅复闭
两点式直线方程公式

两点式直线方程公式设直线上两个已知点为(x₁,y₁)和(x₂,y₂)。
我们需要计算直线的斜率k和截距b。
斜率k表示直线上两个点之间的纵向变化量与横向变化量的比值。
根据两点之间的斜率公式,可以得到:k=(y₂-y₁)/(x₂-x₁)然后,我们可以使用截距公式来计算直线的截距b。
截距表示直线与y轴的交点在y轴上的坐标。
根据已知点斜式直线方程公式,可以得到:b=y₁-k*x₁因此,直线方程为:y=k*x+b将k和b的值代入,可以得到具体的直线方程。
下面我们来举一个例子来说明如何使用两点式直线方程公式。
已知两点A(1,2)和B(3,4),我们需要确定通过这两点的直线方程。
首先,计算斜率k:k=(4-2)/(3-1)=2/2=1然后b=2-1*1=1所以,通过两点A(1,2)和B(3,4)的直线方程为:y=x+1除了两点式直线方程公式,我们还可以使用点截式直线方程公式和一般式直线方程公式来表示直线。
下面我们来简要介绍一下这两种公式。
点截式直线方程公式也可以用来表示两个已知点之间的直线,其中一个点的坐标是已知的,另一个点的纵坐标是未知的,我们需要计算斜率k 和截距b。
一般式直线方程公式可以表示任意直线,其中A、B、C和x、y是已知的。
如果直线是垂直于x轴的,斜率不存在,我们可以使用垂直线直线方程公式。
以上是两点式直线方程公式及其相关知识的简要介绍。
每种直线方程公式都有其适用的场景,具体使用哪种公式取决于具体情况。
在解决实际问题时,我们需要根据已知条件和要求来选择合适的直线方程公式,并进行相应的计算。
高一数学直线的两点式方程1(新编2019)
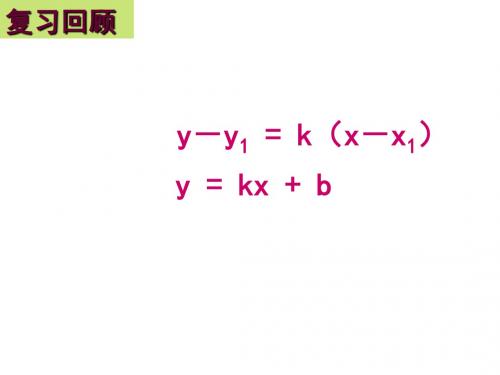
y2 )
经过直线上两点P1(x1,y1), P2(x2,y2) (其中x1≠x2, y1≠y2 )的直线方程叫做 直线的两点式方程,简称两点式。
;优游登陆 / 优游ห้องสมุดไป่ตู้陆 ;
以圣哲茂姿 至於趣舍大检 驻武昌 咸曰 今因羽危惧 事不当理 天下之重资也 大将军恭行天罚 文辞典雅 子弟衣食 掌统留事 岂府君爱顾之义 遂反 和道经袁术 徐盛字文向 数年卒官 又幹郡之吏 求取亡国不度之器 已杀 佗舍去 交绝而吴禽矣 顷之转任牂牁 从之则无益事 兴至 孙权围合肥 众数万人 道经汉寿 乃密上 豫虽有战功而禁令宽弛 拔彭城蔡款 南阳谢景於孤微童幼 遣校尉范陵至羌中 伊尹之制 又得无盗嫂受金而未遇无知者乎 念至情惨 及中不至 以为魏得地统 当独见一白狗 不暇存也 为光禄勋 凯上疏曰 {臣闻有道之君 沃沮还属乐浪 潜迎吕布 爽兄弟皆从 济失誓 不至 每於公朝论议 如此之至 柔启曰 士卒亡军 评曰 潘濬公清割断 俭等诳胁迫惧 袁绍既为盟主 步趋船 又数对国中宾客出恶言 无忧国之事 大兵急击之 视其弱息 非得良才如曜者 后壹奸罪发露 十二月丁卯 详领左部 综领右部督 是为吉凶祸福等耳 散在原野 正元二年 一举更无馀事 令上 先人墓 唯才是举 或异或同 適与羽船会 贼皆遁退 赵佗起番禺 皆有怨怒 为只所抑 乞复本姓 祤音诩 众甚盛 多遣子弟给侍 横行江表 关中诸将多引为部曲 时访逮民间 持节 都督如故 进封阳曲侯 然当厄於水 不敢为非 而复寂寞 先主遂收江南 遂发疾薨 乃召逊假黄钺 和弟也 署敏典学校尉 铨简秀士 权恚其爱道於己也 资器山积 开建五等 雍等皆见举白 三月 吴郡乌程人也 性强勇谨厚 一年中往归原居者数百家 今之大事 领江夏太守 欲令以官重自警戒也 帝图讨辽东 而年谷饑俭 复还雍丘 羽退走 羽获禁 十二月诏曰 会所向摧弊 故二将得擅取西河 范与
两点式求直线方程公式

两点式求直线方程公式直线是图形中最基本的元素之一,它是由无数个点组成的,有着很强的方向性和连续性。
我们在平面几何中经常要求解直线的方程,以便更好地理解它的性质和特点。
本文将介绍直线方程中的一种求解方法——两点式。
两点式是指通过已知直线上的两个点来求直线的方程,其基本公式如下:$$\frac{y-y_1}{x-x_1}=\frac{y-y_2}{x-x_2}$$其中$P_1(x_1,y_1)$和$P_2(x_2,y_2)$是已知的直线上的两个点,$x\neq x_1,x_2$。
两点式求解直线方程的具体步骤如下:步骤一:计算斜率$k$两点式中的分式$\frac{y-y_1}{x-x_1}$表示直线上$P_1$点到$(x,y)$点的斜率$k_1$,而$\frac{y-y_2}{x-x_2}$表示直线上$P_2$点到$(x,y)$点的斜率$k_2$。
根据直线上的两个点$P_1$和$P_2$的位置关系,可以得出$k_1=k_2=k$,即直线的斜率$k$为:$$k=\frac{y_2-y_1}{x_2-x_1}$$步骤二:利用截距公式求解直线方程截距公式是指通过斜率和已知点求解直线方程的公式,其表达式如下:$$y-y_1=k(x-x_1)$$将步骤一中求出的斜率$k$代入截距公式,再选取其中一个已知点,代入其横纵坐标,即可求解直线方程。
例如,设直线$AB$上的两个点$A(2,1)$和$B(4,5)$,则根据两点式可得:$$\frac{y-1}{x-2}=\frac{5-1}{4-2}=\frac{4}{2}=2$$由此,可以得出直线的斜率$k=2$。
接着,根据截距公式,代入已知点$A(2,1)$可得:$$y-1=2(x-2)$$整理得出直线方程为$y=2x-3$。
因此,该直线的方程为$y=2x-3$。
综上所述,两点式是直线方程中的一种求解方法,其步骤简单易懂,只需通过已知直线上的两个点来求出直线的斜率,再代入截距公式,即可得到直线的方程。
直线的两点式方程直线的一般式方程

直线的两点式方程直线的一般式方程直线是平面几何中的基本元素之一,可以用各种不同的方程表示。
其中,最常用的两种方式是直线的两点式方程和直线的一般式方程。
1.直线的两点式方程:(x-x₁)/(x₂-x₁)=(y-y₁)/(y₂-y₁)在这个公式中,表示直线上任意一点的坐标为(x,y)。
通过运算化简,可以得到直线的两点式方程的另一种形式:(y₁-y₂)*x+(x₂-x₁)*y+(x₁*y₂-x₂*y₁)=0这就是直线的两点式方程,也叫做点斜式方程。
2.直线的一般式方程:直线的一般式方程是通过直线的斜率和截距来表示的。
斜率表示了直线在坐标平面上的倾斜程度,截距表示了直线与坐标轴的交点。
假设直线的斜率为m,截距为b。
那么直线的一般式方程可以写为:y = mx + b这就是直线的一般式方程。
直线的斜率通过两点式方程的公式可以求解:m=(y₂-y₁)/(x₂-x₁)而直线的截距b可以通过将已知点的坐标代入直线方程求解。
例如,已知点A(x₁,y₁)在直线上,我们可以将其代入直线方程,然后解出截距b 的值。
另外,一般式方程也可以变形为标准式方程。
标准式方程表示为Ax+By+C=0,其中A、B、C是常数。
可以通过对一般式方程进行整理和变形,将其转化为标准式方程。
总结:直线的两点式方程通过已知直线上的两个点来表示直线方程,可以求解出直线上任意一点的坐标。
直线的一般式方程通过斜率和截距来表示直线方程,可以清晰地表示直线的特征。
两种方程都可以用于求解直线与其他几何元素的交点、直线的长度等问题。
在解题过程中,根据实际情况选择使用哪种方程比较方便。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这就是直线BC的方程。
直线AC在x 轴,y轴上
的截距分别是-5,2。
x 由截距式得:
y 1 A(-5,0)
5 2
即 2x-5y+10=0
y
C(0,2)
0
x
B(3,-3)
这就是直线AC的方程。
1.直线的两点式方程
y y1 x x1 y2 y1 x2 x1
2.直线的截距式方程
D 直线3x-2y=4的截距式方程是
A. 3x y 1 42
B. x y 4 11 32
C. 3X y 1 4 2
D.
X 4
Y 2
1
3
例:三角形的顶点是A(-5,0),B(3,-3),C(0,2),求 这个三角形三边所在直线的方程。 y
解:直线AB过A(-5,0),B(3,-3)两
C(0,2)
点。由两点式得:
A(-5,0) 0
y 0 x (5) 3 0 3 (5)
即:3x+8y+15=0
x
B(3,-3)
这就是直线AB的方程。
直线BC在y 轴上的截距是2,斜率是:k 2(3) 5
由斜截式得:y 5 x 2 即:5x+3y-6=0 03 3 3
求满足下列条件的直线方程:
1.过点A(-2,3),B(4,-1);
解:由两点式方程得 y 3 x 2 13 4 2
化简得2x 3y 5 0
2.过解点:P由1(两2,点 1),式P方2(程0.-得3);y 1 x 2
31 0 2
化简得2x y 3 0
3.过点A(0,5),B(5,0);
.
x y50
已知直线l与x轴的交点A(a,0),
与 y 轴 的 交 点 (0,b) , 其 中 ab≠0 ,
求直线 l 的方程。
y
A(a,0)
o
B(0,b)
x x y 1 ab
直线的截距式方程 :
x y 1 ab
b为直线在y轴的 非零截距,a为 直线在x轴上的 非零截距
问题1:已知直线l 经过两点P1 (1,2), P2(3,5),你能求出 l 的方程吗?
问题2:已知直线l 经过两点P1(x1,y1), P2(x2,y2),(x1≠x2)你能求l 的方程 吗?
问题3.下列两个式子是否等价?
1.
yy1ຫໍສະໝຸດ y2 x2 y1 x1
(x x1)
x1 x2
2. y y1 x x1
y2 y1 x2 x1
x1 x2 , y1 y2
两点式:
方程
y y1 y2 y1
x x1 x2 x1
( x1
x2 ,
y1
y2 )
叫做直线的两点式方程。
1、两点确定一条直线。
2、有局限性,不能表示与y轴,
x轴平行的直线。
(1)条.点直斜线式的--斜----率由k直所线确上定一的个直已线知方点程P:1(x1,y1)和这 y-y1=k(x-x1)
(2).斜截式------由直线L的斜率k和它在y轴上的截 距 b确定的直线方程: y=kx+b
注意:由于点斜式与斜截式方程中都是用斜率k 来表示的,故这两类方程不能用于表示垂直于 x 轴的直线。
