2012年北京一模8题汇编
2012北京17区数学一模新题整合

8. 将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的A .面CDHEB .面BCEFC .面ABFGD .面ADHG8.在正方体的表面上画有如图⑴中所示的粗线,图⑵是其展开图的示意图,但只在A 面上画有粗线,那么将 图⑴中剩余两个面中的粗线画入图⑵中,画法正确的是8.下列图形中,能通过折叠围成一个三棱柱的是A B C D8.如图,圆柱底面直径AB 、母线BC 均为4cm ,动点P 从A 点出发,沿着圆柱的侧面移动到BC 的中点S 的最短距离A.(212π+)cm B.(2412π+)cm C.(214π+)cm D.(242π+)cm7.由n 个相同的小正方体堆成的几何体,其主视图、俯视图如下所示,则n 的最大值是A .16B .18C .19D .20图1图2图322. (本题满分4分)阅读下面材料:小红遇到这样一个问题,如图1:在△ABC 中,A D ⊥BC ,BD=4,DC=6,且∠BAC=45°,求线段AD 的长.小红是这样想的:作△ABC 的外接圆⊙O ,如图2:利用同弧所对圆周角和圆心角的关系,可以知道∠BOC=90°,然后过O 点作OE ⊥BC 于E ,作OF ⊥AD 于F ,在Rt △BOC 中可以求出⊙O 半径及 OE ,在Rt △AOF 中可以求出AF,最后利用AD=AF+DF 得以解决此题。
请你回答图2中线段AD 的长 .参考小红思考问题的方法,解决下列问题:如图3:在△ABC 中,A D ⊥BC ,BD=4,DC=6,且∠BAC=30°,则线段AD 的长 .22.如图①,在矩形A B C D 中,将矩形折叠,使点B 落在A D (含端点)上,落点记为E ,这时折痕与边B C 或边C D (含端点)交于点F .然后再展开铺平,则以B E F 、、为顶点的B E F △称为矩形A B C D 的“折痕三角形”.(1)由“折痕三角形”的定义可知,矩形A B C D 的任意一个“折痕B E F △”一定是一个________三角形;(2)如图②,在矩形A B C D 中,24A B B C ==,,当它的“折痕B E F △”的顶点E 位于边A D 的中点时,画出这个“折痕B E F △”,并求出点F 的坐标; (3)如图③,在矩形A B C D 中,24A B B C ==,.当点F 在OC 上时,在图③中画出该矩形中面积最大的“折痕B E F △”,并直接写出这个最大面积.22.阅读下面材料:如图1,已知线段AB 、CD 相交于点O ,且AB =CD ,请你利用所学知识把线段AB 、CD 转移到同一三角形中. 小强同学利用平移知识解决了此问题,具体做法: 如图2,延长OD 至点E ,使DE =CO ,延长OA 至点F ,使AF =OB ,联结EF ,则△OEF 为所求的三角形.请你仔细体会小强的做法,探究并解答下列问题:如图3,长为2的三条线段AA ′,BB ′,CC ′交于一点O ,并且∠B ′OA =∠C ′OB =∠A ′OC =60°;(1)请你把三条线段AA ′,BB ′,CC ′ 转移到同一三角形中.(简要叙述画法)(2)联结AB ′、BC ′、CA ′,如图4,设△AB ′O 、△BC ′O 、△CA ′O 的面积分别为S 1、S 2、S 3, 则S 1+S 2+S(填“>”或“<”或“=” ) .12.已知如图,△ABC 和△DCE 都是等边三角形,若△ABC 的边长为1,则△BAE 的面积是 .四边形ABCD 和四边形BEFG 都是正方形,若正方形ABCD 的边长为4,则△F AC 的面积是 . ……如果两个正多边形ABCDE …和BPKGY …是正n (n ≥3)边形,正多边形ABCDE …的边长是2a ,则△KCA 的面积是 .(结果用含有a 、n的代数式表示)图4E22.小明在学习轴对称的时候,老师留了这样一道思考题:如图,已知在直线l 的同侧有A 、B 两点,请你在直线l 上确定一点P ,使得PA+PB 的值最小.小明通过独立思考,很快得出了解决这个问题的正确方法,他的作法是这样的:①作点A 关于直线l 的对称点A′.②连结A′B ,交直线l 于点P .则点P 为所求. 请你参考小明的作法解决下列问题:(1) 如图1,在△ABC 中,点D 、E 分别是AB 、AC 边的中点,BC =6,BC 边上的高为4,请你在BC 边上确定一点P ,使得 △PDE 的周长最小.①在图1中作出点P .(三角板、刻度尺作图,保留作图 痕迹,不写作法) ②请直接写出△PDE 周长的最小值 .(2)如图2在矩形ABCD 中,AB =4,BC =6,G 为边AD 的中点,若E 、F 为边AB 上的两个动点,点E 在点F 左侧,且EF =1,当四边形CGEF 的 周长最小时,请你在图2中确定点E 、F 的位置.(三角板、刻度尺作图,保留作图痕迹,不写作法),并直接写出四边形CGEF 周长的最小值 .12.abc 是一个三位的自然数,已知195abc ab a --=,这个三位数是_____________;聪明的小亮在解决这种问题时,采取列成连减竖式的方法(见右图)确定要求的自然数,请你仿照小亮的作法,解决这种问题.如果a b c d 是一个四位的自然数,且 2993abcd abc ab a ---=那么,这个四位数是_____________.动手操作12.在∠A (0°<∠A <90°)的内部画线段,并使线段的两端点分别落在角的两边AB 、AC上,如图所示,从点A 1开始,依次向右画线段,使线段与线段在两端点处互相垂直,A 1A 2为第1条线段.设AA 1=A 1A 2=A 2A 3=1,则∠A = ;若记线段A 2n-1A 2n 的长度为a n (n为正整数),如A 1A 2=a 1,A 3A 4=a 2,则此时a 2= ,a n = (用含n 的式子表示).图1B图1C图222.阅读下面材料:小伟遇到这样一个问题:如图1,在正方形ABCD 中,点E 、F 分别为DC 、BC 边上的点,∠EAF =45°,连结EF ,求证:DE +BF =EF .小伟是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.他的方法是将△ADE 绕点A 顺时针旋转90°得到△ABG (如图2),此时GF 即是DE +BF .请回答:在图2中,∠GAF 的度数是 .参考小伟得到的结论和思考问题的方法,解决下列问题:(1)如图3,在直角梯形ABCD 中,AD ∥BC (AD >BC ),∠D =90°,AD =CD =10,E 是CD 上一点,若∠BAE =45°, DE =4,则BE = .(2)如图4,在平面直角坐标系xOy 中,点B 是x 轴上一 动点,且点A (3 ,2),连结AB 和AO ,并以AB 为边向上作 正方形ABCD ,若C (x ,y ),试用含x 的代数式表示y , 则y = .22. 问题探究:(1)如图1,在边长为3的正方形ABCD 内(含边)画出使∠BPC =90°的一个点P ,保留作图痕迹;(2)如图2,在边长为3的正方形ABCD 内(含边)画出使∠BPC =60°的所有的点P ,保留作图痕迹并简要说明作法;(3)如图3,已知矩形ABCD ,AB =3,BC =4,在矩形ABCD 内(含边)画出使∠BPC =60°,且使△BPC 的面积最大的所有点P ,保留作图痕迹.22.阅读下面材料:小明遇到这样一个问题:如图1,△ABO 和△CDO 均为等腰直角三角形,F ED AB C B EDA G F ED AB C C图1图2图3CDAOBx y 图4F E D A B CEDA GF E D A BC图1图2CD AOBx y 图4图3图2图1A D CBA BCD D CBA∠AOB =∠COD =90︒.若△BOC 的面积为1, 试求以AD 、BC 、OC+OD 的长度为三边长的三角形的面积.图1 图2小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他利用图形变换解决了这个问题,其解题思路是延长CO 到E , 使得OE =CO , 连接BE , 可证△OBE ≌△OAD , 从而得到的△BCE 即是以AD 、BC 、OC+OD 的长度为三边长的三角形(如图2).请你回答:图2中△BCE 的面积等于 . 请你尝试用平移、旋转、翻折的方法,解决下列问题: 如图3,已知△ABC , 分别以AB 、AC 、BC 为边向外作正方形ABDE 、AGFC 、BCHI , 连接EG 、FH 、ID .(1)在图3中利用图形变换画出并指明以EG 、FH 、ID 的长度为三边长的一个三角形(保留画图痕迹); (2)若△ABC 的面积为1,则以EG 、FH 、ID 的长度为三边长的三角形的面积等于 .图322. 阅读下列材料:问题:如图1,在正方形ABCD 内有一点P ,PA =5,PB =2,PC =1,求∠BPC 的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC 绕点B 逆时针旋转90°,得到了△BP ′A (如图2),然后连结PP ′. 请你参考小明同学的思路,解决下列问题: (1) 图2中∠BPC 的度数为 ;(2) 如图3,若在正六边形ABCDEF 内有一点P ,且PA =132,PB =4,PC =2,则∠BPC的度数为 ,正六边形ABCDEF 的边长为 .ODAIGFAB CDE图1 图2 图322.阅读下列材料:小明遇到一个问题:已知:如图1,在△ABC中,∠BAC=120°,∠ABC=40°,试过△ABC的一个顶点画一条直线,将此三角形分割成两个等腰三角形.他的做法是:如图2,首先保留最小角∠C,然后过三角形顶点A画直线交BC于点D. 将∠BAC分成两个角,使∠DAC=20°,△ABC即可被分割成两个等腰三角形.喜欢动脑筋的小明又继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.他的做法是:如图3,先画△ADC ,使DA=DC,延长AD到点B,使△BCD也是等腰三角形,如果DC=BC,那么∠CDB =∠ABC,因为∠CDB=2∠A,所以∠ABC= 2∠A.于是小明得到了一个结论:当三角形中有一个角是最小角的2倍时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.请你参考小明的做法继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.请直接写出你所探究出的另外两条结论(不必写出探究过程或理由).12.如图,直角三角形纸片ABC中,∠ACB=90°,AC=8,BC=6.折叠该纸片使点B与点C重合,折痕与AB、BC的交点分别为D、E. (1) DE的长为;(2) 将折叠后的图形沿直线AE剪开,原纸片被剪成三块,其中最小一块的面积等于.CB A D22.将矩形纸片分别沿两条不同的直线剪两刀,可以使剪得的三块纸片恰能拼成一个等腰三 角形(不能有重叠和缝隙). 小明的做法是:如图1所示,在矩形ABCD 中,分别取AD 、AB 、CD 的中点P 、E 、 F ,并沿直线PE 、PF 剪两刀,所得的三部分可拼成等腰三角形△PMN (如图2). (1)在图3中画出另一种剪拼成等腰三角形的示意图;(2)以矩形ABCD 的顶点B 为原点,BC 所在直线为x 轴建立平面直角坐标系(如图4),矩形ABCD 剪拼后得到等腰三角形△PMN ,点P 在边AD 上(不与点A 、D 重合),点M 、N 在x 轴上(点M 在N 的左边).如果点D 的坐标为(5,8),直线PM 的解析式为=y kx b ,则所有满足条件的k 的值为 .图4 备用12.如图,在正方形ABCD 中,AB =1,E 、F 分别是BC 、CD 边上点,(1)若CE =12CB ,CF =12CD ,则图中阴影部分的面积是 ;(2)若CE =1nCB ,CF =1nCD ,则图中阴影部分的面积是 (用含n 的式子表示,n 是正整数).P E FDA P E F D A BCA。
#北京海淀2012年高考一模试题和答案(理科全套)

北京海淀2012年高考一模语文试题第Ⅰ卷(选择题共27分)一、本大题共5小题,每小题3分,共15分。
1.下列词语中,字形和加点的字的读音全部正确的一项是()A.镌刻余音绕粱牵掣(zhi) 揆情度(duo)理B.观瞻激浊扬清商贾(gu) 良莠不齐C.棉薄两袖清风迄(qi)今矫(jiao)揉造作D. 斧正闻过饰非聒(guo)噪若即(ji)若离2.下列句子中,加点的成语使用不恰当的是()A.春天的颐和园,小草带着泥土的芬芳钻了出来,柳枝之昆明湖畔轻轻摇曳,桃花在枝头尽情绽放,真是秀色可餐。
B.中华民族几千年的文明积淀和不绝如缕的文化传统,是我国新时期文化发展的起点,是我们民生振兴的基石。
C.在全球经济一体化的浪潮下,一个经济体爆发危机,就会冲击到其他经济体,因此,任何开放国家都难以独善其身。
D.福岛核事故发生一周年之际,日本政府首次组织记者进入核电站采访,让他们按照规定路线走马观花的转了一遭。
3.下列句子中,没有语病的一句是()A.虽然中国公民在苏丹遭劫持是一起偶发事件,但中国公民出国要清楚的了解海外安全形势,防止各类安全风险,采取有效措施。
B.男子网坛两大巨头的决战持续近六小时,成为史上最长的大满贯决赛展现观众面前,这场决赛开启了世界男子网球赛的新时代。
C.文物局提出针对当前首都城市的发展和古都名城的保护,相关单位应加强文物保护力度,落实各项监管责任。
D.麦当劳(中国)有限公司销售过期食品,国家食品监管安全司要求其立即进行整改,以防止此类问题再次出现。
4.下列有关文学常识的表述,有错误的一项是()A.中国第一部纪传体通史《史记》是由司马迁撰写的,后人称赞它“不虚美,不隐恶”,具有秉笔直书的“实录”精神。
B.诸葛亮的《出师表》、李密的《陈情表》分别体现了中国古代文化中的忠、孝传统,这两篇文章言辞恳切,感人至深。
C.巴金的《家》描写了一个封建大家庭的分化和没落,反映了封建宗法制度的崩溃,它奠定了巴金在中国文坛上的巨匠地位。
(5)2012年北京市各城区一模试题压轴题汇编.几何综合
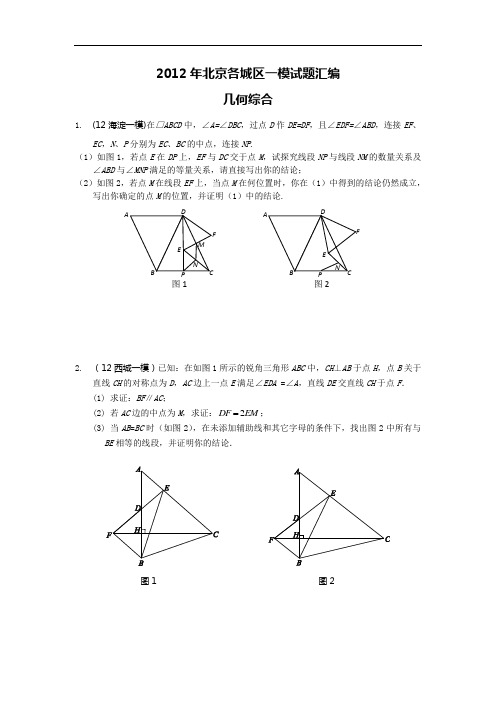
2012年北京各城区一模试题汇编几何综合1. (12海淀一模)在□ABCD 中,∠A=∠DBC ,过点D 作DE=DF ,且∠EDF=∠ABD ,连接EF 、EC ,N 、P 分别为EC 、BC 的中点,连接NP .(1)如图1,若点E 在DP 上,EF 与DC 交于点M ,试探究线段NP 与线段NM 的数量关系及∠ABD 与∠MNP 满足的等量关系,请直接写出你的结论;(2)如图2,若点M 在线段EF 上,当点M 在何位置时,你在(1)中得到的结论仍然成立,写出你确定的点M 的位置,并证明(1)中的结论.2. (12西城一模)已知:在如图1所示的锐角三角形ABC 中,CH ⊥AB 于点H ,点B 关于直线CH 的对称点为D ,AC 边上一点E 满足∠EDA =∠A ,直线DE 交直线CH 于点F . (1) 求证:BF ∥AC ;(2) 若AC 边的中点为M ,求证:2DF EM ;(3) 当AB =BC 时(如图2),在未添加辅助线和其它字母的条件下,找出图2中所有与BE 相等的线段,并证明你的结论.图1 图2图2图13. (12丰台一模) 已知:△ABC 和△ADE 是两个不全等的等腰直角三角形,其中BA =BC ,DA =DE ,联结EC ,取EC 的中点M ,联结BM 和DM .(1)如图1,如果点D 、E 分别在边AC 、AB 上,那么BM 、DM 的数量关系与位置关系是 ;(2)将图1中的△ADE 绕点A 旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.C B AEMMEABC4. (12石景山一模)(1)如图1,在矩形ABCD 中,AB=2BC ,M 是AB 的中点.直接写出∠BMD 与∠ADM 的倍数关系;(2)如图2,若四边形ABCD 是平行四边形, AB=2BC ,M 是AB 的中点,过C 作CE ⊥AD 与AD 所在直线交于点E .①若∠A 为锐角,则∠BME 与∠AEM 有怎样的倍数关系,并证明你的结论; ②当︒<∠<︒A 0时,上述结论成立;当︒<∠≤︒180A 时,上述结论不成立.M D BA CEADC5. (12昌平一模)如图,在四边形ABCD 中,对角线AC 、BD 相交于点O ,直线MN 经过点O ,设锐角∠DOC =∠α,将△DOC 以直线MN 为对称轴翻折得到△D ’OC ’,直线A D ’、B C ’相交于点P .(1)当四边形ABCD 是矩形时,如图1,请猜想A D ’、B C ’的数量关系以及∠APB 与∠α 的大小关系;(2)当四边形ABCD 是平行四边形时,如图2,(1)中的结论还成立吗?(3)当四边形ABCD 是等腰梯形时,如图3,∠APB 与∠α 有怎样的等量关系?请证明.图3图2图1D CBANC'OMPD'D CBAN C'O MPD'D'PMOC'N A BCD6. (12平谷一模)如图,已知四边形ABCD 是正方形,对角线ACBD 相交于O .(1) 如图1,设 E 、F 分别是AD 、AB 上的点,且∠EOF =90°,线段AF 、BF 和EF 之间存在一定的数量关系.请你用等式直接写出这个数量关系;(2) 如图2,设 E 、F 分别是AB 上不同的两个点,且∠EOF =45°,请你用等式表示线段AE 、BF 和EF 之间的数量关系,并证明. 图 1图 2F ODBACAE图1图 2A7. (12延庆一模) 如图1,已知:已知:等边△ABC ,点D 是边BC 上一点(点D 不与点B 、点C 重合),求证:BD+DC > AD 下面的证法供你参考:把ACD ∆绕点A 瞬时间针旋转60得到ABE ∆,连接ED ,则有ABE ACD ∆≅∆,DC=EB∵AD=AE,60=∠DAE ∴ADE ∆是等边三角形 ∴AD=DE在DBE ∆中,BD+EB > DE 即:BD+DC >AD实践探索:请你仿照上面的思路,探索解决下面的问题: (1)如图2,点D 是等腰直角三角形△ABC边上的点(点D 不与B 、C 重合),求证:BD+DC>2AD(2) 如果点D 运动到等腰直角三角形△ABC 外或内时,BD 、DC 和AD 之间又存在怎样的数量关系? 直接写出结论.创新应用:(3) 已知:如图3,等腰△ABC 中, AB=AC ,且∠BAC=α(α为钝角), D 是等腰△ABC 外一点,且∠BDC+∠BAC =180º, BD 、DC 与AD 之间存在怎样的数量关系?写出你的猜想,并证明.DA图3CA图1CBD图28. (12房山一模)如图1,在△ABC 中,∠ACB =90°,AC =BC =5,以点B 为圆心,以2为半径作圆.⑴设点P 为☉B 上的一个动点,线段CP 绕着点C 顺时针旋转90°,得到线段CD ,联结DA ,DB ,PB ,如图2.求证:AD =BP ;⑵在⑴的条件下,若∠CPB =135°,则BD =___________;⑶在⑴的条件下,当∠PBC =_______° 时,BD 有最大值,且最大值为__________;当∠PBC =_________° 时,BD 有最小值,且最小值为__________.图1BC图2DCBP9. (12密云一模)已知:正方形ABCD 中,45MAN ∠=,绕点A 顺时针旋转,它的两边分别交CB 、DC (或它们的延长线)于点M 、N .(1)如图1,当MAN ∠绕点A 旋转到BM DN =时,有BM DN MN +=.当MAN ∠ 绕点A 旋转到BM DN ≠时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)当MAN ∠绕点A 旋转到如图3的位置时,线段BM DN ,和MN 之间有怎样的等量关系?请写出你的猜想,并证明.10. (12通州一模)已知四边形ABCD ,点E 是射线BC 上的一个动点(点E 不与B 、C两点重合),线段BE 的垂直平分线交射线AC 于点P ,联结DP ,PE. (1)若四边形ABCD 是正方形,猜想PD 与PE 的关系,并证明你的结论.(2)若四边形ABCD 是矩形,(1)中的PD 与PE 的关系还成立吗? (填:成立或不成立).(3)若四边形ABCD 是矩形,AB =6,cos ∠ACD =35,设AP=x ,△PCE 的面积为y ,当AP>12AC时,求y 与x 之间的函数关系式.11. (12东城一模) 已知∠ABC =90°,点P 为射线BC 上任意一点(点P 与点B 不重合),分别以AB 、AP 为边在∠ABC 的内部作等边△ABE 和△APQ,连结QE 并延长交BP 于点F . (1)如图1,若AB =32,点A 、E 、P 恰好在一条直线上时,求此时EF 的长(直接写出结果);(2)如图2,当点P 为射线BC 上任意一点时,猜想EF 与图中的哪条线段相等(不能添加辅助线产生新的线段),并加以证明;(3)若AB =32,设BP =x ,以QF 为边的等边三角形的面积y ,求y 关于x 的函数关系式.A DB CA D12. (12朝阳一模) 在矩形ABCD 中,点P 在AD 上,AB =2,AP =1,将三角板的直角顶点放在点P 处,三角板的两直角边分别能与AB 、BC 边相交于点E 、F ,连接EF . (1)如图,当点E 与点B 重合时,点F 恰好与点C 重合,求此时PC 的长;(2)将三角板从(1)中的位置开始,绕点P 顺时针旋转,当点E 与点A 重合时停止,在这个过程中,请你观察、探究并解答: ① ∠PEF 的大小是否发生变化?请说明理由;② 直接写出从开始到停止,线段EF 的中点所经过的路线长.13. (12大兴一模)已知:如图,N 、M 是以O 为圆心,1为半径的圆上的两点,B 是MN 上一动点(B 不与点M 、N 重合),∠MON=90°,BA ⊥OM 于点A ,BC ⊥ON 于点C ,点D 、E 、F 、G 分别是线段OA 、AB 、BC 、CO 的中点,GF 与CE 相交于点P ,DE 与AG 相交于点Q .(1)四边形EPGQ (填“是”或者“不是”)平行四边形; (2)若四边形EPGQ 是矩形,求OA 的值; (3)连结PQ ,求223PQ OA 的值.14. (12顺义一模)问题:如图1, 在Rt △ABC 中,90C ∠=︒,30ABC ∠=︒,点D 是射线CB 上任意一点,△ADE 是等边三角形,且点D 在ACB ∠的内部,连接BE .探究线段BE 与DE 之间的数量关系. 请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.(1) 当点D 与点C 重合时(如图2),请你补全图形.由BAC ∠的度数为 ,点E 落在 ,容易得出BE 与DE 之间的数量关系为 ; (2) 当点D 在如图3的位置时,请你画出图形,研究线段BE 与DE 之间的数量关系是否与(1)中的结论相同,写出你的猜想并加以证明.图1D EBCADB C AABC (D )图图2D B CA 图315. (12门头沟一模)已知:在△ABC 中,BC =2AC ,∠DBC =∠ACB ,BD =BC ,CD 交线段AB于点E .(1)如图l ,当∠ACB =90°时,直接写出线段DE 、CE 之间的数量关系; (2)如图2,当∠ACB =120°时,求证:DE =3CE ;(3)如图3,在(2)的条件下,点F 是BC 边的中点,连接DF ,DF 与AB 交于G ,△DKG和△DBG 关于直线DG 对称(点B 的对称点是点K ),延长DK 交AB 于点H .若BH =10,求CE 的长.图 1EDACB图 2EDACBF G KH图 3EDACB16. (12怀柔一模)探究:(1)如图1,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45°,试判断BE 、DF 与EF 三条线段之间的数量关系,直接写出判断结果: ; (2)如图2,若把(1)问中的条件变为“在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E 、F 分别是边BC 、CD 上的点,且∠EAF=21∠BAD ”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;(3)在(2)问中,若将△AE F 绕点A 逆时针旋转,当点分别E 、F 运动到BC 、CD 延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明..17. (12燕山一模)已知:如图,点P 是线段AB 上的动点,分别以AP 、BP 为边向线段AB的同侧作正△APC 和正△BPD ,AD 和BC 交于点M.(1)当△APC 和△BPD 面积之和最小时,直接写出AP : PB 的值和∠AMC 的度数; (2)将点P 在线段AB 上随意固定,再把△BPD 按顺时针方向绕点P 旋转一个角度α,当α<60°时,旋转过程中,∠AMC 的度数是否发生变化?证明你的结论.(3)在第(2)小题给出的旋转过程中,若限定60°<α<120°,∠AMC 的大小是否会发生变化?若变化,请写出∠AMC 的度数变化范围;若不变化,请写出∠AMC 的度数.CM DA P B。
2012北京市各区中考数学一模试卷及答案试题试卷_1 (2)

顺义区2012届初三第一次统一练习 数学学科参考答案及评分细则二、填空题(本题共16分,每小题4分,)9.4;10.25()x x y -; 11.11.4; 12, 2)π+,π. 三、解答题(本题共30分,每小题5分) 13()12cos303-︒+--1213⎛⎫=+-- ⎪⎝⎭……………………………………………… 4分 113=+ 43= …………………………………………………………………… 5分 14.解: 221x y x y +=⎧⎨-=⎩①②①+②,得 33x =.1x =. …………………………………………………… 2分 把1x =代入①,得 12y +=.1y =. ………………………………………………………… 4分 ∴原方程组的解为 1,1.x y =⎧⎨=⎩ ………………………………………………… 5分15.证明:∵AB=AC ,∴B C ∠=∠. …………………………………………………………… 1分 在△ABD 和△ACE 中,,,,AB AC B C BD CE =⎧⎪∠=∠⎨⎪=⎩∴ △ABD ≌△ACE .……………………………………………………… 3分 ∴ AD=AE . ……………………………………………………………… 4分∴∠ADE =∠AED . ……………………………………………………… 5分16.解:6931x x x x -⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭2693x x x x x -+-=÷ …………………………………………………… 2分 2(3)3x xx x -=-3x =- ……………………………………………………………………… 4分当2012x =时,原式=201232009-=.…………………………………… 5分17.解:(1)∵点(4,)A m 在反比例函数4y x=(0x >)的图象上, ∴414m ==. …………………………………………………………… 1分 ∴(4,1)A .将(4,1)A 代入一次函数y x b =-+中,得 5b =.∴一次函数的解析式为5y x =-+. …………………………………… 2分(2)由题意,得 (0,5)B , ∴5OB =.设P 点的横坐标为P x .∵OBP △的面积为5, ∴1552p x ⨯=.…………………………………………………………… 3分 ∴2P x =±.∴点P 的坐标为(2,3)或(-2,7). ………………………………… 5分 18.解:设A 户型的每户窗户改造费用为x 元,则B 户型的每户窗户改造费用为(500)x -元. ……………………………… 1分 根据题意,列方程得5400004800005x x =-. 解得 4500x =.经检验,4500x =是原方程的解,且符合题意.…………………………… 4分 ∴5004000x -=.答:A 户型的每户窗户改造费用为4500元,B 户型的每户窗户改造费用为4000 元.…………………………………… 5分MF EDCBAFE DCO BA四、解答题(本题共20分,每小题5分)19.解:(1)∵在□ABCD 中,∠B=60°,AB=4,∠ACB=45°,∴∠D=60°,CD=AB=4,AD ∥BC . ……………………………… 1分 ∴∠DAC=45°. 过点C 作CM ⊥AD 于M , 在Rt △CDM 中,sin 4sin 6023CM CD D ==︒=cos 4cos602DM CD D ==︒=.………………………………… 2分在Rt △ACM中,∵∠MAC=45°, ∴AM CM==∴2AD AM DM =+=.…………………………………… 3分∵EF ⊥AD ,CM ⊥AD , ∴EF ∥CM .∴12EF CM ==在Rt △AEF 中,AF EF ==4分∴22DF AD AF =-=-=.……………………… 5分20.(1)证明:连结OD .∵AB 是⊙O 的直径,∴∠ADB=90°. ……………………………………………………… 1分 ∵∠A=30°, ∴∠ABD=60°.∴∠BDC =1302ABD ∠=︒. ∵OD=OB ,∴△ODB 是等边三角形. ∴∠ODB=60°.∴∠ODC=∠ODB+∠BDC =90°. 即OD ⊥DC .∴CD 是⊙O 的切线.…………………………………………………… 2分(2)解:∵OF ∥AD ,∠ADB=90°,∴OF ⊥BD ,∠BOE=∠A =30°. ……………………………………… 3分∴112DE BE BD ===. 在Rt △OEB中,OB=2BE=2,OE ==.………… 4分 ∵OD=OB=2,∠C=∠ABD -∠BDC =30°,∠DOF=30°, ∴CD =tan 30DF OD =︒=∴CF CD DF =-== ……………………………5分21.解:(1)此次共调查了100名学生. …………………………………………………1分(2)填表:…………………………………………………3分(3)补全统计图如下:到校方式条形统计图 到校方式扇形统计图.…………………………………………………………………………5分22.解:(1)四边形DFCE 的面积S = 6 ,△DBF 的面积1S = 6 ,△ADE 的面积2S = 32 . …………………………………… 3分(2)2S = 214S S (用含S 、1S 的代数式表示). ………… 4分 (3)□DEFG 的面积为12. ………………………………………… 5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.解:(1)△=244(1)(3)k k k --+=2244812k k k --+=812k -+ ……………………………………………………………… 1分∵方程有两个不相等的实数根, ∴10,0.k -≠⎧⎨∆>⎩ 即 10,8120.k k -≠⎧⎨-+>⎩∴k 的取值范围是32k <且1k ≠. …………………………………… 3分 (2)当方程有两个相等的实数根时,△=812k -+=0.∴32k =. ………………………………………………………………… 4分 ∴关于y 的方程为2(6)10y a y a +-++=.∴2'(6)4(1)a a ∆=--+2123644a a a =-+--21632a a =-+2(8)32a =--.由a 为正整数,当2(8)32a --是完全平方数时,方程才有可能有整数根. 设22(8)32a m --=(其中m 为整数),32p q =(p 、q 均为整数), ∴22(8)32a m --=.即(8)(8)32a m a m -+--=.不妨设8,8.a m p a m q -+=⎧⎨--=⎩两式相加,得 162p q a ++=.∵(8)a m -+与(8)a m --的奇偶性相同,∴32可分解为216⨯,48⨯,(2)(16)-⨯-,(4)(8)-⨯-, ∴18p q +=或12或18-或12-.∴17a =或14或1-(不合题意,舍去)或2.当17a =时,方程的两根为1172y -±=,即12y =-,29y =-.…… 5分 当14a =时,方程的两根为822y -±=,即13y =-,25y =-.…… 6分当2a =时, 方程的两根为422y ±=,即13y =,21y =. ………… 7分24.解:(1)∵抛物线y =mx 2+2mx +n 经过点A (-4,0)和点B (0,3),∴1680,3.m m n n -+=⎧⎨=⎩ ∴3,83.m n ⎧=-⎪⎨⎪=⎩. ∴抛物线的解析式为:233384y x x =--+.………………………… 2分 (2)令3y =,得2333384x x --+=,得10x =,22x =-, ∵抛物线向右平移后仍经过点B ,∴抛物线向右平移2个单位.……… 3分∵233384y x x =--+ 233(21)388x x =-++++2327(1)88x =-++. ………… 4分∴平移后的抛物线解析式为2327(1)88y x =--+. …………………… 5分(3)由抛物线向右平移2个单位,得'(2,0)A -,'(2,3)B .∴四边形AA ’B ’B 为平行四边形,其面积'236AA OB ==⨯=.设P 点的纵坐标为P y ,由'OA P △的面积=6, ∴1'62P OA y =,即1262P y ⨯= ∴6P y =, 6P y =±.………………………………………………… 6分当6P y =时,方程2327(1)688x --+=无实根, 当6P y =-时,方程2327(1)688x --+=-的解为16x =,24x =-.∴点P 的坐标为(6,6)-或(4,6)--.……………………………… 7分25.解:(1)完成画图如图2,由BAC ∠的度数为 60°,点E 落在 AB 的中点处 ,容易得出BE 与DE 之间的数量关系 为 BE=DE ;…………… 3分(2)完成画图如图3.猜想:BE DE =.证明:取AB 的中点F ,连结EF .∵90ACB ∠=︒,30ABC ∠=︒,∴160∠=︒,12CF AF AB ==. ∴△ACF 是等边三角形.∴AC AF =. ① …… 4分∵△ADE 是等边三角形,∴260∠=︒, AD AE =. ②∴12∠=∠. ∴12BAD BAD ∠+∠=∠+∠.即CAD FAE ∠=∠.③ ………………………………………… 5分 由①②③得 △ACD ≌△AFE (SAS ). …………………………… 6分 ∴90ACD AFE ∠=∠=︒. ∵F 是AB 的中点,∴EF 是AB 的垂直平分线.∴BE=AE . ……………………………………………………… 7分 ∵△ADE 是等边三角形, ∴DE=AE .∴BE DE =. …………………………………………………… 8分EAB C (D )图221F EDB C A图3。
2012北京海淀高考一模数学文(含解析)

海淀区第二学期期中练习 高三数学试卷(文科)2012.04一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|1}A x x ==,{|(2)0}B x x x =-<,那么A B I =( ). A .∅ B . {1}- C .{1} D .{1,1}-2.在等比数列{}n a 中,26a =,318a =-,则1234a a a a +++=( ).A .26B .40C .54D .803.已知向量=(12x +a ,),()=1,x -b .若a 与b 垂直,则||b =( ).A .1 BC .2D .44.过双曲线221916x y -=的右焦点,且平行于经过一、三象限的渐近线的直线方程是( ).A .34150x y +-=B .34150x y --=C .43200x y -+=D .43200x y --=5.执行如图所示的程序框图,输出的k 值是( ).A .5B .6C .7D .86.若满足条件020x y x y y a -≥⎧⎪+-≤⎨⎪≥⎩的整点(,)x y 恰有9个,其中整点是指横、纵坐标都是整数的点,则整数a 的值为( ). A .3- B . 2- C .1- D .07.已知函数2,1,()1,1,x ax x f x ax x ⎧-+≤=⎨->⎩若1212,,x x x x ∃∈≠R ,使得12()()f x f x =成立,则实数a 的取值范围是( ).A .2a <B .2a >C .22a -<<D .2a >或2a <-8.在棱长为1的正方体''''ABCD A B C D -中,若点P 是棱上一点, 则满足'2PA PC +=的点P 的个数为( ). A .4 B .6 C .8 D .12二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上. 9.复数2i1i-在复平面内所对应的点的坐标为 .10.若tan 2α=,则sin 2=α .11.以抛物线24y x =上的点0(,4)x 为圆心,并过此抛物线焦点的圆的方程是 . 12.已知三条侧棱两两垂直的正三棱锥的俯视图如图所示,那么此 三棱锥的体积是 ,左视图的面积是 .13.设某商品的需求函数为1005Q P =-,其中,Q P 分别表示需求量和价格,如果商品需求弹性EQ EP大于1(其中'EQ Q P EP Q =-,'Q 是Q 的导数),则商品价格P 的取值范围是 .14.已知函数1,,()0,.x f x x ∈⎧=⎨∈⎩R Q Q ð (Ⅰ)则()()______f f x =;(Ⅱ)下面三个命题中,所有真命题的序号是 . ①函数()f x 是偶函数;②任取一个不为零的有理数T ,()()f x T f x +=对x ∈R 恒成立;③存在三个点112233(,()),(,()),(,()),A x f x B x f x C x f x 使得ABC △为等边三角形.俯视图D ’C ’B ’A ’DCBA3 / 17三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)已知函数()sin sin()3f x x x π=+-.(Ⅰ)求()f x 的单调递增区间;(Ⅱ)在ABC △中,角A ,B ,C 的对边分别为,,a b c .已知()f A =a =, 试判断ABC △的形状.16.(本小题满分13分)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].Array(Ⅰ)求直方图中x的值;(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少x名学生可以申请住宿.时间5 / 1717.(本小题满分14分)已知菱形ABCD 中,4AB =,60BAD ∠=o (如图1所示),将菱形ABCD 沿对角线BD 翻折,使点C 翻折到点1C 的位置(如图2所示),点,,E F M 分别是11,,AB DC BC 的中点.(Ⅰ)证明:BD ∥平面EMF ; (Ⅱ)证明:1AC BD ⊥;(Ⅲ)当EF AB ⊥时,求线段1AC 的长.E 图2图1AMF C 1D B ACBD18.(本小题满分13分)已知函数211()ln (0)22f x a x x a a =-+∈≠R ,.(Ⅰ)求()f x 的单调区间;(Ⅱ)是否存在实数a ,使得对任意的[)1,x ∈+∞,都有()0f x ≤?若存在,求a 的取值范围;若不存在,请说明理由.7 / 1719.(本小题满分13分)已知椭圆2222: 1 (0)x yC a ba b+=>>的右顶点(2,0)A O为坐标原点.(Ⅰ)求椭圆C的方程;(Ⅱ)已知P(异于点A)为椭圆C上一个动点,过O作线段AP的垂线l交椭圆C于点,E D,求DEAP的取值范围.20.(本小题满分14分)对于集合M ,定义函数1,,()1,.M x M f x x M -∈⎧=⎨∉⎩对于两个集合M ,N ,定义集合{()()1}M N M N x f x f x ∆=⋅=-. 已知{}246810A =,,,,,{}124816B =,,,,.(Ⅰ)写出(1)A f 和(1)B f 的值,并用列举法写出集合A B ∆; (Ⅱ)用()Card M 表示有限集合M 所含元素的个数.(ⅰ)求证:当()()Card X A Card X B ∆+∆取得最小值时,2X ∈; (ⅱ)求()()Card X A Card X B ∆+∆的最小值.9 / 17海淀区第二学期期中练习高三数学试卷(文科)参考答案及评分标准一.选择题:本大题共8小题,每小题5分,共40分.二.填空题:本大题共6小题,每小题5分,共30分. 9.(1,1)- 10.4511.22(4)(4)25x y -+-= 12 ;13.(10,20) 14.1;①②③ 三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)(Ⅰ)解:()sin sin()3f x x x π=+-1sin sin 2x x x =+- ………………………………………2分3sin 2x x =1cos 2x x ⎫-⎪⎪⎭)6x π-.…………………………………4分由22,262k x k k ππππ-<-<π+∈Z ,得:222,33k x k k πππ-<<π+∈Z .所以()f x 的单调递增区间为2(2,2)33k k πππ-π+,k ∈Z .……………6分(Ⅱ)解:因为()f A =)6A π-=.所以1sin()62A π-=.…………………………7分因为 0A <<π,所以 5666A ππ-<-<π.所以 3A π=. …………………………………9分因为 sin sin a b A B=,a =, 所以 1sin 2B =. ………………………………………11分因为a b >,3A π=,所以6B π=.所以2C π= .所以ABC △为直角三角形. ………………………………………13分16.(本小题满分13分) (Ⅰ)解:由直方图可得200.025200.0065200.0032201x ⨯+⨯+⨯+⨯⨯=.所以0.0125x =. …………………………………6分(Ⅱ)解:由直方图可知,新生上学所需时间不少于1小时的频率为:0.003220=0.12⨯⨯.………………………………………9分因为6000.1272⨯=.所以600名新生中有72名学生可以申请住宿.…………………………13分17.(本小题满分14分)(Ⅰ)证明:因为点,F M 分别是11,C D C B 的中点,所以FM BD ∥. ………………………………………2分 又FM ⊂平面EMF ,BD ⊄平面EMF ,所以BD ∥平面EMF . ………………………………………4分 (Ⅱ)证明:在菱形ABCD 中,设O 为,AC BD 的交点,则AC BD ⊥. ………………………………5分 所以在三棱锥1C ABD -中,1,C O BD AO BD ⊥⊥.又1,C O AO O =I所以BD ⊥平面1AOC . ………………7分 又1AC ⊂平面1AOC ,所以BD ⊥1AC . ………………………9分 (Ⅲ)解:连结1,DE C E .在菱形ABCD 中,,60DA AB BAD =∠=o ,所以ABD △是等边三角形.所以DA DB =. ………………………10分 因为E 为AB 中点,所以 DE AB ⊥. 又EF AB ⊥,EF DE E =I .所以AB ⊥平面DEF ,即AB ⊥平面1DEC .…12分O EMFC 1DB AEMF C 1DBA11 / 17又1C E ⊂平面1DEC , 所以AB ⊥1C E .因为,4AE EB AB ==,1BC AB =,所以114AC BC ==. ……………………………………14分 18.(本小题满分13分)(Ⅰ)解:()f x 的定义域为(0,)+∞.2'()a x af x x x x-+=-=. ………………………………………2分当0a <时,在区间(0,)+∞上,'()0f x <.所以()f x 的单调递减区间是(0,)+∞. ………………………………………3分 当0a >时,令'()0f x =得x =x =. 函数()f x ,'()f x 随x 的变化如下:所以()f x 的单调递增区间是,单调递减区间是)+∞.…………6分 综上所述,当0a <时, ()f x 的单调递减区间是(0,)+∞;当0a >时,()f x 的单调递增区间是,单调递减区间是)+∞. (Ⅱ)由(Ⅰ)可知:当0a <时, ()f x 在[1,)+∞上单调递减.所以()f x 在[1,)+∞上的最大值为(1)0f =,即对任意的[1,)x ∈+∞,都有()0f x ≤. ……………………………7分当0a >时,1,即01a <≤时,()f x 在[1,)+∞上单调递减.所以()f x 在[1,)+∞上的最大值为(1)0f =,即对任意的[1,)x ∈+∞,都有()0f x ≤. ………………………………10分1>,即1a >时,()f x 在[1上单调递增, 所以(1)f f >. 又(1)0f =,所以0f >,与对于任意的[1,)x ∈+∞,都有()0f x ≤矛盾.………12分 综上所述,存在实数a 满足题意,此时a 的取值范围是(,0)(0,1]-∞U .……13分19.(本小题满分13分)(Ⅰ)解:因为(2,0)A 是椭圆C 的右顶点,所以2a =.又c a =,所以c 所以222431b a c =-=-=.所以椭圆C 的方程为2214x y +=. ………………………3分(Ⅱ)当直线AP 的斜率为0时,||4AP =,DE 为椭圆C 的短轴,则||2DE =.所以||1||2DE AP =. …………………5分 当直线AP 的斜率不为0时,设直线AP 的方程为(2)y k x =-,00(,)P x y ,则直线DE 的方程为1y x k=-. ……………6分由22(2),14y k x x y =-⎧⎪⎨+=⎪⎩得224[(2)]40x k x +--=. 即2222(14)161640k x k x k +-+-=.所以202162.41k x k +=+ 所以20282.41k x k =+- …………………8分所以||AP即||AP =类似可求||DE =所以2||||DE AP = ………………………………11分设t =则224k t =-,2t >.13 / 1722||4(4)1415(2).||DE t t t AP t t-+-==> 令2415()(2)t g t t t -=>,则22415'()0t g t t+=>. 所以 ()g t 是一个增函数.所以2||41544151||22DE t AP t -⨯-=>=. 综上,||||DE AP 的取值范围是1[,)2+∞. ………………………………13分 (20)(本小题满分14分)(Ⅰ)解:(1)=1A f ,(1)=1B f -,{1,6,10,16}A B ∆=.………………………3分 (Ⅱ)解:设当()()Card X A Card X B ∆+∆取到最小值时,X W =.(ⅰ)证明:假设2W ∉,令{2}Y W =U .那么 ()()Card Y A Card Y B ∆+∆()1()1C a r d W A C a r d W B =∆-+∆-()()C a r d W A C a r d W B <∆+∆.这与题设矛盾.所以 2W ∈,即当()()Card X A Card X B ∆+∆取到最小值时,2X ∈.………7分 (ⅱ)同(ⅰ)可得:4W ∈且8W ∈.若存在a X ∈且a A B ∉U ,则令{}X Z a =ð. 那么()()Card Z A Card Z B ∆+∆()1()1C a r d X A C a r d X B =∆-+∆-()()C a r d X A C a r d X B <∆+∆.所以 集合W 中的元素只能来自A B U .若a A B ∈U 且a A B ∉I ,同上分析可知:集合X 中是否包含元素a ,()()Card X A Card X B ∆+∆的值不变.综上可知,当W 为集合{}161016,,,的子集与集合{}248,,的并集时,()()Card X A Card X B ∆+∆取到最小值4. ………………………14分北京市海淀区高三统一测试 数学(文科)选填解析一、 选择题 1.【答案】C【解析】解:由题可知{}1,1A =-,()0,2B =,故{}1A B =I ,满足题意. 故选C .2.【答案】B【解析】解:由题意得16a q =,2118a q =-,可得12a =-,3q =-, 故123426185440a a a a +++=-+-+=. 故选B .3.【答案】B【解析】解:因为a 与b 垂直,则()()1,21,120x x x x ⋅=+⋅-=--+=a b ,即1x =,所以b 故选B .4.【答案】D【解析】解:可知双曲线的5c =,故右焦点为()5,0, 经过一、三象限的渐近线的方程为43y x =, 故所求直线的斜率为43, 由点斜式可知()4053y x -=-.故选D .5.【答案】A【解析】解:如下列表故输出为5.15 / 17故选A .6.【答案】C【解析】解:如图可知当1a =-时,若满足条件020x y x y y a -≥⎧⎪+-≤⎨⎪≥⎩的整点(,)x y 恰有9个.故选C .7.【答案】A【解析】解:本题可采用数形结合和分类讨论的方式得到结论,但对于小题,特征法排除法更有效, 当0a =时,如图一满足题意,故可排除B ,D ;当3a =-时,如图二满足题意. 故选A .8.【答案】B【解析】解:讨论可分为四组:第一组AB,AD,AA',当点P 与点A 重合时'PA PC +P 与点,,B D A '重合时'PA PC +取到最大值1,故在三条棱上各存在一点满足'2PA PC +=;第二组CC ,C D ,C B ''''',与第一组同理可知CC ,C D ,C B '''''各存在一点满足'2PA PC+=;第三组BC ,当点P 与点B 或C重合时'PA PC +取到最大值1当点P 为点BC 的 中点时'PA PC +2,故在棱BC 上不存在满足条件的点; 第四组A D '',讨论与第三组一样,在棱A D ''上不存在满足条件的点; 综上,共有六点满足题意. 故选B .二、 填空题 9.【答案】(1,1)-图一【解析】解:由2i 2i 1i 22i 1i 1i 1i 1i 2+-+=⋅==-+--+, 复数2i1i-在复平面内所对应的点的坐标为(1,1)-. 故答案为(1,1)-.10.【答案】45【解析】解:2222sin cos 2tan 24sin 2sin cos tan 1415ααααααα====+++.故答案为45.11.【答案】22(4)(4)25x y -+-=【解析】解:由题可知0016=44x x ⇒=,焦点坐标为()1,0 所以满足条件的圆的圆心为()4,4,半径为5r .故答案为22(4)(4)25x y -+-=.12; 【解析】解:由题可知该立体图形的三视图 如图所示,因为,,PA PB PC 两两垂直且2AB BC CA ===,所PA PB PC ==所以1132P ABC V -=⨯⨯; 立体图形的左视图如图所示,易知PC PD ⊥,PC =1PD =,所以)112CDP S =⨯=△.; .13.【答案】(10,20)【解析】解:由题可知'511005EQ Q pP EP Q p-=-=->-, 所以22010010202020p p p p p -->⇒<⇒<<--. 故答案为(10,20).DPC PD CB A17 / 1714.【答案】1; ①②③【解析】解:(Ⅰ)1,,()0,,x f x x ∈⎧=⎨∈⎩RQ Q Q ð,()f x ∴∈Q , 故(())=1f f x ;(Ⅱ)① 正确.当x ∈Q ,则x -∈Q ,易知()()1f x f x =-=; 当x ∈R Q ð,则x -∈R Q ð,易知()()0f x f x =-=, 综上()()()f x f x x =-∈R .② 正确.因为x ∈Q 或x ∈R Q ð,T ∈Q ,所以x T +∈Q 或x T +∈R Q ð, 故()()f x T f x +=对x ∈R 恒成立.当以90BAC ∠=o 时,则()11(,1)A x x ∈Q ,()22(,0)B x x ∈R Q ð,()33(,0)C x x ∈R Q ð为顶点, 易知121x x -=,与已知矛盾(1x ∈R Q ð,2x ∈Q ,3x ∈Q 同理可证);当以11190B AC ∠=o时,则()111(,1)A x x ∈R Q ð,()122(,0)B x x∈R Q ð,()133(,0)C x x ∈Q 为顶 点,易知12x x =,与已知矛盾(1x ∈Q ,2x ∈Q ,3x∈R Q ð同理可证); ③ 正确.如图设()22(,1)C x x ∈Q , ()11(,0)A x x ∈R Q ð,()22(,0)B x x ∈R Q ð,为顶点的等边三角形,由题可知 212x x -==,不妨设(1,1)C , (1A ,(1B ,满足题意. (1x ∈Q ,2x ∈Q ,3x ∈R Q ð同理可证). 故答案为1; ①②③.。
[数学]2012年北京各城区中考一模数学试题汇编
![[数学]2012年北京各城区中考一模数学试题汇编](https://img.taocdn.com/s3/m/e0e170791ed9ad51f01df2f2.png)
2012年北京各城区一模试题汇编第8题汇总:1.(12海淀一模)2.(12西城一模)对于实数c 、d ,我们可用min{ c ,d }表示c 、d 两数中较小的数,如min{3,1-}=1-.若关于x 的函数y = min{22x ,2()a x t -}的图象关于直线3x =对称,则a 、t 的值可能是A .3,6B .2,6- C.2,6 D .2-,63.(12丰台一模)如图,矩形ABCD 中,AB =3,BC =5,点P 是BC 边上的一个动点(点P 不与点B 、C 重合),现将△PCD 沿直线PD 折叠,使点C 落到点C’处;作∠BPC’的角平分线交AB 于点E .设BP =x ,BE =y ,则下列图象中,能表示y 与x 的函数关系的图象大致是A .B .C .D .E PC’A DBCA 、CA第8题图D7.(12延庆一模) 将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的A .面CDHEB .面BCEFC .面ABFGD .面ADHG8.(12房山一模) 如图,梯形ABCD 中,AB ∥CD ,∠A =30°,∠B =60°,AD =32,CD =2,点P 是线段AB 上一个动点,过点P 作PQ ⊥AB 于P ,交其它边于Q ,设BP 为x ,△BPQ 的面积为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( ).xy 6312O xy 6312O A Bxy 6312O xy 6312O C D9.(12密云一模)在正方体的表面上画有如图⑴中所示的粗线,图⑵是其展开图的示意图,但只在A 面上画有粗线,那么将 图⑴中剩余两个面中的粗线画入图⑵中,画法正确的是10.(12通州一模)如图,在平行四边形ABCD中,AC = 4,BD = 6,P是BD上的任一点,过P作EF∥AC,与平行四边形的两条边分别交于点E,F.设BP=x,EF=y,则能大致反映y与x之间关系的图象为()A B C D11.(12顺义一模)12.(12东城一模)如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B点运动,同时动点N自A点出发沿折线AD—DC—CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是A B C D13.(12朝阳一模)已知关于x 的一元二次方程02=++n mx x 的两个实数根分别为a x =1,b x =2(b a <),则二次函数n mx x y ++=2中,当0<y 时,x 的取值范围是 A .a x < B .b x > C .b x a << D .a x <或b x >第12题汇总:1.(12海淀一模)2.(12西城一模)如图,直角三角形纸片ABC 中,∠ACB =90°,AC=8,BC =6.折叠该纸片使点B 与点C 重合,折痕与AB 、BC 的交点分别为D 、E . (1) DE 的长为 ;(2) 将折叠后的图形沿直线AE 剪开,原纸片被剪成三块,其中最小一块的面积等于 .3.(12丰台一模)在数学校本活动课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A 出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D ,第二次逆时针方向跳2步到达顶点B ,第三次顺时针方向跳3步到达顶点C ,第四次逆时针方向跳4步到达顶点C ,… ,以此类推,跳动第10次到达的顶点是 ,跳动第2012次到达的顶点是 .ADCB4.(12石景山一模)一个正整数数表如下(表中下一行中数的个数是上一行中数的个数的2倍):则第4行中的最后一个数是 ,第n 行中共有 个数, 第n 行的第n 个数是 .5.(12昌平一模)己知□ABCD 中,AD =6,点E 在直线AD 上,且DE =3,连结BE 与对角线AC 相交于点M ,则MCAM= .6.(12平谷一模)abc 是一个三位的自然数,已知195abc ab a --=,这个三位数是_____________;聪明的小亮在解决这种问题时,采取列成连减竖式的方法(见右图)确定要求的自然数,请你仿照小亮的作法,解决这种问题.如果abcd 是一个四位的自然数,且2993abcd abc ab a ---=那么,这个四位数是_____________.7.(12延庆一模) 将1、2、3、6按右侧方式排列.若规定(m,n )表示第m 排从左向右第n 个数,则(7,3)所表示的数是 ;(5,2)与(20,17)表示的两数之积是111122663263323第1排第2排第3排第4排第5排8.(12房山一模)如图,已知Rt △ABC 中,∠ACB =90°,AC =6,BC = 8,过直角顶点C 作CA 1⊥AB ,垂足为A 1,再过A 1作A 1C 1⊥BC ,垂足为C 1,过C 1作C 1A 2⊥AB ,垂足为A 2,再过A 2作A 2C 2⊥BC ,垂足为C 2,…,这样一直作下去,得到了一组线段CA 1,A 1C 1,C 1A 2,A 2C 2,…,A n C n ,则A 1C 1= ,A n C n = .9.(12密云一模)在∠A (0°<∠A <90°)的内部画线段,并使线段的两端点分别落在角的两边AB 、AC 上,如图所示,从点A 1开始,依次向右画线段,使线段与线段在两端点处互相垂直,A 1A 2为第1条线段.设AA 1=A 1A 2=A 2A 3=1,则∠A = ;若记线段A 2n-1A 2n 的长度为a n (n 为正整数),如A 1A 2=a 1,A 3A 4=a 2,则此时a 2= ,a n = (用含n 的式子表示).10.(12通州一模)已知如图,△ABC 和△DCE 都是等边三角形,若△ABC 的边长为1,则△BAE 的面积是 .四边形ABCD 和四边形BEFG 都是正方形,若正方形ABCD 的边长为4,则△FAC 的面积是 .……如果两个正多边形ABCDE …和BPKGY …是正n (n ≥3)边形,正多边形ABCDE …的边长是2a ,则△KCA 的面积是 .(结果用含有a 、n 的代数式表示)ABCA 1A 2A 3A 4A 5 C 1 23 4 5 12题图第12题图E11.(12顺义一模)12.(12东城一模) 如图,正方形ABCD 的边长为10,内部有6个全等的正方形,小正方形的顶点E 、F 、G 、H 分别落在边AD 、AB 、BC 、CD 上,则DE 的长为 .13.(12朝阳一模)如图,在正方形ABCD 中,AB =1,E 、F 分别是BC 、CD 边上点,(1)若CE =12CB ,CF =12CD ,则图中阴影部分的面积是 ;(2)若CE =1n CB ,CF =1nCD ,则图中阴影部分的面积是 (用含n 的式子表示,n 是正整数).第22题汇总: 1.(12海淀一模)A2.(12西城一模)阅读下列材料:问题:如图1,在正方形ABCD内有一点P,PA=5,PB=2,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.请你参考小明同学的思路,解决下列问题:(1) 图2中∠BPC的度数为;(2) 如图3,若在正六边形ABCDEF内有一点P,且P A=132,PB=4,PC=2,则∠BPC的度数为,正六边形ABCDEF的边长为.图1 图3CB A D3.(12丰台一模) 将矩形纸片分别沿两条不同的直线剪两刀,可以使剪得的三块纸片恰能拼 成一个等腰三角形(不能有重叠和缝隙).小明的做法是:如图1所示,在矩形ABCD 中,分别取AD 、AB 、CD 的中点P 、E 、F ,并沿直线PE 、PF 剪两刀,所得的三部分可拼成等腰三角形△PMN (如图2). (1)在图3中画出另一种剪拼成等腰三角形的示意图;(2)以矩形ABCD 的顶点B 为原点,BC 所在直线为x 轴建立平面直角坐标系(如图4),矩形ABCD 剪拼后得到等腰三角形△PMN ,点P 在边AD 上(不与点A 、D 重合),点M 、N 在x 轴上(点M 在N 的左边).如果点D 的坐标为(5,8),直线PM 的解析式为=y kx b ,则所有满足条件的k 的值为 .图1 图2 图3图4 备用P E FDAPE FD A4.(12石景山一模)生活中,有人用纸条可以折成正五边形的形状,折叠过程是将图①中.(1)将,若将展开,展开后的平面图形是 ;(2)若原长方形纸条(图①)宽为2cm ,求(1)中展开后平面图形的周长(可以用三角函数表示).5.(12昌平一模) 问题探究:(1)如图1,在边长为3的正方形ABCD 内(含边)画出使∠BPC =90°的一个点P ,保留作图痕迹;(2)如图2,在边长为3的正方形ABCD 内(含边)画出使∠BPC =60°的所有的点P ,保留作图痕迹并简要说明作法;(3)如图3,已知矩形ABCD ,AB =3,BC =4,在矩形ABCD 内(含边)画出使∠BPC =60°,且使△BPC 的面积最大的所有点P ,保留作图痕迹.图① 图② 图③图3图2图1A DCBABCDD CBA图1图26.(12平谷一模)如图①,在矩形ABCD 中,将矩形折叠,使点B 落在AD (含端点)上,落点记为E ,这时折痕与边BC 或边CD (含端点)交于点F .然后再展开铺平,则以B E F 、、为顶点的BEF △称为矩形ABCD 的“折痕三角形”.(1)由“折痕三角形”的定义可知,矩形ABCD 的任意一个“折痕BEF △”一定是一个________三角形;(2)如图②,在矩形ABCD 中,24AB BC ==,,当它的“折痕BEF △”的顶点E 位于边AD 的中点时,画出这个“折痕BEF △”,并求出点F 的坐标;(3)如图③,在矩形ABCD 中,24AB BC ==,.当点F 在OC 上时,在图③中画出该矩形中面积最大的“折痕BEF △”,并直接写出这个最大面积.7.(12延庆一模)阅读下面材料:小红遇到这样一个问题,如图1:在△ABC 中,AD ⊥BC ,BD=4,DC=6,且∠BAC=45°,求线段AD 的长.图3小红是这样想的:作△ABC 的外接圆⊙O ,如图2:利用同弧所对圆周角和圆心角的关系,可以知道∠BOC=90°,然后过O 点作OE ⊥BC 于E ,作OF ⊥AD 于F ,在Rt △BOC 中可以求出⊙O 半径及 OE ,在Rt △AOF 中可以求出AF,最后利用AD=AF+DF 得以解决此题。
2012北京中考一模各区单选汇编

22. Yao Ming is my favorite star. Do you like ____?A. sheB. herC. heD. him23. Daming is in the hospital ___ his father is ill.A. becauseB. butC. andD. or24. There’re some beautiful flowers ____ our classroom.A. onB. inC. atD. of25. - Excuse me, can I sit here?- Of course you ___.A. mayB. shouldC. canD. must26. Linda is much ____ than Tom.A. tallB. tallerC. tallestD. the tallest27. Have you read ___ English stories?A. anyB. someC. fewD. many28. Our teacher often tells us ____ more books in English.A. readB. to readC. readingD. reads29. We ___ a good time last weekend.A. hadB. haveC. will haveD. have had30. Keep quiet! The children ____.A. sleptB. have sleptC. had sleptD. are sleeping31. If I have a dream, I ____ working on it seriously.A. keepB. keptC. will keepD. keeping32. This interesting story ____ by Alice last year.A. was writtenB. is writtenC. was writingD. is writing33. It’s important for us ____ more ways than knowledge itself.A. learnB. learningC. to learnD. learned34. Can you show me ____?A. where was the bookB. where the book wasC. where is the bookD. where the book is22. John is in trouble now. Let’s go and help .A. himB. hisC. herD. hers23. I was born May 14. What about you?A. atB. inC. onD. for24. Hurry up, you will be late for school.A. soB. orC. andD. but25. —do you usually go to visit your grandmother? —By bus.A. HowB. WhenC. WhereD. Why26. —Who is in your school, Mr. Wang, Mr. Gao or Miss Li?—Miss Li, of course.A. popularB. more popularC. most popularD. the most popular27. There’s in the meeting room. Shall we have a talk there?A. somebodyB. anybodyC. nobodyD. everybody28. —Must I answer the question in English?—No, you . You can answer it in Chinese.A. shouldn’tB. can’tC. mustn’tD. needn’t29. —Have you seen Mr. Smith?—Yes. Look, he the flowers in the garden.A. watersB. is wateringC. wateredD. has watered30. —My sister is ill in hospital.—I’m sorry that.A. hearB. heardC. to hearD. hearing31. Rose English since 2002. She’s got a lot of teaching experience.A. has taughtB. will teachC. teachesD. taught32. Mr. Green his lessons when I went into his office.A. preparesB. preparedC. is preparingD. was preparing33. A park here next year. Then people nearby can come for a walk.A. will buildB. will be builtC. has builtD. was built33. —Lisa, could you tell me last night?—Oh, I went to the cinema.A. where you wentB. where did you goC. where you will goD. where will you go22. I’m thirsty, Steven. Please pass ____ a bottle of water.A. mineB. IC. meD. my23. Everything begins to grow ______spring.A. inB. onC. atD. to24. I got up early this morning, ______ I didn’t catch the first bus.A. andB. butC. orD. so25. --______is it from here to the Capital Airport?--Nearly sixty kilometers.A. How longB. How muchC. How oftenD. How far26. Lisa sent for a doctor because she felt much __________.A. illB. worseC. worstD. the worst27. --______you swim? -- No, I can’t.A. CanB. MayC. MustD. Need28. My watch works very well. There is _______wrong with it.A. somethingB. anythingC. nothingD. everything29. My parents and I _______ abroad last year.A. goB. will goC. are goingD. went30. --Mark, would you like _________tennis with me after school?--Yes, I’d love to.A. playB. playingC. playedD. to play31. My cousin is a secretary. She ______in that company for over six years.A. will workB. is workingC. has workedD. works32. Their car broke down while they ________in the desert.A. droveB. were drivingC. are drivingD. will drive33. The park _________by the cleaners every two days.A. is sweptB. was sweptC. has sweptD. will sweep34. –Do you know ____________for London tomorrow?-- At 6:00 o’clock in the morning.A. when did he leaveB. when he leftC. when is he leavingD. when he is leaving22. Our classroom is ______ the second floor.A. forB. fromC. onD. to23. I got up early ______ the traffic was bad this morning.A. andB. butC. soD. or24. — ______ have you been in China?— Three years.A. How muchB. How longC. How oftenD. How far25. Our school is ______ in the town.A. largeB. largerC. largestD. the largest26. These people are good pilots. They ______ fly very well.A. canB. mayC. couldD. might27. — You must come to dinner with us.—I’m sorry, I can’t. What about _____ time?A. someB. anyC. anotherD. other28. He ______too much, so he didn’t feel well.A. ateB. eatsC. will eatD. is eating29. You can find Tom in the classroom. He _______ the window.A. is cleaningB. was cleaningC. cleanedD. clean30. Everyone wants ______ the book as soon as possible.A. readB. readsC. readingD. to read31. Bill’s uncle ______ in Beijing since last year.A. workB. workedC. has workedD. will work32. I ______ my clothes this time yesterday.A. washB. washedC. am washingD. was washing33. The computer _______ away from his room last night.A. takesB. tookC. is takenD. was taken34. I’m going to the librar y. Can you tell me _________?A. where is itB. where it isC. where was itD. where it was22. My parents gave __________ a nice toy bear for my birthday.A. IB. mineC. myD. me23 Tom and his family traveled all night to London and got there __________ Sunday morning.A. forB. onC. atD. to24. —__________ do you go to visit your grandparents? —Once a week.A. How manyB. How muchC. How oftenD. How long25. I’m hung ry. Mum, I want_____ to eat.A. everythingB. anythingC. nothingD. something26. I’d like to go shopping with you, __________ I’m too busy today.A. butB. andC. soD. or27. —How do you like Shu-How Lin?— V ery much. I think he is one of __________players in NBA now.A. the most popularB. more popularC. popularD. most popular28. --Hi, is Mr Wang in the room?-- Sorry, he isn’t in. He ____________the headmaster’s office.A. has beenB. wentC. has goneD. will go29. The children will climb the hill if it __________ tomorrow.A. won’t rainB. didn’t rainC. isn’t rainingD. doesn’t rain30. —__________ you play golf? —No. But I can play tennis.A. CanB. MayC. MustD. Should31. My little sister had a bad cold. The doctor asked her __________ in bed for a few weeks.A. stayingB. to stayC. stayedD. stays32. —Where’s your father, M ike? —He __________ in the kitchen.A. cooksB. cookedC. is cookingD. has cooked33. Today Chinese __________ by more and more people around the world.A. speakB. spokeC. was spokenD. is spoken34. —Do you know __________ the MP4 player last week?—Sorry, I have no idea.A. how much did she pay forB. how much does she pay forC. how much she paid forD. how much she pays for22. — Hi, Mary. Could you lend ______ your pen? — OK. Here you are.A. IB. meC. myD. mine23. _______ March, 12th, we planted trees in a park.A. InB. OnC. AtD. To24. — ________ did you go to the doctor, Tim? — Two weeks ago.A. HowB. WhereC. WhatD. When25. I phoned you at six yesterday evening, ______ nobody answered.A. becauseB. orC. butD. so26. — Look here, please. Who can do this problem? —I ____, Miss Li.A. canB. needC. shouldD. must27. Sam, you’re much ______ than I last saw you.A. thinB. thinnerC. thinnestD. the thinnest28. — This is a really interesting story. I enjoy________ it.A. readingB. readC. to readD. reads29. — What are the kids doing?—They ______ the flowers in the garden.A. waterB. wateredC. have wateredD. are watering30. — Jim, how about going to the movie Mission Impossible IV tonight?—Well, I ______ it already.A. seeB. sawC. have seenD. will see31. I will let you know as soon as I ______ back.A. getB. gotC. will getD. have got32. A talk on pop music ______ in the school hall next Sunday.A. is givenB. givesC. will be givenD. will give33. Look, there ______ little water in the river! How come?A. beB. amC. isD. are34. — Do you know ______ yesterday afternoon?—Sorry, I’ve no idea.A. where is TomB. where Tom isC. where was TomD. where Tom was22. Send __________a postcard from Australia when you are there.A. IB. meC. myD. mine23. – What did you do _____ April 22?-- We turned off the lights for Earth Hour.A. inB. atC. onD. for24. Hurry up, ________ you can’t finish the work on time.A. andB. soC. butD. or25. ---_________ do they go to the village school?---Once a month.A. How oftenB. How longC. How farD. How many26. E-mails are _________than letters, so they are popular among us.A. fastB. fasterC. the fastestD. fastest27. --- Can you translate the article into Chinese?--- Yes, I ________.A. needB. mustC. mayD. can28. The problem is so hard that almost _____________ can work it out.A. nobodyB. somebodyC. everybodyD. anybody29. Parents always tell me not ___________ any chance because it can help you grow up.A.to missB. missC. missingD. missed30. Ms Lee _______a good rest last night and she felt better this morning.A. hasB. hadC. is havingD. will have31. She _____________ when I saw her yesterday morning.A. runB. ranC. was runningD. has run32. Jeremy Shu-How Lin _____ in NBA since 2010.A. playB. playedC. will playD. has played33. Green products ______________by more and more people in their daily lifeA. useB. usedC. are usedD. were used34. Could you tell me _______________next summer?. A. what are you going to do B. what you are going to doC. what did you doD. what you did22.—Alice, is this your dictionary?—Let me see. Oh, no. ____is in my schoolbag.A. MyselfB. MeC. MyD. Mine23. –When was Peter born? — He was born ____ 1995.A. inB. onC. atD. for24. Lucy and Lily ____sisters. They are in the same school.A. beB. amC. isD. are25. —_____schoolbag is this ? —I guess it’s Lily’s.A. WhatB. WhoC. WhoseD. Which26.I knock at the door several times but ____answered, so I left.A. somebodyB. nobodyC. anybodyD. everybody27.—Can I wear any clothes I like to school?—No, you can’t. You ____wear your school uniform.A. canB. mayC.needD. must28. Money is important, _____it’s not the most important thing.A. andB. butC. orD. so29. I have had this novel for three weeks. I ____ it in London.A. buyB. boughtC. have boughtD. had bought30. James, I’m too tired. Let’s stop _____a rest.A. to haveB. to havingC. havingD. have31. The children _____computer games when I came in.A. playB. had playC. are playingD. were playing32. —Who runs fastest in your class?—Tom does. He always runs ____ than any other student.A. fastB. fasterC. fastestD. the fastest33.The 30th Olympic Games ____in London on July 27th, 2012.A. is heldB. will holdC. holdD. will be held34. —Lily, please tell me ______the English Party?—Next Saturday evening.A. when will you haveB. when you will haveC. when did you haveD. when you had22. This man is __________ father, Mr. Smith.A. IB. meC. myD. mine23. The students from England left Beijing __________ Saturday afternoon.A. inB. onC. atD. of24. —__________ is your sister’s school? —Between the hospital and the library.A. WhenB. WhatC. WhoD. Where25. —Which dress is __________, the red one or the blue one?—Hard to say. You decide!A. beautifulB. more beautifulC. most beautifulD. the most beautiful26. There is a strong wind, __________ I want to close all the windows.A. soB. orC. butD. because27. —There isn’t __________ in the cup, Linda. It’s empty.—Sorry, I’ll go and get something to drink now.A. everythingB. somethingC. anythingD. nothing28. —Must we clean the classroom today?—No, you __________. You can do it tomorrow morning.A. can’tB. mustn’tC. needn’tD. shouldn’t29. Tony’s mother is a teacher and she __________ lunch at school every day.A. haveB. hasC. hadD. having30. The foreign children __________ the Forbidden City last Sunday.A. visitB. visitsC. visitedD. visiting31. Look! They __________ in the river.A. swimB. swamC. have swumD. are swimming32. Miss Jackson __________ Chinese for several years.A. learnsB. learnedC. has learnedD. will learn33. The letters __________ by Ann next week.A. sendB. are sentC. will sendD. will be sent34. —Do you know ___________? —At eight yesterday morning.A. when they arrive in BeijingB. when they arrived in BeijingC. when do they arrive in BeijingD. when did they arrive in Beijing22.—Hi, Lucy, could you lend ______ your MP4?—OK, here you are.A. IB. me c. my D. mine23. The 30th London Olympic Games will be held _______ July 27, 2012.A. inB. on c. at D. from24. —_____ did your family spend New Year?—In our hometown.A. WhyB. WhenC. WhereD. How25. —Can you play the piano?—Yes , I _________ , and I’m good at it .A. mayB. canC. needD. must26. —There isn’t _______ good on TV .—Let’s go to the cinema .A. somethingB. nothingC. everythingD. anything27. The story is quite interesting , ___________ it’s too long.A. andB. orC. butD. so28. Keep quiet, please. All the students _____________ in the library now.A. are readingB. will readC. were readingD. read29. Food and vegetables are much_________ than before.A. expensiveB. most expensiveC. more expensiveD. the most expensive30. Lily _______ me a book as a birthday present tomorrow.A. givesB. will giveC. gaveD. has given31. Our teacher always tells us ___________ more English in and after class.A. speakB. spokenC. speakingD. to speak32. John’s car is not here. I think he ___________ somewhere.A. goesB. wentC. has goneD. has been33. More trees and flowers ________________in and around the city next year.A. will be plantedB. are plantingC. will plantD. are planted34. Do you know ______________ the meeting yesterday?A. where did he haveB. where he hadC. where does he haveD. where he has22. Jimmy is coming to Beijing. I’ll meet him _____the airport .A. inB. atC. byD. for23. Lin Shuhao is very popular and he’s ____ favorite basketball player.A. IB. meC. myD. mine24. ________ shall we meet after school? At the school gate.A. WhereB. WhenC. WhoD. What25. I think Zhou Libo is _____ one among all the actors in China.A. funnyB. funnierC. funniestD. the funniest26. Most of the children like to talk, _____ they don’t like to write.A. soB. andC. butD. or27. Although he’d eaten up two bowls of rice,he still didn’t feel ____.A. enough fullB. full enoughC. enough fullyD. fully enough28. Guo Mingyi is a kind-hearted man. He _____ many poor students go to school.A. helpB. will helpC. helpedD. has helped29. The refrigerator is used for_______ food and vegetables fresh.A. keepB. keepingC. keptD. keeps30. When I stepped into the classroom, I saw the teacher _____ out the test papers.A. handsB. handedC. to handD. handing31. --______ I use your computer to send an email to my friend?--Sure. Here you are.A. MayB. MustC. ShouldD. Need32. It is cooler than it was yesterday. Remember to put on more _____.A. waterB. foodC. ice-creamsD. clothes33. --When _____ the opening ceremony for London Olympic Games ____?--On July 27th ,2012.A. do; holdB. did; holdC. was; be heldD. will; be held34. --Can you tell me ______ your grandparents’ home last time?-- In my father’s car.A. how you visitB. how you visitedC. how did you visitD. how will you visit22.— I took a lot of pictures in Africa. — Really? Could you show ______ to me?A. itB. theirC. theyD. them23.— When is the Dragon Boat Festival this year? —It’s ______ June 6.A. atB. inC. onD. from24.— Would you like some more coffee? — Yes. Just ______. Thanks.A. littleB. fewC. a littleD. a few25.— ______ will your father come back from New York? — In two days.A. How longB. How soonC. How oftenD. How many26.— How is your daughter today? — Thanks to the new medicine, she feels much ____ now.A. badB. wellC. worstD. better27.There ______ a library and three bookshops in the town.A. isB. areC. beD. were28.Dentists advise people ______ too many sweets.A. to eatB. not to eatC. eatingD. not eat29.— Oh, I left my dictionary in your house. —Don’t worry. I ______ it to school tomorrow.A. will takeB. takeC. tookD. was taking30.— Your hat looks really nice. — I ______ it in a small shop last week.A. boughtB. have boughtC. will buyD. buy31.—Look! The light is still on in our teacher’s office.— Probably she ______ her work yet.A. doesn’t finishB. didn’t finishC. hasn’t finishedD. won’t finish32.— Guess what? Our team won the school basketball match.— Congratulations! You ______ be very proud.A. canB. mustC. wouldD. may33.— Teachers often say that mistakes should ______ in time.—I think so. It’s really good advice.A. correctB. be correctingC. have correctedD. be corrected34.— Mary, could you tell me ______?— One for each classroom, 50 altogether.A. how many computers did you buyB. how many computers you boughtC. where did you buy the computersD. where you bought the computers22. Mike is my good friend. He often helps _______with my English.A. IB. meC. myD. mine23. —When do you usually go to the chess club? —_______ Friday afternoon.A. AtB. InC. OfD. On24. —Can you play football? —Yes, _______ I can't play i t very well.A. butB. orC. so D . and25. —___were you late for school this morning? —Because I got up late and missed the bus.A. WhereB. WhenC. WhyD. What26. Mike has been working hard and now he is one of _______ students in his class.A. goodB. betterC. bestD. the best27. —Must I clean my room right now?—No, you _______. You can clean it after dinner.A. shouldn’tB. wouldn’tC. mustn’tD. needn’t28. My sister has two skirts. One is red, ________ is black.A. otherB. the other C others D. another29. —May I speak to Mr. Green?—He ______ a meeting now. Can I take a message?A. haveB. hadC. is havingD. will have30. —I hope you will enjoy your trip.—Thanks. I _______ you as soon as I arrive there.A. callB. calledC. will callD. have called31. Aunt Li often asks her son _______ too much meat. It’s bad for his healthA. don’t eatB. not to eatC. not eatD. to not eat32. My aunt is a writer. She ______ more than ten books since 1980.A. writesB. wroteC. will writeD. has written33. Today computers are really helpful. They_______ in both cities and towns.A. useB. will useC. are usedD. are using34.—Can you tell me_______ your grandparents? —Last Saturday.A. when will you visitB. when you will visitC. when did you visitD. when you visited22.Ruth and Tom are my American friends. _______ will come to China next month.A. TheirB. ThemC. TheyD. Theirs23. ---When do people in your hometown plant trees? ---- ________ March.A. OnB. InC. AtD. To24. My sister likes pop songs very much, she doesn’t like country music.A. norB. butC. orD. so25. ---Kate, would you like _________ to drink ? ---No, thanks. I’m not thirsty.A. somethingB. anythingC. nothingD. everything26. --- Which film do you like _________, Let The Bullet Fly or The Crazy Stone?--- I prefer The Crazy Stone.A. mostB. wellC. the bestD. better27. There many students in the school library every day.A. hasB. haveC. isD. are28. --- _______ you say the sentence in English? --- Yes, I can.A. MayB. CanC. MustD. Need29. The environment will be more and more beautiful if everyone _______his best to protect it.A. tryB. triesC. will tryD. has tried30. --Do you know __________the Capital Museum?--Next Friday.A. when will they visitB. when they will visitC. when did they visitD. when they visited31. Don’t make any noise. The teachers _____________a meeting.A. were havingB. haveC. are havingD. will have32. I’m looking forward to Stephon Marbury in Beijing.A. seeB. seeingC. sawD. seen33. Zhang Hong went to Japan in 2006. He ___________ there for 5 years.A. livedB. livesC. is livingD. has lived34. --- I saw you get on the NO. 901 bus. Where did you go?--- I ________ to the hospital to see a friend.A. wentB. goC. am goingD. have gone。
2012北京市语文中考各区一模试题汇--名著阅读

2012北京市语文中考各区一模试题汇编名著阅读【东城】8.名著阅读(3分)儒家经典《孟子》相传所作。
它长于言辞,善于用例。
《生于忧患,死于安乐》一文开头一连列举了六个历史人物在逆境中成长的例子,是为了阐明的观点;《鱼我所欲也》则用的事例,论证了即使普通人也有“舍生取义”之心的看法。
答案:孟子及其门人生于忧患(乞人)不受嗟来之食(共3分。
共3空,每空1分)【西城】8.名著阅读(3分)《诗经》是我国最早的一部诗歌总集,收录了从西周到①时期的诗歌305篇,故也称“②”,这些诗歌分为“风”“雅”“颂”三个部分,其中《蒹葭》属于“风”“雅”“颂”中的“③”。
答案:春秋诗三百风(国风)评分标准:共3分。
共3空,每空1分,该空有错不得分。
【朝阳】8.名著阅读(3分)强调人的道德修养是儒家思想的重要组成部分,“己所不欲勿施于人”,孔子告诫我们要胸怀宽广,宽恕待人;①认为人都有“本心”,道义尊严比生命更为重要,《②》一文中的“舍生取义”和③的故事讲的都是这个道理。
答案:①孟子②鱼我所欲也③不受嗟来之食(行道之人和乞丐不接受施舍)(共3分。
每空1分,有错该空不得分)【海淀】8.名著阅读(3分)我国第一部诗歌总集《诗经》,收入自西周初年至春秋中叶五百多年的诗歌305篇。
先秦称为“诗”,或“诗三百”。
西汉时被①尊为经典,始称“诗经”。
《诗经》中的许多诗歌采用了起兴的表现方法,如《关雎》中“关关雎鸠,在河之洲”,就是以雎鸠起兴,引出淑女和君子;又如《蒹葭》中“②”,就是用③起兴,引出④。
答案:①儒家②蒹葭苍苍,白露为霜③蒹葭④伊人(共3分。
共4空,①②空,每空1分;③④空每空0.5分)【通州】8.名著阅读(3分)《论语》是①家学派的经典著作之一,由孔子的弟子及其再传弟子编撰而成。
记录了②的言行,集中体现了孔子的政治主张、道德观念、教育原则及学习方法等,如“礼让为国”、“见贤思齐”、“有教无类”。
关于学习方法的语录“学而不思则罔,思而不学则殆”,阐述了③的辩证关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E
C (2012昌平一模)8.如图,已知□ABC
D 中,AB =4,AD =2,
E 是AB 边上的一动点(与点A 、B 不重合),设AE =x ,DE 的延长线交CB 的延长线于点
F ,设BF =y ,则下列图象能正确反
映y
与x 的函数关系的是
(2012延庆一模)8. 将图1围成图2的正方体,则图1中的红心“”标志所在的正方
形是正方体中的
(2012西城一模)8.对于实数c 、d ,我们可用min{ c ,d }表示c 、d 两数中较小的数,如min{3,1-}=1-.若关于x 的函数y = min{22x ,2()a x t -}的图象关于直线3x =对称,则a 、t 的值可能是
A .3,6
B .2,6-
C .2,6
D .2-,6
(通州2012一模)8.如图,在平行四边形ABCD 中,AC = 4,BD = 6,P 是 BD 上的任一点,过P 作EF ∥AC ,与平行四边形的两 条边分别交于点E ,F .设BP=x ,EF=y ,则能大致反 映y 与x 之间关系的图象为( )
A B C D
(2012顺义一模)8.如图,在Rt △ABC 中,90ACB ∠=︒,60A ∠=︒,AC =2, D 是AB 边上一个动点(不与点A 、B 重合),E 是BC 边上 一点,且30CDE ∠=︒.设AD=x , BE=y ,则下列图象中, 能表示y 与x 的函数关系的图象大致是 F
E
D C
B A
D
C B A
(2012门头沟一模)8. 如图,在正方形ABCD 中,AB =3cm ,动点M 自A 点出发沿
AB 方向以每秒1cm 的速度运动,同时动点N 自A 点出发沿折 线AD —DC —CB 以每秒3cm 的速度运动,到达B 点时运动同 时停止,设△AMN 的面积为y (cm 2),运动时间为x (秒),
N
M D
C
B
A
则下列图象中能大致反映y 与x 之间的函数关系的是
(2012怀柔一模)8. 如图,在矩形ABCD 中, AB =4,BC =6,当直角三角板顶点
P 在BC 边上移动时,直角边MP 始终经过点A ,设直角三角板的另一直角
边PN 与CD 相交于点Q .BP =x ,CQ=y ,那么y 与x 之间的函数图象大致是
8.(2012丰台一模)如图,矩形ABCD 中,AB =3,BC =5,点P 是BC 边上的一个动点
(点P 不与点B 、C 重合),现将△PCD 沿直线PD 折叠,使点C 落到点C’处;作∠BPC’的角平分线交AB 于点E .设BP =x ,BE =y ,
则下列图象中,能表示y 与x 的函数关系的图象大致是
A .
B .
C .
D .
(房山2012一模)8.如图,梯形ABCD 中,AB ∥CD ,∠A =30°,∠B =60°,AD =32,CD =2,点P 是线段AB 上一个动点,过点P 作PQ ⊥AB 于P
,交其它边于Q ,设BP 为x ,△BPQ 的面积为y ,则下列图象中,能表示y 与x 的函数关
E
P
C’
A
D
B
C
系的图象大致是( ).
x
y 63
12O
x
y 63
12
O B
x
y 63
1
2O
x
y 63
12
O
(东城2012一模)8. 如图,在正方形ABCD 中,AB =3cm ,动点M 自A 点出发沿AB 方向以每秒1cm 的速度向B 点运动,同时动点N 自A 点出发沿折线AD —DC —CB 以每秒3cm 的速度运动,到达B 点时运动同时停止.设△AMN 的面积为y (cm 2
),运动时间为x (秒),则下列图象中能大致反映y 与x 之间的函数关系的是
A B C D
(大兴2012一模)8.如图,圆柱底面直径AB 、母线BC 均为4cm ,动点P 从A 点出发,
沿着圆柱的侧面移动到BC 的中点S 的最短距离 A.(212π+)cm B.(2412π+)cm C.(214π+)cm D.(242π+)cm
(朝阳2012一模)8.已知关于x 的一元二次方程02
=++n mx x 的两个实数根分别为
a x =1,
b x =2(b a <),则二次函数n mx x y ++=2中,当0<y 时,x 的取值范围
是
A .a x <
B .b x >
C .b x a <<
D .a x <或b x >。
