电工学第2章
中南大学电工学第2章正弦交流电路_02

例3 电路如图所示,图中各仪表均为交流电流表,其读数是 电路如图所示,图中各仪表均为交流电流表, 电流表的有效值。已知A 的读数为8A 8A, 的读数为60A 60A, 电流表的有效值。已知A1的读数为8A,A2的读数为60A,A3的 读数为66A 求电流表A 66A。 的读数,并画出相量图。 读数为66A。求电流表A和A4的读数,并画出相量图。 I4 I 解:由于电路为并联电 A A4 A3 路,则可设 I3 + A1 A2 US= US 0 V 1 US I1 I j L ω R j L 2 ω 则由已知条件得 I1= 8 0 A, 2= 60 -90 A,I3= 66 90 A , I , 根据KCL有 有 根据 I4= I2+I3= 60 -90 +66 90 =6 90 A I= I1+I4= 8 0 +6 90 =10 36.9 A 故表A的读数为 的读数为6A。 故表 的读数为10A,表A4的读数为 。 的读数为 , 的读数为 相量图如图。 相量图如图。 I2 I2 I4 I I1 US I3
▲额定视在功率 额定视在功率 SN = UN IN —— 额定容量 ▲有功功率守恒 有功功率守恒: 有功功率守恒 P = ∑Pi =∑ Ui Ii cosϕ i ▲无功功率守恒 无功功率守恒: 无功功率守恒 Q = ∑Q i = ∑ Ui Ii sinϕ i ▲视在功率不守恒 视在功率不守恒: 视在功率不守恒 S ≠∑S i =∑ Ui Ii
& I 1 = 10 90 ° A = j10 A & & & I = I 1 + I 2 = 10 0 ° A
& & U L = I ( j10 )V = j100 V
电工学 第二章 电路的分析方法

例4、用叠加原理求图示电路中的I。 1mA 4kΩ + 10V - 2kΩ I 2kΩ
2kΩ
解:
电流源单独作用时 电压源单独作用时: 10 2 44 mA 1 257mA II 1 mA .0.25mA 4 2 [2+4//2] 4 4 2 [(2+2)//2] 2 I=I′+I″= 1.507mA
返回
第三节 电压源与电流源的等 效变换
等效变换的概念 二端电阻电路的等效变换 独立电源的等效变换 电源的等效变换 无源二端网络的输入电阻 和等效电阻
返回
一、等效变换的概念
1、等效电路
两个端口特性相同,即端口对外的 电压电流关系相同的电路,互为等效电 路。
返回
2、等效变换的条件 对外电路来说,保证输出电压U和 输出电流I不变的条件下电压源和电流 源之间、电阻可以等效互换。
1 1 2 2 S
-US+R2I2+R3I3+R4I4 =0
返回
第二节 叠加原理
叠加原理
原理验证
几点说明
返回
一、叠加原理
在由多个 独立电 源共同 作用的 线性 电路中,任一支路的电流(或电压)等于各 个独立电源分别单独作用在该支路中产 生的电流(或电压)的叠加(代数和) 。
不作用的恒压源短路,不作用的恒流 源开路。
US2单独作用
= 4/3A
返回
三、几点说明
叠加原理只适用于线性电路。
电路的结构不要改变。将不作用的恒压
源短路,不作用的恒流源开路。
最后叠加时要注意电流或电压的方向:
若各分电流或电压与原电路中电流或
电压的参考方向一致取正,否则取负。 功率不能用叠加原理计算。
04电工(第2章交流2RLC串联电路,交流电路分析,功率因数提高)

消耗有功功率为: P PR UI cos
当U、P 一定时 cos
I
供电线路功耗
希望将cos 提高
供电局一般要求用户的cos >0.85 ,否则受处罚
常用电路的功率因数
纯电阻电路
纯电感电路或 纯电容电路
cos 1 ( 0) cos 0 ( 90)
R-L-C串联电路
电动机 空载 满载
0 cos 1
第4讲
第2章 正弦交流电路
2.4 正弦交流电路的分析计算 2.5 正弦交流电路的功率
清华大学电机系电工学教研室 唐庆玉编
海南风光
本课内容
第2章 正弦交流电路
2.1 正弦电压与电流 2.1.1正弦量的参考方向和电源模型 2.1.1 周期、频率和角频率 2.1.2 相位、初相位和相位差 2.1.3 最大值和有效值
例3(教材例2.20)
已知: R1 、R2、R3 、R4 、L、C、u、i、,求支路电流i1、 i2 、i3 。
A
A
R1 i1 R2 i2 R3 i3 R4
R1
I1 R2
I2 R3
I3 R4
u
+
L
+ C uS
相量模型
i
-
U
-
+
+
jX L
jX
US
C-
I
B
B
结点电位法
U I
VA 1
R1 1
1
R1 R2 jX L R3 jX C
i 2I sint
u 2U sin(t )
UIZ
Z
R2
X
2 L
i
+
+
电工学-第二章习题答案
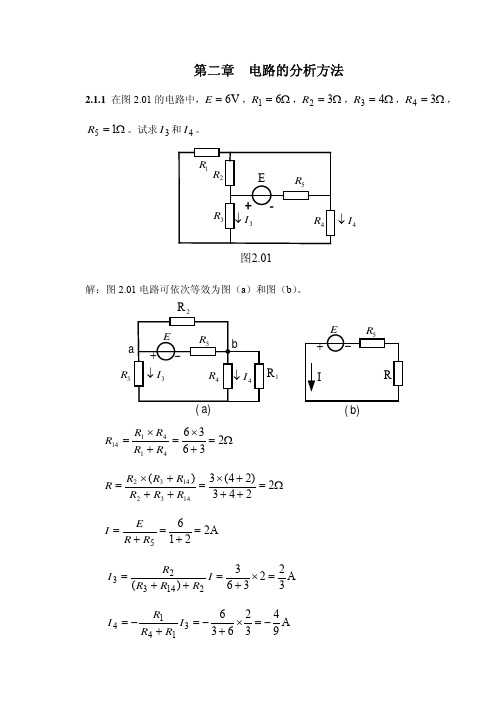
第二章 电路的分析方法2.1.1 在图2.01的电路中,V 6=E ,Ω=61R ,Ω=32R ,Ω=43R ,Ω=34R ,Ω=15R 。
试求3I 和4I 。
4I ↓图2.01解:图2.01电路可依次等效为图(a )和图(b )。
R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。
Ω=1R A2S =图2.12解:根据电压源与电流源的等效变换,图2.12所示电路可依次等效为图(a )和图(b ),由图(b )可求得A 2.15.023=+=I由图(a )可求得:A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中,(1)当将开关S 合在a 点时,求电流1I ,2I 和3I ;(2)当将开关S 合在b 点时,利用(1)的结果,用叠加定理计算电流321,I I I 和 。
I图2.19I (a)I (b)解:(1)当将开关S 合在a 点时,图2.19所示电路即为图(a ),用支路电流法可得:=+=+=+12042130423231321I I I I I I I 解得:===A 25A 10A 15321I I I(2)开关S 合在b 点时,利用叠加原理图2.19所示电路可等效为图(a )和图(b ),其中图(a )电路中130V 和120V 两个电压源共同作用时所产生的电流已在(1)中求得,即:A 151=,I A 102=,I A 253=,I由图3(b )可求得:A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则:A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20(a )所示,V 10ab ,,V 124321=====U R R R R E 。
电工学课后答案-第2章-电路的瞬态分析习题及答案
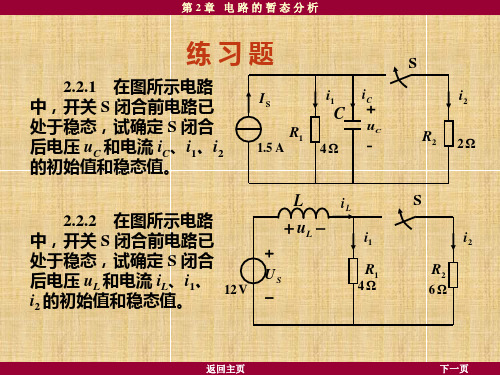
然后,根据,由换路后 (S 闭合时) 的电路求得
i1 ( 0 ) i2 (0 ) R2 R 1 R2 R1 R1 R 2 iL (0) iL (0) 6 46 4 46 3 A 1 .8 A 3 A 1 .2 A
iL
R2
6Ω
L
1H
返 回
第2章 电路的暂态分析
2.4.2图所示电路原 已处于稳态。试求 S 闭合 后的 i2 、iL 和 uL,并画出 其变化曲线。
i1
IS
S
i2
R3
7Ω
R1
24 A
R2
3Ω
uL
iL
1 .5 Ω
L
0 .4 H
a
S
b
R1
3Ω
2.4.3图所示电路 原已处于稳态。在 t = 0 时将开关 S 从 a 端改合 到 b 端。试求换路后的 iL 和 uL,并说明是什么 响应。
uC U 0 e iC C
30 e U0 R
10
4
C
t
V 3e
10
4
R
t
uC
d uC dt
t
e
A
上一题 下一题
返 回练习题题集
上一页
第2章 电路的暂态分析
2.3.2在图所示电路原已处于稳态,在 t = 0 时,将开 关 S 闭合,试求响应 uC 和 iC,并说明是什么响应?
100 t
)V
e
15 e
mA
返 回练习题题集
上一页
上一题
下一题
第2章 电路的暂态分析
电子电工学第2章-1 交流电路的稳态分析

2. 频率f:每秒钟内周期量重复的次数。 单位:赫兹、Hz。
频率与周期的关系: 3. 角频率ω
f 1 T
u
把单位时间正弦量经 历的弧度称为角频率。
2
0
或
T (rad/s )
2f
2π t
T
已知:频率f=50Hz,问正弦量变化一周所需要 的时间,即周期T=?角频率ω =?
u
i
2
ui
U LI
2
t 0
2. 电感元件特性方程的相量形式
由u、i的三角函数式写出其相量表达式:
U Ue j u I Ie j i
求 I I1m I2m ?
Im I1m I2m 58
+j
I1m
I m
+1 0
i 5sin(t 8 )( A)
I2m
需要记住的几个相量:
I1 3 j4 553
I2 3 j3 3 245
I3 1 j 3 260
(3)
Um U R Im I
U I
R
瞬时功率:
2. 功率
p(t
)
ui 2UI
2U sint sin2 t i
u
2I sint i
UI 1 cos 2t i
说明:
p(t)≥0,电阻只消耗功率,以发热的形式表现出来。 p(t)包含两部分: UI——恒定量 UIcos2(ω t+ ψi)——正弦量,但频率为u、i两倍
i
e
L
i 2I sint i Im sint i
电工学第二章

4.电容器的主要参数
(1)标称电容量 电容器的外壳上标出的电容量值称为标称电容量。
(2)允许偏差 电容器的允许偏差常用的有±2%、±5%、±10%、
用介电常数较大的物质作为电容器的电介质 可显著增大电容,而且能做成很小的极板间隔,因 而应用很广。
任何两个导体之间都存在着电容。
3. 电容器的充电和放电
(1)电容器的充电 当开关S置于A端,电源E通过电阻R 对电容器C开始充电。起初,充电电流 较大,但随着电容器C 两端电荷的不断积累,形成的电压 越来越高,它阻碍了电源 对电容器的充电,使充电电流越来越小,当电容器两端电压 达到了最大值E时,则不再变化,电流为零。故在直流稳态电 路中,电容相当于开路,这就是电容的隔直作用。
检测电感器
电感器的直流电阻很小,通常只有几欧或 几十欧,线径越细,圈数越多,电阻值越大。 一般情况下用万用表R×1电阻挡测量,只要能 测出电阻值,即可认为电感器是正常的;如果 测量结果为无穷大,说明电感器已经开路。
§2-3纯电阻、纯电感、纯电容交流电路
一、纯电阻交流电路
交流电路中如果只考虑电阻的作用,这种电 路称为纯电阻电路。
电容量也简称电容。
它只与电容器的极板正对面积、极板间距离 以及极板间电介质的特性有关;而与外加电压的 大小,电容器带电多少等外部条件无关。
C S
d
式中S、d、C的单位分别是m2、m、F,介电常 数ε的单位是F/m。
真空中的介电常数ε0≈8.86×10-12F/m ,某种介 质的介电常数ε与ε0之比,称该介质的相对介电常 数,用εr表示 。
电工学 第七版 上册 (秦曾煌 著) 高等教育出版社 课后答案第二章

第2.7.5题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
第2.7.7题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
第2.7.8题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
第2.6.2题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
第2.6.3题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
第2.6.4题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
I
=
R5
+
E
R2(R3
+
R1R4 R1 + R4
)
R2
+
(R3
+
R1R4 R1 + R4
)
=
1+
6
3
×
(4
+
6 6
× +
33 )
3
+
(4
+
6 6
× +
3 3
)
= 2A
而后应用分流公式得出I3和I4
I3
=
R2
+
R2
R3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
举例 在图中,已知直流发电机 的电动势E1=7V,内阻r1=0.2 Ω, 蓄电池组的电动势E2=6.2V,内 阻r2=0.2 Ω。负载电阻R3=3.2 Ω。 用节点电压法求各支路电流和 负载的端电压。
二、应用举例
解:负载两端的电压即为节点电压。
G1 1 1 5S r1 0.2 G2 1 1 5S r2 0.2 G3 1 1 5 S r3 3.2 16
i f u
2、非线性电阻电路的动态分析 动态分析内容:关注变化量 U S、 IQ、 UQ 动态分析工具:微变等效电路 i
+ _ us
R u
微变:(微小变化) 等效:(线性代替非线性)
i
rd
Q
在Q点附近的 电路模型
i u
u rd i
up
u
2.9 PSpice例题分析
I U
U R I
(常数)
一、非线性电阻的描述
非线性电阻: 电阻值随电压/电流的变化而变化。 非 线 性 特 性 I2 I1 I
U I
Q2
Q1 U1 U2 U
R
工作点不同 电阻不一样
Q1 : Q2 :
U1 R1 R2
I1 I2
U2
二、非线性电阻电路的电阻
1、静态电阻 2、动态电阻U R ຫໍສະໝຸດ tg Ib)有源二端网络
图4-10 二端网络的表示符号
二、无源线性二端网络的等效电阻
1. 任何一个无源线性二端网络,其端电压与端钮电 流间总是线性关系,它们的比值是一个常数。因 此,一个无源线性二端网络总可以用一个等效电 阻 Req 来代替,该等效电阻也称为网络的输入电
阻。
2.无源线性二端网络等效电阻Req的求解
I
i
u r tg i
Q i u
Q
u
U
适用于分析微变 电压引起微变电 流的情况
适用于外加固定电压的情况
三、非线性电阻电路的分析
的电压和电流。静态分析工具:图解法
R E
线性部分
1、静态分析内容:电路加上恒定直流电压时,求各处
+
i
u
非线性部分
i
E/R IQ Q u UQ E
_
u E iR
(1)串联
us us1 us2 ... usn usk
k 1
n
图2-15
电压源的串联
(2)并联
n个电压源,只有在各电压源电压值相等,极性一致的情况 下才允许并联,否则违背KVL。其等效电路为其中的任一电压
源,
图2-17 同值电压源的并联
2.电流源的连接 (1)并联
is is1 is2 ... isn isk
五、诺顿定理
任何一个有源线性二端网络,对外电路来说,可以
用一个电流源与一个电阻并联组合的电路模型来等效。
该电流源的电流等于有源二端网络的短路电流 Isc ; 电阻等于将有源二端网络变为无源二端网络后的等效 电阻 Req 。
对于戴维南定理和诺顿定理应注意以下几点:
(1)戴维南定理和诺顿定理只要求被等效的有源二端网络是线性 的,而该二端网络所连接的外电路可以是任意网络(线性或非 线性、有源或无源) ,但被等效的有源二端网络与外电路之间 不能有控制和被控制关系。 (2)在求戴维南等效电路或诺顿等效电路中的电阻 Req 时,应将 有源二端网络中的所有独立源置零,而受控源应保留不变。 (3)当 Req ≠ 0 和 Req ≠∞时,有源二端网络既有戴维南等效电路 又有诺顿等效电路。
图c中得 U " 8V 1 叠加得 '
2.5 置换定理
一、置换定理内容
线性或非线性的任意网络中,若已知第 k 条支路 的电流为 ik ,端电压为 uk ,则该支路可用以下三种 元件中的任意一种来替代: ( 1 )电压值为 uk 的电压源; ( 2 )电流值为 ik 的电流源; ( 3 )阻值为 uk/ik 的电阻。
图2-42 PSpice电路图
图2-44 PSpice电路图
图2-45 仿真波形
4.叠加定理只能用来计算线性电路的电压或电流,而不能用来计算功率。
5.叠加定理被用于含有受控源的电路时,所谓电源的单独作用只是对独立 电源而言。
例2-2
用叠加定理求图4-3a电路中的电压U1
图2-3 图b中得
例2-2图
解:根据叠加定理,图a为图b和图c的叠加
U1' 12V
U1 U1 U1" 4V
流、电压是会发生变化的。 2.替代定理不仅适用于线性电路,也适用于非线性 电路。
2.6 等效电源定理
一、二端网络
具有两个端钮与外电路相连接的网络,不论其内
部结构如何,都称为二端网络,也称为一端口网
络。
根据网络内部是否含有独立电源,二端网络可分
为有源二端网络和无源二端网络。
二端网络的表示符号:
a)无源二端网络
图2-24 例2-8图
解:用电源等效变换法将图2-24a所示电路按图2-24b、c 、d的变换过程简 94 化成图2-24d,在该图中可求得电流 0.5 A I
1 2 7
2.2 支路电流法
一 . 支路电流法
支路电流法是电路分析中最基本的方法, 它是以各支路电流为变量,根据KCL、KVL
替换后,电路其余各支路电压、电流将保持不变。这就
是替代定理。也称置换定理。
替代定理示图
图4-7
替代定理示图
已知I1=2A,则可将I1支路用一个大小为2A的电流源来替代。
二、注意事项
1.替代不是等效变换,被等效变换的支路在外电路 参数变化时,等效电路的参数不会变,而被替
代支路在外电路参数变化时,被替代支路的电
2.7 最大功率传输定理
最大功率传输定理:
当RL= Req 时, PL 为最大。即:当负载电阻等于电源 内阻时,负载可获得最大功率。这种工作状态称为“匹 配”. 此时,负载上的最大功率为:
Pmax
2 U OC 4 Req
图4-21
负载获得最大功率示意图
图2-33 功率随负载变化的曲线
2.8 非线性电阻电路 线性电阻: 电阻两端的电压与通过的电流成正比; 或电阻值不随电压/电流的变化而变化。
5I1 10 5I 2 25 0
15I3 5I 2 10 0
解方程组得
I1 2 A , I 2 1A , I 3 1A
对外围回路可用KVL进行检验
5 2 15 1 25 0
图3-2 例3-1图
2.3 节点电压法 一、节点电压法
1.两个节点之间的电压称为节点电压。
图2-20 电流源与支路的串联
二. 两种实际电源模型间的等效变换
1.两种实际电源模型:
图2-21
两种实际电源模型
2.等效变换条件: us is Rs
或
注意:
1 Gs Rs
1 Rs Gs
is us Gs
电源的等效变换仅对端钮(或外电路)等效. 对于变换过的每个元件都是不等效的.
例2-8 用电源等效变换法求图2-24a所示电路中的电流I.
( 1 )直接利用电阻的串、并联或 Y-等效变换逐步 化简的方法。这种方法适用于电路结构和元件参 数已知的情况。
( 2 )外加电源法适用于结构和元件参数不清楚的网
络和含有受控源的无源线性二端网络。
三、戴维南定理内容
任何一个有源线性二端网络,对外电路来说, 可以用一个电压源与一个电阻相串联组合的电 路模型来等效。该电压源的电压等于有源二端 网络的开路电压 Uoc ;电阻等于将有源二端网 络变为无源二端网络后的等效电阻Req 。
U AB
EG G
E1G1 E2G2 7 5 6.2 5 6.4V G1 G2 G3 55 5 16
二、应用举例
各支路电流为
E1 U AB 7 6.4 I1 3A r1 0.2 E2 U AB 6.2 6.4 I2 1A r2 0.2 U AB 6.4 I3 2A R3 3.2
I1" I " R2 4 I " 0.4I " R1 R2 64
" " " U s rI1 I1 R1 (10 6) (0.4I " ) 6.4I "
U s" Req " 6.4 I
( 3)在图d等效电路中求U3
U3 Uoc Req I s (6 6.4 4) 19.6V
k 1
n
图2-16 电流源的并联
(2)串联
n个电流源,只有在各电流源电流值相等且方向一致的情况 下才允许串联,否则违背KCL,其等效电路为其中的任一电流 源.
图2-18 同值电流源的串联
3.与电压源并联的任何元件或支路,对外电路均
可视为开路.
图2-19 电压源与支路的并联
4.与电流源串联的任何元件或支路,对外电路均 可视为短路.
图4-15
例4-6图
解:( 1 )在图b中求开路电压Uoc(注意图中I=0的条件)
Uoc= (1×4+3×2+6)V=16V ( 2)在图c中求Req
Req=6Ω
( 3)在图d等效电路中求电流I
I
U oc 16 2A Req RL 6 2
例 4-8 用戴维南定理求图4-17a电路中的电压U3.已知R1=6Ω ,R2=4Ω ,
列写电路方程而求解的方法。
二.支路电流法步骤
1.选定b条支路的电流参考方向,作为电路变量。 2.对(n-1)个独立节点列写KCL电流方程。 3.选定[b-(n-1)]个独立回路,指定绕行方向列写 KVL电压方程。 4. 联立求解上述b个方程,得到待求的各支路电流和其 它需求的电量。
