特殊三角形复习
特殊三角形复习
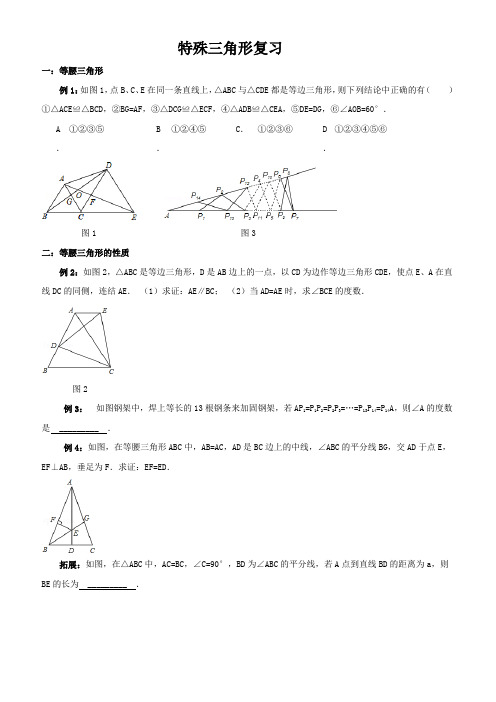
特殊三角形复习一:等腰三角形 例1:如图1,点B 、C 、E 在同一条直线上,△ABC 与△CDE 都是等边三角形,则下列结论中正确的有( ) ①△ACE ≌△BCD ,②BG=AF ,③△DCG ≌△ECF ,④△ADB ≌△CEA ,⑤DE=DG ,⑥∠AOB=60°.A . ①②③⑤B . ①②④⑤C . ①②③⑥D .①②③④⑤⑥图1 图3二:等腰三角形的性质 例2:如图2,△ABC 是等边三角形,D 是AB 边上的一点,以CD 为边作等边三角形CDE ,使点E 、A 在直线DC 的同侧,连结AE . (1)求证:AE ∥BC ; (2)当AD=AE 时,求∠BCE 的度数.图2例3: 如图钢架中,焊上等长的13根钢条来加固钢架,若AP 1=P 1P 2=P 2P 3=…=P 13P 14=P 14A ,则∠A 的度数是 _________ .例4:如图,在等腰三角形ABC 中,AB=AC ,AD 是BC 边上的中线,∠ABC 的平分线BG ,交AD 于点E ,EF ⊥AB ,垂足为F .求证:EF=ED .拓展:如图,在△ABC 中,AC=BC ,∠C=90°,BD 为∠ABC 的平分线,若A 点到直线BD 的距离为a ,则BE 的长为 _________ .三,等腰三角形的判定例5:等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.例6:如图,A、B两点在正方形网格的格点上,每个方格都是边长为1的正方形、点C也在格点上,且△ABC为等腰三角形,则符合条件的点C共有_________ 个.例7:如图,△ABC中,AD平分∠BAC,∠B=2∠C,求证:AB+BD=AC.四,直角三角形的性质例8:如图,已知:△ABC中,AD是高,CE是中线,DC=BE,DG⊥CE,G是垂足.求证:(1)G是CE的中点;(2)∠B=2∠BCE.例9:已知∠BAC=90°,AB=AC,M是AC边的中点,AD⊥BM交BC于D,交BM于E,求证:∠AMB=∠DMC.四,直角三角形的判定例10:如图,在△ABC 与△ADE 中,∠BAC=∠DAE=90°,AB=AC ,AD=AE ,点C 、D 、E 在同一条直线上,连接BD 、BE .把以下所有正确结论的序号都填在写在横线上: _________ .①BD=CE ; ②∠ACE+∠DBC=45°; ③BD ⊥CE ; ④BE 2=2(AB 2+AD 2).五,直角三角形全等的判定例11: 在△ABC 中,AB=CB ,∠ABC=90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF .(1)求证:Rt △ABE ≌Rt △CBF ;(2)若∠CAE=30°,求∠ACF 的度数.课后练习一.选择题1.如图1,正方形ABCD 中,点E 、F 分别在BC 、CD 上,△AEF 是等边三角形,连接AC 交EF 于G ,下列结论:①BE=DF ,②∠DAF=15°,③AC 垂直平分EF ,④BE+DF=EF ,⑤S △CEF =2S △ABE .其中正确结论有( )个.A.2 B. 3 C . 4 D . 5图1 图2 图3 图42.如图2,OP 平分∠BOA ,∠BOA=45°,PC ∥OA ,PD ⊥OA ,若PC=4,则PD 等于( )A 4BCD 2....二.填空题1.如图3,矩形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,则DE的长为_________ .2.如图4,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= _________ 度.3.如图所示,每个小方格都是边长为1的正方形,点A,B是方格纸的两个格点(即正方形的顶点),在这个6×6的方格纸中,找出格点C,使△ABC的面积为1个平方单位的直角三角形的个数是_________ 个.4.如图a,P是等边△ABC内任意一点,由P向边BC、AC、AB分别引垂线段PD、PE、PF,AM⊥BC,AM=6cm,则PD+PE+PF= _________ .图a 图b 图c5.如图b,在△ABC中,AB=AD=DC,∠BAD=32°,则∠BAC= _________ °.6.如图c,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于_________ .三.解答题1.已知,在△ABC中,AB=AC,P为底边BC上一点,PE⊥AB,PF⊥AC,CH⊥AB,垂足分别为E、F、H.(1)求证:PE+PF=CH;(2)P为BC延长线上的点时,其它条件不变,求证:PE﹣PF=CH.2.如图:已知在△ABC中,∠ACB=90°,AC=BC=1,点D是AB上任意一点,AE⊥AB,且AE=BD,DE与AC相交于点F.(1)试判断△CDE的形状,并说明理由.(2)是否存在点D,使AE=AF?如果存在,求出此时AD的长,如果不存在,请说明理由.3.如图,已知在△ABC中,AB=AC,D是BC边上任意一点,E在AC边上,且AD=AE.(1)若∠BAD=40°,求∠EDC的度数;(2)若∠EDC=15°,求∠BAD的度数;(3)根据上述两小题的答案,试探索∠EDC与∠BAD的关系.4.如图,△ABC是等腰三角形,D、E分别是腰AB及AC延长线上的点,且DG=GE,请证明:BD=CE.5.如图所示,在△ABC中,BD、CE分别是边AC、AB上的高,点F在边BC上,BF=CF.求证:△DEF是等腰三角形.6.如图,△ABC是等腰三角形,D,E分别是腰AB及AC延长线上的一点,且BD=CE,连接DE交底BC于G.求证GD=GE.7.如图△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.求证:DB=DE.8.如图所示,AOB是一钢架,且∠AOB=10°,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH…,添加的钢管长度都与OE相等,则最多能添加这样的钢管_________ 根.9.已知:如图,在△ABC中,AB=AC,点D,E在边BC上,且BD=CE.求证:AD=AE.10.在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE.求证:AD=CE.11.如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB.求证:BD=CE.12.如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.求证:AM=AN.13.如图,已知在等边三角形ABC的边AC、BC上各取一点P、Q,且AP=CQ,AQ、BP相交于点O,(1)求证:△ABP≌△ACQ;(2)求∠BOQ的度数.14.如图,P是等边△ABC内一点,∠PBQ=60°,且BQ=BP,连接CQ.猜想AP与CQ之间的大小关系,并证明.15.已知:如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC.求证:DC=AD.16.如图,已知△ABC中,AB=AC,∠A=100°,BD平分∠ABC,求证:BC=BD+AD.17.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,将△ADC沿AC边所在的直线折叠,使点D落在点E处,得四边形ABCE.求证:EC∥AB.18.如图所示,一根长2a的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.(1)请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由.(2)在木棍滑动的过程中,当滑动到什么位置时,△AOB的面积最大?简述理由,并求出面积的最大值.19.如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.(1)求证:BE=CE;(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.20.如图所示的一块地,AD=12m,CD=9m,∠ADC=90°,AB=39m,BC=36m,求这块地的面积.21.如图,正方形ABCD中,边长为4,F为DC的中点,E为BC上一点,且CE=BC.求证:AF⊥FE.22.如图,∠B=∠C=90°,M是BC中点,DM平分∠ADC,求证:AM平分∠DAB.23.已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在边BC上,求证:AB=AC;(2)如图2,若点O在△ABC的内部,求证:AB=AC;(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.。
初中二年级数学上册第2章 特殊三角形单元复习

第2章特殊三角形单元复习1.掌握图形的对称及轴对称图形的定义,会作一个图形关于直线的对称图形,理解轴对称的性质.2.了解等腰三角形的定义,掌握等腰三角形的性质与判定;了解直角三角形的定义,掌握直角三角形的性质与判定;理解中垂线、角平分线的性质与判定.3.理解等腰三角形和直角三角形这两个基本图形在几何中的地位和作用,能将复杂的几何问题转化为基本图形解决.考点一:轴对称与轴对称图形例1 (湖州市吴兴区)下列图形中,属于轴对称图形的是()A. B. C. D.例2 (宁波市北仑区)“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题:如图所示,将军在观望烽火之后从山脚上的点A出发,奔向小河旁边的点P饮马,饮马后再到点B宿营,若点A,B到水平直线l(l表示小河)的距离分别是3,1,A,B两点之间水平距离是3,则AP+PB的最小值为.如果两个图形关于某条直线对称,那么对称轴是任何一组对应点所连线段的垂直平分线.由轴对称的性质可以得到以下结论:①如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称;②如果两个图形是轴对称图形,我们只要找到一组对应点,作出连结它们的线段的垂直平分线,就可以得到这两个图形的对称轴;③轴对称图形的对称轴是任何一组对应点所连线段的垂直平分线.1.(台州市椒江区)如图所示,P是直线l外一个定点,A为直线l上一个定点,点P关于直线l的对称点记为P1,将直线l绕点A顺时针旋转30°得到直线l′,此时点P2与点P关于直线l′对称,则∠P1AP2等于()A.30°B.45°C.60°D.75°2.(宁波市北仑区)如图所示为由5个边长为单位1的小正方形拼成的图形,请你在图上添加一个小正方形,使添加后的图形是一个轴对称图形,要求画出三种.考点二:等腰三角形的性质与判定例3 (杭州市江干区)一个等腰三角形的一个内角是另一个内角的2倍,则这个三角形底角为(A)A.72°或45°B.45°或36C.36°或90°D.72°或90°例4 (宁波市镇海区)如图所示,AB∠CD,CE平分∠ACD交AB于点E.(1)求证:∠ACE是等腰三角形.(2)若AC=13cm,CE=24cm,求∠ACE的面积.1.等腰三角形的性质:①等腰三角形的两腰相等;②等腰三角形的两个底角相等(等边对等角);③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(三线合一).2.等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边).3.在①等腰、②底边上的高、③底边上的中线、④顶角平分线四个元素中,从中任意取出两个元素当成条件,就可以得到另外两个元素为结论.3.(绍兴市柯桥区)在∠ABC中,与∠A相邻的外角是140°,要使∠ABC是等腰三角形,则∠B的度数是.4.(嘉兴市)如图所示,∠ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC=.(第4题)5.(杭州市江干区)证明命题“等腰三角形底边上的中点到两腰的距离相等”是真命题.考点三:直角三角形的性质与判定例5 (杭州市余杭区)如图所示,在∠ABC中,∠ACB=90°,∠A=26°,BC=BD,则∠ACD的度数是(C)A.64B.42°C.32°D.26°例6 (天台县)如图所示,在Rt∠ABC中,CM平分∠ACB交AB于点M,过点M作MN∠BC交AC于点N,且MN平分∠AMC,若AN=1.(1)求∠B的度数.(2)求CN的长.直角三角形是一种特殊的三角形,它除了具有一般三角形的性质外,还具有一些特殊的性质:①直角三角形两直角边的平方和等于斜边的平方(勾股定理);②在直角三角形中,两个锐角互余;③在直角三角形中,斜边上的中线等于斜边的一半;④直角三角形的两直角边的乘积等于斜边与斜边上高的乘积;⑤在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半;如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.6.(杭州市拱墅区)在Rt∠ABC中,∠C=90°,∠A-∠B=70°,则∠A的度数为()A.80°B.70°C.60°D.50°7.(绍兴市越城区)如图所示,在∠ABC中,∠ACB=90°,点D在BC上,E是AB的中点,AD,CE相交于点F,且AD=DB.若∠B=20°,则∠DFE等于()A.30°B.40°C.50°D.60°8.(嘉善县)如图所示,在∠ABC中,D是BC中点,E是AB上一点,F是AC上一点.若∠EDF=90°,且BE2+FC2=EF2,求证:∠BAC=90°.考点四:线段的中垂线与角平分线例7 (德清县)如图所示,已知∠AOE=∠BOE=15°,EF∠OB,EC∠OB于点C,EG∠OA于点G,若EC=√3,则OF的长度是()A.2√3B.√3C.3D.2例8 (杭州市西湖区)在∠ABC中,∠BAC=α,边AB的垂直平分线交边BC于点D,边AC的垂直平分线交边BC于点E,连结AD,AE,则∠DAE的度数为.(用含α的代数式表示)1.角平分线的性质:角的平分线上的点到角的两边的距离相等.注意:①这里的距离是指点到角的两边垂线段的长;②该性质可以独立作为证明两条线段相等的依据,不必证明全等.2.线段垂直平分线的性质:①垂直平分线垂直且平分其所在线段;②垂直平分线上任意一点,到线段两端点的距离相等;③三角形三条边的垂直平分线相交于一点,这一点到三个顶点的距离相等.9.(宁波市江北区)如图所示,在∠ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于点D,交AB于点E,CD=2,则AC=.(第9题)(第10题)10.(杭州市临安区)如图所示,AB∠CD,∠ABC和∠DCB的平分线BP,CP交于点P,过点P作PA∠AB于点A,交CD于点D.若AD=10,则点P到BC的距离是,∠BPC=.考点五:勾股定理例9 (嘉兴市)如图所示的图案由赵爽弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=27,S3=1,则S1的值是.例10 (慈溪市)如图所示,在Rt∠ABC中,∠ACB=90°,BC=6,AB的垂直平分线交AB于点D,交AC 于点E,若CD=5,则AE=.1.勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.2.勾股定理公式a2+b2=c2的变形有a=√c2−b2,b=√c2−a2及c=√a2+b2.3.勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.运用勾股定理的逆定理解决问题的实质就是判断一个角是不是直角.然后进一步结合其他已知条件来解决问题.11.(湖州市南浔区)如图1所示,以直角三角形ABC的各边为边分别向外作正方形,再把较小的两张正方形纸片按如图2所示的方式放置在最大的正方形内,三个阴影部分面积分别记为S1,S2,S3,若S1=1,S2=2,S3=3,则两个较小正方形纸片的重叠部分(四边形DEFG)的面积为()图1 图2A.5B.5.5C.5.8D.612.(临海市)如图所示,在∠ABC中,AB=4,BC=2,AC=2√3.(第12题)(1)求证:∠ABC是直角三角形.(2)D是AC上的中点,求BD的长.考点六:等边三角形与直角三角形例11 (杭州市临安区)在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作等边三角形,作得两个等边三角形的另一顶点分别为D,E.(1)如图1所示,连结CD,AE,求证:CD=AE.(2)如图2所示,若AB=1,BC=2,求DE的长.(3)如图3所示,将图2中的等边三角形BEC绕点B作适当的旋转,连结AE,若有DE2+BE2=AE2,试求∠DEB的度数.图1 图2 图31.等边三角形是特殊的等腰三角形;等边三角形的三条边都相等,三个内角都相等,且都等于60°;等边三角形是轴对称图形,它有三条对称轴;等边三角形的任意一角的平分线都垂直平分对边,三边的垂直平分线都是对称轴.2.等腰直角三角形是另一种特殊的三角形,具备等腰三角形和直角三角形的所有性质.即两个锐角相等且都是45°;斜边上的中线、斜边所对角的角平分线、斜边上的高三线合一.13.(余姚市)如图所示,∠BAC=90°,B是射线AM上的一个动点,C是射线AN上一个动点,且线段BC 的长度不变,点D是点A关于直线BC的对称点,连结AD.若2AD=BC,则∠ABD的度数是.(第13题)14.(杭州市余杭区)如图所示,∠ABC和∠DCE都是等腰直角三角形,∠ACB=∠DCE=90°.(第14题)(1)求证:BD=AE.(2)若∠ABD=∠DAE,AB=8,AD=6,求四边形ABED的面积.本章主要易错点1.注意轴对称与轴对称图形的区别,轴对称是指两个图形的关系,而轴对称图形是指一个图形本身的特征.2.“等边对等角”“等角对等边”指的是同一个三角形中边角之间的转化关系,不能与全等混淆.3.等腰三角形“三线合一”的“三线”是指底边的中线、高线和顶角平分线.4.勾股定理描述直角三角形边之间的关系,主要应用于线段长度的计算,注意其前提条件是在直角三角形中,因此构造直角三角形是应用勾股定理最重要的一个步骤.5.等腰三角形中按边分类、直角三角形中按直角分类是特殊三角形问题中常见的分类讨论,要注意合理分类. 练习1.(杭州市江干区)用反证法证明“三角形中必有一个内角不小于60°”时,应当假设这个三角形中( )A.有一个内角小于60°B.每一个内角都小于60°C.有一个内角大于60°D.每一个内角都大于60°2.(湖州市吴兴区)如图所示,在∠ABC 中,AB =AC =5,BC =8,CD 是AB 边上的高,则线段AD 的长度为( )A. 125B. 245C. 135D. 75(第2题)(第3题)(第4题)(第5题)(第6题)3.(杭州市江干区)如图所示,在Rt∠ABC 中,∠C =90°,BC =6,DE 是斜边AB 的中垂线,交AC 于点E ,∠EBC 的周长为14,则AB = .4.(嘉兴市)如图所示,已知正方形ABCD 的边长是2cm ,E 是CD 边的中点,点F 在BC 边上移动,当AE 恰好平分∠FAD 时,CF = cm.5.(杭州市萧山区)如图所示,在∠ABC 中,AB =AC ,∠BAC =120°,S ∠ABC =8√3,M ,P ,N 分别是边AB ,BC ,AC 上任意一点. (1)AB 的长为 .(2)PM+PN 的最小值为 .6.(嵊州市)如图所示,∠ABC 是边长为12的等边三角形,点D ,E 分别在AB ,BC 上,且BE =BD =10,P 是线段DE 上的一个动点,分别作点P 关于AB ,AC ,BC 的对称点P 1,P 2,P 3,若连结P 1,P 2,P 3所得的三角形是等腰三角形,则DP = .。
浙教版八年级三角形及特殊三角形总复习

浙教版八年级三角形及特殊三角形总复习在八年级的数学学习中,三角形及特殊三角形是一个重要的知识点板块。
这部分内容不仅在数学学科中具有基础地位,还在实际生活中有着广泛的应用。
接下来,让我们一起对浙教版八年级三角形及特殊三角形进行一次全面的总复习。
一、三角形的基本概念三角形是由三条线段首尾顺次相接所组成的封闭图形。
它有三个顶点、三条边和三个内角。
三角形的内角和为 180 度,这是三角形的一个重要性质。
在三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
这个性质在判断三条线段能否组成三角形时非常有用。
二、三角形的分类1、按角分类三角形可以分为锐角三角形、直角三角形和钝角三角形。
锐角三角形的三个内角都小于 90 度;直角三角形有一个内角等于 90 度;钝角三角形有一个内角大于 90 度小于 180 度。
2、按边分类三角形可以分为等边三角形、等腰三角形和不等边三角形。
等边三角形的三条边都相等;等腰三角形有两条边相等;不等边三角形的三条边都不相等。
三、特殊三角形1、等腰三角形(1)性质等腰三角形的两腰相等,两底角相等。
等腰三角形顶角的平分线、底边上的中线和底边上的高相互重合,简称“三线合一”。
(2)判定如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)。
2、等边三角形(1)性质等边三角形的三条边相等,三个内角都等于 60 度。
(2)判定三个角都相等的三角形是等边三角形;有一个角是 60 度的等腰三角形是等边三角形。
3、直角三角形(1)性质直角三角形的两条直角边的平方和等于斜边的平方(勾股定理)。
直角三角形中,30 度角所对的直角边等于斜边的一半。
(2)判定如果一个三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形。
四、三角形的全等1、全等三角形的概念能够完全重合的两个三角形叫做全等三角形。
2、全等三角形的性质全等三角形的对应边相等,对应角相等。
3、全等三角形的判定(1)“边边边”(SSS):三边对应相等的两个三角形全等。
浙教版八年级上册数学第二章特殊三角形全部知识点、考点及练习

浙教版八年级上册数学第二章特殊三角形全部知识点、考点及练习浙教版数学八年级上册第二章《特殊三角形》复习一、知识结构本章主要学习了等腰三角形的性质与判定、直角三角形的性质与判定以及勾股定理、HL 定理等知识,这些知识点之间的结构如下图所示:等腰Rt两直角三角形全等的判定直角三角形的性质和判定等边三角形的性质和判定等腰三角形的性质和判定直角三角形等边三角形等腰三角形特殊三角形二、重点回顾1.等腰三角形的性质:等腰三角形两腰_______;等腰三角形两底角______(即在同一个三角形中,等边对_____);等腰三角形三线合一,这三线是指________________、________________、________________,也就是说一条线段充当三种身份;等腰三角形是________图形,它的对称轴有_________条。
2.等腰三角形的判定:有____边相等的三角形是等腰三角形;有_____相等的三角形是等腰三角形(即在同一个三角形中,等角对_____)。
注意:有两腰相等的三角形是等腰三角形,这句话对吗?3.等边三角形的性质:等边三角形各条边______,各内角_______,且都等于_____;等边三角形是______图形,它有____条对称轴。
4.等边三角形的判定:有____边相等的三角形是等边三角形;有三个角都是______的三角形是等边三角形;有两个角都是______的三角形是等边三角形;有一个角是______的______ 三角形是等边三角形。
5.直角三角形的性质:直角三角形两锐角_______;直角三角形斜边上的中线等于_______;直角三角形两直角边的平方和等于________(即勾股定理)。
30°角所对的直角边等于斜边的________6.直角三角形的判定:有一个角是______的三角形是直角三角形;有两个角_______的三角形是直角三角形;两边的平方和等于_______的三角形是直角三角形。
七年级数学《特殊三角形》复习课件

EF=
BE+CF
3 1
2
变式3
如图:BO和CO分别是 △ABC的两个外角∠EBC
E
B1 3 O
2
、∠BCF的角平分线,过 A
F
点O作直线EF∥BC交AB
C
与AC延长线于E,F点,
猜想EF与BE,CF三者有何
数量关系?说明理由.
EF= BE+CF
A
E
D
A
M
D
Q
E
B
B C
CFΒιβλιοθήκη 解题反思EB
D
A
C
F
1 角平分线
.
2 多题归一
.
平行线 等腰三角形
我来当老师
你能仿造刚才的题目,自己编 一到题吗?请你的同学解答.
编题要求:题目条件中有角平分线和 平行线,结论是线段之间的数量关系.
我来当老 师
A
M
D
Q
E
B
C
F
E
B
D
A
C
F
编题要求:题目条件中有角平分线和 平行线,结论是线段之间的数量关系
我来当老师
你能仿造刚才的题目,自己编 一到题吗?请你的同学解答.
A
E
1 2
B
3
D
C
变式1
如图:△ABC中,CD、CE分别
是∠ACB的内角和外角的平分线,过D
点作DE∥BF交AC于Q,交CM于E,
则DQ=EQ,请说明理由.
A
M
D
Q
3
6E
15
24
B
CF
变式2
如图,在△ABC中, BO、CO分别平 分∠ABC、∠ACB,过点O作直线EF∥BC 交AB于E,交AC于F.猜想EF与BE、CF有 何关系?说明理由.
中考复习特殊三角形

中考复习特殊三角形中考对于每一位初中生来说都是一次重要的挑战,而数学中的特殊三角形更是考点中的重点。
特殊三角形包括等腰三角形、等边三角形和直角三角形,它们各自具有独特的性质和判定方法。
接下来,让我们一起深入复习这些特殊三角形的知识。
一、等腰三角形等腰三角形是指至少有两边相等的三角形。
相等的两条边称为这个三角形的腰,另一边称为底边。
两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
1、性质(1)等腰三角形的两腰相等。
(2)等腰三角形的两底角相等(简写成“等边对等角”)。
(3)等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)。
2、判定(1)如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)。
(2)有两条边相等的三角形是等腰三角形。
在解题中,我们常常利用等腰三角形的性质和判定来求解角度、边长等问题。
例如,已知一个等腰三角形的顶角为 80°,那么底角的度数就可以通过“(180°顶角)÷ 2”来计算,即(180° 80°)÷ 2 = 50°。
二、等边三角形等边三角形又称正三角形,为三边相等的三角形,其三个内角相等,均为 60°。
1、性质(1)等边三角形的三条边都相等。
(2)等边三角形的三个内角都相等,且均为 60°。
(3)等边三角形是轴对称图形,有三条对称轴。
2、判定(1)三边相等的三角形是等边三角形。
(2)三个角都相等的三角形是等边三角形。
(3)有一个角是 60°的等腰三角形是等边三角形。
等边三角形在实际问题中也有广泛的应用。
比如在建筑设计中,利用等边三角形的稳定性可以增强结构的牢固性。
三、直角三角形直角三角形是一个角为直角的三角形。
直角所对的边称为斜边,其余两边称为直角边。
1、性质(1)直角三角形两直角边的平方和等于斜边的平方(勾股定理)。
(2)在直角三角形中,两个锐角互余。
特殊三角形复习

M
E
A
例4. 如图2-8-6,在△ABC中AB=AC=CB, AE=CD, AD、BE相交于P,BQ⊥AD于Q. 请说明BP=2PQ的理由.
思路 在Rt△BPQ中,本题的结论等价于证明∠PBQ=30°
证明 ∵AB=CA,∠BAE=∠ACD=60°, AE=CD, ∴△BAE≌△ACD ∴∠ABE=∠CAD ∴∠BPQ=∠ABE+∠BAP =∠CAD+∠BAP=60° 又∵BQ⊥AD ∴∠PBQ=30° ∴BP=2PQ 说明 本题把证明线段之间的关系转化为证明角的度数,这种转换问题的方 法值得同学们细心体会。
2 2
D
B
C
E
49 — 3
2、当BC为腰时,设∠B为顶角,分下面几种情况讨论:
(1) 顶角B为锐角时,如图: ∵ AD=1/2BC=1/2AB AD ⊥BC ∴ ∠B= 300 ∴ ∠BAC= ∠C= 1/2(1800﹣300 )= 750
B
D
C
A
(2)当顶角B为钝角时,如图:
D ∵ AD ⊥BC AD=1/2BC=1/2AB ∴ ∠ABD= 300 ∴ ∠BAC= ∠C= 1/2 ∠ABD = 150 B C
互余 。 1 在直角三角形中,两个锐角_______ 两直角边 的平方和等于_______ 斜边 的平方。 2、直角三角形_____________ 如果用字母a,b和c分别表示直角三角形的两条直角边和 2 2 2 b c a 斜边,那么_____+ _____=_____。 较小 两边的平方和等于______ 较大 一边 3、如果三角形中_______ 斜边 所对的角是 的平方,那么这个三角形是直角三角形,________ 直角。 30 度,那么它所对 4、在直角三角形中,如果一个锐角等于 _____ 斜边 的一半。 的直角边等于_________ 斜边的一半 那么这 5、在直角三角形中,如果一条直角边等于___________, 条直角边所对的角等于300。
特殊三角形(等腰三角形与直角三角形)2024年中考数学一轮复习之核心考点精讲精练(原卷版)

考点16.特殊三角形(等腰三角形与直角三角形)(精讲)【命题趋势】特殊的三角形重在掌握基本知识的基础上灵活运用,也是考查重点,年年都会考查,分值为10分左右,预计2024年各地中考还将出现,并且在选择、填空题中考查等腰(等边)三角形性质与判定和勾股(逆)定理、直角三角形的性质、尺规作图等知识点结合考查,这部分知识需要学生扎实地掌握基础,并且会灵活运用。
在解答题中会出现等腰三角形与直角三角形的性质和判定,这部分知识主要考查基础。
【知识清单】1:等腰(等边)三角形的性质与判定(☆☆☆)1)等腰三角形的定义:有两边相等的三角形角等腰三角形。
2)等腰三角形的性质:(1)等腰三角形的两个底角相等(简称“等边对等角”)。
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称“三线合一”)。
3)等腰三角形的判定:若某三角形有两个角相等,那这两个角所对的边也相等(简称“等角对等边”)。
4)等边三角形的定义:三条边都相等的三角形叫等边三角形,它是特殊的等腰三角形。
5)等边三角形的性质:(1)等边三角形的三条边相等;(2)三个内角都相等,且每个内角都是60°;(3)等边三角形(边长为a6)等边三角形的判定:(1)三边相等或三个内角都相等的三角形是等边三角形;(2)有一个角是60°的等腰三角形是等边三角形。
2:垂直平分线的性质与判定(☆☆)1)垂直平分线的定理:经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线)。
2)垂直平分线的性质:线段的垂直平分线上的点到这条线段两个端点的距离相等。
3)垂直平分线的判定:到一条线段两个端点距离相等的点在这条线段的垂直平分线上。
3:勾股定理与逆定理及其应用(☆☆)1)勾股定理:直角三角形的两条直角边a、b的平方和等于斜边c的平方,即:a2+b2=c2.2)勾股定理的逆定理:若三角形的三条边a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形.4:直角三角形的性质及计算(☆☆☆)1)直角三角形的定义:有一个角是直角的三角形叫做直角三角形.2)直角三角形的性质:(1)直角三角形两个锐角互余;(2)直角三角形斜边上的中线等于斜边的一半;(3)在直角三角形中,30°角所对的直角边等于斜边的一半。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C B
C Q ①设△AQP的面积为y(cm2),求y与t之间的函数关系式; A ②是否存在某一时刻t,使线段PQ恰好把 Rt△ACB的周长
和面积同时平分?若存在,求出此时的值,若不存在,说明
理由。
小结
拓展
回味无穷
变式2.
过E点作EM⊥BC于M,连接FM,判断四边形AEMF的 形状,并说明理由。
G A F B E
D
M
C
巩固
提高
A
1、如图,在△ABC中,AB=AC , D为AC边上一点,且BD=BC=AD, 则∠ A的度数为( D) ° A 20 ° B 25 ° C 30 ° D 36 2、如图,在Rt△ABC中,∠ACB =90。,AB的垂直平分线分别交BC、 AB于点M、N,BC=2 3 。 (1)若AC= 3 ,则△AMC周长为
在同一个三角形中, 等角对等边
1、有一个角等于90· 的三角形是直角三角形; 2、如果三角形中两边 的平方和等于第三边的 平方,那么这个三角形 是直角三角形。
A. 1个
B. 2个
C. 3个
D. 4个
课前
诊断
6、如图,在Rt△ABC中, 。 ∠BAC=90 A 。 ∠ACB=45 , AD⊥BC于D。 B D C (1)图中等腰直角三角 形的个数为( C )
证明: △AEF是等腰三角形 理由:∵ ∠BAC=90° ∴ ∠1 + ∠4 = 90° ∵ AD⊥BC ∴ ∠ ADB= 90° B ∴ ∠2 +∠5 = 90° 又∵ BE平分∠ABC ∴ ∠1 = ∠2 ∴ ∠4 = ∠5 ∵ ∠3 = ∠5 ∴ ∠3 = ∠4 ∴ △AEF是等腰三角形
F3
1 5 2
A、1个 B、2个
直角三角形斜边上的中 线等于斜边的一半
C、3个 D、4个
2 (2)若AB=2,则线段AD的长为_______
知识
结构
定义
定义
三 角 特殊三角形 形
等腰三角形 性质 特殊 等边三角形 性质
判定
定义 直角三角形 性质 判定
判定
例题
讲解
如图(1),在Rt△ABC中,∠BAC=90° , ∠ACB=45°, AD⊥BC于D,BE平分∠ABC分别交AC、AD于点E 和点F。请判断△AEF的形状,并说明理由. A
D B C
B
N M
15 3 3 ,线段CN的长为____ 2 ___
等边 三角形 (2)若AC=2 ,则△CAN是_____
C
A
拓展
பைடு நூலகம்
延伸
如图,在Rt△ACB中, ∠C=
D A E P
B
90。,AC=4cm,BC=3cm,沿BE折叠后,点 C落在AB边上的点D处,连接DE,
(1)求△ABE的面积.
(2)若点P由B出发沿BA方向向点A匀 速运动,速度为1cm/s;点Q由点A出发沿 AC方向向点C匀速运动,速度为2cm/s; 连接PQ,如下图所示。若设运动的时间t (s)(0<t<2),解答下列问题
课前
诊断
等腰三角形两 底角相等
1、已知等腰三角形一个内角
的度数为40°,那么它的
底角的度数是
70 ° 、70 °或40 ° 、40 ° ___________________
2、已知等腰三角形的两边长 分别是3和7,则它的周长
17 是_____
等腰三角形两 腰相等
3、已知等边三角形的边长为 2cm,则该等边三角形的
4
E C
D
变式1. 将△ABE绕点A逆时针旋转90 °得到△ ACG,线段BE 与CG有什么关系呢?说明理由。 证明: BE ⊥ CG且 BE = CG 理由:延长BE交CG于H点 ∵ △ ACG 是由△ABE旋转所得 G ∴ △ ACG ≌ △ABE A ∴ BE =CG , ∠G =∠3 H 3 4 ∵ ∠1 + ∠3= 90 ° F E 2 1 ∴∠CHB=∠G+∠1=90 ° B C D ∴ BE ⊥ CG ∴ BE ⊥ CG且 BE = CG
面积为______ 3
等腰三角形底边上 的中线,顶角的平分 线,底边上的高三 线合一
4、如果三角形一个外角的平分线 平行与三角形的第三边,那么 这个三角形一定是( A) A 等腰三角形 B 等边三角形 C 直角三角形 D 不等边三角形 5、有四个三角形,分别满足下列 条件:其中直角三角形有( C ) (1) 一个内角等于另外两个内 角之和; (2) 三个内角之比为3∶4∶5; (3) 三边之比为5∶12∶13; (4) 三边长分别为7、24、25.
