统计学课件(第四版)第四章
合集下载
概率论与数理统计第四版第四章
定理2的结果用于计算卡方分布的期望值和方差。
解：让定理2 xedx 4成为随机变量。
尝试证明定理5。
证明：因为，让定理1让总体x服从[0，b]上的均匀分布，并且B是未知的。
尝试找到未知样本值（1.3、0.6、1.7、2.2、0.3、1.1）以找到未知样本，即样本，尝试进行分析：X的概率密度是给定样本值的概率密度，要求使用尽可能小的值，并且最大值应为（相对于给定样本值，如果可能的话）。
最大似然估计方法用于估计总体的未知参数，并且总体θ的概率密度是lnln的样本。
（1）样本方差s的无偏估计。
（2）对于任何α，它也是λ的无偏估计。
解决方案：（1）无偏估计原因。
（2）因为x 是λ的无偏估计，所以它也是λ的无偏估计。
11.对于已知平方差的正常总体，要使总体置信区间的平均值不大于给定正数l的样本大小n是多少？当已知总体的置信区间为-3.0％时，正常解的置信区间为-3.0％，并且已知总体的置信区间为-0.9％。
总体平均值的95％置信区间为315.5％。
因此，正常总体平均值的95％置信区间是样本值，而正常总体平均值的95％置信区间为（-2.751，3.501）。
质量指标数据如下：0.143、0.142、0.143、0.137批次：0.140、0.142、0.136、0.138、0.140。
测试数据独立且未知。
尝试找出95％的置信区间，是否可以认为这两个批次的产品质量存在显着差异？样本值0023的95％置信区间为（-0.002，0.006）。
14.某种容量为100的电子管的寿命样本的标准偏差为45。
给出了这些管的寿命种群（设置为正常种群）的标准偏差σ的95％置信区间。
因为05的95％置信区间为（1566.212747.74），所以标准偏差的95％置信区间为（39.58,52.42）。
15.为了检查两名工人的生产技能的稳定性，在一天中从他们的产品中选择了容量分别为25和15的两个样本，样本的方差计算如下。
让这两个样本来自正常总体，并尝试找到方差。
统计学 第四版 (贾俊平 著) 中国人民大学出版社 第四章课后答案
解: （1）
62.75
2 33.9375
82 64
（2） 可能的样本个数：
（3）由题可得所有样本的样本均值如下表：
第（3）小题图表
（4）利用SPSS软件得到Q-Q图：
（5）
x i 1
xi 64
m
62.75
33.9375 x 4.1193 2 n
0 4
(2) P（X≤2 ）=
4.3 求标准正态分布的概率： （1）P ( 0 ≤ Z ≤ 1.2) ; （2）P ( -0.48 ≤ Z ≤ 0); （3）P (Z > 1.33)。
解: （1）P ( 0 ≤ Z ≤ 1.2) = P ( 1.2) -P ( 0 )= 0.3849 （2）P ( -0.48 ≤ Z ≤ 0 ) = P ( 0) -P (-0.48)= 0.1844 （3）P (Z > 1.33) = P ( -1.33) = 0.0918
(1 )
500 0.4 0.6 0.0219089 500
（2）
（3）由中心极限定理可知 p的分布近似正态分布
4.7 假设一个总体共有8个数值： 54，55，59，63，64，68，69，70.从该总体 中按重复抽样方式抽取n=2的随机样本。
（1）计算总体的均值和方差。 （2）一共有多少个可能的样本？ （3）抽出所有可能的样本，并计算出每个样本的均值。 （4）画出样本均值的正态概率图，判断样本均值是否服从正态分布。 （5）计算所有样本均值的平均数和标准差，并与总体的均值和标准差进行对比得 到的结论是什么？
E ( x ) 200
n 50 5 100
（2 ） x
（3） 由中心极限定理可知 X 的概率分布近似服从正态分布
62.75
2 33.9375
82 64
（2） 可能的样本个数：
（3）由题可得所有样本的样本均值如下表：
第（3）小题图表
（4）利用SPSS软件得到Q-Q图：
（5）
x i 1
xi 64
m
62.75
33.9375 x 4.1193 2 n
0 4
(2) P（X≤2 ）=
4.3 求标准正态分布的概率： （1）P ( 0 ≤ Z ≤ 1.2) ; （2）P ( -0.48 ≤ Z ≤ 0); （3）P (Z > 1.33)。
解: （1）P ( 0 ≤ Z ≤ 1.2) = P ( 1.2) -P ( 0 )= 0.3849 （2）P ( -0.48 ≤ Z ≤ 0 ) = P ( 0) -P (-0.48)= 0.1844 （3）P (Z > 1.33) = P ( -1.33) = 0.0918
(1 )
500 0.4 0.6 0.0219089 500
（2）
（3）由中心极限定理可知 p的分布近似正态分布
4.7 假设一个总体共有8个数值： 54，55，59，63，64，68，69，70.从该总体 中按重复抽样方式抽取n=2的随机样本。
（1）计算总体的均值和方差。 （2）一共有多少个可能的样本？ （3）抽出所有可能的样本，并计算出每个样本的均值。 （4）画出样本均值的正态概率图，判断样本均值是否服从正态分布。 （5）计算所有样本均值的平均数和标准差，并与总体的均值和标准差进行对比得 到的结论是什么？
E ( x ) 200
n 50 5 100
（2 ） x
（3） 由中心极限定理可知 X 的概率分布近似服从正态分布
统计学(中国人民大学出版社)第四版PPT
对总体特征作出推断
推断统计
中国人口状况？ —普查？ —抽样？ 总量？结构？ 总体
抽样
推断
样本
描述统计与推断统计的关系
概率论
（包括分布理论、大数定律 和中心极限定理等）
样本数据
描述统计
（统计数据的搜集、整 理、显示和分析等）
推断统计
（利用样本信息和概率 论对总体的数量特征进 行估计和检验等）
反映客观 现象的数 据
资本主义的兴起：统计扩展到社会经济各方面。
统计学作为一门系统的科学，距今只有300多年的历史。
发展(三个时期) （一）统计学的萌芽期（17世纪中－18世纪中）
1、德国的记述学派（国势学派〕 康令 （1606－1681） 阿痕瓦尔（1719－1772； 1764年首创统计学一词） 他们在大学中开设“国势学”采用记述性材料，讲述国家“显著事项” 籍以说明管理国家的方法。重质轻量 2、政治算术学派 代表人物：英国的威廉«配第、约翰«格朗特等。威廉«配第的代表作《政治 算术》对当时的英、荷、法等国的“国富和力量”进行了数量的计算和比较。
农林牧渔业统计报表制度 工业统计报表制度 建筑业统计报表制度 固定资产投资统计报表制度 科技统计报表制度 城镇劳动力调查制度; 人口变动情况抽样调查方案 ; 农村住户抽样调查方案; 价格统计报表制度
城市住户调查方案
2002年批准实施的一次性调查项目; 2001年已批准实施一次性调查项目; 第三次全国工业普查实施方案; 基本单位普查制度; 农业普查制度; 工业普查制度
频率% 56.0 25.5 4.5 5.0 1.0 8.0
120 100 80 60 40 20 0
112
51 9
电视 网络 杂志
统计学原理第四章PPT学习教案
（二）比例相对指标 （轻重工业比例）
比例相对指标是总体中不同部分数量对比的相对指标，用以分析总 体范围内各个局部、各个分组之间的比例关系和协调平衡状况。
比例相对指标
总体中某一部分数量 总体中另一部分数值
第8页/共41页
第二节 相对指标
（三）比较相对指标
比较相对指标是不同单位的同类现象数量对比而确定的相对指标， 用以说明某一同类现象在同一时间内各单位发展的不平衡程度，以 表明同类实物在不同条件下的数量对比关系。
第9页/共41页
第二节 相对指标
（四）强度相对指标 强度相对指标是两个性质不同但有一定联系的总量指标之间的对比， 用来表明某一现象在另一现象中发展的强度、密度和普遍程度。它和 其他相对指标的根本区别就在于它不是同类现象指标的对比。强度相 对强指度标相以对双指重标计量另单一位个表有示联，系某是而种一性现质种象不复总名量同指数的标。现象总量指标 强度相对指标的分子分母位置可以互换，因而有正指标、逆指标之分。 实际应用时应注意与平均指标的区别。
水泥——（80/100）=80% 第二季度 生铁——（618/600）=103%，钢材—— （300/350）=85.71%
水泥——（180/200）=90% 2）求上半年（一，二季度合并）进货 情况， 解法同 上 生铁——（618+500）/（600+500）= 101.64% 钢材——（300+300）/（250+350）= 100% 水泥——（180+80）/300=86.67% 3）上半年累计计划完成程度执行情况 （计划 期一年 ，实际 期半年 ） 生铁——（618+500）/2000=55.9% 钢材——（600）/1000=60% 水泥——260/500=52%
统计学(第四版)袁卫庞皓贾俊平杨灿(04)第4章参数估计(贾俊平)
4 -2
统计学
STATISTICS
4.1 参数估计的一般问题
一、估计量与估计值 二、点估计与区间估计 三、评价估计量的标准
统计学
STATISTICS
估计量与估计值
统计学
估计量与估计值
STATISTICS (estimator & estimated value)
1. 估计量：用于估计总体参数的随机变量
P(ˆ ) 较大的样本容量
B
较小的样本容量
A
4 - 16
ˆ
统计学 4.2 一个总体参数的区间估计
STATISTICS
一、总体均值的区间估计 二、总体比率的区间估计 三、总体方差的区间估计
统计学
STATISTICS
一个总体参数的区间估计
总体参数 均值 比率 方差
4 - 18
符号表示 样本统计量
x
p
4 - 11
统计学
STATISTICS
影响区间宽度的因素
1. 总体数据的离散程度，用 来测度
2.
样本容量， x
n
3. 3. 置信水平 (1 - )，影响 z 的大小
4 - 12
统计学
STATISTICS
评价估计量的标准
统计学
STATISTICS
无偏性
(unbiasedness)
无偏性：估计量抽样分布的数学期望等于被 估计的总体参数
(point estimate)
1. 用样本的估计量直接作为总体参数的估计值
▪ 例如：用样本均值直接作为总体均值的估计 ▪ 例如：用两个样本均值之差直接作为总体均值
之差的估计
2. 没有给出估计值接近总体参数程度的信息
统计学第四章课件
合人们的认识规律，通常用xG 来表示。
一、分布的集中趋势
1. 简单几何平均数
简单几何平均数适用于资料未进行分组 的情况。其计算公式为
（4-8）
式中， xG 为几何平均数；xi为变量值；n为
变量值个数；Ⅱ为连乘符号。
一、分布的集中趋势
【例4-6】 某企业生产某种产品要经过三个连续的作业车间才能完 成。若某月份第一车间粗加工产品的合格率为95％，第二车间精加工产 品的合格率为93％，第三车间最后装配的合格率为90％，则该产品的企 业合格率（三个车间的平均合格率）为多少?
一、分布的集中趋势
此外，从上述表达式中可以看出，加权算术平均 数受两个因素的影响：一是各组的标志值，二是各组 的单位数或频率。当各组的标志值不变时，其出现的 次数f对于平均数的大小起着权衡轻重的作用，统计学 称其为权数。当各组次数相等时，影响平均数的因素 就只有一个，即各组的标志值，这时加权算术平均数 就等于简单算术平均数。可见，简单算术平均数是加 权算术平均数的特例。
一、分布的集中趋势
【例4-13】 表4-9为某企业工人工资资料，试计算其中位数。
表4-9 某企业工人工资资料
一、分布的集中趋势
确定中位数的方法如下： ①计算累计频数，见表4-9第3栏和第4栏。 ②利用公式∑f/2确定中位数的项次，∑f/2=120/2=60。 ③通过观察，找到中位数(以向上累计为例)，从向上累计频数可知，从 第41个工人到第80个工人都包含在了第三组中。由此可以判断，第60个 工人也应在第三组里。 ④利用公式求得中位数近似值(以上限公式为例)。
一、分布的集中趋势
解：中位数的位置=（n+1）/2=（11+1）÷2=6，则 中位数为第6号位置的零件数，即Me=x(6)=24件。
一、分布的集中趋势
1. 简单几何平均数
简单几何平均数适用于资料未进行分组 的情况。其计算公式为
（4-8）
式中， xG 为几何平均数；xi为变量值；n为
变量值个数；Ⅱ为连乘符号。
一、分布的集中趋势
【例4-6】 某企业生产某种产品要经过三个连续的作业车间才能完 成。若某月份第一车间粗加工产品的合格率为95％，第二车间精加工产 品的合格率为93％，第三车间最后装配的合格率为90％，则该产品的企 业合格率（三个车间的平均合格率）为多少?
一、分布的集中趋势
此外，从上述表达式中可以看出，加权算术平均 数受两个因素的影响：一是各组的标志值，二是各组 的单位数或频率。当各组的标志值不变时，其出现的 次数f对于平均数的大小起着权衡轻重的作用，统计学 称其为权数。当各组次数相等时，影响平均数的因素 就只有一个，即各组的标志值，这时加权算术平均数 就等于简单算术平均数。可见，简单算术平均数是加 权算术平均数的特例。
一、分布的集中趋势
【例4-13】 表4-9为某企业工人工资资料，试计算其中位数。
表4-9 某企业工人工资资料
一、分布的集中趋势
确定中位数的方法如下： ①计算累计频数，见表4-9第3栏和第4栏。 ②利用公式∑f/2确定中位数的项次，∑f/2=120/2=60。 ③通过观察，找到中位数(以向上累计为例)，从向上累计频数可知，从 第41个工人到第80个工人都包含在了第三组中。由此可以判断，第60个 工人也应在第三组里。 ④利用公式求得中位数近似值(以上限公式为例)。
一、分布的集中趋势
解：中位数的位置=（n+1）/2=（11+1）÷2=6，则 中位数为第6号位置的零件数，即Me=x(6)=24件。
统计学第四版(贾俊平著)中国人民大学出版社第四章课后答案PPT课件
4.3 求标准正态分布的概率：
（1）P ( 0 ≤ Z ≤ 1.2) ; （2）P ( -0.48 ≤ Z ≤ 0); （3）P (Z > 1.33)。
解:
（1）P ( 0 ≤ Z ≤ 1.2) = P ( 1.2) -P ( 0 )= 0.3849 （2）P ( -0.48 ≤ Z ≤ 0 ) = P ( 0) -P (-0.48)= 0.1844 （3）P (Z > 1.33) = P ( -1.33) = 0.0918
统计学第四章课后习题
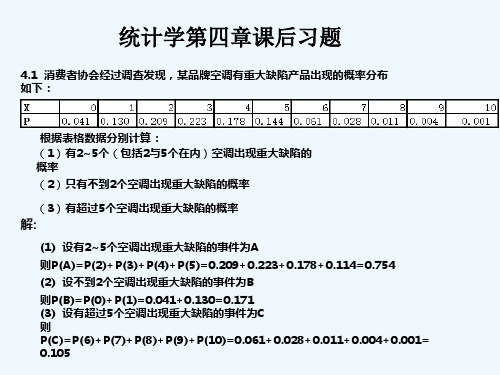
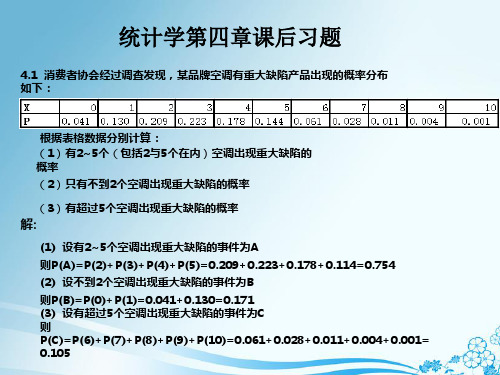
4.1 消费者协会经过调查发现，某品牌空调有重大缺陷产品出现的概率分布 如下：
根据表格数据分别计算： （1）有2~5个（包括2与5个在内）空调出现重大缺陷的 概率 （2）只有不到2个空调出现重大缺陷的概率
（3）有超过5个空调出现重大缺陷的概率
解:
(1) 设有2~5个空调出现重大缺陷的事件为A 则P(A)=P(2)+P(3)+P(4)+P(5)=0.209+0.223+0.178+0.114=0.754 (2) 设不到2个空调出现重大缺陷的事件为B 则P(B)=P(0)+P(1)=0.041+0.130=0.171 (3) 设有超过5个空调出现重大缺陷的事件为C 则 P(C)=P(6)+P(7)+P(8)+P(9)+P(10)=0.061+0.028+0.011+0.004+0.001= 0.105
用样本均值 X 估计总体均值
（1）X 的期望是多少？ （2）X 的标准差是多少？ （3）X 的概率分布是什么？
解:
（1） E(x) 200
（2）
x
统计学第四章课件
（2） f=27， f-1=16 ） =27，
f+1=20
d=10
L=170 ，U=180
11 M0 =170 + ×10 11+ 7 7 M0 =180 − ×10 11+ 7
M0 =176.11
二、中位数（median） 中位数（median） 1、中位数：是指处在中间位置的变量值 中位数： (n +1) / 2 位置的数
注意： 注意： 无论给出的数据如何，一定要转化为绝对数! 无论给出的数据如何，一定要转化为绝对数!
计划完成程度计算例子
计划完成程度=实际完成绝对数/ 计划完成程度=实际完成绝对数/计划完成绝对数
•
例1 ：某年工业增加值计划指标为200万元， 某年工业增加值计划指标为200万元 万元， 实际完成增加值220万元 实际完成增加值220万元 计划完成程度=220/200=110% 计划完成程度=220/200=110% (超计划10%) 超计划10%)
② 确定中位数 Me 设中位数组的上下限为L 设中位数组的上下限为L 和K ，组距为d ，则中 组距为dm n − Sm+1 Me =U − 2 ×d fm
某电脑公司120天销售额分组 某电脑公司120天销售额分组
销售量分组 140－ 140－150 150－ 150－160 160－ 160－170 170－ 170－180 180－ 180－190 190－ 190－200 200－ 200－210 210－ 210－220 220－ 220－230 230－ 230－240 合计 频数 4 9 16 27 20 17 10 8 4 5 120
§4.2 相对指标 三、相对指标的种类和计算方法 结构相对指标(比重，频率) 结构相对指标(比重，频率) 结构相对数指标： 结构相对数指标：反映同一时期总体内部组成 状况的相对指标 结构相对指标计算 结构相对指标=部份/ 结构相对指标=部份/全部 例如：女工占全厂职工的比重为40%， 例如：女工占全厂职工的比重为40%，而女工 工作量占全厂工作量的45% 工作量占全厂工作量的45%
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
间估计； 掌握必要抽样数目的确定方法。
目录
4.1抽样推断的一般问题 4.2抽样误差 4.3抽样估计的方法 4.4抽样组织设计
4.1抽样推断的一般问题
4.1.1抽样推断的意义与特点
1.意义
对于无限总体，统计上无法进行全面调查了解，只有借助于抽样 推断的方法来认识总体的数量特征。
许多产品的例行质量检验是带有破坏性的或消耗性的。对这些总 体只能进行抽样调查。
4.2抽样误差
4.2.3抽样平均误差
抽样平均误差实际上是样本指标的标准差。 通常用μ表示。
4.2抽样误差
1.计算抽样平均误差的理论公式
抽取样本 样本平均数 x 误差 x X
2
xX
10 10
10
10 20
15
10 30
20
10 40
25
10 50
30
20 10
15
20 20
20
20 30
25
第4章 抽样推断
抽样估计
抽样估计的一般 问题
抽样误差
抽样估计的方法
抽样组织设计
抽样估计的意义 基本概念
抽样误差
抽样平均误差 抽样极限误差
点估计
区间估计 基本原则 必要抽样单位数
的确定
常用的抽样组织 形式
总体和样本 总体指标和样本指标 重复抽样和不重复抽
样 抽样误差的含义
主要影响因素
理论公式 计算公式
的资料，应选用数值较大的那个；
2. 用样本标准差S代替全及标准差σ； 3. 在大规模调查前，先搞个小规模的试验性的调查来
确定S，代替σ；
4. 用估计的方法。
例
某灯泡厂从一天所生产的产品10,000个中抽 取100个检查其寿命，得平均寿命为2000小时 (一般为重复抽样)，根据以往资料：σ=20小 时，
不重复抽样
不重复抽样（sampling without replacement）也叫不重置抽样，是 指每次从总体中抽取一个单位记录其标志表现后不再放回，从剩余的 单位中抽取下一个单位。
4.2抽样误差
4.2.1抽样误差的含义
在统计调查中，调查资料与实际情况不一致， 两者的偏离称为统计误差。
登记误差
统计误差
代表性误差
系统性误差
随机误差
实际误差 抽样平均误差
抽样误差即指随机误差，这种误差是抽 样调查固有的误差，是无法避免的。
4.2抽样误差
4.2.2影响抽样误差的主要因素
1. 全及总体标志变异程度。——正比关系 2. 抽样单位数目的多少。——反比关系 3. 不同的抽样方式。 4. 不同的抽样组织形式。
4.1抽样推断的一般问题
4.1.2有关抽样的基本概念
1.总体和样本
全及总体：所要调查观察的全部事物。 总体单位数用N表示。
抽样总体：抽取出来调查观察的单位。 抽样总体的单位数用n表示。 n ≥ 30 大样本 n < 30 小样本
4.1抽样推断的一般问题
4.1.2有关抽样的基本概念
2.总体指标和样本指标 总体指标
202 2(小时) x 100
根据以往资料，产品质量不太稳定，若σ=200 小时，
于是： 20(小时)
抽样平均误差( )
x
n
2500 10(元) 25
(n为样本配合总数 )
4.2抽样误差
以上资料编成次数分配表如下：
x
10 15 20 25 30 35 40 45 50 合计
样本数f (即次数分配)
1 2 3 4 5 4 3 2 1
25
xX
-20 -15 -10
-5 0 5 10 15 20 -
样本指标主要有：样本平均数： x 样本比率 p（或 q）
样本方差： s 2 样本标准差： s
4.1抽样推断的一般问题
4.1.2有关抽样的基本概念
3.重复抽样和不重复抽样
重复抽样
重复抽样（sampling with replacement）也叫重置抽样，是指每次 抽取一个单位记录其标志表现后又放回，重新参加下一次的抽选。
45
50 10
30
50 20
35
50 30
40
50 40
45
50
50
50
合
计
-
2
误差 x X x X
5
25
10
100
-5
25
0
0
5
25
10
100
15
225
0
0
5
25
10
100
15
225
20
400
-
2 500
4.2抽样误差
抽样平均误差
(样本指标 总体指标)2
可能组成的样本总数
(x X )2
总体指标是根据全及总体所有单位的标志值计算出来的，反映总体的 数量特征。总体指标也称为总体参数(Parameter)，或参数。
总体指标主要有：总体平均数：X
总体比率 P（或 Q）
总体方差： 2
总体标准差：
4.1抽样推断的一般问题
4.1.2有关抽样的基本概念
2.总体指标和样本指标 样本指标
由样本总体各个单位的标志值计算的综合指标称为样本指标，样本指标又称为 样本统计量（Statistic），简称为统计量。
20 40
30
20 50
35
30 10
20
30 20
ห้องสมุดไป่ตู้
25
30 30
30
-20
400
-15
225
-10
100
-5
25
0
0
-15
225
-10
100
-5
25
0
0
5
25
-10
100
-5
25
0
0
接左：
抽取样本 样本平均数 x
30 40
35
30 50
40
40 10
25
40 20
30
40 30
35
40 40
40
40 50
对于某些现象，虽然可以进行全面调查，但需要花费大量的人力、 物力、财力和时间，若采用抽样调查，可以达到事半功倍的效果。
对全面调查的资料进行评价与修正。
在对工业生产过程的质量控制。
4.1抽样推断的一般问题
4.1.1抽样推断的意义与特点
2.特点
抽样调查是由部分推算整体的一种认识方法； 抽样推断是建立在随机取样的基础上的； 抽样推断是运用概率估计的方法； 抽样推断的误差可以事先计算并加以控制。
2
(x X) f f
4.2抽样误差
∴抽样误差是所有可能出现的样本指标的标准 差。它是由于抽样的随机性而产生的样本指标 与总体指标之间的平均离差。
4.2抽样误差
2.抽样平均误差的计算公式
（1）平均数的抽样平均误差 重复抽样
x
n
或 2
x
n
4.2抽样误差
取得σ的途径有：
1. 用过去全面调查或抽样调查的资料，若同时有n个σ
无偏性 一致性 有效性
总体平均数的区间估 计
总体成数的区间估计
影响因素 计算公式
简单随机抽样 类型抽样 等距抽样 整群抽样
本章学习目标
理解抽样估计的概念、特点、作用以及几个 基本概念；
掌握抽样误差的含义和影响抽样误差的主要 因素；
熟练掌握抽样平均误差的计算； 熟练掌握抽样估计的两种方法：点估计和区
目录
4.1抽样推断的一般问题 4.2抽样误差 4.3抽样估计的方法 4.4抽样组织设计
4.1抽样推断的一般问题
4.1.1抽样推断的意义与特点
1.意义
对于无限总体，统计上无法进行全面调查了解，只有借助于抽样 推断的方法来认识总体的数量特征。
许多产品的例行质量检验是带有破坏性的或消耗性的。对这些总 体只能进行抽样调查。
4.2抽样误差
4.2.3抽样平均误差
抽样平均误差实际上是样本指标的标准差。 通常用μ表示。
4.2抽样误差
1.计算抽样平均误差的理论公式
抽取样本 样本平均数 x 误差 x X
2
xX
10 10
10
10 20
15
10 30
20
10 40
25
10 50
30
20 10
15
20 20
20
20 30
25
第4章 抽样推断
抽样估计
抽样估计的一般 问题
抽样误差
抽样估计的方法
抽样组织设计
抽样估计的意义 基本概念
抽样误差
抽样平均误差 抽样极限误差
点估计
区间估计 基本原则 必要抽样单位数
的确定
常用的抽样组织 形式
总体和样本 总体指标和样本指标 重复抽样和不重复抽
样 抽样误差的含义
主要影响因素
理论公式 计算公式
的资料，应选用数值较大的那个；
2. 用样本标准差S代替全及标准差σ； 3. 在大规模调查前，先搞个小规模的试验性的调查来
确定S，代替σ；
4. 用估计的方法。
例
某灯泡厂从一天所生产的产品10,000个中抽 取100个检查其寿命，得平均寿命为2000小时 (一般为重复抽样)，根据以往资料：σ=20小 时，
不重复抽样
不重复抽样（sampling without replacement）也叫不重置抽样，是 指每次从总体中抽取一个单位记录其标志表现后不再放回，从剩余的 单位中抽取下一个单位。
4.2抽样误差
4.2.1抽样误差的含义
在统计调查中，调查资料与实际情况不一致， 两者的偏离称为统计误差。
登记误差
统计误差
代表性误差
系统性误差
随机误差
实际误差 抽样平均误差
抽样误差即指随机误差，这种误差是抽 样调查固有的误差，是无法避免的。
4.2抽样误差
4.2.2影响抽样误差的主要因素
1. 全及总体标志变异程度。——正比关系 2. 抽样单位数目的多少。——反比关系 3. 不同的抽样方式。 4. 不同的抽样组织形式。
4.1抽样推断的一般问题
4.1.2有关抽样的基本概念
1.总体和样本
全及总体：所要调查观察的全部事物。 总体单位数用N表示。
抽样总体：抽取出来调查观察的单位。 抽样总体的单位数用n表示。 n ≥ 30 大样本 n < 30 小样本
4.1抽样推断的一般问题
4.1.2有关抽样的基本概念
2.总体指标和样本指标 总体指标
202 2(小时) x 100
根据以往资料，产品质量不太稳定，若σ=200 小时，
于是： 20(小时)
抽样平均误差( )
x
n
2500 10(元) 25
(n为样本配合总数 )
4.2抽样误差
以上资料编成次数分配表如下：
x
10 15 20 25 30 35 40 45 50 合计
样本数f (即次数分配)
1 2 3 4 5 4 3 2 1
25
xX
-20 -15 -10
-5 0 5 10 15 20 -
样本指标主要有：样本平均数： x 样本比率 p（或 q）
样本方差： s 2 样本标准差： s
4.1抽样推断的一般问题
4.1.2有关抽样的基本概念
3.重复抽样和不重复抽样
重复抽样
重复抽样（sampling with replacement）也叫重置抽样，是指每次 抽取一个单位记录其标志表现后又放回，重新参加下一次的抽选。
45
50 10
30
50 20
35
50 30
40
50 40
45
50
50
50
合
计
-
2
误差 x X x X
5
25
10
100
-5
25
0
0
5
25
10
100
15
225
0
0
5
25
10
100
15
225
20
400
-
2 500
4.2抽样误差
抽样平均误差
(样本指标 总体指标)2
可能组成的样本总数
(x X )2
总体指标是根据全及总体所有单位的标志值计算出来的，反映总体的 数量特征。总体指标也称为总体参数(Parameter)，或参数。
总体指标主要有：总体平均数：X
总体比率 P（或 Q）
总体方差： 2
总体标准差：
4.1抽样推断的一般问题
4.1.2有关抽样的基本概念
2.总体指标和样本指标 样本指标
由样本总体各个单位的标志值计算的综合指标称为样本指标，样本指标又称为 样本统计量（Statistic），简称为统计量。
20 40
30
20 50
35
30 10
20
30 20
ห้องสมุดไป่ตู้
25
30 30
30
-20
400
-15
225
-10
100
-5
25
0
0
-15
225
-10
100
-5
25
0
0
5
25
-10
100
-5
25
0
0
接左：
抽取样本 样本平均数 x
30 40
35
30 50
40
40 10
25
40 20
30
40 30
35
40 40
40
40 50
对于某些现象，虽然可以进行全面调查，但需要花费大量的人力、 物力、财力和时间，若采用抽样调查，可以达到事半功倍的效果。
对全面调查的资料进行评价与修正。
在对工业生产过程的质量控制。
4.1抽样推断的一般问题
4.1.1抽样推断的意义与特点
2.特点
抽样调查是由部分推算整体的一种认识方法； 抽样推断是建立在随机取样的基础上的； 抽样推断是运用概率估计的方法； 抽样推断的误差可以事先计算并加以控制。
2
(x X) f f
4.2抽样误差
∴抽样误差是所有可能出现的样本指标的标准 差。它是由于抽样的随机性而产生的样本指标 与总体指标之间的平均离差。
4.2抽样误差
2.抽样平均误差的计算公式
（1）平均数的抽样平均误差 重复抽样
x
n
或 2
x
n
4.2抽样误差
取得σ的途径有：
1. 用过去全面调查或抽样调查的资料，若同时有n个σ
无偏性 一致性 有效性
总体平均数的区间估 计
总体成数的区间估计
影响因素 计算公式
简单随机抽样 类型抽样 等距抽样 整群抽样
本章学习目标
理解抽样估计的概念、特点、作用以及几个 基本概念；
掌握抽样误差的含义和影响抽样误差的主要 因素；
熟练掌握抽样平均误差的计算； 熟练掌握抽样估计的两种方法：点估计和区