拉氏变换分析 习题课
第4章 拉氏变换作业参考答案
第四章 习题解4-1 根据拉氏变换定义，求下列函数的拉普拉斯变换。
（1）ate --1（2）()()t t 5cos 73sin 2+ （3）tet 3-（4）()t et5cos 4-（5）()[]tb e at --cos 1（6）()tett 22531-++（7）5232++t t （8）()te t 732--δ（9）()t Ω2cos （10）t t e e βα--- （11）()t et5cos 22-（12）()ϕω+t cos解：（1）)(111]1[a s s a s s e L at +=+-=-- （2）()()2579657323]5cos 73sin 2[222222+++=+++⨯=+s s s s s s t t L （3）23)3(1][+=-s et L t（4）())](21[)](21[]5cos [)54()54(45544t j t j t t j t j t te e e jL e e e j L t eL --+-----+=+= 25)4(5)541541(212++=+++-+=s j s j s j （5）()[]()]cos []cos 1[at e e L e at L t b t b tb ----=-22)(1ab s a b s ++++=（6）由于1!][+=n ns n t L ,由s 域频移特性得()]53[]531[222222t t t t e t te e L e t t L ----++=++ 3232)2(207)2(10)2(3)2(1+++=+++++=s s s s s s （7）32232526526]523[ss s s s s t t L ++=++=++ （8）()732]32[7+-=--s et L tδ（9）()()22242121]2cos 2121[]cos [Ω+⋅+=Ω+=Ωs ss t L t L （10）))((11][βααββαβα++-=+-+=---s s s s e eL t t（11）在（9）的计算结果基础上由s 域频移特性得()25)2(221)2(21]5cos [222+++⋅++=-s s s t e L t （12）()]sin sin cos cos []cos [ϕωϕωϕωt t L t L -=+222222s i n c o s s i n c o s ωϕωϕωϕωωϕ+-=+-+=s s s s s4-7 求下列函数的拉普拉斯反变换。
拉氏变换习题课
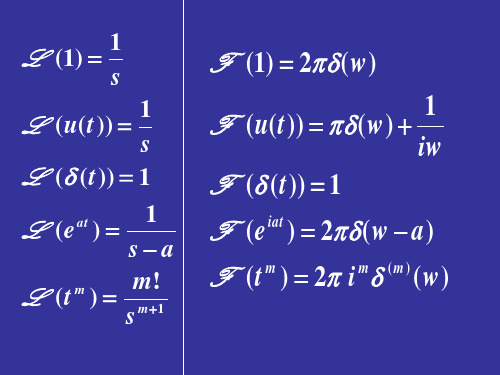
2.( 4 )因为L f ( t) = F ( s) , 由相似性质，有 t L f = aF ( as) a 在利用位移性质， - at t L e f = aF ( as)|s→s+ a s→s+ a = aF ( a(s+ a)
3.
(1)因为（由位移性质）L
s + w0
2 2
|s=β +iw =
β + iw
(β + iw) + w0
2 2
5) f (t ) = e u(t t0 )
iw0t
解： （e u(t t0 ) = F（u(t t0 ) |w→ww ） ） F
iw0t
0
1 ) = e ( + πδ（w）|w→ww iw 1 it ( ww ) ( =e + πδ(w w0 )) i(w w0 )
s2t
s s 1 11 s =L 2 2 2 (10) L 2 2 ( s +1)( s + 4) 3 s +1 s + 2 1 1 s 1 1 s 1 1 L 2 L 2 2 = cost cos2t 3 3 s +1 3 s + 2 3
p100 3.( 2) L
)=
)
u
(t)
L
( f(t)) = L
1 ( u (t)) = s
i 1 snt 2.(1)因为 ct ， ， L = ar an s 所以由相似性质 有 t 1 1 ar an , ct s a a 1 snat 1 i a 即 L ct = aar an s, a t i a snat 所以 L ct = ar an s t i snat L = at
复变函数拉氏变换部分习题解答分析(复拉)(精品)
得z =
+ iy =
1 u+iv
=
u u2 +v 2
−
v i. u2 +v 2
v 又由 y = 1 得 − u2 + = 1, u2 + v 2 + v = 0. v2 π 3
4.求角形域 0 < arg(z ) < 解 arg(w) = arg(¯ z ), 解 将x = 一 判断题
z +¯ z 2 ,y
作业卷（二） 1.若 f ′ (z ) 在区域 D 内处处为零, 则 f (z ) 在 D 内必恒为常数. √ . 在 D 内 f ′ (z ) = ux + ivx ≡ 0, ux = vx = 0. 从而 vy = ux = 0, uy = −vx = 0. 综上结论成立. 2.若 u(x, y ) 和 v (x, y ) 可导,则 f (z ) = u + iv 也可导. 1
= 0, 1, 2, z = −3,
3 2
±
3 2
√
3i.
4.复变函数 w =
z −2 z +1
的实部 u(x, y ) =
, 虚部 v (x, y ) =
x2 −x+y 2 −2 , (x+1)2 +y 2 π 4
. v (x, y ) = .
3y . (x+1)2 +y 2
分析:将 z = x + iy 代入, 分离实部、虚部, 得 u(x, y ) = 5.设 z1 = 2i, z2 = 1 − i, 则 Arg(z1 z2 ) = 分析: arg(z1 ) = π , arg(z2 ) = − π 4 , Arg(z1 z2 ) = √ 2 6.复数 z = − 12 − 2i 的三角表示式为 分析: 4[cos(− 5 6 π) + i sin(− 5 6 π )], 4e
习题课-拉氏变换
1 1 1 F ( s) = F δ( t) + f3 ( 0− ) = ∴ 3 s s s 这是应用微分性质应特别注意的问题。 这是应用微分性质应特别注意的问题。
12
(3)
f1′( t) =3 ( t) δ
t
f 2′ ( t ) = δ ( t )
( 1) o
f 3′ ( t ) = δ ( t )
x3 (t ) 1
o 1 2 3
t
14
解：Y( s) =Y ( s) +Y ( s) =Y ( s) +H( s) F( s) x f x
Y ( s) =Y ( s) +Y f ( s) =Y ( s) +H( s) X1 ( s) 1 x 1 x 1 =Y ( s) +H( s) =1+ x s +1 Y2 ( s ) = Yx ( s ) + Y2 f ( s ) = Yx ( s ) + H ( s ) X 2 ( s )
f (t )
1
o
ROC：整个s平面 ：整个 平面
1
2
6t
方法三： 方法三：利用微分性质求解 信号的波形仅由直线组成， 信号的波形仅由直线组成，信号导数的拉氏变换 容易求得，或者信号经过几次微分后出现原信号， 容易求得，或者信号经过几次微分后出现原信号，这 时利用微分性质比较简单。 时利用微分性质比较简单。 微分两次，所得波形如图9-2（ ）所示。 将 f ( t)微分两次，所得波形如图 （b）所示。
1
2
2
1 −s 1 −s 1 2 −2s −s 1 −2s −s 1 −2s 1 −s =− e + e − − ( e −e ) + 2e −e + e − e s s s s s s s 1 −s 2 = 2 (1−e ) 5 ROC：整个 平面 ：整个s平面 s
第4章 拉氏变换--2
−at
n −at
对s微分特性 微分特性
1 1 ′ −at L te =− = s + a ( s + a)2
′ 1 2 2 −at L t e =− = 2 ( s + a) ( s + a)3
L
t e =
第一种情况：单阶实数极点
A s) ( F(s) = (s − p1 )(s − p2 )⋯ s − pn ) ( kn k1 k2 →F(s) = + +⋯+ s − pn վ s − p1 s + k2e p2t + ... + kne pnt
10
F(s)的一般形式 F(s)的一般形式
ai,bi为实数，m,n为正整数。 m< n , F(s)为有理真分式 为实数， 为正整数。 为正整数 当 < 分解 零点 极点
( A s) am(s − z1 )(s − z2 )⋯ s − zm ) ( F(s) = = B(s) bn(s − p1 )(s − p2 )⋯ s − pn ) (
[
]
微分和积分特性 初值和终值定理 卷积定理
[
]
( −1) t f (τ)dτ = F(s) + f (0− ) L f (t) = ∞ F(s)ds L∫ ∫ −∞ s s t s
W.Hong, Institute of Optoelectronic science and technology, Wuhan National Lab for Optoelctronics, HUST
∫
∞.
0
f ( nT ) ∑ δ T ( t − nT ) e − st dt
拉氏变换习题课
at
F (1) 2 ( w )
1 F ( u( t )) ( w ) iw F ( ( t )) 1
F (e ) 2 ( w a )
te- 3tsi 4 由积分性质，L n2tdt 0 1 1 4 s+ 3 - 3t = L te si n2t 2 2 s s s+ 3 + 4
t
1 利用象函数的微分性质，有
sinkt ∞ L = s L sinkt ds= t ∞ k s∞ π s s s s2 + k 2 ds= arctan k |s = 2 - arctan k = arccotk
p100 2.求下列函数的Lapl ace逆变换：
2 F s =
s
s- a s- b
1 a b a - b s- a s- b b aeat - bebt 1 s- b = a - b
st
解：A 部分分式法 : F s = 1 1 L F s = a- b L
e- 3tsin2t ∞ e- 3tsin2t ds 2L = s L t ∞ 2 s+ 3 = ds= arccot 2 2 s (s+ 3) + 4 2
3
f t tL
-1
F s dt s 1 1 -1 2 2 s - 1
bs a
s F ( )) a
最新第5章 拉氏变换分析 习题课精品课件
d f t
dt
d2 dt 2
f
t
1
1
1
o
1
1
2t
o
1
2t
2
图4-2（b） 第七页，共25页。
显然(xiǎnrán)
L
d2 f dt
t
2
Lδ t 2δ t 1 δ t 2
1 es
2
根据(gēnjù)微分性质
L
d2 d
f t
t
2
s2F
s
f 0
sf
0
由图4-2（b）可以(kěyǐ)看出
1
F s F1sF1s
而
F1s
1 s
1
es
所以(suǒyǐ)
Fs
1 s2
1 es
2
o
1
t
图4-2（c）
第九页，共25页。
例4-3
应用微分(wēi fēn)性质求图4-3（a） f1t , f2(t), f3 t 象函数(há
下中面的说明应用微分性质应注意的问题，图4-3（b）是
f1t ,
2r1
(t)
r2
(t)
e(t)
r1 (t)
dr2 (t) dt
2r2
(t)
0
第二十二页，共25页。
解：对方程组求拉氏变换(biànhuàn)，有： S R1(s) -r1(0) +2R1(s)- R2(s)=1/S (1) - R1(s)+S R2(s)- r2(0)+2 R2(s)=0 (2)
f 0 0, f 0 0
于是
s2F s 1 es 2
F s 1 1 es 2 s 2 第八页，共25页。
拉氏变换详解
t
t
t时，f1 (t ) 1(t ) 0 f1 (t ) f 2 ( )d f1 (t ) 1(t ) f 2 ( )d
0 0
10
t
L[ f 1 (t ) f 2 ( ) d ]
0 t
f 2 ( ) d f 1 ( )e
0 0
s ( )
d d F2 ( s ) F1 ( s )
11
f 2 ( )e
0
s
d f 1 ( )e
0变换
1. 定义：从象函数F(s)求原函数f(t)的运算 1 L [ F ( s )] 。 称为拉氏反变换。记为 由F(s)可按下式求出 1 C j 1 st f (t ) L [ F ( s)] F ( s )e ds(t 0) 2 j C j 式中C是实常数，而且大于F(s)所有极点的 实部。 直接按上式求原函数太复杂，一般都用查 拉氏变换表的方法求拉氏反变换，但F(s)必 12 须是一种能直接查到的原函数的形式。
0
0 st 0
等式两边对s趋向于0取极限
st 左边 lim f ( t ) e dt lim f ( t ) e dt s 0 s 0
f (t ) dt f (t ) 0 lim f (t ) f (0) t
0
右边 lim [ sF ( s ) f (0)] lim sF ( s ) f (0) s 0 s 0 lim f (t ) lim sF ( s ) t s 0
0
0
0
拉普拉斯变换、复频域分析习题课
拉普拉斯变换、复频域分析习题课1. 求下列函数的拉氏变换。
（1）1at e-- （2）sin 2cos t t + （3）2t te - （4）sin(2)t e t -（5）(12)t t e -+ （11）1()t t e e αββα---- （13）(2)(1)t te u t --- （15）()ta t e f a-，设已知[()]()L f t F s = 解：（1）11[1]()at a L e s s a s s a --=-=++ （2）2221221[sin 2cos ]111s s L t t s s s ++=+=+++ （3）221[](2)t L te s -=+ （4）22[sin(2)](1)4t L e t s -=++ （5）23[(12)](1)ts L t e s -++=+ （11）11111[()]()()()t t L e e s s s s αββαβααβαβ---=+=--++++ （13）由于(2)(1)(1)(1)[(1)](1)t t t teu t e t e e u t -------=-+- （15）[()](1)ta t L e f aF as a-=+2求下列函数的拉氏变换，注意阶跃函数的跳变时间。
（1）()(2)tf t e u t -=- （2）(2)()(2)t f t e u t --=- （3）(2)()()t f t e u t --= （4）()sin(2)(1)f t t u t =-（5）()(1)[(1)(2)]f t t u t u t =----解：（1）因为(2)2()(2)t f t ee u t ---=-，所以 222(1)11[()]11s s L f t e e e s s ---+==++ （2）21[()]1s L f t e s -=+ （3）因为2()()t f t e e u t -=，所以2[()]1e Lf t s =+ （4） ()sin[2(1)2](1) {sin[2(1)]cos 2cos[2(1)]sin 2}(1)f t t u t t t u t =-+-=-+-- 2222cos 2sin 22cos 2sin 2[()]()444s s s s L f t e e s s s --+=+=+++ （5）()(1)(1)(2)(2)(2)f t t u t t u t u t =-------222221111[()][1(1)]s s s s s L f t e e e s e e s s s s-----=--=-+ 3求下列函数的拉普拉斯逆变换。
2.2拉氏变换练习题及答案
s
2
s
j
s
j
2
s2
2
s2
2
f
(t)
L1[
s2
s
2
]
cos t
以上8个函数的拉氏变换及反变换要记住，其它函数可查表。
2 拉氏变换运算法则
若有： L[ f (t)] f (t)estdt F(s) 0
1）线性定理
La f1(t) b f2(t) a F1(s) b F2(s)
s
s(s 2)(s 3)
2s2 12s 6 k1 k2 k3
X(s)
s(s 2)( s 3) s s 2 s 3
求K1、K2、K3的方法有两种：
第一种方法：待定系数法
第二种方法：留数法
k1
2s2 12s 6 s(s 2)(s 3)
6）微分定理：
f (t ) k1 k2e 2t k3e 3t
L f nt snFs sn-1 f 0 sn-2 f 0 sf n-2 0 f n1 0
当n=1时： L f t s F s f 0 当n=2时： L f t s2 F s sf 0 f 0
s
A
∴ s 的拉氏反变换变换为： L1[A / s] A1(t)
3) 斜坡函数（速度函数）：
0, t 0 f (t) Bt, t 0
B=1时称为单位斜 坡函数。
L[Bt]
B s2
L1[B / S 2 ] Bt
f (t) f (t) Bt
7.利用拉氏变换的性质求下列函数的拉氏变换.
7．利用拉氏变换的性质求下列函数的拉氏变换.（1）()teet fatbt-=. （2）()ttt f2sin2=.（3）()tttt fωωωcossin-=（4）()ttt fωsh=.解（1）&()[]=t f&⎰∞=⎥⎦⎤⎢⎣⎡-satbttee&[]duee atbt-⎰∞∞--=--=⎪⎭⎫⎝⎛---=s s bsasaubuduaubulnln11|（2）&()[]=t f&[]2222)1(2sindsdtt-=&[]t2sin()3222224161242+-=⎪⎭⎫⎝⎛+=sssdsd（3）&()[]=t f&[]=-tttωωωcossin&[]ωω-tsin&[]ttωcosdsdsωωω++=22&[]⎪⎭⎫⎝⎛+++=2222cosωωωωωωsst()22232ωω+=s（4）&()[]=t f&[]dsdttsh-=ω&[]tshω()222'21121ωωωω-=⎪⎭⎫⎝⎛+---=ssss8．求下列函数的拉氏逆变换.（1）().412+=ssF（2）().14ssF=（3）()().114+=ssF（4）().31+=ssF（5）().9322++=sssF（6）()()().313-++=ssssF（7）().612-++=ssssF（8）().134522+++=ssssF解（1）()=t f&()[]211=-sF&ts2sin214221=⎥⎦⎤⎢⎣⎡+-（2）()=t f&!31141=⎥⎦⎤⎢⎣⎡-s&313161!3ts=⎥⎦⎤⎢⎣⎡+-（3）由&341611ts=⎥⎦⎤⎢⎣⎡-及位移性质&()[]()t feasF at=--1得()=t f&()[]=-sF1&()t e ts--=⎥⎦⎤⎢⎣⎡+3416111（4）()=t f&()[]=-sF1&tes3131--=⎥⎦⎤⎢⎣⎡+（5）()=t f&()[]21=-sF&+⎥⎦⎤⎢⎣⎡+-921ss&tts3sin3cos29321+=⎥⎦⎤⎢⎣⎡+-（6）()=t f&()[]=-sF1&()()⎥⎦⎤⎢⎣⎡-++-3131sss=&231133211=⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛+---ss&213-s11-⎥⎦⎤⎢⎣⎡-&⎥⎦⎤⎢⎣⎡+-111stt ee--=21233（7）()=t f&()[]=-sF1&=⎥⎦⎤⎢⎣⎡-++-6121sss&⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛++--3223511ss53=&52211+⎥⎦⎤⎢⎣⎡--s&tt ees321525331--+=⎥⎦⎤⎢⎣⎡+（8）()=t f&()[]=-sF1&=⎥⎦⎤⎢⎣⎡+++-1345221sss&()()⎥⎦⎤⎢⎣⎡++++-22132122ss2=&()()31322221+⎥⎦⎤⎢⎣⎡+++-ss&()⎥⎦⎤⎢⎣⎡++-221323s()ttetete ttt3sin3cos6313sin313cos2222+=+=---9．设()()t ftf21,均满足拉氏变换存在定理的条件（若它们的增长指数均为c）且&()[](),11sFtf=&()[](),22sFtf=，则乘积()()t f t f21的拉氏变换一定存在，且&()()[]()()⎰∞+∞--=ii2121i21ββπdqqsFqFtftf其中.Re,0cs+>>ββ证由于()()t ftf21,均满足拉氏变换存在定理的条件以及增长指数均为c，知乘积()()t f t f21也一定满足拉氏变换存在的定理的条件且增长指数为.2c根据拉氏存在定理的证明当c>β时，&()()[]()()⎰+∞-=2121,dtetftftftf st在0Re cs+≥β上存在且一致收敛.由于()()⎰∞+∞-=ii11i21ββπdteqFtf qt而&()()[]()()⎰+∞-=2121dtetftftftf st()()⎰⎰+∞-∞+∞-⎪⎭⎫⎝⎛=2i i 1i21dt e t f dq e q F st qt ββπ()()⎰⎰+∞--∞+∞-=0)(2i i 1i 21dtdq e t f q F q s ββπ()()dqq s F q F -=⎰∞+∞-2i i 1i 21ββπ10．求下列函数的拉氏逆变换（像原函数），并用另一种方法加以验证.（1）().122a s s F +=（2）()()().b s a s s s F --=（3）()()()2b s a s cs s F +++=（4）()()222222a sa s s F ++=（5）()().1322s a s s F +=（6）()()()b s a s s s F ++=1（7）().144a s s F -= （8）()()22112--+=s s s s s F（9）()().1122-=s s s F （10）()()()4122++=s s ss F（1）解法1 ()=t f &()[]=-s F 1&⎥⎦⎤⎢⎣⎡+⋅-2211a s a aa 1=&a ata s a sin 221=⎥⎦⎤⎢⎣⎡+- 解法2()⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+=i ,Res i ,Res 2222a a s e a a s e t f st st a at a e a e at at sin i 2i 2i i =-=-解法3 ()=t f &=⎥⎦⎤⎢⎣⎡+-2211a s &⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+---i 1i 1i 211a s a s a i 21a =（&-⎥⎦⎤⎢⎣⎡--i 11a s &⎥⎦⎤⎢⎣⎡+-i 11a s ） ()a at e e a at at sin i 21i i =-=-（2）解法1 ()=t f &()[]=-s F 1&()()⎥⎦⎤⎢⎣⎡---b s a s s1()()()()⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡--=b b s a s se a b s a s se st st ,Res ,Res()bt at bt at be ae b a a b be b a ae --=-+-=1解法2 ()=t f&()[]=-sF1&()()⎥⎦⎤⎢⎣⎡---bsass1=&⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-----bsbasaba11ba-=1（a&bas-⎥⎦⎤⎢⎣⎡--11&⎥⎦⎤⎢⎣⎡--bs11()btat beaeba--=1（3）解法1 ()=t f&()[]s F1-()()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-++++⎥⎥⎦⎤⎢⎢⎣⎡-+++=bbsasecsabsasecs stst,Res,Res22()()bsstateascsdsdabeac-=-⎪⎭⎫⎝⎛+++--=2()()btbtat ebacatebabcebaac-----+--+--=22解法2 ()=t f&()[]=-sF1&()()⎥⎦⎤⎢⎣⎡+++-21bsascs=&()()()⎥⎦⎤⎢⎣⎡+⋅--++⋅--++⋅---2221111bsbabcbsbacaasbaac()2baac--=&()211bacaas--+⎥⎦⎤⎢⎣⎡+-&baacbs--+⎥⎦⎤⎢⎣⎡+-11&()⎥⎥⎦⎤⎢⎢⎣⎡+-211bs ()()btbtat tebabcebacaebaac-----+--+--=22（4）解法1 ()=t f&()[]=-sF1&()⎥⎥⎦⎤⎢⎢⎣⎡++-2222212asas=&⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛+++⋅-'222212123assasaaa23=&21221+⎥⎦⎤⎢⎣⎡+-asa&⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛+'221assattatacos21sin23-=解法2 ()=t f&()[]s F1-()()⎥⎥⎦⎤⎢⎢⎣⎡-+++⎥⎥⎦⎤⎢⎢⎣⎡++=i,2Resi,2Res2222222222aeasasaeasas stst()()i222i222i2i2asstasst easasdsdeasasdsd-==-++++=ta t a t a t a te e a te e a i i i i 41i 4341i 43-----= at t at a cos 21sin 23-=（5）解法1 ()=t f &()2322111a s a s =⎥⎦⎤⎢⎣⎡+-&()⎥⎦⎤⎢⎣⎡+--223111a s s s(12a =&-⎥⎦⎤⎢⎣⎡-311s &())1221⎥⎦⎤⎢⎣⎡+-as s⎰-=t t a 03221(1&)1221dt a s ⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛-=⎰t atdt a t a 032sin 12121()at a t a cos 1121432--=解法2 ()=t f &()⎥⎦⎤⎢⎣⎡+-32211s a s()()()⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡+=i ,Res i ,Res 0,Res 322322322a s a s e a s a s e s a s e stst st()()3i 3i 02222i i 2i i 221a a e a a e a s e ds d ta t a s st --+⎪⎪⎭⎫ ⎝⎛+=-=()at a t a cos 1121422--=（6）解法1 ()=t f &()()⎥⎦⎤⎢⎣⎡-+-b s a s s 11=&()()⎥⎦⎤⎢⎣⎡+⋅--+⋅-+⋅-b s b a b a s b a a s ab 1111111=ab 1&()b a a s -+⎥⎦⎤⎢⎣⎡-111&()b a b a s -1-⎥⎦⎤⎢⎣⎡+-11&⎥⎦⎤⎢⎣⎡+-b s 11()()bt at e b a b e b a a ab -----+=111解法2 ()=t f &()()⎥⎦⎤⎢⎣⎡++-b s a s s 11()()()()()()⎥⎦⎤⎢⎣⎡-+++⎥⎦⎤⎢⎣⎡-+++⎥⎦⎤⎢⎣⎡++=b b s a s s e a b s a s s e b s a s s e stst st ,Res ,Res 0,Res()()bt at e b a b e b a a ab -----+=111（7）解法1 ()=t f&⎥⎦⎤⎢⎣⎡--4411as=&⎥⎦⎤⎢⎣⎡+-⎪⎭⎫⎝⎛+---22331211141asaaasasa()ataeeaatat sin214133--=-()atatasinsh213-=解法2 ()=t f&⎥⎦⎤⎢⎣⎡--4411as⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-=i,Resi,Res,Res,Res44444444aaseaaseaaseaase stststst()()3i3i33i4i444aeaeaeae t ataatst-++-=--()atatasinsh213-=（8）解法1 ()=t f&()=⎥⎦⎤⎢⎣⎡--+-221112ssss&()⎥⎦⎤⎢⎣⎡-+-+--2112121sss=&+⎥⎦⎤⎢⎣⎡--s11&+⎥⎦⎤⎢⎣⎡--121s&()⎥⎦⎤⎢⎣⎡--2112stt tee221++-=解法2()=t f&()⎥⎦⎤⎢⎣⎡--+-221112ssss()()⎥⎦⎤⎢⎣⎡--++⎥⎦⎤⎢⎣⎡--+=1,112Res0,112Res2222stst essssessss12121=⎪⎪⎭⎫⎝⎛-++-=sstesssdsdtt tee221++-=（9）解法1 ()=t f&()[]=-sF1&()⎥⎦⎤⎢⎣⎡--11221ss=&()teessstt--=⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛+----21111112121tsht-=解法2 ()()()()⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=1,1Res1,1Res0,1Res222222ssessesset fstststtteesedsd ttsst-=-+⎪⎪⎭⎫⎝⎛-=-=sh2212（10）解法1 ()=t f &()()⎥⎦⎤⎢⎣⎡++-41221s s s =&⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-+-4131221s s s s(31=&-⎥⎦⎤⎢⎣⎡+-121s s &()t t s s 2cos cos 31)421-=⎥⎦⎤⎢⎣⎡+-解法2 =)(t f &()()⎥⎦⎤⎢⎣⎡++-41221s s s()()()()()()()()⎥⎦⎤⎢⎣⎡-+++⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡-+++⎥⎦⎤⎢⎣⎡++=i 2,41Res i 2,41Res i ,41Res i ,41Res 22222222s s se s s se s s se s s se stst st st ()()()()()i 41i 4i 2i 41i 4i 24i i 2i 4i i 2i 2i 22i 22i 2i -+-++++--++=--tt t t e e e e6666i 2i 2i i t t t t e e e e --+++= ()t t 2cos cos 31-=。
第14 章 Laplace 变换 1. 求下列函数的拉氏变换 (1) (2) 解 (1
第14 章 Laplace 变换1． 求下列函数的拉氏变换 （1）1cos wtw- （2）chwt 解 （1）{}{}220sin 1cos sin ()tL wt wt wL Lwzdz w p p p w -⎧⎫===⎨⎬+⎩⎭⎰（2）{}{}22111122wt wt pL chwt L e e p w p w p w-⎧⎫=+=+=⎨⎬-+-⎩⎭ 2．求下列函数的逆拉氏变换 （1）2845p p p +++； （2）222()p p a + 其中a ＞0。
解 （1）111222821645(2)1(2)1p p L L L p p p p ---⎧⎫⎧⎫⎧⎫++=+⎨⎬⎨⎬⎨⎬++++++⎩⎭⎩⎭⎩⎭22cos 6sin tt et e t --=+（2）1222sin ()2pt at L p a a -⎧⎫=⎨⎬+⎩⎭3. 设11()sin f t wt w=，2()f t chwt =，其中w ≠0,求12()()f t f t *。
解法1 由于{}{}{}1212L f f L f L f *=⋅ {}12211()sin L f t L wt w p w⎧⎫==⎨⎬+⎩⎭ {}{}222()pL f t L chwt p w ==-所以 {}1222221pL f f p w p w*=⋅+- 2222222()2()p pw p w w p w =--+2211cos 22L chwt L wt w w ⎧⎫⎧⎫=-⎨⎬⎨⎬⎩⎭⎩⎭2211cos 22L chwt wt w w ⎧⎫=-⎨⎬⎩⎭1221(cos )2f f chwt wt w *=- 解法2 由卷积定义求1201()()sin ()tf t f t w chw t d wτττ*=-⎰()()01sin 2w t w t te e w d w ττττ---+=⎰ ()()0011sin sin 22t t w t w t e w d e w d w w ττττττ---=+⎰⎰ 22221111sin cos sin 4444wt wt wt e wt w w w w =--++-2211cos 44wtt e w w -+ 2211cos 222wt wt e e wt w w -+=-21(cos )2chwt wt w =- 4．求解'1(0)0x x x +=⎧⎨=⎩解 对方程施行Laplace 变换，并注意初始条件：x(0)=0,我们有 [][][]'1L x L x L +=[][]1pL x L x p+=[]11111(1)1(1)L x p p p p p p ==-=-++--[]11111(1)tx L L x L e p p ---⎡⎤==-=-⎢⎥--⎣⎦5. 求解2'3(0)2tx x e x -⎧-=-⎨=⎩解 对方程两边施以Laplace 变换，并注意初始条件x(0)=0,则有[][]2'3tL x L x L e -⎡⎤-=-⎣⎦[][]3(0)2pL x x L x p ---=+ []311(1)(2)21L x p p p p -==--++-11211()()21t tx t L x L e e p p ---⎡⎤==-=-⎢⎥+-⎣⎦6. 求解01"(0),'(0)tx x e x x x x ⎧+=⎨==⎩解 对方程两边施以Laplace 变换得[][]"tL x L x L e ⎡⎤+=⎣⎦[][]20111p L x px x L x p --+=- 解得 []0122221111121212111x p x p L x p p p p p =--++-++++ 所以 101222211111()21212111x p x p x t L p p p p p -⎡⎤=--++⎢⎥-++++⎣⎦01111()cos ()sin 222t e x t x t =+-+- 7. 求解01"(0),'(0)tx x e x x x x ⎧-=⎨==⎩解 对方程两边施以Laplace 变换得 [][]"t L x L x L e ⎡⎤-=⎣⎦[][]201'(0)1p L x p xx L x p ---=- []201111p L x px x p ⎡⎤-=++⎣⎦- 解得 []2111()2(1)4(1)4(1)L x t p p p =-+--+ 012211x p x p p ++-- []101111()(())244t t t x t L L x t te e e x cht x sht --==-+++8. 求解"'2"'4(0)1,'(0)2,"(0)2x x x x x x --=⎧⎨===-⎩解 对方程两边施行Laplace 变换，并注三个初始条件，则有[][][][]"'2"'4L x L x L x L -+=[][]322(0)'()"(0)2(0)'(0)p x p x px x x p L x px x ⎡⎤------+⎣⎦[]4(0)L x x p-=[][][]3224222241p L x p p p L x p pL x p--+-+++-=[]224(1)5p p L x p p-=+- 解得 []222254()(1)(1)(1)p L x t p p p p p =-+--- 23421p p p =+-- 所以 []1()()342tx t L L x t t e -==+-9. 求解21"'2(0)'(0)"(0)0t x x t e x x x ⎧+=⎪⎨⎪===⎩ 解 对方程两边施以Laplace 变换并利用初始条件有 [][]21"'2tL x L x L t e ⎡⎤+=⎢⎥⎣⎦[][]3221(0)'(0)"(0)(1)p L x p x px x L x p ---+=-解得 []331()(1)(1)L x t p p =-+- 当331231,,ii p p e p e ππ-=-==是一阶极点，p=1是三阶极点，由留数计算公式：22331111Re ()lim 2(1)(1)ptpt p p d s F p e e dp p p →=⎡⎤⎡⎤=⎢⎥⎣⎦!+-⎣⎦2133448t t tt e te e =-+31311(1)Re ()|(1)24ptptt p p e p s F p e e p -=-=--⎡⎤==-⎣⎦+3332(1)Re ()|3i i pt ptp e p e e p s F p e p ππ==-⎡⎤==⎣⎦3Re ()iptp es F p e π-=⎡⎤=⎣⎦所以221331()44824t t t t t x t t e te e e -=-+--21cos 32te10. 求解3''21'4'30(0)(0)0x y x x y y x y ++=⎧⎪++=⎨⎪==⎩解 对方程组两边施行Laplace 变换，并设[][](),(),X L x t Y L y t ==得 1(32)(43)0p X pY p pX p Y ⎧++=⎪⎨⎪++=⎩解得 221111111765(116)5(1)431133(11176)25(1)10(116)Y p p p p p X p p p p p p --⎧==+⎪++++⎪⎨+⎪==--⎪++++⎩所以 [][]61116111113()251011()55t t t tx t L X e e y t L Y e e ------⎧==--⎪⎪⎨⎪==-+⎪⎩11. 求解0sin ()sin()()ta t G t t z G z dz =--⎰，a 为常数。
拉氏变换习题解答
(4) & ⎡ ⎣ f ( t )⎤ ⎦=
∫
+∞
0
sin t cos te − st dt =
⎡ −( s −2 i) t +∞ e −( s + 2 i)t +∞ ⎤ 1 ⎛ 1 1 ⎞ 1 1 ⎢e 0 0 ⎥ = − = ⎜ − ⎟= 2 ⎥ ⎢ 4 i − (s − 2 i ) − (s + 2 i ) 4i ⎝ s − 2i s + 2i ⎠ s + 4 ⎥ ⎢ ⎦ ⎣
2
(5) f ( t ) = sinh kt ； (1) & ⎡ ⎣ f ( t )⎤ ⎦=
(6) f ( t ) = cosh kt ； (7) f ( t ) = cos t ;
+∞
解
∫
0
t (e − e )e − st sin e − st dt = ∫ dt 0 2 2i
+∞
it 2
−it 2
（2）& [ f (t )] =
+∞ − st
(4) f (t ) = δ (t ) cos t − u (t )sin t.
f (t )e dt = ∫ 3e dt − ∫ e dt =
2
− st
4
− st
3e − st −s
|
2
0
0
0
2
+
3e − st s
|
4 2
=
1 (3 − 4e −2 s + e −4 s ) s
第十五章 拉普拉斯变换典型习题解答与提示.
第十五章 拉普拉斯变换典型习题解答与提示习 题 15-11．（1）提示：2()f t t =， ￡20[()]()ptpt f t f t edt t e dt +∞+∞--==⎰⎰，求广义积分后可得￡32[()]f t p =，(0)p >； （2）提示：4()tf t e -=，￡40[()]()pt t pt f t f t e dt e e dt +∞+∞---==⎰⎰，￡1[()](4)4f t p p =>-+； （3）因302()12404t f t t t ≤<⎧⎪=-≤<⎨⎪≥⎩，则￡242[()]()3(1)ptptpt f t f t edt edt e dt +∞---==+-⎰⎰⎰24024,(0)31,(0)pt pt p e e p p p --=⎧⎪=⎨-+≠⎪⎩4234,(0)4,(0)p pe e p pp --⎧+-≠⎪=⎨⎪=⎩； （4）因()tf t te -=， 则￡2(1)(1)0001[()]()1ptp tp t f t f t edt tedt td e p +∞+∞--+-+⎛⎫===- ⎪+⎝⎭⎰⎰⎰ (1)(1)0111p t p t te e dt p p +∞+∞-+-+=-+++⎰ (1)21(1)(1)p tep p +∞-+=->-+21(1)(1)p p =>-+。
2．（1）￡231[()](263)(0)f t p p p p=+->； （2）￡2262[()](0)41pf t p p p =->++； （3）因()1tf t te =+，则￡[()]f t =￡(1)+￡()tte1(1)[p=+-￡()]t e ' （微分性） 222111(1)(1)(1)p p p p p p p -+=+=>--； （4）因3()sin 4tf t e t =，又因￡24(sin 4)()16t F p p ==+，则由位移性知￡24[()](3)(3)(3)16f t F p p p =-=>-+； （5）方法一 因22()tf t t e-=，又￡232[]()(0)t F p p p ==>，则由位移性知 ￡32[()](2)(2)(2)f t F p p p =+=>-+； 方法二 因￡21(),(2)2tep p -=>-+，则由微分性知 ￡2312[()](1)(2)2(2)f t p p p ''⎛⎫=-=>- ⎪++⎝⎭； （6）因21()sin (1cos 2)2f t t t ==-，则￡1[()][2f t =￡(1)-￡22112(cos 2)](0)24(4)p t p p p p p ⎛⎫=-=> ⎪++⎝⎭； （7）因1()sin 2cos 2sin 42f t t t t ==， 则￡1[()]2f t =￡22142(sin 4)(0)21616t p p p =⨯=>++；（8）因()sin()sin cos cos sin f t t t t ωϕωϕωϕ=+=+， 则￡[()]cos f t ϕ=￡(sin )sin t ωϕ+￡2222cos sin (cos )p t p p ωϕϕωωω=+++22cos sin (0)p p p ωϕϕω+=>+； （9）因11()(21)222f t t t t μμμ⎡⎤⎛⎫⎛⎫=-=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， 则由延滞性知￡121[()](0)p f t ep p-=>； （10）因3()sin 2tf t tet -=，又￡22(sin 2)(0)4t p p =>+， 则由位移性知￡322(sin 2)(3)(3)4t e t p p -=>-++，故再由微分性知 ￡22224(3)[()](3)(3)4[(3)4]p f t p p p '⎡⎤+=-=>-⎢⎥++++⎣⎦； （11）因4()cos 24tf t et π-⎛⎫=+ ⎪⎝⎭，又因￡cos 242t π⎡⎤⎛⎫+= ⎪⎢⎥⎝⎭⎣⎦￡222(cos 2sin 2)244p t t p p ⎫-=-⎪++⎝⎭2224p p -=+，则由位移性知￡22[()](4)2(4)4p f t p p +=⨯>-++。
拉氏变换逆变换例题
拉氏变换逆变换例题拉氏变换和逆变换是信号处理中常用的工具，本文将提供几个拉氏变换和逆变换的例题，帮助读者更好地理解这些概念。
例题1：求函数f(t)=sin(2πt)的拉氏变换。
解：根据拉氏变换的定义，我们有：F(s) = ∫0∞ e^(-st) sin(2πt) dt这个积分可以通过分部积分来求解。
设u = sin(2πt)，dv = e^(-st) dt，则du/dt = 2πcos(2πt) 和 v = (-1/s) e^(-st)。
因此，F(s) = (∫0∞ u dv) = [(uv) |0∞ - ∫0∞ v du/dt dt]= [(sin(2πt) (-1/s) e^(-st)) |0∞ - ∫0∞ (-1/s) e^(-st) 2πcos(2πt) dt]= [(0 - 0) - (2π/s) ∫0∞ e^(-st) cos(2πt) dt]= (2π/s) [(1/(s^2 + 4π^2)]因此，f(t)=sin(2πt)的拉氏变换为F(s) = (2π/s) [(1/(s^2 + 4π^2)]例题2：求函数F(s) = (s + 2)/(s^2 + 4s + 5)的拉氏逆变换。
解：我们可以通过部分分式分解来求解逆变换。
设F(s) = A/(s + α) + B/(s + β)，则F(s) = A/(s + α) + B/(s + β) = (As + Aα + Bs + Bβ)/(s^2 + (α + β)s + αβ)比较系数可得：Aα + Bβ = 2，A + B = 1，Aβ + Bα = 0。
解得A = 2/(3-2i)，B = 1/(3-2i)。
因此，F(s) = (s + 2)/(s^2 + 4s + 5) = 2/(3-2i) /(s + (2-i)) + 1/(3-2i) /(s + (2+i))我们可以使用拉氏逆变换的表格或者将其转化为指数函数，最终得到f(t) = (2/5) e^(-2t) sin(t) + (1/5) e^(-2t) cos(t) 以上就是本文的拉氏变换和逆变换例题，希望能对读者在学习信号处理中有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
- R1(s)+S R2(s)- r2(0)+2 R2(s)=0 (2) 联立（1）和（2）求解得
R1(s)=2/(3S)+1/(S+1)+1/[3(S+3)] R2(s)=1/(3S)+1/(S+1)-1/[3(S+3)] 所以：r1(t)=(2/3)u(t)+e-tu(t)+(1/3)e-3tu(t) r2(t)=(1/3)u(t)+e-tu(t)-(1/3)e-3tu(t) 即为所求。
阶跃响应
gt y2t yzi t et ut
则
y3t yzi t gt 1 gt 3 2et ut et1 ut 1 et3 ut 3
例4-5
2Ω 1H
电路如图4-5（a）所示
e t
iL 0
1F
vC t
（1）求系统的冲激响应。
4-5(a)
（2）求系统的起始状态 iL 0 、vC 0 , 使系统的零输
0
因而
f3t
t δ xd
0
x
f30
t δ xd x
0
F2 s
1 s
F δ
t
1 s
f20
3 s
F3 s
1 s
F δ
t
1 s
f3 0
1 s
这是应用微分性质应特别注意的问题。
由图4-3（b）知
L f1t sFs 0 3
则F1 s
3 s
L f2t sFs 2 1
Hale Waihona Puke 则F2s3 s
f3
R(s)=[2/（S+1）-3/（S+2）+1/（S+3）]
所以，rzs(t)=(2e-t-3e-2t+e-3t)u(t) ③ 全响应r(t)=rzs(t)+rzi(t)=(2e-t+4e-2t-4e3t)u(t)
从而求得系统的起始状态
vC 0 1 iL 0 0
例4-6
用拉普拉斯变换分析法求下列系统 的响应r1(t)和r2(t)。已知r1(0)=2， r2(0)=1，e(t)= u(t)。
dr1 (t) dt
2r1 (t)
r2
(t)
e(t)
r1 (t)
dr2 (t) dt
2r2
(t)
0
解：对方程组求拉氏变换，有：
入响应等于冲激响应。
（3）求系统的起始状态，使系统对 ut的激励时的完 全响应仍为ut 。
（1）求系统的冲激响应。
系统冲激响应ht 与系统函数H s是一对拉氏变换的关系。
对H s求逆变换可求得ht ，这种方法比在时域求解微分方
程简便。
利用s域模型图4-5（b）可直写出图4-5（a）电路的系
统函数
1
方法一：按定义式求解 方法二：利用线性叠加和时移性质求解 方法三：利用微分性质求解 方法四：利用卷积性质求解
方法一： 按定义式求解
F s f testd t 0
1 t estd t 2 2 t estd t
0
1
1
t 1 est 1 1 estd t 2 1 estd t 2 t estd t
F
s
L
t
t
1
L
t
1
t
1
t
1
1 s2
1 s
e
s
例4-2
求三角脉冲函数 f t如图4-2（a）所示的象函数
t
f t 2 t
0
f t
0t1
1 t 2
1
其他
o
1
2t
4-2（a）
和傅里叶变换类似，求拉氏变换的时，往往要借助基 本信号的拉氏变换和拉氏变换的性质，这比按拉氏变 换的定义式积分简单，为比较起见，本例用多种方法 求解。
例4-7 已知某LTI系统的系统函数为
H(S) S 5 S2 5S 6
初始条件为r(0)=2，r’(0)=1，求输入 e(t)=e-tu(t)时的全响应。
解：H(S) S 5 S 5 S2 5S 6 (S 2)(S 3)
① 设：rzi(t)=c1e-2t+c2e-3t，代入初始条件得： c1=7，c2=-5 所以，rzi(t)=(7e-2t-5e-3t)u(t) ②E(s)=1/(S+1)， R(s)=H(s)E(s)=(S+5)/[(S+1)(S+2)(S+3)]
2
图4-2（b）
显然
d2 f t
L
dt2
Lδ t 2δ t
1δ t
2
1 es
2
根据微分性质
L
d2 f dt
t
2
s2F
s
f 0
sf
0
由图4-2（b）可以看出
f 0 0, f 0 0
于是
s2Fs 1 es 2
Fs
1 s2
1 es
2
方法四：利用卷积性质求解
由图4-5(b)可以写出
Vos
E s
1 s vC 0 2s
1
iL
0
11 s s vC 0
s
Es s 2vC0 iL 0
s2 2s 1
s2 2s 1
1
零状态响应 零输入响应
上式中第二项只和系统起始状态有关，因此该项是零输入
响应的拉氏变换。依题意的要求，该项应和 H相s等，
拉氏变换有单边和双边拉氏变换,为了区别起见,本书
以 Fs表示 f t 单边拉氏变换,以 FB s表示 f t 双边拉氏
变换。若文字中未作说明,则指单边拉氏变换。单边拉氏 变换只研究 t 0 的时间函数,因此,它和傅里叶变换之间有 一些差异,例如在时移定理,微分定理和初值定理等方面。 本例只讨论时移定理。请注意本例各函数间的差异和时移 定理的正确应用。
y3 t 。
x3 t
1
o 123 t
y1t yzi t yzs t yzi t ht
y2
t
yzi
t
y(1) zs
t
yzi
t
h ( 1)
t
yzi
t
gt
y1t y2t ht h(1) t t 2et
Hs 1 Hs 1 2
s
s1
ht t et ut
yzi t y1t yzs t 2 et ut
f1t 3 t
3 o
f2 t 2 εt
3
2
t
o
图4-3（a）
1
t
o
f3 t εt
t
f1t 3 t
(3)
o
t
(1) f2t t
o
t
图
4-4（b)
(1) f3t t
o
t
（1）对于单边拉氏变换, 由于f1 t f2 t t , 故二者的象
函数相同，即
F1 s
F2 s
3 s
2虽然F1s F2s，但f1t f2t，因而
s
0
s 0
0
1
1 es s
1 s2
es
1 s2
2 e2s s
2 es s
2 e2s s
1 s2
es
1 s2
1 es
2
方法二： 利用线性叠加和时移性质求解
由于 于是
f t t t 2t 1 t 1 t 2 t 2
L
t
t
1 s2
L f t t0 F s est0
Fs
从而得
s 2vC0 iL0 1
故系统的起始状态
vC 0 0 iL 0 1
通过本例可以看出，改变系统的起始状态可以使系统 的完全响应满足某些特定要求。本质上，系统的零输 入响应完全由系统的起始状态决定，对一个稳定系统 而言，零输入响应是暂态响应中的一部分，因此，改 变系统的起始状态只能改变系统的暂态响应，使暂态 响应满足某些特定要求，例如，本例要求暂态响应为 零。
1 s2
1 2es e2s
1 s2
1 es
2
方法三：利用微分性质求解
信号的波形仅由直线组成，信号导数的象函数容易求
得，或者信号经过几次微分后出现原信号，这时利用微分
性质比较简单。
将 f t 微分两次，所得波形如图4-2（b）所示。
d f t
dt
d2 dt 2
f
t
1
1
1
o
1
1
2t
o
1
2t
Hs
Vo s Es
R
sC sL
1
sC Es
冲激响应
s2
1 2s
1
2
s
iL 0
1 s
vC
0
1 s 4-5(b)
Vo s
ht L1Hs t et ut
（2）求系统的起始状态
为求得系统的零输入响应，应写出系统的微分方程或给 出带有初值的s域模型。下面我们用s域模型求解。图45(a)电路的s域模型如图4-5(b)。
内容摘要
一．拉普拉斯变换
拉氏变换的定义和收敛域 典型信号的拉氏变换
二．单边拉氏变换逆变换的求法
部分分式展开法 围线积分法
三．拉氏变换的基本性质
四．用拉普拉斯变换法分析电路
五．系统函数
系统函数的定义 由零极点的决定系统的时域特性 由零极点的分析系统的稳定性 由零极点的分析系统的频响特性
例4-1 求下列函数的拉氏变换 f t t t 1
L f1t L f2t