第三章 电阻电路的一般分析习题共33页文档
第03章电阻电路的一般分析

例3 列支路电流法方程。
a
解:
I1 7
+ 70V
–
I2
1+
5U
_
7 I3 11 +
U 2-
节点a: –I1–I2+I3=0 回路1: 7I1–11I2 - 70 +5U =0 回路2: 11I2+7I3 - 5U =0 增补方程:
b
U=7I3
(1-18)
§3.4 网孔电流法
网孔电流——假想每个网孔中有一个网孔电流。方向可 任意假设。
(1-22)
理想电流源(恒流源)支路的处理
①若恒流源支路仅有一个网孔电流穿过,则该网孔电 流= ± 该恒流源电流(同方向取+,否则取-)。 ②非上述情况时:设恒流源两端电压,当作恒压源列方 程。然后增补恒流源电流与网孔电流的关系方程。
例2 列网孔电流方程。
R1
R2 im2 I3s
+ im1 I5s
第三章
电阻电路的一般分析
重点: 1.支路电流法; 2. 网孔电流法; 3.回路电流法; 4.节点电压法。
对于简单电路,通过电阻串、并联关系或 Y—△等效变换关系即可求解。如:
i总 R
R
R i=?
+
-u
2R
2R
2R 2R
i总
i总
u 2R
+
- u 2R
111 u i i总 2 2 2 16R
例4 列网孔电流方程。
解:网孔电流方向如图所示。 (R1 + R3)i1-R3i3=-U2
+
U1 _
R1
iS
R3 i1
+
第三章 电阻电路的一般分析习题
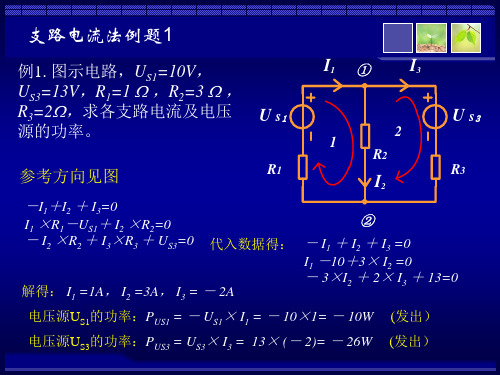
例1. 图示电路,US1=10V, US3=13V,R1=1 ,R2=3 , R3=2,求各支路电流及电压 源的功率。 参考方向见图
-I1+I2 + I3=0 I1 ×R1-US1+ I2 ×R2=0 - I2 ×R2 + I3×R3 + US3=0
I1 U s1
1 R1
①
11Im1-3Im2-4=-27
8Im2-3Im1-8=27 解得 Im1=-1A, Im2=4A, Im3=2A 支路电流为 I1= Im2= 4A, I2=Im3-Im1= 3A,
R2
I6
Im1 I2 Im3 IS
I3 Im2 Us I4
R5 R4
I1
I5
I3=Im2-Im1= 3A
I4=Im3-Im2=-2A, I5=Im3= 2A, I6=Im1=-1A 注意: 电路的最外围支路存在电流源时,仍旧可用网孔电流 法求解支路电流。
I1
U1 R1 Us 1 1 R2 I2
U1
2
R3 I3
I1+I2 - I3=0 I1×R1-I2×R2-US1=0 I2×R2+ U1 + I3×R3=0
②补充受控源控制变量关系式(控制变 量表示为支路电流)
U1=-R1×I1
I1
U1 R1
U1
代入数据
Us 1 1
I1+I2 - I3=0 I1-2×I2-1=0 2×I2+3×U1 + 3×I3=0 U1=-I1
该电路包含一个无伴电压源支路受控电压源选结点1为参考结点列结点电压方程23525454554111110111suuurrrrruuuirrrr???????????????????????3uu?u553uiruu????964808uvuvuv???????44408suuiar???33316uiar????13408iiia????
邱关源《电路》笔记及课后习题(电阻电路的一般分析)【圣才出品】

第3章电阻电路的一般分析3.1 复习笔记一、电路图论的基本概念1.图(G)图(G)是具有给定连接关系的结点和支路的集合,其中每条支路的两端都连到相应的结点上,允许孤立结点的存在,没有结点的支路不能称为图。
路径:从G的一个结点出发,依次通过图的支路和结点(每一支路和结点只通过一次),到达另一个结点(或回到原出发点),这种子图称为路径。
连通图:当G的任意两结点都是连通的,称G为连通图。
有向图:赋予支路方向的图称为有向图。
2.树(T)满足下列三个条件的子图,称为G的一棵树:①连通的;②包含G的全部结点;③本身没有回路。
树支与连支:属于树的支路称为树支;不属于树的支路称为连支。
基本回路:对于G的任意一个树,有且只有一条连支回路,这种回路称为单连支回路或基本回路。
树支数:对于有n个结点,b条支路的连通图,树支数=n-1。
推论:连枝数=b-n+1;基本回路数=连支数=b-n+1。
二、KCL和KVL的独立方程数KCL的独立方程数:对一个具有n个结点的电路而言,其中任意的(n-1)个结点的KCL方程是独立的。
KVL的独立方程数:对一个具有n个结点和b条支路的电路而言,其KVL的独立方程数为(b-n+1)。
三、电路的分析方法1.支路电流法(1)支路电流法是以b个支路电流为变量列写b个方程,并直接求解。
其方程的一般形式为(2)支路电流法解题步骤①标出各支路电流的方向;②依据KCL列写(n-1)个独立的结点方程;③选取(b-n+1)个独立回路,标出回路绕行方向,列写KVL方程。
注:①独立结点选择方法:n个结点中去掉一个,其余结点都是独立的;②独立回路选择方法:先确定一个树,再确定单连支回路(基本回路),仅含唯一的连支,其余为树支。
2.网孔电流法(1)网孔是最简单的回路,即不含任何支路的回路。
网孔数=独立回路数=b-n+1。
网孔电流法是以网孔电流为未知量,根据KVL对全部网孔列出方程求解。
(2)网孔电流法解题步骤①局部调整电路,当电路中含有电流源和电阻的并联组合时,可转化为电压源和电阻的串联组合;②选取网孔电流,指定网孔电流的参考方向;③依据KVL列写网孔电流方程,自阻总为正,互阻视流过的网孔电流方向而定,两电路同向取“+”,异向取“-”。
电阻电路的一般分析例题-精选
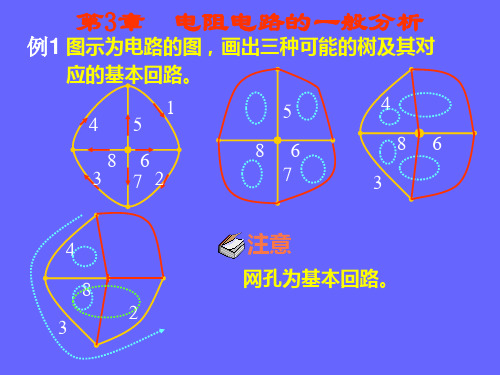
i3 150/4
2 3 2
解得:
+
-2
I(i1i2)12 A0 110V
U 2 i3 1 0 1 0 2 0 1V 95
③用结点电压表示控制量。 u3 un3 i un2 R2
100V
例14 求电压U和电流I
解1 应用结点法
1 I 1
-
-
-
+
un110V 0
90V
U
un2 10 101 201 V0 + 20A +
0 .5 u n 10 .5 u n 2u n 320 2 2 3 2
+
U1
_
R1
R3 1
iS
3
R5 R4
2
R2 gU1
4+_ U1i gU1增补方程:U 1R 1(i1i2)
例9 求电路中电压U,电流I和电压源产生的功率
2A
i2
解 i1 2A i2 2A
2A i1
1 3A + 3 i4 U
i3 3A
2 +
6 i4 3 i1 i2 4 i3 4
1
解得:
+
-
u n3 2 0 5 0 10 15 V 75110V
Uun3 12 019 V5
I (u n2 9)/0 1 1A 20
100V
解2 应用回路法
i1 20A
i2 i1 120
1 -
I 1
1 -
90V
U
-
+
2i1 4i3 110
+ 20A +
R 1 5u n 1 R 1 4u n 2 (R 1 4 R 1 3 R 1 5)u n 3 g3 u u R S 5
第3章 电阻电路的一般分析

解2. I1 7 + 70V –
a
增补方程:I2=6A 11 由于I2已知,故只列写两个方程。 a:–I1+I3=6 7
I2
1 6A b
I3
避开电流源支路取回路: 1: 7I1+7I3=70
返 回 上 页 下 页
例6.
I1 7
+ 70V –
列写支路电流方程(电路中含有受控源)。 a
I2 1 + 5U _ b 11 2 I3 + 7 U _ 解
返 回
支路、结点、路径、回路和网孔的概念。 (1)连通图 图G的任意两结点间至少有一条路径 时,称图G为连通图。非连通图至少 存在两个分离部分。
(2) 子图
若图G1中所有支路和结点都是图G中 的支路和结点,则称G1是G的子图。
返 回
上 页
下 页
(3)树 (Tree)
T是连通图G的一个子图, 并满足条件:
依据:
KCL、KVL以及元件的VCR。
方法: 根据列方程时所选变量不同,可分为支路电流法、
网孔电流法、回路电流法和结点电压法。
返 回 上 页 下 页
对于线性电阻电路,电路方程是一组线性代数方程。
例1
3
I1 R1 uS1 + –
a I2 I3
R2 + – b 2 独立? R3 求I1、I2和I3?
1 uS2
独立回路=2,选为网孔。
+ –
R3
i1 il 1 i3 il 2 i2 il 2 il 1
uS2
b
回路1:R1 il1-R2(il2- il1) +uS2-uS1=0 回路2:R2(il2- il1)+ R3 il2 -uS2=0 自电阻 (R1+ R2) il1 -R2 il2 = uS1-uS2
第三章电阻电路的一般分析

第三章 电 阻 电 路 的 一 般 分 析
②回路(Loop)
L是连通图的一个子图,构成一条 闭合路径,并满足:(1)连通,(2)
1 23 75
6 84
回路
每个结点关联2条支路。
23
12
75
5
84
不 是 回 路
1)对应一个图有很多的回路;
明 2)基本回路的数目是一定的,为连支数; 确 3)对于平面电路,网孔数等于基本回路数。
返回 上页 下页
第三章 电 阻 电 路 的 一 般 分 析
引言
1.电路的图
i
n5 b8
R1 R2
R3 R5
R4
抛开元 件性质
1
8 3
5
2
4
+ uS _ R6
元件的串联及并联 组合作为一条支路
1
3
5
2
4
6
7
6
一个元件作 为一条支路
n4b6
有向图
返回 上页 下页
第三章 电 阻 电 路 的 一 般 分 析
注意
R1lill usl1 R2lill usl 2
Rllill usll
Rkk: 自电阻(总为正) Rjk: 互电阻
+ : 流过互阻的两个网孔电流方向相同;
- : 流过互阻的两个网孔电流方向相反; 0 : 无关。
返回 上页 下页
第三章 电 阻 电 路 的 一 般 分 析
例1 用网孔电流法求解电流 i
线性电路的一般分析方法 • 普遍性:对任何线性电路都适用。 • 系统性:计算方法有规律可循。
方法的基础
• 电路的连接关系—KCL,KVL定律。 • 元件的电压、电流关系特性。 复杂电路的一般分析法就是根据KCL、KVL及元 件电压和电流关系列方程、解方程。根据列方程时所 选变量的不同可分为支路电流法、回路电流法和结点 电压法。
第三章电阻电路的一般分析课本分部习题.

第三章 电阻电路的一般分析电路的一般分析是指方程分析法,它是以电路元件的约束特性 (VCR 和电路的拓扑约束特性(KCL,KVL 为依据,建立以支路电流或回路电流,或结点电压为变量的回路方程组,从中解岀所要求的电流、电压、功率等。
方程 分析法的特点是:(1 )具有普遍适用性,即无论线性和非线性电路都适用;(2)具有系统性,表现在不改变电路结构,应用 KCL ,KVL,元件的VCR 建立电路变量方程,方程的建立有一套固定不变的步骤和格式,便于 编程和用计算机计算。
本章的重点是会用观察电路的方法,熟练运用支路法、回路法和结点电压法的“方程通式”写岀支路电流方 程、回路方程和结点电压方程,并加以求解。
3-1在一下两种情况下,画出图示电路的图,并说明其节点数和支路数 (1每个元件作为一条支路处理; (2电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。
解:(1每个元件作为一条支路处理时,图(a 和(b 所图(a1中节点数.',支路数图(b1中节点数’ ,支路数 -(2电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图 图分别为题解图(a2和(b2。
(a 和图(b 所示电路的图(a2中节点数■' ■",支路数图(b2中节点数■■-■'■,支路数--示电路的图分别为题解 3-1 图(a1 和(b13-2指出题3-1中两种情况下,KCL,KVL 独立方程数各为多少?解:题3- 1中的图(a 电路,在两种情况下,独立的 KCL 方程数分别为(1 , 丨 ' :(2独立的KVL 方程数分别为(1 • ■ I (2 ';■打-■讣, '图(b 电路在两种情况下,独立的 KCL 方程数为独立的KVL 方程数分别为(1 • ; - (2 ■■- C - I 寸 - . .?3-3对题图(a 和(b 所示-,各画出4个不同的树,树支数各为多少?解:一个连通图 '的树-是这样定义的:(1■包含|的全部结点和部分支路;(2 ■■本身是连通的且又不包含回路。
第3章 电阻电路的一般分析答案
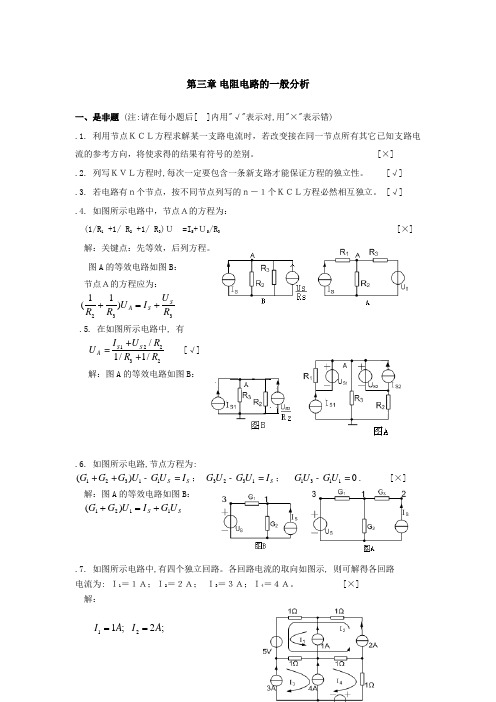
第三章 电阻电路的一般分析一、是非题 (注:请在每小题后[ ]内用"√"表示对,用"×"表示错).1. 利用节点KCL方程求解某一支路电流时,若改变接在同一节点所有其它已知支路电流的参考方向,将使求得的结果有符号的差别。
[×] .2. 列写KVL方程时,每次一定要包含一条新支路才能保证方程的独立性。
[√] .3. 若电路有n个节点,按不同节点列写的n-1个KCL方程必然相互独立。
[√] .4. 如图所示电路中,节点A的方程为: (1/R 1 +1/ R 2 +1/ R 3)U =I S +US /R 3 [×]解:关键点:先等效,后列方程。
图A 的等效电路如图B :节点A的方程应为: 332)11(R U I U R R S S A +=+ .5. 在如图所示电路中, 有 12232/1/1/S S A I U R U R R +=+ [√]解:图A 的等效电路如图B :.6. 如图所示电路,节点方程为:12311()S S G G G U GU I ++-=; 3231S G U G U I -=; 13110GU GU -=. [×]解:图A 的等效电路如图B :S S U G I U G G 1121)(+=+.7. 如图所示电路中,有四个独立回路。
各回路电流的取向如图示, 则可解得各回路 电流为: I1=1A;I2=2A; I3=3A;I4=4A。
[×] 解:;11A I = ;22A I =;33A I = ;7344A I =+=二、选择题(注:在每小题的备选答案中选择适合的答案编号填入该题空白处,多选或不选按选错论).1.对如图所示电路,下列各式求支路电流正确的是 C_。
(A) 12112E E I R R -=+; (B) 222E I R =(C) AB L LUI R =.2. 若网络有b 条支路、n 个节点,其独立KCL方程有_C_个,独立KVL方程有_D__个,共计为_A_个方程。
