2018年高考数学一轮复习课时跟踪检测4文新人教A版!
2018年高考数学一轮复习 课时跟踪检测18 文 新人教A版

课时跟踪检测(十八)[高考基础题型得分练]1.下列与9π4的终边相同的角的表达式中正确的是( )A .2k π+45°(k ∈Z )B .k ·360°+9π4(k ∈Z )C .k ·360°-315°(k ∈Z )D .k π+5π4(k ∈Z )答案:C解析:与9π4的终边相同的角可以写成2k π+9π4(k ∈Z ),但是角度制与弧度制不能混用,所以只有C 正确.2.已知角α的终边经过点(-4,3),则cos α=( ) A.45 B.35 C .-35D .-45答案:D解析:由三角函数的定义知, cos α=-4-2+32=-45 . 3.已知点P (tan α,cos α)在第三象限,则角α的终边在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限答案:B解析:由题意知,tan α<0,cos α<0,∴α是第二象限角.4.已知圆O :x 2+y 2=4与y 轴正半轴的交点为M ,点M 沿圆O 顺时针运动π2弧长到达点N ,以ON 为终边的角记为α,则tan α=( )A .-1B .1C .-2D .2 答案:B解析:圆的半径为2,π2的弧长对应的圆心角为π4,故以ON 为终边的角为{α⎪⎪⎪⎭⎬⎫α=2k π+π4,k ∈Z ,故tan α=1.5.已知点P ⎝ ⎛⎭⎪⎫sin 3π4,cos 3π4落在角θ的终边上,且θ∈[0,2π),则θ=( )A.π4 B.3π4 C.5π4D.7π4答案:D解析:由sin 3π4>0,cos 3π4<0知,角θ是第四象限的角,∵tan θ=cos3π4sin3π4=-1,θ∈[0,2π),∴θ=7π4.6.若α是第三象限角,则y =⎪⎪⎪⎪⎪⎪sin α2sinα2+⎪⎪⎪⎪⎪⎪cos α2cosα2的值为( )A .0B .2C .-2D .2或-2答案:A解析:∵α是第三象限角,∴2k π+π<α<2k π+3π2(k ∈Z ),∴k π+π2<α2<k π+3π4(k ∈Z ),∴α2是第二象限角或第四象限角. 当α2是第二象限角时,y =sin α2sin α2-cosα2cosα2=0, 当α2是第四象限角时,y =-sin α2sin α2+cosα2cosα2=0,故选A. 7.[2017·湖南株洲六校联考]已知P ,Q 是圆心在坐标原点O 的单位圆上的两点,分别位于第一象限和第四角限,且P 点的纵坐标为45,Q 点的横坐标为513,则cos ∠POQ =( )A.3365B.6365C .-6365D .-3365答案:D解析:因为P ,Q 是圆心在坐标原点O 的单位圆上的两点,分别位于第一象限和第四象限,且P 点的纵坐标为45,Q 点的横坐标为513,所以点P ,Q 的坐标分别为P ⎝ ⎛⎭⎪⎫35,45,Q ⎝ ⎛⎭⎪⎫513,-1213,所以cos ∠POQ =OP →·OQ →|OP →||OQ →|=35×513+45×⎝ ⎛⎭⎪⎫-1213=-3365.故选D.8.[2017·河南商丘一模]已知锐角α的终边上一点P (sin 40°,1+cos 40°),则α等于( )A .10°B .20°C .70°D .80°答案:C解析:由题意可知,sin 40°>0,1+cos 40°>0,点P 在第一象限,OP 的斜率tan α=1+cos 40°sin 40°=1+2cos 220°-12sin 20°cos 20°=cos 20°sin 20°=sin 70°cos 70°=tan 70°,由α为锐角,可知α为70°.故选C.9.函数y =sin x -32的定义域为________. 答案:⎣⎢⎡⎦⎥⎤2k π+π3,2k π+2π3,k ∈Z 解析:∵sin x ≥32,作直线y =32交单位圆于A ,B 两点,连接OA ,OB ,则OA 与OB 围成的区域(图中阴影部分)即为角α的终边的范围,故满足条件的角α的集合为{x ⎪⎪⎪⎭⎬⎫2k π+π3≤x ≤2k π+2π3,k ∈Z .10.在直角坐标系中,O 是原点,A 点坐标为(3,-1),将OA 绕O 逆时针旋转450°到B 点,则B 点的坐标为________.答案:(1,3)解析:设B (x ,y ),由题意知,|OA |=|OB |=2,∠BOx =60°,且点B 在第一象限, ∴x =2cos 60°=1,∴y =2sin 60°=3, ∴B 点的坐标为(1,3).11.函数y =lg(3-4sin 2x )的定义域为________. 答案:⎝ ⎛⎭⎪⎫k π-π3,k π+π3(k ∈Z ) 解析:∵3-4sin 2x >0, ∴sin 2x <34,∴-32<sin x <32. ∴x ∈⎝⎛⎭⎪⎫k π-π3,k π+π3(k ∈Z ).[冲刺名校能力提升练]1.集合⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪k π+π4≤α≤k π+π2,k ∈Z 中的角所表示的范围(阴影部分)是( )A B C D 答案:C解析:当k =2n (n ∈Z )时,2n π+π4≤α≤2n π+π2,此时α表示的范围与π4≤α≤π2表示的范围一样;当k =2n +1(n ∈Z )时,2n π+π+π4≤α≤2n π+π+π2,此时α表示的范围与π+π4≤α≤π+π2表示的范围一样.2.已知A (x A ,y A )是单位圆(圆心在坐标原点O )上任意一点,将射线OA 绕O 点逆时针旋转30°,交单位圆于点B (x B ,y B ),则x A -y B 的取值范围是( )A .[-2,2]B .[-2,2]C .[-1,1] D.⎣⎢⎡⎦⎥⎤-12,12 答案:C解析:设x 轴正方向逆时针到射线OA 的角为α,根据三角函数的定义得x A =cos α,y B =sin(α+30°),所以x A -y B =cos α-sin(α+30°)=-32sin α+12cos α=sin(α+150°)∈[-1,1].3.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角α∈(0,π)的弧度数为( )A. π3B. π2C. 3 D .2答案:C解析:设圆半径为r ,则其内接正三角形的边长为3r ,所以3r =αr ,则α= 3. 4.一扇形的圆心角为120°,则此扇形的面积与其内切圆的面积之比为________. 答案:(7+43)∶9解析:设扇形半径为R ,内切圆半径为r .则(R -r )sin 60°=r ,即R =⎝⎛⎭⎪⎫1+233r .又S 扇=12|α|R 2=12×2π3×R 2=π3R 2=7+439πr 2,∴S 扇πr 2=7+439.5.已知角α的终边在直线3x +4y =0上,求sin α,cos α,tan α的值. 解:∵角α的终边在直线3x +4y =0上, ∴在角α的终边上任取一点P (4t ,-3t )(t ≠0), 则x =4t ,y =-3t ,r =x 2+y 2=t2+-3t2=5|t |,当t >0时,r =5t ,sin α=y r =-3t 5t =-35,cos α=x r =4t 5t =45,tan α=y x =-3t 4t =-34;当t <0时,r =-5t ,sin α=y r =-3t -5t =35,cos α=x r =4t -5t =-45,tan α=y x =-3t 4t =-34.综上可知,sin α=-35,cos α=45,tan α=-34或sin α=35,cos α=-45,tan α=-34.6.已知一扇形的圆心角为α (α>0),所在圆的半径为R .(1)若α=60°,R =10 cm ,求扇形的弧长及该弧所在的弓形的面积; (2)若扇形的周长是一定值C (C >0),当α为多少弧度时,该扇形有最大面积? 解:(1)设弧长为l ,弓形面积为S 弓, 则α=60°=π3,R =10,l =π3×10=10π3 (cm), S 弓=S 扇-S △=12×10π3×10-12×102×sin π3=503π-5032=50⎝ ⎛⎭⎪⎫π3-32 (cm 2). (2)扇形周长C =2R +l =2R +αR , ∴R =C2+α, ∴S 扇=12α·R 2=12α·⎝ ⎛⎭⎪⎫C 2+α2 =C 2α2·14+4α+α2=C 22·14+α+4α≤C 216. 当且仅当α2=4,即α=2时,扇形面积有最大值C 216.百度文库是百度发布的供网友在线分享文档的平台。
2018版高考数学(人教A版理科)一轮复习课时跟踪检测46含答案
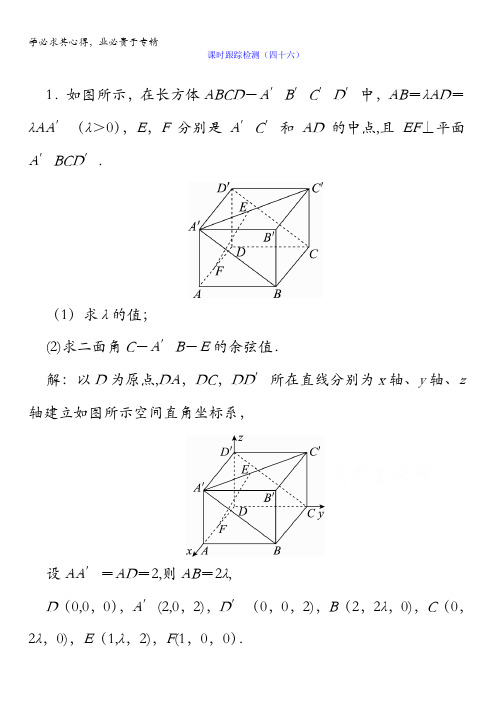
课时跟踪检测(四十六)1.如图所示,在长方体ABCD-A′B′C′D′中,AB=λAD=λAA′(λ>0),E,F分别是A′C′和AD的中点,且EF⊥平面A′BCD′.(1)求λ的值;(2)求二面角C-A′B-E的余弦值.解:以D为原点,DA,DC,DD′所在直线分别为x轴、y轴、z 轴建立如图所示空间直角坐标系,设AA′=AD=2,则AB=2λ,D(0,0,0),A′(2,0,2),D′(0,0,2),B(2,2λ,0),C(0,2λ,0),E(1,λ,2),F(1,0,0).(1)错误!=(0,-λ,-2),错误!=(2,0,0),错误!=(0,2λ,-2),∵EF⊥D′A′,EF⊥A′B,∴错误!·错误!=0,错误!·错误!=0,即-2λ2+4=0,∴λ=错误!。
(2)设平面EA′B的一个法向量为m=(1,y,z),则错误!∵错误!=(0,2错误!,-2),错误!=(-1,错误!,0),∴错误!∴y=错误!,z=1,∴m=错误!.由已知得错误!为平面A′BC的一个法向量,又错误!=(0,-错误!,-2),∴cos〈m,错误!〉=错误!=错误!=-错误!。
又二面角C-A′B-E为锐二面角,故二面角C-A′B-E的余弦值为错误!。
2.如图所示的几何体,四边形ABCD中,有AB∥CD,∠BAC=30°,AB=2CD=2,CB=1,点E在平面ABCD内的射影是点C,EF∥AC,且AC=2EF.(1)求证:平面BCE⊥平面ACEF;(2)若二面角D-AF-C的平面角为60°,求CE的长.(1)证明:在△ABC中,BC2=AB2+AC2-2AB·AC cos 30°,解得AC=错误!,所以AB2=AC2+BC2,由勾股定理知∠ACB=90°,所以BC⊥AC.又EC⊥平面ABCD,BC⊂平面ABCD,所以BC⊥EC.又AC∩EC=C,所以BC⊥平面ACEF,所以平面BCE⊥平面ACEF.(2)解:因为EC⊥平面ABCD,又由(1)知BC⊥AC,所以可以以C为原点,建立如图所示的空间直角坐标系C-xyz。
2018年高考数学一轮复习课时跟踪检测28文新人教A版

课时跟踪检测(二十八)[高考基础题型得分练]1.[2017·广东惠州二调]已知向量AB →=(3,7),BC →=(-2,3),则-12AC →=( )A.⎝ ⎛⎭⎪⎫-12,5B.⎝ ⎛⎭⎪⎫12,5C.⎝ ⎛⎭⎪⎫-12,-5D.⎝ ⎛⎭⎪⎫12,-5 答案:C解析:因为向量AC →=AB →+BC →=(1,10),则-12AC →=⎝ ⎛⎭⎪⎫-12,-5,故选C.2.下列各组向量:①e 1=(-1,2),e 2=(5,7);②e 1=(3,5),e 2=(6,10);③e 1=(2,-3),e 2=⎝ ⎛⎭⎪⎫12,34,能作为表示它们所在平面内所有向量的基底是( )A .①B .①③C .②③D .①②③ 答案:B解析:②中,e 1=12e 2,即e 1与e 2共线,所以不能作为基底.3.已知点A (1,3),B (4,-1),则与向量AB →同方向的单位向量为( ) A.⎝ ⎛⎭⎪⎫35,-45 B.⎝ ⎛⎭⎪⎫45,-35C.⎝ ⎛⎭⎪⎫-35,45D.⎝ ⎛⎭⎪⎫-45,35答案:A解析:∵AB →=OB →-OA →=(4,-1)-(1,3)=(3,-4), ∴与AB →同方向的单位向量为AB →|AB →|=⎝ ⎛⎭⎪⎫35,-45.4.在△ABC 中,点P 在BC 上,且BP →=2PC →,点Q 是AC 的中点,若PA →=(4,3),PQ →=(1,5),则BC →=( )A .(-2,7)B .(-6,21)C .(2,-7)D .(6,-21) 答案:B解析:AQ →=PQ →-PA →=(-3,2),∵Q 是AC 的中点,∴AC →=2AQ →=(-6,4), PC →=PA →+AC →=(-2,7),∵BP →=2PC →,∴BC →=3PC →=(-6,21).5.已知向量a =(1,2),b =(1,0),c =(3,4).若λ为实数,(a +λb )∥c ,则λ的值为( )A.14B.12 C .1 D .2 答案:B解析:∵a +λb =(1+λ,2),c =(3,4), 且(a +λb )∥c ,∴1+λ3=24,∴λ=12,故选B.6.设向量a =(x,1),b =(4,x ),且a ,b 方向相反,则x 的值是( ) A .2 B .-2 C .±2 D .0 答案:B解析:∵a 与b 方向相反,∴b =m a ,m <0,则有(4,x )=m (x,1),∴⎩⎪⎨⎪⎧4=mx ,x =m ,解得m =±2.又m <0,∴m =-2,x =m =-2.7.[2017·江苏杭州五校联盟一诊]已知三个向量m =⎝ ⎛⎭⎪⎫a ,cos A 2,n =⎝ ⎛⎭⎪⎫b ,cos B 2,p=⎝⎛⎭⎪⎫c ,cos C 2共线,其中a ,b ,c ,A ,B ,C 分别是△ABC 的三条边及相对三个角,则△ABC的形状是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰直角三角形答案:B解析:∵m =⎝ ⎛⎭⎪⎫a ,cos A 2与n =⎝ ⎛⎭⎪⎫b ,cos B 2共线,∴a cos B 2=b cos A2,由正弦定理得sin A cos B 2=sin B cos A2,∵sin A =2sin A 2cos A 2,sin B =2sin B 2cos B2,∴2sin A 2cos A 2cos B 2=2sin B 2cos B 2cos A2,化简得sin A 2=sin B2.又0<A 2<π2,0<B 2<π2,∴A 2=B2,可知A =B . 同理,由n =⎝ ⎛⎭⎪⎫b ,cos B 2与p =⎝ ⎛⎭⎪⎫c ,cos C 2共线得到B =C ,∴在△ABC 中,A =B =C ,可得△ABC 是等边三角形.故选B.8.[2017·河南八市质检]已知点M 是△ABC 的边BC 的中点,点E 在边AC 上,且EC →=2AE →,则向量EM →=( )A.12AC →+13AB →B.12AC →+16AB →C.16AC →+12AB →D.16AC →+32AB → 答案:C解析:如图,∵EC →=2AE →, ∴EM →=EC →+CM →=23AC →+12CB →=23AC →+12(AB →-AC →)=12AB →+16AC →. 9.若三点A (2,2),B (a,0),C (0,b )(ab ≠0)共线,则1a +1b的值为________.答案:12解析:AB →=(a -2,-2),AC →=(-2,b -2), 依题意,有(a -2)(b -2)-4=0,即ab -2a -2b =0, 所以1a +1b =12.10.[2017·四川雅安模拟]已知向量a =(3,1),b =(0,-1),c =(k ,3).若a-2b 与c 共线,则k =________.答案:1解析:∵a -2b =(3,3),且(a -2b )∥c , ∴3×3-3k =0,解得k =1.11.已知向量AC →,AD →和AB →在正方形网格中的位置如图所示,若AC →=λAB →+μAD →,则λμ=________.答案:-3解析:建立如图所示的平面直角坐标系xAy , 则AC →=(2,-2),AB →=(1,2),AD →=(1,0),由题意可知,(2,-2)=λ(1,2)+μ(1,0),即⎩⎪⎨⎪⎧2=λ+μ,-2=2λ,解得⎩⎪⎨⎪⎧λ=-1,μ=3,所以λμ=-3.[冲刺名校能力提升练]1.[2017·湖南长沙调研]如图,在△OAB 中,P 为线段AB 上的一点,OP →=xOA →+yOB →,且BP →=2PA →,则( )A .x =23,y =13B .x =13,y =23C .x =14,y =34D .x =34,y =14答案:A解析:由题意知,OP →=OB →+BP →,又BP →=2PA →,所以OP →=OB →+23BA →=OB →+23(OA →-OB →)=23OA →+13OB →,所以x =23,y =13.2.[2016·江西南昌十校联考]已知a =(3,1),若将向量-2a 绕坐标原点逆时针旋转120°得到向量b ,则b 的坐标为( )A .(0,4)B .(23,-2)C .(-23,2)D .(2,-23)答案:B解析:∵a =(3,1),∴-2a =(-23,-2), 易知向量-2a 与x 轴正半轴的夹角α=150°(如图).向量-2a 绕坐标原点逆时针旋转120°得到向量b ,在第四象限,与x 轴正半轴的夹角β=30°,∴b =(23,-2),故选B.3.[2017·甘肃兰州一中期中]如图所示,两个不共线向量OA →,OB →的夹角为θ,M ,N 分别为OA 与OB 的中点,点C 在线段MN 上,且OC →=xOA →+yOB →(x ,y ∈R ),则x 2+y 2的最小值为( )A.24 B.18 C.22 D.12答案:B解析:∵M ,N ,C 三点共线,∴存在实数t 使得NC →=tNM →(0≤t ≤1),∴OC →=ON →+NC →=ON →+tNM →=ON →+t (OM →-ON →)=(1-t )ON →+tOM →=1-t 2OA →+t 2OB →.∴⎩⎪⎨⎪⎧x =1-t2,y =t2,∴x 2+y 2=1-t2+t24=14(2t 2-2t +1)(0≤t ≤1). 令f (t )=2t 2-2t +1(0≤t ≤1),函数f (t )图象开口向上且以t =12为对称轴,∵t =12∈[0,1],∴f (t )min =f ⎝ ⎛⎭⎪⎫12=2×14-2×12+1=12. ∴(x 2+y 2)min =14×12=18,故选B.4.在梯形ABCD 中,已知AB ∥CD ,AB =2CD ,M ,N 分别为CD ,BC 的中点.若AB →=λAM →+μAN →,则λ+μ=________.答案:45解析:解法一:由AB →=λAM →+μAN →,得 AB →=λ·12(AD →+AC →)+μ·12(AC →+AB →),则⎝ ⎛⎭⎪⎫μ2-1AB →+λ2AD →+⎝ ⎛⎭⎪⎫λ2+μ2AC →=0, 得⎝⎛⎭⎪⎫μ2-1AB →+λ2AD →+⎝ ⎛⎭⎪⎫λ2+μ2⎝⎛⎭⎪⎫AD → +12AB →=0, 得⎝ ⎛⎭⎪⎫14λ+34μ-1AB →+⎝ ⎛⎭⎪⎫λ+μ2AD →=0. 又AB →,AD →不共线,∴由平面向量基本定理,得 ⎩⎪⎨⎪⎧14λ+34μ-1=0,λ+μ2=0,解得⎩⎪⎨⎪⎧λ=-45,μ=85.∴λ+μ=45.解法二:(回路法)连接MN 并延长交AB 的延长线于T ,由已知易得AB =45AT ,∴45AT →=AB →=λAM →+μAN →,即AT →=54λAM →+54μAN →,∵T ,M ,N 三点共线,∴54λ+54μ=1.∴λ+μ=45.5.已知O (0,0),A (1,2),B (4,5)及OP →=OA →+tAB →,试问: (1)当t 为何值时,P 在x 轴上?在y 轴上?在第三象限?(2)四边形OABP 能否成为平行四边形,若能,求出相应的t 的值;若不能,请说明理由. 解:(1)∵OA →=(1,2),AB →=(3,3), ∴OP →=OA →+tAB →=(1+3t,2+3t ).若点P 在x 轴上,则2+3t =0,解得t =-23;若点P 在y 轴上,则1+3t =0,解得t =-13;若点P 在第三象限,则⎩⎪⎨⎪⎧1+3t <0,2+3t <0,解得t <-23.(2)若四边形OABP 为平行四边形,则OP →=AB →,∴⎩⎪⎨⎪⎧1+3t =3,2+3t =3.∵该方程组无解,∴四边形OABP 不能成为平行四边形.6.已知A (-2,4),B (3,-1),C (-3,-4).设AB →=a ,BC →=b ,CA →=c ,且CM →=3c ,CN →=-2b .(1)求3a +b -3c ;(2)求满足a =m b +n c 的实数m ,n ; (3)求M ,N 的坐标及向量MN →的坐标.解:由已知,得a =(5,-5),b =(-6,-3),c =(1,8). (1)3a +b -3c =3(5,-5)+(-6,-3)-3(1,8) =(15-6-3,-15-3-24)=(6,-42). (2)∵m b +n c =(-6m +n ,-3m +8n ),∴⎩⎪⎨⎪⎧-6m +n =5,-3m +8n =-5,解得⎩⎪⎨⎪⎧m =-1,n =-1.即所求实数m 的值为-1,n 的值为-1. (3)设O 为坐标原点,∵CM →=OM →-OC →=3c , ∴OM →=3c +OC →=(3,24)+(-3,-4) =(0,20),即M (0,20).又CN →=ON →-OC →=-2b , ∴ON →=-2b +OC →=(12,6)+(-3,-4) =(9,2),即N (9,2),∴MN →=(9,-18).。
2018年高考数学一轮复习 课时跟踪检测61 文 新人教A版

课时跟踪检测(六十一)[高考基础题型得分练]1.(2017·海南海口模拟)某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解答下列问题.(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.①求所抽取的2名同学中至少有1名同学来自第5组的概率;②求所抽取的2名同学来自同一组的概率.解:(1)由题意可知,样本总人数为80.16=50,∴b=250=0.04,∴y =b10=0.004,a =16,x =0.032.(2)①由题意可知,第4组共有4人,记为A ,B ,C ,D ,第5组共有2人,记为X ,Y . 从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有AB ,AC ,AD ,BC ,BD ,CD ,AX ,AY ,BX ,BY ,CX ,CY ,DX ,DY ,XY ,共15种情况.设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E ,有AX ,AY ,BX ,BY ,CX ,CY ,DX ,DY ,XY ,共9种情况.∴P (E )=915=35.②设“随机抽取的2名同学来自同一组”为事件F ,有AB ,AC ,AD ,BC ,BD ,CD ,XY ,共7种情况.∴P (F )=715.2.某足球队两名主力队员各进行了5组罚点球训练,每组罚10次,罚中次数如下表:场?(2)若从这两名队员的5组中各随机抽取一组分析罚点球的技术和心理因素,求选出的一组中甲恰好罚中次数多于乙的罚中次数的概率.解:(1)计算甲、乙的罚中次数的平均值得x 甲=6+5+7+9+85=7,x乙=4+8+9+7+75=7,所以两人罚中次数的平均值相等,s 2甲=-2+-2+-2+-2+-25=2,s 2乙=-2+-2+-2+-2+-25=145,s 2甲<s 2乙,甲罚中次数的方差较小,相对更稳定,应派甲队员出场.(2)记甲队员的5组次数分别为A 1,A 2,A 3,A 4,A 5,乙队员的5组次数分别为B 1,B 2,B 3,B 4,B 5,随机抽取各一组所有可能的情况有25种,分别为:(A 1,B 1),(A 1,B 2),(A 1,B 3),(A 1,B 4),(A 1,B 5),(A 2,B 1),…,(A 5,B 5),其中甲恰好罚中次数多于乙的罚中次数的有(A 1,B 1),(A 2,B 1),(A 3,B 1),(A 4,B 1),(A 5,B 1),(A 4,B 2),(A 4,B 4),(A 4,B 5),(A 5,B 4),(A 5,B 5),共10种情况,故所求概率为P =1025=25.3.在等差数列{a n }和等比数列{b n }中,a 1=b 1=1,b 4=8,{a n }的前10项和S 10=55.(1)求a n 和b n ;(2)现分别从{a n }和{b n }的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.解:(1)设数列{a n }的公差为d ,数列{b n }的公比为q . 依题意得S 10=10+10×92d =55,b 4=q 3=8,解得d =1,q =2,所以a n =n ,b n =2n -1.(2)分别从{a n }和{b n }的前3项中各随机抽取一项,得到的基本事件有9个:(1,1),(1,2),(1,4),(2,1),(2,2),(2,4),(3,1),(3,2),(3,4).符合题意的基本事件有2个:(1,1),(2,2).故所求的概率P =29.[冲刺名校能力提升练]1.一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机抛掷两次,正四面体面朝下的数字分别为b ,c .(1)z =(b -3)2+(c -3)2,求z =4的概率;(2)若方程x 2-bx -c =0至少有一根x ∈{1,2,3,4},就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.解:(1)因为是抛掷两次,因此基本事件(b ,c ):(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.当z =4时,(b ,c )的所有取值为(1,3),(3,1), 所以P (z =4)=216=18.(2)①若方程一根为x =1,则1-b -c =0, 即b +c =1,不成立.②若方程一根为x =2,则4-2b -c =0, 即2b +c =4,所以 ⎩⎪⎨⎪⎧ b =1,c =2.③若方程一根为x =3,则9-3b -c =0,即3b +c =9,所以 ⎩⎪⎨⎪⎧b =2,c =3.④若方程一根为x =4,则16-4b -c =0,即4b +c =16,所以 ⎩⎪⎨⎪⎧b =3,c =4.由①②③④知(b ,c )的所有可能取值为(1,2),(2,3),(3,4), 所以方程为“漂亮方程”的概率为P=316.2.某班甲、乙两名同学参加100米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论);(2)经过对甲、乙两位同学的若干次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.解:(1)甲、乙两人10次训练的成绩的茎叶图:从统计图中可以看出,乙的成绩较为集中,差异程度较小,所以选派乙同学代表班级参加比赛更好.(2)设甲同学的成绩为x,乙同学的成绩为y,则|x-y|<0.8,得x-0.8<y<0.8+x,如图,阴影部分面积即为3×3-2.2×2.2=4.16,则P (|x -y |<0.8)=P (x -0.8<y <0.8+x )=4.163×3=104225.3.已知集合P ={x |x (x 2+10x +24)=0},Q ={y |y =2n -1,1≤n ≤2,n ∈N *},M =P ∪Q .在平面直角坐标系中,点A 的坐标为(x ′,y ′),且x ′∈M ,y ′∈M ,试计算:(1)点A 正好在第三象限的概率; (2)点A 不在y 轴上的概率;(3)点A 正好落在区域x 2+y 2≤10上的概率. 解:由集合P ={x |x (x 2+10x +24)=0}, 可得P ={-6,-4,0},由Q ={y |y =2n -1,1≤n ≤2,n ∈N *},可得Q ={1,3},则M =P ∪Q ={-6,-4,0,1,3}, 因为点A 的坐标为(x ′,y ′),且x ′∈M ,y ′∈M ,所以满足条件的点A 的所有情况为(-6,-6),(-6,-4),(-6,0),(-6,1),(-6,3),…,(3,3),共25种.(1)点A 正好在第三象限的可能情况为(-6,-6),(-6,-4),(-4,-6),(-4,-4),共4种,故点A 正好在第三象限的概率P 1=425.(2)点A 在y 轴上的可能情况为(0,-6),(0,-4),(0,0),(0,1),(0,3),共5种, 故点A 不在y 轴上的概率P 2=1-525=45.(3)点A 正好落在区域x 2+y 2≤10上的可能情况为(0,0),(1,0),(0,1),(3,1),(1,3),(3,0),(0,3),(1,1),共8种,故点A 落在区域x 2+y 2≤10上的概率P 3=825.。
高中数学 课时跟踪训练1 任意角 新人教A版必修4-新人教A版高一必修4数学试题

课时跟踪训练(一)(时间45分钟) 题型对点练(时间20分钟)题组一 任意角的概念 1.给出下列说法: ①锐角都是第一象限角; ②第一象限角一定不是负角; ③第二象限角是钝角;④小于180°的角是钝角、直角或锐角.其中正确命题的序号为________(把正确命题的序号都写上).[解析]①正确;②错,若顺时针旋转终边落在第一象限,则为负角;③错,第二象限角不都是钝角,钝角都是第二象限角;④错,小于180°的角包括负角和零角.[答案]①2.将时钟拨快20分钟,则分针转过的度数是________.[解析] 时钟拨快20分钟,相当于转了13小时.因为时针转过1小时,分针转-360°,所以时针转13小时,分针转过的度数为13×(-360°)=-120°.[答案] -120°3.写出图(1),(2)中的角α,β,γ的度数.[解] 题干图(1)中,α=360°-30°=330°; 题干图(2)中,β=-360°+60°+150°=-150°;γ=360°+60°+(-β)=360°+60°+150°=570°.题组二 终边相同的角与象限角4.与405°角终边相同的角是( )A .k ·360°-45°,k ∈ZB .k ·180°-45°,k ∈ZC .k ·360°+45°,k ∈ZD .k ·180°+45°,k ∈Z[解析] 因为405°=360°+45°,所以与405°终边相同的角为k ·360°+45°,k ∈Z .[答案] C5.-435°角的终边所在的象限是( ) A .第一象限 B .第二象限 C .第三象限D .第四象限[解析] 因为-435°=-360°-75°,而-75°为第四象限角,所以-435°为第四象限角.[答案] D6.若角α,β的终边相同,则α-β的终边在( ) A .x 轴的非负半轴 B .y 轴的非负半轴 C .x 轴的非正半轴D .y 轴的非正半轴[解析]∵角α,β终边相同,∴α=k ·360°+β(k ∈Z ),∴α-β=k ·360°(k ∈Z ),故α-β的终边在x 轴的非负半轴上.[答案] A题组三 角αn,(n ∈N *)所在象限的确定7.已知α为第一象限角,则α2所在的象限是( )A .第一象限或第二象限B .第一象限或第三象限C .第二象限或第四象限D .第二象限或第三象限[解析] 由于k ·360°<α<k ·360°+90°,k ∈Z , 得k ·180°<α2<k ·180°+45°,当k 为偶数时,α2为第一象限角;当k 为奇数时,α2为第三象限角.[答案] B8.已知角2α的终边在x 轴的上方,那么α是( ) A .第一象限角 B .第一、二象限角 C .第一、三象限角D .第一、四角限角[解析] 由题意知k ·360°<2α<180°+k ·360°(k ∈Z ),故k ·180°<α<90°+k ·180°(k ∈Z ),按照k 的奇偶性进行讨论.当k =2n (n ∈Z )时,n ·360°<α<90°+n ·360°(n ∈Z ),∴α在第一象限;当k =2n +1(n ∈Z )时,180°+n ·360°<α<270°+n ·360°(n ∈Z ),∴α在第三象限.故α在第一或第三象限.[答案] C综合提升练(时间25分钟)一、选择题1.给出下列四个命题:①-75°角是第四象限角;②225°角是第三象限角;③475°角是第二象限角;④-315°角是第一象限角,其中真命题有( )A .1个B .2个C .3个D .4个[解析]①正确;②正确;③中475°=360°+115°,因为115°为第二象限角,所以475°也为第二象限角,正确;④中-315°=-360°+45°,因为45°为第一象限角,所以-315°也为第一象限角,正确.[答案] D2.终边在直线y =-x 上的所有角的集合是( ) A .{α|α=k ·360°+135°,k ∈Z } B .{α|α=k ·360°-45°,k ∈Z } C .{α|α=k ·180°+225°,k ∈Z } D .{α|α=k ·180°-45°,k ∈Z }[解析] 因为直线y =-x 为二、四象限角平分线,所以角终边落到第四象限可表示为k ·360°-45°=2k ·180°-45°,k ∈Z ;终边落到第二象限可表示为k ·360°-180°-45°=(2k -1)·180°-45°,k ∈Z ,综上可得终边在直线y =-x 上的所有角的集合为{α|α=k ·180°-45°,k ∈Z }.[答案] D3.若φ是第二象限角,那么φ2和90°-φ都不是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角[解析]∵φ是第二象限角,∴k ·360°+90°<φ<k ·360°+180°,k ∈Z , ∴k ·180°+45°<φ2<k ·180°+90°,k ∈Z ,∴φ2是第一或第三象限角,而-φ是第三象限角, ∴90°-φ是第四象限角,故选B. [答案] B 二、填空题4.与角-1560°终边相同的角的集合中,最小正角是________,最大负角是________. [解析] 由于-1560°÷360°=-4×360°-120° 即最大负角为-120°,最小正角为240°. [答案] 240° -120°5.若α,β两角的终边互为反向延长线,且α=-120°,则β=________. [解析] 由题意知,β角的终边与60°角终边相同,则β=k ·360°+60°,k ∈Z . [答案]k ·360°+60°,k ∈Z 三、解答题6.已知α,β都是锐角,且α+β的终边与-280°角的终边相同,α-β的终边与670°角的终边相同,求角α,β的大小.[解] 由题意可知,α+β=-280°+k ·360°,k ∈Z ,∵α,β都是锐角,∴0°<α+β<180°. 取k =1,得α+β=80°.① ∵α-β=670°+k ·360°,k ∈Z .∵α,β都是锐角,∴{ 0°<α<90°-90°<-β<0°, ∴-90°<α-β<90°.取k =-2,得α-β=-50°.② 由①②,得α=15°,β=65°.7.如图,分别写出适合下列条件的角的集合:(1)终边落在射线OB上;(2)终边落在直线OA上;(3)终边落在阴影区域内(含边界).[解](1)终边落在射线OB上的角的集合为S1={α|α=60°+k·360°,k∈Z}.(2)终边落在直线OA上的角的集合为S2={α|α=30°+k·180°,k∈Z}.(3)终边落在阴影区域内(含边界)的角的集合为S3={α|30°+k·180°≤α≤60°+k·180°,k∈Z}.。
2018年高考数学一轮复习课时跟踪检测31文新人教A版

课时跟踪检测(三十一)[高考基础题型得分练]1.数列0,1,0,-1,0,1,0,-1,…的一个通项公式是a n 等于( ) A.-1n+12 B .cos n π2C .cosn +12π D .cosn +22π答案:D解析:令n =1,2,3,…,逐一验证四个选项,易得D 正确. 2.设a n =-3n 2+15n -18,则数列{a n }中的最大项的值是( ) A.163 B.133C .4D .0 答案:D解析:∵a n =-3⎝ ⎛⎭⎪⎫n -522+34,由二次函数的性质,得当n =2或3时,a n 最大,最大值为0.3.已知数列{a n },a 1=-14,a n =-1a n -1+1(n >1),则当a n =-14时,n 的值可以为( )A .14B .15C .16D .17答案:C解析:由题意,得a 1=-14,a 2=-43,a 3=3,a 4=-14,…,则a 3m -2=-14(m ∈N *),a 16=-14,故选C.4.[2017·河北保定调研]在数列{a n }中,已知a 1=1,a n +1=2a n +1,则其通项公式为a n =( )A .2n-1 B .2n -1+1C .2n -1D .2(n -1) 答案:A解析:解法一:由a n +1=2a n +1,可求a 2=3,a 3=7,a 4=15,…,验证可知a n =2n-1. 解法二:由题意知a n +1+1=2(a n +1),∴数列{a n +1}是以2为首项,2为公比的等比数列,∴a n +1=2n ,∴a n =2n-1. 5.数列{a n }的前n 项和为S n ,若a 1=1,a n +1=3S n (n ≥1),则a 6=( ) A .3×44B .3×44+1C .45D .45+1 答案:A解析:当n ≥1时,a n +1=3S n ,则a n +2=3S n +1,∴a n +2-a n +1=3S n +1-3S n =3a n +1,即a n +2=4a n +1,∴该数列从第2项开始是以4为公比的等比数列.又a 2=3S 1=3a 1=3,∴a n =⎩⎪⎨⎪⎧1,n =1,3×4n -2,n ≥2,∴a 6=3×46-2=3×44,故选A.6.[2016·云南一模]在数列{a n }中,a 1=12,a 2=13,a n a n +2=1,则a 2 016+a 2 017=( )A.56B.52C.72 D .5答案:C解析:因为a 1=12,a 2=13,a n a n +2=1,所以a 3=2,a 4=3,a 5=12,a 6=13,即数列{a n }是周期数列,周期为4,则a 2 016+a 2 017=a 4+a 1=3+12=72,故选C.7.在数列{a n }中,已知a 1=2,a 2=7,a n +2等于a n a n +1(n ∈N *)的个位数,则a 2 015=( ) A .8 B .6 C .4 D .2 答案:D解析:由题意得a 3=4,a 4=8,a 5=2,a 6=6,a 7=2,a 8=2,a 9=4,a 10=8.所以数列中的项从第3项开始呈周期性出现,周期为6,故a 2 015=a 335×6+5=a 5=2.8.已知数列{a n }满足a n +1=a n -a n -1(n ≥2),a 1=1,a 2=3,记S n =a 1+a 2+…+a n ,则下列结论正确的是( )A .a 2 014=-1,S 2 014=2B .a 2 014=-3,S 2 014=5C .a 2 014=-3,S 2 014=2D .a 2 014=-1,S 2 014=5 答案:D解析:由a n +1=a n -a n -1(n ≥2),知a n +2=a n +1-a n ,则a n +2=-a n -1(n ≥2),a n +3=-a n ,…,a n +6=a n .又a 1=1,a 2=3,a 3=2,a 4=-1,a 5=-3,a 6=-2,所以当k ∈N 时,a k +1+a k +2+a k +3+a k +4+a k +5+a k +6=a 1+a 2+a 3+a 4+a 5+a 6=0,所以a 2 014=a 4=-1,S 2 014=a 1+a 2+a 3+a 4=1+3+2+(-1)=5.9.在数列{a n }中,a 1=1,对于所有的n ≥2,n ∈N *,都有a 1·a 2·a 3·…·a n =n 2,则a 3+a 5=________.答案:6116解析:由题意知a 1·a 2·a 3·…·a n -1=(n -1)2, ∴a n =⎝⎛⎭⎪⎫n n -12(n ≥2),∴a 3+a 5=⎝ ⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫542=6116.10.设{a n }是首项为1的正项数列,且(n +1)a 2n +1-na 2n +a n +1·a n =0(n =1,2,3,…),则它的通项公式a n =________.答案:1n解析:∵(n +1)a 2n +1+a n +1·a n -na 2n =0, ∴(a n +1+a n )[(n +1)a n +1-na n ]=0, 又a n +1+a n >0,∴(n +1)a n +1-na n =0, 即a n +1a n =n n +1,∴a 2a 1·a 3a 2·a 4a 3·a 5a 4·…·a n a n -1=12×23×34×45×…×n -1n ,∵a 1=1,∴a n =1n. 11.[2017·山西四校第二次联考]已知{a n }满足a 1=1,a n +1·a n =2n(n ∈N *),则S 2 016=________.答案:3×101 008-3解析:因为a n ·a n +1=2n,所以a n +2·a n +1=2n +1,所以a n +2a n=2,因此a 1,a 3,a 5,…构成一个以1为首项,2为公比的等比数列,a 2,a 4,a 6,…构成一个以2为首项,2为公比的等比数列.从而S 2 016=(a 1+a 3+…+a 2 015)+(a 2+a 4+…+a 2 016)=1-21 0081-2+2×1-21 0081-2=3×21008-3.12.已知a n =n 2+λn ,且对于任意的n ∈N *,数列{a n }是递增数列,则实数λ的取值范围是________.答案:(-3,+∞)解析:因为{a n }是递增数列,所以对任意的n ∈N *,都有a n +1>a n ,即(n +1)2+λ(n +1)>n 2+λn ,整理,得2n +1+λ>0,即λ>-(2n +1).(*)因为n ≥1,所以-(2n +1)≤-3,要使不等式(*)恒成立,只需λ>-3.[冲刺名校能力提升练]1.[2017·山西四校联考]已知数列2 008,2 009,1,-2 008,…,这个数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前2 016项之和S 2 016=( )A .1B .4 018C .2 010D .0答案:D解析:依题意,该数列为2 008,2 009,1,-2 008,-2 009,-1,2 008,2 009,1,…,按此规律,可知该数列的周期为6,且这6项之和为0.所以这个数列的前2 016项之和S 2 016=S 336×6=S 6=0.2.[2017·湖北宜昌一模]已知函数f (x )=⎩⎪⎨⎪⎧3-a x -3,x ≤7,a x -6,x >7,若数列{a n }满足a n =f (n ),且数列{a n }是递增数列,则实数a 的取值范围是( )A.⎣⎢⎡⎭⎪⎫94,3B.⎝ ⎛⎭⎪⎫94,3C .(2,3)D .(1,3) 答案:C解析:由已知得a n =f (n )=⎩⎪⎨⎪⎧3-a n -3,n ≤7,a n -6,n >7(n ∈N *),若数列{a n }是递增数列,则⎩⎪⎨⎪⎧3-a >0,a >1,3-a ×7-3<a 8-6,解得2<a <3,故实数a 的取值范围是(2,3).3.[2016·北京海淀期末]若数列{a n }满足:a 1=19,a n +1=a n -3(n ∈N *),则数列{a n }的前n 项和数值最大时,n 的值为( )A .6B .7C .8D .9 答案:B解析:∵a 1=19,a n +1-a n =-3,∴数列{a n }是以19为首项,-3为公差的等差数列, ∴a n =19+(n -1)×(-3)=22-3n . 设{a n }的前k 项和数值最大,则有⎩⎪⎨⎪⎧a k ≥0,a k +1≤0,k ∈N *,∴⎩⎪⎨⎪⎧22-3k ≥0,22-3k +1≤0,∴193≤k ≤223,∵k ∈N *,∴k =7. ∴满足条件的n 的值为7.4.[2016·江西南昌调研]一牧羊人赶着一群羊通过4个关口,每过一个关口,守关人将拿走当时羊的一半,然后退还1只给牧羊人,过完这些关口后,牧羊人只剩下2只羊,则牧羊人在过第一个关口前有________只羊.答案:2解析:记此牧羊人通过第1个关口前、通过第2个关口前、……、通过第4个关口前剩下的羊的只数组成数列{a n }(n =1,2,3,4),则由题意得a 2=12a 1+1,a 3=12a 2+1,a 4=12a 3+1,而12a 4+1=2,解得a 4=2,因此得a 3=2,…,a 1=2. 5.[2017·甘肃天水一模]已知数列{a n }中,a 1=1,且a n +a n +1=2n.求数列{a n }的通项公式.解:∵a n +a n +1=2n,①∴a n +1+a n +2=2n +1,②②-①,得a n +2-a n =2n, 由a 1=1,a 1+a 2=2,得a 2=1. 当n 为奇数时,a n =(a n -a n -2)+(a n -2-a n -4)+…+(a 3-a 1)+a 1=2n -2+2n -4+…+2+1=13×2n +13; 当n 为偶数时,a n =(a n -a n -2)+(a n -2-a n -4)+…+(a 4-a 2)+a 2=2n -2+2n -4+…+22+1=13×2n -13. 故a n=⎩⎪⎨⎪⎧13×2n+13,n 为奇数,13×2n-13,n 为偶数.6.已知数列{a n }中,a n =1+1a +2n -1(n ∈N *,a ∈R ,且a ≠0).(1)若a =-7,求数列{a n }中的最大项和最小项的值; (2)若对任意的n ∈N *,都有a n ≤a 6成立,求a 的取值范围. 解:(1)∵a n =1+1a +2n -1(n ∈N *,a ∈R ,且a ≠0),又∵a =-7,∴a n =1+12n -9.结合函数f (x )=1+12x -9的单调性, 可知1>a 1>a 2>a 3>a 4,a 5>a 6>a 7>…>a n >1(n ∈N *).∴数列{a n }中的最大项为a 5=2,最小项为a 4=0.(2)a n =1+1a +2n -1=1+12n -2-a2.∵对任意的n ∈N *,都有a n ≤a 6成立, 结合函数f (x )=1+12x -2-a 2的单调性,知5<2-a 2<6,∴-10<a <-8.故a 的取值范围为(-10,-8).。
新教材高中数学课时跟踪检测四等差数列的性质及其应用新人教A版选择性必修第二册

课时跟踪检测(四) 等差数列的性质及其应用1.在等差数列{a n }中,a 1+a 9=10,则a 5=( ) A .5 B .6 C .8 D .9解析:选A 由等差中项的性质得a 1+a 9=2a 5=10,所以a 5=5. 2.在等差数列{a n }中,a 1=2,a 3+a 5=10,则a 7=( ) A .5 B .8 C .10D .14解析:选B 法一:设等差数列的公差为d ,则a 3+a 5=2a 1+6d =4+6d =10,所以d =1,a 7=a 1+6d =2+6=8.法二:由等差数列的性质可得a 1+a 7=a 3+a 5=10,又a 1=2,所以a 7=8. 3.已知数列{a n }为等差数列,若a 1+a 5+a 9=π,则cos(a 2+a 8)的值为( ) A .-12 B .-22 C.12 D .32解析:选A ∵数列{a n }为等差数列,a 1+a 5+a 9=π, ∴a 1+a 5+a 9=3a 5=π,解得a 5=π3,∴a 2+a 8=2a 5=2π3,∴cos(a 2+a 8)=cos 2π3=-cos π3=-12.故选A.4.在等差数列{a n }中,a 2 016=log 27,a 2 022=log 2 17,则a 2 019=( )A .0B .7C .1D .49解析:选A ∵数列{a n }是等差数列,∴由等差数列的性质可知2a 2 019=a 2 016+a 2 022=log 27+log 217=log 21=0,故a 2 019=0.5.在等差数列{a n }中,若a 1,a 2 019为方程x 2-10x +16=0的两根,则a 2+a 1 010+a 2 018=( )A .10B .15C .20D .40解析:选B 因为a 1,a 2 019为方程x 2-10x +16=0的两根,所以a 1+a 2 019=10.由等差数列的性质可知,a 1 010=a 1+a 2 0192=5,a 2+a 2 018=a 1+a 2 019=10,所以a 2+a 1 010+a 2 018=10+5=15.故选B.6.某人练习写毛笔字,第一天写了4个大字,以后每天比前一天都多写,且多写的字数相同,第三天写了12个大字,则此人每天比前一天多写________个大字.解析:由题意可知,此人每天所写大字数构成首项为4,第三项为12的等差数列,即a 1=4,a 3=12,所以d =12-43-1=4. 答案:47.设数列{a n },{b n }都是等差数列,若a 1+b 1=7,a 3+b 3=21,则a 5+b 5=________. 解析:由{a n },{b n }都是等差数列可知{a n +b n }也是等差数列,设{a n +b n }的公差为d , 所以a 3+b 3=(a 1+b 1)+2d , 则2d =21-7,即d =7. 所以a 5+b 5=(a 1+b 1)+4d =35. 答案:358.在等差数列{a n }中,a 1=8,a 5=2,若在数列{a n }中每相邻两项之间插入一个数,使之成为新的等差数列,那么新的等差数列的公差是________.解析:法一:设新的等差数列的公差为d .由a 1=8,a 5=2,得a 3=a 1+a 52=8+22=5,a 2=a 1+a 32=8+52=132,所以d =a 2-a 12=132-82=-34.法二:设新的等差数列为{b n },其公差为d ,则b 1=a 1=8,b 9=a 5=2,所以d =b 9-b 19-1=2-88=-34. 答案:-349.首项为a 1,公差d 为正整数的等差数列{a n }满足下列两个条件: (1)a 3+a 5+a 7=93;(2)满足a n >100的n 的最小值是15. 试求公差d 和首项a 1的值. 解:∵a 3+a 5+a 7=93, ∴3a 5=93,∴a 5=31, ∴a n =a 5+(n -5)d . 令a n >100,得n >69d+5.∵满足a n >100的n 的最小值是15, ∴14≤69d+5<15,∴6910<d ≤723,又d 为正整数,∴d =7,a 1=a 5-4d =3.10.某产品按质量分10个档次,生产最低档次的产品的利润是8元/件,每提高一个档次,利润每件增加2元,同时每提高一个档次,产量减少3件,在相同的时间内,最低档次的产品可生产60件.试问:在相同的时间内,应选择生产第几档次的产品可获得最大利润?(设最低档次为第1档次)解:设在相同的时间内,从低到高每档产品的产量分别为a 1,a 2,…,a 10, 每件产品的利润分别为b 1,b 2,…,b 10,则{a n },{b n }均为等差数列,且a 1=60,d 1=-3,b 1=8,d 2=2, 则a n =60-3(n -1)=-3n +63,b n =8+2(n -1)=2n +6,所以利润f (n )=a n b n =(-3n +63)(2n +6)=-6n 2+108n +378=-6(n -9)2+864. 显然,当n =9时,f (n )max =f (9)=864.即在相同的时间内生产第9档次的产品可以获得最大利润.1.(多选)《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).关于这个问题,下列说法正确的是( )A .甲得钱是戊得钱的2倍B .乙得钱比丁得钱多12钱C .甲、丙得钱的和是乙得钱的2倍D .丁、戊得钱的和比甲得钱多13钱解析:选AC 依题意,设甲、乙、丙、丁、戊所得钱分别为a -2d ,a -d ,a ,a +d ,a +2d ,且a -2d +a -d =a +a +d +a +2d ,即a =-6d ,又a -2d +a -d +a +a +d +a +2d =5a =5,∴a =1,d =-16,即a -2d =1-2×⎝ ⎛⎭⎪⎫-16=43,a -d =1-⎝ ⎛⎭⎪⎫-16=76,a +d =1+⎝ ⎛⎭⎪⎫-16=56,a +2d =1+2×⎝ ⎛⎭⎪⎫-16=23, ∴甲得43钱,乙得76钱,丙得1钱,丁得56钱,戊得23钱,则有如下结论:甲得钱是戊得钱的2倍,故A 正确;乙得钱比丁得钱多76-56=13钱,故B 错误;甲、丙得钱的和是乙得钱的43+176=2倍,故C 正确;丁、戊得钱的和比甲得钱多56+23-43=16钱,故D 错误.故选A 、C.2.[多选]下面是关于公差d >0的等差数列{a n }的四个说法,其中正确的是( ) A .数列{a n }是递增数列 B .数列{na n }是递增数列 C .数列⎩⎨⎧⎭⎬⎫a n n 是递增数列D .数列{a n +3nd }是递增数列解析:选AD a n =a 1+(n -1)d ,d >0,∴a n -a n -1=d >0,A 正确;na n =na 1+n (n -1)d ,∴na n -(n -1)a n -1=a 1+2(n -1)d 与0的大小关系和a 1的取值情况有关. 故数列{na n }不一定递增,B 不正确; 对于C :a n n =a 1n +n -1nd ,∴a n n -a n -1n -1=-a 1+d n n -1,当d -a 1>0,即d >a 1时,数列⎩⎨⎧⎭⎬⎫a n n 递增, 但d >a 1不一定成立,C 不正确; 对于D :设b n =a n +3nd , 则b n +1-b n =a n +1-a n +3d =4d >0. ∴数列{a n +3nd }是递增数列,D 正确.3.设数列{a n }的前n 项和为S n ,写出一个同时满足条件①②的等差数列{a n }的通项公式a n =________.①S n 存在最小值且最小值不等于a 1; ②不存在正整数k ,使得S k >S k +1且S k +1<S k +2.解析:若a 2<0,则满足①,又由不存在正整数k ,使得S k >S k +1且S k +1<S k +2,则可得S n连续两项取得最小值,即存在n 使得a n =0,则可得{a n }的通项公式可以是a n =2n -6.答案:2n -6(答案不唯一)4.已知{a n }是等差数列,且a 1+a 2+a 3=12,a 8=16. (1)求数列{a n }的通项公式;(2)若从数列{a n}中依次取出第2项,第4项,第6项,…,第2n项,按原来的顺序组成一个新数列{b n},试求数列{b n}的通项公式.解:(1)设{a n}的公差为d.∵a1+a2+a3=12,∴a2=4.∵a8=a2+(8-2)d,∴16=4+6d,解得d=2.∴a n=a2+(n-2)d=4+(n-2)×2=2n.(2)a2=4,a4=8,a6=12,a8=16,…,a2n=2×2n=4n.当n>1时,a2n-a2(n-1)=4n-4(n-1)=4.∴{b n}是以4为首项,4为公差的等差数列.∴b n=b1+(n-1)d=4+4(n-1)=4n.5.下表是一个“等差数阵”:ij(1)写出a45的值;(2)写出a ij的计算公式,以及2 020这个数在“等差数阵”中所在的一个位置.解:(1)a45表示数阵中第4行第5列的数.先看第1行,由题意4,7,…,a15,…成等差数列,公差d=7-4=3,则a15=4+(5-1)×3=16.再看第2行,同理可得a25=27.最后看第5列,由题意a15,a25,…,a45成等差数列,∴a45=a15+3d=16+3×(27-16)=49.(2)该“等差数阵”的第1行是首项为4,公差为3的等差数列a1j=4+3(j-1);第2行是首项为7,公差为5的等差数列a2j=7+5(j-1);第i行是首项为4+3(i-1),公差为2i+1的等差数列,∴a ij=4+3(i-1)+(2i+1)(j-1)=2ij+i+j=j(2i+1)+i.要求2 020在该“等差数阵”中的位置,也就是要找正整数i,j,使得j(2i+1)+i =2 020,∴j =2 020-i 2i +1.又∵j ∈N *,∴当i =1时,得j =673.∴2 020在“等差数阵”中的一个位置是第1行第673列.。
2018年高考数学一轮复习课时跟踪检测49文新人教A版

所以 a 2= 6, b 2= 1, 则 c 2= a 2-b 2= 5.课时跟踪检测(四十九)[高考基础题型得分练]1.椭圆x 2 + my = 1的焦点在y 轴上,长轴长是短轴长的两倍,贝U m 的值为(1A.4B.C. 2D.答案: 解析: 2 1 2由题意知,a = m b = 1,且a = 2b ,1•m=4,X 22.已知实数4, m,9构成一个等比数列,则圆锥曲线-+ y = 1的离心率为(B. .7答案:C解析:因为实数4, m,9构成一个等比数列, 所以可得m = 36, 解得m= 6或m=- 6.当圆锥曲线为椭圆时,即2 2m / =1的方程为x + y =1所以离心率e =a =5 _30 6= 当曲线是双曲线时可求得离心率为 .7. 2 23. [2017 •河北邯郸一模]椭圆12 + 3 = 1 的焦点为F i , F 2,点P 在椭圆上,如果线段PF 2的中点在y 轴上,那么|PB |是|PF |的( A. 7倍 B. 5倍 C. 4倍 D. 3倍答案:A解析:设线段PF 的中点为D,1 则 |0D = 2I PF 1I 且 OD/ PF , ODL x 轴,••• PF 丄 x 轴,••• |PF | = b =△=€•a 2、p 2又••• |PF | + I PF = 4西,• |PE|= 4 .3_f= =-2.■■- | PFJ 是| PF | 的 7倍.2 2x y4•已知椭圆C : ; + £= 1的左、右焦点分别为 F l , F 2,椭圆C 上的点A 满足AF 丄F 1F 2.43若点P 是椭圆C 上的动点,贝U F i P- F 2A 勺最大值为于2贝y c 的方程是()2土=12x 2D -+y =14B.3<3 2_ 9C.4D. 15 ~4答案:B解析:设向量FP, F 2A 的夹角为0 . 由条件知| AR|为椭圆通径的一半,b 2 3即 | AF = - = ©T T 3 T则 F 1P - F 2A = ?| F 1P COS 0 ,于是FP-只需FP 在 F 2A 上的投影值最大,易知此时点P 在椭圆短轴的上顶点,T T 3 T所以 FP- F 2A = x| F 1P |cos 3.3故选B.5. [2017 •陕西西安质量检测 ]已知中心在原点的椭圆 C 的右焦点为F (1,0),离心率等—1,=—1,点与线段AB 中点的直线的斜率为■,则b 的值为( 2 aB.2*3 3 C症C.2D.2,3 27答案:B解析:设 A (X 1, yj , B (X 2, ax 2 + by 1 = 1, ax 2+ by ! = 1,y 2),则即 ax 1 — ax 2=— ( by 2 — by 2), 22by 1 — by 22 2 = ax 1 — ax 2.b y — y 2y 1 + y 2 a X 1 — X 2 X 1 + X 2答案:A解析:设椭圆C 的焦距为2c (c <a ), 由于直线 AB 的方程为bx + ay — ab = 0,ab•/ b 2 = a 2 — c 2,「. 3a 4— 7a 2c 2+ 2c 4= 0,解得a 2= 2c 2或3a 2= c 2(舍去)」e =#答案:C 解析:依题意,所求椭圆的焦点位于c1x轴上,2 2因此其方程是++警=X 故选C.6. [2017 •甘肃兰州诊断]已知椭圆 C:2 2x y 云+令=1( a >b >0)的左、右焦点分别为 F 1, F 2, 右顶点为A,上顶点为B,若椭圆C 的中心到直线AB 的距离为半| F 1F 2I ,则椭圆C 的离心率e =( )B.~2D.7. [2 017 •江西师大附中模拟]椭圆ax 2+ by 21与直线y = 1 — x 交于A , B 两点,过原••• a x(-1)x• b=孚,故选B.2 2& [2017 •山东青岛模拟]设椭圆m2+ £= 1(m>0, n>0)的右焦点与抛物线y2= 8x的焦点1相同,离心率为2,则此椭圆的方程为 ________ .2 2答案:16+务=1解析:抛物线y2= 8x的焦点为(2,0),•吊—n2= 4,①• m= 4,n2= 12,2 2•椭圆方程为~+12= 1.2 29. _________ [2017 •湖南长沙一模]椭圆r :争+碁=1(a>b>0)的左、右焦点分别为F1, F2,焦距为2c,若直线y=J3(x+ c)与椭圆r的一个交点M满足/ MFF2= 2/ MFF,则该椭圆的离心率等于_________________ .答案:3 —1解析:依题意得/ MFF2= 60°,/ MFF1 = 30°,/ RMF= 90°,设| MF| = m则有| MF| = 3m I尸冋=2m该椭圆的离心率是e=丨田_J3_1| MF| + | MI2| = 32x10. 在平面直角坐标系xOy中,已知△ ABC的顶点A( —4,0)和C(4,0),顶点B在椭圆忑5答案:5解析:sin A+ sin C | BQ + | BA 2a a 5 sin B =|AQ = 2c= c = 4.2 2 21 2e= 2=m代入①得,2+ y9 = 1上,则S in A+ Sin C的值为sin Bxv 2 y11. [2017 •山东三校联考]椭圆C:孑+話=1(a>b>0)的右焦点为F,双曲线x -3 = 1的一条渐近线与椭圆C交于A, B两点,且AF丄BF则椭圆C的离心率为____________ .答案:3 —12解析:不妨取双曲线x2—V3 = 1的一条渐近线的方程为y= .3x,记椭圆C的左焦点为F1,由题意得| OA = | OB = | OF = | OF| = c,•••四边形AFBF为矩形,△ AFC是正三角形,••• | AF = c, | AF| = Q3c,c 2c•椭圆C的离心率e=a=亦=l FF l = % = 3_1= |AF + |AF| = c+ 3c = 3_12. 已知椭圆的左焦点为R,右焦点为冃,若椭圆上存在一点P,满足线段PR相切于以椭圆的短轴为直径的圆,切点为线段 __________________________ PF的中点,则该椭圆的离心率为.答案:£设| F1F2| = 2c, |PF| = 2|CM = 2b, 由椭圆的定义,得|PF a| = 2a_ 2b.2 2 2由勾股定理,得4b + (2 a—2b) = 4c ,2 yl5解得b= 3a, c = -ya,所以椭圆的离心率e =靑[冲刺名校能力提升练]2 21. [2017 •广东汕头一模]已知椭圆X +吕=1上有一点P , F i , F 2是椭圆的左、右焦点, 若厶F i PR 为直角三角形,则这样的点P 有( )A. 3个B. 4个C. 6个D. 8个答案:C解析:当/ PF 1F 2为直角时,根据椭圆的对称性知,这样的点 P 有2个;同理当/ PF 2F 1为直角时,这样的点 P 有2个;当P 点为椭圆的短轴端点时,/ F i PR 最大,且为直角,此时这样的点P 有2个.故符合要求的点 P 有6 个.+ y =0的对称点A 是椭圆C 上的点,则椭圆 C 的离心率为( 1 A.- 1 BYC© C.2D. 3 — 1答案:D解析:解法一:设A (m n ),则—/3 =— 1,解得A |,彳-,-2 3-2代入椭圆C 中,有石+ 4b 2=1,.22只 2 2 , 2. 2「•be + 3a - = 4a b ,/ 22、 2 小22 ,2,2 2、/• (a — c )c + 3a c = 4a (a — c ),4介 2 2 ,4…c — 8a c + 4a = 0,二 e — 8e + 4 = 0,2. [2017 •河北唐山模拟m- - n+ 2=0,]椭圆C:2 2F ,若F 关于直线e = 4±2 , 3,•/ 0<e<1,二e= . 3— 1.解法二:借助于椭圆的定义,本题还有如下简捷解法:设F '是椭圆的右焦点,连接 AF, AF . 由已知得厶AFF 是直角三角形,其中/ A = 90°,/ AFF = 30°,2c—— =3— 1,故选D.c + 3c '2 2x y3.已知F 1, F 2是椭圆G 尹^2= 1(a >b >0)的两个焦点,P 为椭圆答案:3••• I FF I = 2c ,. | AF | =0c , |AF | = c , 2c|FF |e= 2a = | AF | + | AF IC 上的一点,且 PF丄PF 2.若厶PFF 2的面积为 9,则 b =解析:设| PF| = r1, | PF| =「2,则r 1+「2= 2a,2,2 2r 1+「2= 4c ,2 22「1「2= (「1 +「2) —(r 1 +r ) =4a2—4c2= 4b2,1 2又S PF_,F2=歹1r2= b = 9,「. b= 3.4. [2017 •河北保定一模]与圆C: (x+ 3)2+ y2= 1外切,且与圆 2 2G: (x —3) + y = 81内切的动圆圆心P的轨迹方解析:设动圆的半径为r,圆心为F(x, y),则有|PG| = r + 1, | PG| = 9- r.所以| PG| + | PG| = 10> | CC ,即P在以2x P的轨迹方程为去+255.已知椭圆G的对称中心为原点O,焦点在x轴上,左、右焦点分别为F1和F2,且|尸冋=2,点1, 2在该椭圆上.(1)求椭圆G的方程;⑵过F1的直线I与椭圆C相交于A, B两点,若△ AFB的面积为^2#,求以F2为圆心且与直线I相切的圆的方程.解:(1)由题意知c = 1,2 a=gj + p gj + 22= 4,解得a= 2,故椭圆G的方程为x(2)①当直线I 丄x 轴时,可取A — 1, — 2 , B — 1, 2 , △ AFB 的面积为3,不符合题意.②当直线I 与x 轴不垂直时,设直线I 的方程为y = k (x + 1),代入椭圆方程得(3 + 4k 3 4 5)x 22 2+ 8k x + 4k — 12= 0,显然△ >0 成立,设 A (X 1, y 1), B (X 2, y 2),3 求椭圆C 的方程;4 在x 轴上是否存在定点经过以 MN 为直径的圆?若存在, 求定点坐标;若不存在,请说明理由.X 1+ X 2= — 8 k 2 3 +4k 2,X 1X 2 = 4k 2— 123+ 4k 2,可得| AB = 1 + k2—X1 + X2 2—4x1X212 k2+l=3 + 4k2,又圆F2的半径r =2| k|_ 1 + k2'•••△ AFB的面积为12| k| .. k2+ 1 12 2 r= 3+ 4k2=十,化简得17k4+ k2—18= 0,得k=± 1,• r = 2,圆的方程为(x —1)2+ y2= 2.2 2x y6. [2017 •湖南四校联考]在平面直角坐标系xOy中,椭圆C:二+ 2= 1(a>b>0)的离心a b率e= 1,且过点(0 , 3),椭圆C的长轴的两端点为A B,点P为椭圆上异于A, B的动点, 1| AB. 2 2 22 c a — b 1解:⑴ a a 4 b 2= 32 2 x y•••椭圆C 的方程为匚+石=1. 4 3y oy o 则 k l =,k 2=x^, 2 y ok i k 2= ―22 X o — 4x o — 42 4 — x o 3X 4 3x 2— 4 =— 4,由 I PA :y = k i (x + 2)知 M 4,6 k i ), 由 l PB : y = k 2(x — 2)知 N (4,2 k 2), • MN 的中点Q4,3总+ k 2),1•••以 MN 为直径的圆的方程为(x — 4)2+ (y — 3k 1— k 2)2=二(6k 1 — 2k ?)2 = (3k 1 — k"2, 4 令y = o ,得x — 8x + 16+ 9k 1 + 6k 〔k 2+ k 2=9k 1— 6k 1 k 2 + k 2,2•- x — 8x + 16+ 12k 1k 2= o , • x 2 — 8x + 16+ 12X-3 = o ,2 即 x — 8x + 7 = o ,解得 x = 7 或 x = 1,•••存在定点(1,o) , (7,o)经过以MN 为直径的圆. ⑵设PA PB 的斜率分别为 k i , k 2, F (x o , y o ),31 - 42 2 T。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时跟踪检测(四)
[高考基础题型得分练]
1.下图中可作为函数y =f (x )的图象的是( )
A B C D
答案:D
解析:由函数的定义知只有D 是“多对一”函数,而A ,B ,C 均为“一对多”,故选D.
2.已知f ⎝ ⎛⎭⎪⎫12x -1=2x -5,且f (a )=6,则a =( ) A .-7
4
B.7
4 C.43 D .-43
答案:B
解析:令t =1
2x -1,则x =2t +2,f (t )=2(2t +2)-5=4t -1,由f (a )=6知,4a -1
=6,解得a =7
4
.
3.若二次函数g (x )满足g (1)=1,g (-1)=5,且图象过原点,则g (x )的解析式为( ) A .g (x )=2x 2
-3x B .g (x )=3x 2-2x C .g (x )=3x 2+2x D .g (x )=-3x 2-2x 答案:B
解析:设g (x )=ax 2
+bx +c (a ≠0), ∵g (1)=1,g (-1)=5,且图象过原点,
∴⎩⎪⎨⎪
⎧
a +
b +
c =1,a -b +c =5,c =0,
解得⎩⎪⎨⎪
⎧
a =3,
b =-2,
c =0,
∴g (x )=3x 2
-2x . 4.函数y =
13x -2
+lg(2x -1)的定义域是( )
A.⎣⎢⎡⎭⎪⎫23,+∞
B.⎝ ⎛⎭⎪⎫12,+∞
C.⎝ ⎛⎭
⎪⎫23,+∞ D.⎝ ⎛⎭
⎪⎫12,23 答案:C
解析:由⎩
⎪⎨
⎪⎧
3x -2>0,2x -1>0,得x >2
3
,故选C.
5.[2017·豫南豫北十校模拟]已知f (x )是定义在R 上的奇函数,且当x >0时,f (x )=⎩⎪⎨⎪⎧
cos πx 6,0<x ≤8,log 2x ,x >8,
则f (f (-16))=( )
A .-12
B .-32
C.12
D.
32
答案:C
解析:因为f (x )为奇函数,
所以f (f (-16))=-f (f (16))=-f (4)=-cos 2π3=1
2
,故选C.
6.[2017·云南师范大学附属中学月考]已知f (x )=⎩⎪⎨⎪⎧
sin π8x ,x ≥0,f x ++2,x <0,
则
f (-2 016)的值为( )
A .810
B .809
C .808
D .806
答案:B
解析:f (-2 016)=f (-2 011)+2=f (-2 006)+4=…=f (-1)+403×2=f (4)+
404×2=808+sin ⎝ ⎛⎭
⎪⎫π8×4=809. 7.[2017·安徽六校联考]已知函数f (x )=x |x |,若f (x 0)=4,则x 0的值为( ) A .-2 B .2 C .-2或2 D. 2
答案:B
解析:当x ≥0时,f (x )=x 2
,f (x 0)=4, 即x 2
0=4,解得x 0=2.
当x <0时,f (x )=-x 2
,f (x 0)=4,即-x 2
0=4,无解.
所以x 0=2,故选B.
8.[2017·河北唐山期末]已知f (x )=⎩⎪⎨⎪
⎧
-2a x +3a ,x <1,
ln x ,x ≥1
的值域为R ,那么a
的取值范围是( )
A .(-∞,-1] B.⎝
⎛⎭⎪⎫-1,12
C.⎣⎢⎡⎭⎪⎫-1,12
D.⎝ ⎛⎭
⎪⎫0,12 答案:C
解析:要使函数f (x )的值域为R ,
需使⎩
⎪⎨
⎪⎧
1-2a >0,
ln 1≤1-2a +3a ,∴⎩⎪⎨⎪⎧
a <12,a ≥-1,
∴-1≤a <1
2
.
即a 的取值范围是⎣
⎢⎡⎭⎪⎫-1,12. 9.已知函数f (x )=⎩⎪⎨⎪
⎧
x 2
+2ax ,x ≥2,2x
+1,x <2,
若f (f (1))>3a 2
,则a 的取值范围是________.
答案:(-1,3)
解析:由题意知,f (1)=2+1=3,f (f (1))=f (3)=32
+6a ,若f (f (1))>3a 2
,则9+6a >3a 2
,即a 2
-2a -3<0,解得-1<a <3.
10.已知实数a ≠0,函数f (x )=⎩⎪⎨
⎪⎧
2x +a ,x <1,
-x -2a ,x ≥1.
若f (1-a )=f (1+a ),则a 的值
为________.
答案:-3
4
解析:当a >0时,1-a <1,1+a >1, 此时f (1-a )=2(1-a )+a =2-a ,
f (1+a )=-(1+a )-2a =-1-3a ,
由f (1-a )=f (1+a ),得2-a =-1-3a , 解得a =-3
2,不合题意,舍去.
当a <0时,1-a >1,1+a <1,
此时f (1-a )=-(1-a )-2a =-1-a ,
f (1+a )=2(1+a )+a =2+3a ,
由f (1-a )=f (1+a ),得-1-a =2+3a , 解得a =-3
4
.
综上可知,a 的值为-3
4
.
[冲刺名校能力提升练]
1.[2017·湖北武汉调考]函数f (x )=⎩⎪⎨⎪
⎧
πx 2
,-1<x <0,e x -1
,x ≥0
满足f (1)+f (a )=
2,则a 的所有可能值为( )
A .1或-
2
2
B .-
22 C .1 D .1或
22
答案:A 解析:∵f (1)=e 1-1
=1且f (1)+f (a )=2,
∴f (a )=1,
当-1<a <0时,f (a )=sin(πa 2
)=1, ∵0<a 2
<1,∴0<πa 2
<π, ∴πa 2
=π2⇒a =-22;
当a ≥0时,f (a )=e
a -1
=1⇒a =1.
2.[2017·福建四地六校联考]若f (x )对于任意实数x 恒有2f (x )-f (-x )=3x +1,则
f (1)=( )
A .2
B .0
C .1
D .-1 答案:A
解析:令x =1,得2f (1)-f (-1)=4,① 令x =-1,得2f (-1)-f (1)=-2,② 联立①②得f (1)=2.
3.[2017·福建福州质检]已知函数f (x )=⎩⎪⎨⎪⎧
2x
,x ≥2,
x -3,x <2,若关于x 的方程f (x )
=k 有两个不同的实根,则实数k 的取值范围是( )
A .(-1,1)
B .(0,1)
C .(0,1]
D .(-1,0)
答案:B
解析:由题意得,函数f (x )=2
x
在[2,+∞)上是减函数,且0<f (x )≤1,f (x )=(x -
1)3
在(-∞,2)上是增函数,且f (x )<1,若关于x 的方程f (x )=k 有两个不同的实根,则0<k <1.
4.已知函数f (x )满足对任意的x ∈R 都有f ⎝ ⎛⎭⎪⎫12+x +f ⎝ ⎛⎭⎪⎫12-x =2成立,则f ⎝ ⎛⎭⎪⎫18+f ⎝ ⎛⎭⎪⎫28+…+f ⎝ ⎛⎭
⎪⎫78=________.
答案:7
解析:由f ⎝ ⎛⎭⎪⎫12+x +f ⎝ ⎛⎭
⎪⎫12-x =2,得
f ⎝ ⎛⎭⎪⎫18+f ⎝ ⎛⎭⎪⎫78=2, f ⎝ ⎛⎭⎪⎫28+f ⎝ ⎛⎭⎪⎫68=2, f ⎝ ⎛⎭
⎪⎫38+f ⎝ ⎛⎭
⎪⎫58
=2, 又f ⎝ ⎛⎭⎪⎫48=12⎣⎢⎡⎦
⎥⎤f ⎝ ⎛⎭⎪⎫48+f ⎝ ⎛⎭⎪⎫48 =1
2
×2=1, ∴f ⎝ ⎛⎭⎪⎫18+f ⎝ ⎛⎭⎪⎫28+…+f ⎝ ⎛⎭
⎪⎫78 =2×3+1=7.
5.已知函数f (x )(x ∈R )满足f (x )=2bx
ax -1
(a ≠0),f (1)=1,且使f (x )=2x 成立的实数x 只有一个,求函数f (x )的解析式.
解:由f (x )=
2bx
ax -1
(a ≠0),f (1)=1, 得a =2b +1.①
又f (x )=2x 只有一个解,即
2bx ax -1
=2x 只有一个解,也就是2ax 2
-2(1+b )x =0(a ≠0)只有一个解,所以b =-1,代入①中得a =-1,所以f (x )=
2x x +1
.。
