2018-2019学年人教A版必修2 1.1.1 柱、锥、台、球的结构特征 作业
高一数学人教A版必修2第1章1.1柱、锥、台、球的结构特征课件(共19张PPT)

(2)
(5)
(8)
高一数学人教A 版必修2 第1 章1 . 1 柱、锥、台、球的结构特征课件(共1 9 张P P T )
(3) (6) (9)
高一数学人教A 版必修2 第1 章1 . 1 柱、锥、台、球的结构特征课件(共1 9 张P P T )
(2)
(3)
(4)
(6)
(7)
(1)
(5)
高一数学人教A 版必修2 第1 章1 . 1 柱、锥、台、球的结构特征课件(共1 9 张P P T )
问题三:用一个平面去截一个球,截面是什么平面 图形?
高一数学人教A 版必修2 第1 章1 . 1 柱、锥、台、球的结构特征课件(共1 9 张P P T )
想一想:
高一数学人教A 版必修2 第1 章1 . 1 柱、锥、台、球的结构特征课件(共1 9 张P P T )
球、圆柱、圆锥、圆台过轴的截面分别是什么图形?
问题一:下面图形中,为棱锥的是 ( )
(1)
(2)
(3)
高一数学人教A 版必修2 第1 章1 . 1 柱、锥、台、球的结构特征课件(共1 9 张P P T )
高一数学人教A 版必修2 第1 章1 . 1 柱、锥、台、球的结构特征课件(共1 9 张P P T )
问题2:如图,长方体ABCD-A’B’C’D’中被截去一部分, 其中FG∥B’C’,剩下的几何体是什么?截去的几何体呢?
高一数学人教A 版必修2 第1 章1 . 1 柱、锥、台、球的结构特征课件(共1 9 张P P T )
高一数学人教A 版必修2 第1 章1 . 1 柱、锥、台、球的结构特征课件(共1 9 张P P T )
思考: 以下平面图形绕着定直线旋 转所得旋转体的结构如何?举出实物
人教A高中数学必修二1.1.1柱、锥、台、球的结构特征2

多面体
旋转体
顶点
面
轴
棱
课堂练习: 下列物体中,哪些具有多面体的形状,哪些具有旋 转体的形状?
问题3:视察下列多面体,它们共同的特点是什么?
C'
D'
之间的部分,这样的多面体叫做棱台.
2.分类:由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做
三棱台、四棱台、五棱台……
3.表示:棱台ABCD-A'B'C'D'
D’
C’
D
A’
B’
C
D’
D A’
A
B
A
C’ 上底面
侧棱
B’
C
侧面
下底面
B
顶点
课堂练习: 4.(P 9第2题)判断下列几何体是不是棱台,为什么?
C'
E'
D'
C'
A'
B'
A'
B'
A'
B'
D
E
D
C
C
C
A
B
A
B
A
B
1.定义: 有两个面互相平行,其余各面都是四边形,并且每相邻
两个四边形的公共边都互相平行,由这些面所围成的多 面体叫做棱柱。
E’ F’ A’
D’
2.分类: 棱柱的底面是三角形、四边形、五边
B’ C’
形……的棱柱分别叫做三棱柱、四棱柱、
S
顶点 2.分类: 底面是三角形、四边形、
1.1.柱、锥、台、球的结构特征-人教A版必修二教案

1.1.柱、锥、台、球的结构特征-人教A版必修二教案一、柱体的结构特征柱体是一种线塑体,它具有以下结构特征:1.每个截面都是圆形,而且圆心在这个截面的中心;2.每个截面之间距离相等,所以从任意角度看上去,都是圆形。
柱体在物理世界中十分常见,例如水管、电线杆等。
由于其圆形结构,柱体具有抗弯和抗压的能力较强,因此被广泛使用。
二、锥体的结构特征锥体是一种线塑体,它具有以下结构特征:1.由一个圆锥顶点到底面任意一点的直线段为母线,锥体的结构由该直线段和底面围成;2.底面是个圆形。
锥体在构造物理学中有着广泛的应用,例如锥形漏斗、冰淇淋锥等。
锥体在制作过程中,需要注意底面的圆心和母线的长度,以确保最终产品符合需求。
三、台体的结构特征台体是一种线塑体,它具有以下结构特征:1.由一个圆台顶点到底面圆心的直线段为轴线,台体的结构由该直线段和上下两个圆台围成;2.上下两个圆台面积大小相等。
台体的结构在物理实验中被广泛使用,例如水流研究、电场模拟等。
在设计制作台体时,需注意两个圆台的形状和尺寸,以达到理想的实验效果。
四、球体的结构特征球体是一种线塑体,它具有以下结构特征:1.每个表面都是一个圆形,而且所有圆心都在同一点;2.所有体内点到同一点的距离相等。
球体在物理学、地理学、天文学等领域有着广泛的应用。
例如在天文观测中,我们所看到的星星通常是球体形状的天体。
制作球体时,通常需要注意表面的光滑度、圆心位置和直径等因素。
五、小结本文介绍了四种线塑体:柱体、锥体、台体和球体,以及它们的结构特征。
在物理世界中,这四种形态常常出现,有着广泛的应用。
熟悉这些塑体的结构特征,对于理解相关的物理现象和设计制作模型等都十分重要。
以上仅为基础知识的介绍,希望能够引起读者对这些形体结构的关注,进而领悟常见的物理现象和背后的原理。
高中数学 1.1.1 柱、锥、台、球的结构特征教案 新人教A版必修2

第一章空间几何体本章教材分析柱体、锥体、台体和球体是简单的几何体,复杂的几何体大都是由这些简单的几何体组合而成的.有关柱体、锥体、台体和球体的研究是研究比较复杂的几何体的基础.本章研究空间几何体的结构特征、三视图和直观图、表面积和体积等.运用直观感知、操作确认、度量计算等方法,认识和探索空间几何图形及其性质.本章中的有关概念,主要采用分析具体实例的共同特点,再抽象其本质属性空间图形而得到.教学中应充分使用直观模型,必要时要求学生自己制作模型,引导学生直观感知模型,然后再抽象出有关空间几何体的本质属性,从而形成概念.本章内容是在义务教育阶段学习的基础上展开的.例如,对于棱柱,在义务教育阶段直观认识正方体、长方体等的基础上,进一步研究了棱柱的结构特征及其体积、表面积.因此,在教材内容安排中,特别注意了与义务教育阶段“空间与图形”相关内容的衔接.值得注意的是在教学中,要坚持循序渐进,逐步渗透空间想象能力面的训练.由于受有关线面位置关系知识的限制,在讲解空间几何体的结构时,少问为什么,多强调感性认识.要准确把握这方面的要求,防止拔高教学.重视函数与信息技术整合的要求,通过电脑绘制简单几何体的模型,使学生初步感受到信息技术在学习中的重要作用.为了体现教材的选择性,在练习题安排上加大了弹性,教师应根据学生的实际,合理地进行取舍.本章教学时间约需7课时,具体分配如下(仅供参考):1.1.1 柱、锥、台、球的结构特征约1课时1.1.2 简单组合体的结构特征约1课时1.2.1 中心投影与平行投影约1课时1.2.2 空间几何体的三视图1.2.3 空间几何体的直观图约1课时1.3.1 柱体、锥体、台体的表面积与体积约1课时1.3.2 球的体积和表面积约1课时本章复习约1课时§1.1 空间几何体的结构§1.1.1 柱、锥、台、球的结构特征一、教材分析本节教材先展示大量几何体的实物、模型、图片等,让学生感受空间几何体的结构特征,从整体上认识空间几何体,再深入细节认识,更符合学生的认知规律.值得注意的是:由于没有点、直线、平面的有关知识,所以本节的学习不能建立在严格的逻辑推理的基础上,这与以往的教材有较大的区别,教师在教学中要充分注意到这一点.本节教学尽量使用信息技术等手段,向学生展示更多具有典型几何结构特征的空间物体,增强学生的感受.二、教学目标1.知识与技能(1)通过实物操作,增强学生的直观感知.(2)能根据几何结构特征对空间物体进行分类.(3)会用语言概述棱柱、棱锥、圆柱、圆锥、棱台、圆台、球的结构特征。
高中数学人教版必修二:1.1.1柱、锥、台、球的结构特征

理解棱柱的定义
⑤棱柱两个互相平行的面以外的面 都是平行四边形吗? 答:是.
E′ F′ A′ B′
D′
C′
⑥为什么定义中要说“其余各面都 是四边形,并且相邻两个四边形的公共 边都互相平行,”而不简单的只说“其 余各面是平行四边形呢”?
答:满足“有两个面互相平行,其 余各面都是平行四边形的几何体”这样 说法的还有右图情况,如图所示.所以 定义中不能简单描述成“其余各面都是 平行四边形”.
答:满足“有两个面互相平行,其 余各面都是平行四边形的几何体”这样 说法的还有右图情况,如图所示.所以 定义中不能简单描述成“其余各面都是 平行四边形”.
2.棱锥的结构特征
观察下列几何体,有什么相同点?
1、棱锥的概念
有一个面是多边形,其余各面是有 一个公共顶点的三角形, 由这些面所围 成的几何体叫做棱锥。
上底面 侧棱 侧面 高 顶点 下底面
2.棱台的分类:
由三棱锥、四棱锥、五棱锥……截得的 棱台分别叫做三棱台、四棱台、五棱台…… 用顶点各底面各顶点的字母表示 3.棱台的表示:
棱台ABCD-A‘B’C‘D’
三棱台
四棱台
五棱台
辨析
判断:下列几何体是不是棱台,为什么?
(1)
(2)
棱柱、棱锥、棱台的结构特征比较
3、圆台与棱台统称为台体。
O'
底面 轴 侧面 母线
O
底面
判断题:
(1)在圆柱的上下底面上各取一点,这两点的连
线是圆柱的母线.
(
)
(2)圆台所有的轴截面是全等的等腰梯形.( )
(3)与圆锥的轴平行的截面是等腰三角形.( )
圆柱与棱柱统 称为柱体。
圆台与棱台统 称为台体。
人教A版高中数学必修2课件1.1.1柱、锥、台、球的结构特征课件

柱、锥、台、球的结构特征
【棱台的结构特征】
(2)棱台的分类 由三棱锥、四棱锥、五棱锥、…截得的棱台, 分别叫做三棱台、四棱台、五棱台、…
(3)棱台的表示法 用表示棱台的各顶点的字母表示,如上图所示的 棱台可表示为棱台ABCD-A′B′C′D′.
柱、锥、台、球的结构特征
【球的结构特征】 (1)球的有关概念 ①球的定义:以半圆的直径所在直 线为旋转轴,半圆面旋转一周形成 的旋转体叫做球体,简称球. ②各部分名称:半圆的半径叫做球 的半径;半圆的圆心叫做球心;半 圆的直径叫做球的直径. ③图示:
柱、锥、台、球的结构特征
【棱锥的结构特征】
棱锥的分类 按底面多边形的边数分类: 三棱锥(底面是三角形);四 棱锥(底面是四边形);五棱 锥(底面是五边形)· · · · · n棱锥 (底面是n边形); (3)棱锥的表示法 用表示顶点和底面各顶点的字 母表示,如上图所示的棱锥表 示为四棱锥S-ABCD.
柱、锥、台、球的结构特征
【典型例题】 【分析】 充分利用空间几何体的结构特征.
【解】 (1)不正确,当截面和底面平行 时,这种说法是正确的;当截面与底面 不平行时,这种说法是错误的. 对棱锥来说,截面截掉的部分是棱锥, 但当截面与底面不平行时,截面和底面 之间的部分不是棱台,如图(1);对圆锥 来说,只要截面和底面不平行,截面和 底面之间的部分既不是圆台,截掉的部 分也不是圆锥,如图(5).
台,故该几何体为圆台.
【点评】 根据圆柱、圆锥、圆台的结构特 征进行判断.
知识点—— 柱、锥、台、球 的结构特征
柱、锥、台、球的结构特征
【棱柱的结构特征】 (1)棱柱的有关概念 ①定义:一般地,有两个面互相平行,其余各 面都是四边形,并且每相邻两个四边形的公共 边都互相平行,由这些面所围成的多面体叫做 棱柱. ②各部分名称:棱柱中,两个互相平行的面叫 做棱柱的底面,简称底;其余各面叫做棱柱的 侧面;相邻侧面的公共边叫做棱柱的侧棱;侧 面与底面的公共顶点叫做棱柱的顶点. ③图示:
人教A版数学必修2 柱、锥、台、球的结构特征

分类:
三棱台 四棱台 五棱台 等
分类标准: 底面多边形的 边数
思考9:
用一个平行于棱锥底面的平面去截棱锥, 截面与底面的形状关系如何?
相似多边形
棱台的结构特征和表示:
结构特征: • 两个底面是相似多边形; • 侧面都是梯形; • 侧棱延长后交于一点.
表示:棱台ABC-A1B1C1
小结 : 1.棱柱:
棱锥的分类及表示
分类标准: 底面多边形的边数
三棱锥
棱锥S-ABC
四棱锥
棱锥S-ABCD
五棱锥
棱锥P-ABCDE
思考8: 观察并对比以下两个多面体.
思考II中多面体与I中四棱锥有何关系?
棱台的概念及分类:
棱锥被平行于棱锥
底面的平面所截后,
截面和底面之间的部 分叫做棱台.
(上底面、下底面、侧面、 侧棱、顶点 )
思考2:
为了研究方便,我们把棱柱中两个互相平行的 面叫做棱柱的底面,其余各面叫做棱柱的侧面, 相邻侧面的公共边叫做棱柱的侧棱,侧面与底面 的公共顶点叫做棱柱的顶点. 你能指出上面棱柱 的底面、侧面、侧棱、顶点吗?
顶点
侧面
侧棱
底面
棱柱的分类及表示
分类标准: 底面多边形的边数
D
三棱柱
四棱柱
五棱柱
棱柱ABC-A'B'C' 棱柱ABCD-A1B1C1D1 棱柱ABCDE-A'B'C'D'E'
• 第一个图中其余各面是几边形?第二个图中 其余各面是几边形?
• 第一个图中其余各面的公共边位置关系如何? 第二个图中有同样的特征吗?
棱柱的结构特征:
• 有两个面互相平行; • 其余各面都是四边形 ; • 每相邻两个四边形的公共边互相平行 。
新课标人教A版高中数学必修2知识点总结
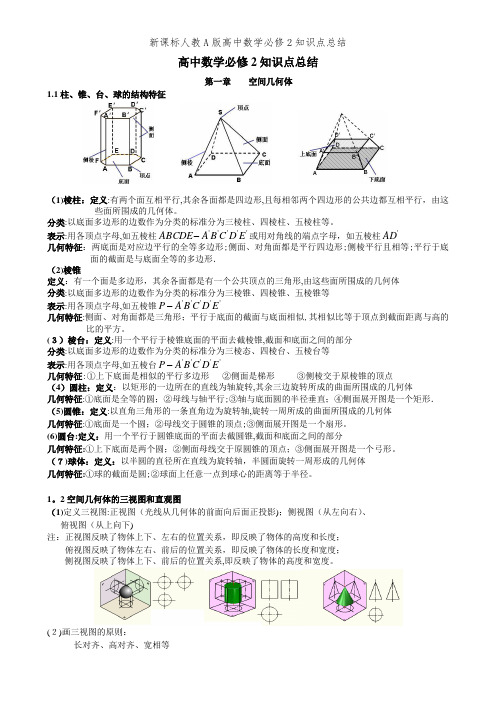
高中数学必修2知识点总结第一章 空间几何体1.1柱、锥、台、球的结构特征(1)棱柱:定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱'''''E D C B A ABCDE -或用对角线的端点字母,如五棱柱'AD几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.(2)棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体 分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥'''''E D C B A P -几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
(3)棱台:定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分 分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如五棱台'''''E D C B A P -几何特征:①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形. (5)圆锥:定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体 几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
(6)圆台:定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[A基础达标]
1.下列说法正确的是()
A.棱柱的底面一定是平行四边形
B.棱锥的底面一定是三角形
C.棱锥被平面分成的两部分不可能都是棱锥
D.棱柱被平面分成的两部分可能都是棱柱
解析:选D.棱柱和棱锥的底面可以是任意多边形,故选项A、B均不正确;可沿棱锥的侧棱将其分割成两个棱锥,故C错误;用平行于棱柱底面的平面可将棱柱分割成两个棱柱.2.具备下列条件的多面体是棱台的是()
A.两底面是相似多边形的多面体
B.侧面是梯形的多面体
C.两底面平行的多面体
D.两底面平行,侧棱延长后交于一点的多面体
解析:选D.由棱台的定义可知,棱台的两底面平行,侧棱延长后交于一点.
3.
纸质的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开,外面朝上展平得到如图所示的平面图形,则标“△”的面的方位是()
A.南B.北
C.西D.下
解析:选B.将所给图形还原为正方体,并将已知面“上”、“东”分别指向上面、东面,则标记“△”的为北面.
4.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱共有对角线()
A.20条B.15条
C.12条D.10条
解析:选D.
如图,在五棱柱ABCDE A1B1C1D1E1中,从顶点A出发的对角线有两条:AC1,AD1,同理从B,C,D,E点出发的对角线均有两条,共有2×5=10(条).
5.有下列说法:
①有两个面互相平行,其余各面都是平行四边形的几何体的侧棱一定不相交于一点,故一定不是棱台;②两个互相平行的面是平行四边形,其余各面是四边形的几何体不一定是棱台;
③两个互相平行的面是正方形,其余各面是四边形的几何体一定是棱台.
其中正确的说法的序号有()
A.0个B.1个
C.2个D.3个
解析:选C.①正确,因为具有这些特征的几何体的侧棱一定不相交于一点,故一定不是棱台;②正确,如图所示;③不正确,当两个平行的正方形全等时,一定不是棱台.故选C.6.如图,已知四边形ABCD是一个正方形,E,F分别是边AB和BC的中点,沿DE,EF,FD折起得到一个空间几何体,则这个空间几何体是________(只填几何体的名称).
解析:折起后是一个三棱锥(如图所示).
答案:三棱锥
7.在下面的四个平面图形中,是侧棱都相等的四面体的展开图的为__________.(填序号)
解析:由于③④中的图组不成四面体,只有①②可以.
答案:①②
8.在正方体上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是________.(写出所有正确结论的编号)
①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.
解析:在正方体ABCD-A1B1C1D1上任意选择4个顶点,它们可能是如下各种几何体的4个
顶点,这些几何体是:①矩形,如四边形ACC1A1;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体,如A-A1BD;④每个面都是等边三角形的四面体,如A-CB1D1;
⑤每个面都是直角三角形的四面体,如A-A1DC,故填①③④⑤.
答案:①③④⑤
9.已知半径为10的球的两个平行截面的周长分别是12π和16π.试求这两个截面间的距离.解:如图所示,
设球的大圆为圆O,C,D分别为两截面圆的圆心,AB为过C,O,D的直径,由题意得两截面圆半径分别为6和8,
在Rt△COE中,OC=102-62=8,
在Rt△DOF中,OD=102-82=6,
当两截面在球心同侧时(如图(1)),CD=OC-OD=8-6=2.
当两截面在球心异侧时(如图(2)),CD=OC+OD=8+6=14.
所以两截面间的距离为2或14.
10.
如图所示,在侧棱长为23的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°,过A作截面AEF,求△AEF周长的最小值.
解:如图,将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,则线段AA1的长即为所求△AEF的周长的最小值.
取AA1的中点D,
连接VD,则VD⊥AA1,∠AVD=60°.
在Rt△VAD中,AD=VA·sin 60°=3,
所以AA1=2AD=6,
即△AEF周长的最小值为6.
[B能力提升]
11.
关于如图所示几何体的正确说法为()
①这是一个六面体.
②这是一个四棱台.
③这是一个四棱柱.
④此几何体可由三棱柱截去一个三棱柱得到.
⑤此几何体可由四棱柱截去一个三棱柱得到.
A.①②③B.①③④
C.①②④⑤D.①③④⑤
解析:选D.①正确.因为有六个面,属于六面体的范围.
②错误.因为侧棱的延长线不能交于一点,所以不正确.
③正确.如果把几何体放倒就会发现是一个四棱柱.
④⑤都正确.如图所示.
12.一个三棱锥,如果它的底面是直角三角形,那么它的三个侧面()
A.至多有一个是直角三角形
B.至多有两个是直角三角形
C.可能都是直角三角形
D.必然都是非直角三角形
解析:选C.注意到答案特征是研究侧面最多有几个直角三角形,这是一道开放性试题,需要研究在什么情况下侧面的直角三角形最多.在如图所示的长方体中,三棱锥A-A1C1D1的三个侧面都是直角三角形.
13.已知正四棱锥V-ABCD中,底面面积为16,侧棱的长为211,则该棱锥的高是________.
解析:如图,取正方形ABCD的中心O,连接VO、AO,则VO就是正四棱锥V-ABCD的高.因为底面面积为16,所以AO=22.
因为侧棱的长为211,
所以VO=VA2-AO2=44-8=6.
所以正四棱锥V-ABCD的高为6.
答案:6
14.(选做题)如图,在一个长方体的容器中装有少量水,现在将容器绕着其底部的一条棱倾斜,在倾斜的过程中,
(1)水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)水的形状也不断变化,可以是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底部的一个顶点,试着讨论水面和水的形状.
解:(1)不对,水面的形状就是用一个与棱(倾斜时固定不动的棱)平行的平面截长方体时截面的形状,因而是矩形,不可能是其他非矩形的平行四边形.
(2)不对,水的形状就是用与棱(将长方体倾斜时固定不动的棱)平行的平面将长方体截去一部分后,剩余部分的几何体是棱柱,水比较少时,是三棱柱,水多时,可能是四棱柱;但不可能是棱台或棱锥.
(3)用任意一个平面去截长方体,其截面形状可以是三角形,四边形,五边形,六边形,因而水面的形状可以是三角形,四边形,五边形,六边形;水的形状可以是棱锥,棱柱,但不可能是棱台.。
