2015-2016年湖北省荆州市洪湖一中高二(上)期中数学试卷及参考答案(文科)
湖北省荆州中学2015-2016学年高二上学期第一次月考化学试卷.pdf

荆州中学高二年级第一次质量检测化学卷 可能用到的相对原子质量:C:12 H:1 O:16 一、选择题(共16题,每小题3分,每小题只有一个正确答案) 1.下列说法或表示法正确的是( ) A.氢气与氧气反应生成等量的水蒸气和液态水,前者放出热量多 B.需要加热的反应说明它是吸热反应 C.在稀溶液中:H+(aq)+OH-(aq)H2O(l) ?ΔH?=-57.3?kJ·mol?-1,若将含0.5mol?H2SO4的稀硫酸与含1mol?NaOH的溶液混合,放出的热量等于57.3kJ D.1mol?S完全燃烧放热297.3?kJ,热化学方程式为: S+O2 SO2? ΔH=-297.3?kJ·mol-1 2.下列说法正确的是( ) A.强酸跟强碱的反应热一定是中和热 B.1molC完全燃烧放热383.3kJ,其热化学方程为: C+O2=CO2 ΔH=-383.3kJ·mol-1 C.在稀溶液中,酸与碱发生中和反应生成1 mol H2O时的反应热叫做中和热 D.表示中和热的离子方程式为: H+(aq)+OH-(aq) H2O(l);ΔH=57.3KJ·mol-1 3.在298K、100kPa时,已知:(1)2H2O(g) O2(g)+2H2(g) ΔH1 (2)Cl2(g)+H2(g)=2HCl(g)ΔH2? (3)2Cl2(g)+2H2O(g)=4HCl(g)+O2(g)? ?ΔH3 则ΔH3与ΔH1和ΔH2间的关系正确的是 AΔH3=ΔH1+2ΔH2? ? B.ΔH3=ΔH1+ΔH2 CΔH3=ΔH1-2ΔH2? ?D.ΔH3=ΔH1-ΔH2 ΔH=+131.4kJ·mol-1下列判断正确的是( ) A.反应物能量总和大于生成物能量总和 B.CO(g)+H2(g) C(s)+H2O(g) ?ΔH=+131.4kJ·mol-1 C.水煤气反应中,生成1?mol?H2(g)吸收131.4?kJ热量 D.水煤气反应中生成1体积CO(g)吸收131.4?kJ热量 5.已知化学方程式:2SO2(g)+O2(g)2SO3(g) ?ΔH=-QkJ·mol-1(Q>0)。
洪湖一中2014—2015学年度上学期高二年级期中考试

洪湖一中2014—2015学年度上学期高二年级期中考试英语试卷限时:120分钟满分:150分命题人:罗英第一部分:听力(共两节,满分30分)做题时,先将答案划在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题,每题1.5分,共7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What does the man mean?A. He’d like to come along with the womanB. The weather is quite hot.C. He knows the way to the river.2. How many cars can be parked in front of this building now?A. 30B. 60C. 903. Where is the woman going?A. To AustraliaB. To SingaporeC. To America4. What’s the man’s opinion of his new boss?A. His boss is frank.B. His boss is very kind.C. His boss is rude.5. What does the woman mean?A. The Edwards are quite well-off.B. The Edwards should cut down on their living expenses.C. It’ll be unwise for the Edwards to buy another house.第二节(共15小题,每题1.5分,共22.5分)听下面5段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
(全优试卷)湖北省高二数学(理)上学期期中试题word版

荆州中学2015~2016学年度上学期期 中 考 试 卷年级:高二科目:数学(理科)一、选择题(60分,每小题5分,每题的四个选项中有且仅有一个是正确的)1.荆州市某重点学校为了了解高一年级学生周末双休日在家活动情况,打算从高一年级1256名学生中抽取50名进行抽查,若采用下面的方法选取:先用简单随机抽样从1256人中剔除6人,剩下1250人再按系统抽样的方法进行,则每人入选的机会( ) A. 不全相等 B. 均不相等 C. 都相等 D. 无法确定2.已知点(,1,2)A x B 和点(2,3,4),且AB =,则实数x 的值是( ) A.3-或4 B.6-或2 C.3或4- D.6或2- 3.某店一个月的收入和支出总 共记录了N 个数据1a ,2,,N a a ⋅⋅⋅, 其中收入记为正数,支出记为负数. 该店用右边的程序框图计算月总收入S 和月净盈利V ,那么在图中空白的判断框和处理框中,应分别填入下列四个 选项中的( )A .0,A V S T >=-B .0,A V S T <=-C .0,A V S T >=+D .0,A V S T <=+4.用斜二测画法作出一个三角形的直观图,则原三角形面积是直观图面积的( ) A.21倍 B. 22倍 C. 2倍 D. 42倍5.如图(1)所示的一个几何体,在图中是该几何体的俯视图的是( )(1)6.已知,a b为两条不同的直线,,αβ为两个不同的平面,且,ab αβ⊂⊂,给出下列结论:①若a ∥b ,则α∥β ;②若α∥β,则a ∥b ;③若a ⊥b ,则α⊥β; ④若α⊥β,则a ⊥b ;其中正确结论的个数是( )A B C Dx y O x y O x y O xyOA. 0B. 1C. 2D. 37.将一圆形纸片沿半径剪开为两个扇形,其圆心角之比为3∶4. 再将它们卷成两个圆锥侧面,则两圆锥的高之比为( )A. 3∶4B. 9∶16C. 27∶64D. 8. 在同一直角坐标系中,方程y ax =与y x a =+的图形正确的是( ).A.B. C. D.9. 若()2,1P -为圆()22125x y -+=的弦AB 的中点,则直线AB 的方程为 ( )A. 230x y +-=B. 10x y +-=C. 30x y --=D.250x y --=10. 已知点)3,2(-A 、(3,2),B --若直线l 过点)1,1(P ,且与线段AB 相交,则直线l 的斜率的取值k 范围是( )A. (]3,4,4⎡⎫-∞-+∞⎪⎢⎣⎭ B. 13,,44⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭ C. 34,4⎡⎤-⎢⎥⎣⎦ D. 3,44⎡⎤⎢⎥⎣⎦11.若直线42y kx k =++与曲线y =则实数k 的取值范围是( ) A .[)1,+∞ B. 31,4⎡⎫--⎪⎢⎣⎭ C. 3,14⎛⎤⎥⎝⎦D. (],1-∞-12.若圆C 与圆()()22:261D x y ++-=关于直线:50l x y -+=对称,则圆C 的方程为( )A. 22(2)(6)1x y ++-= B. 22(6)(2)1x y -++= C. 22(1)(3)1x y -+-= D. 22(1)(3)1x y +++=二、填空题(共20分,每小题5分)13.过圆22:1O x y +=上一点(),M a b 的切线方程为 .14.已知x 与y 之间的一组数据如右图所示,当m 变化时,y 与x 的回归直线方程ˆy b x a =+必过定点 .15. 若四面体的四个顶点到平面α的距离相等,则这样的平面α的个数是 . 16.荆州市为了解7080-岁的老人的日平均睡眠时间(单位:h ),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:的值为 .三、解答题17.(本小题满分10分)某地区100位居民的人均月用水量(单位:t )的频率分布直方图及频数分布表如下:(1)根据频率分布直方图估计这组数据的众数与平均数;(2)当地政府制定了人均月用水量为3t 的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?18.(本小题满分12分)已知一条光线从点()2,3A -射出,经过x 轴反射后,反射光线与圆()()22:321C x y -+-=相切,求反射光线所在直线的方程.19.(本小题满分12分)在2015年全运会上两名射击运动员甲、乙在比赛中打出如下成绩:甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8; 乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;(1)用茎叶图表示甲、乙两人的成绩;并根据茎叶图估计他们的中位数;(2)已知甲、乙两人成绩的方差分别为1.69与0.81,分别计算两个样本的平均数x x 乙甲、和标准差s s 乙甲、,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.20.(本小题满分12分)设()00,M x y 是直线():00l mx ny p mn ++=≠外一定点,且点M 到直线l 的距离是d,试证明:d =.21.(本小题满分12分)在三棱锥A BCD -中,AB BCD ⊥面,BC CD ⊥,点E 在棱AC 上,且BE AC ⊥.(Ⅰ)试证明:BE ACD ⊥面;(Ⅱ)若2AB BC CD ===,过直线BE 任作一个平面与直线 AD 相交于点P ,得到三棱锥A BCD -的一个截面BEP ∆, 求BEP ∆面积的最小值;(Ⅲ)若2AB BC CD ===,求二面角B AD C --的正弦值.22.(本小题满分12分)已知圆22:1O x y +=和定点()2,1A ,由圆O 外一点(,)P a b 向圆O引切线,PQ PM ,切点为,Q M ,且满足PQ PA =. (1)求实数,a b 间满足的等量关系;(2)若以P 为圆心的圆P 与圆O 有公共点,试求圆P 的半径 最小时圆P 的方程;(3)当P 点的位置发生变化时,直线QM 是否过定点,如果PABCDE是,求出定点坐标,如果不是,说明理由.荆州中学2015~2016学年度上学期期 中 考 试 卷年级:高二 科目:数学(理科) 出题人:审题人:参考答案一、选择题 CDCBC ADCCA BC 二、填空题10ax by +-=; )4,23(; 7; 6.42 三、解答题17. 解:(1)由图知,这组数据的众数为2.25, 平均数为2.02. (2)人均月用水量在3t 以上的居民的比例为6%+4%+2%=12%,即大约是有12%的居民月均用水量在3t 以上,88%的居民月均用水量在3t 以下,因此,政府的解释是正确的.18.解:A 关于x 轴的对称点(2,3)A '--。
【全国百强校】湖北省荆州中学2015-2016学年高二上学期期中考试文数试题解析(解析版)

第Ⅰ卷(共60分)一、 选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有 一项是符合题目要求的.1.荆州市某重点学校为了了解高一年级学生周末双休日在家活动情况,打算从高一年级1256名学生中抽取50名进行抽查,若采用下面的方法选取:先用简单随机抽样从1256人中剔除6人,剩下1250人再按系统抽样的方法进行,则每人入选的机会( )A. 不全相等B. 均不相等C. 都相等D. 无法确定 【答案】C考点:抽样方法。
2.已知点(,1,2)A x B 和点(2,3,4),且AB =,则实数x 的值是( ). A.3-或4 B.6-或2 C.3或4- D.6或2- 【答案】D 【解析】试题分析:由空间两点间距离公式得,6242312222=-+-+-)()()(x ,解得6=x 或2-=x 。
故选D 。
考点:空间两点间距离公式。
3.某店一个月的收入和支出总共记录了N 个数据1a ,2,,N a a ⋅⋅⋅,其中收入记为正数,支出记为负数。
该店用右边的程序框图计算月总收入S 和月净盈利V ,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的( )A .0,A V S T >=-B .0,A V S T <=-C .0,A V S T >=+D .0,A V S T <=+【答案】C考点:程序框图的应用。
4.用斜二测画法作出一个三角形的直观图,则原三角形面积是直观图面积的( ) A.21倍 B. 22倍 C. 2倍 D. 42倍【答案】B 【解析】试题分析:设原三角形的底边长为a,高为h,则直观图中底边长仍为a ,高为42452hh =︒⋅sin ,所以原三角形面积与直观图面积的比值为222442==⋅h a ah 2121,即原三角形面积是直观图面积的22倍。
考点:斜二测画法。
5.如图(1)所示的一个几何体,在图中是该几何体的俯视图的是( )【答案】C 【解析】试题分析:对于原几何体中能够看到的棱或边界在三视图中画实线,不能看到的棱或边界在三视图中画虚线或不画,结合几何体及选项易知选C 。
(全优试卷)湖北省高二数学(文)上学期期中试题word版
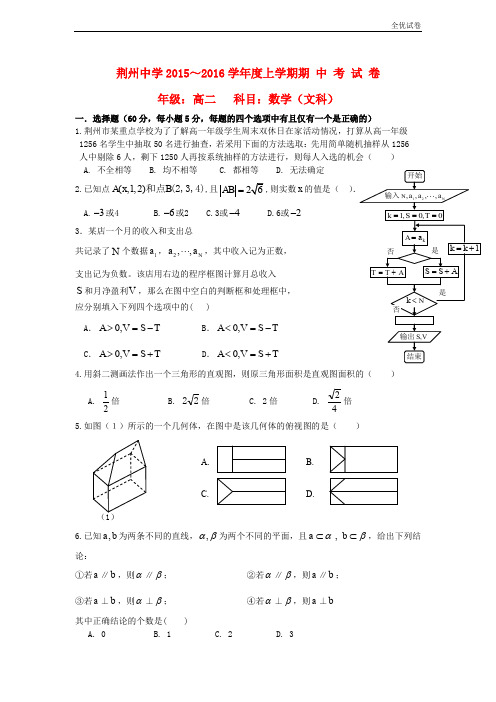
荆州中学2015~2016学年度上学期期 中 考 试 卷年级:高二 科目:数学(文科)一.选择题(60分,每小题5分,每题的四个选项中有且仅有一个是正确的)1.荆州市某重点学校为了了解高一年级学生周末双休日在家活动情况,打算从高一年级1256名学生中抽取50名进行抽查,若采用下面的方法选取:先用简单随机抽样从1256人中剔除6人,剩下1250人再按系统抽样的方法进行,则每人入选的机会( ) A. 不全相等 B. 均不相等 C. 都相等 D. 无法确定2.已知点(,1,2)A x B 和点(2,3,4),且AB =,则实数x 的值是( )A.3-或4B.6-或2C.3或4-D.6或2- 3.某店一个月的收入和支出总共记录了N 个数据1a ,2,,N a a⋅⋅⋅,其中收入记为正数,支出记为负数。
该店用右边的程序框图计算月总收入S 和月净盈利V ,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的( )A .0,A V S T >=-B .0,A V S T <=-C .0,A V S T >=+D .0,A V S T <=+4.用斜二测画法作出一个三角形的直观图,则原三角形面积是直观图面积的( ) A.21倍 B. 22倍 C. 2倍 D. 42倍5.如图(1)所示的一个几何体,在图中是该几何体的俯视图的是( )(1)6.已知,a b 为两条不同的直线,,αβ为两个不同的平面,且,a b αβ⊂⊂,给出下列结论:①若a ∥b ,则α∥β; ②若α∥β,则a ∥b ; ③若a ⊥b ,则α⊥β; ④若α⊥β,则a ⊥b 其中正确结论的个数是( )A. 0B. 1C. 2D. 3A. B. C. D.x y O x y O x y O xyO7.将一圆形纸片沿半径剪开为两个扇形,其圆心角之比为3∶4. 再将它们卷成两个圆锥侧面,则两圆锥的之底面积比为( ) A. 3∶4 B. 9∶16 C. 4:3 D. 16:9 8.在同一直角坐标系中,方程y ax =与y x a =+的图形正确的是( )A. B. C. D.9.若()2,1P -为圆()22125x y -+=的弦AB 的中点,则直线AB 的方程为 ( )A. 230x y +-=B. 10x y +-=C. 30x y --=D. 250x y --=10.已知点)3,2(-A 、(3,2),B --若直线l 过点)1,1(P ,且与线段AB 相交,则直线l 的斜率的取值k 范围是 ( )A. (]3,4,4⎡⎫-∞-+∞⎪⎢⎣⎭ B. 13,,44⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭C. 34,4⎡⎤-⎢⎥⎣⎦D. 3,44⎡⎤⎢⎥⎣⎦11.若直线42y kx k =++与曲线y =k 的取值范围是( )A. [)1,+∞B. 31,4⎡⎫--⎪⎢⎣⎭ C. 3,14⎛⎤ ⎥⎝⎦D. (],1-∞- 12.若圆C 与圆()()22:261D x y ++-=关于直线:0l x y -=对称,则圆C 的方程为( ) A. 22(2)(6)1x y ++-= B. 22(6)(2)1x y -++= C. 22(1)(3)1x y -+-= D. 22(1)(3)1x y +++=二、填空题(共20分,每小题5分)13.过圆22:1O x y +=外一点()1,2M -的切线方程为 .14.已知x 与y 之间的一组数据如右图所示,当m 变化时,y 与x 的回归直线方程ˆy b x a =+必过定点 .15.在三棱锥的四个面中,直角三角形最多可有 个.16.荆州市为了解7080-岁的老人的日平均睡眠时间(单位:h ),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:的值为 .三、解答题17. (本小题满分10分)某地区100位居民的人均月用水量(单位:t )的频率分布直方图及频数分布表如下:(1)根据频率分布直方图估计这组数据的众数与平均数;(2)当地政府制定了人均月用水量为3t 的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?18.(本小题满分12分)已知一条光线从点()2,3A -射出,经过x 轴反射后,反射光线与圆()()22:321C x y -+-=相切,求反射光线所在直线的方程.19.(本小题满分12分)在2015年全运会上两名射击运动员甲、乙在比赛中打出如下成绩:甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8; 乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;(1)用茎叶图表示甲、乙两人的成绩;并根据茎叶图估计他们的中位数;(2)已知甲、乙两人成绩的方差分别为1.69与0.81,分别计算两个样本的平均数x x 乙甲、和标准差s s 乙甲、,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.20.(本小题满分12分)已知点()3,4,(6,3)A B --到直线:10l ax y ++=的距离相等,求a 得值.21.(本小题满分12分)在三棱锥A BCD -中,AB BCD ⊥面,BC CD ⊥,点E 在棱AC 上,且BE AC ⊥.(Ⅰ)试证明:BE ACD ⊥面;(Ⅱ)若2AB BC CD ===,过直线BE 任作一个平面与直线 AD 相交于点P ,得到三棱锥A BCD -的一个截面BEP ∆, 求BEP ∆面积的最小值;(Ⅲ)若2AB BC CD ===,求二面角B AD C --的正弦值.22.(本小题满分12分)已知圆22:1O x y +=和定点()2,1A ,由圆O 外一点(,)P a b 向圆O 引切线PQ ,切点为Q ,且满足PQ PA =. (1) 求实数,a b 间满足的等量关系; (2) 求线段PQ 长的最小值;(3) 若以P 为圆心的圆P 与圆O 有公共点,试求圆P 的半径最小时圆P 的方程.PABCDE荆州中学2015~2016学年度上学期期 中 考 试 卷年级:高二 科目:数学(文科) 出题人:审题人:参考答案一、选择题CDCBC ABCCA BB 二、填空题34501x y x ++==和; )4,23(; 4; 6.42三、解答题17. 解:(1)由图知,这组数据的众数为2.25, 平均数为2.02.(2)人均月用水量在3t 以上的居民的比例为6%+4%+2%=12%,即大约是有12%的居民月均用水量在3t 以上,88%的居民月均用水量在3t 以下,因此,政府的解释是正确的.18.解:A 关于x 轴的对称点(2,3)A '--。
2015-2016学年湖北省荆州市公安一中高二(上)12月月考数学试卷(理科)

2015-2016学年湖北省荆州市公安一中高二(上)12月月考数学试卷(理科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共12小题,共60.0分)1.一个盒子里有6只好晶体管,4只坏晶体管,任取两次,每次取一只,每次取后不放回,则若已知第一只是好的,则第二只也是好的概率为()A. B. C. D.【答案】C【解析】解:根据题意,已知第一只是好的,则盒子里还有5只好晶体管,4只坏晶体管,∴若已知第一只是好的,则第二只也是好的概率为故选C.根据题意,已知第一只是好的,则盒子里还有5只好晶体管,4只坏晶体管,,故可求概率.本题考查等可能事件的概率,考查学生的计算能力.2.从1,2,3,4,5中随机取出二个不同的数,其和为奇数的概率为()A. B. C. D.【答案】C【解析】解:由题意可得:从数字1,2,3,4,5中,随机抽取2个数字共有不同的取法有:C52=10.其中这两个数字之和为奇数的取法有:(1,2),(1,4).(2,3),(2,5),(3,4),4,5),共有6种取法.所以这两个数字之和为奇数的概率为:=故选C.首先计算出所以基本事件总数为:C52=10,再计算出这两个数字之和为奇数的取法,进而计算出事件发生的概率.本题考查等可能事件的概率,解题的关键是熟练掌握古典概率模型的特征,并且结合排列与组合解决概率问题3.C+C=()A.466B.478C.512D.526【答案】A【解析】解:由题意可得:,n∈N*,解得n=10.原式=+=+31=466.故选:A.由题意可得:,n∈N*,解得n.再利用组合数的计算公式即可得出.本题考查了组合数的计算公式、不等式的解法,考查了推理能力与计算能力,属于中档题.4.已知X~B(n,p),E(X)=8,D(X)=1.6,则n,p的值为()A.100和0.8B.20和0.4C.10和0.8D.10和0.2【答案】C【解析】解:因为X~B(n,p),含义为n次独立事件,每次发生的概率为p.所以:EX=8,DX=1.6,即np=8,np(1-p)=1.6,可解得p=0.8,n=10,故选:C.1由已知X~B(n,p),EX=8,DX=1.6,求n的值.首先要知道X~B(n,p)是二项分布即表示n次独立事件,每次发生的概率为p.又有公式EX=np,DX=np (1-p),求解即可得到答案.此题主要考查二项分布的问题.对于X~B(n,p),要理解每一个字母所代表的含义,是此题解答的关键.题目考查的是概念性问题,属于基础题型.5.我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有()A.12B.18C.24D.48【答案】C【解析】解:把甲、乙看作1个元素和戊全排列,调整甲、乙,共有种方法,再把丙、丁插入到刚才“两个”元素排列产生的3个空位种,有种方法,由分步计算原理可得总的方法种数为:=24故选C分两大步:把甲、乙看作1个元素和戊全排列,调整甲、乙,共有种方法,再把丙、丁插入到刚才“两个”元素排列产生的3个空位种,有种方法,由分步计算原理可得答案.本题考查简单的排列组合问题,捆绑法和插空法结合是解决问题的关键,属中档题.6.在长为1cm的线段AB上任取一点C,现以AC、BC为邻边作矩形,则该矩形面积不小于cm2的概率为()A. B. C. D.【答案】B【解析】解:设AC=x,则BC=1-x矩形的面积S=x(1-x)≥,∴x2-x+≤0∴≤x<≤由几何概率的求解公式可得,该矩形面积不小于cm2的概率为P==.故选:B.设AC=x,则BC=1-x,由矩形的面积S=x(1-x)≥可求x的范围,利用几何概率的求解公式可求.本题主要考查了二次不等式的解法,与区间长度有关的几何概率的求解公式的应用,属于基础题.7.某班新年联欢会原定的6个节目已排成节目单,开演前又增加了3个新节目,如果将这3个节目插入节目单中,那么不同的插法种数为()A.504B.210C.336D.120【答案】A【解析】解:∵由题意知将这3个节目插入节目单中,原来的节目顺序不变,∴三个新节目一个一个插入节目单中,原来的6个节目形成7个空,在这7个位置上插入第一个节目,共有7种结果,原来的6个和刚插入的一个,形成8个空,有8种结果,同理最后一个节目有9种结果根据分步计数原理得到共有插法种数为7×8×9=504,故选A.由题意知将这3个节目插入节目单中,原来的节目顺序不变,三个新节目一个一个插入节目单中,原来的6个节目形成7个空,在这7个位置上插入第一个节目,共有7种结果;用同样的方法插入第二个和第三个节目,根据分步乘法计数原理得到结果.本题考查分步计数原理,是一个实际问题,解题时注意题目条件中对于原来6个节目的顺序要求不变,所以采用插入法.8.一个课外兴趣小组共有5名成员,其中3名女性成员、2名男性成员,现从中随机选取2名成员进行学习汇报,记选出女性成员的人数为X,则X的数学期望是()A. B. C. D.【答案】D【解析】解:一个课外兴趣小组共有5名成员,其中3名女性成员、2名男性成员,现从中随机选取2名成员进行学习汇报,记选出女性成员的人数为X,则X的可能取值为0,1,2,P(X=0)==,P(X=1)==,P(X=2)==,∴X的分布列为:EX==.故选:D.X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列,由此能求出EX.本题考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.9.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=()A.0.6B.0.4C.0.3D.0.2【答案】C【解析】解:∵随机变量X服从正态分布N(2,σ2),μ=2,得对称轴是x=2.P(ξ<4)=0.8∴P(ξ≥4)=P(ξ≤0)=0.2,∴P(0<ξ<4)=0.6∴P(0<ξ<2)=0.3.故选C.根据随机变量X服从正态分布N(2,σ2),看出这组数据对应的正态曲线的对称轴x=2,根据正态曲线的特点,得到P(0<ξ<2)=P(0<ξ<4),得到结果.本题考查正态曲线的形状认识,从形态上看,正态分布是一条单峰、对称呈钟形的曲线,其对称轴为x=μ,并在x=μ时取最大值从x=μ点开始,曲线向正负两个方向递减延伸,不断逼近x轴,但永不与x轴相交,因此说曲线在正负两个方向都是以x轴为渐近线的.10.(+)n的展开式中,只有第9项的二项式系数最大,则展开式中含x3的项是第几项()A.5B.6C.7D.8【答案】C【解析】解:∵(+)n的展开式中,只有第9项的二项式系数最大,∴n=16,∴(+)n=(+)16,由,令,得n=6.∴展开式中含x3的项是第7项.故选:C.由题意可得n值,写出二项展开式的通项,由x的指数等于3求得r,则答案可求.本题考查二项式定理的应用,关键是区分项的系数与二项式系数,是基础题.11.如图,花坛内有五个花池,有五种不同颜色的花卉可供栽种,每个花池内只能种同种颜色的花卉,相邻两池的花色不同,则最多有几种栽种方案()A.180种B.240种C.360种D.420种【答案】D【解析】解:若5个花池栽了5种颜色的花卉,方法有种,若5个花池栽了4种颜色的花卉,则2、4两个花池栽同一种颜色的花;或者3、5两个花池栽同一种颜色的花,方法有2种,若5个花池栽了3种颜色的花卉,方法有种,故最多有+2+=420种栽种方案,故选D.若5个花池栽了5种颜色的花卉,方法有种,若5个花池栽了4种颜色的花卉,方法有2种,若5个花池栽了3种颜色的花卉,方法有种,相加即得所求.本题主要考查排列、组合以及简单计数原理的应用,体现了分类讨论的数学思想,属于中档题.12.在(1+x)6(1+y)4的展开式中,记x m y n项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)=()A.45B.60C.120D.210【答案】C【解析】解:(1+x)6(1+y)4的展开式中,含x3y0的系数是:=20.f(3,0)=20;含x2y1的系数是=60,f(2,1)=60;含x1y2的系数是=36,f(1,2)=36;含x0y3的系数是=4,f(0,3)=4;∴f(3,0)+f(2,1)+f(1,2)+f(0,3)=120.故选:C.由题意依次求出x3y0,x2y1,x1y2,x0y3,项的系数,求和即可.本题考查二项式定理系数的性质,二项式定理的应用,考查计算能力.二、填空题(本大题共4小题,共20.0分)13.已知集合M={1,-2,3},N={-4,5,6,-7},从两个集合中各取一个元素作为点的坐标,则在直角坐标系中,第一、第二象限不同点的个数为______ .【答案】14【解析】解:由题意知本题是一个分类和分步的综合问题,M中的元素作点的横坐标,N中的元素作点的纵坐标,在第一象限的点共有2×2个,在第二象限的点共有1×2个.N中的元素作点的横坐标,M中的元素作点的纵坐标,在第一象限的点共有2×2个,在第二象限的点共有2×2个.∴所求不同的点的个数是2×2+1×2+2×2+2×2=14(个).故答案为:14.本题首先分类在每一类中又分步,M中的元素作点的横坐标,N中的元素作点的纵坐标,N中的元素作点的横坐标,M中的元素作点的纵坐标,分别可以得到在第一和第二象限中点的个数,根据分类加法原理得到结果.本题考查分步计数原理和分类计数原理,是一个综合题目,首先分类,每类方法并不都是一步完成的,必须在分类后又分步,综合利用两个原理解决.其中a,b,c成等差数列,若.则Dξ的值是______ .【答案】【解析】解:∵a,b,c成等差数列,∴2b=a+c,∵a+b+c=1,Eξ=-1×a+1×c=c-a=.联立三式得,,,∴.故答案为:要求这组数据的方差,需要先求出分布列中变量的概率,这里有三个条件,一个是三个数成等差数列,一个是概率之和是1,一个是这组数据的期望,联立方程解出结果.这是一个综合题目,包括等差数列,离散型随机变量的期望和方差,主要考查分布列和期望的简单应用,通过解方程组得到要求的变量,这与求变量的期望是一个相反的过程,但是两者都要用到期望的公式.15.若的展开式中,各项系数的和与各项二项式系数的和之比为64,则n=______ .【答案】6【解析】解:令x=1,可得的展开式中,各项系数的和为4n,而它的各项二项式系数的和2n,根据题意可得=2n=64,∴n=6,故答案为:6.由条件求得展开式的各项系数的和与各项二项式系数的和,从而根据各项系数的和与各项二项式系数的和之比为64,求得n的值.本题主要考查二项式定理的应用,注意各项系数的和与各项二项式系数的和的区别,属于基础题.16.将6本不同的书,分给甲、乙、丙三人,每人至少1本,则不同的分配方法种数为______ .【答案】540【解析】解:分为3类:①411,C61×C51×C31=90;②321,C61×C51×A33=360种;③222,C62×C42×C22=90种,故共有90+360+90=540种.故答案为:540.分为3类:411,321,222,利用排列组合知识,即可得出结论.本题考查排列、组合及简单计数问题,正确区分无序不均匀分组问题.有序不均匀分组问题.无序均匀分组问题.是解好组合问题的一部分;本题考查计算能力,理解能力.三、解答题(本大题共6小题,共70.0分)17.2015年3月22日,长沙某协会在“保护湘江,爱我母亲河”活动中共计放生了青鱼、草鱼、鲫鱼数百万尾.若这些鱼中三种鱼所占比例一样,现从中抽取5尾检查鱼的健康状况,求其中青鱼的尾数X的分布列及其数学期望.【答案】解:由题意可得:X~B,.∴P(X=k)=.的分布列为:EX=5×=.【解析】由题意可得:X~B,.可得P(X=k)=,进而得出分布列与数学期望.本题考查了二项分布列与数学期望,考查了推理能力与计算能力,属于中档题.18.在某次物理考试中,考生的成绩ξ服从正态分布,即ξ:N(70,100),已知满分为100分.(1)试求考试成绩ξ位于区间(50,90)内的概率;(2)若这次考试共有1000名学生参加,试估计这次考试及格(不小于60分)的人数.(附:若ξ:N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544,P(μ-3σ<ξ<μ+3σ)=0.9974)【答案】解:(1)∵考生的成绩ξ服从正态分布,即ξ~N(70,100),∴正态曲线关于x=70对称,且标准差为10,根据3σ原则知P(50<x<90)=P(70-2×10<x<70+2×10)=0.9544,(2)P(60<x<80)=P(70-10<x<70+10)=0.6826,考试成绩ξ位于区间(60,80)上的概率为0.6826,则考试成绩在60分以上的概率是=0.5+×0.6826=0.8413∴估计这次考试及格(不小于60分)的人数为1000×0.8413≈841人.【解析】(1)根据考生的成绩ξ~N(70,100),得到正态曲线关于x=70对称,根据3σ原则知P(50<x<90)=P(70-2×10<x<70+2×10)=0.9544;(2)P(60<x<80)=P(70-10<x<70+10)=0.6826,再根据对称性得到结果.本题考查正态分布曲线的特点及曲线所表示的意义,解题的关键是注意利用正态曲线的对称性.19.设(2x-1)5=a0+a1x+a2x2+…a5x5,求:(1)a0+a1+…+a5;(2)|a0|+|a1|+…+|a5|;(3)a1+a3+a5;(4)(a0+a2+a4)2-(a1+a3+a5)2.【答案】解:∵(2x-1)5=a0+a1x+a2x2+…+a5x5,(1)∴令x=1,可得a0+a1+…+a5=1①.(2)在(2x+1)5中,令x=1,可得|a0|+|a1|+…+|a5|=35=243.(3)在(2x-1)5=a0+a1x+a2x2+…a5x5,中,令x=-1,可得a0-a1+a2-a3+a4-a5=-243②,①-②可得2(a1+a3+a5)=244,∴a1+a3+a5=122.(4)①+②可得2(a0+a2+a4)=-242,∴a0+a2+a4=-121,∴(a0+a2+a4)2-(a1+a3+a5)2=(-121)2-1222=-243.【解析】(1)在所给的等式中,令x=1,可得a0+a1+…a5=1①;(2)在(2x+1)5中,令x=1,可得|a0|+|a1|+…+|a5|的值.(3)在所给的等式中,令x=-1,可得a0-a1+a2-a3+a4-a5=-243②,①-②可得a1+a3+a5的值.(4)①+②可得a0+a2+a4的值,从而求得(a0+a2+a4)2-(a1+a3+a5)2的值.本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.20.某地为了改善居民的居住环境,争创国家卫生城市,在市民意见网站发布一项调查,每个住户在调研所居住的环境卫生后进行自主打分,最高分是10分.上个月该网站共有100个住户进行了打分,所有住户打分的平均分作为居民对该城市卫生现状满意度的参考分值,将这些打分结果分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.(1)分别求第三、四、五组的频率;(2)该网站在打分结果较高的第三、四、五组中用分层抽样的方法抽取6个住户.①已知甲住户和乙住户均在第三组,求甲、乙同时被选中的概率;②政府决定在这6个住户中随机抽取2个作具体了解,设第四组中有X个住户被选中,求X的分布列和数学期望.【答案】解:(1)由频率分布直方图得第三组的频率为:0.150×2=0.3,第四组的频率为:0.1×2=0.2,第五组的频率为:0.05×2=0.1.(2)①该网站在打分结果较高的第三、四、五组中用分层抽样的方法抽取6个住户,则第三组抽:6×=3人,第四组抽:6×=2人,第五组抽:6×=1人,∵第三组共有100×0.3=30个住户,甲住户和乙住户均在第三组,∴甲、乙同时被选中的概率p==.②第四组中有X个住户被选中,由题意得X的可能取值为0,1,2,P(X=0)==,P(X=1)==,P(X=2)==.∴X的分布列为:EX==.【解析】(1)由频率分布直方图能求出第三、四、五组的频率.(2)①该网站在打分结果较高的第三、四、五组中用分层抽样的方法抽取6个住户,第三组抽3人,由第三组共有100×0.3=30个住户,甲住户和乙住户均在第三组,能求出甲、乙同时被选中的概率.②第四组中有X个住户被选中,由题意得X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意频率分布直方图的性质的合理运用.21.已知在(-)6(a>0)的展开式中,常数项为60.(1)求a;(2)求含x的项的系数;(3)求展开式中所有的有理项.【答案】解:(-)6(a>0)的展开式中,通项公式T r+1==a6-r(-1)r.(1)令-6=0,解得r=4,∴a2=60,解得a=2.(2)令-6=,解得r=5,∴含x的项的系数==-12.(3)由x的指数为-6(r=0,1,2,…,6),只有当r=4,6时,有理项分别为:T5=60,T7=x3.【解析】(-)6(a>0)的展开式中,通项公式T r+1=a6-r(-1)r.(1)令-6=0,解得r即可得出.(2)令-6=,解得r即可得出.(3)由x的指数为-6(r=0,1,2,…,6),只有当r=4,6时,为有理项.本题考查了二项式定理的通项公式的应用,考查了推理能力与计算能力,属于基础题.22.某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于80小于90为二等品,小于80为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利30元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.(1)计算新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的概率;(2)记甲乙分别生产一件产品A给工厂带来的盈利和记为X,求随机变量X的概率分布和数学期望.【答案】解:(1)甲生产一件产品A为一等品、二等品、三等品的概率分别为,,,…(3分)乙生产一件产品A为一等品、二等品、三等品的概率分别为,,,…(6分)新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的情形有:三件都是一等品;二件是一等品、一件是二等品或一件是一等品、二件是二等品,概率为:p=()3+3•()2•+3••=.…(8分)(2))随机变量X的所有可能取值为100,80,60,40,20,-20.P(X=100)==,P(X=80)==,P(X=60)==,P(X=40)==,高中数学试卷第11页,共12页P(X=20)==,P(X=-20)==,∴随机变量X的概率分布为:随机变量X的数学期望EX=+=56(元)…(12分)【解析】(1)由已知条件,利用互斥事件的概率加法公式能求出他们生产产品A为一等品、二等品、三等品的概率.(2))随机变量X的所有可能取值为100,80,60,40,20,-20.分别求出相对应的概率,由此能求出随机变量X的概率分布和数学期望.本题考查概率的计算,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.高中数学试卷第12页,共12页。
湖北省荆州中学2015-2016学年高二上学期期中考试物理试题

MN静电计荆州中学2015~2016学年度上学期期 中 考 试 卷(考试范围:静电场、恒定电流、磁场 考试时间:90分钟 满分:110分)一、选择题(每小题5分共50分,其中1—7题为单选题,8—10题为多选题。
)1.在电磁学发展过程中,许多科学家做出了贡献,下列说法中符合物理学发展史的是( )A .奥斯特发现了点电荷的相互作用规律B .库仑发现了电流的磁效应C .安培发现了磁场对运动电荷的作用规律D .法拉第最早引入电场的概念,并发现了磁生电的条件和规律 2.把一根柔软的螺旋弹簧竖直悬挂起来,使它的下端刚好与杯里的水银面相接触,并组成如图所示电路图,当开关S 接通后,将看到的现象是( ) A. 弹簧向上收缩 B. 弹簧上下跳动 C. 弹簧被拉长 D. 弹簧仍静止不动3.如图所示,质量为m 、长为L 的直导线用两绝缘细线悬挂于'O O 、,并处于匀强磁场中.当导线中通以沿x 负方向的电流I ,且导线保持静止时,悬线与竖直方向的夹角为θ.则磁感应强度的方向和大小不可能的是 ( )A .z 正向,tan mg IL θ B .y 负向,mgILC .x 负向,IL mgD .沿悬线向上,sin mg IL θ4.一根导线两端加上电压U ,导体中自由电子定向移动的平均速率为v ,现将导线均匀拉长至横截面半径为原来的1/2,然后两端加上电压U ,则导线中自由电子定向移动的平均速率为: ( )A .2v B .22v C .4vD .42v5.如图所示,由两块相互靠近的平行金属板组成的平行板电容器的极板N 与静电计相接,极板M 接地.用静电计测量平行板电容器两极板间的电势差U .在两板相距一定距离d 时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器所带电量Q 不变,下面哪些操作将使静电计指针张角变大 ( )A .将M 板向下平移B .将M 板沿水平向右方向靠近N 板C .在M 、N 之间插入云母板(介电常数ε>1)D .在M 、N 之间插入金属板,且不和M 、N 接触6.如图所示,长为L 、倾角为θ的光滑绝缘斜面固定在水平面上,斜面处于电场中.一电荷量为+q 、质量第7题图abdc O为m 的小球以速度v 0由斜面底端A 沿斜面上滑,到达顶端B 的速度仍为v 0,则 A .若电场是匀强电场,则场强大小一定为qmgB .若电场是匀强电场,A 、B 两点间的电势差一定为qmgLC .不论电场是否是匀强电场,小球在B 点的电势能一定大于在A 点的电势能D .不论电场是否是匀强电场,A 、B 两点间的电势差一定为qmgLsin 7.如图所示,电源电动势为E,内阻为r.电路中的R 2 、R 3为滑动变阻器,R 0为定值电阻,R 1为光敏电阻(其电阻随光照强度增大而减小).当电键S 闭合时,电容器中一带电微粒恰好处于静止状态.有关下列说法中正确的是 ( )A.若断开电键S,电容器所带电荷量变大,带电微粒向上运动B.只调节电阻R 3的滑动端P 2向上端移动,电源消耗的功率变大,电阻R 3中有向上的电流C.只调节电阻R 2的滑动端P 1向下端移动时,电压表示数变大,带电微粒向下运动D.只逐渐增大R 1的光照强度,电阻R 0消耗的电功率变大,电阻R 3 中有向上的电流8.下列运动情况可能出现的是 ( ) A.带电粒子绕通稳恒电流的长直导线只受磁场力作用做匀速圆周运动B.电子绕一正电荷只受电场力作用做匀速圆周运动C.电子在两等量同种正电荷连线中垂面上,只受电场力作用绕连线中点做匀速圆周运动D.带电粒子在匀强磁场中只受磁场力作用做匀加速直线运动9.如图所示,空间中有两个点电荷Q 1和Q 2,在两电荷所在平面上有a 、b 、c 、d 四点,其中a 、b 位于电荷连线的延长线上, c 点位于两电荷连线的中点,d 点位于两电荷连线的垂直平分线上.则以下判正确的是 ( ) A .若a 点的电场强度为零,则说明Q 1和Q 2为异种电荷,且|Q 1| < |Q 2| B .若c 点的电势为零,则说明Q 1和Q 2是异种电荷,且|Q 1|=|Q 2|C .若b 点的电场强度为零,则说明Q 1和Q 2是同种电荷,且|Q 1| > |Q 2|D .无论两电荷是同种电荷还是异种电荷,d 点的电场强度都不可能为零 10.如图所示,垂直纸面向里的匀强磁场分布在正方形abc d 区域内,O 点是cd 边的中点,一个带正电的粒子仅在磁场力的作用下,从O 点沿纸面以垂直于cd 边的速度射入正方形内,经过时间t 0刚好从c 点射出磁场,现设法使该带电粒子从O 点沿纸面以与Od 成300的方向,以大小不同的速率射入正方形内,下列说法中正确的是( )Q 1Q 2 a b c d第9题图A .若该带电粒子在磁场中经历的时间是035t ,则它一定从cd 边射出磁场B .若该带电粒子在磁场中经历的时间是043t ,则它一定从ad 边射出磁场C .若该带电粒子在磁场中经历的时间是045t ,则它一定从bc 边射出磁场D .若该带电粒子在磁场中经历的时间是0t ,则它一定从ab 边射出磁场二 、实验题(本题共2小题,共13分)11.(4分) 用游标卡尺和螺旋测微器测量一圆柱形小零件的长和直径时如下图所示,读出游标卡尺示数为__________cm ,螺旋测微器示数为__________cm12.(9分) 小灯泡灯丝的电阻会随温度的升高而变大.某同学为研究这一现象,用实验得到如下数据(I 和U 分别表示小灯泡上的电流和电压):I/(A) 0.12 0.21 0.29 0.34 0.38 0.42 0.45 0.47 0.49 0.50 U(V)0.200.400.600.801.001.201.401.601.802.00(1)在左下框中画出实验电路图.可用的器材有:电压表、电流表、滑动变阻器(变化范围0~10Ω)、电源、小灯泡、电键、导线若于. (2)在右图中画出小灯泡的U —I 曲线. (3)若将该小灯泡接在电动势是1.5V ,内 阻是2.0Ω的电池两端,小灯泡的实际功率为 (保留两位有效数字)。
2015-2016学年湖北省荆州市洪湖一中高二上学期期中数学试卷与解析(文科)

2015-2016学年湖北省荆州市洪湖一中高二(上)期中数学试卷(文科)一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)直线的倾角为()A.B.C. D.2.(5分)已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是()A.﹣2 B.﹣4 C.﹣6 D.﹣83.(5分)点(1,﹣2,3)关于x轴的对称点坐标为()A.(1,2,﹣3)B.(﹣1,﹣2,3) C.(﹣1,2,﹣3) D.(﹣1,2,3)4.(5分)已知直线l1:ax+(a+2)y+1=0,l2:x+ay+2=0.若l1⊥l2,则实数a的值是()A.0 B.2或﹣1 C.0或﹣3 D.﹣35.(5分)与直线x﹣y﹣4=0和圆x2+y2+2x﹣2y=0都相切的半径最小的圆的方程是()A.(x+1)2+(y+1)2=2 B.(x+1)2+(y+1)2=4 C.(x﹣1)2+(y+1)2=2 D.(x﹣1)2+(y+1)=46.(5分)执行如图所示的程序框图,输出的结果是()A.11 B.12 C.13 D.147.(5分)用秦九韶算法计算多项式f(x)=12+35x﹣8x2+79x3+6x4+5x5+3x6在x=﹣4时的值时,V3的值为()A.﹣845 B.220 C.﹣57 D.348.(5分)如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是()A.x>60?,i=i+1 B.x<60?,i=i+1 C.x>60?,i=i﹣1 D.x<60?,i=i﹣1 9.(5分)用“辗转相除法”求得360和504的最大公约数是()A.72 B.36 C.24 D.252010.(5分)与⊙D:(x+1)2+(y﹣2)2=相切且在两坐标轴上的截距相等的直线的条数有()A.1 B.2 C.3 D.411.(5分)若点P(x,y)为不等式组所表示区域内任一点,则x2+y2+1的最小值为()A.B.1 C.2 D.12.(5分)若要(x﹣1)2+(y+2)2=4上恰有两个点到直线2x+y+m=0的距离等于1,则m的一个可能值是()A.3 B.C.2 D.二、填空题:本大题共4个小题,每小题5分,共20分,把答案填写在题中的横线上.13.(5分)某程序框图如图所示,该程序运行后输出的值是.14.(5分)某程序的流程图如图所示,若使输出的结果不大于37,则输入的整数的最大值为15.(5分)已知直线l与圆O:x2+y2=1在第一象限内相切于点C,并且分别与x,y轴相交于A、B两点,则|AB|的最小值为.16.(5分)已知点P(x,y)满足约束条件,且z=2x+4y的最小值为6.(1)常数k=;(2)的取值范围为.三、解答题:本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(10分)已知点P是直线3x+4y+8=0上的动点,PA、PB是圆(x﹣1)2+(y ﹣1)2=1的两条切线,A、B为切点,C为圆心,求四边形PACB面积S的最小值.18.(12分)求适合下列各条件的直线的方程:(1)自点P(﹣3,3)发出的光线射到x轴上,被x轴反射,其反射光线与⊙C:(x﹣2)2+(y﹣2)2=1相切;(2)直线过定点P(5,10)且与原点的距离为5.19.(12分)已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,(1)求点P的轨迹C的方程(2)过点A的直线与轨迹C有公共点,求的斜率k的取值范围.20.(12分)已知⊙C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0.(1)求证:对任意实数m,直线与⊙C总有两个不同的公共点;(2)求直线被⊙C截得的线段最短时直线的方程.21.(12分)据报我国正分别在大连和上海建造两航母,而建造航母必需特种钢.为建造航母的需要,要将两种不同的特种钢板截成A、B、C三种规格,每张钢板可同时截成三种规格的小钢板的块数如下表所示:今需要A、B、C三种规格的成品分别15、18、27块.问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少?22.(12分)已知⊙C:(x﹣6)2+y2=4,直线过点P(0,2)且斜率为k.(1)若直线与⊙C有公共点,求k的取值范围;(2)若直线与⊙C交于不同两点A、B,是否存在常数k,使以AB为直径的圆过⊙C的圆心C?若存在,试求出k的值;若不存在,请说明理由.2015-2016学年湖北省荆州市洪湖一中高二(上)期中数学试卷(文科)参考答案与试题解析一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)直线的倾角为()A.B.C. D.【解答】解:由3x+y+2=0,得直线斜率为﹣,设直线的倾斜角为α(0≤α<π),则tanα=﹣,∴α=.故选:C.2.(5分)已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是()A.﹣2 B.﹣4 C.﹣6 D.﹣8【解答】解:圆x2+y2+2x﹣2y+a=0 即(x+1)2+(y﹣1)2=2﹣a,故弦心距d==.再由弦长公式可得2﹣a=2+4,∴a=﹣4,故选:B.3.(5分)点(1,﹣2,3)关于x轴的对称点坐标为()A.(1,2,﹣3)B.(﹣1,﹣2,3) C.(﹣1,2,﹣3) D.(﹣1,2,3)【解答】解:点(1,﹣2,3)关于x轴的对称点坐标为(1,2,﹣3).故选:A.4.(5分)已知直线l1:ax+(a+2)y+1=0,l2:x+ay+2=0.若l1⊥l2,则实数a的值是()A.0 B.2或﹣1 C.0或﹣3 D.﹣3【解答】解:∵直线l1:ax+(a+2)y+1=0,l2:x+ay+2=0,且l1⊥l2,∴a+a(a+2)=0,解得a=0或a=﹣3故选:C.5.(5分)与直线x﹣y﹣4=0和圆x2+y2+2x﹣2y=0都相切的半径最小的圆的方程是()A.(x+1)2+(y+1)2=2 B.(x+1)2+(y+1)2=4 C.(x﹣1)2+(y+1)2=2 D.(x﹣1)2+(y+1)=4【解答】解:由题意圆x2+y2+2x﹣2y=0的圆心为(﹣1,1),半径为,∴过圆心(﹣1,1)与直线x﹣y﹣4=0垂直的直线方程为x+y=0,所求的圆的圆心在此直线上,排除A、B,∴圆心(﹣1,1)到直线x﹣y﹣4=0的距离为=3,则所求的圆的半径为,故选:C.6.(5分)执行如图所示的程序框图,输出的结果是()A.11 B.12 C.13 D.14【解答】解:框图首先给变量x,y,z赋值,x=0,y=1,z=2,判断2≤10成立,执行x=1,y=2,z=3;判断3≤10成立,执行x=2,y=3,z=5;判断5≤10成立,执行x=3,y=5,z=8;判断8≤10成立,执行x=5,y=8,z=13;判断13≤10不成立,跳出循环,输出z=13.故选:C.7.(5分)用秦九韶算法计算多项式f(x)=12+35x﹣8x2+79x3+6x4+5x5+3x6在x=﹣4时的值时,V 3的值为()A.﹣845 B.220 C.﹣57 D.34【解答】解:∵多项式f(x)=12+35x﹣8x2+79x3+6x4+5x5+3x6=(((((3x+5)x+6)x+79)x﹣8)x+35)x+12,当x=﹣4时,∴v0=3,v1=3×(﹣4)+5=﹣7,v2=﹣7×(﹣4)+6=34,v3=34×(﹣4)+79=﹣57.故选:C.8.(5分)如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是()A.x>60?,i=i+1 B.x<60?,i=i+1 C.x>60?,i=i﹣1 D.x<60?,i=i﹣1【解答】解:把大于60的数找出来,根据流程图可知当满足条件时输出x,故判断框中应填x>60,处理框用来计数的,则处理框应填i=i+1.故选:A.9.(5分)用“辗转相除法”求得360和504的最大公约数是()A.72 B.36 C.24 D.2520【解答】解:∵504÷360=1 (144)360÷144=2 (72)144÷72=2∴360和504的最大公约数是72故选:A.10.(5分)与⊙D:(x+1)2+(y﹣2)2=相切且在两坐标轴上的截距相等的直线的条数有()A.1 B.2 C.3 D.4【解答】解:作出⊙D:(x+1)2+(y﹣2)2=如图,由图可知,当直线过原点时,设直线方程为y=kx,即kx﹣y=0,由D(﹣1,2)到切线的距离等于圆的半径得:,解得k1=﹣1,k2=﹣7,此时切线方程有两条;当截距相等不为0时,设切线方程为x+y=a,即x+y﹣a=0,由,解得a=0或a=2.∴与⊙D:(x+1)2+(y﹣2)2=相切且在两坐标轴上的截距相等的直线的条数有3条.故选:C.11.(5分)若点P(x,y)为不等式组所表示区域内任一点,则x2+y2+1的最小值为()A.B.1 C.2 D.【解答】解:作出不等式组对应的平面区域,设z=x2+y2,则z的几何意义是区域内的点到原点的距离的平方,由图象知A到原点的距离最小,由得,即A(1,0),此时x2+y2+1取得最小值为12+02+1=1+1=2,故选:C.12.(5分)若要(x﹣1)2+(y+2)2=4上恰有两个点到直线2x+y+m=0的距离等于1,则m的一个可能值是()A.3 B.C.2 D.【解答】解:由圆的方程(x﹣1)2+(y+2)2=4,得到圆心A的坐标为(1,﹣2),圆的半径为2,设圆心A到直线2x+y+m=0的距离为d,据图形可知:当1<d<3时,圆上恰有两点到直线2x+y+m=0的距离等于1,由d=,代入得:1<<3,解得:<m<3,因为<3<3,所以m可能等于3.故选:A.二、填空题:本大题共4个小题,每小题5分,共20分,把答案填写在题中的横线上.13.(5分)某程序框图如图所示,该程序运行后输出的值是16.【解答】解:程序在运行过程中各变量的值如下表示:a b 是否继续循环循环前 1 1/第一圈 2 2 是第二圈 3 4 是第三圈 4 16 否则输出的结果为16故答案为:16.14.(5分)某程序的流程图如图所示,若使输出的结果不大于37,则输入的整数的最大值为5【解答】解:模拟执行程序,可得S=0,n=0若满足条件,n<i,经过第一次循环得到S=2,n=1,若满足条件,n<i,经过第二次循环得到S=5,n=2,若满足条件,n<i,经过第三次循环得到S=10,n=3,若满足条件,n<i,经过第四次循环得到S=19,n=4,若满足条件,n<i,经过第五次循环得到S=36,n=5,若满足条件,n<i,经过第六次循环得到S=69,n=6,∵输出的结果不大于37,∴n的最大值为4,∴i的最大值为5.故答案为:5.15.(5分)已知直线l与圆O:x2+y2=1在第一象限内相切于点C,并且分别与x,y轴相交于A、B两点,则|AB|的最小值为2.【解答】解:设直线AB的方程为,即bx+ay﹣ab=0由题意,直线l与圆O相切于第一象限,∴又∵(a>0,b>0),∴|AB|=≥2∴a=b时,线段|AB|的最小值为2故答案为:2.16.(5分)已知点P(x,y)满足约束条件,且z=2x+4y的最小值为6.(1)常数k=﹣3;(2)的取值范围为[﹣,] .【解答】解:(1)作出不等式组对应的平面区域,由z=2x+4y,得y=,平移直线y=,由图象可知当直线经过点A时,直线y=的截距最小,此时z最小为6,由,得,即A(3,0),同时A也在直线x+y+k=0上,代入解得k=﹣3.(2)的几何意义为区域内的点到定点D(﹣7,2)的斜率,由图象知DC的斜率最大,DA的斜率最小,由得,即C(3,9)则DC的斜率k==,DA的斜率k==﹣,则的取值范围为[﹣,]故答案为:(1)﹣3;(2)[﹣,]三、解答题:本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(10分)已知点P是直线3x+4y+8=0上的动点,PA、PB是圆(x﹣1)2+(y ﹣1)2=1的两条切线,A、B为切点,C为圆心,求四边形PACB面积S的最小值.【解答】解:由题意(如图)可设PC=d,则由圆的知识和勾股定理可得PB=PA=,∴四边形PACB面积S=2××PA×BC=,当d取最小值时S取最小值,由点P在直线上运动可知当PC与直线垂直时d取最小值,此时d恰为点C到已知直线的距离,由点到直线的距离公式可得d==3,∴四边形PACB面积S的最小值为2.18.(12分)求适合下列各条件的直线的方程:(1)自点P(﹣3,3)发出的光线射到x轴上,被x轴反射,其反射光线与⊙C:(x﹣2)2+(y﹣2)2=1相切;(2)直线过定点P(5,10)且与原点的距离为5.【解答】解:(1)点P(﹣3,3)关于x轴的对称点P′(﹣3,﹣3),设反射光线所在直线方程为:y+3=k(x+3),即kx﹣y+3k﹣3=0.∵反射光线与⊙C:(x﹣2)2+(y﹣2)2=1相切,∴=1,解得k=或.∴反射光线所在的直线为:x﹣y+﹣3=0,或﹣3=0,化为:4x﹣3y+3=0,或3x﹣4y﹣3=0.(2)斜率不存在时,直线x=5满足条件.斜率存在时,设直线方程为:y﹣10=k(x﹣5),即kx﹣y+10﹣5k=0.由题意可得:=5,解得:k=.∴直线的方程为:x﹣y+10﹣5×=0,解得3x﹣4y+25=0.综上可得:所求的直线方程为:x=5或3x﹣4y+25=0.19.(12分)已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,(1)求点P的轨迹C的方程(2)过点A的直线与轨迹C有公共点,求的斜率k的取值范围.【解答】解:(1)设AM中点P(x,y),则M(2x﹣4,2y),代入圆的方程得(2x﹣4)2+4y2=4,即(x﹣2)2+y2=1.(2)设过点A的直线方程为y=k(x﹣4),即kx﹣y﹣4k=0,∵过点A的直线与轨迹C有公共点,∴圆心(2,0)到直线的距离d=≤1,∴﹣≤k≤.20.(12分)已知⊙C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0.(1)求证:对任意实数m,直线与⊙C总有两个不同的公共点;(2)求直线被⊙C截得的线段最短时直线的方程.【解答】(1)证明:∵直线l的方程为mx﹣y+1﹣m=0,∴m(x﹣1)﹣y+1=0,令x﹣1=0,﹣y+1=0,∴x=1,y=1,∴直线l恒过定点A(1,1),∴12+(1﹣1)2=1<5,∴定点A(1,1)在圆内,∴直线l与圆C相交;(2)解:直线被⊙C截得的线段最短时,CA⊥l,∵k CA=0,∴直线l的方程为x=1.21.(12分)据报我国正分别在大连和上海建造两航母,而建造航母必需特种钢.为建造航母的需要,要将两种不同的特种钢板截成A、B、C三种规格,每张钢板可同时截成三种规格的小钢板的块数如下表所示:今需要A 、B 、C 三种规格的成品分别15、18、27块.问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少?【解答】解:设需要第一种钢板x 张,第二种钢板y 张,钢板总数z 张,则目标函数 z=x +y作出可行域如图所示,作出直线x +y=0.作出一组平行直线x +y=t (其中t 为参数). 其中经过可行域内的点且和原点距离最近的直线, 经过直线 x +3y=27和直线 2x +y=15的交点,直线方程为.由于和都不是整数,而最优解(x ,y )中,x ,y 必须都是整数,所以,可行域内点不是最优解.经过可行域内的整点(横坐标和纵坐标都是整数的点),且与原点距离最近的直线是x +y=12.经过的整点是B (3,9)和C (4,8),它们是最优解.故要截得所需三种规格的钢板,且使所截两种钢板的张数最少的方法有两种,第一种截法是截第一种钢板3张、第二种钢板9张;第二种截法是截第一种钢板4张、第二种钢板8张.两种方法都最少要截两种钢板共12张.22.(12分)已知⊙C:(x﹣6)2+y2=4,直线过点P(0,2)且斜率为k.(1)若直线与⊙C有公共点,求k的取值范围;(2)若直线与⊙C交于不同两点A、B,是否存在常数k,使以AB为直径的圆过⊙C的圆心C?若存在,试求出k的值;若不存在,请说明理由.【解答】解:(1)直线的方程为:y=kx+2,由题意可得:≤2,解得.(2)设A(x1,y1),B(x2,y2).假设存在常数k,使以AB为直径的圆过⊙C的圆心C,则=(x1﹣6)(x2﹣6)+y1y2=(x1﹣6)(x2﹣6)+(kx1+2)(kx2+2)=(k2+1)x1x2+(2k﹣6)(x1+x2)+40=0.联立,化为:(1+k2)x2+(4k﹣12)x+36=0.∴x1+x2=,x1x2=,∴(k2+1)×+(2k﹣6)+40=0.化为8k2+12k+1=0.解得k=.∵,∴k=.存在常数k=,使以AB为直径的圆过⊙C的圆心C.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2016学年湖北省荆州市洪湖一中高二(上)期中数学试卷(文科)一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)直线的倾角为()A.B.C. D.2.(5分)已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是()A.﹣2 B.﹣4 C.﹣6 D.﹣83.(5分)点(1,﹣2,3)关于x轴的对称点坐标为()A.(1,2,﹣3)B.(﹣1,﹣2,3) C.(﹣1,2,﹣3) D.(﹣1,2,3)4.(5分)已知直线l1:ax+(a+2)y+1=0,l2:x+ay+2=0.若l1⊥l2,则实数a的值是()A.0 B.2或﹣1 C.0或﹣3 D.﹣35.(5分)与直线x﹣y﹣4=0和圆x2+y2+2x﹣2y=0都相切的半径最小的圆的方程是()A.(x+1)2+(y+1)2=2 B.(x+1)2+(y+1)2=4 C.(x﹣1)2+(y+1)2=2 D.(x﹣1)2+(y+1)=46.(5分)执行如图所示的程序框图,输出的结果是()A.11 B.12 C.13 D.147.(5分)用秦九韶算法计算多项式f(x)=12+35x﹣8x2+79x3+6x4+5x5+3x6在x=﹣4时的值时,V3的值为()A.﹣845 B.220 C.﹣57 D.348.(5分)如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是()A.x>60?,i=i+1 B.x<60?,i=i+1 C.x>60?,i=i﹣1 D.x<60?,i=i﹣1 9.(5分)用“辗转相除法”求得360和504的最大公约数是()A.72 B.36 C.24 D.252010.(5分)与⊙D:(x+1)2+(y﹣2)2=相切且在两坐标轴上的截距相等的直线的条数有()A.1 B.2 C.3 D.411.(5分)若点P(x,y)为不等式组所表示区域内任一点,则x2+y2+1的最小值为()A.B.1 C.2 D.12.(5分)若要(x﹣1)2+(y+2)2=4上恰有两个点到直线2x+y+m=0的距离等于1,则m的一个可能值是()A.3 B.C.2 D.二、填空题:本大题共4个小题,每小题5分,共20分,把答案填写在题中的横线上.13.(5分)某程序框图如图所示,该程序运行后输出的值是.14.(5分)某程序的流程图如图所示,若使输出的结果不大于37,则输入的整数的最大值为15.(5分)已知直线l与圆O:x2+y2=1在第一象限内相切于点C,并且分别与x,y轴相交于A、B两点,则|AB|的最小值为.16.(5分)已知点P(x,y)满足约束条件,且z=2x+4y的最小值为6.(1)常数k=;(2)的取值范围为.三、解答题:本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(10分)已知点P是直线3x+4y+8=0上的动点,PA、PB是圆(x﹣1)2+(y ﹣1)2=1的两条切线,A、B为切点,C为圆心,求四边形PACB面积S的最小值.18.(12分)求适合下列各条件的直线的方程:(1)自点P(﹣3,3)发出的光线射到x轴上,被x轴反射,其反射光线与⊙C:(x﹣2)2+(y﹣2)2=1相切;(2)直线过定点P(5,10)且与原点的距离为5.19.(12分)已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,(1)求点P的轨迹C的方程(2)过点A的直线与轨迹C有公共点,求的斜率k的取值范围.20.(12分)已知⊙C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0.(1)求证:对任意实数m,直线与⊙C总有两个不同的公共点;(2)求直线被⊙C截得的线段最短时直线的方程.21.(12分)据报我国正分别在大连和上海建造两航母,而建造航母必需特种钢.为建造航母的需要,要将两种不同的特种钢板截成A、B、C三种规格,每张钢板可同时截成三种规格的小钢板的块数如下表所示:A规格B规格C规格规格类型钢板类型第一种钢板211第二种钢板123今需要A、B、C三种规格的成品分别15、18、27块.问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少?22.(12分)已知⊙C:(x﹣6)2+y2=4,直线过点P(0,2)且斜率为k.(1)若直线与⊙C有公共点,求k的取值范围;(2)若直线与⊙C交于不同两点A、B,是否存在常数k,使以AB为直径的圆过⊙C的圆心C?若存在,试求出k的值;若不存在,请说明理由.2015-2016学年湖北省荆州市洪湖一中高二(上)期中数学试卷(文科)参考答案与试题解析一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)直线的倾角为()A.B.C. D.【解答】解:由3x+y+2=0,得直线斜率为﹣,设直线的倾斜角为α(0≤α<π),则tanα=﹣,∴α=.故选:C.2.(5分)已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是()A.﹣2 B.﹣4 C.﹣6 D.﹣8【解答】解:圆x2+y2+2x﹣2y+a=0 即(x+1)2+(y﹣1)2=2﹣a,故弦心距d==.再由弦长公式可得2﹣a=2+4,∴a=﹣4,故选:B.3.(5分)点(1,﹣2,3)关于x轴的对称点坐标为()A.(1,2,﹣3)B.(﹣1,﹣2,3) C.(﹣1,2,﹣3) D.(﹣1,2,3)【解答】解:点(1,﹣2,3)关于x轴的对称点坐标为(1,2,﹣3).故选:A.4.(5分)已知直线l1:ax+(a+2)y+1=0,l2:x+ay+2=0.若l1⊥l2,则实数a的值是()A.0 B.2或﹣1 C.0或﹣3 D.﹣3【解答】解:∵直线l1:ax+(a+2)y+1=0,l2:x+ay+2=0,且l1⊥l2,∴a+a(a+2)=0,解得a=0或a=﹣3故选:C.5.(5分)与直线x﹣y﹣4=0和圆x2+y2+2x﹣2y=0都相切的半径最小的圆的方程是()A.(x+1)2+(y+1)2=2 B.(x+1)2+(y+1)2=4 C.(x﹣1)2+(y+1)2=2 D.(x﹣1)2+(y+1)=4【解答】解:由题意圆x2+y2+2x﹣2y=0的圆心为(﹣1,1),半径为,∴过圆心(﹣1,1)与直线x﹣y﹣4=0垂直的直线方程为x+y=0,所求的圆的圆心在此直线上,排除A、B,∴圆心(﹣1,1)到直线x﹣y﹣4=0的距离为=3,则所求的圆的半径为,故选:C.6.(5分)执行如图所示的程序框图,输出的结果是()A.11 B.12 C.13 D.14【解答】解:框图首先给变量x,y,z赋值,x=0,y=1,z=2,判断2≤10成立,执行x=1,y=2,z=3;判断3≤10成立,执行x=2,y=3,z=5;判断5≤10成立,执行x=3,y=5,z=8;判断8≤10成立,执行x=5,y=8,z=13;判断13≤10不成立,跳出循环,输出z=13.故选:C.7.(5分)用秦九韶算法计算多项式f(x)=12+35x﹣8x2+79x3+6x4+5x5+3x6在x=﹣4时的值时,V3的值为()A.﹣845 B.220 C.﹣57 D.34【解答】解:∵多项式f(x)=12+35x﹣8x2+79x3+6x4+5x5+3x6=(((((3x+5)x+6)x+79)x﹣8)x+35)x+12,当x=﹣4时,∴v0=3,v1=3×(﹣4)+5=﹣7,v2=﹣7×(﹣4)+6=34,v3=34×(﹣4)+79=﹣57.故选:C.8.(5分)如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是()A.x>60?,i=i+1 B.x<60?,i=i+1 C.x>60?,i=i﹣1 D.x<60?,i=i﹣1【解答】解:把大于60的数找出来,根据流程图可知当满足条件时输出x,故判断框中应填x>60,处理框用来计数的,则处理框应填i=i+1.故选:A.9.(5分)用“辗转相除法”求得360和504的最大公约数是()A.72 B.36 C.24 D.2520【解答】解:∵504÷360=1 (144)360÷144=2 (72)144÷72=2∴360和504的最大公约数是72故选:A.10.(5分)与⊙D:(x+1)2+(y﹣2)2=相切且在两坐标轴上的截距相等的直线的条数有()A.1 B.2 C.3 D.4【解答】解:作出⊙D:(x+1)2+(y﹣2)2=如图,由图可知,当直线过原点时,设直线方程为y=kx,即kx﹣y=0,由D(﹣1,2)到切线的距离等于圆的半径得:,解得k1=﹣1,k2=﹣7,此时切线方程有两条;当截距相等不为0时,设切线方程为x+y=a,即x+y﹣a=0,由,解得a=0或a=2.∴与⊙D:(x+1)2+(y﹣2)2=相切且在两坐标轴上的截距相等的直线的条数有3条.故选:C.11.(5分)若点P(x,y)为不等式组所表示区域内任一点,则x2+y2+1的最小值为()A.B.1 C.2 D.【解答】解:作出不等式组对应的平面区域,设z=x2+y2,则z的几何意义是区域内的点到原点的距离的平方,由图象知A到原点的距离最小,由得,即A(1,0),此时x2+y2+1取得最小值为12+02+1=1+1=2,故选:C.12.(5分)若要(x﹣1)2+(y+2)2=4上恰有两个点到直线2x+y+m=0的距离等于1,则m的一个可能值是()A.3 B.C.2 D.【解答】解:由圆的方程(x﹣1)2+(y+2)2=4,得到圆心A的坐标为(1,﹣2),圆的半径为2,设圆心A到直线2x+y+m=0的距离为d,据图形可知:当1<d<3时,圆上恰有两点到直线2x+y+m=0的距离等于1,由d=,代入得:1<<3,解得:<m<3,因为<3<3,所以m可能等于3.故选:A.二、填空题:本大题共4个小题,每小题5分,共20分,把答案填写在题中的横线上.13.(5分)某程序框图如图所示,该程序运行后输出的值是16.【解答】解:程序在运行过程中各变量的值如下表示:a b 是否继续循环循环前 1 1/第一圈 2 2 是第二圈 3 4 是第三圈 4 16 否则输出的结果为16故答案为:16.14.(5分)某程序的流程图如图所示,若使输出的结果不大于37,则输入的整数的最大值为5【解答】解:模拟执行程序,可得S=0,n=0若满足条件,n<i,经过第一次循环得到S=2,n=1,若满足条件,n<i,经过第二次循环得到S=5,n=2,若满足条件,n<i,经过第三次循环得到S=10,n=3,若满足条件,n<i,经过第四次循环得到S=19,n=4,若满足条件,n<i,经过第五次循环得到S=36,n=5,若满足条件,n<i,经过第六次循环得到S=69,n=6,∵输出的结果不大于37,∴n的最大值为4,∴i的最大值为5.故答案为:5.15.(5分)已知直线l与圆O:x2+y2=1在第一象限内相切于点C,并且分别与x,y轴相交于A、B两点,则|AB|的最小值为2.【解答】解:设直线AB的方程为,即bx+ay﹣ab=0由题意,直线l与圆O相切于第一象限,∴又∵(a>0,b>0),∴|AB|=≥2∴a=b时,线段|AB|的最小值为2故答案为:2.16.(5分)已知点P(x,y)满足约束条件,且z=2x+4y的最小值为6.(1)常数k=﹣3;(2)的取值范围为[﹣,] .【解答】解:(1)作出不等式组对应的平面区域,由z=2x+4y,得y=,平移直线y=,由图象可知当直线经过点A时,直线y=的截距最小,此时z最小为6,由,得,即A(3,0),同时A也在直线x+y+k=0上,代入解得k=﹣3.(2)的几何意义为区域内的点到定点D(﹣7,2)的斜率,由图象知DC的斜率最大,DA的斜率最小,由得,即C(3,9)则DC的斜率k==,DA的斜率k==﹣,则的取值范围为[﹣,]故答案为:(1)﹣3;(2)[﹣,]三、解答题:本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(10分)已知点P是直线3x+4y+8=0上的动点,PA、PB是圆(x﹣1)2+(y ﹣1)2=1的两条切线,A、B为切点,C为圆心,求四边形PACB面积S的最小值.【解答】解:由题意(如图)可设PC=d,则由圆的知识和勾股定理可得PB=PA=,∴四边形PACB面积S=2××PA×BC=,当d取最小值时S取最小值,由点P在直线上运动可知当PC与直线垂直时d取最小值,此时d恰为点C到已知直线的距离,由点到直线的距离公式可得d==3,∴四边形PACB面积S的最小值为2.18.(12分)求适合下列各条件的直线的方程:(1)自点P(﹣3,3)发出的光线射到x轴上,被x轴反射,其反射光线与⊙C:(x﹣2)2+(y﹣2)2=1相切;(2)直线过定点P(5,10)且与原点的距离为5.【解答】解:(1)点P(﹣3,3)关于x轴的对称点P′(﹣3,﹣3),设反射光线所在直线方程为:y+3=k(x+3),即kx﹣y+3k﹣3=0.∵反射光线与⊙C:(x﹣2)2+(y﹣2)2=1相切,∴=1,解得k=或.∴反射光线所在的直线为:x﹣y+﹣3=0,或﹣3=0,化为:4x﹣3y+3=0,或3x﹣4y﹣3=0.(2)斜率不存在时,直线x=5满足条件.斜率存在时,设直线方程为:y﹣10=k(x﹣5),即kx﹣y+10﹣5k=0.由题意可得:=5,解得:k=.∴直线的方程为:x﹣y+10﹣5×=0,解得3x﹣4y+25=0.综上可得:所求的直线方程为:x=5或3x﹣4y+25=0.19.(12分)已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,(1)求点P的轨迹C的方程(2)过点A的直线与轨迹C有公共点,求的斜率k的取值范围.【解答】解:(1)设AM中点P(x,y),则M(2x﹣4,2y),代入圆的方程得(2x﹣4)2+4y2=4,即(x﹣2)2+y2=1.(2)设过点A的直线方程为y=k(x﹣4),即kx﹣y﹣4k=0,∵过点A的直线与轨迹C有公共点,∴圆心(2,0)到直线的距离d=≤1,∴﹣≤k≤.20.(12分)已知⊙C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0.(1)求证:对任意实数m,直线与⊙C总有两个不同的公共点;(2)求直线被⊙C截得的线段最短时直线的方程.【解答】(1)证明:∵直线l的方程为mx﹣y+1﹣m=0,∴m(x﹣1)﹣y+1=0,令x﹣1=0,﹣y+1=0,∴x=1,y=1,∴直线l恒过定点A(1,1),∴12+(1﹣1)2=1<5,∴定点A(1,1)在圆内,∴直线l与圆C相交;(2)解:直线被⊙C截得的线段最短时,CA⊥l,∵k CA=0,∴直线l的方程为x=1.21.(12分)据报我国正分别在大连和上海建造两航母,而建造航母必需特种钢.为建造航母的需要,要将两种不同的特种钢板截成A、B、C三种规格,每张钢板可同时截成三种规格的小钢板的块数如下表所示:规格类型钢板类型A规格B规格C规格第一种钢板211第二种钢板123今需要A、B、C三种规格的成品分别15、18、27块.问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少?【解答】解:设需要第一种钢板x张,第二种钢板y张,钢板总数z张,则目标函数z=x+y作出可行域如图所示,作出直线x+y=0.作出一组平行直线x+y=t(其中t为参数).其中经过可行域内的点且和原点距离最近的直线,经过直线x+3y=27和直线2x+y=15的交点,直线方程为.由于和都不是整数,而最优解(x,y)中,x,y必须都是整数,所以,可行域内点不是最优解.经过可行域内的整点(横坐标和纵坐标都是整数的点),且与原点距离最近的直线是x+y=12.经过的整点是B(3,9)和C(4,8),它们是最优解.故要截得所需三种规格的钢板,且使所截两种钢板的张数最少的方法有两种,第一种截法是截第一种钢板3张、第二种钢板9张;第二种截法是截第一种钢板4张、第二种钢板8张.两种方法都最少要截两种钢板共12张.22.(12分)已知⊙C:(x﹣6)2+y2=4,直线过点P(0,2)且斜率为k.(1)若直线与⊙C有公共点,求k的取值范围;(2)若直线与⊙C交于不同两点A、B,是否存在常数k,使以AB为直径的圆过⊙C的圆心C?若存在,试求出k的值;若不存在,请说明理由.【解答】解:(1)直线的方程为:y=kx+2,由题意可得:≤2,解得.(2)设A(x1,y1),B(x2,y2).假设存在常数k,使以AB为直径的圆过⊙C的圆心C,则=(x1﹣6)(x2﹣6)+y1y2=(x1﹣6)(x2﹣6)+(kx1+2)(kx2+2)=(k2+1)x1x2+(2k﹣6)(x1+x2)+40=0.联立,化为:(1+k2)x2+(4k﹣12)x+36=0.∴x1+x2=,x1x2=,∴(k2+1)×+(2k﹣6)+40=0.化为8k2+12k+1=0.解得k=.∵,∴k=.存在常数k=,使以AB为直径的圆过⊙C的圆心C.第21页(共21页)。
