电路基础第4章
电路与电子技术基础第4章习题参考答案

τ=
L 1 = R0 7
(s)
利用三要素公式,可得
i (t ) = 4 + (0 − 4)e −7t = 4(1 − e −7 t ) ( A)
4-4 电路如题图 4-3(a)所示,i(t)=10mA、R=10kΩ、L=1mH。开关接在 a 端为时已久, 在 t=0 时开关由 a 端投向 b 端,求 t≥0 时,u(t)、iR(t)和 iL(t),并绘出波形图。
《电路与电子技术基础》第四章参考答案
第6页
u c (t ) = U oc (1 − e τ )(V)
根据已知条件,得:Uoc=20V,τ=2s。因为τ=R0C,所以 R0=2/0.2=10Ω 当电容 C=0.05F 时,时间常数τ=10×0.05=0.5s。电容电压初始值为 uc(0+)=5V,稳态值 为 uc(∞)=20V,由三要素公式,可以得到全响应
u c (0 _ ) = 1 × 2 = 2(V)
开关闭合后
u c (0 + ) = u c (0 _ ) = 2(V)
τ = R0 C = (2 // 1) × 3 = 2(s)
u c (∞) = 1 × (1 // 2) =
所以
2 (V) 3
− t
u c (t ) = u c (∞) + (u c (0) − u c (∞))e 2 2 + (2 − )e −0.5t 3 3 2 − 0.5t − 0.5t = 2 e2 ) 1 3 + 3 (1 − e 14243 零输入响应 =
uc (0) = 3 × 2 = 6(V)
当开关投向 b 时电容电压的初始值
uc (0 + ) = uc (0 − ) = 6(V)
电工基础 第4章正弦交流电

u = U m sin(ωt + u )
i = I m sin(ωt + i )
4.1.2正弦交流电的基本特征和三要素 . . 正弦交流电的基本特征和三要素
两个同频率正弦量的相位角之 差或初相位角之差,称为相位 相位 差,用 表示。 图4.3中电压u和电流i的相位差 为
= (ωt + u ) (ωt + i ) = u i
第4章 正弦交流电路 章
4.1交流电路中的基本物理量 . 交流电路中的基本物理量 4.2正弦量的相量表示 4.3电路基本定律的相量形式 4.4 电阻、电感、电容电路 4.5 谐振电路 . 4.6正弦交流电路中的功率 . 正弦交流电路中的功率
第4章 正弦交流电路 章
4.1交流电路中的基本物理量 . 交流电路中的基本物理量
U m = 220 2V = 311.1V
U= U m 220 2 = V = 220V 2 2
4.1.2正弦交流电的基本特征和三要素 . . 正弦交流电的基本特征和三要素
2.频率与周期 . 正弦量变化一次所需的时间(秒)称为周期T,如图4.2所示。每秒内变化 的次数称为频率f,它的单位是赫兹(Hz)。 频率是周期的倒数,即
电路与电子技术基础第四章习题答案
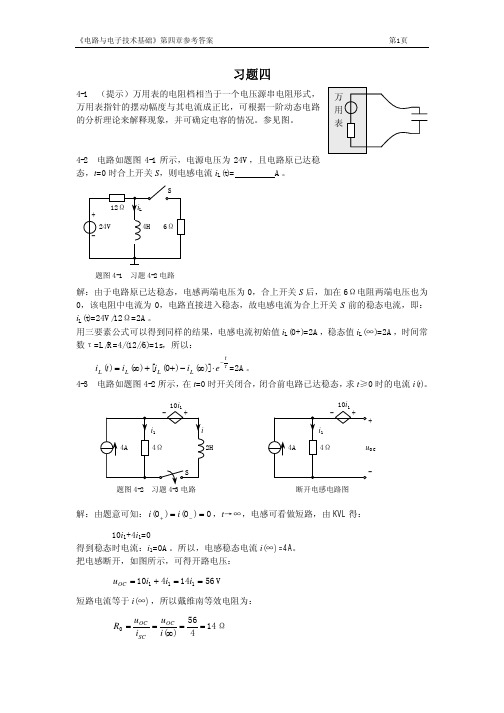
解:本题是求零输入响应,即在开关处于 a 时,主要是电感储能,当开关投向 b 后, 讨论由电感的储能所引起的响应。所以对图(a)t≥0 时的电路可列出 di L L + Ri L = 0 t≥0 dt 及 iL(0)=i(t)=10(mA) 其解为: i L (t ) = 10e
而
t≥0
i R (t ) = −i L (t ) = −10e −10 t (mA)
7
t≥0
其波形图见图(b)、图(c)所示。 4-5 电路如题图 4-4 所示,开关接在 a 端为时已久,在 t=0 时开关投向 b 端,求 3Ω电 1Ω a b 阻中的电流。 i (t ) 解:因为 u c (0) = 3 × 2 = 6(V ) (注意:当稳态以后电容为开路,所以流过 1 3A Ω和电容串联支路的电流为零, 因此电容两端的电 压就是并联支路 2Ω支路两端的电压) 当开关投向 b 时电流的初始值为
S 12Ω + 24V iL 4H 6Ω
题图 4-1
习题 4-2 电路
解:由于电路原已达稳态,电感两端电压为 0,合上开关 S 后,加在 6Ω电阻两端电压也为 0,该电阻中电流为 0,电路直接进入稳态,故电感电流为合上开关 S 前的稳态电流,即: iL(t)=24V/12Ω=2A。 用三要素公式可以得到同样的结果,电感电流初始值 iL(0+)=2A,稳态值 iL(∞)=2A,时间常 数τ=L/R=4/(12//6)=1s,所以:
当 t=0 时,开关打开,由于电感电流、电容电压均不跃变,有: i L (0 + ) = i L (0 − ) = 0.03( A) 1k u c (0 + ) = u c (0 − ) = 120(V ) 当 t≥0 时,根据基尔霍夫定律有
(完整版)数字电路基础-阎石第五版-第4章

用与或非门实现
AG R 00 01 11 10
01 0 1 0
Z (RAG RAG RAG)
10 1 1 1
4.3 若干常用的组合逻辑电路
§4.3.1 编码器
编码:用二进制代码来表示某一信息(文 字、数字、符号)的过程。
实现编码操作的电路称为编码器。
编
高?低?
码 器
码?
一、二进制编码器 输入端:2n
(A B)CI
AB
S A B CI CO (A B)CI AB
S A B CI CO (A B)CI AB
这是一个全 加器电路
§4.2.2 组合逻辑电路的设计方法
根据实际逻辑问题
步骤:
确定输入、输出 列出真值表
最简单逻辑电路
设计
选择所需
门电路
写出表达式
并简化
画逻辑电路图
根据设
计要求
分析题意,将设计 要求转化为逻辑关
形式变换
系,这一步为设计
组合逻辑电路的根关据键设计所用
芯片要求
例1:设计三人表决电路(A、B、C)。每人 一个按键,如果同意则按下,不同意则不按。 结果用指示灯表示,多数同意时指示灯亮, 否则不亮。用与非门实现.
解:
1.首先指明逻辑符号取“0”、“1”的含义。三 个按键A、B、C按下时为“1”,不按时为“0”。 输出量为 L,多数赞成时是“1”,否则是“0”。
(( DC A) (DCB) (DCB))
解: Y2 ((DBA)(DC)) DBA DC
Y1 ((DCA)(DCB)(DCB)) DCA DCB DCB
Y0 ((DB)(DC)) DB DC
由真值表知:该电路可用来判别输入的4位二 进制数数值的范围。
《电路分析基础》_第4章

RO
+
– B
40 RO 8 // 10 4.44 9
A
10 280 uoc 10 ( 20 10) 15.6V 10 8 18
此例从一个侧面证明了戴维南定 理的正确性。也反映了其简便性。
RO
4.44
15.6V B
uoc
+
–
戴维南定理也可以在单口外加电流源i ,用叠加定理计算端 口电压表达式的方法证明。
—
i NS
+ –
a
+
RO
u
b 含源单口网络的VCR表达式:
uoc
–
b
u =K1+K2i = uoc+ Roi
其中:
uoc等于该网络NS的端口开路电压;
a + u
—
i RO
+ –
i
NS
a
+
端口开路时: i =0 u = uoc
u
uoc
–
b
b
RO等于该网络中所有独立源置零时所得网络NR 的等效电阻Rab。 独立源置零
I
+ +
I
º +
5V _
5V _
º
5V _
与电压源并联的元件称为多余元件,多余元件的存在与否并 不影响端口电压的大小,端口电压总等于电压源电压。
us
is
提示:多余元件的存在会使电压源的电流有所改变,但电压源 的电流可为任意值。
总结:一个理想电压源与任何一条支路并联后,对外 等效为理想电压源。 i
(3)外加电压源,求入端电流:
网孔法列方程
( R1+R2 )I + R1IS = - US - U
电气基础知识:第四章 线性电路基本定理

i 52 2.6A 12 8
+
- UocRo
16
例4:图示电路,用戴维南定理求电流I。
+ Uoc -
解:移去待求支路求:Uoc 40V
Ro
除去独立电源求: Ro =7
I 40 10 A 75 3
画出戴维南等效电路,并接入待求支路求响应。 17
3、含受控源电路分析
例5:图示电路,用戴维南定理求电流I2。
Us
I0
Us R1
Is
R0
R1R2 R1 R2
R1 R2
Is Isc
Ro Io
Uo
Ro
Us R1
U0
Io Ro
(U s
/ R1 ( R1
I s )R1R2 R2 )
(Ro :除源输入电阻)
+
R1
Uoc
-
(Io : 短路电流Isc )
(Uo : 开路电压Uoc )
10
二、定理:
1、线性含源单口网络对外电路作用可等效为一
30
三、定理应用: 例1:求图示电路中电流I。
I
I4
I0
解:I0 =1A I4 = -0.25A
I1
I3
I2
I1 =0.5A
I2 =0.5A
I= -Io -I4 = -0.75A
31
例2:已知条件如图所示,求图(b)的电压源电压us。
4A
us
(a)
10A ++
U2o0cV --
4A
us
(b)
Ro = 2 Uoc = 20V us = 100V
Ro
u i
=6
画出等效电路,有 R=Ro =6
电路理论基础第四章习题解答西安电子科技大学出版社
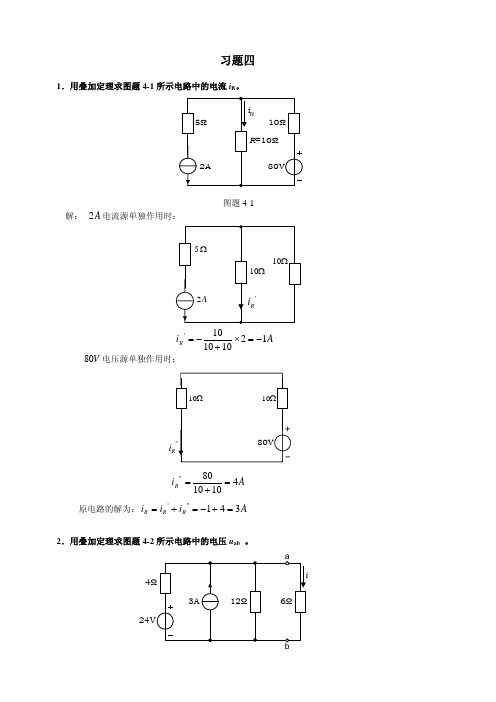
习题四1.用叠加定理求图题4-1所示电路中的电流i R 。
图题4-1解: A 2电流源单独作用时:A i R 12101010'−=×+−=V 80电压源单独作用时:i A i R 4101080''=+=原电路的解为:A i i i R R R 341'''=+−=+=2.用叠加定理求图题4-2所示电路中的电压u ab 。
4图题4-2解:V 24电压源单独作用时:Ω6Ω=+×==46126126//121RV R R u ab 1224411'=×+=A 3电流源单独作用时:Ω4Ω6''A i 13623611214161''=×=×++=V i u ab 6616''''=×=×= 原电路的解为:V u u u ab ab ab 18612'''=+=+=3.用叠加定理求图题4-3所示电路中的电流i 。
6A图题4-3解: A 6电流源单独作用时:ΩΩ6A i 4612612'−=×+−= V 36电压源单独作用时:Ω6Ω6ΩΩA i 261236''−=+−=原电路的解为:()()A i i i 624'''−=−+−=+=4.图题4-4所示电路中,R =6Ω,求R 消耗的功率。
图题4-4解: 将R 支路以外的部分看作一个二端电路。
可采用叠加原理求oc u :12⎟⎠⎞⎜⎝⎛++××+×+=26363212636oc u V 1688=+=求其等效电阻:eqRΩ=++×=426363eq R 原电路简化为:Ri=eq R u oc =RA R R u i eq oc R 6.14616=+=+=W R i P R R 36.1566.122=×=×=5.图题4-5所示电路中, R 1=1.5Ω R 2=2Ω,求(a )从a、b 端看进去的等效电阻;(b )i 1与i s 的函数关系。
电路分析基础第四章4-4,5,6

例 例4-6-2 如图所示电路,试问当电阻 R 等于何值时?它可获
4 6
得最大功率, 最大功率等于多少。
2
i
2 2
2i 4 I
4i
U
解:
Uoc = 2i-2i+6 = 6V
R0
R R0 4Ω
Uoc
R
P
UOC 2
62
4R0 4 4
2.25W
4i 2I 8i 0
2i 6I 10i U
dP dRL
d dRL
(
uS2 RL RS RL
)
2
uS2
(
RS
RL )2 2RL (RS ( RS RL )4
RL
)
uS2 ( RS (RS
RL ) RL )3
0
RS RL 0, RL RS
最大功率传递定理的表述
若一个实际电源模型为一个可变负载电阻RL提供
能量。只有当负载电阻RL等于电源内电阻Rs时,负
Uoc' R 0 'R 3
R 3 rm R 0 'R 3
Uoc'
I sc
R
R3 3 (R
rm 0 'rm
)
U
oc
'
R0
Uoc I sc
R 3 (R 0 'rm ) R0 'R 3
I2
U2 Uoc R0 r0 R2
(R0'R3 )U2 (R 3 rm )Uoc' R3 (R0'rm ) (r0 R2 )(R 0'R3 )
I a 3I1 6I3 I1 2I3
I 6Ω
8 3
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章 正弦交流电路本章要点● 正弦交流电量的三要素。
● 两同频率正弦电量之间的相位关系。
● 正弦量的相量表示方法。
● 单一参数(R 、L 、C )电路及其组合电路分析。
● 串联谐振与并联谐振。
●功率因数的提高。
本章先介绍正弦交流电的基本特征和相量表示法,然后从单一参数电路出发,并以RLC 串联电路为典型电路,讨论交流电路中电压和电流之间的关系以及基尔霍夫定律的相量形式,从而得出分析交流电路的一般方法。
同时还讨论正弦交流电路中的功率和能量交换,最后介绍电路的谐振和功率因数的提高。
正弦交流电路的基本理论和基本分析方法是学习交流电机、电器及电子技术的重要基础,是本课程的重要内容之一。
4.1 正弦交流电的基本概念在前面的章节中我们所分析的电路都是直流电路,其特点是电流和电压的大小和方向都不随时间变化,是恒定的,如图4.1所示。
而在实际中应用最多的还是交流电,其特点是电流和电压大小和方向都随时间作周期变化,且在一个周期内,其平均值为零。
在交流电中,正弦交流电应用最广泛。
所谓正弦交流电就是大小随时间按正弦规律变化,其波形如图4.2所示。
正弦交流电流流过的电路称为正弦交流电路。
o u ,it图4.1 直流电 图4.2 正弦交流电的波形图otI ,U4.1.1 正弦交流电量的三要素在分析计算正弦交流电路时,我们首先要写出正弦交流电量的数学表达式,并画出它的波形图。
为此,必须像直流电路那样,预先设定交流电量的正方向。
如图4.3(a )所示的一段电路,通过正弦电流i ,其正方向用箭头标示在电路中。
当i 的实际方向与正方向一致时,是正值,对应波形图的正半周;反之,i 的实际方向与正方向相反时,是负值,对应波形图的负半周。
其正弦电流i 的波形图如图4.3(b )所示。
与该波形图相对应的正弦电流的数学表达式为:)sin(i t I i ϕω+=m (4-1)式(4-1)称为正弦电流的瞬时值表达式。
正弦电量在每一瞬间的数值,称为瞬时值。
规定用小写字母i ,u ,e 分别表示正弦电流、电压和电动势的瞬时值。
利用它们的瞬时值表达式可以计算出任一瞬时该正弦电量的数值。
此值的正负与规定的正方向比较,便可确定该瞬时电量的实际方向。
式(4-1)和图 4.3(b )表明:一个正弦电量的特征表现在它变化的最大值,又称振幅值(m I ),随时间变化的快慢(ω)和起始值(0=t 时的数值,它取决于0=t 时的角度i ϕ)三个方面。
描述这三个特征的物理量是最大值、角频率(频率)和初相角,这三个物理量通常又被称为正弦量的三要素。
1.最大值正弦电量瞬时值中的最大值称为最大值或振幅值,用带m 下标的大写字母来表示。
如m I 、m U 、m E 分别表示正弦电流、电压和电动势的最大值。
最大值表示了正弦量的变化幅度。
对于一个确定的正弦量,其最大值是一个常数。
2.周期、频率和角频率周期、频率和角频率这三个物理量都是用来表示正弦电量随时间变化的快慢的。
正弦量重复变化一周所需要的时间,称为周期,用大写字母T 表示,其单位是秒(s )。
单位时间(1秒)内正弦量变化的周期数,称为频率,用小写字母f 来表示,频率的单位图4.3 正弦电量的正方向和波形图t ωi(a )(b )Ti ϕo im I是赫兹(H Z )。
根据上述定义可知,频率与周期互为倒数,即: Tf 1=(4-2)(注:在我国,发电厂提供的正弦交流电能的频率是50=f H Z ,其周期02.0501==T 秒,这一频率称为工业标准频率,简称工频。
) 正弦量的变化快慢还可以用角频率ω来表示。
由于正弦量变化一周相当于变化了π2弧度。
角频率ω就是正弦电量在单位时间(1s )内变化的电角度,即:f Tπ2π2==ω (4-3)角频率的单位是弧度/秒(rad/s ),工频交流电量的角频率是rad/s π(rad/s)314100==ω。
在交流电的波形中(图4.4),其横坐标既可以用时间(秒)t 来表示,也可以用电角度t ω(弧度)来表示,一个周期时间T 与π2弧度相对应。
3.初相位正弦量在每一瞬时的状态是不同的,具体表现在每一瞬时的数值(包括正、负号)及变化趋势不同。
我们以图4.5所示的正弦电流i 为例,当1t t =时,对应波形图上的b 点,其瞬时值为b 点在纵坐标轴上的截距,变化趋势是由小变大,而正弦量在这一瞬时的状态则是由该瞬时对应的电角度(i t ϕω+1)所决定。
我们把正弦电量在任意瞬时的电角度(ϕω+t )称为相位角,简称为相位。
它反映了正弦量随时间变化的进程,决定了它在每一瞬时的状态。
当0=t 时,正弦电量的相位角i ϕ称为初相角,又称初相位。
正弦电量在任何瞬时的相位都与初相位有关。
iT2Tt ωπ3π2 π 0图4.4 正弦电量波形图时间轴的标注 图4.5 正弦电量的初相角i a1t ωoi ϕbt ωa '初相位i ϕ的大小和正负与选择0=t 这一计时起点有关,如在图4.4中,若选择a '点为计时起点,则初相角为i ϕ;若选择a 点为计时起点,则初相角为零。
在以上的讨论中我们都规定,正弦量瞬时值由负值向正值变化所经过的零值点为正弦量的零点,以正弦量零点到计时点之间的电角度为初相角。
由于正弦电量是周期性变化的,所以初相角一般都在绝对值小于π的主值范围内取值,即取π≤i ϕ。
现将初相角为零、为正和为负的波形图及瞬时值表达式分述如下:(1)如图 4.6(a )所示,正弦量的零点与计时起点重合,其初相角0=i ϕ,其瞬时值表达式为:t I i ωsin m =(2)如图4.6(b )所示,初相角为正,即0>i ϕ。
这时按时间增长的方向,计时起点选择在正弦量零点之后(即正弦量零点在原点左侧),其瞬时值表达式为:)sin(m i t I i ϕω+=(3)如图 4.6(c )所示,初相角为负值,即0<i ϕ。
此时,按时间增长的方向,计时起点选在正弦量零点之前(即正弦量零点在原点右侧),其瞬时值表达式为:)sin(m i t I i ϕω-=显然同一个正弦量,当选择不同的计时起点时,其初相角i ϕ就不同;0=t 时,该正弦电量的初始瞬时值也不同,可能是正值(0>ϕ时),也可能是负值(0<ϕ时),或者是零(0=ϕ时)。
且它们的瞬时值表达式也不相同。
ωii 0)(<i ϕc0)(>i ϕb0)(=i ϕao t ωiϕ o t ω t ω i ϕoi图4.6 正弦电量的初相角与计时起点的关系例4.1 正弦电压)60314sin(52.190︒+=t u V ,试求(1)最大值、角频率和初相角。
(2)该电压从计时起点开始需经过多长时间才第一次出现最大值。
解 (1)根据该正弦电压的瞬时值表达式可知:其最大值52.190m =U V ;角频率rad/s 314=ω;频率π2ω=f =50H Z ;初相角rad π360u u ==︒ϕϕ或。
(2)该正弦电压第一次出现最大值的时间应为︒=︒+9060)(t ω,即: 314t +60°=90°将度数化为弧度数,可得:314t =632πππ=-t=67.13146=πms4.1.2 两同频率正弦电量之间的相位关系在同一线性电路中,若电源都是同频率的正弦电量,则各支路电流、电压也都是同频率的正弦电量。
但是它们随时间变化的进程不同,为了描述同频率正弦电量随时间变化进程的先后,我们引出了相位差这一概念。
两个同频率正弦电量的相位之差称为相位差,且用字母ϕ来表示。
例如正弦电压)sin(u m ϕω+=t U u ,正弦电流)sin(m i t I i ϕω+=,则u 与i 的相位差:i i t t ϕϕϕωϕωϕ-=+-+=u u )()( (4-4)由此可见,两同频率正弦电量的相位差就是它们的初相位之差。
下面介绍两同频率正弦电量相位关系的几种情况:(1)有两个同频率的正弦电压1u 和2u ,它们的初相位分别是1ϕ和2ϕ。
当1ϕ=2ϕ时,它们之间的相位差021=-=ϕϕϕ,波形如图4.7(a )所示,这时1u 和2u 的变化进程一致,同增同减,同时达到正弦电量的零点和正、负最大值。
我们称1u 和2u 同相。
(2)当1ϕ>2ϕ时,相位差021>-=ϕϕϕ,波形如图4.7(b )所示。
从波形图可见,1u 总比2u 先经过零点和先达到最大值,即1u 的变化进程领先于2u ,称为1u 在相位上超前2u 一个相位角ϕ,或者说2u 滞后于1u 相位角ϕ。
(3)若1ϕ<2ϕ,则相位差021<-=ϕϕϕ,波形如图4.7(c )所示。
这时1u 滞后2u 一个相位角ϕ,也就是2u 超前于1u 一个相位角ϕ。
(4)当π±=-=21ϕϕϕ时,波形图如图4.7(d )所示,这时1u 与2u 的相位相反,称为反相。
通过上述讨论可知,当选择不同的计时起点时,正弦电量的初相角就不同。
但是两同频率正弦量之间的相位差则与计时起点无关。
注意:不同频率的正弦电量之间没有确定的相位差,也无法确定它们之间的超前与滞后关系。
因此,讨论它们之间的相位差没有意义。
例4.2 求两个正弦电流)120sin(1.141︒--=t i ωA ,)60cos(05.72︒-=t i ωA 的相位差12ϕ。
解 把电流写成标准的解析式,求出二者的初相,再求出相位差。
)60sin(1.14)180120sin(1.141︒+=︒+︒-=t t i ωω A )30sin(05.7)9060sin(05.72︒+=︒+︒-=t t i ωω A根据解析式和相位差的定义可得:︒=︒=306021ϕϕ,,12ϕ︒=30在正弦量的分析计算中,经常要比较同一电路中多个同频率正弦量之间的相位关系,为了方便起见,可以选取其中某一个正弦量作为参考,即令其初相角为零,我们把初相角为零的正弦量称为参考正弦量。
这样其它的正弦量的初相角应等于与参考正弦量图4.7 两同频率正弦量的相位关系u21<-=ϕϕϕ(c ) t ω2ϕu1ϕ o(b ) 021>-=ϕϕϕot ω2ϕ1ϕu(d )1u 、2u 反相t ωou(a )0=ϕ1ut ω21ϕϕ o之间的相位差(即初相差)。
各正弦量必须以同一时刻为计时的起点才能比较相位差,故一个电路中只能有一个参考正弦量,而选择哪一个则是任意的。
例 4.3 三个正弦电压t u 314sin 311A =V ,)3/314sin(311B π-=t u V ,)3/314sin(311C π+=t u V ,若以B u 为参考正弦量,写出三个正弦电压的解析式。
解 先求出A u 、C u 与B u 的相位差,由已知得:3)3(0AB ππ=--=ϕ 32)3(3CB πππ=--=ϕ以B u 为参考正弦量,它们的解析式为:t u 314sin 311B =V)3314sin(311A π+=t u V )32314sin(311C π+=t u V4.1.3 正弦量的有效值在实际应用中,用瞬时值或最大值来表示交流电量在电路中产生的效果既不确切,又不方便。
