余角和补角2
7下2.1余角与补角2

余角与补角
平度朝阳中学 郭晓燕
胶莱河大坝的底部是石块堆积而成,量角 器无法伸入大坝底部测量,如何测量大坝的倾 斜角?(∠1即为倾斜角) 胶莱河大坝
1
余
胶莱河大坝的底部是石块堆积而成,量角 器无法伸入大坝底部测量,如何测量大坝的倾 斜角?(∠1即为倾斜角) ∠1=180°- ∠2 胶莱河大坝
所以∠AOC =∠BOD D
借助三角板尽可能多的画出∠AOB的余角。
C E
A
1
∠AOC和∠BOD的大 小有什么关系?为 你发现了什么? 什么?
B
2 O
D
N
A B
∠1=∠2 ON⊥DE于O
1 2 3 D O 4 E
图中∠3与∠4有什么关系?为什么?
因为∠3是∠1的余角, ∠4也是∠1的余角, 所以∠3=∠4。 (同角的余角相等)
因为∠1 +∠3=90°,
所以∠1 与∠3互余。
胶莱河大坝
3
1
N A B
∠1=∠2 ON⊥DE于O
1 2 3 D O 4 E
在上图中,还有哪些角互为余角?
N
A B
1 2 3 D O 4 E
如果两个角的和是平角,那 么称这两个角互为补角。(互补)
胶莱河大坝的底部是石块堆积而成,量角 器无法伸入大坝底部测量,如何测量大坝的倾 斜角? (∠1即为倾斜角) ∠1=180°- ∠2
N
A B
∠1=∠2 ON⊥DE于O
1 2 3 D O 4 E
在上图中,各角与∠3有什么关系?
N
A B
∠1=∠2
ON⊥DE于O
如果两个角的和是直角,
1 2 那么称这两个角互为余角。(互余) 3 D O 4 E
余角和补角2

再 见
(2)互补、互余的两角是否一定有公共顶点或公共边? )互补、互余的两角是否一定有公共顶点或公共边?
(3)∠1 + ∠2 + ∠3 )
= 180°,能说∠1 、∠2、 ∠3 互补吗? 互补吗? ° 能说 ∠ 、
(4)所有的角都有余角,补角? 所有的角都有余角,补角? 所有的角都有余角
二、看谁答得快
∠α 30° ° 45° ° 62°23′ ° ∠α 的余角 60 ° 45 ° ∠α 的补角 150 ° 135 ° 117 ° 37 ′
∠3
相等的角 互补的角
∠2=∠4 , ∠
∠AOC=∠BOC=∠DOE=900 ∠ ∠
∠1=∠3 ∠
∠AOE
∠DOB
大显身手 已知∠1与∠2互余,∠2与∠3 互补, ∠3=155°,求∠1的度 数?
本节课有何收获? 本节课有何收获?
1余角补角概念及应用 余角补角概念及应用 如果两个角的和等于 和等于90° 直角 直角)就 如果两个角的和等于 ° (直角 就 互余” 说这两个角 “互余” 如果两个角的和等于 和等于180° (平角 , 平角), 如果两个角的和等于 ° 平角 互补” 就说这两个角 “互补” 2余角补角性质及应用 余角补角性质及应用 同 (等) 角的余角相等 同 (等) 角的补角相等
1
α
2
1
O
B D
α
2
β
(2)图中∠α的余角∠1,∠2的大小有什么关系? 为什么? 因 为 ∠ 1 = 9 0 ° - ∠ α ; ∠ 2 = 9 0 ° - ∠° α °
因 为 ∠1 = 9 0 -∠ α ; ∠ 2 = 9 0 -∠ β
所 以 ∠ 1 = ∠ 2 又因为∠α=∠β
4.3.3余角和补角 (第2课时)

教师:提出问题,引导、画图并举例 说明. 学生:根据已有知识思考、回答、认 识理解,学会画图,认识始边,终边. 总结:谁在前谁为始边, 后为终边, 如: 东偏南 60°,即东为始边,向南旋转 确定角的度数为 60°.不能弄错角.
尝 中,发现灯塔 A 在它南偏 东 60°的方向上。同时,在它北偏东 40°、南偏 西 10°、西北方向上又分别发现了客轮 B、货轮 C 和海岛 D。仿照表示灯塔方位的方法,画出表示客 轮 B 、货轮 C 和海岛 D 方向的射线. 解:
自 主 探 究
【问题1】 如图: ∠1 与∠2 互补, ∠3 与∠4 互补 , 教师:提出问题, 如果∠1=∠3,那么∠2 与∠4 相等吗?为什么? 学生:尝试分析,怎样说明、验证∠2 与∠4 的关系?组内讨论、分析. 师:根据学生阐述情况,引导学生证 明得出结论. 2 1 说明:验证方法是多样的,注意倾听 分析:怎么验证∠2 与∠4 相等?测量、叠合、理 学生的方法,评判、鼓励. 论验证. ( 组织学生讨论解决。 ) 结论:补角性质:等角(或同角)的补角相等 【问题 2】 如图: ∠1 与∠2 互余, ∠3 与∠4 互余 ,
认识角的互余、互补关系及其性质,确定方位 1.通过简单的推理,归纳出余角、补角的性质,并能用规范的语言描述性质. 2.方位角的实际应用.
【教学环节安排】
环 节 情 境 引 入 教 学 问 题 设 计 教学活动设计
教师提出问题,学生回顾回答.为本 节课的学习做准备.
【问题】 什么是互余的角?什么是互补的角?两 角互补,两角互余与位置有关吗?
教师:出示例 4,引导学生分析,板 演出所求方位角并标明. 学生:理解,认识,尝试画出. 师:出示题目,鼓励学生分析,写出 过程.
解:
展 示 作 业 设 计
数学补角和余角的概念

数学补角和余角的概念
数学中的角是描述两条射线或线段之间的旋转的概念。
当两条射线或
线段相交时,形成了一个角,可以用度数或弧度来度量。
本文将重点
介绍数学中的补角和余角的概念。
一、补角的概念
所谓补角,是指两个角的和等于90度的角。
比如,如果两个角的度数
分别是40度和50度,那么它们的补角就是由这两个角组成的角,其
度数为90度减去40度再减去50度,即为90度减去90度等于0度。
因此,两个角40度和50度的补角是0度。
二、余角的概念
余角是指两个角的和等于180度的角。
举个例子,如果某个角的度数
为60度,那么它的余角就是钝角120度;如果某个角的度数为30度,则其余角为150度。
三、其他注意事项
1. 补角和余角是角度的概念。
当我们用弧度来度量角的时候,其对应
的概念分别是补角和余角的弧度。
2. 补角和余角是互补的,即它们的和等于180度。
因此,在计算某个
角的补角或余角时,我们只需要用90度或180度减去该角度即可。
3. 在解题时,补角和余角的概念非常常用,特别是在数学中的三角函
数中,例如正弦、余弦和正切等函数的定义和计算中,常常用到补角
和余角的概念。
总的来说,补角和余角是数学中非常基础而重要的概念。
掌握了它们的概念和计算方法,有助于我们更好地理解和应用数学知识。
余角和补角的概念及性质的运用(2)
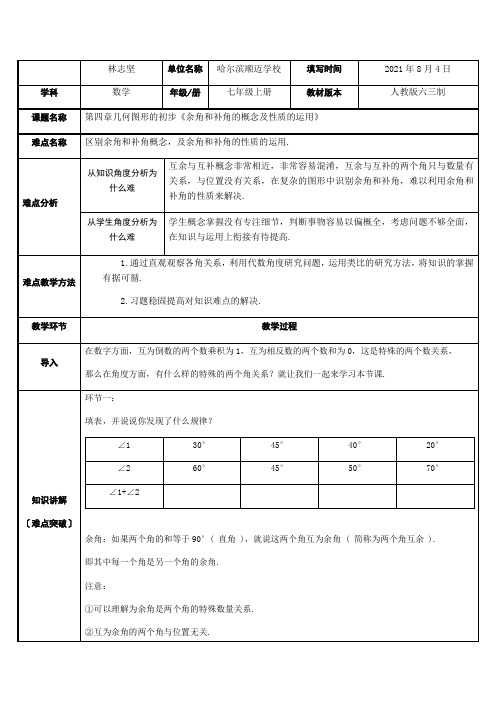
符号语言因为∠1与∠2互为余角/∠1与∠2互余/∠1是∠2的余角/∠2是∠1的余角所以∠1+∠2=90°思考:如图,∠COA=∠BOD=90°,图形中有哪几对余角.余角的性质:如果两个角都是同一个角的余角,那么这两个角相等.简单说成:同角的余角相等.符号语言:因为∠1+∠3=90°,∠2+∠3=90°,所以∠1=∠2.余角的性质:如果两个角是等角的余角,那么这两个角相等.简单说成:等角的余角相等符号语言:因为∠1+∠4=90°,∠2+∠3=90°,∠3=∠4,所以∠1=∠2.环节二:填表,并说说你发现了什么规律?∠1 30°45°40°20°∠2 150°135°140°160°∠1+∠2补角:如果两个角的和等于180°( 平角 ),就说这两个角互为补角 ( 简称为两个角互补 ). 即其中每一个角是另一个角的补角.注意:①可以理解为补角是两个角的特殊数量关系.②互为补角的两个角与位置无关.符号语言因为∠1与∠2互为补角/∠1与∠2互补/∠1是∠2的补角/∠2是∠1的补角所以∠1+∠2=180°思考:如图,∠COA=∠BOD=180°,∠1、∠2、∠3中有哪几对补角.补角的性质:如果两个角都是同一个角的补角,那么这两个角相等.简单说成:同角的补角相等符号语言:因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2.补角的性质:如果两个角是等角的补角,那么这两个角相等. 简单说成:等角的补角相等符号语言:因为∠1+∠4=180°,∠2+∠3=180°,∠3=∠4,所以∠1=∠2.课堂练习〔难点稳固〕°,那么它的余角是,它的补角是.解析:90°-50°=40°,180°-50°=130°.∠1与∠2互余,∠3与∠2互补,且∠3=120°,那么∠1= .解析:因为∠3+∠2=180°,∠3=120°,所以∠2=60°,又因为∠1+∠2=90°,所以∠1=30°.∠1与∠2互余,∠3与∠2互余,且∠3=50°,那么∠1= .解析:∠1和∠3都是∠2的余角,根据同角的余角相等,所以∠1=∠3=50°.小结。
第七课时余角与补角(2)(方位角)

B
1 2 A
东
东
例2:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方 向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°) 方向上又分别发现了客轮 B, 货轮 C 和海岛 D. 仿照表示灯塔方位 的方法画出表示客轮B,货轮C和海岛D方向的射线.
∴ 射线 OA 的方向就是南偏东 60°,即灯塔A所在的方向。 射线OB的方向就是北偏东40°, 即客轮B所在的方向。
北 D E 45° 45° 西 C H 射线OA OB OC OD
射线OE (2)西北方向:_________ 射线OF 西南方向:__________ 东 A 射线OG 东南方向:__________
O
F
B
南
射线OH 东北方向 :__________ G
北
(3)南偏西25°
B 西 70° O 60° 25° A 南
32°
∠AOB=180°-32°-43°
=105°
43°
说出B在A的 北偏东40°
那么A在B的 南偏西40°
北
● ●
B B
西
B
●
40 40° ° 70°
●
A
65°
●B
东
●
B
南
A看B的方向是北偏东30°,那么B看 A的方向是( C )
(A)南偏东60°(B)南偏西60°
(C)南偏东30° (D)南偏西30°
5米
西
B 500
400
8 、 12
C
射线OA 东 北偏西70° 射线OB 南偏东60° 射线OC
例1 如图,OA是表示北偏东30°方向的一条 射线,仿照这条射线,画出表示下列方向的角:
人教版七年级上数学:4.3.3余角和补角(2)学案

2143西北西南东南东北北西南东数学:4.3.3《余角和补角(2)》学案(人教版七年级上)【学习目标】:1、掌握余角和补角的性质。
2、了解方位角,能确定具体物体的方位。
【重点难点】掌握余角和补角的性质;方位角的应用; 【导学指导】 一、知识链接1.70°的余角是 ,补角是 ;2.∠α(∠α <90°)的它的余角是 ,它的补角是 ; 二、自主学习 1.探究补角的性质:例3、如图, ∠1与∠2互补,∠3与∠4互补, ∠1= ∠3,那么∠2与∠4相等吗?为什么?分析:(1)∠1与∠2互补,∠2等于什么?∠2=1800- ,∠3与∠4互补,∠4等于什么? ∠4=1800 - 。
(2)当∠1= ∠3时,∠2与∠4有什么关系?为什么?∠2=∠4(等量减等量,差相等)上面的结论,用文字怎么叙述?补角的性质:等角的 相等。
2.探究余角的性质:如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?余角性质:等角的 相等 3.方位角:(1)认识方位:正东、正南、正西、正北、东南、 西南、西北、东北。
(2)找方位角:乙地对甲地的方位角 ; 甲地对乙地的方位角1 2 3 4南北西例4:如图.货轮O 在航行过程中,发现灯塔A 在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C 和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C 和海岛D 方向的射线。
(师生共同完成)【课堂练习】:1、α∠和β∠都是AOB ∠的补角,则α∠ β∠;2、如果9031,9021=∠+∠︒=∠+∠,则32∠∠与的关系是 , 理由是 ;3、A 看B 的方向是北偏东21°,那么B 看A 的方向( )A 南偏东69°B 南偏西69°C 南偏东21°D 南偏西21°4、在点O 北偏西60°的某处有一点A ,在点O 南偏西20°的某处有一点B ,则∠AOB 的度数是( ) A 100° B 70° C 180° D 140° 【要点归纳】:补角的性质:余角的性质:【拓展训练】:1. 如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E 在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?【总结反思】:2019-2020学年七年级数学上学期期末模拟试卷一、选择题1.如图,两轮船同时从O 点出发,一艘沿北偏西50°方向直线行驶,另一艘沿南偏东25°方向直线行驶,2小时后分别到达A ,B 点,则此时两轮船行进路线的夹角∠AOB 的度数是( )A.165°B.155°C.115°D.105°2.锐角4720'的余角是( ) A.4240'B.4280'C.5240'D.13240'3.在海上,灯塔位于一艘船的北偏东40方向,那么这艘船位于这个灯塔的( ) A.南偏西50°B.南偏西40°C.北偏东50°D.北偏东40°4.下列方程的变形中,正确的是( ) A .由3+x =5,得x =5+3B .由3x ﹣(1+x )=0,得3x ﹣1﹣x =0C .由102y =,得y =2 D .由7x =﹣4,得74x =-5.一个两位数的个位数字是x ,十位数字是y ,这个两位数可表示为( ) A.xyB.C.D.6.如果代数式4y 2-2y +5的值是7,那么代数式2y 2-y +1的值等于( ) A .2 B .3 C .-2 D .4 7.若代数式2x a y 3z c与4212b x y z -是同类项,则( ) A.a=4,b=2,c=3 B.a=4,b=4,c=3C.a=4,b=3,c=2D.a=4,b=3,c=48.下列代数式中:1x ,2x y +,213a b ,x y π-,54y x,0,整式有( ) 个 A.3个B.4个C.5个D.6个9.若一个代数式与代数式2ab 2+3ab 的和为ab 2+4ab-2,那么,这个代数式是( ) A .3ab 2+7ab-2 B .-ab 2+ab-2 C .ab 2-ab+2 D .ab 2+ab-2 10.和数轴上的点一一对应的是( ) A .整数 B .实数 C .有理数 D .无理数11.实数1 ,1- ,0 ,12- 四个数中,最大的数是( ) A.0B.1C.1-D.12-12.冰箱冷藏室的温度零上5℃,记作+5℃,保鲜室的温度零下7℃,记作 A .7℃ B .-7℃ C .2℃ D .-12℃ 二、填空题13.若一个角是34︒,则这个角的余角是_______︒.14.如图,点P 是∠AOB 内任意一点,且∠AOB=40°,点M 和点N 分别是射线OA 和射线OB 上的动点,当△PMN 周长取最小值时,则∠MPN 的度数为_____.15.有甲、乙两桶油,从甲桶到出14到乙桶后,乙桶比甲桶还少6升,乙桶原有油30升,设甲有油x 升,可列方程为_____.16.去括号合并:(3)3(3)a b a b --+=_________.17.计算:()()35---=______;()225323a a b b ---=______.18.若a,b 是整数,且ab =12,|a|<|b|,则a+b=________ .19.一个两位数,个位上的数字是十位上数字的3倍,它们的和是12,那么这个两位数是____. 20.比较大小:-3__________0.(填“< ”“=”“ > ”) 三、解答题21.如图,点O 在直线AB 上,OM 平分∠AOC ,ON 平分∠BOC ,如果∠1:∠2=1:2,求∠1的度数.22.如图,在四边形ABCD 中, //AD BC ,B D ∠=∠延长BA 至点E ,连接CE ,且CE 交AD 于点F ,EAD ∠和ECD ∠的角平分线相交于点P .(1)求证:①//AB CD ;②2EAD ECD APC ∠+∠=∠; (2)若70B ∠=︒,60E ∠=︒,求APC ∠的度数;(3)若APC m ∠=︒,EFD n ∠=︒请你探究m 和n 之间的数量关系. 23.解方程(1)3x-7(x-1)=3-2(x+3) (2)12x -=413x --1 24.为实施“学讲计划”,某班学生计划分成若干个学习小组,若每组5人,则多出4人,若每组6人,则有一组只有2人,该班共有多少名学生?25.先化简,再求值:已知|2a +1|+(4b -2)2=0,求3ab 2-[2221522a b ab ab ⎛⎫+-+ ⎪⎝⎭]+6a 2b 的值. 26.先化简,再求值:2(﹣3xy+52x 2)+5(2xy ﹣x 2),其中x =﹣2,y =12.27.现从小欣作业中摘抄了下面一道题的解题过程:计算:24÷(13-18-16); 解:24÷(13-18-16)=24÷13-24÷18-24÷16=72-192-144 =-264;观察以上解答过程,请问是否正确?若不正确,请写出正确的解答.28.某粮库3天内粮食进出库的吨数如下:(“+”表示进库,“-”表示出库)(1)经过这3天,库里的粮食是增多了还是减少了?(2)经过这3天,仓库管理员结算发现库里还存有480吨粮食,那么3天前库里存粮多少吨? (3)如果进出的装卸费都是每吨5元,那么这3天要付多少元装卸费?【参考答案】*** 一、选择题 1.B 2.A 3.B 4.B 5.C 6.A7.C 8.B 9.A 10.B 11.B 12.B 二、填空题 13.56 14.100°15.(1﹣ SKIPIF 1 < 0 )x ﹣(30+ SKIPIF 1 < 0 x )=6 解析:(1﹣14)x ﹣(30+14x )=6 16.-10 SKIPIF 1 < 0 解析:-10b17.SKIPIF 1 < 0 解析:223a b + 18.7,8,13 19.39 20.< 三、解答题 21.30°22.(1)①见解析,②见解析;(2)65°;(3)12m n =,见解析. 23.(1)x=5;(2)x=1. 24.4425.a 2b +1;98.26.4xy ,-4.27.错误,正确的解法见解析.28.(1)库里的粮食减少了;(2)3天前库里存粮食是525吨;(3)3天要付装卸费825元.2019-2020学年七年级数学上学期期末模拟试卷一、选择题1.如图是某几何体的表面展开图,则该几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱2.如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于()A.90°B.80°C.70°D.60°3.∠A 的余角与∠A 的补角互为补角,那么 2∠A 是()A.直角B.锐角C.钝角D.以上三种都有可能4.若关于x的一元一次方程1﹣46x a+=54x a+的解是x=2,则a的值是()A.2B.﹣2C.1D.﹣15.同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了()A.10场B.11场C.12场D.13场6.某车间有22名工人,生产某种由一个螺栓套两个螺母的产品,每人每天生产螺母20个或螺栓12个,若分配x名工人生产螺栓,其他工人生产螺母,恰好使每天生产的螺栓和螺母配套,则下面所列方程中正确的是()A.20x=12(22-x)B.12x=20(22-x)C.2×12x=20(22-x)D.20x=2×12(22-x)7.下列计算正确的是()A.3a+2a=5a2B.3a-a=3 C.2a3+3a2=5a5D.-a2b+2a2b=a2b8.下列算式中,计算结果为a3b3的是()A.ab+ab+ab B.3ab C.ab•ab•ab D.a•b39.下列图形都是由同样大小的黑、白圆按照一定规律组成的,其中第①个图形中一共有2个白色圆,第②个图形中一共有8个白色圆,第③个图形中一共有16个白色圆,按此规律排列下去,第⑦个图形中白色圆的个数是()A .96B .86C .68D .5210.如果|a ﹣1|+(b+2)2=0,则a ﹣b 的值是( ) A .-1 B .1 C .-3 D .311.计算(﹣8)﹣(﹣5)的结果等于( ) A .-3 B .-13 C .-40 D .312.在下面的四个有理数中,最小的是( ) A .﹣1 B .0 C .1 D .﹣2 二、填空题13.如图,在△ABC 中,∠ABC 与∠ACB 的平分线交于点O ,过点O 作DE//BC ,分别交AB,AC 于点D,E,若AB=4,AC=3,则△ADE 的周长是_______________。
6.8 余角和补角 课件2

(1)互余的两个角必定都是锐角。 (2) =90°,那么它是余角。
(3)一个角的补角必定是钝角。 ( ) (4)两个角互补,那么这两个角中,必定一个是锐角, 另一个是钝角。 ( ) (5)一个角的余角一定比这个角的补角小。 ( ) (6)若 AOB与 BOC互补,则A、O、C同在一直线
已知一个角的补角比这个角的余角的3倍大10 度,求这个角的补角的度数.
巩固练习3
如下图,∠DOB为平角,∠AOC为直角, ∠AOD=20°,则∠COD的补角是多少度?
再见
上。 (
( (
) )
×
)
⑺若∠1+∠2+∠3=180°,那么∠1、∠2、∠3互为 补角。 (
×
)
A 1 2
B
C
3 O∠2=∠3 ,∠3源自∠α 互余, ∠2和∠β互余 D同角 或等角的余角相等 。
3
α
∠α =∠β
β
2
A
C 2 O 3 1 B β D 2 α 3
同角 或等角 的补角相等 。
∠2=∠3,∠2和∠α互补,∠3和∠β互补
60
°
80
°
100
°
120
°
150
°
170
°
1、若 =60°32′,则 的余角是 ________ , 29 ° 的补角是 _________, 119°28′ 28′
2、若一个角的度数是X°,则它的余角的 90-X,180-X 度数和补角的度数分别是_________
150° 3、60°的余角的补角是___________
1 1 x ∴ AC = AB 3 3 ∵ CP=AP -AC
∵ CP=1.5cm
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
东
A
B
余角和补角
龙伏中学 吴 柳
你还记得吗?
你叙述一下具有什么关系的两个角叫互为余 角和互为补角吗? 1.互为余角的定义 :如果两个角的和是一 个直角,那么这两个角叫互为余角.其中 一个角叫做另一个角的余角. 2.互为余角、互为补角的定义 :如果两 个角的和是一个平角,那么这两个角叫互 为补角.其中一个角叫做另一个角的补角 .
因为,∠1=∠3 所以,180° —∠1=180° — ∠3 又因为, ∠1与∠2,∠2=180° — ∠1; ∠3与∠4互补,∠4=180° — ∠3; 所以: ∠2=∠4
由此,我们可以猜想:
等角的补角相等 相等 等角的余角
动脑想一想,动手画一画
按照上北下南,左西右东的规定画出表示东南西北的十字线,然 后在图上画出表示下列方向的射线: 北 (1)北偏西30° 北偏西30° 北偏东15° (2)南偏东60° 30°15° (3)北偏东15°
恭喜你,你已经顺利地完成了本课时的学习 任务。请别忘了用心做好今天的作业。
1、认真阅读教材P137和P138。 2、完成P140第7题和 第8题。 3、想一想,议一议:
如图:A地和B地都是海上观测站,从A地发现它的北偏东 60°方向有一艘船,同时,从A地发现这艘船在它的北偏 东30°方向。试在图中确定这艘船的位置。
考考你!
如图, O 是直线 AB 上一点, OC 是∠ AOB 的平 分线
①∠AOD的补角是____________ <DOB
<DOC ②∠AOD的余角是 ____________ <DOA ③∠DOB的补角是____________
让我们认真想一想
问题:如下图,∠1与∠2互补,∠3与∠4互补, 如果∠1=∠3,那么∠2=∠4成立吗?为什么?
(4)西南方向
(南偏西45°)
西 45°
东
西南方向 (南偏西45°)
60°
南偏东60°
南
问题:如图(1),货轮O在航行过程中,发现灯 塔A在它南偏东60度的方向上,同时,在它北偏 东40度、南偏西10度、西北(即北偏西45度)方 向上又分别发现了客轮B、客轮C和海岛D。仿照 表示灯塔方位的方法,画出表示客轮B、客轮C和 海岛D方向的射线。
北 西 0 南 60° A A 东 东
(1)
北
海岛C 40°
轮船B
西
45° 客轮 60° 灯塔A
东
南
北 B C 西 45°
40° 东
0
6ห้องสมุดไป่ตู้°
南
A
静下来,仔细的回味一下,这节课你有 什么收获?说出来与大家一起分享。
提示:
1 补角和余角的性质: 等角的补角相等 等角的补角相等
2 如何表示物体所处的方位?
