第3课时 三角函数的图象
《3.3三角函数的图象与性质》 学案

23 / 24
课程小结 1.求三角函数的单调区间时,应先把函数式化成 y=Asin(ωx+φ)(ω>0)的形式,再根据三角函数的单调区间,求出 x 所在的区间.应特别注意,考虑问题应在函数的定义域内. 注意区分下列两种形式的函数单调性的不同: π (1)y=sinωx-4; π (2)y=sin4-ωx. 2.周期性是函数的整体性质,要求对于函数整个定义域内的每一个 x 值都满足 f(x+T)=f(x),其中 T 是不为零的常 数.如果只有个别的 x 值满足 f(x+T)=f(x),或找到哪怕只有一个 x 值不满足 f(x+T)=f(x),都不能说 T 是函数 f(x)的周 期.
24 / 24
x π A.y=sin2+6 π C.y=sin2x+6
18 / 24
【巩固】 4.函数 y= 1 的定义域为________. tan x- 3
19 / 24
π π 5.已知函数 f(x)=cosωx+6(ω>0)的图象上的两个相邻的最高点和最低点的横坐标之差为2,则函数在[0,2π]上的 零点个数为________.
k∈Z}
R
4 / 24
考点 2
正弦函数、余弦函数、正切函数的单调性及最值 函数 y=sin x 递增区间: π π 2kπ-2,2kπ+2(k∈Z) 单调性 递减区间: π 3 2kπ+2,2kπ+2π(k∈ Z) π x=2kπ+2(k∈Z)时,ymax 最 值 π =1 x=2kπ-2(k∈Z)时, ymin=-1 y=cos x y=tan x
π π π π 【解析】(1)由 y=sin x 的对称轴为 x=kπ+2(k∈Z),即 3×12+φ=kπ+2(k∈Z),得 φ=kπ+4(k∈Z). π π 又|φ|<2,所以 k=0,故 φ=4. π (2)由题意,得 y=cos(3x+φ)是奇函数,故 φ=kπ+2,(k∈Z).
3-3第三章 三角函数、解三角形

解析
1 3 1 3 2 (1)f(x)=1-2sin x+2sinx=-2 sinx-2 所以当 sin x = 时, f ( x ) f(x)min + , max= , 2 2 2 当 sinx=-1 时,
2
=-3,故选 C. (2)要使函数 y=lg (2sinx-1)+ 1-2cosx有意义,
π π 2.函数 f(x)=sin 2x-4在区间0,2 上的最小值为(
)
A.-1 2 C. 2
2 B.- 2 D.0
π π π 3π 解析 由 0≤x≤2得-4≤2x-4≤ 4 ,结合 y=sinx 的图象易得 B.
π x ≠ k π + , k ∈ Z x π 3 . 3.[教材改编]函数 y=-tanx+ +2 的定义域为______________________
)
π π π π kπ π kπ 5π 解析 由 kπ-2<2x-3<kπ+2(k∈Z)得,2 -12<x< 2 +12(k∈Z), 所以函数 f(x)=tan2x-3 的单调递增
kπ π kπ 5π 区间为 2 -12, 2 +12 (k∈Z),故选 B.
) B.2 D.5
π π π π π π +2 解析 ∵f(x)在 6,2 =0, 上单调递减,且 f +f =0,∴f6 6 2 2 π ∵f(x)=sinωx+ 3cosωx=2sinωx+3 , π+π π π π ∴f6 2=f3=2sin3ω+3 =0, 2 π π 1 2π π π ∴3ω+3=kπ(k∈Z),又2· ω ≥2-6,ω>0, ∴ω=2.
三角函数的图象与性质
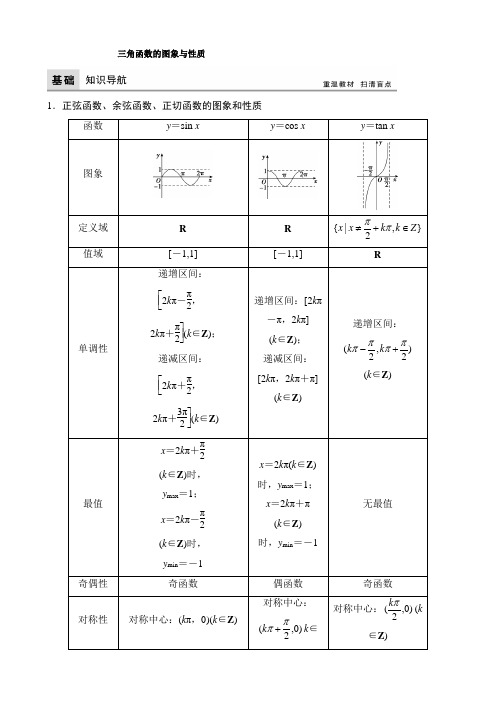
三角函数的图象与性质1.正弦函数、余弦函数、正切函数的图象和性质2.(1)y =sin x 在]2,0[π上是增函数.(√)(2)y =sin x 在第一、四象限是增函数.(×) (3)所有的周期函数都有最小正周期.(×) (4)y =tan x 在整个定义域上是增函数.(×) (5)y =k sin x +1(x ∈R )的最大值为k +1.(×) (6)y =sin|x |为偶函数.(√)(7)y =|sin x |和y =sin|x |的周期都是π.(×) (8)y =tan x 的对称中心为(k π,0)(k∈Z ).(×) (9)若sin x >22,则x >π4.(×)(10)y =sin x 与y =cos x 同时为增的区间是)2,22(πππk k -,k ∈Z .(√)考点一 有关三角函数的定义域、值域问题[例1] (1)函数y =lg sin x +1-2cos x 的定义域是________. 解析:由题意,得⎩⎨⎧sin x >0,1-2cos x ≥0,∴sin x >0且cos x ≤12,作单位圆中三角函数线(图略),得2k π+π3≤x ≤2k π+π,k ∈Z , ∴函数的定义域为},232|{Z k k x k x ∈+<≤+ππππ.答案:},232|{Z k k x k x ∈+<≤+ππππ(2)函数y =2sin )36(ππ-x (0≤x ≤9)的最大值与最小值之和为( ) A .2-3 B .0 C .-1 D .-1- 3 解析:利用三角函数的性质先求出函数的最值. ∵0≤x ≤9,∴-π3≤π6x -π3≤7π6, ∴sin )36(ππ-x ∈]1,23[-.∴y ∈[-3,2],∴y max +y min =2- 3. 答案:A(3)当x ∈]67,6[ππ时,函数y =3-sin x -2cos 2x 的最小值是________,最大值是________.解析:∵x ∈]67,6[ππ,∴sin x ∈]1,21[-.又y =3-sin x -2cos 2x =3-sin x -2(1-sin 2x )=22)41(sin -x +78.∴当sin x =14时,y min =78,当sin x =-12或sin x =1时,y max =2. 答案:78 2[方法引航] 1.求三角函数的定义域实际上是解简单的三角不等式,常借助三角函数线或三角函数图象来求解.2.求解三角函数的值域(最值)常见的有以下几种类型:(1)形如y =a sin x +b cos x +c 的三角函数化为y =A sin(ωx +φ)+k 的形式,再求最值(值域). (2)形如y =a sin 2x +b sin x +c 的三角函数,可先设sin x =t ,化为关于t 的二次函数求值域(最值).(3)形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(最值).1.若将本例(1)变为y =1-2cos x ,其定义域为________.解析:1-2cos x ≥0,∴cos x ≤12.如图,当x ∈(0,2π)时,cos π3=cos 53π=12,∴cos x ≤12,x ∈)35,3(ππ∴x ∈R 时,cos x ≤12的解集为},23523|{Z k k x k x ∈+≤≤+ππππ答案:},23523|{Z k k x k x ∈+≤≤+ππππ2.若在本例(2)中,x 的范围变为“-1≤x ≤9”,其它不变,如何选答案. 解析:-1≤x ≤9时,-π2≤π6x -π3≤76π. -1≤sin )36(ππ-x ≤1,y ∈[-2,2],y max +y min =0. 答案:B3.若将本例(3)中的函数换为“y =sin x -cos x +sin x cos x ,x ∈[0,π]”,如何求解? 解:令t =sin x -cos x ,又x ∈[0,π],∴t =2sin )4(π-x ,t ∈[-1,2].由t =sin x -cos x ,得t 2=1-2sin x cos x ,即sin x cos x =1-t 22.∴原函数变为y =t +1-t22,t ∈[-1,2].即y =-12t 2+t +12=-12(t -1)2+1.∴当t =1时,y max =1;当t =-1时,y min =-12(-2)2+1=-1.考点二 三角函数的单调性和周期性[例2] (1)(2016·高考山东卷)函数f (x )=(3sin x +cos x )(3cos x -sin x )的最小正周期是( )A.π2 B .π C.32π D .2π解析:法一:由题意得f (x )=3sin x cos x -3sin 2x +3cos 2x -sin x cos x =sin 2x +3cos2x =2sin )32(π+x .故该函数的最小正周期T =2π2=π.故选B.法二:由题意得f (x )=2sin )6(π+x ×2cos )6(π+x =2sin )32(π+x .故该函数的最小正周期T =2π2=π.故选B. 答案:B(2)(2016·湖北武汉模拟)设函数f (x )=A sin(ωx +φ))2||,0,0(πϕϖ<>>A 与直线y =3的交点的横坐标构成以π为公差的等差数列,且x =π6是f (x )图象的一条对称轴,则下列区间中不是函数f (x )的单调递增区间的是( ) A.]0,3[π-B.]65,34[ππ--C.]67,32[ππD.]3,65[ππ-- 解析:由题意得A =3,T =π,∴ω=2.∴f (x )=3sin(2x +φ),又f )6(π=3或f )6(π=-3, ∴2×π6+φ=k π+π2,k ∈Z ,φ=π6+k π,k ∈Z , 又∵|φ|<π2,∴φ=π6,∴f (x )=3sin )62(π+x ,令-π2+2k π≤2x +π6≤π2+2k π,k ∈Z ,得-π3+k π≤x ≤π6+k π,k ∈Z , 故当k =-1时,f (x )的增区间为]65,34[ππ--,当k =0时,f (x )的增区间为]6,3[ππ-,当k =1时,f (x )的增区间为]67,32[ππ,故选D. 答案:D(3)已知ω>0,函数f (x )=sin )4(πϖ+x 在),2(ππ上单调递减,则ω的取值范围是( )A.]45,21[B.]43,21[C. ]21,0( D .(0,2] 解析:由π2<x <π得π2ω+π4<ωx +π4<πω+π4,由题意知)4,42(ππϖπϖπ++⊆]23,2[ππ,∴⎩⎪⎨⎪⎧π2ω+π4≥π2,πω+π4≤3π2,∴12≤ω≤54,故选A.答案:A[方法引航] 形如y =A sin (ωx +φ)的函数的单调区间的求法 (1)代换法,①若A >0,ω>0,把ωx +φ看作是一个整体,由2π-+2k π≤ωx +φ≤2π+2k π(k∈Z )求得函数的增区间,由2π+2k π≤ωx +φ≤23π+2k π(k ∈Z )求得函数的减区间.,②若A >0,ω<0,则利用诱导公式先将ω的符号化为正,再利用①的方法,或根据复合函数的单调性规律进行求解.(2)图象法:画出三角函数图象,利用图象求函数的单调区间.,对于已知函数的单调区间的某一部分确定参数ω的范围的问题,首先,明确已知的单调区间应为函数的单调区间的子集;其次,要确定已知函数的单调区间,从而利用它们之间的关系可求解.1.已知函数f (x )=2sin )42(πϖ-x (ω>0)的最大值与最小正周期相同,则函数f (x )在[-1,1]上的单调增区间为________. 解析:由题知2π2ω=2,得ω=12π,∴f (x )=2sin )4(ππ-x ,令-π2+2k π≤πx -π4≤π2+2k π,k ∈Z ,解得-14+2k ≤x ≤34+2k ,k ∈Z ,又x ∈[-1,1],所以-14≤x ≤34,所以函数f (x )在[-1,1]上的单调递增区间为]43,41[-.答案:]43,41[-2.若将本例(3)改为f (x )=sin ωx 在),2(ππ上为增函数(ω>0),如何求ω的范围?解:当π2<x <π时,ωπ2<ωx <ωπ (ω>0) ∴),2(ϖπϖπ⊆]2,0[π∴ωπ≤π2,∴ω≤12,∴ω∈]21,0(. 考点三 三角函数的奇偶性、对称性[例3] (1)A .y =cos )22(π+x B .y =sin )22(π+x C .y =sin 2x +cos 2x D .y =sin x +cos x解析:对于A ,y =cos )22(π+x =-sin 2x ,T =π为奇函数,故选A.答案:A(2)(2016·高考全国甲卷)若将函数y =2sin 2x 的图象向左平移π12个单位长度,则平移后图象的对称轴为( )A .x =k π2-π6(k ∈Z )B .x =k π2+π6(k ∈Z )C .x =k π2-π12(k ∈Z )D .x =k π2+π12(k ∈Z ) 解析:法一:将函数y =2sin 2x 的图象向左平移π12个单位长度,得到y =2sin 2)12(π+x =2sin )62(π+x 的图象.由2x +π6=π2+k π(k ∈Z )得,∴x =π6+k 2π.(k ∈Z ),即平移后图象的对称轴为x =k π2+π6(k ∈Z ). 法二:∵y =2sin 2x 的对称轴为x =π4+k 2π,向左平移π12个单位后为x =π4-π12+k 2π=π6+k2π,故选B. 答案:B(3)(2017·吉林长春模拟)函数f (x )=sin(2x +φ))2|(|πϕ<向左平移π6个单位后是奇函数,则函数f (x )在]2,0[π上的最小值为________.解析:函数f (x )=sin(2x +φ))2|(|πϕ<向左平移π6个单位后得到函数为f )6(π+x =sin ])6(2[ϕπ++x =sin )32(ϕπ++x ,因为此时函数为奇函数,所以π3+φ=k π(k ∈Z ),所以φ=-π3+k π(k ∈Z ).因为|φ|<π2,所以当k =0时,φ=-π3,所以f (x )=sin )32(π-x .当0≤x ≤π2时,-π3≤2x -π3≤2π3,即当2x -π3=-π3时,函数f (x )=sin )32(π-x 有最小值为sin )3(π-=-32.答案:-32(4)(2017·湖南六校联考)若函数f (x )=a sin ωx +b cos ωx (0<ω<5,ab ≠0)的图象的一条对称轴方程是x =π4ω,函数f ′(x )的图象的一个对称中心是)0,8(π,则f (x )的最小正周期是________.解析:由题设,得f )4(ϖπ=±a 2+b 2,即22(a +b )=±a 2+b 2,∴a =b . 又)8(πf '=0,∴aω)8sin 8(cos ϖπϖπ-=0,∴tan ω8π=1,∴ω8π=k π+π4,∴ω=8k +2,(k ∈Z ) 而0<ω<5,0<8k +2<5,∴k =0,ω=2,∴f (x )=a (sin 2x +cos 2x )=2a sin )42(π+x ,∴T =2π2=π.答案:π[方法引航] 函数f (x )=A sin (ωx +φ)的奇偶性和对称性(1)若f (x )=A sin (ωx +φ)为偶函数,则当x =0时,f (x )取得最大或最小值;若f (x )=A sin (ωx +φ)为奇函数,则当x =0时,f (x )=0.(2)对于函数y =A sin (ωx +φ),其对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点,因此在判断直线x =x 0或点(x 0,0)是否是函数的对称轴或对称中心时,可通过检测f (x 0)的值进行判断.(3)求形如y =A sin (ωx +φ)或y =A cos (ωx +φ)的函数图象的对称轴或对称中心时,都是把“ωx +φ”看作一个整体,然后根据y =sin x 和y =cos x 的图象的对称轴或对称中心进行求解.1.已知函数f (x )=a sin x +b cos x (a ,b 为常数,a ≠0)在x =π4处取得最小值,则函数g (x )=f )43(x -π是( ) A .偶函数且它的图象关于点(π,0)对称 B .偶函数且它的图象关于点)0,23(π对称 C .奇函数且它的图象关于点)0,23(π对称 D. 奇函数且它的图象关于点(π,0)对称解析:选D.因为f (x )=a 2+b 2sin(x -φ)在x =π4处取得最小值,所以π4-φ=2k π-π2,k ∈Z ,故φ=3π4-2k π,k ∈Z ,得f (x )=a 2+b 2sin )43(π-x ,g (x )=f )43(x -π=-a 2+b 2sin x ,所以g (x )为奇函数,且其图象关于点(π,0)对称.2.已知f (x )=cos(3x +φ)-3sin(3x +φ)为偶函数,则φ可以取的一个值为( ) A.π6 B.π3 C .-π6 D .-π3解析:选D.由已知得f (x )=2cos )]3(3[πϕ++x 为偶函数,由诱导公式可知φ+π3=k π.(k ∈Z )当k =0时,φ=-π3.(也可由f (-x )=f (x )恒成立求.)[易错警示]求y =A sin(ωx +φ)的单调区间的A ,ω的符号处理借助于y =sin x 的单调区间求y =A sin(ωx +φ)的单调区间时,首先保证ω>0,然后再看A 的正负,结合整体“ωx +φ”,求x 的范围.[典例] 已知函数y =sin )23(x -π,则函数在[-π,0]上的单调递减区间为________.[解析] y =sin )23(x -π=-sin )32(π-x ,令2k π-π2≤2x -π3≤2k π+π2(k ∈Z ),得k π-π12≤x ≤k π+5π12,k ∈Z . 所以y =sin )23(x -π在[-π,0]上的减区间为]0,12[π-.[答案] ]0,12[π-[警示] 当ω>0,A <0时,y =A sin(ωx +φ)的增区间是利用2k π+π2≤ωx +φ≤32π+2k π,(k ∈Z )求得x ,减区间是利用2k π-π2≤ωx +φ≤π2+2k π,(k ∈Z )求得x .[高考真题体验]1.(2016·高考全国乙卷)已知函数f (x )=sin(ωx +φ)(ω>0,|φ|≤π2),x =-π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在)365,18(ππ上单调,则ω的最大值为( )A .11B .9C .7D .5解析:选B.先根据函数的零点及图象对称轴,求出ω,φ满足的关系式,再根据函数f (x )在)365,18(ππ上单调,则)365,18(ππ的区间长度不大于函数f (x )周期的12,然后结合|φ|≤π2计算ω的最大值.因为f (x )=sin(ωx +φ)的一个零点为x =-π4,x =π4为y =f (x )图象的对称轴,所以T 4·k =π2(k 为奇数).又T =2πω,所以ω=k (k 为奇数).又函数f (x )在)365,18(ππ上单调,所以π12≤12×2πω,即ω≤12.若ω=11,又|φ|≤π2,则φ=-π4,此时,f (x )=sin )411(π-x ,f (x )在)443,18(ππ上单调递增,在)365,443(ππ上单调递减,不满足条件.若ω=9,又|φ|≤π2,则φ=π4,此时,f (x )=sin )49(π+x ,满足f (x )在)365,18(ππ上单调的条件.故选B.2.(2016·高考浙江卷)设函数f (x )=sin 2x +b sin x +c ,则f (x )的最小正周期( ) A .与b 有关,且与c 有关 B .与b 有关,但与c 无关 C .与b 无关,且与c 无关D .与b 无关,但与c 有关解析:选B.由于f (x )=sin 2x +b sin x +c =1-cos 2x2+b sin x +c .当b =0时,f (x )的最小正周期为π;当b ≠0时,f (x )的最小正周期为2π.c 的变化会引起f (x )图象的上下平移,不会影响其最小正周期.故选B.3.(2014·高考课标全国卷Ⅰ)在函数①y =cos|2x |,②y =|cos x |,③y =cos )62(π+x ,④y =tan )42(π-x 中,最小正周期为π的所有函数为( )A .②④B .①③④C .①②③D .①③ 解析:选C.①中,y =cos|2x |=cos 2x ,周期T =π,①符合; ②中,y =|cos x |=1+cos 2x2,周期T =π,②符合; ③中,周期T =π,③符合;④中,周期T =π2,④不符合. ∴符合条件的函数为①②③.4.(2012·高考课标全国卷)已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图象的两条相邻的对称轴,则φ=( )A.π4B.π3C.π2D.3π4解析:选A.由于直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图象的两条相邻的对称轴,所以函数f (x )的最小正周期T =2π,所以ω=1,所以π4+φ=k π+π2(k ∈Z ),又0<φ<π,所以φ=π4. 5.(2016·高考北京卷)已知函数f (x )=2sin ωx cos ωx +cos 2ωx (ω>0)的最小正周期为π. (1)求ω的值;(2)求f (x )的单调递增区间.解:(1)因为f (x )=2sin ωx cos ωx +cos 2ωx =sin 2ωx +cos 2ωx =2sin )42(πϖ+x ,所以f (x )的最小正周期T =2π2ω=πω.依题意,πω=π,解得ω=1. (2)由(1)知f (x )=2sin )42(π+x函数y =sin x 的单调递增区间为]22,22[ππππ+-k k (k ∈Z ). 由2k π-π2≤2x +π4≤2k π+π2(k ∈Z ),得k π-3π8≤x ≤k π+π8(k ∈Z ). ∴f (x )的单调递增区间为]8,83[ππππ+-k k k ∈Z . 6.(2015·高考安徽卷)已知函数f (x )=(sin x +cos x )2+cos 2x . (1)求f (x )的最小正周期;(2)求f (x )在区间]2,0[π上的最大值和最小值.解:f (x )=sin 2x +2sin x cos x +cos 2x +cos 2x =1+sin 2x +cos 2x =2sin )42(π+x +1,所以函数f (x )的最小正周期为T =2π2=π. (2)由(1)的计算结果知,f (x )=2sin )42(π+x +1.当x ∈]2,0[π时,2x +π4∈]45,4[ππ,由正弦函数y =sin x 在]45,4[ππ上的图象知,当2x +π4=π2,即x =π8时,f (x )取最大值2+1;当2x +π4=5π4,即x =π2时,f (x )取最小值0. 综上,f (x )在]2,0[π上的最大值为2+1,最小值为0.课时规范训练 A 组 基础演练1. 函数f (x )=cos )42(π+x 的最小正周期是( )A.π2 B .π C .2π D .4π解析:选B.由周期公式T =2π2=π.2.下列函数中周期为π且为偶函数的是( )A .y =sin )22(π-xB .y =cos )22(π-xC .y =sin )2(π+xD .y =cos )2(π+x解析:选A.y =sin )22(π-x =-cos 2x 为偶函数,且周期为π.3.与函数y =tan )42(π+x 的图象不相交的直线是( )A .x =π2B .y =π2C .x =π8D .y =π8 解析:选C.2x +π4=π2+k π,k ∈Z ,得x =π8+k π2,k ∈Z ,k =0时,x =π8.4.将函数y =sin x 的图象向左平移π2个单位,得到函数y =f (x )的图象,则下列说法正确的是( )A .y =f (x )是奇函数B .y =f (x )的周期为πC .y =f (x )的图象关于直线x =π2对称 D .y =f (x )的图象关于点)0,2(π-对称解析:选D.由题意知,f (x )=cos x ,所以它是偶函数,A 错;它的周期为2π,B 错;它的对称轴是直线x =k π,k ∈Z ,C 错;它的对称中心是点)0,2(ππ+k ,k ∈Z ,D 对.5.已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f )4(π+x =f (-x )成立,且f )8(π=1,则实数b 的值为( )A .-1B .3C .-1或3D .-3解析:选C.由f )4(π+x =f (-x )可知函数f (x )=2cos(ωx +φ)+b 关于直线x =π8对称,又函数f (x )在对称轴处取得最值,故±2+b =1,∴b =-1或b =3.6.函数f (x )=sin )42(π-x 在]2,0[π上的单调递增区间是________.解析:由2k π-π2≤2x -π4≤π2+2k π,k ∈Z ,得k π-π8≤x ≤38π+2k π,k ∈Z ,在]2,0[π上的单调增区间为]83,0[π. 答案:]83,0[π 7.已知函数y =cos x 与y =sin(2x +φ)(0≤φ<π),它们的图象有一个横坐标为π3的交点,则φ的值是________.解析:由题得cos π3=sin )32(ϕπ+,即sin )32(ϕπ+=12.∵0≤φ<π,∴23π≤2π3+φ<5π3,∴2π3+φ=5π6,则φ=π6. 答案:π68.设函数y =sin(ωx +φ)(ω>0,φ∈)2,2(ππ-)的最小正周期为π,且其图象关于直线x =π12对称,则在下面四个结论:①图象关于点)0,4(π对称;②图象关于点)0,3(π对称;③在]6,0[π上是增函数;④在]0,6[π-上是增函数中,所有正确结论的序号为________.解析:∵T =π,∴ω=2.又2×π12+φ=k π+π2(k ∈Z ),∴φ=k π+π3(k ∈Z ).∵φ∈)2,2(ππ-,∴φ=π3,∴y =sin )32(π+x ,由图象及性质可知②④正确. 答案:②④9.设函数f (x )=sin(2x +φ)(-π<φ<0),y =f (x )图象的一条对称轴是直线x =π8. (1)求φ;(2)求函数y =f (x )的单调增区间.解:(1)令2×π8+φ=k π+π2,k ∈Z ,∴φ=k π+π4,k ∈Z ,又-π<φ<0,则φ=-3π4. (2)由(1)得:f (x )=sin )432(π-x ,令-π2+2k π≤2x -3π4≤π2+2k π,k ∈Z ,可解得π8+k π≤x ≤5π8+k π,k ∈Z ,因此y =f (x )的单调增区间为]85,8[ππππk k ++,k ∈Z .10.已知函数f (x )=2cos x (sin x +cos x ).(1)求f )45(π的值; (2)求函数f (x )的最小正周期及单调递增区间. 解:(1)f )45(π=2cos 5π4)45cos 45(sin ππ+=-2cos π4)4cos 4sin (ππ--=2. (2)因为f (x )=2sin x cos x +2cos 2x =sin 2x +cos 2x +1=2sin )42(π+x +1,所以T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z . 所以f (x )的单调递增区间为]8,83[ππππ+-k k ,k ∈Z . B 组 能力突破1.函数y =sin(ωx +φ)(ω>0且|φ|<π2),在区间]32,6[ππ上单调递减,且函数值从1减小到-1,那么此函数图象与y 轴交点的纵坐标为( )A.12B.22C.32 D.6+24 解析:选A.由题意知T 2=2π3-π6=π2,∴T =π=2πω, ∴ω=2.将点)1,6(π代入y =sin(2x +φ)得sin )3(ϕπ+=1,又|φ|<π2,∴φ=π6,故y =sin )62(π+x .令x =0,则y =12.2.若函数y =f (x )+cos x 在]434[ππ,-上单调递减,则f (x )可以是( )A .1B .cos xC .-sin xD .sin x 解析:选C.-sin x +cos x =cos x -sin x =2cos )4(π+x ,∵-π4≤x ≤3π4,∴0≤x +π4≤π,∴函数y =-sin x +cos x 在]434[ππ,-上为减函数.3.函数f (x )=tan )32(π-x 的单调递增区间是( )A.]1252,122[ππππ+-k k (k ∈Z ) B.)1252,122(ππππ+-k k (k ∈Z )C.)32,6(ππππ++k k (k ∈Z ) D.]125,12[ππππ+-k k (k ∈Z ) 解析:选 B.由k π-π2<2x -π3<k π+π2(k ∈Z )得,k π2-π12<x <k π2+5π12(k ∈Z ),所以函数f (x )=tan )32(π-x 的单调递增区间为)1252,122(ππππ+-k k (k ∈Z ).4.设函数f (x )=3sin )42(ππ+x ,若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________. 解析:f (x )=3sin )42(ππ+x 的周期T =2π×2π=4, f (x 1),f (x 2)应分别为函数f (x )的最小值和最大值,故|x 1-x 2|的最小值为T2=2. 答案:25.已知a >0,函数f (x )=-2a sin )62(π+x +2a +b ,当x ∈]2,0[π时,-5≤f (x )≤1.(1)求常数a ,b 的值;(2)设g (x )=f )2(π+x 且lg g (x )>0,求g (x )的单调区间.解:(1)∵x ∈]2,0[π,∴2x +π6∈]67,6[ππ.∴sin )62(π+x ∈⎣⎢⎡⎦⎥⎤-12,1,∴-2a sin )62(π+x ∈[-2a ,a ].∴f (x )∈[b,3a +b ],又∵-5≤f (x )≤1, ∴b =-5,3a +b =1,因此a =2,b =-5.(2)由(1)得,f (x )=-4sin )62(π+x -1,g (x )=f )2(π+x =-4sin )672(π+x -1=4sin )62(π+x -1,又由lg g (x )>0,得g (x )>1,∴4sin )62(π+x -1>1,∴sin )62(π+x >12,∴2k π+π6<2x +π6<2k π+5π6,k ∈Z ,∴g (x )的增区间:2k π+π6<2x +π6≤2k π+π2,即k π<x ≤k π+π6, g (x )的减区间为2k π+π2≤2x +π6<2k π+56π,即k π+π6≤x <k π+π3,故g (x )增区间为]6,(πππ+k k ,减区间为)3,6[ππππ++k k k ∈Z .。
《第3讲 三角函数的图像与性质》

【反思归纳】 (1)三角函数定义域的求法 ①应用正切函数 y=tan x 的定义域求函数 y=Atan(ωx+φ)的定义 域. ②转化为求解简单的三角不等式求复杂函数的定义域. (2)简单三角不等式的解法 ①利用三角函数的图象求解. ②利用三角函数线求解.
【即时训练】 (1)函数 y=lg(2sin x-1)+ 1-2cos x的定义域为 ________.
2020届高考第一轮复习理科数学
第三章 三角函数、解三角形
第3讲 三角函数的图像与性质
(第三课时)
三角函数的周期性、奇偶性、对称性(多维探究)
角度一 三角函数的周期性
例 3. (1)(2018 潍坊模拟)下列函数中,最小正周期为 π,且图象关于直线
x=π3对称的是( B )
(A)y=sin2x-π3
故 y=f(t)=12(t+1)2-1(- 2≤t≤ 2),从而知: f(-1)≤y≤f( 2),即-1≤y≤ 2+12. 即函数的值域为[-1, 2+12].
(2)y=2cos(π3+x)+2cos x
=
π 3cos
x-2sin
π 3sin
x+2cos
x
=3cos x- 3sin x
=2
【答案】 (1)[-32,3] (2) 1 (3)[-12- 2,1]
1.(2018·高考全国卷Ⅰ)已知函数 f(x)=2cos2x-sin2x+2,则 () A.f(x)的最小正周期为 π,最大值为 3 B.f(x)的最小正周期为 π,最大值为 4 C.f(x)的最小正周期为 2π,最大值为 3 D.f(x)的最小正周期为 2π,最大值为 4 2.求下列函数的值域: (1)y=sin x+cos x+sin xcos x;(2)y=2cos(π3+x)+2cos x. (《金榜题名》第 54 页 典例 2 【即时训练】)
苏教版高中数学必修第一册7.3.2 第3课时 正切函数的图象与性质【授课课件】

值域 周期 奇偶性 单调性
对称性
R π 奇函数 在开区间kkππ--π2,kπ+π2(k∈Z)上都是增函数 无对称轴,对称中心为k2π,0(k∈Z)
1
2
3
4
第3课时 正切函数的图象与性质 必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
正切函数在定义域内是单调函数吗? [提示] 不是.
1
2
3
4
第3课时 正切函数的图象与性质 必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
1.思考辨析(正确的打“√”,错误的打“×”)
(1)正切函数在定义域上是增函数.
()
(2)正切函数的对称轴方程为 x=kπ+π2,k∈Z.
()
(3)正切函数的对称中心为(kπ,0),k∈Z.
2.(变条件)将本例(2)中的函数改为“y=lg tan x”,结果又如 何?
[解] 因为函数 y=lg x 在(0,+∞)上为增函数, 所以函数 y=lg tan x 的增区间就是函数 y=tan x(tan x>0)的增区 间,即kπ,π2+kπ,k∈Z.
1
2
3
4
第3课时 正切函数的图象与性质 必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
握正切函数的性质.(重点)
培养直观想象素养.
2.能利用正切函数的图象及性质 2.通过正切函数的性质的应用,提 解决有关问题.(难点、易错点) 升逻辑推理素养.
1
2
3
4
第3课时 正切函数的图象与性质 必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
2015年高考数学一轮复习课时训练第3节 三角函数的图象与性质

第3节三角函数的图象与性质课时训练练题感提知能【选题明细表】A组一、选择题1.(2013福州模拟)已知函数f(x)=3cos(2x-)在[0,]上的最大值为M,最小值为m,则M+m等于( C )(A)0 (B)3+(C)3-(D)解析:∵x∈[0,],∴(2x-)∈[-,],∴cos(2x-)∈[-,1],∴f(x)∈[-,3],∴M+N=3-.故选C.2.y=sin(x-)的图象的一个对称中心是( B )(A)(-π,0) (B)(-,0)(C)(,0) (D)(,0)解析:令x-=kπ,k∈Z得x=+kπ,k∈Z,于是(-,0)是y=sin(x-)的图象的一个对称中心.故选B.3.使函数f(x)=sin(2x+ϕ)为R上的奇函数的ϕ值可以是( C )(A)(B)(C)π (D)解析:要使函数f(x)=sin(2x+ϕ)为R上的奇函数,需ϕ=kπ,k∈Z.故选C.4.(2013揭阳二模)设函数f(x)=cos(2π-x)+cos(-x),则函数的最小正周期为( C )(A)(B)π (C)2π(D)4π解析:函数f(x)=cos x+sin x=2sin(x+),故其最小正周期为2π,故选C.5.(2013洛阳市模拟)已知函数f(x)=2sin(ωx+ϕ)(ω>0)的图象关于直线x=对称,且f()=0,则ω的最小值是( B )(A)1 (B)2 (C)3 (D)4解析:设函数的周期为T,则T的最大值为4×(-)=π,≤π,ω≥2.故选B.6.(2013佛山质检(二))函数f(x)=sin(πx+),x∈[-1,1],则( A )(A)f(x)为偶函数,且在[0,1]上单调递减(B)f(x)为偶函数,且在[0,1]上单调递增(C)f(x)为奇函数,且在[-1,0]上单调递增(D)f(x)为奇函数,且在[-1,0]上单调递减解析:∵f(x)=sin(πx+)=cos πx,∴f(x)是[-1,1]上的偶函数,又由f(x)在[-1,0]上单调递增,在[0,1]上单调递减,可得应选A.二、填空题7.(2013年高考江苏卷)函数y=3sin(2x+)的最小正周期为.解析:T==π.答案:π8.函数f(x)=sin x+cos x的值域是.解析:∵f(x)=sin x+cos x=2sin,又x∈,∴x+∈,∴2sin∈[-1,2].答案:[-1,2]9.函数y=2sin(3x+ϕ)的一条对称轴为x=,则ϕ= . 解析:∵函数y=sin x的对称轴为x=+kπ(k∈Z),又函数的一条对称轴为x=,∴3×+ϕ=+kπ(k∈Z),∴ϕ=+kπ(k∈Z),又|ϕ|<,∴k=0,故φ=.答案:10.函数y=cos(-2x)的单调减区间为.解析:y=cos(-2x)=cos(2x-),由2kπ≤2x-≤2kπ+π(k∈Z),得kπ+≤x≤kπ+(k∈Z).所以函数的单调减区间为[kπ+,kπ+](k∈Z)答案:[kπ+,kπ+](k∈Z)三、解答题11.(2013汕头质检(二))已知向量a=(,),b=(cos x,sin x).若函数f(x)=a·b,求函数f(x)的最小正周期和单调递增区间. 解:∵f(x)=a·b=cos x+sin x=sin(x+),∴f(x)的最小正周期T==2π.令-+2kπ≤x+≤+2kπ(k∈Z),解得-+2kπ≤x≤+2kπ(k∈Z),∴函数f(x)的单调递增区间为[-+2kπ,+2kπ],k∈Z.12.(2013年高考天津卷)已知函数f(x)=-sin(2x+)+6sin xcos x-2cos2x+1,x∈R.(1)求f(x)的最小正周期;(2)求f(x)在区间[0,]上的最大值和最小值.解:(1)f(x)=-sin 2x-cos 2x+3sin 2x-cos 2x=2sin 2x-2cos2x=2sin(2x-).所以f(x)的最小正周期T==π.(2)由(1)f(x)=2sin(2x-),2x-∈[-,],则sin(2x-)∈[-,1].所以f(x)在[0,]上最大值为2,最小值为-2.13.已知a>0,函数f(x)=-2asin(2x+)+2a+b,当x∈[0,]时, -5≤f(x)≤1.(1)求常数a,b的值;(2)求f(x)的单调区间.解:(1)∵x∈[0,],∴2x+∈[,].∴sin(2x+)∈[-,1],∴-2asin(2x+)∈[-2a,a].∴f(x)∈[b,3a+b].又∵-5≤f(x)≤1,∴b=-5,3a+b=1,因此a=2,b=-5.(2)由(1)得f(x)=-4sin(2x+)-1,由-+2kπ≤2x+≤+2kπ得-+kπ≤x≤+kπ,k∈Z,由+2kπ≤2x+≤+2kπ得+kπ≤x≤π+kπ,k∈Z,∴f(x)的单调递增区间为[+kπ,+kπ](k∈Z),单调递减区间为[-+kπ,+kπ](k∈Z).B组14.(2013广州市毕业班综合测试(二))若函数y=cos(ωx+)(ω∈N*)的一个对称中心是(,0),则ω的最小值为( B )(A)1 (B)2 (C)4 (D)8解析:依题意得cos(ω·+)=0,(ω+1)=kπ+,ω=6k+2(其中k∈Z).又ω是正整数,因此ω的最小值是2,故选B.15.(2013广州市高三调研)已知函数f(x)=(1-cos 2x)·cos2 x,x∈R,则f(x)是( C )(A)最小正周期为的奇函数(B)最小正周期为π的奇函数(C)最小正周期为的偶函数(D)最小正周期为π的偶函数解析:因为f(x)=(1-cos 2x)·cos2 x=2sin2 xcos2 x=sin22x=×=,所以最小正周期T==,且是偶函数,故选择C. 16.若函数f(x)=sin ωx(ω>0)在区间[0,]上单调递增,在区间[,]上单调递减,则ω= .解析:因为当0≤ωx≤,即0≤x≤时,函数是增函数;当≤ωx≤,即≤x≤时,函数是减函数,∴=,ω=.答案:。
三角、反三角函数图像

六个三角函数值在每个象限的符号:
sinα·cscα cosα·secα tanα·cotα
三角函数的图像和性质:
函数
y=sinx
y=cosx
y=tanx
y=cotx
定义域
R
R
{x|x∈R且x≠kπ+ ,k∈Z}
{x|x∈R且x≠kπ,k∈Z}
值域
[-1,1]x=2kπ+ 时ymax=1
奇偶性
arcsin(-x)=-arcsinx
arccos(-x)=π-arccosx
arctan(-x)=-arctanx
arccotห้องสมุดไป่ตู้-x)=π-arccotx
周期性
都不是同期函数
恒等式
sin(arcsinx)=x(x∈[-1,1])arcsin(sinx)=x(x∈[- , ])
cos(arccosx)=x(x∈[-1,1]) arccos(cosx)=x(x∈[0,π])
y=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosy
y=tanx(x∈(- , )的反函数,叫做反正切函数,记作x=arctany
y=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty
理解
arcsinx表示属于[- , ]
且正弦值等于x的角
arccosx表示属于[0,π],且余弦值等于x的角
在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)
在(kπ- ,kπ+ )内都是增函数(k∈Z)
在(kπ,kπ+π)内都是减函数(k∈Z)
.反三角函数:
《三角函数图象》教案设计

第三届全国中小学“教学中的互联网搜索”优秀教案评选教案设计函数sin()y A x ωϕ=+的图象(一)学校:江苏省沭阳高级中学 姓名:李秋香 学科:数学通讯地址:江苏省宿迁市沭阳县学府中路1号 联系电话:0527—83582838 邮编:223600全国中小学“教学中的互联网搜索”优秀教案评选《函数sin()y A x ωϕ=+的图象》教案设计一、 教案背景:1.高中数学苏教版必修4第一章第三节,《函数)sin(ϕω+=x A y 的图象》教学设计2.课时:二课时3.课前准备:在百度上搜索“视频: 弹簧振子简谐运动振动图像形成动画” 二、、教材分析: 1、本节的作用和地位三角函数是中学数学的重要内容之一,它的基础主要是几何中的相似形和圆,研究方法主要是代数变形和图象分析,因此三角函数的研究已经初步把几何与代数联系起来了,三角函数知识,既是解决生产实际问题的工具,又是学习中学后继内容和高等数学的基础.2、本节高考要求:(1)了解三角函数sin()y A x ωϕ=+的实际意义及其参数,,A ωϕ对函数图象变化的影响; (2)能借助计算机画出sin()y A x ωϕ=+的图象,会用五点法画出sin()y A x ωϕ=+的简图;(3)会画出sin()y A x ωϕ=+的简图,能由正弦曲线y=sinx 通过平移、伸缩变换得到sin()y A x ωϕ=+的图象.3、本节课教学目标: 知识目标:1、结合实例,了解三角函数sin()y A x ωϕ=+的实际意义及其参数,,A ωϕ对函数图象变化的影响;2、会用“五点法”画出函数y = A sin(ωx +ϕ)的简图,掌握它们与y =sin x 的转换关系; 能力目标:经历对函数sin y x =到sin()y A x ωϕ=+的图象变换规律的探索过程,体会数形结合以及从特殊到一般的数学思想.情感态度价值观目标:通过学生对问题的自主探究,培养学生动与静的辨证关系,善于从运动的观点观察问题,培养学生解决问题抓主要矛盾的思想;领悟物质运动具有规律性的马克思主义哲学思想;唤起学生追求真理,乐于创新的情感需求;引发学生渴求知识的强烈愿望,树立科学的人生观、价值观.4、教学重点:函数sin()y A x ωϕ=+的图象及其参数,,A ωϕ对函数图象变化的影响.5、教学难点:函数sin()y A x ωϕ=+的图象与正弦曲线sin y x =的关系.6、教学方法:教师引导,学生自主探索.7、教学手段:网络化多媒体教学. 三、教学过程:1、创设情境,引入新课1、如图所示,是一个弹簧振子在做简谐运动(用电脑演示).【百度搜索】/v_show/id_XMTUxNDY5MzQ0.html 由物理学知识可知,小球离开平衡位置的位移与时间t 的关系为:s i n ()(0,s A t A ωϕω=+>>.其中A 为物体振动时离开平衡位置的最大距离,称为振幅;2T πω=为物体往复振动一次所需要的时间,称为周期;12f T ωπ== 为单位时间内往复振动的次数,称为频率; t ωϕ+称为相位,当0t =时的相位ϕ称为初相.在物理和工程技术的许多问题中,都要遇到形如sin()y A x ωϕ=+的函数(其中A ,ω,ϕ都是常数,且0A >,0ω>)如交流电、振动和波等.因此我们有必要画好这些函数的图象.【百度搜索】/show/ZebAZp-4Rm2_9AlP.html?loc=youce_tuijian2、从解析式来看,sin()y A x ωϕ=+与函数sin y x =存在怎样的关系?从图象来看,它与函数sin y x =的图象有什么关系?采用什么研究方法? 如何作出函数sin()y A x ωϕ=+的图象?2、学生活动1、书40页练习4,52、给出下列函数,说出它的振幅、周期、初相并用“五点法”作出下列函数的简图. (1)sin()6y x π=-(2)3sin y x = (3)sin 2y x =3、从作出的图象观察它们与sin y x =的图象存在联系: 如何由sin sin()y x y x ϕ=→=+? 如何由sin sin y x y A x =→=?如何由sin sin()y x y x ω=→=? 3、建构数学 1、 平移变换函数sin()y x ϕ=+的图象是将sin y x =的图象向左平移(当0ϕ>)或向右(当0ϕ<)平移ϕ个单位长度而得到的. 2、 伸缩变换sin y A x =的图象(A>0A 1≠且)是把sin y x =的图象上所有点的纵坐标伸长(A >1)或缩短(01A <<)到原来的A 倍(横坐标不变),而得到的.sin y x ω= (>01ωω≠且)的图象是将sin y x =的图象上所有点纵坐标不变,横坐标伸长(0<<1ω)或缩短(ω>1)到原来的1ω倍而得到的.【百度搜索】/html/jiaoyuwenzhai/2011/1128/484.html4、数学应用例1.已知函数sin()3y x π=-的图象为C .(1) 为了得到sin y x =的图象,只需把C 上的所有点 (2) 为了得到sin()4y x π=+的图象,只需把C 上的所有点(3) 为了得到2sin y x =的图象,只需把C 上的所有点 (4) 为了得到cos()3y x π=-的图象,只需把C 上的所有点变式训练:1、函数sin y x =的图象向左平移6π,所得函数的解析式是 2、函数sin 2y x =的图象向左平移6π,所得函数的解析式是【百度搜索】/view/5bdb184769eae009581becdd.html例2. 用“五点法”作出下列函数的简图,并说出它们与y =sin x 的图象间的关系. (1)sin 3y x = (2)2sin2x y = (3)sin()23x y π=+变式训练:如何变换函数sin y x =可以得到函数思考:如何变式训练:如何变换函数sin y x =可以得到函数sin(2)3y x π=+的图象?【百度搜索】1、/s/blog_62277ac40100fhzz.html2、/view/9c80d2fe770bf78a652954ac.html3、/p-01872229637.html 5、回顾小结1.三角函数sin()y A x ωϕ=+的实际意义及其参数,,A ωϕ对函数图象变化的影响; 2.由正弦函数s i n y x =的图象经过平移变换和伸缩变换得到如sin()y x ϕ=+、sin y A x =、sin y x ω=,sin()(0,0)s A t A ωϕω=+>>的图象,学习时可以类比()(),(),()y f x y f x m y kf x y f nx ==+==与之间的关系.3.注意通过数形结合,化归思想的来学习新的知识. 6、课后作业1、课本P 45 7,92、思考函数sin y A x =、sin y x ω=分别有哪些性质.【百度搜索】/view/bea41e0d76c66137ee06195c.html 7、板书设计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
延伸·拓展
5.已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶 函数,其图象关于点M(3π/4,0)对称,且在区间[0, π/2]上是单调函数.求φ和ω的值.
返回
误解分析
1.在能力· 思维· 方法4中,由于φ没有给出范围,所 以极易求出不合题意的φ值,解题时要结合“零点” 观察
2.设函数y=sin2x+acos2x的图象关于直线x=-π/6对 称,求a的值
【解题回顾】此二种方法都应用了三角函数图象 的知识解一,抓住的是正弦曲线在与对称轴交 点处取得函数最大或最小值的特点解二,充分 应用了图形对称以及待定系数法的数学方法,显 示了数形结合的灵活性.
1 3 2 sin x cos x 1x R 3.已知函数 y cos x 2 2 (1)当y取得最大值时,求自变量x的集合;
返回
能力·思维·方法
1.先将函数y=f(x)的图象右移π/8个单位,然后再把 图象上每一点的横坐标扩大为原来的两倍,所得 的图象恰好与函数y=3sin(x+π/6)的图象相同.求f(x) 的解析式
【解题回顾】此题为逆向求解对函数y=Asin(ωx+ φ)的图象作变换时应该注意:横坐标的扩大与压缩 只与ω有关,与其他参量无关;图象的左右平移应 先把ω提到括号外,然后根据加减号向相应方向移 动
2.由y=sinx作y=sin(2x+π/3)图象,如果先把横坐标 缩短为原来的1/2倍,得y=sin2x后再平移,应向左 平移π/6,切勿左移π/3.
返回
3.图象的对称性 函数y=Asin(ωx+φ)(A>0,ω>0)的图象具有轴对 称和中心对称.具体如下: (1)函数y=Asin(ωx+φ)的图象关于直线x=xk(其中 ωxk+φ=kπ+π/2,k∈Z)成轴对称图形. (2)函数y=Asin(ωx+φ)的图象关于点(xj ,0)(其中 ωxj+φ=kπ,k∈Z)成中心对称图形.
(2)该函数图象可由y=sinx(x∈R)的图象经过怎样的 平移和伸缩变换得到? 【解题回顾】当A>0,ω>0时,函数y=Asin(ωx+
φ)的图象可用“五点法”作出,也可用下列图象变 换方法作出,先把y=sinx的图象向左(φ>0)或向右(φ <0)平移|φ|的单位,再把各点横坐标缩短(ω>1)或 伸长(0 < ω<1)到原来的1/ω倍(纵坐标不变),再把 各点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的 A 倍 ( 横 坐 标 不 变 ) ; 而 函 数 y=Acos(ωx+φ) 和 y=Atan(ωx+φ) 的 图 象 均 可 仿 上 变 换 由 y=cosx 和 y=tanx作出.
4.函数y=|tgx|·cosx(0≤x<3π/2,且x≠π/2) 的图象是( C )
5.关于函数f(x)=2sin(3x-3π/4),有下列命题: ①其最小正周期是2π/3; ②其图象可由y=2sin3x向左平移π/4个单位得到; ③其表达式可改写为y=2cos(3x-π/4); ④在x∈[π/12,5π/12]上为增函数. ①④ 其中正确的命题的序号是_________
4.如下图,函数y=Asin(ωx+φ)(A>0,ω>0)的图像上 相邻的最高点与最低点的坐标分别为(5π/12,3)和 (11π/12,-3).求该函数 的解析式
【解题回顾】这类问题的求解难点是φ的确定,除 以上方法外,常用移轴方法:做平移,移轴公式为 x=x′+π/6,y=y′,则易知函数在新坐标系中的方程 是 y′=3sin2x′, 而 x′=x-π/6, 故所 求 函 数 y=3sin[2(xπ/6)] 返回
(A)函数y=f(x)· g(x)的周期为2π
(B)函数y=f(x)· g(x)的最大值为1
(C)将f(x)的图象向左平移π/2单位后得g(x)的图象
3.将函数y=f(x)sinx的图象向右平移π/4个单位后再 作关于x轴对称的曲线,得到函数y=1-2sin2x,则 f(x)是( B ) (A)cosx (B)2cosx (C)sinx (D)2sinx
返回
课前热身
1.给出四个函数: (A)y=cos(2x+π/6) (B)y=sin(2x+π/6)
(C)y=sin(x/2+π/6)
(D)y=tan(x+π/6)
)
则同时具有以下两个性质的函6,0)对称. 2.已知f(x)=sin(x+π/2),g(x)=cos(x-π/2),则下列结论 中正确的是( D )
第3课时 三角函数的图象
要点·疑点·考点 课
前 热 身 能力·思维·方法 延伸·拓展
误
解 分 析
要点·疑点·考点
1.三角函数线 右面四个图中, 规定了方向的 MP、OM、 AT 分 别 叫 做 角α的正弦线, 余弦线,正切 线.
2.三角函数的图象 (1)y=sinx、y=cosx、y=tanx、y=cotx的图象(略) (2)y=Asin(ωx+φ)的图象及作法 (3)三角函数的图象变换 ①振幅变换:y=sinx→y=Asinx 将y=sinx的图象上各点的纵坐标变为原来的A倍(横 坐标不变); ②相位变换:y=Asinx→y=Asin(x+φ) 将y=Asinx的图象上所有点向左(φ>0)或向右(φ<0) 平移|φ|个单位; ③周期变换:y=Asin(x+φ)→y=Asin(ωx+φ) 将 y=Asin(x+φ) 图 象 上 各 点 的横 坐 标 变为 原 来 的 1/ω 倍(纵坐标不变).
