竖曲线习题
竖曲线计算公式
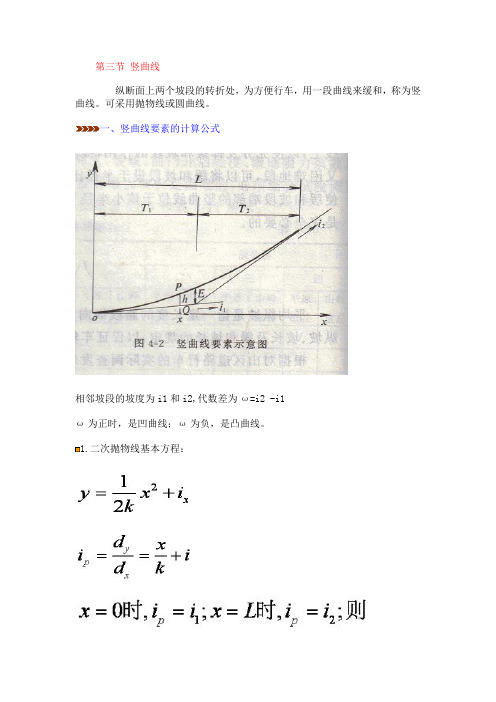
第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
1.二次抛物线基本方程:或ω:坡度差(%);L:竖曲线长度;R:竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:二、竖曲线最小半径(三个因素)1.缓和冲击对离心加速度加以控制。
ν(m/s)根据经验,a=0.5~0.7m/s2比较合适。
我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。
(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时,Lmin = 2ST - 4/ω2.当L≥ST时,ST为停车视距。
以上两个公式,第二个公式计算值大,作为有效控制。
按缓和冲击、时间行程和视距要求(视距为最不利情况)计算各行车速度时的最小半径和最小长度,见表4-13。
表中:(1)一般最小半径为极限最小半径的1.5~2倍;(2)竖曲线最小长度为3s行程的长度。
(二)凹曲线最小半径和长度1.夜间行车前灯照射距离要求:1)L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。
例:设ω=2%=0.02;则L=ωR竖曲线最小长度L=V/1.2速度V=120km/h V=40km/h 一般最小半径R凸17000 700一般最小半径R凹6000 700 L凸340 14L凹120 14 例题4-3ω=-0.09 凸形;L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号=k5+030 - T =K4+940起始高程=427.68 - 5%*90=423.18m桩号k5+000处:x1=k5+000-k4+940=60m切线高程=423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程=426.18 - 0.90=425.28m 桩号k5+100处:x2=k5+100-k4+940=160m切线高程=423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程=431.18 - 6.40=424.78m。
竖曲线计算原理

式中: 式中:R——抛物线顶点 抛物线顶点 处的曲率半径
A
B
一、竖曲线要素的计算公式 竖曲线的基本方程式: 1.竖曲线的基本方程式:设变坡点相邻两纵坡坡 度分别为i 抛物线竖曲线有两种可能的形式: 度分别为i1和i2。抛物线竖曲线有两种可能的形式: 包含抛物线底( (1)包含抛物线底(顶)部; 不含抛物线底( (2)不含抛物线底(顶)部。
2.时间行程不过短 .时间行程不过短 最短应满足3 行程。 最短应满足3s行程。
Lmin V V = t= 3.6 1.2 则 Rmin V = = ω 1.2ω L min
3.满足视距的要求: 满足视距的要求: 凸形竖曲线: 凸形竖曲线:坡顶视线受阻 凹形竖曲线: 凹形竖曲线:下穿立交 4. 凸形竖曲线主要控制因素:行车视距。 凸形竖曲线主要控制因素:行车视距。 凹形竖曲线的主要控制因素:缓和冲击力。 凹形竖曲线的主要控制因素:缓和冲击力。
1 2 y= x + i1 x 2k 式中: 式中:k——抛物线顶点 抛物线顶点 处的曲率半径 ;
B
i1——竖曲线顶 竖曲线顶 点处切线的坡度。 (底)点处切线的坡度。
A
对竖曲线上任一点P 其切线的斜率(纵坡) 对竖曲线上任一点P,其切线的斜率(纵坡)为
iP = dy x = + i1 dx k
当x=0时,ip=i1; 时 当x=L时, i = L + i = i 时 p 1 2
T2 Lω Tω E= ,E上任一点竖距 : )竖曲线上任一点竖距h:
x2 x2 h = PQ = y P − yQ = + i1 x − i1 x = 2R 2R
下半支曲线在竖曲线终点的切线上的竖距h’ 下半支曲线在竖曲线终点的切线上的竖距 ’为:
竖曲线习题
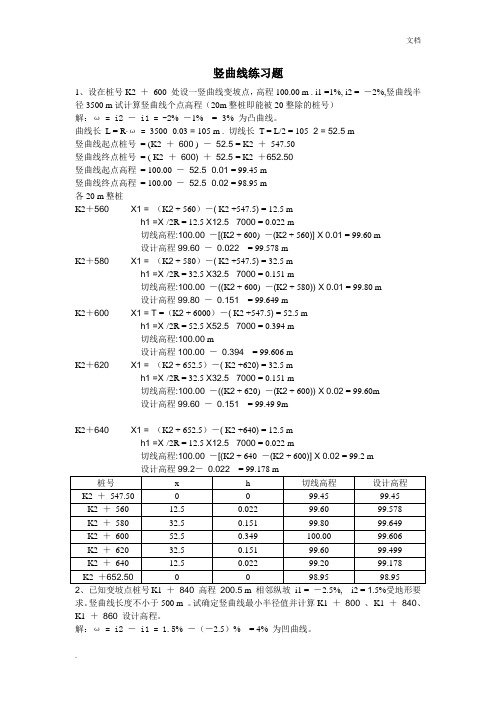
竖曲线练习题1、设在桩号K2 +600 处设一竖曲线变坡点,高程100.00 m . i1 =1%, i2 = -2%,竖曲线半径3500 m试计算竖曲线个点高程(20m整桩即能被20整除的桩号)解:ω = i2 - i1 = -2% -1% = -3% 为凸曲线。
曲线长L = R∙ω = 3500×0.03 = 105m . 切线长T = L/2 = 105÷2 = 52.5 m竖曲线起点桩号= (K2 +600 ) -52.5 = K2 +547.50竖曲线终点桩号= ( K2 +600) +52.5 = K2 +652.50竖曲线起点高程= 100.00 -52.5×0.01 = 99.45 m竖曲线终点高程= 100.00 -52.5×0.02 = 98.95 m各20 m整桩K2+560 X1 = (K2 + 560)-( K2 +547.5) = 12.5 mh1 =X²/2R = 12.5 X12.5 ÷7000 = 0.022 m切线高程:100.00 -[(K2 + 600) -(K2 + 560)] X 0.01 = 99.60 m设计高程99.60 -0.022 = 99.578 mK2+580 X1 = (K2 + 580)-( K2 +547.5) = 32.5 mh1 =X²/2R = 32.5 X32.5 ÷7000 = 0.151 m切线高程:100.00 -((K2 + 600) -(K2 + 580)) X 0.01 = 99.80 m设计高程99.80 -0.151 = 99.649 mK2+600 X1 = T =(K2 + 6000)-( K2 +547.5) = 52.5 mh1 =X²/2R = 52.5 X52.5 ÷7000 = 0.394 m切线高程:100.00 m设计高程100.00 -0.394 = 99.606 mK2+620 X1 = (K2 + 652.5)-( K2 +620) = 32.5 mh1 =X²/2R = 32.5 X32.5 ÷7000 = 0.151 m切线高程:100.00 -((K2 + 620) -(K2 + 600)) X 0.02 = 99.60m设计高程99.60 -0.151 = 99.49 9mK2+640 X1 = (K2 + 652.5)-( K2 +640) = 12.5 mh1 =X²/2R = 12.5 X12.5 ÷7000 = 0.022 m切线高程:100.00 -[(K2 + 640 -(K2 + 600)] X 0.02 = 99.2 m求。
测量学习题09 10 11 12 测设-路线

习题九一、填空1、测设的基本工作包括和。
2、平面点位放样的基本操作是和。
3、测设点的平面位置,采用的方法有、、和等方法。
二、问答题1、什么是测设,测设和测定的区别是什么?2、简述全站仪放样已知距离的基本步骤。
3、已知经纬仪角度放样的方法有哪些,简述其步骤。
4、简述角度交会法放样点的平面位置的基本步骤。
5、高程放样有几种情况,每种情况下采用怎样的方法测设?三、计算题1、如图的高墩台的高程放样,已知BM A的高程为41.582米,墩台顶的设计高为45.261米,安置好水准仪后,测得读数a=1.853米,则墩台要达到设计高,B点尺的读数b应该为多少?2、如图深基坑的高程放样中,已知点BM A高程为31.524米,基底设计高程为10.056米,安置好仪器后,读数分别为:a=1.235m,c1=0.254m,c2=21.587m,则基坑要达到设计高,B点尺的读数b应该为多少?3、已知某点B的设计高程为87.831m,附近已知水准点的BM A,其高程为87.534m,为放样B点的高程,在其间架设水准仪,读出BM A尺上读数a为1.644m,则B点要达到设计高:(1)B点尺读数b应该为多少?(2)简述放样B点设计高的步骤。
4、已知αMN =300 º25′17″,X M=14.228m,Y M=77.564m,X A=47.337m,Y A=73.556m,试计算置仪器于M点,如采用全站仪用极坐标法测设A点(1)计算测设所需的数据;(2)并简述测设步骤。
习题十一、填空1、路线转角是指,位于称为右转角,位于称为左转角。
2、路线里程桩,按其所表示的里程数,可分为和两种。
3、园曲线的主点为、和。
4、园曲线测设时,按桩距在曲线上设桩,通常有和两种方法。
5、园曲线的详细测设方法(传统作业)主要有和两种。
6、缓和曲线是指,它采用的形式有、和,常采用形式。
7、在园曲线上设置缓和曲线后,曲线长度增长了,切线长度近似增长了。
工程测量习题集

一、填空题:1、地下施工测量中,地下控制应和地面控制采用相同的的坐标系统和高程系统。
这可以通过联系测量来实现。
2、地下建筑物施工测量一般采用现场标定法和解析法。
3、隧道贯穿误差包括纵向贯穿误差、横向贯穿误差和高程贯穿误差。
4、隧道施工精度主要取决于横向贯穿误差和高程贯穿误差。
5、在施工期间,临时水准点的密度应保证放样时只设1个测站,即能将高程传递到建筑物上。
6、隧道中线方向进洞的类型有直线进洞和曲线进洞两种类型。
7、地下导线的三种类型是施工导线、根本导线和主要导线。
8、对于直线型的隧道而言,常用的平面测量类型有中线法和串线法。
9、隧道施工中的测量工作主要任务有定方向、检查施工进度和计算土方量。
二、简答题1、举例说明什么是地下工程2、地下建筑物的施工测量主要包括哪些内容?3、常用的地下建筑物施工测量方法4、地下施工测量的内容5、贯穿误差概念、分类及来源6、什么是进洞数据的推算7、直线进洞数据有哪些?8、曲线进洞的过程9、地下控制测量的内容10、地下导线的特点地下导线布设时的考前须知11、隧道开挖中测量常用的方法,各有何优缺点?12、施工测量的内容有哪些?13、贯穿误差的测定方法14、调整贯穿误差的方法15、地下高程测量与地面高程测量有何不同之处?16、地下工程的地面控制测量有哪些方法和技术?17、地下工程测量有哪些特点?18、何谓联系测量?20、高程联系测量有几种方法?21、简述隧道施工和竣工测量的内容。
22、在深基坑或高楼施工时,通常采用什么方法传递高程的?三、判断题1、隧道的贯穿精度主要取决于纵向贯穿误差和高程贯穿误差。
2、隧道的横向贯穿误差仅受导线测角误差的影响。
第九章竖井联系测量与陀螺经纬仪测量一、填空题1、竖井联系测量是将地面控制中的坐标、方向及高程经由竖井传递到地下去。
2、按照地下控制网与地面上联系的不同,定向方法可以分为一井定向、两井定向、横洞〔斜井〕定向和陀螺经纬仪定向。
3、一井定向在地面上测量的数据有两吊锤线的坐标X、Y以及连线的方向角。
《铁路选线》习题

《铁路设计基础》套题练习适用专业:铁道工程技术专业编写:刘淑娟班级:学号:姓名:注:每位同学必须人手一册,自觉动手练习,有问题集体处理。
第一章铁路能力习题一一、填空题1、铁路运送货物的生产量用(吨 公里)衡量。
2、铁路设计使用的规程和规范主要有:(铁路技术管理)规程,(铁路线路设计)规范。
3、近期通过能力是指运营后的第( 5 )年通过能力。
4、远期运量是指运营后的第(10 )年运量。
5、初期为交付运营后第( 3 )年的客货运量。
6、(机车牵引力)是与列车运行方向相同并可由司机根据需要调解的外力。
7、根据列车运行阻力的性质可分为(基本)阻力、(附加)阻力和(起动)阻力三类。
8、我国《列车牵引计算规程》中规定:以(轮周牵引力)来衡量和表示机车牵引力的大小。
.9、机车车钩牵引力是指机车用来牵引列车的牵引力,其值等于轮周牵引力减去机车全部(运行阻力)。
10、列车阻力是(机车)阻力和(车辆)阻力之和。
11、单位阻力的单位是(N/t )。
12、列车在曲线上运行比在直线上运行的阻力大,增大的部分称为(曲线附加阻力)。
13、牵引质量就是机车牵引的车列质量,也称(牵引力吨数)。
14、列车的制动距离是指(制动空走距离)和(有效制动距离)之和。
紧急制动时,对于时速120KM及以下列车,我国目前规定允许的最大制动距离为(800 )米。
15、铁路每昼夜可以通过的列车对数称为(通过能力)。
16、铁路输送能力是铁路(单方向每年)能运送的货物吨数。
17、设计线的吸引范围按运量性质划分为(直通吸引范围)和(地方吸引范围)两种。
18、铁路能力是指(运输)能力和(通过)能力。
19、正线数目是指连接并贯穿(车站)的线路的数目。
二、判断题(正确打√错误打×)1、设计线的主要技术标准在一定程度上影响线路走向的选择,同样的运输任务,采用大功率机车,可采用较大的坡度值,使线路有可能更靠近短直方向。
(√)2、紧坡地段和缓坡地段的定线方法是相同的。
竖曲线计算公式ppt课件

已知连续三个以上变坡点桩号、高程、竖曲线半径或已知一个变坡点桩号、 高程、竖曲线半径及相邻两条坡段的纵坡度,可以计算该测段内任意点的设计 高程。 计算竖曲线要素及起终点桩号; 判断计算点所在的坡段,按直线比例内插法计算切线高程; 判断计算点与竖曲线是位置关系,计算竖曲线的纵距; 判断凸、凹,切线高程与纵距的代数和即为设计高程(凸型竖曲线的纵距为 负值,凹型为正)。
视距长度st1lt2211121211222trhdrtrdh????则222222222222trhdrtrdh????则ltrhldt?????21111222111trhlt???211llrht??222222lltrhlldt???????222llllrht????rd221abs有极小值视距长度
(2)竖曲线切线长T: T = T1 = T2
T L R
22
(3)竖曲线上任一点竖距h:
h
PQ
yP
yQ
xP2 2R
(yA
i1x)
i1
xA R
xP2 2R
2xRA2
xA R
(xA
xP)
h(xPxA)2 x2
x
2R 2R
下半支曲线的竖距h:
(L x)2 h
2R
▪若设计算点离开竖曲线终点的距离为. x’,则 x’= L – x
设计高程 HS = HT - y1 = 136.55 – 1.50=135.05m (凸竖曲线应减去改正值)
.
(2)K6+180.00:位于下半支(>K6+100) 按变坡点分界计算:
横距:x2= ZD – Lcz = 6235.00 – 6180.00 =55m
竖曲线计算示意图及说明
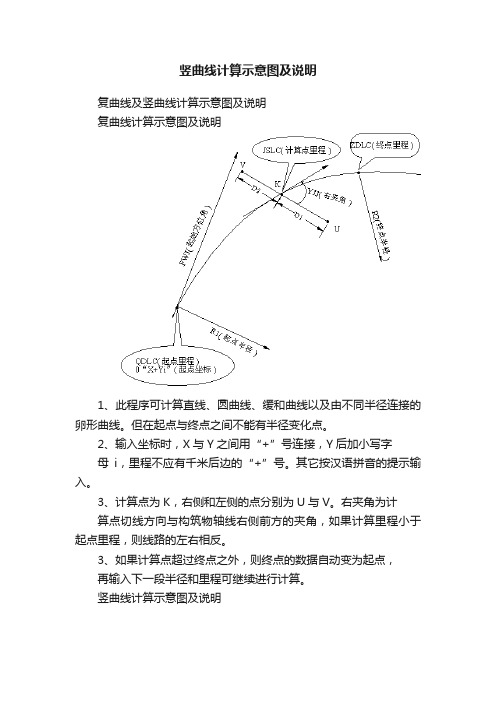
竖曲线计算示意图及说明
复曲线及竖曲线计算示意图及说明
复曲线计算示意图及说明
1、此程序可计算直线、圆曲线、缓和曲线以及由不同半径连接的卵形曲线。
但在起点与终点之间不能有半径变化点。
2、输入坐标时,X与Y之间用“+”号连接,Y后加小写字
母i,里程不应有千米后边的“+”号。
其它按汉语拼音的提示输入。
3、计算点为K,右侧和左侧的点分别为U与V。
右夹角为计
算点切线方向与构筑物轴线右侧前方的夹角,如果计算里程小于起点里程,则线路的左右相反。
3、如果计算点超过终点之外,则终点的数据自动变为起点,
再输入下一段半径和里程可继续进行计算。
竖曲线计算示意图及说明
1、竖曲线只能计算两个变坡点之间的高程。
按上图中所示的汉语拼音提示输入数据。
2、如果计算里程超过终点里程,则终点自动变为起点,然后再按提示输入下一个变坡点的数据,继续进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
竖曲线练习题
1、设在桩号K2 +600 处设一竖曲线变坡点,高程m . i1 =1%, i2 = -2%,竖曲线半径3500 m试计算竖曲线个点高程(20m整桩即能被20整除的桩号)
解:ω= i2 -i1 = -2% -1% = -3% 为凸曲线。
曲线长L = Rω= 3500× = 105 m . 切线长T = L/2 = 105÷2 = m
竖曲线起点桩号= (K2 +600 ) -= K2 +
竖曲线终点桩号= ( K2 +600) += K2 +
竖曲线起点高程= -× = m
竖曲线终点高程= -× = m
各20 m整桩
K2+560 X1 = (K2 + 560)-( K2 + = m
h1 =X2/2R = ÷7000 = m
切线高程: -[(K2 + 600) -(K2 + 560)] X = m
设计高程-= m
K2+580 X1 = (K2 + 580)-( K2 + = m
h1 =X2/2R = ÷7000 = m
切线高程: -((K2 + 600) -(K2 + 580)) X = m
设计高程-= m
K2+600 X1 = T =(K2 + 6000)-( K2 + = m
h1 =X2/2R = ÷7000 = m
切线高程: m
设计高程-= m
K2+620 X1 = (K2 + )-( K2 +620) = m
h1 =X2/2R = ÷7000 = m
切线高程: -((K2 + 620) -(K2 + 600)) X =
设计高程-= 9m
K2+640 X1 = (K2 + )-( K2 +640) = m
h1 =X2/2R = ÷7000 = m
切线高程: -[(K2 + 640 -(K2 + 600)] X = m
长度不小于500 m 。
试确定竖曲线最小半径值并计算K1 +800 、K1 +840、K1 +860 设计高程。
解:ω= i2 -i1 = % -(-)% = 4% 为凹曲线。
T = L/2 推出R = 2T/ω= 100/ = 2500 m
E = T2/2R =2500/5000 = m
竖曲线起点桩号= (K1 +840 ) -50 = K1 +790
竖曲线终点桩号= ( K1 +840) +50 = K1 +890
K1+800 X1 = (K1 + 800)-( K1+790) = 10 m
h1 =X2/2R = 100 ÷5000 = m
切线高程: -[(K1+ 840) -(K1 + 800)] X = m
设计高程+=
K1+860 切线高程: m
设计高程+=
K1+860 X1 = (K1 + 890)-( K1+860) = 30 m
h1 =X2/2R = 900 ÷5000 = m
切线高程: -[(K1+ 860) -(K1 + 800)] X = m
设计高程+=
3、某公路连续的三个变坡点桩号分别为:K8 + 700、K9 + 100、K9 + 380.对应连续设计标高分别为:m、m、m。
在变坡点K9 + 100处竖曲线半径为3000 m。
求(1)该竖曲线要素及起始点桩号(2)桩号K8 + 980、K9 + 100 K9 + 060、K9 + 150、K9 + 220设计高程.
解:(1)i1 =(-)÷ 400 = -=(-)÷ 280 =
ω= i2 -i1 = + = 为凹曲线
曲线长L = Rω= 3000× = 129 m . 切线长T = L/2 = 129÷2 = m
中心竖距 E = T2/2R = ÷6000 = m
竖曲线起点桩号= (K9 + 100 ) -= K9 +
竖曲线终点桩号= (K9 + 100) += K9 +
(2)
K9 + 060 X1 = (K9 + 060)-( K9 + = m
h1 =X2/2R = X ÷ 6000 = m
切线高程: +[(K9+ 100) -(K9 + 060)] X = m
设计高程+=
K9 + 150 X1 = (K9 + )-( K9 +150) = m
h1 =X2/2R = X ÷ 6000 = m
切线高程: +[(K9+ 150) -(K9 + 100)] X = m
设计高程: +=
K8 + 980 设计高程: +[(K9+ 100) -(K8 + 980)] X = m
K9 + 220 设计高程: +[(K9+220) -(K9 + 100)] X = m。
