格林公式
合集下载
格林公式
1 2 3
= ∫L Pdx + Qdy + ∫L Pdx + Qdy + ∫L Pdx + Qdy
1 2 3
= ∫L Pdx + Qdy
L3
D3
D2
L2
( L1, L2 , L3对D来说为正方向 )
D1
L1
L
证明(3)
若区域不止由一条闭曲 线所围成.添加直线段 AB,CE. 则 D 的边界曲线由 AB, L2 ,BA, AFC,CE, L3 , EC 及 CGA 构成. D 由(2)知
o
L
B
x
解 引入辅助曲线 L , L = OA + AB + BO
应用格林公式 ,
(
P = 0, Q = x 有
y
− ∫∫ dxdy = ∫ xdy
L D
A
D
= ∫OA xdy + ∫AB xdy + ∫BO xdy , 由于 ∫OA xdy = 0,
o
L
B
x
∫BO xdy = 0,
1 2 ∴ ∫ xdy = − ∫∫ dxdy = − πr . AB 4 D
∂P ∂ 2u ⇒ = ∂y ∂x∂y
=
∂ u ∂Q = ∂y∂x ∂x
2
(4) ⇒ (1) :
（1）对 D内任意一条闭路径 L, ∫ Pdx + Qdy = 0;
L
∂Q ∂P (4) = , ∀( x , y ) ∈ D . ∂x ∂y
D′
L D
设 L 是 D 内一条闭路径， L 所围有界闭区域 D ′ ⊂ D , 则在 D ′内 ∂ Q = ∂ P , ∂x ∂y
= ∫L Pdx + Qdy + ∫L Pdx + Qdy + ∫L Pdx + Qdy
1 2 3
= ∫L Pdx + Qdy
L3
D3
D2
L2
( L1, L2 , L3对D来说为正方向 )
D1
L1
L
证明(3)
若区域不止由一条闭曲 线所围成.添加直线段 AB,CE. 则 D 的边界曲线由 AB, L2 ,BA, AFC,CE, L3 , EC 及 CGA 构成. D 由(2)知
o
L
B
x
解 引入辅助曲线 L , L = OA + AB + BO
应用格林公式 ,
(
P = 0, Q = x 有
y
− ∫∫ dxdy = ∫ xdy
L D
A
D
= ∫OA xdy + ∫AB xdy + ∫BO xdy , 由于 ∫OA xdy = 0,
o
L
B
x
∫BO xdy = 0,
1 2 ∴ ∫ xdy = − ∫∫ dxdy = − πr . AB 4 D
∂P ∂ 2u ⇒ = ∂y ∂x∂y
=
∂ u ∂Q = ∂y∂x ∂x
2
(4) ⇒ (1) :
（1）对 D内任意一条闭路径 L, ∫ Pdx + Qdy = 0;
L
∂Q ∂P (4) = , ∀( x , y ) ∈ D . ∂x ∂y
D′
L D
设 L 是 D 内一条闭路径， L 所围有界闭区域 D ′ ⊂ D , 则在 D ′内 ∂ Q = ∂ P , ∂x ∂y
格林公式
L D
8
64 3
o
A x
例 3计算
2xydx x2dy 其中 L 为抛物线 yx2 L
上从O(0 0)到B(1 1)的一段弧
解 这里P2xy Qx2
P Q 2x 所 以 积 分 因为 y x
L
2 xydx x 2 dy 与 路 径 无 关
M
计算抛物线 ( x y ) ax ( a 0 )
曲线 AMO 表示为
解：ONA为直线 y=0
y ax x , x [ 0 , a ]
1
N
A ( a ,0 )
A
L xdy 2
1
ydx
2 ONA
xdy ydx
1
2 AMO
xdy ydx
1
2 AMO
L
x 2
解
P y Q x
y x
(x
2
2 xy ) 2 x
4
P y
Q x
，
(x y ) 2x
2
原积分与路径无关
故原式
1 0
x dx
2
1 0
( 1 y ) dy
4
23 15
.
例2. 计算 圆周
其中L 为上半 从 O (0, 0) 到 A (4, 0)
(2) 对D 中任一分段光滑曲线 L, 曲线积分 与路径无关, 只与起止点有关. (3) 在 D 内每一点都有
P y Q x .
L Pd x Qd y
例1 计算 ( x 2 xy ) dx ( x y ) dy 其中L为由点
格林公式
L1 : y 1 ( x : 1 2) L L1 L2 , 其中， 取积分路径： L2 : x 2 ( y : 1 3)
y
2 2 3 2
则
(2, 3) ．
(2,1)
4 1 ( x 1)d x 1 (2 y )d y 3
(1,1)
．
o
x
例6
y
L
o
D A(2,0) x l
5d xd y
D
0
2
8 5 x d x . 3 2
2
例4
计算
其中L为一无重点且不过原点
的分段光滑逆时针向闭曲线. 解 令 则
y
L
D
o
x
记 L 所围成的闭区域为 D .
(1) 当( 0, 0) D 时, 由格林公式知
(2) 当(0,0) D 时, 作位于 D 内圆周 l : x 2 y 2 r 2 ,
D
yx
o
x
1 0 d x x (1 x )d y . 3
1 1
例3
计0,0)到点A(2,0)的上半圆周 x y 2 x .
解
令 P x 2 2 y , Q 3 x ye y , 则
设 l : y 0 ( x : 2 0), 则 利用格林公式 , 得
1 故 . 0d x y d y xy d x y ( x )d y 0 0 (0,0) 2
(1,1) 2
计算
解
令
则
y
(1,1) ．
o
故原曲线积分在全平面内与路径无关．
(1,0)
x
L1 : y 0 ( x : 0 1) 取积分路径：L L1 L2 , 其中， L2 : x 1 ( y : 0 1) 2 2 4 ( x 2 xy )d x ( x y )d y 故 L
微积分 格林公式
A.
证明 : 例2、
2 xydx
D
x dy 0 , D 分段光滑 .
2
求 例3、 e
D
y
2
dxdy , D 是以 O ( 0 , 0 ), A ( 1 ,1 ), B ( 0 ,1 ) 为顶点 .
xdy ydx
的三角形闭区域
设 例4、 D 是包含原点的有界闭区
y
Q ( x , y ) dy
y0
y0
Q ( x 0 , y ) dy
例7、 已知 du
xdy ydx x
2
y
2
( x 0 ), 求 u ( x , y ).
P 全微分方程： ( x , y ) dx Q ( x , y ) dy 0
(
Q x
P y
)
例8、 解全微分方程 作业
(4)
Q x
P y
在 G 内处处成立 .
关键：
Q x
P y
P ( x , y ) dx
L
Q ( x , y ) dy 与路径无关
.
例5、计算
L
(x
2
2 xy ) dx ( x
2
y ) dy , 其中 L 为
4
由点 O ( 0 , 0 )到点 B ( 1 ,1 )的曲线弧 y sin
( x, y)
( x0 , y)
( x, y)
( x0 , y0 )
(1 )
u 按（1）： ( x , y ) u 按（2）： ( x , y )
( x, y0 ) ( x0 , y0 )
格林公式
L
综上所述，格林公式成立。
(注意格林公式成立的条件)
机动 目录 上页 下页 返回 结束
例 1：计算 F ( x , y ) dr ，其中 L （1） F ( x, y ) yi xj ， L 是由 x y, x 1, y 0 围
成的三角形闭路，其方向为逆时针方向； yi xj （2） F ( x , y ) 2 ， L ： x 2 y 2 a 2 , ( a 0) ，其 x y2 方向为逆时针方向。
1
2
x
则称曲线积分 L Pdx Qdy 在 D 内与路径无关，
否则称与路径有关。
机动
目录
上页
下页
返回
结束
定理 2：设 D 是平面上的一个单连通域，函数 P ( x , y )，
Q ( x , y ) 在 D 内具有一阶连续偏导数，则以下
四个条件相互等价：
（1）对 D 内的任意一条分段光滑的闭曲线 L ，
机动 目录 上页 下页 返回 结束
两式相加得
（2） 若区域 D 由分段光滑的闭 曲线围成。如图，将 D 分成三个 既是 X 型又是Y 型的区域 D1 , D2 , D3 。则
L3 D3
D2
L2
D1
L1
D
L
Q P Q P ( x y )dxdy D D ( x y )dxdy D 1 D2 3
时针方向。
解： 记 L所围成的闭区域为 D ，令
y x P 2 Q 2 2, x y x y2
则当 x y 0 时, 有
2 2
Q y2 x2 P 2 2 2 x ( x y ) y
机动 目录 上页 下页 返回 结束
综上所述，格林公式成立。
(注意格林公式成立的条件)
机动 目录 上页 下页 返回 结束
例 1：计算 F ( x , y ) dr ，其中 L （1） F ( x, y ) yi xj ， L 是由 x y, x 1, y 0 围
成的三角形闭路，其方向为逆时针方向； yi xj （2） F ( x , y ) 2 ， L ： x 2 y 2 a 2 , ( a 0) ，其 x y2 方向为逆时针方向。
1
2
x
则称曲线积分 L Pdx Qdy 在 D 内与路径无关，
否则称与路径有关。
机动
目录
上页
下页
返回
结束
定理 2：设 D 是平面上的一个单连通域，函数 P ( x , y )，
Q ( x , y ) 在 D 内具有一阶连续偏导数，则以下
四个条件相互等价：
（1）对 D 内的任意一条分段光滑的闭曲线 L ，
机动 目录 上页 下页 返回 结束
两式相加得
（2） 若区域 D 由分段光滑的闭 曲线围成。如图，将 D 分成三个 既是 X 型又是Y 型的区域 D1 , D2 , D3 。则
L3 D3
D2
L2
D1
L1
D
L
Q P Q P ( x y )dxdy D D ( x y )dxdy D 1 D2 3
时针方向。
解： 记 L所围成的闭区域为 D ，令
y x P 2 Q 2 2, x y x y2
则当 x y 0 时, 有
2 2
Q y2 x2 P 2 2 2 x ( x y ) y
机动 目录 上页 下页 返回 结束
格林公式积分方向
格林公式积分方向
格林公式是对一个闭合曲面S（也可以是一个曲线）上的散度和旋度进行积分，公式分别为：
∬S ∇·F dS = ∫L F · dr
其中，∇·F是F的散度（divergence），F是一个向量场，dS 是曲面元素面积，L是曲线路径，F · dr是向量场F在曲线路径上的微分。
在格林公式中，曲面和曲线都有一个方向，这个方向一般是由右手法则确定的。
对于曲面S来说，曲面元素面积dS的方向垂直于曲面且向外指，根据右手法则，曲线L的方向应该是沿着曲面的边界，也就是沿着曲面S的边缘的方向。
所以，在使用格林公式时，需要注意曲面和曲线的方向。
如果方向选取不当，会导致计算结果的正负错误。
一般来说，在确定曲面和曲线的方向时，可以根据实际问题的几何特点和物理规律进行选择，以保证计算结果的正确性。
10.3 格林(Green)公式
lim P ( , y )
x 0
lim P( , y ) P( x, y )
同理可得
u y
Q ( x , y ).
又由于P ( x , y ), Q ( x , y ) 连续，
所以 u ( x , y ) 可微，且
du P ( x , y ) dx Q ( x , y ) dy .
D.
由条件（1）有
Q x
,
( x, y ) E .
由格林公式有
Pdx Qdy
L
( x
E
Q
P y
) dxdy 0 .
（2）
（3）： 设
L 1 , L 2是 D
D
内任意两条由 A 到
B 的曲线， 则 L 2 L1
是
内一条正向闭曲线。由条
件（2）有
A
其中 AB 在 D 内； 与起点 A 和终点 B 有关，
即 du Pdx Qdy .
（4） Pdx Qdy 在 D 内是某一函数 u ( x , y ) 的全微分，
证 （1）
（2）： 设
L
为 D 中任一条闭曲线，
它所围成的区域记为 E , 由于D 是单连通
L
D
E
区域， 所以 E
P y
偏导数， L 是 D 的正向边界曲线， 则有
P ( x , y ) dx Q ( x , y ) dy
L
( x
D
Q
P y
) dxdy
（格林公式）
例1 求 L
xdy 2 ydx , 其中 L 是圆周 x 2 y 2 1,
§11.2(2)格林公式
Q P ∫∫D( x y )dxdy = ∫L Pdx + Qdy
4
2) 若D不满足以上条件, 则可通过加辅助线将其分割 为有限个上述形式的区域 , 如图 Q P ∫∫D( x y ) dxdy
y
1 D2 D
L
= ∑∫∫
k =1 n
n
Dk
(
Q P ) dxdy x y
Dn
o
x
= ∑∫
k =1
du = xy2 dx + x2 ydy. (0,0)( Nhomakorabea, y) .
= ∫ x 0 dx + ∫
0
x
y 2 x y dy 0
(x,0)
=∫
y 2 x y dy 0
18
xd y y d x 在右半平面 ( x > 0 ) 内存在原函 例6. 验证 2 2 x +y y 数 , 并求出它. (x, y) y x , Q= 2 证: 令 P = 2 2 x +y x + y2 2 2 o (1,0) ( x,0) x P y x Q 则 = 2 = ( x > 0) 2 2 x (x + y ) y 由定理 2 可知存在原函数 定理
Q P ∫∫ x y dxdy = ∫ Pdx + Qdy ( 格林公式 ) D L
或
∫∫ P
D
x
y
Q
dxdy = ∫ Pdx + Qdy
L
2
证明: 证明 1) 若D 既是 X - 型区域 , 又是 Y - 型区域 , 且 1(x) ≤ y ≤ 2 (x) y E D: d a ≤ x ≤b
y0 x0 x0 y y0 x
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
E
F
积分中L的方向.
oA
Bx
D
Q x
P y
dxdy
L
Pdx
Qdy
44
(2)求曲线积分时, 可利用格林公式简化计算, 若积分路径不是闭曲线, 可添加辅助线;
(3) 可用积分法求 d u P d x Q d y
在域D内的原函数:
思考题
1. 若区域 如图
为复连通域，试描
y
D
C
G
述格林公式中曲线
E
F
积分中L的方向.
oA
Bx
D
Q x
P y
dxdy
L
Pdx
Qdy
37
设区域D既是X-型 d
又是Y-型,
x
即平行于
1
(
y)
E y 2(x)
D
B
坐标轴的直线和 L 至多交于两点.
A c
oa
x 2( y) Cy 1(x)
bx
D {( x, y)1( x) y 2( x),a x b}
D {( x, y)1( y) x 2( y),c y d }
7
证明
Ñ L 2xydx x2dy 0.
14
证明 Ñ L 2xydx x2dy 0.
证: 因 P 2x y, Q x2, 则
利用格林公式
Q P
(
D
x
y
)dxdy
Ñ L Pdx
Qdy
得 Ñ L 2x y d x x2 d y 0d x d y 0 D 15
例3 计算
xdy ydx L x2 y2
Q P
Q P
( )dxdy
( )dxdy
D x y
x D1 D2 D3 y
9
Q P
Q P
Q P
( )dxdy ( )dxdy ( )dxdy
D1 x y
D2 x y
D3 x y
L1 Pdx Qdy L2 Pdx Qdy L3 Pdx Qdy
L Pdx Qdy
du x y2 dx x2 yd y
32
du x y2 dx x2 yd y
(x, y)
x
x 0dx
y x2 y dy
0
0
。
y x2 y d y 0
。
(0,0)
( x,0)
注
是全微分方程
的通解.
33
小结
一、格林公式
ÑL P d x Qd y
Q P
D
x
y
d
xd
y
L是D的取正向的边界曲线.
Q ex cos y, P ex cos y 1
x
y
AO : y 0,
y
D
d xd
y
0 1
xdx
L
D
1
o
Ax
82
23
注:
求曲线积分时, 可利用格林公式简化计算.
若积分路径不是闭曲线, 可添加辅助线, 使其成为封闭曲线，利用格林公式后， 再减去辅助线上的曲线积分.
4.平面上曲线积分与路径无关的等价条件
y
D
o
L Ax
Ñ 原式
(ex sin y x y) dx (ex cos y 1) d y
L AO
(ex sin y x y) dx (e x cos y 1) d y AO
Ñ 原式 (ex sin y x y)dx (ex cos y 1)d y L AO (ex sin y x y) dx (ex cos y 1) d y AO
定理1
的曲线积分之间的联系
设闭区域D由分段光滑的曲线L围成,
函数P x, y ,Q x, y在D上有一阶连续
偏导数，则有
L
D
(
Q x
P y
)dxdy
Ñ L
Pdx
Qdy
D
其中L取正向.?
格林公式
4
y
L
D
y
L1
D
L2
o
x
o
x
L正向：逆时针
L由L1与L2组成
规 边界曲线L的正向: 当观察者沿边界 定 行走时,区域D总在他的左边.
y y
Q ( x2 y4 ) 2x x x
O
x
P Q 原积分与路径无关
y x
29
(x,y) P x, ydx Q x, ydy
( x0 , y0 ) x
x0 P( x, y0)dx
y
Q(x, y)dy
y0
( x2 2xy)dx ( x2 y4 )dy L
B(1,1)( x2 2xy)dx ( x2 y4 )dy
Q dxdy
D x
Ñ d
dy
2 ( y) Qdx
证
Q dxdy
Q( x, y)dy
c
1 ( y) x
D x
L
d
c
Q(
2
(
y),
y)dy
d
c
Q(
1(
y),
y)dy
y
C¼BE Q( x, y)dy C¼AE Q( x, y)dy d
E
x 1( y)
Q( x, y)dy Q( x, y)dy
在D内具有一阶连续偏导数,则以下四个条件等价:
(1)沿D 中任意光滑闭曲线L,有 Ñ L Pdx Qd y 0.
(2)对D中任一分段光滑曲线L,曲线积分
Pdx Qd y 与路径无关, 只与起止点有关. L
(3)
在D内是某一函数
的全微分,
即 du( x, y) P d x Q d y
(4)在D 内每一点都有 P Q .
y x
27
由定理2知：当满足 Q P 时， x y
积分与路径无关，可以取路径为平行于
坐标轴的折线，即 x0, y0 x, y0 x, y
(x,y)
P x, y dx Q x, y dy
( x0 , y0 )
y
或
x
x0 P( x, y0 )dx
y
Q(x, y)dy
D
解 令 P 0, Q xe y2
y
则 Q P e y2 , x y
B
A
1
D
应用格林公式,有
e y2dxdy
xe y2 dy o
x
1
D
OA AB BO
xe y2dy 1 xex2dx 1 (1 e1 ).
OA
0
2
43
思考题
若区域 如图
为复连通域，试描
y
D
C
G
述格林公式中曲线
1 2 (abcos2 absin2 )d 20
ab
21
例4 计算 ex sin y x y dx e x cos y 1 dy L
其中L：x2 y2 x( y 0)从O0,0到A1,0
的上半圆周.
解 为了使用格林公式, 添加辅助线段 AO, 它与L所围区域为D , 则
格林短促的一生共发表了十篇论文，数量不多，却 包含了影响19世纪数学物理发展的宝贵思想。
一、格林公式及其应用
1.区域连通性的分类
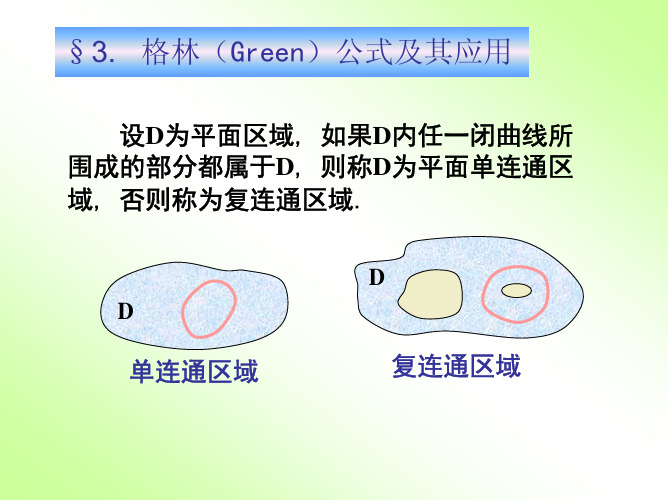
设D为平面区域, 如果D内任一闭曲线所围
成的部分都属于D, 则称D为单连通区域, 否
则称为复连通区域.
有洞
D
D
单连通区域
3
复连通区域
2.格林公式 二重积分与其区域边界上
5
注：
1.格林公式是牛顿—莱布尼兹公式的推广.
b
a f ( x)dx F (b) F (a)
2.若边界L是反方向，则
Q P
(
D
x
y
)dxdy
Ñ L Pdx
Qdy
3.区域是复连通区域时，格林公式也成立， 此时边界必须是区域的整个边界.
Q P
(
D
x
y
)dxdy
Ñ L Pdx
Qdy
证明:(1)特殊情形 y
(2) 计算平面区域面积
格林公式:
D
(
Q x
P y
)dxdy
L
Pdx
Qdy
取 P y, Q x, 得
2 dxdy L xdy ydx
D
闭区域D的面积
1
A 2 L xdy ydx
20
例3
椭圆L： xy
a cos b sin
，0
2
所围面积.
解
由求面积的公式：A
1 2
L
xdy
ydx
其中L为一条无重点,分段光滑且不经过
原点的连续闭曲线, y2
解 记L所围成的闭区域为D,
令P
y x2 y2
,
Q
x2
x
y2
,
则当 x2 y2 0 时, 有
Q x
y2 x2 ( x2 y2 )2
P y
17
(1) 当(0, 0) D 时,由格林公式 y
y0
y
y
y0 Q( x0, y)d y
x P( x, y)dx y0
x0
O
x, y
x0, y0 x, y0
x
x0
x
28
例5 计算 ( x2 2xy)dx ( x2 y4 )dy， L
其中L为由点O(0, 0)到点B(1,1)的曲线弧
y sin x .
2
y
B(1,1)
解 P ( x2 2xy) 2x
C
y
o
40
(x, y) (x,0) x