电磁学_09_稳恒磁场的高斯定理与安培环路定理
2、磁场的高斯定理和安培环路定理

L
B dl o I i
L
S
B dS 0 j dS
S
B 0 j
安培环路定理的物理意义 磁场是有旋场(或磁场是非保守场,磁感应线 是闭合曲线)。
三、安培环路定理的应用
O
R
r
例3、求长直螺线管内的磁场。设螺线管的长度为 L,共有N匝线圈,单位长度上有 n = N/L匝线圈, 通过每匝线圈电流为I。管内中间部分的磁场是均 匀的,方向与管的轴线平行,在管的外侧磁场很 弱,可以忽略不计。
B
a
b
c d [解]: 若螺线管很长,则边缘效应可以忽略,螺 线管可看成是无限长,由对称性可知管内磁场是 均匀的,方向与管的轴线平行,并由右手螺旋定 则确定。在管的外侧磁场很弱,可以忽略不计。
B dl B 2πr μ0 I ,
j I / R2
且 I j s jπr 2 (r <R)
B
1 B μ0 jr 2
μ0 Ir B 2π R 2
0 I B 2R
μ0 I r = R处 B 2π R
B
0 Ir 1 0 jr, ( r R) 2 2 R 2 0 I 1 R2 0 j , r R ) ( 2 r 2 r
例2、求均匀载流无限长圆柱导体内外的磁场分布。
[解]:当r R时 B dl B 2r 0 I
L
I
R
μ0 I B 2π r
I 由 j πR 2
1 R2 B μ0 j 2 r
(r >R)
I jπR2
r
L
L
高斯定理和安培环路定理

r R 时在圆柱面内做一圆周
B cos dl B dl B 2r 0
L L
dI ' dI
P
B0
例 无限大平面电流的磁场.有一无限大的导体平面,均匀地 流着自下而上的面电流.设其电流线密度(垂直于电流线的单 位长度上的电流)为a,求距平面为d的任一点的磁感应强度B.
2、任意两条磁力线在空间不相交。 3、磁力线与电流方向之间可以用右手定则表示。
二.磁通量
磁场的高斯定理
静电场: e E dS qi / 0 S 磁 场: B dS ?
B dN dS
d B dS BS cos
m
通过面元的磁力线条数 —— 通过该面元的磁通量
(1)设闭合曲线L在垂直于无限长载流导线的平面内,电流I穿 过L. 设闭合回路 L为圆形回路( L 与 I 成右螺旋)
载流长直导线的磁感强 度为 0I B 2π R 0I l B d l 2 π R d l 0I l B d l 2 π R l d l
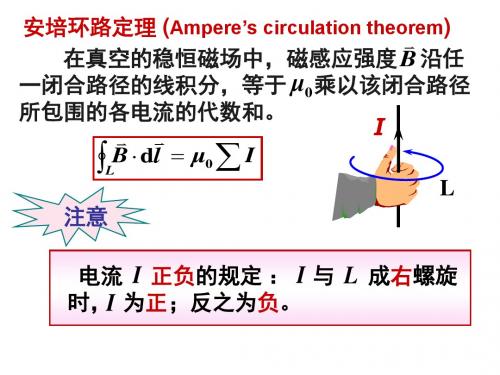
即在真空的稳恒磁场中,磁感应强度 B 沿任
讨论 (1) 积分回路方向与电流方向呈右手螺旋关系 满足右螺旋关系时 I i 0 反之 I i 0
(2) 安培环路定理只适用于闭合的载流导线,对于任意设想 的一段载流导线不成立
例如 图中载流直导线, 设 θ 1 θ 2 / 4 则 L 的环流为:
B dl
L
I
2
L 4a cos1 cos 2 dl
2 2 2a
0 I
a
0 I
4a
2
0 2I
2
L
0 I
磁场的高斯定理和安培环路定理

解:
Bp
发生变化. 发生变化.
I2 I1
∫
L
B dl 不发生变化 P
L
例如: 例如: I1 >0 L I2<0 I1 I2 I3 L I L
I3
∫
L
B dl = o ( I1 I 2 )
∫
L
B dl = o ( I1 + I 3 )
∫ B dl
l
= 4 0 I
二,安培环路定理
∑Ii
i =0
§8-4
稳恒磁场的高斯定理与 安培环路定理
一,稳恒磁场的高斯定理
由磁感应线的闭合性可知, 对任意闭合曲面, 由磁感应线的闭合性可知 , 对任意闭合曲面 , 穿入的磁感应线条数与穿出的磁感应线条数相同, 穿入的磁感应线条数与穿出的磁感应线条数相同 , 因此,通过任何闭合曲面的磁通量为零. 因此,通过任何闭合曲面的磁通量为零.
Φ = BS 2 = (6i + 3 j + 1.5k ) (0.15) i = 0.135Wb ( 2) z Φ = ∫∫ B dS = 0
S
O l
x
l
l
一长直导线通有电流I 距其d 例,一长直导线通有电流I,距其d处有 一长为a 宽为b的长方形, 一长为a,宽为b的长方形,求通过这个 长方形的磁通量. 长方形的磁通量.
n
闭合回路所包围的所有电流 的代数和. 的代数和. 所取的闭合路径上各点的磁 感强度值, 感强度值,是由闭合路径内 外所有的电流产生的. 外所有的电流产生的.即是 由空间所有的电流产生的. 由空间所有的电流产生的.
B
二,安培环路定理
定理的物理意义 由安培环路定理可以看出, 由安培环路定理可以看出,由于 磁场中的磁感强度的环流一般不 为零,所以磁场是非保守场 非保守场. 为零,所以磁场是非保守场.
高二物理竞赛课件:磁场的高斯定理和安培环路定理

作一安培回路如图: bc和 da两边被电流平面 等分。ab和cd 与电流平 面平行,则有
dB' dB
dB''
dl'
l pd c
o dl''
ab
方向如图所示。
结果:在无限大均匀平面电流的两侧的磁场都 为均匀磁场,并且大小相等,但方向相反。
14
是与环共轴的一系列同心圆。
11
设螺绕环的半径为
,共有N 匝线圈。
以平均半径 作圆为安培回路 L得:
R
L
n 为单位长度上的匝数。
其磁场方向与电流满足右手螺旋。 同理可求得在螺绕管外部的磁场为零:
12
例4:设一无限大导体薄平板垂直于纸面放置,
其上有方向垂直于纸面朝外的电流通过,面电流
密度为 j ,求无限大平板电流的磁场分布。
其方向与电流满足右手螺旋法则。
10
例3: 求载流螺绕环内的磁场。 解:设环很细,环的平均半径为R , 总匝数为N,通有电流强度为 I。
磁场的结构与长直螺旋管类似, 环内磁场只能平行于线圈的轴线 (即每一个圆线圈过圆心的垂线)
根据对称性知,在与环共轴的
圆周上磁感应强度的大小相等,
p
方向沿圆周的切线方向。磁感线
表达式
符号规定:穿过回路 L 的电
流方向与 L 的环绕方向服从右 手关系的,I 为正,否则为负。
不穿过回路边界所围面积的电流不计在内。
3
2. 安培环路定理的证明:无限长直电流的磁场 在围绕单根载流导线的垂直平面内的圆回路 。
在围绕单根载流导线的 垂直平面内的任一回路。
r
4
闭合路径L不包围电流 ,在垂直平面内的任一回路
磁场的高斯定理和安培环路定理课件

03
安培环路定理的介绍与推导
安培环路定理的基本概念
总结词
安培环路定理是描述磁场散布的重要定理之一,它指出磁场线总是闭合的,且穿过任意一个封闭曲面的磁通量为 零。
详细描述
安培环路定理是电磁学中的基本定理之一,它描述了磁场线的性质和散布规律。根据安培环路定理,磁场线总是 闭合的,即磁场线不会中断或消失,而是形成一个完整的闭合曲线。此外,安培环路定理还指出,穿过任意一个 封闭曲面的磁通量为零,即磁场线不会从一个区域穿入另一个区域。
磁力线
磁感应强度
描述磁场强弱的物理量,单位是特斯 拉或高斯。
描述磁场散布的几何图形,磁力线闭 合且不相交,磁力线的疏密程度表示 磁场强弱。
高斯定理的背景与定义
高斯定理的背景
磁场在空间中的散布具有闭合性 ,即穿过某一封闭曲面S的磁通量 等于零或无穷大。
高斯定理的定义
穿过任意封闭曲面S的磁通量等于 该封闭曲面所包围的净磁荷量。
04
高斯定理与安培环路定理的比较与联系
两者之间的类似之处
闭合曲面的磁场通量
高斯定理和安培环路定理都涉及到闭合曲面的磁场通量。在高斯定理中,磁场 通量是通过闭合曲面进入或离开某一区域的量,而在安培环路定理中,磁场通 量与电流和闭合曲面的关系是关键。
无源磁场
高斯定理适用于无源磁场,即没有电流源的磁场。同样地,安培环路定理也适 用于无源磁场的情况。
高斯定理的应用场景
01
02
03
磁场散布分析
通过高斯定理可以分析磁 场在空间中的散布情况, 确定磁力线的走向和强弱 。
磁荷检测
高斯定理可以用于检测磁 场中的磁荷散布,例如磁 铁、发电机和电动机中的 磁荷散布。
磁场屏蔽
磁场高斯定理 安培环路定理
R
例题 无限大平板电流的磁场分布。设一无限大导体 薄平板垂直于纸面放置,其上有方向垂直于纸面朝外 的电流通过,面电流密度(即指通过与电流方向垂直 的单位长度的电流)到处均匀。大小为 j 。
解:视为无限多平行长 直电流的场。 分析求场点p的对称性 做 po 垂线,取对称的 长直电流元,其合磁场 方向平行于电流平面。
多电流情况
I1
I2
I3
B B1 B2 B3 B d l 0 ( I 2 I 3 )
l
l
以上结果对任意形状 的闭合电流(伸向无限远 的电流)均成立.
n B dl 0 Ii i 1
安培环路定理
2. 明确几点 (1) 电流正负规定:电流方向与环路方向满足 右手定则时电流 I取正;反之取负。 (2) B 是指环路上一点的磁感应强度,不是任 意点的,它是空间所有电流共同产生的。
I
a
b
B
B d l lb c d d a c B d l B d l B d l B d l Bab
a
得长直载流螺线管内的磁场: B μ0 nI 无限长载流螺线管内部磁场处处相等 , 外 部磁场为零。
B
b
l
在无限大均匀平面电流的两侧的磁场都为均 匀磁场,并且大小相等,但方向相反。
同轴电缆的内导体圆柱
半径为R1,外导体圆筒内外
半径分别为R2、 R3,电缆载 有电流I,求磁场的分布。
课堂练习
0 I B r r R1 2 2 R1 0 I B R1 r R2 2 r 2 2 0 I ( R3 r ) B r R2 2 2 2 r ( R3 R2 )
高二物理竞赛课件:磁场的高斯定理及安培环路定理

l Bdl
0 I dl
2πR
0 I
B
dl
R
l
2) 复杂点情形——任意形状的环路
在r 处
B 0I 2 r
B dl Bdl cos Brd
L
2 0I d 0 2
0I
思考:若I 反向或环路反向?
B dl l
0 I
I
•
d
B
r dl
O
d
r
PB
N
M dl
➢环路不包围直导线
B dl B dl B dl
磁场的高斯定理及安培环路定理
磁场的高斯定理及安培环路定理
一、磁力线 (磁场线、磁感线)
1. 磁场线的大小与方向 方向:切线方向表示该点处的磁场方向 2. 磁场线的性质 (1) 任意两条磁场线不相交 (2) 任意磁场线都是闭合曲线
大小:B dN m
dS
(3) 磁场线与形成磁场的电流互相套连,成右螺关系
dS1
1
B1
B2
dΦ1 B1 dS1 0
当磁力线穿入时
2
2
B d S 0——磁场高斯定理
S
dΦ2 B2 dS2 0
意义:说明磁场是无源场
例1、如图所示,求均匀磁场中下曲面的 磁通量
解法一:直接求解
B
n S2
m dm B dS 很难计算
S1
解法二:利用高斯定理
B d S 0 S
S1
将顶端圆面补全,构成一个闭合曲面。
B d S B d S B d S 0 B d S BSB2cdosS
S
S1
S2
S1
S2
三、安培环路定理
l E dl 0 l B dl ?
磁场的高斯定理和安培环路定理

乘以该闭合路径所包围的各电流的代数和.
B d l B d l B d l B d l B d l 二 安培环路定理的应用举例
二 磁通量 磁场的高斯定理
l 无限长载流螺线管内部磁场处处相等 ,M 外部磁场为零. N NO O P PM
oR
l
B dl0I dl
l 2πRl
设闭合回路 l 为圆形
lBdl0I
回路(l 与 I成右螺旋)
I
o
B
dl
R
若回路绕向化为逆时针时,则
lB dl 20 π I0 2πd0I
l
I
d
dl
B
r
对任意形状的回路
B dl0Ird0Id
2πr 2π
l
l 与 I成右螺旋
Bdl
l
0I
电流在回路之外
d
( 0 I1I2)
I1
I1
I2 I3
L
I1
问 1)B是否与回路 L外电流有关?
2)若 Bdl 0,是否回路 L上各处 B0? L
是否回路 L内无电流穿过?
以上结果对任意形状的闭合电流(伸向无限远的电流)均成立.
二 安培环路定理的应用举例 电流 正负的规定 : 与 成右螺旋时, 为正;
设闭合回路 为圆形回路( 与 成右螺旋)
I
B1
r1
B2
dl1
dl2
r2
l
B12π0Ir1,B22π0Ir2
B 1dl1B 2dl2 20 πId
B 1 d l 1 B 2 d l 2 0
lBdl 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九讲 稳恒磁场的高斯定理与安培环路定理01 磁感应线为描述空间磁场的分布,人为引入一系列假想的曲线(1831年法拉第首次引入)。
曲线的疏密反映磁感应强度的大小,曲线每一点切线方向表示磁感应强度的方向。
这些假想的曲线称为磁感应线。
如图XCH003_106所示,在磁场分布的空间一点选取一面积元dS ,面积元法线方向用单位矢量n表示,该面积元在磁感应强度方向上的投影大小dS ⊥。
磁感应强度大小: m d B dS ⊥Φ= —— 通过垂直B 方向上单位面积的磁感应线条数,也称为磁感应线密度 磁感应强度方向沿该点磁感应线的切线方向,即小磁针放在该点静止时,N 所指的方向。
02 磁通量如图XCH003_106所示,通过dS 的磁通量:m d B dS Φ=⋅02πθ≤< —— m d Φ为正;2πθπ<≤ —— m d Φ为负穿过曲面S 的磁通量:m S B dS Φ=⋅⎰ —— 如图XCH003_097所示规定面元法线方向由里向外为正,如图XCH003_107所示,通过一个闭合曲面S 的磁通量:Sm B dS Φ=⋅⎰ —— 穿过闭合曲面S 的磁通量为净穿过闭合曲面磁感应线的总条数 03 磁场的高斯定理0SB dS ⋅≡⎰ —— 无源场 由于磁感应线是闭合线,因此,对于一个闭合曲面S ,穿入的磁感应线的总数必然等于穿出的磁感应线总数,即通过任一闭合曲面的磁通量总是零。
稳恒磁场的高斯定理是电磁场理论的基本方程之一。
04 安培环路定理1安培环路定理在恒定电流产生的磁场中,磁感应强度沿任一闭合回路L 的线积分,等于闭合回路包围的所有电流代数和的0μ倍。
0int L LB dr I μ⋅=∑⎰ —— 安培环路定理的数学表达式 安培环路定理的证明1) 无限长载流直导线 —— 平面闭合回路L 垂直于导线,回路绕行方向和电流满足右手螺旋关系 导线周围的磁感应强度:02I B rμπ=,如图XCH003_126所示。
0cos 2L L I B dr dr r μθπ⋅=⎰⎰由几何关系:cos dr rd θα=22000022L Id I B dr d ππμαμαππ⋅==⎰⎰⎰ −−→ 0LB dr I μ⋅=⎰2) 无限长载流直导线 —— 平面闭合回路垂直于导线,回路绕行和电流不满足右手螺旋关系,如图XCH003_126_01所示。
0cos 2L L I B dr dr r μθπ⋅=⎰⎰—— cos cos()dr dr rd θπθα-=-= 2000222L Id I B dr πμαμπππ⋅=-=-⋅⎰⎰ 0LB dr I μ⋅=-⎰ —— 电流I 对环路积分的贡献与电流方向有关 —— 规定电流与闭合回路绕行方向满足右手螺旋关系时,对回路积分贡献为正3) 无限长载流直导线 —— 平面闭合回路L 不垂直于导线,绕行方向和电流满足右手螺旋关系 dr 在电流方向和垂直于电流方向投影://dr dr dr ⊥=+ —— 如图XCH003_126_02所示//L L LB dr B dr B dr ⊥⋅=⋅+⋅⎰⎰⎰ 0LB dr ⊥⋅=⎰ —— dr ⊥ 与电流同方向,与磁场垂直//cos L LB dr B dr θ⋅=⎰⎰ —— 如图XCH003_126_03所示 //cos dr rd θα= —— 02I B rμπ= 20002L Id B dr I πμαμπ⋅==⎰⎰4) 无限长载流直导线 —— 平面闭合回路L 不包围电流,如图XCH003_127所示。
12L L L B dr B dr B dr ⋅=⋅+⋅⎰⎰⎰120022L L L I I B dr d d μμααππ⋅=+⎰⎰⎰ 200()22L I I d μμααππ=-⎰ —— 积分方向与电流不是右手螺旋关系00()022L I I B dr μμααππ⋅=+-=⎰ 5) 任意形状电流___闭合回路为非平面___多个电流同时存在的情况可以证明安培环路定理依然成立:0int L LB dr I μ⋅=∑⎰ 如图XCH003_126_04所示。
安培环路定理的意义0int L LB dr I μ⋅=∑⎰ —— 与L 形状大小无关,只与闭合回路包围的电流有关 0int L LB dr I μ⋅=∑⎰ —— 与闭合回路的绕行方向满足右手螺旋关系的电流对积分贡献为正,反之为负,式中的磁感应强度是空间所有电流在积分回路上共同产生的。
闭合回路与包围电流的含义:与闭合回路相铰链的电流为回路包围的电流,如图XCH003_128_01所示的电流1和电流2为回路包围的电流,电流3和电流4则不是。
对环路L 的积分:012()LB dr I I μ⋅=-⎰ 如图XCH003_128_02所示的螺旋型电流,可以看作是电流回路cfabc 和电流回路cdefc 形成的。
对环路L 的积分:0int L LB dr I μ⋅=∑⎰ —— int 2I I I I =+= 02LB dr I μ⋅=⎰05安培环路定理的应用1) 分析电流分布的对称性无限长均匀载流直导线、圆柱面、圆柱体;无限长载流直螺线管、环形载流螺线管;无限大载流平面。
2) 分析磁场分布对称性无限长均匀载流导线、圆柱面、圆柱体:磁力线为环绕中心轴线的同心圆,一个圆环上各点的磁感应强度大小相等,方向沿切线方向。
无限长直螺线管:管内磁场沿轴线方向,同一条磁力线上各点磁感应强度大小相等。
环形螺线管:管内磁场沿环形切线方向,同一个圆环上各点磁感应强度大小相等。
各种电流分布产生的磁场,磁感应强度方向总是与电流方向满足右手螺旋关系。
3) 选取积分回路回路上各点磁感应强度大小为常数、方向沿回路各点切线方向,或回路上部分磁感应强度积分为零,部分磁场为常数;规定闭合回路绕行的正方向。
4) 应用安培环路定理根据0int L LB dr I μ⋅=∑⎰ 进行计算 5) 对于电流分布不对称的情况由安培环路定理计算对称电流的磁场,再应用磁场叠加原理计算。
计算无限长均匀载流圆柱面在空间产生的磁场。
设电流为I ,圆柱面半径为R 。
电流具有轴对称分布特点,磁场具有轴对称性 —— 到轴线距离相同的点,磁感应强度大小相等 假设距轴线r 处点磁感应强度可分解为三个垂直方向:,r a t B B and B ,如图XCH003_129_01所示选取半径为r ,底面积和侧面积分别是S and S '∆∆的圆柱面为高斯面。
应用高斯定理:0SB dS ⋅=⎰ ()0a a r B S B S B S '∆+-∆+∆=0r B = —— 磁场在垂直于轴线方向上无分量再在通电圆柱面外选取一个矩形闭合回路,回路正方向为顺时针,如图XCH003_129_02所示。
应用安培环路定理:0i LB dr I μ⋅=∑⎰ —— ()0a a B l B l '∆+-∆= a aB B '= —— 意味着到轴线距离不相同的点,磁感应强度大小相等 根据电流分布的特点,磁场应该为非均匀分布,因此:0a aB B '== —— 磁场在平行于轴线方向上无分量 通电圆柱面在空间激发的磁场:磁感应线为许多簇同心圆,同一个圆上各点的磁感应强度大小相等,方向沿各点的切线方向。
圆柱面外磁场的计算选取半径()r r R >的圆为闭合回路,如图XCH003_129_03所示应用安培环路定理:02LB dr B r I πμ⋅=⋅=⎰ 02I B rμπ= —— 与无限长载流直导线产生磁场一致 圆柱面内磁场的计算选取半径()r r R <的圆为闭合回路,如图XCH003_129_04所示应用安培环路定理:20LB dr B r π⋅=⋅=⎰ 0B = —— 磁场分布如图XCH003_129_05所示计算无限长均匀载流圆柱导体产生的磁场。
设均匀电流I 在圆柱面内,圆柱体半径为R 。
如图XCH003_141_00所示电流具有轴对称分布特点,磁场具有轴对称性,即到轴线距离相同的点,磁感应强度大小相等;距离不同的点,磁感应强度不同。
磁场线为许多簇同心圆,同一个圆上各点的磁感应强度大小相等,方向沿各点的切线方向。
r R >区域:取半径为()r r R >的圆为闭合回路,如图XCH003_141_01所示应用安培环路定理:02LB dr B r I πμ⋅=⋅=⎰ 02I B rμπ= —— 与无限长载流直导线和通电圆柱面产生磁场一致 r R <区域:取半径为()r r R <的圆为闭合回路,如图XCH003_141_02所示。
应用安培环路定理:02B r I πμ'⋅=22()I I jS r R ππ'== 2022I B r r R πμππ⋅= 022I B r R μπ= 磁场分布如图XCH003_141_03所示计算长直螺线管内部的磁场。
已知长直螺线管单位长度的匝数为n ,导线内通有电流I 。
根据电流分布的对称性,可以得出管内磁感应线是一系列于轴线平行的直线,到轴线相同的点,磁感应强度大小相等。
长直螺线管的外部,可以认为场强近似为0。
P 点的磁感应强度的计算:过P 点作矩形闭合路径L L 的线积分:由于P通电螺绕环,总匝数为N ,导线内通有电流I ,假设螺绕环的半径比环管的截面半径大许多。
求空间磁场分布。
环内的磁力线为同心圆,同一条磁力线上各点的磁感应强度大小相等,如图XCH003_130所示。
区域:12r r r <<:应用安培环路定理:02L B dr B r NI πμ⋅=⋅=⎰ —— 02NI B rμπ= 螺绕环的半径比环管的截面半径大许多:121()2r R r r ≈=+ 02NI B Rμπ= 0B nI μ= —— 2N n R π=:螺绕环单位长度的匝数 1r r <的空间:00i L iB dr I μ⋅==∑⎰ —— 0B = 2r r >的空间:00i L iB dr I μ⋅==∑⎰ —— 0B =空气中有一半径为r 的“无限长”直圆柱金属导体,竖直线OO '为其中心轴线,在圆柱体内挖一个直径为12r 的圆柱空洞,空洞侧面与OO '相切,在未挖洞部分通以均匀分布的电流I ,方向沿OO '向下,如图Q_02178_03所示,在距轴线3r 处有一电子(电量为e -)沿平行于OO '轴方向,在中心轴线OO '和空洞轴线所决定的平面内,向下以速度 v 飞经P 点,求电子经P 点时所受的力。
利用补偿法计算P 点磁感应强度(负电流法)P 点的磁感应强度由电流密度为22(/16)I j r r π=-半径为r 、电流向下的“无限长”直圆柱金属导体和电流密度为:22(/16)I j r r π=-半径为/4r 、电流向上“无限长”直圆柱金属导体共同产生的。
