第六章状态反馈和状态观测器1
实验6_状态反馈与状态观测器

自动控制原理实验报告院系名称:仪器科学与光电工程学院班级:141715班姓名:武洋学号:14171073实验六状态反馈与状态观测器一、实验目的1. 掌握用状态反馈进行极点配置的方法。
2. 了解带有状态观测器的状态反馈系统。
3. 理解系统极点、观测器极点与系统性能、状态估计误差之间的关系。
二、实验内容1. 系统G(s)=10.05s 2+s+1如图2.6.1所示,要求设计状态反馈阵K ,使动态性能指标满足超调量%5%≤σ,峰值时间st p 5.0≤。
图2.6.1二阶系统结构图2.被控对象传递函数为57.103945.3100)(2++=S S s G写成状态方程形式为CX Y Bu AX X =+=式中⎥⎦⎤⎢⎣⎡--=945.357.10310A ;⎥⎦⎤⎢⎣⎡=10B ;[]0100=C为其配置系统极点为S 1,2=−7.35±j7.5; 观测器极点为Z 1,2=0.712±j0.22。
分别计算状态反馈增益阵和观测矩阵,并进行实验验证。
分别改变几组系统极点和观测器极点,各自比较系统阶跃响应差异。
被控对象的模拟电路图如图2.6.2所示。
图2.6.2 模拟电路图带有状态观测器的状态反馈系统方框图如图2.6.3所示图2.6.3 计算机实现带有状态观测器的状态反馈系统图图2.6.3中虚线内表示连续域转换成离散域在计算机中的实现方法: 其中AT e G = B dt t H T⎪⎭⎫ ⎝⎛=⎰0)(ϕAte t =)(ϕ21⨯---K 维状态反馈系数矩阵,由计算机算出。
12⨯---L 维观测器的反馈矩阵,由计算机算出。
---Kr 为使)(t y 跟踪)(t r 所乘的比例系数。
三、 实验原理1. 闭环系统的动态性能与系统的特征根密切相关,在状态空间的分析中可利用状态反馈来配置系统的闭环极点。
这种校正手段能提供更多的校正信息,在形成最优控制率、抑制或消除扰动影响、实现系统解耦等方面获得广泛应用。
6.4 状态观测器-1

0 b 1
渐近状态观测器(8/9)
显然,系统能控能观
0 A Gc 2 1 h0 [2 3 h1 2 h0 0] 2 2 h1 1 3
观测器特征方程为
I ( A G c ) (2 h0 3) (6 h0 2 h1 2) 0
ˆ x
C
ˆ y
∫
图6-4 渐近状态观测器的结构图 下面分析状态估计误差是否能趋于零
渐近状态观测器(5/9)
下面分析状态估计误差是否能趋于零. 先定义如下状态估计 误差:
ˆ x x -x
则有
ˆ ˆ ˆ x ( x - x ) A ( x - x )- G ( y - y ) ˆ ˆ A ( x - x )- G C ( x - x ) ˆ ( A - G C )( x - x )
ˆ ˆ ˆ x Ax Bu G ( y y) ˆ ˆ y Cx
其中G称为状态观测器的反馈矩阵
该状态估计器称为全维状态观测器, 简称为状态观测器, 其结构如下图所示
渐近状态观测器(4/9)
u B
+ +
x'
x
y C
∫
A
+ G + B + 闭环状态观测器 A
ˆ x
+ x ˆ
其中A-GC称为状态观测器的系统矩阵 根据上述误差方程,被控系统(A,B,C)的渐近状态观测器, 亦可简记为( A GC, B, C ) 上述误差方程的解为
x (t ) e
A GC t A GC t
x (0) e
x (0)
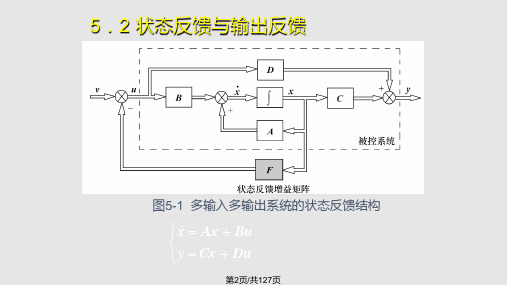
状态反馈与状态观测器
的逆_矩_ 阵,c即
o(A,B,C)
化为能控o (标A准, B型,C)
Tc
的变换矩阵
A Tc 1 ATc ; B Tc 1B ; C CTc
Tc1
B
AB
an1
A n 1 B
a1 1
a1
1
1
1
(5-31)
第19页/共127页
的能o (控A性, B,,但C不) 一
定理5-2 输出反馈不改变被控系统
的能控性与能观o (性A,。B,C)
第8页/共127页
5.4 闭环系统极点配置
状态反证馈明不改5变.2节被已控说系明统,的输能出控反性馈,故H可输等出效反为馈不改变的被状控态系反统馈的,能又控由性F定。理 5H-1C知,
可从系统能观性的PBH秩判据出发证明输出反馈不改变被控系统
(1)若被控系统
o (A, B,C)
x Ax Bu 状态完全能控,且设其特征多项式 y和传C递x函数分别为
第10页/共127页
fo (s) det sI A s n a1s n1 an1s an (5-16)
Go
(s)
C (sI
A)1 B
b1s n1 b2 s n2 bn1s s n a1s n1 an1s
等,即令
,由两个n阶特征多项式对应项系数相等,可得n个关于
的联立代数方程,若
能控,解联立方程可求出唯一解
。
pF (s) p (s)
f1 f2 fn
o (A, B,C)
f1 f2 fn
第20页/共127页
【例5-2】被控系统
的状态o空(A间,表B,达C式) 为
x
1 0
北航_自控实验报告_状态反馈和状态观测器

北航_自控实验报告_状态反馈和状态观测器摘要:本实验通过对一个质点的运动进行实时控制的实验研究,了解了状态反馈和状态观测器的原理和应用。
通过实验验证了状态反馈和状态观测器在控制系统中的重要性和有效性。
1引言状态反馈和状态观测器是控制系统中常用的两种控制方法,可以实现对系统状态的准确估计和实时控制。
在实际控制应用中,状态反馈和状态观测器广泛应用于电力系统、轨道交通系统等领域。
本实验通过对一个质点运动的控制,以实验方式掌握状态反馈和状态观测器的原理和应用。
2实验目的2.1理解状态反馈和状态观测器的原理;2.2 学会使用Matlab编程实现状态反馈和状态观测器;2.3通过实验验证状态反馈和状态观测器的有效性。
3实验内容与方法3.1实验设备本实验所需设备和材料有:计算机、Matlab软件。
3.2系统建模通过对质点的运动进行建模,得到系统的状态空间方程,用于状态反馈和状态观测器的设计。
3.3状态反馈设计根据系统建模和状态反馈的原理,设计状态反馈控制器,并进行仿真实验。
3.4状态观测器设计根据系统建模和状态观测器的原理,设计状态观测器,并进行仿真实验。
4实验结果与分析4.1状态反馈实验结果在进行状态反馈实验时,观察到质点运动的稳定性得到了明显提高,达到了预期的控制效果。
4.2状态观测器实验结果在进行状态观测器实验时,观察到对系统状态的估计准确性得到了明显提高,状态观测器的设计能够很好地预测系统状态变化。
5结论本实验通过对一个质点运动进行实时控制的实验研究,学习并实践了状态反馈和状态观测器的原理和应用。
通过实验验证了状态反馈和状态观测器在控制系统中的重要性和有效性。
实验结果表明,状态反馈和状态观测器能够有效改善系统的稳定性和估计准确性,达到了实时控制的目的。
[1]袁永安.现代控制理论与技术[M].北京:中国电力出版社。
[2]何国平,刘德海.控制系统设计与应用[M].北京:中国电力出版社。
[3]王晓红.状态反馈和状态观测在电力系统控制中的应用[J].电网技术,2024。
chapter6极点配置与状态观测器

K
6.3 状态观测器
用 ~x 代替 x
自然要求:
x~ x
渐近意义下: lim~x x 0 t
6.3 状态观测器
uB B
x ∫
+
A
E + x~ ∫
+
A
x
y
C
+
x~ C ~y 观测器
x~
6.3 状态观测器
u
y
+
E
B
+
x~
∫
x~
~y -
C
+
A
观测器
观测器状态方程
x~ A EC x~ Bu Ey
是否可以利用状态反馈,达到极点的 任意配置?
Im
s平面
0
Re
6.2 极点配置
6.2.1 极点配置定理 定理 6.2.1 给定系统
x Ax Bu :
y Cx Du
通过状态反馈 u v kx 任意配置极点的充
要条件 完全能控。
证: 只就单输入系统的情况证明本定理
6.2 极点配置
Re
响应快 响应慢
6.2 极点配置 在看一例:
Im
s平面
0
Re
稳定
6.2 极点配置
2阶系统 3阶系统
1阶系统
6.2 极点配置
Im
s平面
0
Re
稳定
6.2 极点配置
2阶系统 1阶系统
3阶系统
6.2 极点配置
状态反馈后系统极点
v
uB
-
x
∫
x
y
C
+
A
K
现代控制理论6状态观测器设计ppt课件

C 0
0 0 2
1
1
,B
1
2 0
1
0 1
设计观测器,使其极点配置在-3,-4,-5上。
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
• 例:设系统的系数矩阵为:
1
A
3
0
• 对于完全能控的系统,状态反馈可任意 配置闭环系统的极点,从而使得闭环系 统具有期望的稳态和动态性能。
• 条件:所有的状态变量可测。 • 实际系统,状态变量未必都可以直接测
量到。 • 状态能观性说明:系统是状态能观的,
则系统的任意状态信息必定在系统的输 出中得到反映。
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
• 问题:如何用系统的外部输入输出信息 来确定系统的内部状态?
• 观测器设计问题 • 观测器的输出就是系统状态的估计值。
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
6.1 观测器设计
• 已知系统模型
问题:如何从系统的输入输出数据得到系 统的状态?
现代控制理论第六章

的列向量可以由 [ B AB A B] 的列向量 的线性组合表示。这意味着
rankuc ' ≤ rankuc
n1
系统 也可看成是由系统 K 经过状态反馈
( K,I ) 而获得的,因此,同理有
rankuc rankuc '
所以系统 K 的能控性等价于系统 的能控性,
于是定理得证。
例 6.1.1
系统
1 2 0 & : x x 1 u 3 1
y [1 2]x
完全能控能观,引入反馈
u [3 1]x V
则闭环系统 K的状态空间表达式为
1 2 0 & K : x x 1 v 0 0
1 式(6.3.2)可写为 y(s) G(s)u(s) C (sI A) Bu (s)
y1 ( s ) g11 ( s )u1 ( s ) g12 ( s )u2 ( s ) L L g1 p ( s )u p ( s ) y2 ( s ) g 21 ( s )u1 ( s ) g 22 ( s )u2 ( s ) L L g 2 p ( s )u p ( s ) M M yq ( s ) g q1 ( s )u1 ( s ) g q 2 ( s )u2 ( s ) L L g qp ( s )u p ( s )
y [1 2]x
不难判断,系统 K 仍然是能控的,但已不再 能观测。
6.2 极点配置
6.2.1 极点配臵定理 定理 6.2.1 给定系统
:
& x Ax Bu y Cx Du
u v kx
任意配臵极点的充
通过状态反馈
要条件 完全能控。
现代控制理论之状态反馈与状态观测器介绍课件

状态反馈的设计方法
确定系统状态方程
设计状态反馈控制器
计算状态反馈增益矩阵
验证状态反馈控制器的性能
状态反馈的优缺点
优点:能够有效地减小系统的动态响应时间,提高系统的稳定性和动态性能。
优点:可以实现对系统的解耦控制,使得系统的控制更加简单和直观。
现代控制理论之状态反馈与状态观测器介绍课件
演讲人
01.
状态反馈
02.
03.
目录
状态观测器
状态反馈与状态观测器的关系
状态反馈
状态反馈的基本概念
状态反馈是一种控制策略,通过调整系统的状态来达到控制目标。
状态反馈控制器的设计基于系统的状态方程,通过调整输入信号来影响系统的状态。
状态反馈控制器可以改善系统的动态性能,提高系统的稳定性和鲁棒性。
04
状态反馈与状态观测器的区别
状态反馈需要知道系统的模型,状态观测器不需要知道系统的模型
04
状态反馈用于控制系统,状态观测器用于估计系统状态
03
状态观测器:通过观测系统的输出,估计系统的状态
02
状态反馈:通过调整系统的输入,使系统达到期望的状态
01
状态反馈与状态观测器在实际应用中的选择
状态反馈适用于系统模型已知且可控的情况,能够实现最优控制。
02
状态观测器通过测量系统的输入和输出,利用数学模型来估计系统的内部状态。
04
状态观测器在现代控制理论中具有重要地位,广泛应用于各种控制系统的设计与实现。
状态观测器的设计方法
状态观测器性能评估:通过仿真或实验,评估观测器的性能,如观测精度、响应速度等
