地理信息系统算法第三章
地理信息系统链式编码ppt下载

J(Y)
K(Z)
7 444
454
554 555
6
541
5
405
505
515
4 400
415 500
510
3 044
054
2 040 041 050 051 140 141 150 151
1 004 005 014 015 104 105 004 005
0 000 001 010 011 100 101 110 111
数据量大 几何和属性偏差 面向位置的数据结构,难以建立空间
对象之间的关系
2020/11/15
28
矢量数据结构
矢量数据结构是通过记录坐标的方式,尽可 能地将点、线、面地理实体表现得精确无误。 其坐标空间假定为连续空间,不必象栅格数 据结构那样进行量化处理。因此矢量数据能 更精确地定义位置、长度和大小。
游程长度编码压缩比的大小是与图的复杂程度成 反比的,在变化多的部分,游程数就多,变化少 的部分游程数就少,图件越简单,压缩效率就越 高。
游程长度编码在栅格加密时,数据量没有明显增 加,压缩效率较高,且易于检索,叠加合并等操 作,运算简单,适用于机器存贮容量小,数据需 大量压缩,而又要避免复杂的编码解码运算增加 处理和操作时间的情况。
… 像元n
栅格数据文件
层1 像元1 X,Y,属性值 像元2 X,Y,属性值
…
…
像元n X,Y,属性值
层2
…
层n
栅格数据文件 层1 多边形1 属性值
像元1坐标 …
像元n坐标 多边形N
层2
…
层n
2020/11/15
26
2020/11/15
27
地理信息系统概论-第三章

2024/7/17
22
高斯-克吕格投影的特点:
① 中央经线上没有任何变形,满足中央经线投影后保持长度 不变的条件;
② 除中央经线上的长度比为1外,其他任何点上长度比均大 于1;
③ 在同一条纬线上,离中央经线越远,变形越大,最大值位 于投影带的边缘;
④ 在同一条经线上,纬度越低,变形越大,变形最大值位于 赤道上。
局部比例尺: 由于投影中必定存在某种变形,地图仅能在某些点或线上保 持比例尺,其余位置的比例尺都与主比例尺不相同,即大于 或小于主比例尺。这个比例尺被称为局部比例尺。
一般地图上注明的比例尺是主比例尺,而对用于测量长度的
地图要采用一定的方式设法表示出该图的局部比例尺。这就
是在大区域小比例尺地图(小于1:1 000 000)上常见的图解
地形图上公里网横坐标前2位就是带号, 例如:1∶5万地形图上的坐标为(18576000, 293300),其中18即为带号。
2024/7/17
24
当地中央经线经度的计算
六度带中央经线经度的计算: 当地中央经线经度=6°×当地带号-3°, 例如:地形图上的横坐标为18576000,其所处的六度带的中 央经线经度为:6°×18-3°=105°。
2、建立地图投影的目的: 采用某种数学法则,使空间信息在地球表面上的位置和地 图平面位置一一对应起来,以满足地图制图的要求。
2024/7/17
9
理解地图投影如何改变空间属性的一种简便方法:
观察光穿过地球投射到表面(称为投影曲面)上。 想像一下,地球表面是透明的,其上绘有经纬网。用一 张纸包裹地球。位于地心处的光会将经纬网投影到一张纸上 。现在,可以展开这张纸并将其铺平。纸张上的经纬网形状 与地球上的形状不同。 地图投影使经纬网发生了变形。
黄杏元《地理信息系统概论》配套题库-课后习题(空间数据处理)

第3章空间数据处理1.比较空间内插的移动拟合法、局部函数和按距离加权法等。
答:(1)移动拟合法移动拟合法是指对每一个待插值点用一个多项式曲面拟合改点附近的表面,进而计算出该点的高程。
(2)线性内插法线性内插法是先将所有的已知数据点连接成三角网的形式,使用靠近内插点的三个已知数据点,来确定三角网中的一个三角形形成的空间平面,继而求出该内插点在平面中的高程值。
(3)按距离加权法按距离加权法是移动拟合法的特例,它在使用搜索圆寻找附近数据点的方法上和拟合法相同,但加权平均法在计算待差值点的高程时,可使用加权平均值代替误差方程求解出曲面函数。
权重的计算由于考虑到不同的数据点相对于待差值点的距离不同,对待差值点的影响程度不同,一般采用与距离相关的权函数来计算权重。
2.讨论在空间数据坐标变换中,选择控制点数量及分布的判断标准。
答:若是地图坐标到地图坐标的变换,图面坐标直接在涂上选取,真实坐标按照国家测绘标准,常用的是图廓点坐标,控制点个数与几何变换方法有关,相对较少;若是影像坐标到地图坐标的变换,图面坐标直接从影像上选取明显的像元,真实坐标通过GPS或数字化地图获取,控制点个数与几何变换方法有关,相对较多。
一般选取四个角点为控制点,控制点的分布要均匀布满整个区域。
3.试述克里金内插法的基本原理、优点及实施过程。
答:(1)克里金插值法的原理克里金插值法又称空间自协方差最佳插值法,它将被插值的莫要素(例如地形要素)当做一个区域化地变量来看待。
所谓区域化的变量就是介于完全随机的变量和完全确定的变量之间的一种变量,它随所在区域位置的改变而连续地变化,因此,彼此离得近点之间有某种程度上的空间相关性,而相隔比较远的点之间在统计上看是相互独立无关的。
(2)克里金插值法的优点克里金法广泛地应用于地下水模拟、土壤制图等领域,是一种很有用的地质统计格网化方法。
该方法在数学上可对所研究的对象提供一种最佳线性无偏估计的方法。
它是一种光滑的内插方法,在数据点多时,其内插的结果可信度较高。
地理信息系统 第三章地理空间数据模型

同种属性表为一个层
按专题分层
每个图层对应一个专题,包含某一种 或某一类数据。如地貌层、水系层、道 路层、居民地层等。。
现实世界
获取
地形信息
+
水系信息
+
道路信息
+
植被信息等
存储
空间 数据库
按时间序列分层
即把不同 时间或不同时 期的数据分别 构成各个数据 层
图层i 图层j
点文件i 线文件i
代码有数字、字母、数字和字母混合三类表示形式。
数字型代码
用一个或若干个阿拉伯数字表示对象的代码。特点是结构 简单、使用方便、易于排序,但对对象的特征描述不直观。
字母型代码
用一个或若干个字母表示对象的代码。特点是比同样位数 的数字型代码容量大,还可提供便于识别的信息,易于记 忆,但比同样位数的数字型代码占用更多的计算机空间。
空间数据的分层和分区
地理信息本身具有层次性。分层和分区 是空间数据组织的高级形式,为管理和 使用提供了便利 分层依据地理实体性质 分区依据平面范围
分层
按专题
地貌、水系、植被、交通、居民地等
按时间
不同时间的数据成为不同层,便于对比、处理、表 现。如每年建的住宅用不同的颜色表现
按实体的几何类型
一般按点、线、面、注记
格网型空间索引
将区域用横竖线条划分大小相等和不等 的格网,记录每一个格网所包含的空间 实体。进行空间查询时,首先计算出查 询对象所在格网,然后再在该网格中快 速查询所选空间实体。
一条河流、一个湖泊和一条省界,它们的关键字分别为5,11和 23。河流穿过的栅格为2,34,35,67,68;湖泊覆盖的栅格为 68,69,100,101;省界所通过的栅格为5,37,36,35,67, 99,98,97。
第三章第一节 地理信息系统2

第一节地理信息系统及其应用
四.GIS的工作过 程
数据输入、 存储
数据操作、 分析 可视化表达(地 图、三维视图、 多媒体等)
地理信息输出
[教材图表点拨]
图3—8 地图数字化过程
常见的纸质地图、文字以及非数字形
式的资料,都必须转换为数字形式, 才能被 计算机存储、识别和处理。 实现从图形到数字的转换过程,称为 数字化。图形数据的 输入,常用的 方法是扫描纸质地图后进行数字化
第三章地理信息技术应用
第一节地理信息系统及其应用
二、地理信息系统与城市管理
二、地理信息系统与城市管理
GIS能满足人们对空间信息的要求,帮 助人们进行各种辅助决策。目前,GIS广泛 应用于资源调查、环境评估、灾害预测、国 土管理、城市规划、邮电通信、交通运输、 公安、水利、公共设施、商业金融等人们生 产生活的各个领域。
[阅读指导]
GIS的查询与分析
和用GIS中的地理数据,实现 地理分析、评价、预测和辅助 决策,是GIS的重要应用领域。 网上的电子地图采用图层管理 的方法,用户可以选择需要的 图层进行显示、查询、分析。
例: 甲图为一幅具有林木、河流和住房的景观 图,乙图是根据该图而建立的空间数据模型。 由此比较地图与地理信息系统对地物的表示有 何差异。
4、全球气候监测和预报网络的GIS网络。
5、全球环境管理:如确定全球最敏感的植物产地, 让所在国家同意保护并作为国际债务偿还。
图层 —— 将空间信息按其几何 特征及属性划分成的专题。 专题地图 —— 以表现某一 属性的位置或若干个选定属性之间关 系为主要目的的地图。
[阅读指导]
数字化与GIS数据源
地理数据的采集方法包括实地调查、采样; 传统的测量方法,如三角测量法、三边测量 法;人口普查;生物遥测学;数字摄影技术; 全球定位系统(GPS);现代遥感技术等。其中, 遥感数据已经成为GIs的重要数据来源,利用 卫星拍摄的高分辨率遥感技术影像,人们可 以迅速获得几周前甚至几天前的最新数据, 并且数据真实准确,成本也很低。
地理信息系统下的空间分析——第三章_空间分析的理论问题

4、顺序关系描述 顺序关系中的一类重要关系是方向关系,如东、西、 南、北等。 (1)方向关系的定量描述 方向关系的定量描述主要是使用方位角来进行
(2)方向关系的定性描述 方向关系的定性描述主要有投影法(projection)和锥形 法(cone)。 1)投影法:是将空间目标投影到特定的坐标轴上,通 过各目标投影间的关系去描述与定义方向关系。其中的投 影可以是正射投影,也可以是斜率投影。 2)锥形法:是将空间目标及其周围的区域分成带有方 向性的几个区域,通过各目标本身及方向区域之间的交的 结果来描述空间关系。
7)西南关系
South_West(Pi,Qj)=X(Pi)<X(Qj) And Y(Pi)<Y(Qj) 示意图如下:
8)东南关系
South_East(Pi,Qj)=X(Pi)>X(Qj) And Y(Pi)<Y(Qj) 示意图如下:
以上8种关系通过点的投影可以精确判断。对于任意两点, 上述8种关系必有一种满足。 这些关系具有传递性。 另外,一些关系可进行相互转换,如North_East(Pi,Qj)和 South_West(Qj,Pi)。
课堂练习: 请大家分别算 出8种面面关系 的4元组矩阵
8种面/面关系
………………….
三种点/线拓扑关系。 课堂练习:请大家分别算出3 种点线关系的4元组矩阵。
两种点/点拓扑关系。
课堂练习:请大家分别算出2种点 点关系的4元组矩阵。
三种点/面拓扑关系,请 写出4元组矩阵。
2、空间关系描述结果的评价: 完备性是指空间关系描述结果能包含目标间所有可能的定 性关系; 严密性是要求所推出的一组关系是实际存在的或正确的; 唯一性要求所有关系是互斥的; 通用性指描述方法应能处理各种形状的目标和各类关系。
地理信息系统GIS—第3章矢量数据

空间关系及其表达
绝对空间关系:坐标、角度、方位、距离等 相对空间关系:相邻、包含、关联(连接)
等
相对空间关系的类型
拓扑空间关系:描述空间对象的相邻、包含、关联 关系等。
顺序空间关系:描述空间对象在空间上的排列次序 ,如前后、左右、东、西、南、北等。
地图、遥感影像上的空间关系是通过图形识别的, 在GIS中的空间关系则必须显式的进行定义和表达
地理信息系统
第三章 矢量数据模型
第二章内容回顾
1、什么叫坐标系? 2、为什么要建立坐标系? 3、为什么要建立地球的坐标系? 4、如何建立地球的坐标系统? 5、坐标系统与地图绘制有什么关系?
第二章内容回顾
1. 什么是地图投影? 2. 地图投影主要有几种分类方法? 3. 中国、美国的地图投影主要有哪几种? 4. 在地图投影过程中需要设置哪两部分内容?需要设
3.2 拓扑
Topology一词来自希腊文,它的原意是“形状 的研究”。拓扑学属于数学中几何学的内容, 最早由德国数学家莱布尼茨1679年提出。历 史上著名的哥尼斯堡七桥问题、多面体的欧 拉定理、四色问题等都是拓扑学发展史的重 要问题。
3.2 拓扑-哥尼斯堡七桥问题
问:能不能每座桥都 只走一遍,最后又回 到原来的位置?
空间数据结构
数据结构的概念:
数据结构即指数据组织的形式,是适于计算机存 储、管理和处理的数据逻辑结构。
对空间数据而言,数据结构则是地理实体的空间 排列方式和相互关系的抽象描述。
在地理系统中描述地理要素和地理现象的空间数 据主要包括:空间位置、拓扑关系和属性三个方 面的内容。
常用的空间数据结构
ArcGIS中的矢量数据模型
Coverage Shapefile
地理信息系统第三章
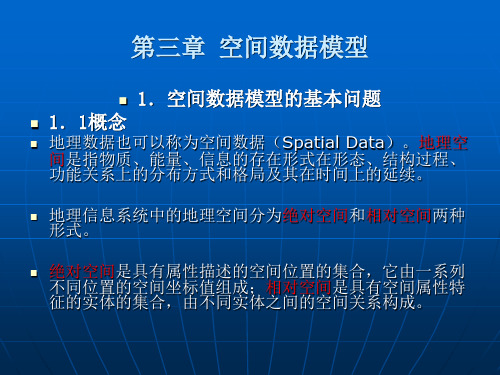
1.3.2三维空间数据模型
三维矢量模型 体模型
1.3.3分布式空间数据模型
分布式空间数据库管理系统 联邦空间数据库(Federated Spatial Database)
1.3.4 CASE工具 (Computer-Aided Software Engineering)
2.场模型
1.2空间数据模型的类型
在GIS中与空间信息有关的信息模型有三个,即基于对象 (要素)(Feature)的模型、网络(Network)模型以及 场(Field)模型。 选择某一种模型而不选择另外一种模型主要是顾及数据的 测量方式。
1.3 GIS空间数据模型的学术前沿
1.3.1时空数据模型 核心问题是研究如何有效地表达、记录和管理现实世界的 实体及其相互关系随时间不断发生的变化。
е1 P1 е5 P2 е2
N1
е6
N4
P3
N5
е3
N2
е4
N3
P4
е7
2.地理空间数据拓扑关系应用价值
(1)确定地理实体间的相对空间位置,无需坐标 和距离 (2)利于空间要素查询 (3)重建地理实体
3.地理空间数据 拓扑关系的表示
N2
е1
P1 е5
N4
е6
P3
N5
е3
结点集合
P2
е2
е4
N3 针
4.4度量空间关系分析
度量空间关系主要是指空间对象之间的距离关系。 这种距离关系可以定量地描述为特定空间中的某种距离, 如A实体距离B实体100m。也可以应用与距离概念相关的术
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
a、b称为长度元素
扁率反映了椭球体的 扁平程度
椭圆的第一偏心率:
a2 −b2 e′ = b 椭圆的第二偏心率:
e= a2 −b2 a
e和e’反映椭球体的扁平程 和 反映椭球体的扁平程 偏心率越大, 度,偏心率越大,椭球愈 扁
3.4.2 地球椭球体的相关公式
W
W 顾及 a = c 1−e2 和 =V 1−e2,则上式又可写为
c N= V (3-13) (3-
卯酉圈曲率半径
由图看出, 由图看出, (3(3-14) 也就是说,卯酉圈曲率半径恰好等于椭球面和短轴之间的一段法线 的长度,亦即卯酉圈的曲率中心位于椭球的旋转轴上。 N与B有关,是纬度B的函数,且随B的增大而增大,变化规律如下表 有关,是纬度B的函数,且随B
3.4.2 地球椭球体的相关公式
2.地球椭球参数间的相互关系 2.地球椭球参数间的相互关系
由前面式子得:
a2 − b2 e2 = a2
a2 − b2 e'2 = b2
b2 2 1− e = 2 a
a2 1+ e = 2 b
2
并得: 推得:
(1− e2 )(1+ e'2 ) = 1
e2 e2 ' = 1+ e 2 '
e2 '
e2 = 1− e2
同理可得: a = b 1+ e'2 L L = a 1− e2 L b
c = a 1+ e'2 L L = c 1− e2 L a
e' = e 1+ e'2 L L = e' 1− e2 L e
V =W 1+ e 2 L L =V 1− e2 L W
椭球面上的常用坐标系及其相互关系
第三章 空间数据的变换算法
3.1 3.2 3.3 3.4 平面坐标变换 球面坐标变换 仿射变换 地图投影变换
3.4 地图投影变换
3.4.1 概述 3.4.2 地球椭球体的相关公式 3.4.3 地图投影变换
3.4.1 概述
地图投影变换的实质是建立两平场之间的一一对应关系。
x = f1(ϑ,γ ) y = f2(ϑ,γ )
子午圈曲率半径
在子午椭圆的一部分上取一微分弧长DK=dS,相应地有( 在子午椭圆的一部分上取一微分弧长DK=dS,相应地有(子午 面直角坐标系)坐标增量dx,点n是微分弧dS的曲率中心,则 面直角坐标系)坐标增量dx,点n是微分弧dS的曲率中心,则 线段Dn及Kn即是子午圈曲率半径,用M 线段Dn及Kn即是子午圈曲率半径,用M表示。 由平面曲线的曲率半径定义公式可得: dS M = (3(3-1)
(3(3-5)
上式代入(3-4)式得, 上式代入(3-4)式得, (3(3-6) 1 e2 cos2 B dx asin B 2 2 2 = −asin B − (W − e cos B) =− dB W W3 W3 又 则有
W2 = 1− e2 sin2 B
dx asin B =− (1− e2 sin2 B − e2 cos2 B) dB W3
∑ ∑
三、 数值解析变换法
当已知新投影的公式,但不知原投影的公式时,可先通过 数值变换求出原投影点的地理坐标φ 数值变换求出原投影点的地理坐标φ,λ,然后代入新投影公 式中,求出新投影点的坐标。即:
x,y
数值变换
Φ,λ
解析变换
X,Y
地球椭球的基本几何参数及相互关系
1.地球椭球的基本几何参数 1.地球椭球的基本几何参数 五个基本几何参数
WGS-84系椭球 WGS-84系椭球 6378137 6356752.3142 6399593.6258 1/298.257223563 0.0066943799013 0.00673949674227
α
e2
e′2
0.006693421622966 0.006738525414683
我国所采用的1954年北京坐标系应用的是克拉索夫斯基椭球 我国所采用的1954年北京坐标系应用的是克拉索夫斯基椭球 1954 参数;以后采用的1980国家大地坐标系应用的是1975 1980国家大地坐标系应用的是1975国际椭 参数;以后采用的1980国家大地坐标系应用的是1975国际椭 球参数; GPS应用的是WGS-84系椭球参数 应用的是WGS 系椭球参数。 球参数;而GPS应用的是WGS-84系椭球参数。
dx 1 M =− ⋅ dB sin B
(3(3-3)
子午圈曲率半径
a cos B 由 x= 式可求得 = 2 2 W 1− e sin B
dW − sin BW − cosB dx dB = a dB W2
acos B
(3(3-4)
dW d 1− e2 sin2 B − 2e2 sin Bcos B − e2 sin Bcos B = = = 2 2 dB dB W 2 1− e sin B
B=0Β B=0Β(在赤道处) 0Β〈B〈90Β 90Β B=90Β B=90Β(在极点处)
M
M0 = a(1− e2 ) = a(1− e2 ) < M < c a M90 = =c 2 1− e c (1+ e'2 )3
(3-10) 说(3-明
M小于赤道a 小于赤道a M随B的增大而增大 M等于极点曲率半径
1.常用的四种坐标系 1.常用的四种坐标系 大地坐标系 空间直角坐标系 子午平面直角坐标系 大地极坐标系
(1)大地坐标系
P点的子午面NPS与起始子午面 NGS所构成的二面角叫做P点大地 经度,P点的法线Pn与赤道面的 夹角B叫P点的大地纬度,P点的 位置用(L、B)表示
(2)空间直角坐标系
以椭球中心O为原点,起始子午面 与赤道面交线为X轴,在赤道面上 与X轴正交的方向为Y轴,椭球体的 旋转轴为Z轴,构成右手坐标系OXYZ,在该坐标系中,P点的位置用 X、Y、Z表示
(3)子午面直角坐标系
设P点的大地经度为L,在过P点 的子午面上,以子午圈椭圆中心 为原点,建立x,y平面直角坐标 系。在该坐标系中,P点的位置 用L,x,y表示
(4)大地极坐标系
M为椭圆体面上任意一点,MN为 过M点的子午线,S为连结MP的 大地线长,A为大地线在M点的 大地方位角。以M为极点、MN为 极轴、S为极径、A为极角,就构 成了大地极坐标系。P点位置用S、 A表示。
X = xc s L o Y = xsi L n Z=y
X (N + H) cos Bcos L ρ = Y = (N + H) cos Bsin L 2 Z N(1− e ) + H sin B
[
]
Y L = r t a c g X
(3(3-7)
子午圈曲率半径
或
dx asin B =− (1− e2 ) 3 dB W
(3(3-8)
(3-8)代入(3-3)则曲率半径为: (3-8)代入(3-3)则曲率半径为:
a(1− e2 ) M= W3
(3(3-9)
由前面 c = a 1+ e'2 L L = c 1− e2 L a c 又可简化为:M = 3 2 2 V V =W 1+ e L L =V 1− e L W B
实现一种地图投影点的坐标变换为另一种地图投影点的坐标 就是要找出上述关系式,其方法为:
解析变换法
数值变换法 数值解析变换法
一、 解析变换法
这类方法是找出两投影间坐标变换的解析计算公式。由于所 反解变换法和 采用的计算方法不同,又可分为反解变换法 正解变换法。 采用的计算方法不同,又可分为反解变换法和正解变换法。 反解变换法(又称间接变换法)是一种中间过渡的方法, 即先解出原地图投影点的地理坐标X 即先解出原地图投影点的地理坐标X、Y,对于x、y的解析关 ,对于x 系式,将其代入新图的投影公式中求得其坐标。即:
各种坐标系间的关系
子午平面直角坐标系同大地坐标系的关系
acos B x= = 2 2 W 1− e sin B
y= a(1− e2 )sin B 1− e2 sin2 B = a bsin B (1− e2 )sin B = W V
acos B
(e)
(f)
(e)(f)两式即为子午面直角坐标x、y同大地纬度B的关系式。
克拉索夫斯基椭球 a b c 6378245 6356863.0187730473 6399698.9017827110 1/298.3
α
1975国际椭球 1975国际椭球 6378140 6356755.2881575287 6399596.6519880105 1/298.257 0.006694384999588 0.006739501819473
通过选择10个以上的两种投影之间的共同点,并组成最小 通过选择10个以上的两种投影之间的共同点,并组成最小 二乘法的条件式,即: n n为点数;Xi、Yi为新投影的实际 为点数;X ′ ( Xi − Xi )2 = min 变换值; Xi’、Yi’为新投影的理论值。 i =1 n 根据求极值原理,可得到两组线性方 (Y −Y′)2 = min i i i =1 程,即可求得各系数的值。
x,y
X,Y
Φ, λ
正解变换法(又称直接变换法)是一种不需要反解出原地 图投影点的地理坐标的解析公式,而是直接求出两种投影点的 图投影点的地理坐标的解析公式,而是直接求出两种投影点的 直角坐标关系式。即:
x,y
Φ,λ
二、 数值变换法
如果原投影点的坐标解析式不知道,或不易求出两投影 之间坐标的直接关系,可以采用多项式逼近的方法,即用数 值变换法来建立两投影间的变换关系式。例如,可采用二元 三次多项式进行变换。二元三次多项式为:
