第三章 连续时间信号与系统的频域分析 (1)
合集下载
信号与线性系统 第四版 管致中 第3章1
11
傅里叶级数的指数形式
可以从三角傅立叶级数直接导出，由欧拉公式：
1 sin nt e jnt e jnt 2j 1 jnt cos nt e e jnt 代入三角形傅氏级数中去， 2
a0 f (t ) an cos nt bn sin nt 2 n 1 n 1
7
例
试将下图所示的方波信号f(t)展开为傅里 f (t) 叶级数。 f (t ) a0 an cos nt bn sin nt 1
2
n 1 n 1
T 2
2 T 2 2 T a0 f (t )dt dt T (1)dt 0 T 0 T 0 T 2
0
T 2
T
n
2
(cos n
T
T 2
8
1)
例
将具有不连续点的周期函数（如 矩形脉冲)进行傅立叶级数展开 后，选取有限项进行合成。当选 取的项数越多，在所合成的波形 中出现的峰起越靠近原信号的不 连续点。当选取的项数很大时， 该峰起值趋于一个常数，大约等 于总跳变值的9%。这种现象称 为吉布斯效应。
______。 B
2
f (t )
周期信号 f (t) 的傅立叶级数中所含有的频率分量是
1
0
T 2
T
t
-1
(A) 余弦项的奇次谐波，无直流 (B) 正弦项的奇次谐波，无直流 (C) 余弦项的偶次谐波，直流 (D) 正弦项的偶次谐波，直流。
奇函数：只含正弦项； 半周镜象对称： 只含奇次谐波
25
例 3 习题3.8
t0
t0+T
信号与系统PPT-cp3-连续时间信号的频谱
（ 0, 2 ）内是一个正交函数集
电气工程学院
3.1 用完备正交函数集表示信号
（2）
n 1
n 1
2
0
sin t cos ntdt 0
sin t 在区间（ 0, 2 ）内与{cos nt }正交。故函数集 cosnt 在区间（0, 2 ）内不是完备正交函数集。
即 （3）
2
0
mn
T
2
1
为指数函数的公共周期
当n , e jn1t 为一完备的正交函数集
电气工程学院
3.1 用完备正交函数集表示信号
3)函数集： Sa [ ( t nT )] （其中n 0, 1, 2) T 对于有限带宽信号类来说是一个完备的正交函数集。
ir
ir
2
0
1 sin(i r )t sin(i r )t 2 cosit cosrtdt 0 2 ir ir 0
2
2
0
cosit cosrtdt
0
1 1 1 2 1 sin 2it dt t sin 2it 2 2 2i 0
m, n 为任意整数
mn
t 1T t 1T t1 cosm1t cosn1tdt t1 sinm1t sinn1tdt 0 t 1T t 1T 2 T 2 cos n tdt sin n tdt 1 1 t1 t1 2 2 T 三角函数的公共周期 1
在 (t1 , t2 ) 内构成归一化正交函数集。
电气工程学院
3.1 用完备正交函数集表示信号
正交复变函数集
设
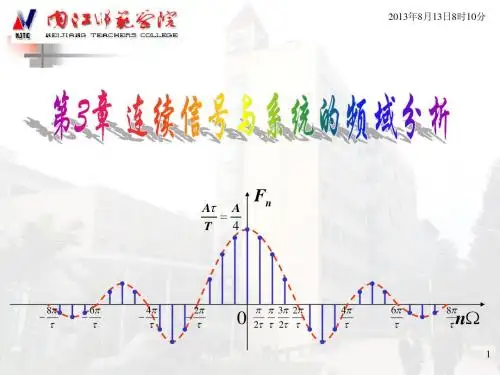
第3章连续信号与系统的频域分析
8
2013年8月13日8时10分
3.0 引言
LTI系统的特性完全可以由其单位冲激响应
来表征，通过对LTI系统单位冲激响应的研究就可
分析LTI系统的特性。
连续时间信号分解为一系列完备正交信号集， 再根据线性叠加原理求解系统的零状态响应。
9
2013年8月13日8时10分
3.1信号的正交分解
3.1.1 矢量的正交分解 1 、正交矢量（2维空间）
3.1.2 信号的正交分解 2、正交函数的两个重要定理 定理2：若 则：
f (t ) c1 g1 (t ) cr gr (t ) cn gn (t ) ci gi (t )
i 1
n
t2
t1
f (t ) dt ci gi (t ) dt
t2 i 1 t1
完备正交函 数集
1,cos t,cos 2t,,sin t,sin 2t,
17
2013年8月13日8时10分
3.2 周期信号的连续时间傅立叶级数
一般地，若 即有：
则有：
f ( t ) 在区间(-∞，+
∞)内，每隔周期T重复，
f (t ) f (t kT )
T 2 T 2
V1 V2 0
V1 V3 0
V2 V3 0
11
2013年8月13日8时10分
3.1信号的正交分解
3.1.1 矢量的正交分解 3 、正交矢量（n维空间）
c3 V3 V3 o V2 c2 V2 V1
V cV1 crVr cnVn 1
V c1 V1
cr
V cos r Vr
3.7 连续信号的抽样定理
2013年8月13日8时10分
3.0 引言
LTI系统的特性完全可以由其单位冲激响应
来表征，通过对LTI系统单位冲激响应的研究就可
分析LTI系统的特性。
连续时间信号分解为一系列完备正交信号集， 再根据线性叠加原理求解系统的零状态响应。
9
2013年8月13日8时10分
3.1信号的正交分解
3.1.1 矢量的正交分解 1 、正交矢量（2维空间）
3.1.2 信号的正交分解 2、正交函数的两个重要定理 定理2：若 则：
f (t ) c1 g1 (t ) cr gr (t ) cn gn (t ) ci gi (t )
i 1
n
t2
t1
f (t ) dt ci gi (t ) dt
t2 i 1 t1
完备正交函 数集
1,cos t,cos 2t,,sin t,sin 2t,
17
2013年8月13日8时10分
3.2 周期信号的连续时间傅立叶级数
一般地，若 即有：
则有：
f ( t ) 在区间(-∞，+
∞)内，每隔周期T重复，
f (t ) f (t kT )
T 2 T 2
V1 V2 0
V1 V3 0
V2 V3 0
11
2013年8月13日8时10分
3.1信号的正交分解
3.1.1 矢量的正交分解 3 、正交矢量（n维空间）
c3 V3 V3 o V2 c2 V2 V1
V cV1 crVr cnVn 1
V c1 V1
cr
V cos r Vr
3.7 连续信号的抽样定理
第三章信号与系统连续时间信号与系统的傅里叶分析
n
n = 2, 4, 6, n = 1, 3, 5,
信号与系统
一、周期信号的傅立叶级数
所以有
an 0
0
bn
4
n
n = 2, 4, 6, n = 1, 3, 5,
f
(t)
4
[sin 0t
1 sin 3
3
0t
1 5
sin
5
0
t
1 n
sin n
0t
]
信号与系统
一、周期信号的傅立叶级数
2 . 复指数形式的傅立叶级数
a
b
0
信号与系统
一、周期信号的傅立叶级数
三角函数集:
{1, cos0t, cos 20t, , cos n0t, , sin 0t, sin 20t, , sin n0t, }
在区间 (t0 ,
t0
T)
内是一完备正交函数集。
T
2 0
正交性:（m 和 n 都是整数）
0
t0 T cos
t0
m0t
cos
信号与系统
§ 3.2 周期信号的 傅立叶级数展开
信号与系统
周期信号
周期信号: 定义在区间 (, ) ，每隔一定时间 T ，按 相同规律重复变化的信号，如图所示 。它可表示为
f (t)=f ( t+mT )
其中 m 为正整数， T 称为信号的周期，周期的倒数称为频率。
f t
1
0 T/2 T
t
1
信号与系统
f (t) a0 a1 cos0t a2 cos 20t b1 sin 0t b2 sin 20t
a0 an cos n0t bn sin n0t
n = 2, 4, 6, n = 1, 3, 5,
信号与系统
一、周期信号的傅立叶级数
所以有
an 0
0
bn
4
n
n = 2, 4, 6, n = 1, 3, 5,
f
(t)
4
[sin 0t
1 sin 3
3
0t
1 5
sin
5
0
t
1 n
sin n
0t
]
信号与系统
一、周期信号的傅立叶级数
2 . 复指数形式的傅立叶级数
a
b
0
信号与系统
一、周期信号的傅立叶级数
三角函数集:
{1, cos0t, cos 20t, , cos n0t, , sin 0t, sin 20t, , sin n0t, }
在区间 (t0 ,
t0
T)
内是一完备正交函数集。
T
2 0
正交性:（m 和 n 都是整数）
0
t0 T cos
t0
m0t
cos
信号与系统
§ 3.2 周期信号的 傅立叶级数展开
信号与系统
周期信号
周期信号: 定义在区间 (, ) ，每隔一定时间 T ，按 相同规律重复变化的信号，如图所示 。它可表示为
f (t)=f ( t+mT )
其中 m 为正整数， T 称为信号的周期，周期的倒数称为频率。
f t
1
0 T/2 T
t
1
信号与系统
f (t) a0 a1 cos0t a2 cos 20t b1 sin 0t b2 sin 20t
a0 an cos n0t bn sin n0t
实验三 连续信号与系统的频域分析
郑慧乐
学号
0174280
同组人：无
实验项目
实验三连续信号与系统的频域分析
☑必修□选修
□演示性实验☑验证性实验□操作性实验□综合性实验
实验地点
H113
实验仪器台号
F0
指导教师
蒋娜
实验日期及节次
week14->2-12
一、实验目的及要求：
1、目的
1．掌握非周期信号的傅里叶变换：fourier函数和ifourier函数；
四、实验结果与数据处理：
1．利用fourier函数求下列信号的傅里叶变换F(jω)，并用ezplot函数绘出其幅度谱和相位谱。
（1）
syms t v w phase im re;%定义变量t,v,w,phase,im re
f=sym('Heaviside(t)-Heaviside(t-2)');%
Fw=fourier(f);
plot([07.0711],[0.7070.707],':');
axis([04001.1]);
grid;
xlabel('角频率(\omega)');
ylabel('幅度');
title('H(j\omega)的幅频特性');
subplot(212);
plot(w,h2*180/pi);
axis([0400200]);
（2）
syms t v w phase im re;%定义变量t,v,w,phase,im re
f=exp(-1*t)*sym('Heaviside(t)');%
Fw=fourier(f);
subplot(311);
学号
0174280
同组人：无
实验项目
实验三连续信号与系统的频域分析
☑必修□选修
□演示性实验☑验证性实验□操作性实验□综合性实验
实验地点
H113
实验仪器台号
F0
指导教师
蒋娜
实验日期及节次
week14->2-12
一、实验目的及要求：
1、目的
1．掌握非周期信号的傅里叶变换：fourier函数和ifourier函数；
四、实验结果与数据处理：
1．利用fourier函数求下列信号的傅里叶变换F(jω)，并用ezplot函数绘出其幅度谱和相位谱。
（1）
syms t v w phase im re;%定义变量t,v,w,phase,im re
f=sym('Heaviside(t)-Heaviside(t-2)');%
Fw=fourier(f);
plot([07.0711],[0.7070.707],':');
axis([04001.1]);
grid;
xlabel('角频率(\omega)');
ylabel('幅度');
title('H(j\omega)的幅频特性');
subplot(212);
plot(w,h2*180/pi);
axis([0400200]);
（2）
syms t v w phase im re;%定义变量t,v,w,phase,im re
f=exp(-1*t)*sym('Heaviside(t)');%
Fw=fourier(f);
subplot(311);
精品文档-信号与系统(第四版)(陈生潭)-第3章
An cos(nt n )
Fne jnt
n 1
n
F0 2 Fn cos(nt n )
其中：
n 1
an
2 T
t0 T t0
fT (t )cosntdt
bn
2 T
t0 T t0
fT (t )sin ntdt
n0,1,2...
1
n1,2...
Fn
T
t0 T t0
fT (t)e jnt dt
fT (t)sin ntdt
A0 a0 An an2 bn2
n 1,2...
n
arctg
bn an
说明：1.周期信号可分解表示为三角函数的线性组合。
2.物理意义：周期信号可分解为众多频率成整数倍
和正（余）弦函数或分量的线性组合。具体有：
a0 A0 直流分量cost, sin t 基波分量 22
fT (t)
Fne jnt
F e j (nt n ) n
F0
2 Fn cos(nt n )
n
n
n1
各谐波分量的角频率nΩ 是基波角频率Ω的n倍且有不同的
振幅和相位，均有傅立叶系数 Fn Fn e jn 反映出来。
为揭示各谐波振幅、初相随角频率变化情况，特画出振幅
及相位随w变化的曲线称其为频谱图。
的模
最小，（此时的C12称为最佳），当C12＝0时，Ve的
模最小，此时V1和V2正交。
2.矢量分解
在平面空间里，相互正交的矢量
V1和V2构成一个正交矢量集，而且为
完备的正交矢量集。平面空间中的任
一矢量V都可表示为V1和V2的线性组合 （如上图）。即：
V=C1V1+C2 V2。式中V1、V2为单位矢量，且V1·V2＝0。其中：
时间管理第三章连续时间系统的频域分析
最新卓越管理方案您可自由编辑第三章.连续时间系统的频域分析一、任意信号在完备正交函数系中的表示法（§6.3---6.4）信号分解的目的：● 将任意信号分解为单元信号之和，从而考查信号的特性。
●简化电路分析与运算，总响应=单元响应之和。
1．正交函数集任意信号)(t f 可表示为n 维正交函数之和：∑==++++=nr r r n n r r t g C t g C t g C t g C t g C t f 12211)()()()()()(原函数()()()t g t g t g r 21,相互正交：⎩⎨⎧=≠=⋅⎰nm K nm dt t g t g m t t n m ,,0)()(21()t g r 称为完备正交函数集的基底。
一个信号可用完备的正交函数集表示,.正弦函数集有许多方便之处,如易实现等，我们主要讨论如何用正弦函数集表示信号。
2．能量信号和功率和信号（§6.6一）设()t i 为流过电阻R 的电流，瞬时功率为R t i t P )()(2=一般说来，能量总是与某一物理量的平方成正比。
令R = 1Ω，则在整时间域内，实信号()t f 的能量，平均功率为：⎰-∞→=222000)(lim T T T dt t f W⎰-∞→=2220000)(1lim T T T dt t f T P讨论上述两个式子，只可能出现两种情况： ①∞<<W 0 (有限值)0=P②∞<<P 0(有限值) ∞=W满足①式的称为能量信号，满足②式称功率信号。
3．帕斯瓦尔定理设{})(t g r 为完备的正交函数集，即()()[]∑⎰∑⎰⎰∞=∞===121222212121)(r t t r r r t t rr t t dt t g C dt t g C dt t f信号的能量 基底信号的能量 各分量此式称为帕斯瓦尔定理 P331 式（6-81） (P93, P350) 左边是信号能量，右边是各正交函数的能量。
第三章 LTI连续系统的频域分析
n π j 2
1 e nπ
j ( nΩ t
π ) 2
例2. 求图示周期锯齿波信号的傅里叶级数。 解法1
2 T 2 T t a0 f (t )dt dt 1 T 0 T 0T
-T 0
f(t)
1
T
2T
3T
t
2 T 2 Tt 2 t sin nt cos nt an 0 f ( t ) cos ntdt 0 cos ntdt 2 [ 2 2 ] 0 T T T n T n 0
谱 相位谱：以频率(角频率)为横坐标，以各谐波的初相
角为纵坐标画出的线图(离散)为相位频谱。简称相位谱。
一、周期矩形脉冲的频谱
1 Fn T
f (t )
A
…
T
T/ 2 T/ 2
f ( t )e
j nΩ t
A d t e j nΩ t dt T / 2
/ 2
…
f ( t ) A T
解法2(自学):可利用傅里叶性质3求解
2
f(t)
1
1 T/ 2 ( j nΩ ) Fn [ (t )]e j nΩ t dt T T/ 2 0 T -T T / 2 1 [e j nΩ t (t ) j nΩe j nΩ t (t )]dt T T/ 2 f ' (t ) j nΩ j nΩ 0 1/ T T T 0 T -T F0 0.5
第三章
LTI连续系统的频域分析
时域分析法: 系统→微分方程(算子方程)→传输算子H﹙p﹚→ 特征根→零输入响应或冲激响应→利用 f(t)*h(t) 求解 任意激励下的零状态响应,最后零输入响应与零状态 响应叠加,得到全响应。
1 e nπ
j ( nΩ t
π ) 2
例2. 求图示周期锯齿波信号的傅里叶级数。 解法1
2 T 2 T t a0 f (t )dt dt 1 T 0 T 0T
-T 0
f(t)
1
T
2T
3T
t
2 T 2 Tt 2 t sin nt cos nt an 0 f ( t ) cos ntdt 0 cos ntdt 2 [ 2 2 ] 0 T T T n T n 0
谱 相位谱：以频率(角频率)为横坐标，以各谐波的初相
角为纵坐标画出的线图(离散)为相位频谱。简称相位谱。
一、周期矩形脉冲的频谱
1 Fn T
f (t )
A
…
T
T/ 2 T/ 2
f ( t )e
j nΩ t
A d t e j nΩ t dt T / 2
/ 2
…
f ( t ) A T
解法2(自学):可利用傅里叶性质3求解
2
f(t)
1
1 T/ 2 ( j nΩ ) Fn [ (t )]e j nΩ t dt T T/ 2 0 T -T T / 2 1 [e j nΩ t (t ) j nΩe j nΩ t (t )]dt T T/ 2 f ' (t ) j nΩ j nΩ 0 1/ T T T 0 T -T F0 0.5
第三章
LTI连续系统的频域分析
时域分析法: 系统→微分方程(算子方程)→传输算子H﹙p﹚→ 特征根→零输入响应或冲激响应→利用 f(t)*h(t) 求解 任意激励下的零状态响应,最后零输入响应与零状态 响应叠加,得到全响应。