反比例函数的图像和性质1教案
数学九年级下册《反比例函数的图像和性质( 1)》教案
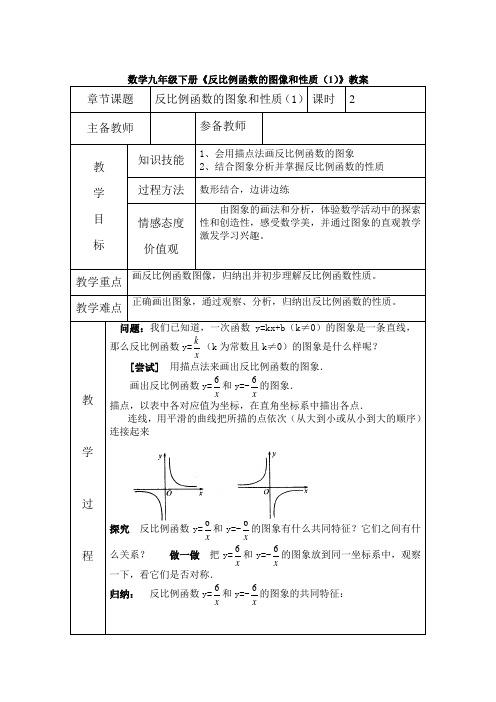
数学九年级下册《反比例函数的图像和性质(1)》教案章节课题反比例函数的图象和性质(1)课时 2 主备教师参备教师教学目标知识技能1、会用描点法画反比例函数的图象2、结合图象分析并掌握反比例函数的性质过程方法数形结合,边讲边练情感态度价值观由图象的画法和分析,体验数学活动中的探索性和创造性,感受数学美,并通过图象的直观教学激发学习兴趣。
教学重点画反比例函数图像,归纳出并初步理解反比例函数性质。
教学难点正确画出图象,通过观察、分析,归纳出反比例函数的性质。
教学过程问题:我们已知道,一次函数y=kx+b(k≠0)的图象是一条直线,•那么反比例函数y=kx(k为常数且k≠0)的图象是什么样呢?21教育网[尝试]用描点法来画出反比例函数的图象.画出反比例函数y=6x和y=-6x的图象.描点,以表中各对应值为坐标,在直角坐标系中描出各点.连线,用平滑的曲线把所描的点依次(从大到小或从小到大的顺序)连接起来探究反比例函数y=6x和y=-6x的图象有什么共同特征?它们之间有什么关系?做一做把y=6x和y=-6x的图象放到同一坐标系中,观察一下,看它们是否对称.归纳:反比例函数y=6x和y=-6x的图象的共同特征:(1)它们都由两条曲线组成.(2)随着x的不断增大(或减小),曲线越来越接近坐标轴(x轴、y轴).(3)反比例函数的图象属于双曲线.此外,y=6x的图象和y=-6x的图象关于x轴对称,也关于y轴对称【归纳】(1)反比例函数y=kx(k为常数,k≠0)的图象是双曲线.(2)当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内,y•值随x值的增大而减小.21·cn·jy·com(3)当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内,y•值随x值的增大而增大.例题 1请你写出一个反比例函数的解析式,使它的图象在第一、三象限.2.如图所示的函数图象的关系式可(• )A.y=x B.y=1xC.y=x2 D.y=1||x目标归结:1.画反比例函数的图象步骤.2.反比例函数的性质.3.反比例函数的图象在哪个象限由k决定,且y值随x值变化只能在“每一个象限内”研究.4.在y=kx(k≠0)中,由于x≠0,同时y≠0,因此双曲线两个分支不可能到达坐标轴.【课后作业】教材习题26.1 P8 3。
17·1·2反比例函数的图象和性质(一)教案

2010-2011学年第二学期阿克苏市第四中学优秀教案学科:数学姓名:任小梅任教年级:八年级17·1·2反比例函数的图象和性质(一)一、教学目标:1.知识与技能:(1)进一步作函数图象的主要步骤,会作反比例函数的图象。
(2)体会函数三种表示方法的相互转换,对函数进行认识上的整合。
2.过程与方法:经历画图、观察、猜想、思考等数学活动,向学生渗透数形结合的思想方法,让学生初步认识具体的反比例函数图像的特征。
3.情感态度与价值观:体会分类讨论思想、数形结合思想的运用。
在动手作图中体会做中的乐趣,养成勤于动手、乐于探索的习惯。
二、教学重、难点:重点:正确的进行描点、画出图像,理解并掌握反比例函数的图像与性质。
难点:归纳反比例函数的性质。
三、教学方法:讲练结合法四、教学准备:小黑板、三角尺、彩色粉笔五、授课类型:新授课六、课时安排:一课时七、教学过程:(一)创设问题情景,引入新课活动1(1)画函数1=xy的图象:(2)求上述函数与x轴、y轴的交点坐3+标。
〖学生独立思考、操作、交流、回答;教师可与学生平等交流,提问学生。
〗(1)列表:(由于一次函数的图象是一条直线,所以只需找两点即可)(2) 描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点. (3) 连线:连接两点即可得13-=x y 的图象令0=x ,则1=y ,一次函数与轴交点坐标为(0,-1),令0=y ,得31=x 一次函数与轴交点的坐标为(31,0)。
问:1、什么叫做反比例函数?如果两个变量x 、y 之间的关系可以表示成xky =(k 为常数且0≠k )的形式,那么y 是x 的反比例函数。
反比例函数的自变量x 不能为零。
2、让学生猜想反比例函数的图象是什么样的?让学生自己尝试作反比例函数x y 6=,x y 4=,x y 6-=,xy 4-=的图象。
(二)探索、研究——揭示反比例函数的特点 活动2〖例2〗画出反比例函数xy 6=与xy 6-=的图象。
11.2反比例函数的图像与性质(1)教案

怀文中学2013—2014学年度第二学期教学设计初二数学(11.2反比例函数的性质和图像(1))主备:王大勇审核:叶兴龙日期:2014-4 教学目标:1.使学生会作反比例函数的图象;2.能理解反比例函数的性质;3.培养提高学生的计算能力和作图能力.教学重难点:1.作反比例函数的图象;2. 理解反比例函数的性质.一.自主探究复习一次函数的相关内容:一次函数y=kx+b(k≠0)的图象是 .当k>0时,y随x的增大而 .当k<0时,y随x的增大而 .二.自主合作探索活动一:1.作反比例函数y=6x的图象:列表:描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点。
连线:用光滑的曲线顺次连结各点,即可得到函数y=6x的图象.2. 你认为作反比例函数图象时应注意哪些问题?列表时,自变量的值可以选取绝对值相等而符号相反的一对一对的数值,这样既可简化计算,又便于描点.探索活动二:作反比例函数y=6x-的图象探索活动三:1. 观察函数y=6x和y=6x-的图象,它们有什么相同点和不同点?ky x =y y yy x x x xA .B .C .D . O O O O 图象分别都是由两支曲线组成的(一般把这两个分支组成的曲线称为双曲线),它们都不与坐标轴相交,两个函数图象都是轴对称图形,它们各自都有两条对称轴。
2. 归纳得出反比例函数图象特征:反比例函数y=k x的图象是由两支曲线组成的,当k>0时,两支曲线分别位于一、三象限内,当k<0 时,两支曲线分别位于第二、四象限内.三.自主展示1. 已知变量y 与x 成反比例,并且当x=2时,y=-3.(1)求y 与x 的函数关系式;(2)求当y=2时x 的值;(3)在直角坐标系内画出(1)小题中函数图象的草图.2. 反比例函数的图象经过点(-2,4),求它的解析式,并画出函数图象,图象分布在哪几个象限?与坐标轴的交点是什么?四.自主拓展1.写出一个图象在第二、四象限的反比例函数的表达式 .2.已知:y 是 x 的反比例函数,且当 x =3 时,y =8,则 y 与 x 的函数关系式为 .3.函数y x =-和xy 2=在同一平面直角坐标系中的图象大致是 ( )4.若反比例函数k y x=的图象经过点()12-,,则这个函数的图象一定经过点 ( ) A.()21-, B.122⎛⎫- ⎪⎝⎭, C.()21--, D.122⎛⎫ ⎪⎝⎭, 5.在同一平面直角坐标系中,直线y x =与双曲线1y x =-的交点个数为 ( ) A.0个 B.1个 C.2个D.无法确定五.自主评价通过这节课的学习,你有什么收获,和大家分享一下吧.教后记:。
11.2 反比例函数的图像与性质(1) 教学案

四明初级中学八年级数学(下)教学案班级: 姓名: 学号:【教学目标】1.能简单分析反比例函数的特征;2.用描点的方法画出反比例函数的图像;3.经历画图、观察、猜想、思考等数学活动,向学生渗透数形结合的数学思想方法.【教学重点】画反比例函数的图像.【教学难点】1.理解用光滑的曲线顺次连接各点;2.根据图像分析函数具有的一些特征,感受数形结合的思想方法.【教学过程】思考、探究:我们已经知道一次函数y kx b =+(k 、b 为常数,k ≠0)的图像是一条直线.让我们一起研究反比例函数k y x=(k 、b 为常数,k ≠0)的图像是怎样的图形. 问题1:已知反比例函数6y x=,请你描述一下这个函数图像具有哪些特征? 思考下列问题:(1)x 、y 所取值的符号有什么关系?这个函数的图像会在哪几个象限?(2)x 、y 的值可以为0吗?这个函数的图像与x 轴、y 轴有交点吗?(3)当x >0时,随着x 的增大,y 怎样变化?当x <0时,随着x 的增大,y 怎样变化?这个函数的图像与x 轴、y 轴的位置关系有什么特征?实践探索一:画反比例函数6y x=的图像.2.在平面直角坐标系中描出相应的点.3.用平滑的曲线分别顺次连接第一和第三象限内的点,得到的两个分支合在一起就是反比例函数的图像.4.根据所画的图像在解决问题1中的问题。
实践探索二:说一说反比例函数6y x=-的图像具有哪些特征,并请在刚才坐标系中画它的图像.达标检测1、反比例函数x y 2=的图像大致是 ( )A B C D2、反比例函数xy 1-=的图像是 ,该函数图像在第 象限。
3、反比例函数xk y 21-=的图像经过点)3,2(-,则k 的值为 ( ) A 6 B -6 C 27 D 27- 4、在同一直角坐标系下,直线1+=x y 与双曲线x y 1=的交点的个数为 ( ) A 0个 B 1个C 2个D 不能确定5、在同一坐标系中画出下列函数的图像:(1) xy 4= (2) x y 4-=6、反比例函数x k y =的图像经过点)4,2(-,求它的解析式,并画出函数图像,图像分布在哪几个象限?拓展延伸7、已知点P 为函数x y 2=图像上一点,且P 到原点的距离为2,则符合条件的点P 有 个。
反比例函数的图象与性质教案

反比例函数的图象与性质教案•相关推荐反比例函数的图象与性质教案范文(通用8篇)作为一名教师,时常会需要准备好教案,教案是教学蓝图,可以有效提高教学效率。
那么大家知道正规的教案是怎么写的吗?下面是小编精心整理的反比例函数的图象与性质教案范文,欢迎阅读与收藏。
反比例函数的图象与性质教案篇1教学目标知识与技能:1、进一步熟悉作函数图象的主要步骤,会作反比例函数的图象。
2、体会函数的三种表示方法的相互转换,对函数进行认识上的整合。
3、培养学生从函数图象中获取信息的能力,初步探索反比例函数的性质。
过程与方法:通过学生自己动手列表,描点,连线,提高学生的作图能力;通过观察图象,概括反比例函数图象的有关性质,训练学生的概括总结能力、情感、态度与价值观:让学生积极参与到数学学习活动中去,增强他们对数学学习的好奇心和求知欲。
教学重难点1) 重点:画反比例函数图象并认识图象的特点。
2)难点:画反比例函数图象。
教学关键:教师画图中要规范,为学生树立一个可以学习的模板。
教学方法:激发诱导,探索交流,讲练结合三位一体的教学方式。
教学手段:教师画图,学生模仿。
教具:三角板,小黑板。
学法:学生动手、动眼,、动耳、采用自主,合作、探究的学习方法。
教学过程一:课前检测:1、什么叫做反比例函数;(一般地,如果两个变量x、y之间的关系可以表示成y= (k为常数,k0)的形式,那么称y是x的反比例函数。
)2、反比例函数的定义中需要注意什么?(1)k为常数,k0(2)从y= 中可知x作为分母,所以x不能为零。
二:激发兴趣导入新课问题1:对于一次函数 y = kx + b ( k 0 )的图象与性质,我们是如何研究的?y=kx+b y=kxK0 一、二、三一、三b0 一、三、四K0 一、二、四二、四b0 二、三、四问题2:对于反比例函数 y=k/x ( k是常数,k 0 ),我们能否象一次函数那样进行研究呢?可以问题3:画图象的步骤有哪些呢?(1)列表(2)描点(3)连线(教学片断:师:上一节课我们研究了反比例函数,今天我们继续研究反比例函数,下面哪位同学说一下自己对反比例函数的了解。
《反比例函数的图象和性质》(第1课时)教案

汇报人:XXX 2024-01-22
contents
目录
• 课程介绍与目标 • 反比例函数概念及性质 • 反比例函数图象分析 • 反比例函数在实际问题中应用 • 学生自主探究活动设计 • 课堂小结与作业布置
CHAPTER 01
课程介绍与目标
教学目标
CHAPTER 05
学生自主探究活动设计
小组合作探究任务布置
分组:将班级学生按照46人一组进行分组,确保 每组学生具有不同的学习 层次和能力特点。
任务布置:给每组学生布 置如下探究任务
探究反比例函数$y = frac{k}{x}$($k$为常数 ,$k neq 0$)的图象特 点;
总结反比例函数的性质, 并与正比例函数性质进行 比较。
例题2
已知反比例函数y=(m+3)/x的图象在每个象限 内,y随x的增大而增大,则m的取值范围是____ 。
解析
将点A的坐标代入函数解析式,得k=2×6=12。 根据k的值,可以确定双曲线的两支分别位于第一 、三象限。在平面直角坐标系中描出点A,并作出 双曲线的两支。
解析
由题意可知,在每个象限内y随x的增大而增大, 说明k<0。因此,m+3<0,解得m<-3。
性反应。
02
环境科学
环境质量与污染物排放之间的关系通常呈现反比例关系。随着污染物排
放量的增加,环境质量逐渐下降。因此,环境保护需要控制污染物的排
放量。
03
社会学
人口增长与资源消耗之间的关系也可能呈现反比例关系。随着人口的增
长,资源消耗速度加快,可能导致资源短缺和环境问题。因此,可持续
发展需要考虑人口增长和资源消耗的平衡。
26.1.1反比例函数的图像与性质(教案)
2.教学难点
(1)反比例函数图像的绘制:学生对反比例函数图像的绘制方法掌握不足,容易在图像的准确性和细节上出现问题。
解决方法:教师可通过示范、指导,让学生动手实践,逐步掌握图像绘制的方法和技巧。
(2)反比例函数性质的推导:学生对反比例函数性质的理解和推导存在困难,如单调性、奇偶性等。
举例:通过实际例子(如速度与时间的关系)引导学生理解反比例函数的定义,突出k值对函数图像的影响。
(2)反比例函数的图像:掌握反比例函数图像的绘制方法,了解图像在坐标平面上的分布特点。
举例:利用数形结合的方法,让学生动手绘制反比例函数图像,观察并总结图像在第一、第三象限的分布情况。
(3)反比例函数的性质:理解反比例函数的单调性、奇偶性等性质,并能应用于实际问题。
3.重点难点解析:在讲授过程中,我会特别强调反比例函数的定义和图像性质这两个重点。对于难点部分,如反比例函数图像的绘制和性质的理解,我会通过举例和比较来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与反比例函数相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。通过改变变量,观察反比例函数图像的变化,从而验证反比例函数的性质。
解决方法:教师可以通过问题引导、小组讨论等方式,帮助学生理解反比例函数的性质,并学会推导方法。
(3)反比例函数在实际问题中的应用:学生在将反比例函数应用于实际问题时,容易忽略条件限制,导致解题错误。
解决方法:教师需提供丰富的实际案例,让学生在练习中学会分析问题、解决问题,提高应用能力。
(4)反比例函数与一次函数、二次函数等其他函数的联系与区别:学生容易混淆不同类型函数的性质和图像。
反比例函数的图象和性质(第1课时)教案.
反比例函数的图象和性质(第1课时)教案[教学目标]知识技能:1、进一步熟悉用描点法作函数图象的主要步骤,会作反比例函数的图象;观察、分析、归纳反比例函数的性质并能初步运用2、通过作图,培养学生的作图能力;逐步提高从函数图象中获取知识的能力,探索并掌握反比例函数的主要性质;过程与方法:1、开展作图经验交流,掌握作图技巧2、通过观察反比例函数图象,分析和探究反比例函数的性质,培养学生的探究,归纳及概括能力。
在探究过程中渗透分类讨论思想和数形结合的思想。
情感态度:1、积极参与探索活动,注意多和同伴交流看法;2、在动手做图的过程中,体会做中学的乐趣,养成勤于动手,乐于探究的好习惯;[教学重点和难点]1、重点:会画反比例函数的图象,理解反比例函数的性质;2、难点:理解反比例函数的性质,并能灵活应用[课型和课时]1、课型:本课为新授课2、课时:本节“反比例函数的图象和性质”共2课时,本课为第1课时。
[授课方法]合作探究式[教学手段]多媒体[教学流程][教学过程]一、预习检测回顾交流创设情境由一名学生主发言以(温故与知新)教师小结:刚才由同学带领大家对函数进行了复习,我们知道对于函数的学习是从定义、图象、性质等方面去研究的,我们已经学习了反比例函数的定义了,下面该学习什么内容了?学生回答:反比例函数的图象与性质。
引出课题二、揭示目标三、问题引导下的再学习合作交流探索新知(实践与探究)(一)画图象1.反比例函数的图象是什么样子呢?我们就来画一画下面6yx=、6yx=-、1yx=、1yx=-几个反比例函数的图象。
以共同体小组为单位,在学案上每组画一个。
教师在学生活动中应重点关注:列表、描点、连线时学生出现的问题。
4.根据指出的问题修改图象。
(二 )、 获取信息 探索性质1.请同学们观察6y x =和6y x =-以及1y x =和1y x=-的图象,回答问题: (1)你能发现它们的共同特征吗?(2)每个函数的图象分别位于哪几个象限?由谁决定? (3)在每个象限内,y 随x 的变化如何变化?小组共同思考这三个问题,请小组长做好记录,代表全组发言。
反比例函数的图象和性质(1)教学设计
17.1.2反比例函数的图象与性质(一)教学设计教学目标一、知识与技能1.进一步熟悉画函数图象的主要步骤,会画反比例函数的图象。
2.体会函数三种表示方法的相互转换,对函数进行认识上的整合。
3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质。
二、过程与方法1.经历反比例函数主要性质的发现过程。
2.体会分类讨论思想、数形结合思想的运用。
三、情感态度与价值观1.积极参与探索活动,多和同伴交流看法。
2.在动手画图的过程中,体会做中学的乐趣,养成勤于动手,乐于探究的好习惯。
教学重点、难点重点:掌握反比例函数的画图。
难点:反比例函数三种表示方法的相互转换。
教具准备1.教师准备:电脑、投影仪、直尺、圆规。
2.学生准备:复习已学过函数有关的图象、性质,预习本节课文内容。
学法解析1.认知起点:本节课是在已经学习了函数、一次函数,对函数的图象、性质等有关概念有了一定经验的基础上学习的。
2.知识线索:回顾旧知识——画反比例函数的图象——探索反比例函数的性质。
3.学习方式:采用教师引导下,师生互动、动手画图、动脑思考、小组合作等方式进行学习。
教学过程一、复习导入(1)什么是反比例函数,其自变量的取值范围是什么?(2)正比例函数y=kx (k≠0)的图像是什么形状,它具有什么样的性质?(3)正比例函数y=kx (k≠0)的图像的位置和增减性是由谁决定的?我们是如何探究得到的?(4)反比例函数的图象会是什么样子呢?反比例函数又具有什么样的性质呢?二、问题探究1.反比例函数的图象是什么样子呢?我们就举个特殊的反比例函数y=6/x画它的图象。
分析:(1)我们第一次画反比例函数的图象时,取几个点?在上一题中我们取几个点?为什么?师生一起完成,后播放多媒体。
2.现在请小组合作画出反比例函数y=-6/x的图象。
师生一起完成,后播放多媒体。
3.小组展示画图情况,表扬其优点,指出其中不足之处。
强调画图是要注意以下三个问题:(1)取点要均衡。
反比例函数的图像和性质1教案
26.1.2 反比例函数的图象和性质第1课时反比例函数的图象和性质一、三维教学目标知识与能力:1、体会并了解反比例函数的图象的意义2、能描点画出反比例函数的图象3、通过反比例函数的图象分析,探索并掌握反比例函数的图象的性质。
过程与方法:通过对比、观察、合作的学习,掌握反比例函数的图像特点和函数性质.情感态度价值观:通过学习了解函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.二、回顾与思考1.反比例函数的概念及表达式形式.2.类比一次函数的作图象法,作反比例函数的图象的方法及一般步骤.三、合作探究例1 画出反比例函数y=6x和y=6x-的函数图象.教师点拨1:1.作反比例函数图象时应注意哪些问题?列表时:自变量的值可以选取一些互为相反数的值,这样即可简化计算,又便于对称描点;列表描点时:要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确的表达函数变化趋势;连线时:一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性. 教师点拨2:比较函数y=6x与y=6x-两个图象,说说它们有什么共同特点?它们之间有什么关系?共同点:图象都是双曲线,关于原点对称。
不同点:分布的象限不同.四、模拟画图例2 在同一坐标系画出反比例函数y=3x 和 y=-3x的函数图象. 解:列表→描点→连线五、归纳新知思考 :观察反比例函数 y=6x , y=6x,与 y=3x 以及y =-3x 的函数图象,回答下列问题: 1、你能发现它们的共同特征以及不同点吗?2、每个函数的图象分别位于那个象限?函数图象的位置由谁决定?3、在每一个象限内,y 随x 的变化如何变化? 正比例函数与反比例函数的比较六、我学我用1.请指出下面的图像中那一个是反比例函数的图像(C)2.如图,这是下列四个函数中哪一个函数的图象( C )3. 认真填一填 (基础题)(1)函数 y=20x的图象在第________象限,在每一象限内,y 随x 的增大而_________. (2) 函数 y=-30x的图象在第________象限,在每一象限内,y 随x 的增大而_________. (3)函数 y=xπ ,当x>0时,图象在第____象限,y 随x 的增大而_________. 变式练习 (中档题)1.已知反比例函数y=4k x-. (1)若函数的图象位于第一、三象限,则k ;(2)若在每一象限内,y 随x 增大而增大,则k .2. 反比例函数y=21a x +-(a 为常数)图象位于( ) A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限思前想后 (综合题)1.已知k <0,函数 y 1=kx , y 2= -k x在同一坐标系中的图象大致是 ( )( A ) ( B ) ( C ) ( D )2.函数y=kx-k 与 y =k x在同一个直角坐标系中的图象可能是教师点拨3:这是反比例函数及一次函数的性质的综合运用,可以采用排除法;也可以让学生分两种情况(k >0和k <0)讨论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题: 反比例函数的图象和性质1
武汉市琴断口中学 施兴娥
教学目标 【知识技能】
1、会用描点法画出反比例函数的图象,说出它的性质;
2、通过画图,理解反比例函数图象是有“间断”的两只曲线,掌握其图象的位置、增减性、对称性与解析式的内在联系,利用相关性质解决有关问题. 【数学思考与问题解决】
1、经历画图,观察、猜想、思考等数学活动,能根据图象数形结合的分析、探究反比例函数的性质,培养学生观察、探究、归纳以及动手的能力。
2、感悟“数形结合”“变化与对应”“无限逼近”等数学思想,并能运用类比、从特殊到一般等研究方法探究反比例函数的性质 【学习重难点】
教学重点:画反比例函数图象和理解反比例函数的性质。
教学难点:探索反比例函数的图象的性质,体会用数形结合思想解数学问题. 【情感态度】
在探究活动中,体验数学活动中的探索性和创造性,感受数学美,体会事物有规律地运动变化的观点,培养严谨的科学态度和勇于探索的精神。
教学设计 【凭风起航】: 1、情景导入
2、正比例函数的解析式:( )。
3、正比例函数的图象是( )。
正比例函数的性质:
当k>0,图象经过原点和( )象限,y 随x 的增大而( )。
当k<0,图象经过原点和( )象限,y 随x 的增大而( ) 画函数图象的步骤是: 微课正比例函数的画法 4、给反比例函数“画像” 5试一试:你能画出反比例函数x 6y =与x 6
-y =的图象吗? y ...
... Y=
x
6
... ... Y=x
6-
...
...
6、y=
x 12,y=x
k
(k>0)的大致图象。
几何画板演示函数图象(k>0)和(k<0)的情况。
7、研究反比例函数图象的性质。
【乘风破浪】
1、(1)当k>0时,反比例函数的图象位于第 象限,在 内y 随x 值的增大而 ;
(2)当k<0时,反比例函数的图象位于第 象限,在 内y 随x 值的增大而 。
2、反比例函数的图象是否具有对称性? 【激流勇进】
1.函数 y= x
5
- 的图象在第___________象限,在每个象限内,y 随 x 的增大而
__________ .
2.函数 y=x m 2
-的图象在二、四象限,则m 的取值范围是 _______.
例1.已知反比例函数y = (m +1)x
m 5
_2 的图象在二、四象限内,求m 的值。
1 .若反比例函数 y= x
k
的图象经过点(2,1),则该反比例函数的图象在第( ) 象限。
【扬帆远航】
1.下列图象中,是反比例函数的图象的是 ( )
2.一次函数y=kx+b (K>0)与反比例函数 x
k y (K>0)
的图象交点的个数为( )
(A ) 0个(B )1个(C )2个(D )无数个
3、若y=x
2
图象上有两点P 1(1,y 1)和P 2(2,y 2),试比较y 1和y 2的大小
4、若x
k
y =
(K>0)图象上有两点P 1(x 1,y 1)和P 2(x 2,y 2),
x
1
<0<x 2,试比较y 1
和y 2
的大小。
5、若 x
k
y =
(K<0)图象上有两点P 1(x 1,y 1)和P 2(x 2,y 2)
0<x 1<x 2,试比较y 1
和y 2
的大小。
课后思考:已知函数2
3)2(m x m y --=为反比例函数. (1)求m 的值;
(2)它的图象在第几象限内?在各象限内,y 随x 的增大如何变化?
(3)当-3≤x ≤21
-时,求此函数的最大值和最小值.
小节:学生总结 送给大家一首诗: 数缺形时少直观 形少数时难入微 数形结合百般好 隔离分家万事休
华罗庚。
