小学数学六年组合图形面积问题
六年级数学拓展题之《12平面组合图形(含答案)》

12.平面组合图形1.正方形ABCD的边长为8厘米,三角形ABC三角形CEF的面积大10平方厘米,求阴影部分的面积。
2.如图,两图中的两个圆的半径都是5厘米,两个图中阴影部分的面积相比较,()。
A.图①大B.图②大C.一样大3.如图,小圆的半径是1厘米,大圆的半径是5厘米,小圆沿着大圆外延滚动直至回到起点位置,(1)小圆扫过的面积是多少平方厘米?(2)小圆圆心经过的长度是多少厘米?(3)小圆一共转了多少圈?4.如图,正方形中阴影部分的面积是53c㎡,那么正方形的面积是多少平方厘米?5.墙角O点处的一木桩上栓着一只羊(如图),栓羊的绳子长4米,墙角两边的墙长2米。
这只羊能吃到草的面积最多是多少?6.如图,已知一个五边形的三条边的长和四个角,试求这个五边形的面积。
(单位厘米)7.如图在大正方形中,三个涂色部分图形周长的和是60厘米,大正方形的面积是多少平方厘米?8.在一个底面是长方形的洗脸盆中,有一个直径6厘米的圆形塑料片在盆地任意滑动。
这个塑料片不可能滑到的面积是多少平方厘米?9.下图中空白部分是一个正方形,求阴影部分的周长和面积。
10.求图中阴影部分的面积,其中A为边的中点。
(单位:cm)11.如图,大正方形的边长比小正方形的长2厘米,小正方形的面积比大正方形小36平方厘米。
小正方形的面积是()平方厘米。
12.如图,大、小两个正方形中阴影部分的面积比是3:1,小正方形的面积是大正方形的( )。
13.已知右图中长方形被分成四部分,三角形BCO的面积是4cm²,三角形CDO 的面积是8cm²,涂色部分的面积是()cm²。
14.如图,涂色部分的面积是10平方厘米,空白部分的面积是多少平方厘米。
15.正方形的面积是12平方厘米,求阴影部分的面积。
参考答案1.222.B3. 24π、12π、54.1005.6π6.187.1448.7.749.21.42、10.2610.9π11.6412.1 913.2014.52.815.3π详细讲解,请参阅“小学六年级数学思维提升培优拓展题讲解之《12平面组合图形》”。
小学数学 多边形面积与组合图形面积(含答案)
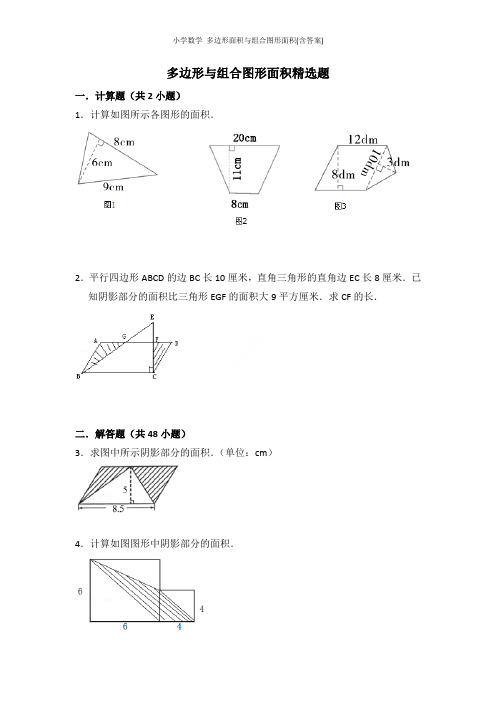
多边形与组合图形面积精选题一.计算题(共2小题)1.计算如图所示各图形的面积.2.平行四边形ABCD的边BC长10厘米,直角三角形的直角边EC长8厘米.已知阴影部分的面积比三角形EGF的面积大9平方厘米.求CF的长.二.解答题(共48小题)3.求图中所示阴影部分的面积.(单位:cm)4.计算如图图形中阴影部分的面积.5.如图所示是学校生态园的平面图,你能算出生态园的面积吗?(单位:m)6.计算下面图形的面积.7.图形由两个正方形组成,求阴影部分的面积.(单位:cm)8.计算阴影部分的面积.9.在如图所示中剪出一个最大的长方形,画出来并求出剩余部分的面积.10.求如图平面图形的面积.11.李大爷家有一块菜地(如图所示)你能用巧妙的方法算出菜地的周长和面积吗?12.一张长8厘米,宽4厘米的长方形纸,从下边的中点和右上角顶点连线一条线段,沿这条线段剪去一个角(如图所示),剩下的面积是多少?13.用篱笆围一块菜地,如图的梯形,一边利用房屋的墙壁,已知梯形上、下底的比为3:5,篱笆长40米,求菜地面积.14.把一个大平行四边形分成3块,(如图)已知图形阴影部分是平行四边形,面积是12平方米,求三角形和梯形的面积各是多少?15.如图,三角形ABC的面积是56平方米,BD=DC,DE垂直于AC,AC=14米.求图中阴影部分的面积.16.李大伯一边利用房屋干墙壁,另三边用篱笆围成一个梯形养鸡场地(如图).篱笆总长是36米.求这个养鸡场的面积是多少?17.求下列图形中阴影部分的面积.18.看图计算如图图形的面积.19.认真观察,巧计算.(用两种方法计算组合图形的面积)20.一块水稻田的形状如下图.如果按照平均每穴30平方分米插秧,大约要插多少穴?21.求组合图形的面积.(1)图1的面积是:;(2)图2的面积是:.22.如图,已知四条线段的长分别是:AB=2厘米,CE=6厘米,CD=5厘米,AF=4厘米,并且有两个直角.求四边形ABCD的面积.23.如图,长方形里有四个三角形,已知其中的三角形的面积,求三角形ADE 的面积.24.(如图)三角形ABC的周长为80厘米,形内有一点P到三角形三条边的距离都是8厘米,求三角形ABC的面积.25.求如图图形的面积.26.我会计算阴影部分的面积.27.如图:ABCE是一个梯形,其中ABCD是长8厘米,宽7厘米的长方形,AF 长是4厘米,求阴影部分的面积?28.如图是由两个完全一样的直角三角形叠在一起而成的,求阴影部分的面积.(单位:厘米)29.计算下列图形的面积.(单位:厘米)30.如图所示,长方形的ABCD面积被线段AE,AF分成三等份,且三角形AEF 的面积是35平方厘米,求长方形的面积.31.图中长方形的面积是432平方厘米,求阴影部分的面积.32.如图所示,已知正方形和三角形有一部分重叠,三角形乙比三角形甲面积大7平方厘米,则X=厘米.33.用篱笆围成一个养鸡场(如图所示),一面靠墙,篱笆总长90米,下底长度是上底长度的3倍.求这个养鸡场的面积.34.如图正方形ABCD的边长是4分米,长方形EFGD的长GD是5分米,求DE 的长.35.已知如图大正方形的边长是5厘米,小正方形的边长是3厘米,求阴影部分的面积.36.如图所示,长方形ABCD的面积是180平方厘米,CD长15厘米,ED长17厘米,求三角形ACE的面积.37.图中的两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积.38.如图ABCD是梯形,∠A=∠B=90°,AB=12cm,BC=6cm,甲、乙两阴影面积之差为24cm2,求ABCD的面积.39.有一块如图形状的菜田,算一算:①占地多少公顷?所需数据在图中选择.(单位:m)②如果每公顷需要施化肥50千克,这块地一共要施肥多少千克?40.你能求出下列图形的周长吗?41.求组合图形的面积.(单位:米)42.如图,一个梯形的上底是5厘米,下底是8厘米.三角形的高是4厘米,并把三角形分为面积相等的甲乙两部分,求阴影部分的面积.43.求如图的面积或阴影面积:44.如图,是大小两个正方形组成的图形,大正方形边长是8厘米,小正方形边长为6厘米,求阴影部分的面积.45.如图,正方形ABCD的边AB、BC分别在三角形BEF的BE、BF边上,顶点D 在EF边上,点D把EF分成两段,DE=12米,DF=15米,求两个阴影三角形的面积和.46.在长方形ABCD中,AD=15厘米,AB=8厘米,四边形EFGO的面积是9平方厘米,阴影部分的面积是多少平方厘米?47.如图是由两个平行四边形组成的,这个图形的面积是多少?48.如图,四边形ACEH是梯形,ACEG是平行四边形,ABGH是正方形,CDFG 是长方形.已知,AC=8厘米,HE=13厘米,求阴影部分的面积.49.图中长方形的面积是180平方厘米,S1的面是45平方厘米,S2的面积是60平方厘米.求阴影部分的面积.50.有一块铁皮,形状如图所示.如要油饰这块铁皮的一面,每平方米用油漆0.6千克,刷完这块铁皮需要多少千克油漆?多边形与组合图形面积精选题参考答案与试题解析一.计算题(共2小题)1.【解答】解:(1)8×6÷2=24(平方厘米)答:三角形的面积是24平方厘米.(2)(8+20)×11÷2=28×11÷2=154(平方厘米)答:梯形的面积是154平方厘米.(3)12×8+10×3÷2=96+15=111(平方分米)答:这个图形的面积是111平方分米.2.【解答】解:设EF长为x厘米,则CF就是8﹣x厘米,根据题干分析可得方程:10×(8﹣x)=10×8÷2+9 80﹣10x=49 10x=31 x=3.18﹣3.1=4.9(厘米);答:CF长为4.9厘米.二.解答题(共48小题)3.【解答】解:8.5×5﹣8.5×5÷2=42.5﹣21.25=21.25(cm2),答:阴影部分的面积为21.25cm2.4.【解答】解:6×6+4×4﹣6×6÷2﹣4×4÷2﹣6×(6﹣4)÷2=36+16﹣18﹣8﹣6=20(平方厘米)答:阴影部分的面积是20平方厘米.5.【解答】解:20﹣12=8(米)16﹣10=6(米)12×16+8×6÷2=192+24216(平方米)答:生态园的面积是216平方米.6.【解答】解:15×4=60(平方米),答:它的面积是60平方米.7.【解答】解:(10+8)×10÷2=18×5=90(平方厘米)答:阴影部分的面积是90平方厘米.8.【解答】解:30×28÷2=30×14=420(平方厘米)答:阴影部分的面积是420平方厘米.9.【解答】解:如图所示,(12﹣6)×(10﹣5)÷2=6×5÷2=15(平方厘米)答:剩余部分的面积是15平方厘米.10.【解答】解:(1)15×30=450(平方厘米)答:平行四边形的面积是450平方厘米.(2)5×2÷2+5×3=5+15=20(平方米)答:这个图形的面积是20平方米.11.【解答】解:周长是:(17+8+23)×2=48×2=96(米)面积是:(17+8)×23﹣(23﹣8)×17=25×23﹣15×17=575﹣255=320(平方米)答:周长是96米,面积是329平方米.12.【解答】解:(8+8÷2)×4÷2=(8+4)×4÷2=12×4÷2=24(平方厘米),答:剩下的面积为24平方厘米.13.【解答】解:如图:5﹣3=240×=8(米)40×=20(米)40×=12(米)(12+20)×8÷2=32×8÷2=128(平方米)答:菜地面积是128平方米.14.【解答】解:因为大平行四边形的对边平行且相等,所以阴影部分的高=12÷3=4(米),所以三角形的面积=×3×4=6(平方厘米),梯形的面积=(3+6)×4=18(平方厘米).答:三角形的面积是6平方厘米,梯形的面积是18平方厘米.15.【解答】解:因为BD=DC,所以三角形ABD和三角形ADC的面积相等,因为三角形ABC的面积是56平方米,所以图中阴影部分的面积为:56÷2=28(平方米)答:阴影部分的面积是28平方米.16.【解答】解:(36﹣10)×10÷2=26×10÷2=130(平方米)答:这个养鸡场的面积是130平方米.17.【解答】解:(2+9+2)×(2+4+2)+2×2×4=13×8﹣16=104﹣16=88(平方厘米)答:阴影部分的面积是88平方厘米.18.【解答】解:(1)8×3=24(平方分米)答:图形的面积是24平方(2)25×14÷2=25×7=175(平方米)答:图形的面积是175960平方厘米.(3)分米.(26+34)×32÷2=60×32÷2=960(平方分米)答:图形的面积是960平方分米.(4)26×20+(26+30)×5÷2=520+56×5÷2=520+140=660(平方厘米)答:图形的面积是60平方厘米.(5)6×7+(8﹣6)×(7﹣2.5)÷2=42+2×4.5÷2=42+4.5=46.5(平方厘米)答:图形的面积是46.5平方厘米.19.【解答】解:(1)如图所示,,4×10+(9+10)×(5﹣4)÷2=40+9.5=49.5(平方厘米)(2)如图所示,,5×9+(4+5)×(10﹣9)÷2=45+4.5=49.5(平方厘米)答:组合图形的面积是49.5平方厘米.20.【解答】解:8×11÷2+(11+22)×10÷2=44+165=209(平方分米)209÷30=6(穴)…29(平方分米)6+1=7(穴)答:大约要插7穴.21.【解答】解:(1)24×8+10×24÷2=192+120=312(平方米)答:组合图形的面积为312平方米.(2)12×6+(12+6)×6÷2=72+18×3=72+54=126(平方米)答:组合图形的面积为126平方米.故答案为:312,126.22.【解答】解:连接AC,就变成ADC和ABC两个三角形,如图:三角形ABC 已知底AB=2(厘米)高就是CE=6(厘米)那么三角形ABC面积就是2×6÷2=6(平方厘米)三角形ADC已知底DC=5(厘米)高就是AF=4(厘米)三角形ADC 面积是5×4÷2=10(平方厘米)ABCD面积是10+6=16(平方厘米)答:四边形ABCD的面积16平方厘米.23.【解答】解:如图:S △ABE面积+S△DEC面积=(AB×EF)÷2+(DC×EG)÷2,因为AB=DC,两个三角形高的和等于AD,所以,S△ABE面积+S△DEC面积=AB×AD÷2=长方形面积的一半;同理,另两个三角形面积的和也是长方形面积的一半,即S△ABE面积+S△EDC面积=S△ADE面积+S△BCE面积,即S△=37+29﹣41=25.24.【解答】解:如图:S△ABC =S△APB+S△APC+S△BPC=AB×BP÷2+AC×PE÷2+BC×PD÷2=PD×(AB+AC+BC)=×8×80=320(平方厘米)答:三角形ABC的面积是320平方厘米.25.【解答】解:(1)14×12÷2=168÷2=84(平方厘米),答:面积是84平方厘米;(2)(12+18)×16÷2=30×16÷2=240(平方米),答:面积是240平方米.26.【解答】解:15×9﹣6×6=135﹣36=99(平方分米)答:阴影部分的面积是99平方分米.27.【解答】解:8×7÷2﹣8×4÷2=28﹣16=12(cm2)答:阴影部分的面积是12平方厘米.28.【解答】解:S=[(8﹣3)+8]×5÷2=65÷2=32.5(平方厘米);答:阴影部分的面阴影积是32.5平方厘米.29.【解答】解:(1)12×8﹣×(12﹣4﹣4)×3,=96﹣6,=90(平方厘米);(2)12×8+×10×(12﹣5),=96+35,=131(平方厘米).30.【解答】解:根据以上分析知:S△EFC=EC×CF=×BC×CD=BC ×CD=×ABCD的面积,四边形AECF的面积=×ABCD的面积,设长方形ABCD 的面积为S,根据题意得:(﹣)×S=35 S=35,S=126.答:这个长方形有面积是126平方厘米.31.【解答】解:432÷36×6÷2=12×6÷2=72÷2=36(平方厘米)答:阴影部分的面积是36平方厘米.32.【解答】解:三角形乙的面积比三角形甲的面积大7平方厘米,根据图形可得:三角形ABE的面积比正方形ABCD 的面积大7平方厘米,所以三角形ABE的面积为:7×7+7=49+7=56(平方厘米),又因为AB=7厘米,所以BE的长度是:56×2÷7=16(厘米),所以CE的长度为:16﹣7=9(厘米),即X=9厘米.答:X的长度是9厘米.故答案为:9.33.【解答】解:3﹣1=290÷(3+3)=15(米)下底:15×3=45(米)高:15×2=30(米)面积:(15+45)×30÷2=30×30=900(平方米)答:这个养鸡场的面积是900平方米.34.【解答】解:4×4÷2=8(平方分米),8×2÷5=3.2(分米).答:DE的长是3.2分米.35.【解答】解:(5+3)×3÷2+5×5÷2﹣3×(3+5)÷2,=8×3÷2+5×5÷2﹣3×8÷2,=12+12.5﹣12,=12.5(平方厘米).答:阴影部分的面积是12.5平方厘米.36.【解答】解:连接ED,AD=BC=180÷15=12(厘米),AE2=172﹣122=145(平方厘米),AE=,三角形ACE的面积是:×12÷2,=6(平方厘米);答:三角形ACE的面积是6平方厘米.37.【解答】解:大三角形面积:10×(10+6)÷2=80(平方厘米),小三角形面积:10×10÷2=50(平方厘米),阴影部分三角形面积:80﹣50=30(平方厘米).答:阴影部分的面积是30平方厘米.38.【解答】解:12×AD÷2﹣12×6÷2=24,6AD﹣36=24,6AD=60,AD=10;梯形的面积为:(6+10)×12÷2,=16×12÷2,=96(平方厘米);答:ABCD的面积是96平方厘米.39.【解答】解:①×(75+125)×40+×125×48=4000+3000=7000(平方米),7000平方米=0.7公顷;答:占地0.7公顷.②0.7×50=35(千克);答:这块地一共要施肥35千克.40.【解答】解:(1)4+3+3=10(2)(5+3)×2=16(3)4+2+3+5+2=16.41.【解答】解:5×4÷2+7×5+(5+12)×3÷2=5×4÷2+7×5+17×3÷2=10+35+25.5=70.5(平方米)答:面积是70.5平方米.42.【解答】解:[5﹣(8﹣5)+5]×4÷2,=[5﹣3+5]×4÷2,=[2+5]×4÷2,=7×4÷2,=28÷2,=14(平方厘米);答:阴影部分的面积为14平方厘米.43.【解答】解:(1)(15+20)×25÷2+12×20÷2=437.5+120=557.5答;图形的面积是557.5.(2)12×8﹣4×8÷2=96﹣16=80答:阴影部分的面积是80.44.【解答】解:阴影部分的面积:6×6÷2=36÷2=18(平方厘米)答:阴影部分的面积是18平方厘米.45.【解答】解:据分析解答如下:12×15÷2=90(平方米);答:两个阴影三角形的面积和是90平方米.46.【解答】解:15×8﹣15×8÷2+9,=120﹣60+9,=69(平方厘米).答:阴影部分的面积是69平方厘米.47.【解答】解:3×7.5=22.5(平方厘米).答:这个图形的面积是22.5平方厘米.48.【解答】解:因为ACEG是平行四边形,所以AC=GE=8厘米又已知HE=13厘米,所以HG=13﹣8=5(厘米)故GB=5厘米所以红色三角形的面积是:8×5÷2=20(平方厘米)即阴影部分的面积是20平方厘米.答:阴影部分的面积是20平方厘米.49.【解答】解:连接BD,则S△BCD=180÷2=90(平方厘米),S△BDF=90﹣60=30(平方厘米),所以BF:BC:=1:3;同理,BE:AB=1:2,因此S△BEF=BE×BF,=×BC×AB,=BC×AB,=×180,=15(平方厘米);阴影部分的面积:180﹣60﹣45﹣15,=180﹣120,=60(平方厘米).答:阴影部分的面积是60平方厘米.50.【解答】解:(3×1.2÷2+5×2.4)×0.6,=(1.8+12)×0.6,=13.8×0.6,=8.28(千克);答:刷完这块铁皮需要8.28千克油漆.。
小学数学 简单组合图形的面积

简单组合图形的面积
一、考点、热点
1.巩固基本图形的面积计算,能根据基本图形的面积用“割补”的方法正确计算出组合图形的面积。
2. 能灵活应用不同方法计算同一个组合图形的面积,体会转化思想,感受解决问题的多样性。
二、知识梳理
1、写出下面这些简单的、基本的图形的面积公式
2、
像这样由几个基本图形拼成的图形,我们就把它叫作组合图形。
3、华丰小学校园里有一块草坪(如右图),它的面积是多少平方米?
分割法:将整体分成几个基本图形,求出它们的面积和。
添补法:用一个大图形减去一个小图形求出组合图形的面积。
试一试
1、如图:校园里有一个花圃你能计算出它的面积是多少平方米吗? (可以尝试着不同的方法)
三、巩固练习
1、判断题。
(1)一个街心公园大约占地面积20平方米。
()
(2)6平方千米50公顷=6500公顷。
()
(3)组合图形面积可以转化为我们学过的简单图形的面积之和或者之差。
()
2、下图空白部分的面积是20平方分米,你能算出下面图形中阴影部分的面积是多少吗?
4、已知下图中平行四边形的面积是240平方厘米,求阴影部分的面积。
5、求下面组合图形的面积
四、过手训练
1、一个平行四边形相邻的两条边分别长8厘米和15厘米,这个平行四边形的一条底边上的高是12厘米,这个平行四边形的面积是多少平方厘米。
(提示:先画图再解答)
2、在长15米,宽12米的长方形地上种草坪,中间横竖各有一条宽2米的小路,求小路的面积。
3、求下面阴影部分的面积
4、两个完全一样的直角三角形重叠在一起,那么阴影部分的面积是多少平方厘米?。
小学数学西南师大六年级上册二圆西师版求组合图形的面积教案

求组合图形的面积教案教科书第35页,课堂活动,练习七第1、2、3题。
【教学目标】1.学会并掌握组合图形的面积计算方法。
2..通过相关习题的练习,加深学生运用求组合图形的面积的方法。
3.经历解决问题的过程,学会从不同的角度去分析解决问题,体会学习圆的面积的现实意义和价值。
【教学重点难点】重点是掌握求组合图形面积的方法;难点是能将组合图形分解成基本图形,运用求组合图形的面积的方法解决稍复杂的问题。
【教学过程】一、导入新课1.出示所学过的几何图形:长方形、正方形、平行四边形、三角形、梯形、圆。
让学生说说怎样求这些图形的面积?2.生活中,有些图形是不规则的,或者是几个图形组合而成的,我们并不能直接求它们的面积。
如何计算它们的面积?解决相关的问题呢?今天就开始学习:求组合图形的面积。
二、探究新知1.掌握求组合图形面积的基本策略。
(教学例1)(1)请看图形,求阴影部分面积(完整地呈现例1)。
(2)怎样算出阴影部分面积?学生讨论分析教学方案1:在学生回答的基础上,板书:阴影部分的面积=(四分之一圆面积-三角形面积)×8S=(4×4×÷4- 4×4÷2)×8=(cm²)学生独立解答两个问题。
教学方案2:先让学生独立尝试其它解答以后,再通过交流反馈,总结出方法。
学生讨论,教师总结:阴影部分的面积=四分之一圆面积×2-正方形面积S=8×8×÷4×2-8×8 =(cm²)(3)小结:像这种组合图形的面积,我们一般把它分割成几个学过的图形,再把它们的面积相加或者相减得到组合图形的面积。
2.掌握求组合图形的不同策略。
(1)呈现变式题:求右图形的面积。
(2)独立思考:这个组合图形可以分解成哪些基本图形?(3)引导学生通过画辅助虚线,整理出各种思路。
(4)请同学们选择一种喜欢的思路来求出组合图形的面积。
小学数学组合图形面积

小学数学组合图形的面积,10种解题思路,值得收藏小学数学组合图形的面积,10种解题思路,值得收藏一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积分析:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差. 例如:下图,求阴影部分的面积。
分析:先求出正方形面积再减去里面圆的面积即可.三、直接求法这种方法是根据已知条件,从整体出发直接求出不规则图形面积.例如:下图,求阴影部分的面积。
分析:通过分析发现阴影部分就是一个底是2、高是4的三角形四、重新组合法这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如:下图,求阴影部分的面积。
分析:拆开图形,使阴影部分分布在正方形的4个角处,如下图。
五、辅助线法这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可例如:下图,求两个正方形中阴影部分的面积。
分析:此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便(如下图)根据梯形两侧三角形面积相等原理(蝴蝶定理),可用三角形丁的面积替换丙的面积,组成一个大三角ABE,这样整个阴影部分面积恰是大正方形面积的一半.六、割补法这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如:下图,若求阴影部分的面积。
分析:把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如:下图,求阴影部分的面积。
分析:可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
小学六年级数学小升初珍藏版复习资料第19讲 组合图形的认识、表面积与体积(解析)

2022-2023学年小升初数学精讲精练专题汇编讲义第19讲 组合图形的认识、表面积与体积小学阶段所学的立体图形主要有长方体、正方体、圆柱体和圆锥体,这四种立体图形的表面积和体积的计算是小升初数学的热点内容,特别是涉及到立体图形的切拼时,立体图形的表面积和体积发生了变化,牢固掌握这些立体图形的特征和有关的计算方法及切拼时表面积和体积的变化规律是解题的关键,本讲将在前面两讲学习的基础上进一步总结整理立体图形切拼时表面积和体积的变化规律。
知识点一:立体图形的表面积和体积计算常用公式: 立体图形 表面积体积 长方体S=2)(bh ah ab ++a :长 b:宽 h :高 S :表面积 V abh = V Sh = 正方体S=26a a :棱长 S :表面积 3V a = V Sh = 圆柱222π2πS rh r =+=+圆柱侧面积个底面积 2πV r h =圆柱圆锥 22ππ360n S l r =+=+圆锥侧面积底面积 注:l 是母线,即从顶点到底面圆上的线段长 21π3V r h =圆锥体 知识点二:解决立体图形的表面积和体积问题时的注意事项(1)要充分利用正方体六个面的面积都相等,每个面都是正方形的特点.(2)把一个立体图形切成两部分,新增加的表面积等于切面面积的两倍;反之,把两个立体图形拼合到一起,减少的表面积等于重合部分面积的两倍。
(3)若把几个长方体拼成一个表面积最大的长方体,应把它们最小的面拼合起来;若把几个长方体拼成一个表面积最小的长方体,应把它们最大的面拼合起来。
2.解答立体图形的体积问题时,要注意以下几点:(1)物体沉入水中,水面上升部分的体积等于物体的体积;把物体从水中取出,水面下降部分的体积等干物体的体积,这是物体全部浸没在水中的情况。
如果物h r hr 知识精讲体不全部浸在水中,那么排开水的体积就等于浸在水中的那部分物体的体积. (2)把一种形状的物体变为另一种形状的物体后,形状变了,但它的体积保持不变.(3)求一些不规则物体体积时,可以通过变形的方法求体积。
小学六年级数学总复习题库-组合图形一

Lorem ipsum dolor sit amet, consectetur adipisicing elit.
• 1、有一个面积是96平方厘米的长方形,长与 宽的比是 ,从一个顶点出发,分别与它对 1 3:2 1 边的 2 和 处相连,求阴影部分的面积。 3
• 3、已知四边形ABCD的边AB=5厘米,AD=4厘米, ∠C=67.5°,∠A=90°,∠D=135°,BH与CD 垂直,BH=7厘米。求四边形ABCD的面积。
• 4、大正方形的边长是4厘米,小正方形的边 长是3厘米,求阴影部分的面积。
• 5、A,B是两个扇形所在圆的圆心,那么两个 阴影部分的面积差是多少?
• 6、如图,ABCD是直角梯形,四边形AEGF、 MBKN都是正方形,且AE=MB,EP=KC=9, DF=PM=4,求三角形DPC的面积。
• 1、一个六边形的六个内角都是120度,连续 四边的长依次是2厘米、3厘米、3厘米、1厘 米,如图。求这个六边形的周长。
• 2、如图,已知四边形ABCD的边BC=7厘米, AD=3厘米,∠B=∠D=90度,∠c=45度,求这 个四边形的面积。
• 3、如图,已知三角形ABD的面积为72平方厘 米,且DC= 1 BD,AE=ED,求四边形CDE=4CD,连接AD,E是AD的中点。已知三角形 ABC的面积是112平方厘米,求四边形CDEF的 面积。
• 5、如图,在长方形ABCD中,AC与BE相交于F, 三角形BCF的面积为6平方厘米,三角形CEF的 面积为4平方厘米。求四边形AFED的面积。
• 2、已知BC=5厘米,AD=3厘米,AE=4厘米, CF=6厘米,∠AED=90°,∠CFD=90°图中四 边形ABCD(阴影部分)的面积是多少?
数学-奥数竞赛-小学六年级奥数--面积计算

二、精讲精练
【例题3】在图中, 正方形的边长是10厘米, 求图中阴影部分的面积。 【思路导航】解法一:先用正方形的面积减去一个整圆的面积, 得空部分的
一半(如图所示), 再用正方形的面积减去全部空白部分。 空白部分的一半:10×10-(10÷2)2×3.14=21.5(平方厘米) 阴影部分的面积:10×10-21.5×2=57(平方厘米) 解法二:把图中8个扇形的面积加在一起, 正好多算了一个正方形(如图所
练习3: 3.求下面各图形中阴影部分的面积(单位:厘米)。
二、精讲精练
【例题4】在正方形ABCD中, AC=6厘米。求阴影部分的面积。
【思路导航】这道题的难点在于正方形的边长未知, 这样扇形的半径 也就不知道。但我们可以看出, AC是等腰直角三角形ACD的斜边。根 据等腰直角三角形的对称性可知, 斜边上的高等于斜边的一半(如图 所示), 我们可以求出等腰直角三角形ACD的面积, 进而求出正方形 ABCD的面积, 即扇形半径的平方。这样虽然半径未求出, 但可以求 出半径的平方, 也可以把半径的平方直接代入圆面积公式计算。
3.14×(30×2)×1/4-30=17.1(平方厘米)
答:阴影部分的面积是17.1平方厘米。
二、精讲精练
练习5: 1.如图所示, 平行四边形的面积是100平方厘米, 求阴影部分的面积。
二、精讲精练
练习5:
2.如图所示,O是小圆的圆心,CO垂直于AB,三角形ABC的面积是45平方 厘米,求阴影部分的面积。
练习4:
2.如图所示, 图形中正方形的面积是50平方厘米, 分别求出每个图形 中阴影部分的面积。
二、精讲精练
练习4:
3.如图所示, 正方形中对角线长10厘米, 过正方形两个相对的顶点以 其边长为半径分别做弧。求图形中阴影部分的面积(试一试, 你能想 出几种办法)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学数学六年组合图形面积问题
1.(2011•东莞)如图中圆的
周长是62.8厘米,如果圆的面
积和长方形的面积相等,计算
涂色部分的周长.
2.求下列图形的面积和
周长
周长:面积:
周长:面积:
3.求图中阴影部分的周长.(单位:厘米)
4.如图所示,三角形ABC的边长都为6cm,分别以A、B、C三点为圆心,边长的一半为半径作弧,求阴影部分的周长.5.(2008•镇海区)如图,三角形AOC是边长为3厘米的正三角形,求阴影部分的面积.6.(2008•兴山县)计算阴影部分的面积.
7.(2008•洛阳)如图:阴影部分的面积是50平方厘米,求图中圆环的面积.
8.梯形面积51平方厘米,图中阴影影部分的面积(单位:厘米)
9.图中两块阴影部分的面积相等,三角形ABC是直角三角形,BC是直径,长20厘米.计算AB 的长度.
10.求阴影部分的面积(单位:厘米)
11.(2012•郑州)ABCD和CDEF 都是正方形,DC等于12厘米,CB等于10厘米,求阴影部分的面积.
12.(2012•郑州)计算如图阴影部分的面积.(单位:分米)
13.(2012•仙游县)求出阴影部分的周长和面积.(单位:厘米)14.(2012•金沙县)如图,求阴影部分的面积.已知:r=10cm.
15.(2012•衡阳)两个正方形
组成下图所示的组合图形.已
知组合图形的周长是52厘米,DG=4厘米,阴影部分的面积是
_________平方厘米.16.(2011•汕头)求下图阴影部分面积.(单位:厘米)
17.(2010•镇海区)图形计算.①一个环形铁片,外圆半径是0.6米,内圆半径是0.4米.它的面积是多少平方米?(π取
3.14,得数保留两位小数)
②求阴影部分的面积.(单位,厘
米)
18.(2010•雨花区)求阴影部分面
积(空白部分面积为80平方厘米)
19.(2010•尤溪县)求下列图形中阴影部分的面积.<单位:厘米>
20.(2009•镇海区)在图中,O是
圆心,OD=4,C是OB的中点.
阴影部分的面积是14π,求直角三
角形OAB的面积.
21.(2009•南岗区)如图,半圆的直径AB长6厘米,半圆绕A点逆时针旋转60°,使直径AB到达AC的位置.求图中阴影部分的面积.
22.(2008•杭州)如果你完成上述题目觉得正确无误后,可考虑解决以下问题,注意:本题不计入总分.两个正方形如图放置,其中D、C、G在同一条直线上,小正方形ECGF的边长为6,连AE、EG、AG,求图中阴影部分的面积.
23.(2008•禅城区)图中,圆周长为12.56厘米,平行四边形ABCD 的面积为21.6平方厘米,求阴影部分的面积.(π取3.14)
24.(2003•重庆)列式计算:
①6除1.5的商,加上3,在乘3,积是多少?
②1与0.5的和除以它们的差的2倍,商是多少?③如图:三角形ABC为直角三角形,BC为圆的直径,BC=20厘米,S1、S2阴
六年数学图形面积问题- 7 - 影部分的面积,且S1=S2,求三角形
ABC的面积?()
25.在如图所示的长方形ABCO
中,三角形ABD的面积比三角形
BCD的面积大10平方厘米,求阴
影部分的面积.
26.如图:三角形ABC是等腰直
角三角形,直角边为4厘米,求阴
影部分面积.
27.计算下图中阴影部分的面积.
(单位:厘米)
28.求图中阴影部分的面积(图中
单位:厘米)
六年数学图形面积问题- 8 - 29.如图中平行四边形的面积是90
平方分米.求阴影部分的面积.
30.求阴影部分的面积:。
