可逆过程与可逆过程体积功的计算
合集下载
02热力学第一定律2
一粒粒取走砂粒
P终,V
终
可逆过程 , 外压和内压相差无穷 小,p环境 = p
P始,V
始
T
T
W p环境 dV
V1
V2
pdV
V1
V2
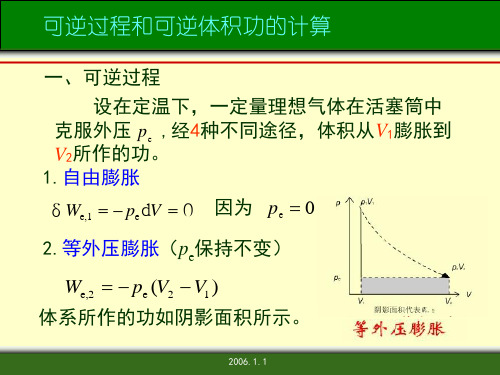
3、可逆过程的体积功：
可逆过程,外压和内压相差无穷小
W pdV
不同过程的体积功
一次 -18 72 二次 -24 48 三次 -26 44 (1)功与过程有 关。同样是膨 胀(压缩)过程， 它们的功各不 相同。
膨胀过程 W/kJ
压缩过程 W/kJ
(2)正、逆过程的功绝对值不相等。W正≠W逆 (3)膨胀次数越多，膨胀功越大。
可逆过程的体积功
P终 p
始
物理化学
第二章 热力学第一定律
第二章
2.1
2.2
热力学第一定律
热力学基本概念
热力学第一定律
2.3
2.4
恒容热、恒压热、焓
变温过程热的计算
第二章 热力学第一定律
2.5 可逆过程和可逆体积功的计算
2.6
2.7 2.8
相变热的计算
化学反应热的计算 气体的节流膨胀
2.1
热力学基本概念
一.系统[体系]和环境
系统（system） 在科学研究时必须先确定研究对象，把 研究的对象称为系统或体系。 环境（surroundings） 系统以外的与系统相联系的那部分物质 称为环境。 隔开系统与环境的界面可以是实际存在 的，也可以是想象的，实际上并不存在的。
根据系统与环境之间的关系，把系统分为三类：
14-可逆过程与可逆功
P2 0.401 100 0.401 T2 T1 ( ) 298 ( ) 118K P 1.00 1 nRT2 1.00 8.314118 3 3 V2 9 . 58 10 m 3 P2 10010
3 W U nCV ,m (T2 T1 ) 1.00 8.314 (118 298 ) 2.24 KJ 2
' e,1 " "
p (V V )
' ' "
p1 (V1 V )
'
整个过程所作的功为三步加和。
上一内容
下一内容 回主目录 返回
功与过程
上一内容
下一内容
回主目录
返回
功与过程
3.可逆压缩 如果将蒸发掉的水气慢慢在杯中凝聚，使压力缓 慢增加，恢复到原状，所作的功为：
Hale Waihona Puke W pi dV上一内容
下一内容 返回
回主目录
功与过程
上一内容
下一内容
回主目录
返回
功与过程
2.多次等外压压缩 第一步：用 p" 的压力将体系从 V2 压缩到V " ； 第二步：用 p' 的压力将体系从V " 压缩到V ' ； 第三步：用 p1 的压力将体系从 V ' 压缩到 V1 。
W p (V V2 )
V2 0.0248 Wr nRT ln 2.0 8.314 298ln V1 0.10 6.9110 J
3
上一内容
下一内容
回主目录
返回
例题：
• 2、1.00mol某单原子理想气体在298K,1.00×１０３ KPa下可逆绝热膨胀到最终状态压力为100KPa,求算 终态体积、终态温度及所做的功。 1 1 1.67 1 解： T2 ( P2 ) 0.401 T1 P1 1.67
3 W U nCV ,m (T2 T1 ) 1.00 8.314 (118 298 ) 2.24 KJ 2
' e,1 " "
p (V V )
' ' "
p1 (V1 V )
'
整个过程所作的功为三步加和。
上一内容
下一内容 回主目录 返回
功与过程
上一内容
下一内容
回主目录
返回
功与过程
3.可逆压缩 如果将蒸发掉的水气慢慢在杯中凝聚，使压力缓 慢增加，恢复到原状，所作的功为：
Hale Waihona Puke W pi dV上一内容
下一内容 返回
回主目录
功与过程
上一内容
下一内容
回主目录
返回
功与过程
2.多次等外压压缩 第一步：用 p" 的压力将体系从 V2 压缩到V " ； 第二步：用 p' 的压力将体系从V " 压缩到V ' ； 第三步：用 p1 的压力将体系从 V ' 压缩到 V1 。
W p (V V2 )
V2 0.0248 Wr nRT ln 2.0 8.314 298ln V1 0.10 6.9110 J
3
上一内容
下一内容
回主目录
返回
例题：
• 2、1.00mol某单原子理想气体在298K,1.00×１０３ KPa下可逆绝热膨胀到最终状态压力为100KPa,求算 终态体积、终态温度及所做的功。 1 1 1.67 1 解： T2 ( P2 ) 0.401 T1 P1 1.67
第二章热力学第一定律公式总结1
r
1
1
(
p2V2
p1V1)
nR(T2 T1) r 1
1 V
( V T
)p
J
( T V
)U
1 V
( V p
)T
J -T
(
T p
)H
1 Cp
H
p
T
可逆相变热: Qp H n Hm (B)
不可逆相变热:设计过程,其中要包含可逆相变
pdV
1
2
QV＝△U
Q U nC dT
V
1
V ,m
Qp＝ H
Qp H
T2 T1
nC
p
,mdT
H= U+ (pV) = U+(p2V2－p1V1)
以公下式所列运公用式条只件适用于封闭体系和热力学平衡态。
(1)H=U+pV 是定义式，适用于任何处于热力学平衡
rUV + RT ni.g rUV + RT i.g
规定 ： Hm(稳定单质,298.15K)＝0i
推论： fHm(稳定单质,T)＝0 fHm(B,298.15K)=Hm(B,298.15K)
由基础热数据求rHm(298.15K):
r
H
nB ( ) nB (0) B
QV rU， Qp r H
r H p rUV + RT i.g
i
r Hm rUm RT i.g
以上两式推导过程如下，可以看出应i 用了两个近似： （1）忽略了凝聚相体积的变化（2）将气体视为理想气体。
关于热力学中体积功的计算
p 外 dV ，因为外压保持不变，是常数，所以积分
得到： W = － p 外 （ V2 － V1 ） 或 W = － p2 （ V2 － V1 ） 。 （ 3 ） 等温可逆过程： 可逆过程中系统无限接近于平衡态， 可逆过程中环境压力与系统压力只相差无穷小的值，即： p 外 = p ʃ dp。 代入 W = －
［ 1］ 傅献彩， 沈文霞， 姚天扬， 等， 物理化学（ 第五版） ［M］． 北京： 高等教 2005 ： 74． 育出版社， ［ 2］ 印永嘉， ．北 奚正楷， 张树永， 等， 物理化学简明教程（ 第四版） ［M］ 2007 ： 13． 京： 高等教育出版社， ［ 3］ 胡英， 吕瑞东， 刘国杰， 等， 物理化学（ 第五版） ［M］． 北京： 高等教育 2007 ： 33． 出版社， ［ 4］ 沈 文 霞， ． 北 京： 科 学 出 版 社， 物 理 化 学 核 心 教 程 （ 第 二 版） ［M］ 2009 ： 34．
热力学中，除了热以外其它各种形式被传递的能量都叫做 功，其中由于体积的膨胀或压缩而与环境间交换的功通常称为 体积功。体积功的概念及计算在热力学中占有非常重要地位 。 首先，功是传递的能量，不是状态函数，功的值与具体的变化 途径有关，相同的始态、 终态之间因为途径不同所做的功不 同。其次，在热力学第一定律的数学表达式 ΔU = Q + W 中就有 功，一般通过计算出功而才计算内能的改变量 。 现在，诸多物 ［1 3 ］ 理化学教科书 通常以如下或类似模型引入体积功的计算公 式。 机械功的计算公式是作用力与力方向上的位移的乘积，即 W δ 机 = Fdl。F 为作用力，dl 为移动的距离。压强 p 与作用力之 F 间又有如下关系： p = ，A 为物体的截面积。 A F外 dAl = p 外 dV δW 机 = A 因此推导得出体积功的公式： δW 体 = － p 外 dV 公式中的 p 外 为环境的压力， dV 是系统体积的改变，负号 代表热力学规定，即系统对环境做功时，功取负值； 反之环境 对系统作功时，功取正值。只有 － p 外 dV 才表示体积功， － pdV （ p 表示系统的压力） 、pV 或 － pV、 － Vdp 等均不表示体积功。 计算某个过程的体积功时，首先对上式取定积分，得： W体 = －
物理化学计算公式的适用条件
可逆相变
⊿H=n⊿HV
任何相变, 但系统始态、终态温度、压力不能变
8.⊿H=ΣνΔHf(生成物)- ΣνΔHf(反应物)
等温等压下的化学反应,对物理化学B来讲,就是25℃, 101.325kPa下的化学反应
9 p1V1γ= p2V2γ, T1V1γ-1=T2V2γ-1
理想气体绝热可逆,而且无相变,无化学反应
等压过程、只要求系统始态、终态无相变、无化学反应、无非体积功，始态终态压力不变
⊿S=n⊿HV/T
等温等压下的任何相-TS
F=U-TS
任何过程
⊿G=⊿H-T⊿S
⊿A=⊿U-T⊿S
等温等压过程
⊿Ssur=-Qsys/Tsur
系统实际过程的热效应，假设环境温度不变
物理化学计算公式的适用条件
热力学第一定律
公式
适用条件
⊿U=nCV⊿T.
无相变、无化学反应、无非体积功的任何过程
⊿U=nCV⊿T=Q
等容可逆过程
⊿H=nCp⊿T.
无相变、无化学反应、无非体积功的任何过程
⊿H=nCp⊿T=Q
等压可逆过程
W=-nRTln（V2/V1）
等温可逆过程
H=U+pV
任何过程
⊿H=n⊿HV=Q
10 W=-pe⊿V
任何过程,但要注意与途径有关
热力学第二定律
公式
适用条件
⊿S=nRln(V2/V1)
等温过程，只要求系统始态、终态无相变、无化学反应、无非体积功，始态终态温度不变
⊿S=nCVln(T2/T1)
等容过程，只要求系统始态、终态无相变、无化学反应、无非体积功，始态终态体积不变
⊿S=nCpln(T2/T1)
⊿S=ΣνS(生成物)- ΣνS(反应物)
⊿H=n⊿HV
任何相变, 但系统始态、终态温度、压力不能变
8.⊿H=ΣνΔHf(生成物)- ΣνΔHf(反应物)
等温等压下的化学反应,对物理化学B来讲,就是25℃, 101.325kPa下的化学反应
9 p1V1γ= p2V2γ, T1V1γ-1=T2V2γ-1
理想气体绝热可逆,而且无相变,无化学反应
等压过程、只要求系统始态、终态无相变、无化学反应、无非体积功，始态终态压力不变
⊿S=n⊿HV/T
等温等压下的任何相-TS
F=U-TS
任何过程
⊿G=⊿H-T⊿S
⊿A=⊿U-T⊿S
等温等压过程
⊿Ssur=-Qsys/Tsur
系统实际过程的热效应，假设环境温度不变
物理化学计算公式的适用条件
热力学第一定律
公式
适用条件
⊿U=nCV⊿T.
无相变、无化学反应、无非体积功的任何过程
⊿U=nCV⊿T=Q
等容可逆过程
⊿H=nCp⊿T.
无相变、无化学反应、无非体积功的任何过程
⊿H=nCp⊿T=Q
等压可逆过程
W=-nRTln（V2/V1）
等温可逆过程
H=U+pV
任何过程
⊿H=n⊿HV=Q
10 W=-pe⊿V
任何过程,但要注意与途径有关
热力学第二定律
公式
适用条件
⊿S=nRln(V2/V1)
等温过程，只要求系统始态、终态无相变、无化学反应、无非体积功，始态终态温度不变
⊿S=nCVln(T2/T1)
等容过程，只要求系统始态、终态无相变、无化学反应、无非体积功，始态终态体积不变
⊿S=nCpln(T2/T1)
⊿S=ΣνS(生成物)- ΣνS(反应物)
热力学第一定律 (2)
2)恒外压膨胀 pamb=50.663kPa 3)恒温可逆膨胀
末态 p1＝50.663kPa V1= 44.8 dm3 T1= 273.15K
求：三个过程的体积功各为多少？
解：
W1＝－pamb(V2－V1) ＝ 0（效率为0，完全不可逆）
W2＝－pamb(V2－V1) ＝－50.663103(44.8－22.4) 10-3 J
由热力学第一定律可得:
Qp U W U (p2V2 p1V1) (U2 p2V2)(U1 p1V1) (dp = 0，W’=0)
3.焓的导出：
定义 : H = U + pV 称H为焓，H为状态函数，广延量 于是：
Qp=H2-H1=H 或 : Qp=dH (dp = 0，W′= 0)
H 的计算：基本公式： H= U+ (pV)
热和功不是状态函数，而是过程函数
1)热 Q
系统与环境由温差而引起的能量交换称为热
显热 单纯pVT变化时，系统吸收或放出的热 热 潜热 相变时，T不变，系统吸收或放出的热
反应热 化学反应时，系统吸收或放出的热
2)功
除热之外，系统与环境交换能量的另一种形式
体积功Biblioteka 功 电功电化学一章讨论 非体积功
表面功
p1，V1，T1
W =?
末态2 p2，V2，T2
V2
W W pambdV pambdV
V1
体积功的计算式
(1)恒(外)压过程(isobaric or constant pamb)
恒外压过程：W＝－pamb(V2－V1)
恒压过程(pamb=p)：W＝－p(V2－V1)
(2)自由膨胀过程(free expansion process)
末态 p1＝50.663kPa V1= 44.8 dm3 T1= 273.15K
求：三个过程的体积功各为多少？
解：
W1＝－pamb(V2－V1) ＝ 0（效率为0，完全不可逆）
W2＝－pamb(V2－V1) ＝－50.663103(44.8－22.4) 10-3 J
由热力学第一定律可得:
Qp U W U (p2V2 p1V1) (U2 p2V2)(U1 p1V1) (dp = 0，W’=0)
3.焓的导出：
定义 : H = U + pV 称H为焓，H为状态函数，广延量 于是：
Qp=H2-H1=H 或 : Qp=dH (dp = 0，W′= 0)
H 的计算：基本公式： H= U+ (pV)
热和功不是状态函数，而是过程函数
1)热 Q
系统与环境由温差而引起的能量交换称为热
显热 单纯pVT变化时，系统吸收或放出的热 热 潜热 相变时，T不变，系统吸收或放出的热
反应热 化学反应时，系统吸收或放出的热
2)功
除热之外，系统与环境交换能量的另一种形式
体积功Biblioteka 功 电功电化学一章讨论 非体积功
表面功
p1，V1，T1
W =?
末态2 p2，V2，T2
V2
W W pambdV pambdV
V1
体积功的计算式
(1)恒(外)压过程(isobaric or constant pamb)
恒外压过程：W＝－pamb(V2－V1)
恒压过程(pamb=p)：W＝－p(V2－V1)
(2)自由膨胀过程(free expansion process)
几种常见过程的体积功
几种常见过程的体积功熊帮云;罗杰;廖爽【摘要】本文给出了热力学中体积功的定义式,并结合定义式,推导出了几种常见过程的体积功的公式,对《普通化学》《无机化学》及《物理化学》等课程中体积功的理解与应用具有指导意义.【期刊名称】《产业与科技论坛》【年(卷),期】2018(017)022【总页数】2页(P69-70)【关键词】体积功;过程推导;热力学【作者】熊帮云;罗杰;廖爽【作者单位】佛山科学技术学院;佛山科学技术学院;佛山科学技术学院【正文语种】中文一、引言在热力学系统中，“功”是系统与环境之间除“热”之外的以其它形式传递的能量[1～2]，是由微观粒子的有序运动所引起的。
热力学中又将“功”分为体积功和非体积功两大类，而其中由于系统体积的变化而与环境之间交换的“功”称为体积功。
体积功的概念及其计算在热力学中占有非常重要地位，对理解系统与环境之间的能量交换非常重要，是正确理解和运用热力学基础知识，特别是热力学第一定律的关键[3]。
正因如此，热力学中的体积功是普通高校化学及材料专业课程，如《普通化学》《无机化学》《物理化学》等课程中的重要知识点。
但是，目前部分高校的《无机化学》和《普通化学》课程所采用的教材，如天津大学无机化学教研室编著的普通高等教育“十二五”普通高等教育本科国家级规划教材《无机化学》和赵士铎主编的普通高等教育“十一五”国家级规划教材中，只是简单地给出了体积功的文字定义，并未对其详加说明，显得比较晦涩难懂，学生不明所以。
再加上“功”不是状态函数，其大小与过程有关，准确地说与系统状态具体的变化途径有关[4]，对于相同的始态、终态，往往因为过程的不同而所做的功也不同。
这就导致学生在对体积功的概念理解不明的情况下，对具体过程的体积功的计算更是无从下手。
经过近两年的教学实践，发现学生对于体积功概念的理解还不透彻，特别是对不同过程的体积功的计算问题更是含混不清。
为此，从学生的实际情况出发，在体积功这部分的教学中，做了一些尝试，不仅考虑到体积功这一非状态函数本身的特点，给出了体积功的定义式，还推导出了教材里没有的几种常见过程的体积功的计算公式，有助于学生理解掌握。
热力学第一定律复习
11/46 11/46
所以上述两过程 W≈0
20112011-4-2
祝大家学习愉快，天天进步！ 祝大家学习愉快，天天进步！
3、相变化
（2）有气体参加的过程 例:蒸发 B（l）→ B（g）
定温、定压，W’ =0 时 可逆相变 定温、定压，
Q p =∆ g H l
W = − p∆V = − p (Vg − Vl ) ≈ − pVg ≈ −nRT
20112011-4-2
祝大家学习愉快，天天进步！ 祝大家学习愉快，天天进步！
13/46 13/46
3、相变化
可逆相变
气液间可逆相变（ 气液间可逆相变（恒T、P）P是液体在T时的饱和蒸汽压。 可逆相变 是液体在T时的饱和蒸汽压。 气固间可逆相变 可逆相变（ 是固体在T时的饱和蒸汽压。 气固间可逆相变（恒T、P）P是固体在T时的饱和蒸汽压。 固液间可逆相变 可逆相变（ 是固体在P时的熔点。 固液间可逆相变（恒T、P）T是固体在P时的熔点。
∆U = Q + W ≈∆ g H − nRT l
[一般在大气压及其平衡温度下的相变（可逆相变） 一般在大气压及其平衡温度下的相变（可逆相变） 焓数据可查文献，是基础热数据， 焓数据可查文献，是基础热数据，其与压力关系不 因此不标明压力] 大，因此不标明压力]
20112011-4-2 祝大家学习愉快，天天进步！ 祝大家学习愉快，天天进步！ 12/46 12/46
由热力学稳定单质生 （6） 标准摩尔生成焓：一定温度下由热力学稳定单质生 ） 标准摩尔生成焓：一定温度下由热力学稳定单质 的物质B的标准摩尔反应焓 的物质 的标准摩尔反应焓， 成化学计量数 νB=1的物质 的标准摩尔反应焓，称为物质 B在该温度下的标准摩尔生成焓。 ∆f H m ( B )表示 在该温度下的标准摩尔生成焓 在该温度下的标准摩尔生成焓。 没有规定温度， 时的数据有表可查。 1）没有规定温度，一般298.15 K时的数据有表可查。 3）由定义可知：稳定态单质的 ∆f Hm ( B) = 0 稳定态单质的 （6） 标准摩尔燃烧焓:一定 标准摩尔燃烧焓:一定温度下， 1mol物质 B 与 氧气进行完全燃烧反应，生成规定的燃烧产物时的 标准摩尔反应焓，称为B在该温度下的标准摩尔燃烧 焓。 ∆ Hm ( B) 表示.单位：J mol-1 c
所以上述两过程 W≈0
20112011-4-2
祝大家学习愉快，天天进步！ 祝大家学习愉快，天天进步！
3、相变化
（2）有气体参加的过程 例:蒸发 B（l）→ B（g）
定温、定压，W’ =0 时 可逆相变 定温、定压，
Q p =∆ g H l
W = − p∆V = − p (Vg − Vl ) ≈ − pVg ≈ −nRT
20112011-4-2
祝大家学习愉快，天天进步！ 祝大家学习愉快，天天进步！
13/46 13/46
3、相变化
可逆相变
气液间可逆相变（ 气液间可逆相变（恒T、P）P是液体在T时的饱和蒸汽压。 可逆相变 是液体在T时的饱和蒸汽压。 气固间可逆相变 可逆相变（ 是固体在T时的饱和蒸汽压。 气固间可逆相变（恒T、P）P是固体在T时的饱和蒸汽压。 固液间可逆相变 可逆相变（ 是固体在P时的熔点。 固液间可逆相变（恒T、P）T是固体在P时的熔点。
∆U = Q + W ≈∆ g H − nRT l
[一般在大气压及其平衡温度下的相变（可逆相变） 一般在大气压及其平衡温度下的相变（可逆相变） 焓数据可查文献，是基础热数据， 焓数据可查文献，是基础热数据，其与压力关系不 因此不标明压力] 大，因此不标明压力]
20112011-4-2 祝大家学习愉快，天天进步！ 祝大家学习愉快，天天进步！ 12/46 12/46
由热力学稳定单质生 （6） 标准摩尔生成焓：一定温度下由热力学稳定单质生 ） 标准摩尔生成焓：一定温度下由热力学稳定单质 的物质B的标准摩尔反应焓 的物质 的标准摩尔反应焓， 成化学计量数 νB=1的物质 的标准摩尔反应焓，称为物质 B在该温度下的标准摩尔生成焓。 ∆f H m ( B )表示 在该温度下的标准摩尔生成焓 在该温度下的标准摩尔生成焓。 没有规定温度， 时的数据有表可查。 1）没有规定温度，一般298.15 K时的数据有表可查。 3）由定义可知：稳定态单质的 ∆f Hm ( B) = 0 稳定态单质的 （6） 标准摩尔燃烧焓:一定 标准摩尔燃烧焓:一定温度下， 1mol物质 B 与 氧气进行完全燃烧反应，生成规定的燃烧产物时的 标准摩尔反应焓，称为B在该温度下的标准摩尔燃烧 焓。 ∆ Hm ( B) 表示.单位：J mol-1 c
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一粒粒取走砂粒
V1
p1 T
-dp
p2 V2
T
8
恒温压缩过程环境所做的功在 p-V 图中的表示
恒外压压缩过程
{p}
p2
W ＝ － p外V＝ － p终(V终－V始 )
定T
{p} p2
恒外压压缩过程
W ＝W1+W2
定T
1
p1
10
4. 理想气体绝热可逆过程
绝热可逆过程 Qr=0： dU δQr δWr
dU δWr
nCV ,mdT pdV
nRT nCV ,mdT dV V dT R 即 : CV ,m dV T V
即 : CV ,mdlnT RdlnV
CV,m为定值，与温度无关：
U 0
H 0
p2 Wr nRTln 4.034kJ p1
U Q WΒιβλιοθήκη Q W 4.034kJ
15
(2)恒温反抗50kPa恒外压膨胀至平衡
n=1mol pg, T1=350K p1 = 200 kPa
是理想气体 dT 0 U 0
反抗50kPa 恒外压膨胀到末态。
c.恒温可逆膨胀到末态
4
始末态相同，途径不同，功不同 解: a. 反抗 50kPa 的恒外压一次膨胀到末态。
W
V2 V1
p外dV = - p外 (V2 V1) = - 3.326 kJ
b.先反抗100 kPa 的恒外压膨胀到中间平衡态，再反抗 50kPa 恒外压膨胀到末态。 W= W1 + W2 = - 4.158 kJ c.恒温可逆膨胀到末态
(1)恒温可逆膨胀到50kPa (2)恒温反抗50kPa恒外压膨胀至平衡 (3)绝热可逆膨胀到50kPa (4)绝热反抗50kPa恒外压膨胀至平衡。
14
(1)dT=0,可逆
n=1mol pg, T1=350K p1 = 200 kPa
是理想气体 dT 0
dT=0,可逆
n=1mol pg, T2= 350K p2 = 50 kPa
V2
V2 Wr nRT ln V1
p2 Wr nRT ln p1
3
例18: 始态 T1 =300 K ，p1 = 150 kPa 的 2 mol某 理想气体，经过下述三种不同途径恒温膨胀到同 样的末态， p2 = 50 kPa 。求各途径的体积功。 a. 反抗 50kPa 的恒外压一次膨胀到末态。 b.先反抗100 kPa 的恒外压膨胀到平衡，再
状态1←←←← →→→→状态2
系统复原,环境复原 系统内部及系统与环境间在一系列无限接近平衡条件 下进行的过程称为可逆过程。
状态1
状态2
系统复原,环境不可能复原 对于不可逆过程，无论采取何种措施使系统恢复原状 时，都不可能使环境也恢复原状. 自然界发生的任何变化都是不可逆过程。
1
2 可逆过程体积功的计算公式
p2 5.48kJ Wr nRTln p1
5
途径a、b、c所做的功在 p-V 图中的表示
一次反抗恒外压膨胀过程 {p} p始 －W ＝p外V＝p终(V终－V始) {p} p始
二次反抗恒外压膨胀过程
－W ＝ －(W1+W2)
定T
定T
p终 V始 V终 {V}
p终 1 2
V始
V终
{V}
6
{p su} {p } p始 －W ＝-( W 1＋ W 2＋ W 3) ＝ (p2V1＋p3V2＋p终V3) －W ＝ -(W 1＋ W 2＋ W 3+…..) p始
p1 V2 {p} p2 V1 {V}
2
V2 V1 {V}
W ＝ W 1＋ W 2＋ W 3
{p }
p2
W ＝ W 1＋ W 2＋ W 3+…..
定T
定T p1 1 2 V2 3 V1 {V} V2 p1 2
V1
{V}
环境对系统做功,可逆过程做最小功(W)
9
总结，可逆过程的特点： (1) 推动力无限小，系统内部及系统和环境间都无限接近平衡， 进行得无限慢， (2)过程结束后，系统若沿原途径逆向进行恢复到始态，则环境 也同时复原。 (3) 可逆过程系统对环境做最大功, 环境对系统做最小功。
T2 V2 CV ,m ln Rln T1 V1
11
V2 T2 T1 V 1
定义： C p ,m CV ,m
R / CV ,m
V2 T2 T1 V 1
1
理想气体 绝热可逆过程 的过程方程
T2 p2 T1 p1
由绝热可逆过程方程求出终态温度T2，再求体积功.
ΔU n CV ,mdT n CV ,m (T2 T1 )
T1
T2
U Q W
Wr ΔU
Q0
13
例19： 某双原子理想气体1mol从始态350K，200kPa 经过如下四个不同过程达到各自的平衡态， 求各过程的Q，W，U及H。
1
1
p1V1 p2V2
12
绝热可逆过程体积功的计算
方法一：
nRT p0V0 dd V Wr pdV V V V1 1 V V V2 1 p V p0V0 dV 0 0 ( V21 V11 ) V1 V 1
V2 2
方法二:
定T 1 2 3 2
定T
V始
V终
{V}
V始
V终
{V}
系统对环境做功,可逆过程做最大功(-W)
7
恒温可逆膨胀途径所做的功在 p-V 图中的表示
p2
p1
δW p环dV
对可逆过程：
δWr p环dV p系 dpdV
p系dV dp dV
p系dV
Wr p系dV
V1 V2
Wr p dV
V1
V2
2
3 理想气体恒温可逆过程
nRT V2 dV nRT ln W r pd V V1 V V1