2-9可逆过程与可逆体积功
合集下载
2-9可逆过程与可逆体积功

2013-7-14
3
例1, 3mol理想气体于恒温298.15K条件下由始态 V1 = 20.0dm3 可逆膨胀到末态V2 = 50.0dm3 . 求始, 末态气体的压力p1 , p2 以及 膨胀过程的可逆功Wr .
n = 3 mol p1 = V1 = 20dm3 T1 = 298.15K 恒温可逆 n = 3 mol p2 = V2 = 50dm3 T2 = 298.15K
2. 可逆体积功(reversible volume work )
W
V2
V1
pd V
pamb p
(1). 理想气体恒温可逆过程
WT ,r pdV nRT dV V1 V1 V
V2 V2
WT ,r
V1 p2 nRTln nRTln V2 p1
nRT V p
2013-7-14
p2 Wr nRT ln p1
4
{ 3 8.314 298.15 ln(20.0 / 50.0 )}J 6814J
(2). 理想气体绝热可逆过程
Wa,r pdV
V2 V1
绝热与恒温的区别?
2013-7-14
5
①. 理想气体绝热可逆过程方程式
T2 T1 V1 V 2
②. 理想气体绝热可逆体积功 不论可逆与否, 绝热过程的功总可以用 W = U 来进行计算 , 这种方法更加简便.
Wa,r U nCV ,m (T2 T2 )
2013-7-14
7
例36 1 mol氧气由0℃, 106Pa,经过(1)绝热可逆膨胀;(2) 对抗恒定外压Psu= 105Pa绝热不可逆膨胀,使气体最后压力为 105Pa,求此两种情况的最后温度及系统对环境所作的功。 解(1)绝热可逆膨胀 绝热可逆膨胀 1molO2 p1 = 106Pa T1 = 273.15K
2.10可逆过程与可逆体积功

气体可逆膨胀压缩过程
以理想气体恒温膨胀压缩过程为例, 以理想气体恒温膨胀压缩过程为例,将盛 有一定量某理想气体的带活塞的气缸与恒温热 源接触, 源接触,以使平衡时系统的温度与热源的温度 相等。 相等。 系统始态为a压力为 末态为z压力为 压力为p 系统始态为 压力为pa;末态为 压力为 z, 压力为 pz=1/5pa 。
理想气体绝热可逆功
Wa,r = ∆U = ∫T nCV ,mdT = nCV ,m (T2 − T1 )
T2
1
T2根据绝热可逆过程方程式求得。 根据绝热可逆过程方程式求得。 或
Wa,r = ∫ − pamb dV = ∫ − pdV = ∫
V1 V1
V2
V2
V2
V1
p1V1γ − γ dV V
p1V1γ 1 1 = γ −1 − γ −1 V1 γ − 1 V2
3)绝热恒外压膨胀 : ∆U = W 绝热恒外压膨胀 绝热 nCV,m (T2 −T1) = -p2(V2 −V1) = -p2V2+p2V1
3 p2 n R(T2 −T ) = nRT1 − nRT2 1 2 p1 3 p2 T2 = 174.8K (T2 −T ) = T −T2 1 1 2 p1 ∆U= nCV,m(T2 −T1) = −5.40×103J
p1V1γ − γ dV V
• P95,39 解:设计变化途径如下: 设计变化途径如下:
n = 5mol T2 = 300K p2 = 50kPa V2
n = 5mol T1 = 300K p1 = 200kPa V1
Байду номын сангаас恒温 可逆
绝热 可逆
n = 5mol T3 p3 = 200kPa V3
2-10可逆过程和可逆体积功

•多次等外压膨胀
(3).外压比内压小一个无穷小的值
外压相当于一堆沙子,每次取一粒,这样的膨胀过程是 无限缓慢的,每一步都接近于平衡态。所作的功:
P终 p始
一粒粒取走砂粒 (剩余砂粒相当前述一 个重物)
(iii)
即 TV 1 常 : 数
结 pg状 方 有 合 态 程
:
pV 常 数
1
Tp
常 数
pV c
b、理想气体绝热可逆体积功
由 热 逆 程 绝 可 方 :
V2 V1
pV p1V1
W的定义式
Wr pdV p1V1
V2
V1
V dV
V2
V2
V2
(2)理想气体绝热可逆体积功
a、 理想气体绝热可逆过程方程式
d U δWr δ Qr 0 nRT 理想气体 nCV,m d T p d V dV V
对 热 逆 程 绝 可 过 ,
CV,m dT dV R T V
pg :C p,m CV, m R γ C p,m CV, m
W p (V V 1)
' '
p终 p始 p1 P1
p'' (V '' V ' )
p2 (V2 V '' )
(ii)
P始,V始 T
V1
1 P 1,V 1 T
p2 V2
2
P2
p终V3
3 P终,V终
P2,V2 T
可逆过程与可逆功

两种功的区别:
A
P0 V0 T P V1 T
B p
p
T
C
p'
P’ V1 T ’
'
p "(V " V ')
p2 (V2 V ")
W3 nRT ln
V2 V1
这种过程近似地可看作可逆过程,所作的功最大。
(二)压缩过程
将体积从 V 压缩到
2
V1 ,有如下三种途径:
1.一次等外压压缩 在外压为 p 下,一次从 V 压 缩到 V ,环境对体系所作的功 (即体系得到的功)为:
上述为理气绝热可逆过程方程式。描述了理气在该种过 程中p、T、V之间的关系。要熟记。
2)理想气体绝热可逆过程体积功
理气绝热可逆功有两种计算方法: ①由热一律 绝热可逆
P80
U Q W
Q 0 U W r ,a
Wr ,a nCV ,m T 所以 ②利用过程方程式
W r ,a
二 可逆过程(reversible process)P76
1.定义
体系由始态到终态发生了一过程,若能在不给 可逆过程: 体系和环境留下任何影响(痕迹)的条件下体 Reversible process 系与环境都恢复到原态,则原过程称为可逆过 程。途径Ⅲ的正逆过程均为可逆过程。
不可逆过程: 体系由始态到终态发生了一过程后,用任何方 法也不能使体系与环境都完全复原,则此过程 irreversible process 称为不可逆过程。途径Ⅰ、Ⅱ为不可逆过程, 自然界的一切实际过程都是不可逆过程,可逆过程是热力学 上的一种假想过程,是一种科学的抽象,实际过程只能无限趋近 它。但是可逆过程的讨论,在热力学中有着重要的意义。
可逆过程与可逆过程体积功
T2
= U
n CV ,mdT
T1
T2
= H
n C p,mdT
T1
7
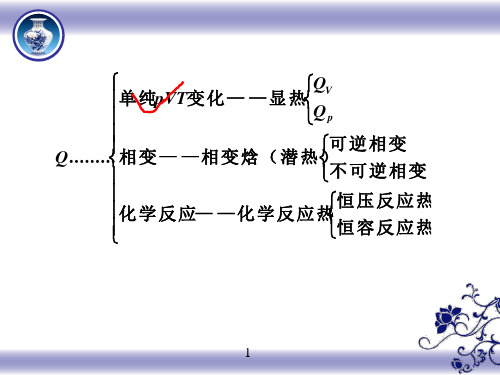
单
纯pVT变
化
—
—
显
热QQVp
Q......... 相
变
—
—
相
变
焓
(
潜
热
)可不
逆 可
相变 逆相
变
化
学
反
应—
—
化
学
反
应
热恒恒
压 容
反 反
应 应
热 热
8
§ 2.5 相变过程热的计算
1. 相及相变
(1)相的定义: 系统内性质完全相同且均匀的部分称为相。 (2)相变:物质从一相转移至另外一相,称为相变。 (3)常见相变:
ln
p2 p1
4. 理想气体绝热可逆过程
T2 T1
V2 V1
1
1 1
T2 T1
p2 p1
4 p1V1 p2V2
5. 绝热可逆过程体积功的计算
方法一:
Wr
pdV
V2 nRT dV V1 V
V2 p0V0
V V1
dV
p0V0
1 V2 V V1
dV p0V0
1
(V21 V11 )
Q Qp H 40.63kJ
28
(2) 100℃下向真空蒸发
H2O(l) T1 373.15K p1
p外0 H
H2O(g) T2 373.15K p2 101.325k Pa
H1
H2O(l) T 373.15K
H 2
p 101.325k Pa
热力学第一定律复习

11/46 11/46
所以上述两过程 W≈0
20112011-4-2
祝大家学习愉快,天天进步! 祝大家学习愉快,天天进步!
3、相变化
(2)有气体参加的过程 例:蒸发 B(l)→ B(g)
定温、定压,W’ =0 时 可逆相变 定温、定压,
Q p =∆ g H l
W = − p∆V = − p (Vg − Vl ) ≈ − pVg ≈ −nRT
20112011-4-2
祝大家学习愉快,天天进步! 祝大家学习愉快,天天进步!
13/46 13/46
3、相变化
可逆相变
气液间可逆相变( 气液间可逆相变(恒T、P)P是液体在T时的饱和蒸汽压。 可逆相变 是液体在T时的饱和蒸汽压。 气固间可逆相变 可逆相变( 是固体在T时的饱和蒸汽压。 气固间可逆相变(恒T、P)P是固体在T时的饱和蒸汽压。 固液间可逆相变 可逆相变( 是固体在P时的熔点。 固液间可逆相变(恒T、P)T是固体在P时的熔点。
∆U = Q + W ≈∆ g H − nRT l
[一般在大气压及其平衡温度下的相变(可逆相变) 一般在大气压及其平衡温度下的相变(可逆相变) 焓数据可查文献,是基础热数据, 焓数据可查文献,是基础热数据,其与压力关系不 因此不标明压力] 大,因此不标明压力]
20112011-4-2 祝大家学习愉快,天天进步! 祝大家学习愉快,天天进步! 12/46 12/46
由热力学稳定单质生 (6) 标准摩尔生成焓:一定温度下由热力学稳定单质生 ) 标准摩尔生成焓:一定温度下由热力学稳定单质 的物质B的标准摩尔反应焓 的物质 的标准摩尔反应焓, 成化学计量数 νB=1的物质 的标准摩尔反应焓,称为物质 B在该温度下的标准摩尔生成焓。 ∆f H m ( B )表示 在该温度下的标准摩尔生成焓 在该温度下的标准摩尔生成焓。 没有规定温度, 时的数据有表可查。 1)没有规定温度,一般298.15 K时的数据有表可查。 3)由定义可知:稳定态单质的 ∆f Hm ( B) = 0 稳定态单质的 (6) 标准摩尔燃烧焓:一定 标准摩尔燃烧焓:一定温度下, 1mol物质 B 与 氧气进行完全燃烧反应,生成规定的燃烧产物时的 标准摩尔反应焓,称为B在该温度下的标准摩尔燃烧 焓。 ∆ Hm ( B) 表示.单位:J mol-1 c
所以上述两过程 W≈0
20112011-4-2
祝大家学习愉快,天天进步! 祝大家学习愉快,天天进步!
3、相变化
(2)有气体参加的过程 例:蒸发 B(l)→ B(g)
定温、定压,W’ =0 时 可逆相变 定温、定压,
Q p =∆ g H l
W = − p∆V = − p (Vg − Vl ) ≈ − pVg ≈ −nRT
20112011-4-2
祝大家学习愉快,天天进步! 祝大家学习愉快,天天进步!
13/46 13/46
3、相变化
可逆相变
气液间可逆相变( 气液间可逆相变(恒T、P)P是液体在T时的饱和蒸汽压。 可逆相变 是液体在T时的饱和蒸汽压。 气固间可逆相变 可逆相变( 是固体在T时的饱和蒸汽压。 气固间可逆相变(恒T、P)P是固体在T时的饱和蒸汽压。 固液间可逆相变 可逆相变( 是固体在P时的熔点。 固液间可逆相变(恒T、P)T是固体在P时的熔点。
∆U = Q + W ≈∆ g H − nRT l
[一般在大气压及其平衡温度下的相变(可逆相变) 一般在大气压及其平衡温度下的相变(可逆相变) 焓数据可查文献,是基础热数据, 焓数据可查文献,是基础热数据,其与压力关系不 因此不标明压力] 大,因此不标明压力]
20112011-4-2 祝大家学习愉快,天天进步! 祝大家学习愉快,天天进步! 12/46 12/46
由热力学稳定单质生 (6) 标准摩尔生成焓:一定温度下由热力学稳定单质生 ) 标准摩尔生成焓:一定温度下由热力学稳定单质 的物质B的标准摩尔反应焓 的物质 的标准摩尔反应焓, 成化学计量数 νB=1的物质 的标准摩尔反应焓,称为物质 B在该温度下的标准摩尔生成焓。 ∆f H m ( B )表示 在该温度下的标准摩尔生成焓 在该温度下的标准摩尔生成焓。 没有规定温度, 时的数据有表可查。 1)没有规定温度,一般298.15 K时的数据有表可查。 3)由定义可知:稳定态单质的 ∆f Hm ( B) = 0 稳定态单质的 (6) 标准摩尔燃烧焓:一定 标准摩尔燃烧焓:一定温度下, 1mol物质 B 与 氧气进行完全燃烧反应,生成规定的燃烧产物时的 标准摩尔反应焓,称为B在该温度下的标准摩尔燃烧 焓。 ∆ Hm ( B) 表示.单位:J mol-1 c
物理化学 第二章 热力学第一定律-2

定义 :
def
H = =U + pV
H为焓,为状态函数,广度量,无绝对值,单位 : J
Qp H
δQ p = dH 即恒压热与过程的焓变在量值上相等。
焓是状态函数,其改变量△H只取决于体系的初态和终态,而
与变化过程无关。故恒压过程热QP量值也仅取决于体系的初态 和终态,而与变化过程无关。
H 的计算的基本公式: H= U+ (pV) 恒压过程 H = Qp
一 、热容
1.定义:在不发生相变化、不发生化学反应和非体积功为零的条 件下,一定量的物质温度升高1K所吸收的热量称为该物质的热 容。 C Q dT
2. 特性 :
1)与物质的量有关
规定物质的质量为1g,或1kg,称为比热容,单位为J.K-1.g-1 或J.K-1.Kg-1。 2)与过程有关 热不是状态函数,与途径有关,所以热容C一般也与途径有关。 对于不同的途径,吸收的热量不同,热容值也不相同。
T,V
途径1 反应b
QV,b=Ub
CO2(g)
T,V
因为: Uc = Ua + Ub , Ua = Uc – Ub 。 所以: Qa = Qc - Qb 。
盖斯定律:一确定化学反应的恒容热或恒压热只取决于过程 的始末态,与中间经过的途径无关。
§2.4 摩尔热容
摩尔热容是实验测定的一类基础数据,用来计算系统发生单纯 PVT变化(无相变、无化学变化)时,过程的热Q及△H、△U。
U n( Ar, g)Cv,m( Ar, g) n(Cu, s)C p,m (Cu, s) (T2 - T1 )
(412.472 2 24.435)(373.15 - 273.15)J 9.876kJ
(2)-01章-热力学第一定律(可逆过程,体积功,焓,热容)
物理化学电子教案—第一章
热力学第一定律及其应用
环境 surroundings
无物质交换 封闭系统
Closed system
U Q W
有能量交换
上一内容 下一内容 回主目录
返回
2020/3/7
热力学第一定律
Joule(焦耳)和 Mayer(迈耶尔)自1840年 起,历经20多年,用各种实验求证热和功的转 换关系,得到的结果是一致的。
也可以表述为:第一类永动机是不可能制成的
第一类永动机(first kind of perpetual motion machine):一种既不靠 外界提供能量,本身也不减少能量,却可以不断对外作功的机器 称为第一类永动机,它显然与能量守恒定律矛盾。
热力学第一定律是人类经验的总结,事实证明违背该定 律的实验都将以失败告终,这足以证明该定律的正确性。
U U2 U1 QW 对于微小变化 dU Q W
热力学能的单位: J
热力学能是状态函数,用符号U表示,它的 绝对值尚无法测定,只能求出它的变化值。
上一内容 下一内容 回主目录
返回
2020/3/7
热力学第一定律的文字表述
热力学第一定律是能量守恒与转化定律在热现 象领域内所具有的特殊形式,说明热力学能、热和 功之间可以相互转化,但总的能量不变。
自然界的一切物质都具有能量,能量有各 种不同形式,能够从一种形式转化为另一种形 式,但在转化过程中,能量的总值不变。
上一内容 下一内容 回主目录
返回
2020/3/7
热力学能
系统总能量通常有三部分组成:
(1)系统整体运动的动能 (2)系统在外力场中的位能 (3)热力学能,也称为内能 热力学中一般只考虑静止的系统,无整体运动, 不考虑外力场的作用,所以只注意热力学能
热力学第一定律及其应用
环境 surroundings
无物质交换 封闭系统
Closed system
U Q W
有能量交换
上一内容 下一内容 回主目录
返回
2020/3/7
热力学第一定律
Joule(焦耳)和 Mayer(迈耶尔)自1840年 起,历经20多年,用各种实验求证热和功的转 换关系,得到的结果是一致的。
也可以表述为:第一类永动机是不可能制成的
第一类永动机(first kind of perpetual motion machine):一种既不靠 外界提供能量,本身也不减少能量,却可以不断对外作功的机器 称为第一类永动机,它显然与能量守恒定律矛盾。
热力学第一定律是人类经验的总结,事实证明违背该定 律的实验都将以失败告终,这足以证明该定律的正确性。
U U2 U1 QW 对于微小变化 dU Q W
热力学能的单位: J
热力学能是状态函数,用符号U表示,它的 绝对值尚无法测定,只能求出它的变化值。
上一内容 下一内容 回主目录
返回
2020/3/7
热力学第一定律的文字表述
热力学第一定律是能量守恒与转化定律在热现 象领域内所具有的特殊形式,说明热力学能、热和 功之间可以相互转化,但总的能量不变。
自然界的一切物质都具有能量,能量有各 种不同形式,能够从一种形式转化为另一种形 式,但在转化过程中,能量的总值不变。
上一内容 下一内容 回主目录
返回
2020/3/7
热力学能
系统总能量通常有三部分组成:
(1)系统整体运动的动能 (2)系统在外力场中的位能 (3)热力学能,也称为内能 热力学中一般只考虑静止的系统,无整体运动, 不考虑外力场的作用,所以只注意热力学能
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
W2 U nCV ,m (T2 T1 ) 1mol 21.05J . K 1 .mol1 ( 203.6 273.15) K 1465 J
由此可见,由同一始态经过可逆与不可逆两种绝热变化不 可能达到同一终态,即 T2 T2 ; U U 。
1molO2 p2 = 105Pa T2= ?K
T2 P1 T1 P2
1
已知该气体 CV, m = 21.05J· 1· 1. mol K
C p,m / CV ,m 1.40
1
p1 T2 T1 p 2 2013-7-14
因不可逆 绝热恒外压膨胀
1molO2 p2 = 105Pa T2= ?K
p1 T2 T1 p 2
1
nRT2 nRT1 W2 pamb V pamb (V2 V1 ) pamb p p 2 1 W2 U nCV ,m (T2 T1 )
p1 = nRT/V1 = {3 8.314 298.15/(20 10-3)} Pa = 371.8 Pa p2 = nRT/V2 = {3 8.314 298.15/(50 10-3)} Pa = 148.7 Pa
因是理想气体, 恒温, 可逆过程, 故 V2 V1 Wr pdV nRT ln or V1 V2
2. 可逆体积功(reversible volume work )
W
V2
V1
pd V
pamb p
(1). 理想气体恒温可逆过程
WT ,r pdV nRT dV V1 V1 V
V2 V2
WT ,r
V1 p2 nRTln nRTln V2 p1
nRT V p
2013-7-14
3
例1, 3mol理想气体于恒温298.15K条件下由始态 V1 = 20.0dm3 可逆膨胀到末态V2 = 50.0dm3 . 求始, 末态气体的压力p1 , p2 以及 膨胀过程的可逆功Wr .
n = 3 mol p1 = V1 = 20dm3 T1 = 298.15K 恒温可逆 n = 3 mol p2 = V2 = 50dm3 T2 = 298.15K
2013-7-14
10
体积功的计算式小结: pamb V pamb (V2 V1 )
例2 例1 恒外压 恒压
pV p(V2 V1 )
W pambdV
v2 v1
恒容过程 dV = 0
0
自由膨胀过程 pamb = 0 凝聚系统(不含气相) V 0
②. 理想气体绝热可逆体积功 不论可逆与否, 绝热过程的功总可以用 W = U 来进行计算 , 这种方法更加简便.
Wa,r U nCV ,m (T2 T2 )
2013-7-14
பைடு நூலகம்
7
例36 1 mol氧气由0℃, 106Pa,经过(1)绝热可逆膨胀;(2) 对抗恒定外压Psu= 105Pa绝热不可逆膨胀,使气体最后压力为 105Pa,求此两种情况的最后温度及系统对环境所作的功。 解(1)绝热可逆膨胀 绝热可逆膨胀 1molO2 p1 = 106Pa T1 = 273.15K
可逆过程与可逆体积功
1. 可逆过程 (reversible process) 推动力无限小,系统内部及系统与环境之间在无 限接近平衡条件下进行的过程, 称为可逆过程.
2013-7-14
1
体积功.exe
结论一 : 当始、 终态确定的条件下, 功与途径有关. 其 中无限多步膨胀途径, 系统对环境作最大功! 结论二 :当始、 终态确定的条件下, 逆向的无限多步 压缩途径, 环境对系统作最小功! 并且与膨胀时的最大 2013-7-14 2 功相等!
V2
V1
pd V
可逆过程
注意:恒外压:pamb保持恒定
恒
2013-7-14
压: p = pamb且保持恒定
11
2013-7-14
p2 Wr nRT ln p1
4
{ 3 8.314 298.15 ln(20.0 / 50.0 )}J 6814J
(2). 理想气体绝热可逆过程
Wa,r pdV
V2 V1
绝热与恒温的区别?
2013-7-14
5
①. 理想气体绝热可逆过程方程式
T2 T1 V1 V 2
1
T2 P1 T1 P2
1
P2 V1 P1 V2
以上三式称为 理想气体绝热 可逆过程方程
应用条件:封闭系统, W =0, 理想气体, 绝热, 可逆过程. 常见错误: 将上式用于绝热非可逆过程!
2013-7-14 6
( 273.15K ) (10)0.286 141.4 K
8
绝热过程: W1 = U = nCV, m(T2- T1) =
1mol21.05 J· 1· 1 (141.4-273.15)K =-2773J mol K
(2)绝热恒外压逆膨胀 1molO2 p1 = 106Pa T1 = 273.15K
2013-7-14 9
nRT2 nRT1 psu p p nCV ,m (T2 T1 ) 2 1
p 1 ( 1) su p1 T2 T1 203.6 K psu 1 ( 1) p 2
