14-可逆过程与可逆功
14 热力学第二定律 玻耳兹曼熵

8.7.2 熵和熵增加原理
1. 熵的存在 根据热力学第二定律, 一切与热 现象有关的实际宏观过程都不可 逆, 并且总是向概率较大的宏观态 进行. 说明: 热力学过程的初态和末态 对应着不同的状态量. 这种不同表 现为初末两态的概率(或包含的微 观状态数)不同, 从而决定了过程 进行的方向.
结论: 可以提出一个物理量对系统 的热力学状态进行描述, 这个物理 量称为熵(S): 对系统热力学状态的 定量描述.
能量守恒, 为何会有能源危机? 可见: 自然界中遵从能量守恒 的过程并非都可以实现! 8.7.1 热力学第二定律的 统计意义 热力学第二定律指出了热传 递方向和热功转化方向的不可 逆性, 即: 大量微观粒子组成的 孤立系统中发生的与热现象有 关的实际宏观过程都不可逆. 这一结论可以从微观角度, 从统计意义上进行解释.
P.5/46
第8章 热力学基础
8.7.1 热力学第二定律的 统计意义 大量微观粒子组成的孤立 系统中发生的与热现象有关 的实际过程都不可逆. 例如: 气体的自由膨胀 容器中有a, b, c 三个分子: A a b
隔 板
a, b, c 三个分子在 A, B 两区的 分布方式:
A
B
abc ab
0 c
bc a
P.7/46
任何自发过程都向平衡态演变.
第8章 热力学基础
结论3: 不可逆过程的实质是 系统从概率较小的宏观状态 向概率较大的宏观状态过度. 或者说从包含微观状态数少 的宏观状态向包含微观状态 数多的宏观状态进行. 这就是 热力学第二定律的统计解释 (微观意义).
孤立系统中, 一切实际过 程都向状态几率增大的方 向进行; 对理想的可逆过程, 状态几率才能保持不变; 状 态几率永不减少.
可逆过程与不可逆过程

可逆过程与不可逆过程可逆过程是指系统沿着一条连续的平衡状态路径从一个平衡状态到另一个平衡状态的过程。
该过程是无损耗的,物质的所有性质和状态都可以完全恢复。
不可逆过程是指系统从一个平衡状态到另一个平衡状态的过程中,无法通过任何方式使所有物质的性质和状态完全恢复原状的过程。
可逆过程满足热力学第一定律和第二定律的要求,而不可逆过程可能违反这些定律。
热力学第一定律,也称为能量守恒定律,指出能量是守恒的,能量不能被创建或销毁,只能从一种形式转化为另一种形式。
热力学第二定律,也称为熵增定律,指出孤立系统的熵将随时间增加,自然趋向于更加混乱的状态。
可逆过程与不可逆过程之间最大的区别在于能量和熵的改变。
可逆过程中,系统的能量改变等于传递给系统的热量减去系统对外做功所消耗的能量,熵保持不变。
而不可逆过程中,系统的能量改变小于传递给系统的热量和系统对外做功所消耗的能量之和,熵增加。
一个常见的例子是理想气体在等温膨胀和绝热膨胀两种过程中的行为。
在等温膨胀中,理想气体与热源保持恒温接触,气体按照等温膨胀的路径发生体积的变化。
这个过程是可逆的,因为系统的能量改变等于传递给系统的热量减去系统对外做功所消耗的能量,同时熵保持不变。
然而,在绝热膨胀中,理想气体与外界没有任何热交换,气体按照绝热膨胀的路径发生体积的变化。
这个过程是不可逆的,因为系统的能量改变小于传递给系统的热量和系统对外做功所消耗的能量之和,同时熵增加。
这两个过程的区别在于热量的流向。
在可逆过程中,热量是平衡地进入和离开系统,系统内部的每个点的温度都与热源相同。
而在不可逆过程中,热量的流动是不平衡的,系统内部的一些点的温度可能高于或低于热源。
可逆过程和不可逆过程在实际中都有广泛的应用。
例如,汽车引擎中的一些过程可以被视为可逆过程,例如理想的等温膨胀和等熵膨胀。
而摩擦、温度梯度和达到平衡所需的时间等因素使得其他过程变得不可逆。
在化学工程中,例如化学反应过程、质量传递过程和传热过程都是不可逆的。
物化03_第一定律,功,可逆过程

δW = p外dV
W = ∫ p外dV
V1 V2
系统,V
(1)被积函数为p外(系统与环境的压力一直相等) (2)此式中的W与第一定律表达式中的W相同吗?
(3) 具体过程的体积功: 等压外过程: = p外∆V W 等压过程: W = p∆V
W = ∫ p外dV
V1 V2
自由膨胀: W = 0 等容过程: W = 0 理气等温可逆膨胀(压缩): = nRT ln V2 W V1
(1) 适用于非敞开系统
Ⅰ
(2)
1 Ⅱ
2
∆U = Q − W = QⅡ − WⅡ Ⅰ Ⅰ
§2-3 功的计算 (How to calculate work)
一、功的分类 体积功 Volume work 功 非体积功 电功 表面功 光 轴功,等
二、体积功的计算
p外 dV
若体积膨胀或压缩dV (即V→V+dV),则
= ∆ (U + pV ) + W '
Q p = ∆H + W '
Q p = ∆H
条件:等压
条件:等压,W’=0
三、热容和简单变温过程热的计算 简单变温过程: δQ 热容 (Heat capacity): C = dT 1. 等容热容
∂U CV = ∂ T V
等容 dU = CV dT
可逆膨胀:理想活塞 p外=p-dp
力学平衡
W = ∫ p外dV = ∫ ( p − dp )dV = ∫ pdV
Байду номын сангаасV1 V1 V1
V2
V2
V2
=∫
V2
V1
nRT V dV = nRT ln 2 V V1
可逆过程与可逆功

两种功的区别:
A
P0 V0 T P V1 T
B p
p
T
C
p'
P’ V1 T ’
'
p "(V " V ')
p2 (V2 V ")
W3 nRT ln
V2 V1
这种过程近似地可看作可逆过程,所作的功最大。
(二)压缩过程
将体积从 V 压缩到
2
V1 ,有如下三种途径:
1.一次等外压压缩 在外压为 p 下,一次从 V 压 缩到 V ,环境对体系所作的功 (即体系得到的功)为:
上述为理气绝热可逆过程方程式。描述了理气在该种过 程中p、T、V之间的关系。要熟记。
2)理想气体绝热可逆过程体积功
理气绝热可逆功有两种计算方法: ①由热一律 绝热可逆
P80
U Q W
Q 0 U W r ,a
Wr ,a nCV ,m T 所以 ②利用过程方程式
W r ,a
二 可逆过程(reversible process)P76
1.定义
体系由始态到终态发生了一过程,若能在不给 可逆过程: 体系和环境留下任何影响(痕迹)的条件下体 Reversible process 系与环境都恢复到原态,则原过程称为可逆过 程。途径Ⅲ的正逆过程均为可逆过程。
不可逆过程: 体系由始态到终态发生了一过程后,用任何方 法也不能使体系与环境都完全复原,则此过程 irreversible process 称为不可逆过程。途径Ⅰ、Ⅱ为不可逆过程, 自然界的一切实际过程都是不可逆过程,可逆过程是热力学 上的一种假想过程,是一种科学的抽象,实际过程只能无限趋近 它。但是可逆过程的讨论,在热力学中有着重要的意义。
可逆过程与可逆过程体积功
T2
= U
n CV ,mdT
T1
T2
= H
n C p,mdT
T1
7
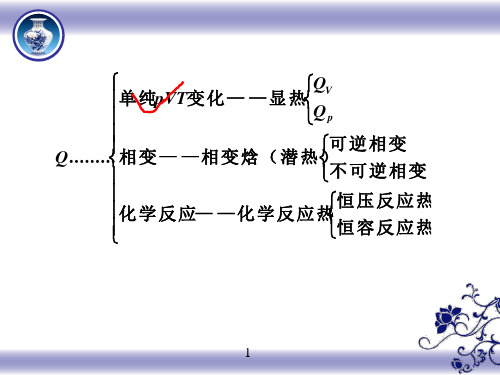
单
纯pVT变
化
—
—
显
热QQVp
Q......... 相
变
—
—
相
变
焓
(
潜
热
)可不
逆 可
相变 逆相
变
化
学
反
应—
—
化
学
反
应
热恒恒
压 容
反 反
应 应
热 热
8
§ 2.5 相变过程热的计算
1. 相及相变
(1)相的定义: 系统内性质完全相同且均匀的部分称为相。 (2)相变:物质从一相转移至另外一相,称为相变。 (3)常见相变:
ln
p2 p1
4. 理想气体绝热可逆过程
T2 T1
V2 V1
1
1 1
T2 T1
p2 p1
4 p1V1 p2V2
5. 绝热可逆过程体积功的计算
方法一:
Wr
pdV
V2 nRT dV V1 V
V2 p0V0
V V1
dV
p0V0
1 V2 V V1
dV p0V0
1
(V21 V11 )
Q Qp H 40.63kJ
28
(2) 100℃下向真空蒸发
H2O(l) T1 373.15K p1
p外0 H
H2O(g) T2 373.15K p2 101.325k Pa
H1
H2O(l) T 373.15K
H 2
p 101.325k Pa
可逆与不可逆过程

自发过程的共同特征
• 无需外力帮助、任其 自然就可发生的过程
• 不可逆过程 • 一个自发过程发生后
不可能使系统和环境 都恢复到原来的状态 而不留下任何影响
自发过程不可逆实质
功可自发地全部变为热, 但热不可能全部转化 为功而不引起任何其 他变化
• 一切自发过程都具有 不可逆性,它们在进行 时都具有确定的方向 和限度,如何知道一个 自发过程进行的方向 和限度呢?
• 热力学第二定律的各种表述在本质上 是等价的,由一种表述的正确性可推 出另外一种表述的正确性。
• 热力学第二定律的现代表述是卡诺的 专著 “Reflexions on Motive Work of Fire” 发表 25 年后由 Clausius 和 Kelvin给出的。
热力学第二定律的本质和熵的统计意义
自发过程的共同特征
2.化学变化: 25℃ Pθ下: H2 + O2
H2O(l)
正过程:自发反应 Q = -285.8KJ, W = 3.7KJ
逆过程:可逆电解 耗电功W’= 237.2KJ,
体系作膨胀功W=-3.7KJ, Q=48.6KJ
• 二个过程的总结果: 体系回到初态,但环境总的
• 付出了W = 3.7+237.2-3.7=237.2KJ 的功,
相反的过程,热量自动由低温物体流到高温物体,使热者 愈热,冷者愈冷,这种现象从未发生过
(2)高压气体向低压气体的扩散。
A p1
p2 B
若 p1 > p2 ,打开活塞后, A 球中气体自动扩散到 B 球。
相反的现象:“低压球中气体自动向高压球扩散,使压 力低的愈低,压力高的愈高”,从未发生过。
(3)溶质自高浓度向低浓度的扩散:
可逆反应与可逆过程概念辨析博客

标题:可逆反应与可逆过程概念辨析在化学领域中,可逆反应与可逆过程是两个重要的概念,它们在化学反应和热力学过程中起着重要的作用。
本文将从深度和广度的角度对可逆反应与可逆过程进行全面评估,以便读者更深入地理解这两个概念。
一、可逆反应与可逆过程的概念1. 可逆反应是指在一定条件下,反应物可以生成生成物,同时生成物也可以再次生成反应物的反应过程。
这种反应是可以在一定条件下前进和后退的。
在化学反应中,可逆反应通常用双箭头表示,表示反应可以进行正向和逆向的反应。
2. 可逆过程是指系统从初始状态到最终状态再返回到初始状态的过程,系统在这个过程中不断与外界交换能量和物质。
在热力学领域,可逆过程是理想化的过程,它是在不产生不可逆损失的条件下进行的过程。
二、深度探讨在化学反应中,可逆反应的性质使得它具有一定的平衡性,也就是反应达到动态平衡时正向反应和逆向反应的速率相等。
这种平衡状态在化学工业生产和生物体内的代谢过程中都有重要应用。
而可逆过程在热力学领域中是一种理想化的状态,它在热力学循环和热力学系统分析中有着重要的作用。
从宏观的角度来看,可逆反应和可逆过程都是一种动态的过程,在这个过程中系统不断地与外界交换能量和物质,达到一种相对稳定的状态。
从微观的角度来看,可逆反应和可逆过程都是由分子和原子之间的相互作用所驱动的,热力学和动力学的原理都可以解释这两个过程的特性。
三、总结与回顾通过对可逆反应与可逆过程的深度探讨,我们可以看到这两个概念在化学和热力学领域中具有重要的意义。
在化学反应中,可逆反应的平衡性使得它成为了化学平衡研究的基础,而可逆过程则在热力学领域中有着重要的理论意义。
在实际应用中,我们需要根据具体的条件来选择合适的反应条件和过程条件,以达到预期的目的。
个人观点与理解在我看来,可逆反应与可逆过程的概念虽然在理论上有所区分,但在实际应用中往往是相互联系的。
化学反应和热力学过程都是由分子和原子之间的相互作用所驱动的,理解这些相互作用的本质对于我们更深入地理解可逆反应与可逆过程具有重要意义。
热力学中的可逆过程与不可逆过程

热力学中的可逆过程与不可逆过程热力学是研究能量转化与能量传递的学科,涉及到了许多重要的概念与原理。
其中,可逆过程与不可逆过程是热力学中的两个重要概念,它们对于各个工程领域和自然科学研究都具有重要意义。
本文将就这两个概念进行探讨,旨在深入了解这两个过程的特点与应用。
一、可逆过程可逆过程是指在系统内发生的过程可以在给定的条件下以相同的顺序反转,达到与初始状态完全相同的过程。
简而言之,可逆过程是可逆的,可以在任何时候完全逆转过程而不产生任何不可逆性和额外的能量损失。
在可逆过程中,系统内的能量转化是无损失的。
一个典型的例子是理想气体的绝热膨胀和绝热压缩。
在绝热条件下,理想气体的膨胀和压缩可以看作是两个可逆过程。
在膨胀过程中,理想气体通过缓慢而均匀地将容器的体积扩大,外部环境对气体进行功的做用将气体的压强降低,使气体内部的分子自发地做功,气体的温度下降,最终达到平衡态。
而在绝热压缩过程中,正好相反,气体的体积缩小,温度升高,最终也可以达到平衡态。
整个过程中,无论是膨胀还是压缩,系统内的能量转化都是完全可逆的,没有能量损失。
二、不可逆过程不可逆过程与可逆过程相反,是指系统中发生的不能在给定条件下逆转的过程。
不可逆过程会导致能量的不可逆转化和能量损失。
在不可逆过程中,系统内的能量转化是有损失的。
例如,我们常见的阻力会造成机械系统的损耗。
当我们让车辆在水平面上运动时,车轮与地面之间的摩擦力会导致能量的损耗,这是一个不可逆过程。
无法将已经转化成摩擦热的能量再次转化回机械能。
另外,自然界中的热传导现象也是不可逆过程的一种。
热传导是指高温物体的热能通过接触媒介传递给低温物体的过程,这个过程是无法逆转的。
热传导的性质决定了热能会自发地从高温物体传递到低温物体,而不会相反。
不可逆过程是现实生活中普遍存在的,它们经常与能量转化和能量损失相关。
不可逆过程是因为存在各种能量转化的限制与损失,无法实现理想化的完全逆转。
三、可逆过程与不可逆过程的应用虽然不可逆过程存在能量转化损失的问题,但在实际应用中,不可逆过程却发挥了重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
We,3 p '(V 'V1 ) p "(V " V ') p2 (V2 V ")
所作的功等于3次作功的加和。
可见,外压差距越小,膨胀 次数越多,做的功也越多。
上一内容
下一内容
2006.1.1 回主目录
返回
2006.1.1
功与过程
上一内容
下一内容
2006.1.1 回主目录
返回
2006.1.1 2006.1.1
功与过程
4.外压比内压小一个无穷小的值 外压相当于一杯水不断蒸发,这样的膨胀过程是 无限缓慢的,每一步都接近于平衡态。所作的功为:
We,4 pedV
pi dV
V1
V2
V2
V1
V1 nRT dV nRT ln V2 V
这种过程近似地可看作可逆过程,所作的功最大。
可逆过程和可逆体积功的计算
一、可逆过程 设在定温下,一定量理想气体在活塞筒中 克服外压 pe ,经4种不同途径,体积从V1膨胀到 V2所作的功。 1.自由膨胀
δ We,1 pe dV 0
因为 pe 0
2.等外压膨胀(pe保持不变)
We,2 pe (V2 V1 )
体系所作的功如阴影面积所示。
Q H n H m
g l g l
10010 8 40.7 2.2610 kJ / m ol 18
6
上一内容
下一内容
回主目录
返回
相变热的计算
• 二、不可逆相变热的计算
需要设计过程,通过可逆相变计算。
例如:
nA(α)
T1 P ΔH1 nA(α)
QP=ΔH
nA(β)
2、理想气体绝热可逆过程
W U nCV ,m (T2 T1 )
上一内容
下一内容
回主目录
返回
绝热过程
绝热过程的功
在绝热过程中,体系与环境间无热的交换,但可 以有功的交换。根据热力学第一定律:
dU Q W
=W
(因为Q 0)
这时,若系统对外作功,热力学能下降,体系温
上一内容
下一内容 回主目录 返回回主目录
返回
功与过程
压缩过程
将体积从 V2 压缩到 V1 ,有如下三种途径: 1.一次等外压压缩
在外压为 p1下,一次从 V2 压 缩到 V1 ,环境对体系所作的功 (即体系得到的功)为:
We',1 p1 (V1 V2 )
' e,3 V2
V1
V2 nRT ln V1
则体系和环境都能恢 复到原状。
上一内容
下一内容 回主目录 返回
功与过程
上一内容
下一内容
回主目录
返回
功与过程
功与过程 小结:
从以上的膨胀与压缩过程看出,功与变化的途 径有关。虽然始终态相同,但途径不同,所作的功 也大不相同。显然,可逆膨胀,体系对环境作最大 功;可逆压缩,环境对体系作最小功。
n Hm 已知的摩尔相变焓。——可查化学手册
摩尔相变焓也是温度的函数,当温度升高时,分子 间相互作用减弱,故蒸发热变小,当温度升高到临 界温度时,蒸发热为零。
上一内容
下一内容 回主目录 返回
相变热的计算
例如: g 水在正常沸点373K时的摩尔相变焓 l H m =40.7kJ/mol, 求100吨水在正常沸点下完全汽化需要吸收多少热?
返回
回主目录
pV K1
TV 1 K2
p1 T K3
式中, K1, K2 , K 3 均为常数, C p / CV 。
上一内容
下一内容
回主目录
返回
可逆体积功的计算
三、可逆体积功的计算 1、理想气体恒温可逆过程
V2 P W nRT ln nRT ln 1 V1 P2
度必然降低,反之,则体系温度升高。因此绝热压缩, 使系统温度升高,而绝热膨胀,可获得低温。
上一内容
下一内容 回主目录 返回
例题:
• 1、某理想气体2.0mol从初始状态298K,200KPa,恒 温可逆膨胀到0.100m3,求过程的功。
解:
nRT 2.0 8.314 298 3 V1 0 . 0248 m 3 P 200 10 1
上一内容
下一内容 返回
回主目录
功与过程
上一内容
下一内容
回主目录
返回
功与过程
2.多次等外压压缩 第一步:用 p" 的压力将体系从 V2 压缩到V " ; 第二步:用 p' 的压力将体系从V " 压缩到V ' ; 第三步:用 p1 的压力将体系从 V ' 压缩到 V1 。
W p (V V2 )
摩尔相变焓: 1mol物质由α变为β相时对应的焓变。 符号: H 单位: KJ / mol
m
•二.摩尔相变焓
上一内容
下一内容
回主目录
返回
相变热的计算
•三.相变热的计算
1、可逆相变热
可逆相变:恒温恒压且没有非体积功的可逆过程
计算公式:
QP H n Hm
(3)体系变化一个循环后,体系和环境均恢复原态, 变化过程中无任何耗散效应; (4)等温可逆过程中,体系对环境作最大功,环境 对体系作最小功。
上一内容
下一内容 回主目录 返回
绝热过程
二、理想气体绝热可逆过程方程式
理想气体在绝热可逆过程中, p,V , T 三者遵循的 关系式称为绝热过程方程式,可表示为:
上一内容
下一内容 回主目录 返回
可逆过程
体系经过某一过程从状态(1)变到状态(2) 之后,如果能使体系和环境都恢复到原来的状态 而未留下任何永久性的变化,则该过程称为热力 学可逆过程。否则为不可逆过程。
上一内容
下一内容
回主目录
返回
可逆过程
可逆过程的特点: (1)状态变化时推动力与阻力相差无限小,体系 与环境始终无限接近于平衡态; (2)过程中的任何一个中间态都可以从正、逆两个 方向到达;
P2 0.401 100 0.401 T2 T1 ( ) 298 ( ) 118K P 1.00 1 nRT2 1.00 8.314118 3 3 V2 9 . 58 10 m 3 P2 10010
3 W U nCV ,m (T2 T1 ) 1.00 8.314 (118 298 ) 2.24 KJ 2
T2 P ΔH3
ΔH2
nA(β)
T平衡 P平衡
上一内容
下一内容 回主目录 返回
T平衡 P平衡
相变热的计算
QP H H1 H 2 H3
H1
T平衡
T1
CP,m ( )dT
H2 n Hm
H3
上一内容
下一内容
T1
T平衡
CP,m ( )dT
上一内容
下一内容 回主目录 返回
总结
• • • •
本课小结: 1、可逆过程要正确理解; 2、可逆过程的特点; 3、理想气体可逆体积功的计算。
作业:
上一内容
下一内容
回主目录
返回
相变热的计算
•一.相变和相变热
相:系统中物理性质和化学性质完全相同的均 匀部分. 相变:系统从一个相变成另一个相的过程称为 相变化
上一内容
下一内容
2006.1.1 回主目录
返回
2006.1.1
功与过程
上一内容
下一内容
2006.1.1 回主目录
返回
2006.1.1
功与过程
3.多次等外压膨胀 (1)克服外压为 p ' ,体积从 V1 膨胀到 V ' ; (2)克服外压为 p ",体积从V ' 膨胀到 V " ; (3)克服外压为 p2 ,体积从V "膨胀到 V2 。
V2 0.0248 Wr nRT ln 2.0 8.314 298ln V1 0.10 6.9110 J
3
上一内容
下一内容
回主目录
返回
例题:
• 2、1.00mol某单原子理想气体在298K,1.00×103 KPa下可逆绝热膨胀到最终状态压力为100KPa,求算 终态体积、终态温度及所做的功。 1 1 1.67 1 解: T2 ( P2 ) 0.401 T1 P1 1.67
' e,1 " "
p (V V )
' ' "
p1 (V1 V )
'
整个过程所作的功为三步加和。
上一内容
下一内容 回主目录 返回
功与过程
上一内容
下一内容
回主目录
返回
功与过程
3.可逆压缩 如果将蒸发掉的水气慢慢在杯中凝聚,使压力缓 慢增加,恢复到原状,所作的功为:
W pi dV
