算法案例 - 简单 - 讲义
四个经典的算法案例
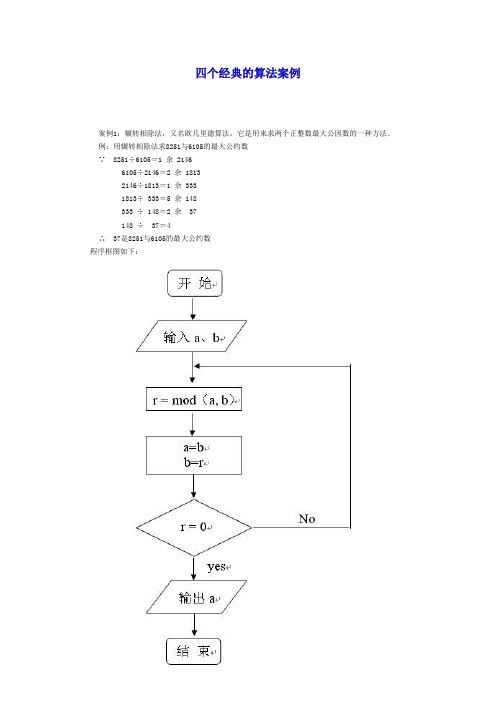
四个经典的算法案例案例1:辗转相除法,又名欧几里德算法,它是用来求两个正整数最大公因数的一种方法。
例:用辗转相除法求8251与6105的最大公约数∵ 8251÷6105=1 余 21466105÷2146=2 余 18132146÷1813=1 余 3331813÷ 333=5 余 148333 ÷ 148=2 余 37148 ÷ 37=4∴ 37是8251与6105的最大公约数程序框图如下:其中 r = mod(a, b) r表示a÷b的余数案例2:秦九韶算法,它是中国南宋时期数学家秦九韶提出的,用来解决多项式的求值问题,在西方被称作霍纳算法。
首先看一道例题:求多项式f(x)=2x5―5x4―4x3+3x2―6x+7当x=5时的值。
根据秦九韶算法:f(x)可表示为f(x)=({[(2x―5)x―4]x+3}x―6)x+7于是令 V0=5则 V1=2V0―5=2×5―5=5V2=V1X―4=5×5―4=21V3=V2X+3=21×5+3=108V4=V3X―6=108×5―6=534V5=V4X+7=534×5+7=2677∴ f(5) = 2677秦九韶算法只用到乘法、加法两个简单运算,不需要乘方运算,它是多项式求值的简化算法。
下面看程序框图,其中a0、a1、a2、a3、a4、a5是f (x) 从右向左的系数。
案例3:排序:是一种基本并且常用的算法,排序的算法很多,可以参阅课本,这里不再叙述。
案例4:进位制例:画程序框图,表示把k进制数a(共有n位),转化为十进制数b的过程框图如下:其中:t = GET a│i│ t表示a右数第i位利用上面的算法,把2进制数110011化为十进制的数即:1×20+1×21+0×22+0×23+1×24+1×25= 51以上是四个经典算法,大家可以从中体会算法的基本思想和算法的基本结构,并尝试用算法的基本语句描述它。
算法的教学实践__案例(3篇)

第1篇一、背景随着信息技术的飞速发展,算法已经成为现代社会不可或缺的一部分。
在计算机科学、数据科学、人工智能等领域,算法的应用越来越广泛。
为了培养学生的逻辑思维能力、问题解决能力和创新意识,将算法融入教学实践显得尤为重要。
本文以某高校计算机科学与技术专业为例,介绍一种算法的教学实践案例。
二、教学目标1. 理解算法的基本概念和特性。
2. 掌握常用算法的设计与实现方法。
3. 能够运用算法解决实际问题。
4. 培养学生的团队合作精神和创新能力。
三、教学内容1. 算法的基本概念:算法的定义、特性、复杂度等。
2. 常用算法:排序算法(冒泡排序、选择排序、插入排序等)、查找算法(二分查找、顺序查找等)、图算法(广度优先搜索、深度优先搜索等)。
3. 算法设计方法:分治法、动态规划、贪心算法等。
4. 算法实现:使用Python语言实现各种算法。
四、教学实践案例1. 案例背景某高校计算机科学与技术专业开设了一门《数据结构与算法》课程,课程内容涉及算法的基本概念、常用算法、算法设计方法以及算法实现等。
为了提高学生的实践能力,教师决定采用案例教学法,通过一个具体的案例让学生在实践中学习算法。
2. 案例描述案例:某公司需要开发一个图书管理系统,实现以下功能:(1)图书信息录入:包括书名、作者、出版社、出版日期、价格等信息。
(2)图书查询:根据书名、作者、出版社等信息进行查询。
(3)图书借阅:实现图书的借阅、归还功能。
(4)图书统计:统计图书的借阅次数、库存数量等信息。
3. 教学过程(1)引入案例教师首先向学生介绍案例背景,让学生了解图书管理系统的功能和需求。
(2)分析问题教师引导学生分析案例中的问题,明确需要解决的问题,如图书信息录入、查询、借阅、统计等。
(3)设计算法教师带领学生一起设计解决案例中问题的算法,如图书信息录入可以使用链表实现,图书查询可以使用二分查找算法,图书借阅可以使用栈实现,图书统计可以使用哈希表实现。
SIMPLE算法及计算例子

SIMPLE算法及计算例子算法是指一系列解决问题的步骤和规则,是计算机科学的基础。
简单算法是指易于理解和实现的算法,适用于一些简单的问题。
下面是几个简单算法及其计算例子。
1.冒泡排序算法:冒泡排序是一种基础的排序算法,它依次比较相邻的元素,如果顺序不对则进行交换,直到整个序列有序为止。
计算例子:假设有一个数字序列[5,3,8,4,2],使用冒泡排序算法将其从小到大进行排序。
-第一次迭代:比较5和3,交换位置,得到序列[3,5,8,4,2]-第二次迭代:比较5和8,位置不变,继续比较下一对数字-第三次迭代:比较8和4,交换位置,得到序列[3,5,4,8,2]-第四次迭代:比较8和2,交换位置,得到序列[3,5,4,2,8]经过第四次迭代后,发现序列已经是有序的,算法结束。
最终的有序序列为[2,3,4,5,8]。
2.欧几里得算法:欧几里得算法用于计算两个非负整数的最大公约数。
算法基于两个数的辗转相除法,即先用较大数除以较小数得到余数,然后用较小数除以余数,依次循环,直到余数为0为止。
计算例子:假设需要计算36和48的最大公约数。
-第一次迭代:48除以36,余数为12-第二次迭代:36除以12,余数为0迭代过程中余数为0时,算法结束,最大公约数为123.线性算法:线性算法用于在一个无序列表或数组中寻找一些元素的位置。
它是一种直观的方法,逐个比较列表中的元素,当找到匹配的元素时返回其位置,否则返回未找到。
计算例子:假设有一个列表[4,2,7,1,9,5],需要找到数字7的位置。
-从列表的第一个元素开始,比较其与目标数字7-第一次比较:4!=7,继续比较下一个元素-第二次比较:2!=7,继续比较下一个元素-第三次比较:7=7,找到匹配,返回位置3最终结果为数字7的位置为3这些是一些简单算法及其计算例子,它们是计算机科学中最基础的算法之一、无论是冒泡排序还是求最大公约数,这些算法都体现了计算机程序处理问题的思维方式和逻辑。
易语言经典算法 实例辅导讲义

易语言经典算法1.取所有质数2.求最小公倍数3.求最大公约数4.汉诺塔5.9X9乘法表6.猫捉老鼠(筛选法)7.水仙花数问题8.计算组合9.身份证升级15位升级到18位10.用冒泡法排序数字11.九宫计算12.奶牛问题13.求阶乘14.折半查找15.给歌手打分16.航线设置17.数字全排列18.借书方案19.求直角三角形20.二分排序21.抢3022.求回文数23.斐波那契数列(递推法)24.分块查找25.求帕斯卡三角(杨辉三角)26.箱子问题(贪婪法)27.寻找文件(递归法)28.求最大公约数(递归法)29.取不重复数(排除法)30.拉丁方31.波松瓦分酒32.皇后问题33.背包问题34.角谷猜想35.邮票组合36.贮油点37.分解质因数38.任意进制转换(大数)39.计算星期几(常用公式)40.计算星期几(蔡勒公式)41.猴子吃桃子42.马踏棋盘43.打鱼还是晒网44.九位累进可除数45.十进制转为二进制46.九连环47.找窃贼48.哥德巴赫猜想49.最小生成数50.农夫过河51.旅游最省钱路径52.马克思手稿中的数学题53.上楼梯(递归).e54.上楼梯(非递归)55.金额大小写转换56.求一元二次方程的根(二分法)57.数字与IP地址间的转换58.八皇后问题(回溯法)59.求N阶幻方60.计算分数的精确值61.找零钱62.求一元二次方程的根(公式法)63.比赛日程(分治法)64.两个有序数组的合并65.统计投色子(2个)的结果66.12小球问题67.改进冒泡排序法68.螺旋数组69.射击环数70.猜数字游戏71.桶排序72.造币厂问题73.直接插入排序74.搬砖75.公车座位巧安排76.韩信点兵(中国剩余定理)77.黑洞数78.矩阵相乘79.螺旋矩阵问题(多循环法)80.买水果问题81.求平方根82.求任意三角形面积83.全排列问题(递推法)84.怎样组合值最大85.取两数之间均匀分布的随机数算法:递归递推法分块查找筛选法枚举法冒泡法二分法贪婪法序号:001使用算法:筛选法问题:取N以内的所有质数数量并显示,问题描述:求N(N>0)个自然数中的所有质数数量,并显示问题分析:先把所有质数以外的数,打上“1“的标志,最后搜索整型数组,找出值为0的个数,就是质数的个数!备注:易语言例程:001.取所有质数.e序号:002使用算法:循环检验问题:求最小公倍数问题描述:求任意2个自然数的最小公倍数问题分析:我们只要认准一个数,先从自身开始和另一个数求余数比较,为0那么这个数就是最小公倍数,如果不为0,那么把这个数不断翻倍再比较。
五大经典算法以及案例

五大经典算法以及案例
1. 排序算法:使用冒泡排序算法对一个包含10个随机整数的数组进行排序。
案例:
给定数组:[4, 9, 2, 5, 1, 8, 3, 7, 6, 10]
排序后的数组:[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
2. 查找算法:使用二分查找算法在一个有序整数数组中查找目标值。
案例:
给定有序数组:[1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
目标值:11
查找结果:目标值在数组中的位置为5。
3. 图遍历算法:使用深度优先搜索算法遍历一个无向图。
案例:
给定无向图的邻接矩阵表示:
[0, 1, 1, 0, 0]
[1, 0, 0, 1, 1]
[1, 0, 0, 0, 1]
[0, 1, 0, 0, 0]
[0, 1, 1, 0, 0]
从节点1开始进行深度优先搜索的遍历结果:1 -> 2 -> 4 -> 3 -> 5
4. 动态规划算法:使用动态规划算法求解斐波那契数列的第n项。
案例:
求解斐波那契数列的第10项:
斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55
第10项为55。
5. 贪心算法:使用贪心算法解决背包问题。
案例:
给定背包容量为10,物品列表如下:
物品1:重量4,价值8
物品2:重量3,价值5
物品3:重量1,价值2
物品4:重量5,价值12
通过贪心算法选择物品装入背包的方案:
选择物品2,物品3,物品4装入背包,总重量为9,总价值为19。
C语言简单算法举例

穷举法
▪ 基本思想:首先根据问题的部分条件预估 答案的范围,然后在此范围内对所有可能 的情况进行逐一验证,直到全部情况均通 过了验证为止。若某个情况使验证符合题 目的全部条件,则该情况为本题一个答案。 若全部情况验证结果均不符合题目的全部 条件,则说明该问题无解。
转到S5 S4: 若y%100=0且y%400=0,则输出输出y”是闰年”,
否则输出“不是闰年”然后转到S5 S5: y=y+1 S6: 当y≤2500时,转至S2继续执行,否则,算法停
止
对于一个大于或等于3的正整数,判断它是不 是一个素数
S1: 输入n的值
S2: i=2 (i作为除数)
▪ 所谓素数,指除1和该
▪ 算法结束,变量p就是 所求结果。
举例:求5!的算法用流程图表示
开始 p=1 i=2 p=p×i i=i+1 N i>5
Y
打印 ` p
结束
求 1-1/2+1/3-1/4+…+1/99-1/100 S1:sum=1 S2:deno=2 S3:sign=1 S4:sign=(-1) ×sign S5:term=sign ×(1/deno) S6:sum=sum+term S7:deno=deno+1 S8:若deno≤100,返回S4;否则结束
简单算法举例
▪ 求1×2×3×4×5 ▪ S1: p=1
▪ S2: i=2 ▪ S3: p=p×i ▪ S4: i=i+1 ▪ S5: 若i≤5,返回S3;否则
结束
▪ 设两个变量。一个变 量p代表被乘数,一个 变量i代表乘数。不另 设变量存放乘积结果, 而直接将每一步的乘 积放在被乘数变量中。
算法案例(完整版)

例2 已知10b1(2)=a02(3),求数字a, b的值.
10b1(2)=1×23+b×2+1=2b+9. a02(3)=a×32+2=9a+2. 所以2b+9=9a+2,即9a-2b=7.
故a=1,b=1.
小 结
1. k进制数使用0~(k-1)共k个数字, 但左侧第一个数位上的数字(首位数字) 不为0. 2.用 an an-1 a2 a1(k ) 表示k 进制数,其中k称为基数,十进制数不标 注基数. 3. 把k进制数化为十进制数的一般算式 是: an an-1 a2 a1(k )
第一步,输入a和n的值. 第二步,令b=0,i=1. i-1 b 第三步, = b + ai ´ 2 , i=i+1. 第四步,判断i>n 是否成立.若是,则输 出b的值;否则,返回第三步.
同样地,把k进制数 a = an an-1 a2 a1(k )
化为十进制数b的算法和程序框图如何设 计? 第一步,输入a,k和n的值. 第二步,令b=0,i=1.
“更相减损术”在中国古代数学专著《 九章算术》中记述为:
可半者半之,不可半者,副置分母、 子之数,以少减多,更相减损,求其等 也,以等数约之.
例1 分别用辗转相除法和更相减损 术求168与93的最大公约数. 辗转相除法:168=93×1+75,
93=75×1+18, 75=18×4+3, 18=3×6.
a=rnrn-1„r1r0(2)
知识探究(二):十进制化k进制的算法
思考1:根据上面的分析,将十进制数a化 为二进制数的算法步骤如何设计? 第一步,输入十进制数a的值. 第二步,求出a除以2所得的商q,余数r. 第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的二进制数.
随机算法最简单的例子

随机算法最简单的例子-概述说明以及解释1.引言1.1 概述在编写长文《随机算法最简单的例子》之前,我们首先来谈谈文章的概述。
随机算法(Random Algorithm)是计算机科学中的一个重要概念,其核心思想是通过随机选择的方式进行计算或决策。
随机算法广泛应用于各个领域,如密码学、仿真、优化问题等。
本文旨在介绍随机算法的基本概念、原理,以及其在实际问题中的广泛应用。
首先,我们将详细定义随机算法,并解释其基本原理。
紧接着,我们将探讨随机算法在各个领域的应用,例如抛硬币问题、随机数生成器、随机洗牌算法和随机选择算法等。
通过这些具体案例的分析,我们将进一步说明随机算法的实际应用价值以及其优缺点。
最后,我们将总结随机算法的重要性、发展方向以及应用前景。
通过阅读本文,读者将能够全面了解随机算法的基本概念和原理,并且了解其在各个领域中的应用。
我们希望本文能够为读者提供一个简单明了的随机算法的入门指南,并且激发对于随机算法更深入探索的兴趣。
在随机算法的广阔领域中,随机选择了本文的出现,希望读者在阅读过程中也能够感受到这种随机性带来的惊喜和创造力。
让我们开始探索随机算法的奇妙世界吧!1.2 文章结构文章结构部分的内容:本文主要分为四个部分:引言、正文、案例分析和结论。
下面将对每个部分进行简要介绍。
在引言部分,首先对随机算法进行概述,指出随机算法是指一种具有随机性质的算法。
接着介绍文章的结构,即分为引言、正文、案例分析和结论四个部分。
然后说明本文的目的,即探索随机算法的最简单的例子,并指出通过分析这些例子,可以更好地理解随机算法的定义、原理、应用以及它们的优缺点。
最后进行总结,概括了本文的主要内容和观点。
在正文部分,我们将详细介绍随机算法的定义、原理、应用以及它们的优缺点。
首先,阐述随机算法的定义,即一种具有随机性质的算法,可以生成一系列不确定的结果。
其次,解释随机算法的原理,包括随机数生成器的原理、随机洗牌算法的原理和随机选择算法的原理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法案例
知识讲解
一、更相减损术
1.概念:求两个整数的最大公约数的算法.
2.步骤:以两个数中较大的数减去较小的数,以差数和较小的数构成一对新的数,对这一对数再用大数减小数,以同样的操作一直做下去,直到产生一对相等的数,此数就是这两个数的最大公约数.
3.等值算法:用“更相减损术”设计出来的算法求最大公约数的算法称为“等值算法”,用等值算法可以求任意两个正整数的最大公约数.
4.原理:《九章算法》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数.以具体的例子来说明更相减损术求最大公约数的原理:以求117和182的最大公约数为例:(117182)(11765)(6552)(5213)(1339)(1326)(1313),,,,,,,,
→→→→→→
每次操作后得到的两个数与前两个数的最大公约数相同,而且逐渐减少,故总能得到相等的两个数,即为所求的最大公约数.
二、辗转相除法
1.概念:辗转相除法又称欧几里得算法,是由欧几里得在公元前300年左右首先提出来的求两个数的最大公约数的算法.
2.步骤:对于给定的两个数,以其中较大的数除以较小的数得到一个余数,将较小的数与余数看成一对新的数,重复上面的步骤,直到余数为零为止,此时上一步中较小的数即为所求的最大公约数.
如:(117182)(11765)(6552)(5213)(130)
,,,,,,故13即为所求.
→→→→
三、秦九韶算法
1.用途:秦九韶算法求多项式的值
2.具体内容:已知一个多项式函数,计算多项式在某点处的函数值的一种算法,是我国古
代数学家秦九韶提出的,具体如下: 对任意一个n 元多项式1110()n n n n f x a x a x a x a --=++++,
改写成如下形式:12110()()n n n n f x a x a x a x a ---=++
++ 231210(())n n n n a x a x a x a x a ---=++
+++
=
1210((()))n n n a x a x a x a x a --=+++++,
求多项式的值时,先计算最内层括号内的一次多项式的值,即11n n v a x a -=+, 然后由内向外逐层计算一次多项式的值, 即212n v v x a -=+,323n v v x a -=+,
,10n n v v x a -=+.
这样,求一个n 次多项式的值,就转化为求n 个一次多项式的值. 令1(1)(())k n n n k n k v a x a x a x a ----=++++,则递推公式为01n
k
k n k v a v v x a --=⎧⎨=+⎩,
其中12k n =,,,.
到目前为止,此算法仍然是世界上多项式求值的最先进的算法.
3.秦九韶算法与其它算法的比较:1110()n n n n f x a x a x a x a --=++
++,
(1)直接求和法:先计算各个单项式的值,再把它们相加,乘法次数为
(1)
(1)212
n n n n ++-+++=
,加法次数n ; (2)逐项求和法:先计算x 的各项幂的值,再分别相乘,计算幂值需要乘法1n -次,将幂值与多项式系数k a 相乘需要乘法n 次,故共需要乘法21n -次,加法n 次. 注:此方法对直接求和法有所改进,但仍然比秦九韶算法计算量大很多. (3)秦九韶算法:计算量仅为乘法n 次,加法n 次.
4.秦九韶算法的特点:
1)化高次多项式求值为一次多项式求值; 2)减少了运算次数,提高了效率; 3)步骤重复执行,容易用计算机实现.
注意:利用秦九韶算法计算多项式的值关键是能正确地将所给多项式改写,然后由内向外逐
次计算,由于后项计算用到前项的结果,故应认真、细心,确保中间结果的准确性.若在多项式中有几项不存在时,可将这些项的系数看成0,即把这些项看做0·x n
四、进位制
内容:K 进制数的基数为K ,K 进制数是由0~1K -之间的数字构成. 将十进制的数转化为
K 进制数的方法是除K 取余法.把K 进制数1
10110(0,0,
,)n n n n a a a a a K a a a K --<<≤< 化
为十进制数的方法为11
10()110n n n n k n n a a a a a k a k a k a ---=++
++.
典型例题
一.选择题(共5小题)
1.(2016•渭南一模)函数f(x)=lnx的零点所在的区间是()A.(1,2) B.(1,e) C.(e,3) D.(3,+∞)
【解答】解:函数f(x)=lnx在(0,+∞)上连续,
且f(e)=1<0,f(3)=ln3﹣1>0,
故选:C.
2.(2015•醴陵市)下列图象表示的函数中,不能用二分法求零点的是()A.B.C.
D.
【解答】解:由函数图象可得,A中的函数有零点,但函数在零点附近两侧的符号相同,故不能用二分法求零点;
除.
B,C,D中的函数存在零点且函数在零点附近两侧的符号相反,故能用二分法求函数的零点,
故选:A.
3.(2015•惠州模拟)若函数f(x)=x3+x2﹣2x﹣2的一个正数零点附近的函数值用二分法计算,那么方程x3+x2﹣2x﹣2=0的一个近似根(精确到0.1)为()A.1.2 B.1.3 C.1.4 D.1.5
【解答】解:由参考数据可得f(1.43750)>0,f(1.40625)<0,又因为题中要求精确到0.1,
所以近似根为1.4
故选:C.
4.(2017秋•辽阳县期末)方程x3﹣x﹣3=0的实数解落在的区间是()A.[﹣1,0]B.[0,1]C.[1,2]D.[2,3]
【解答】解:令f(x)=x3﹣x﹣3,
易知函数f(x)=x3﹣x﹣3在R上连续,
f(1)=﹣3<0,f(2)=8﹣2﹣3=3>0;
故f(1)•f(2)<0,
故函数f(x)=x3﹣x﹣3的零点所在的区间为[1,2];
故选:C.
5.(2015春•淄博期末)根据表格内的数据,可以断定方程e x﹣x﹣2=0的一个根所在的区间是()
A.(﹣1,0)B.(0,1) C.(1,2) D.(2,3)
【解答】解:由上表可知,
令f(x)=e x﹣x﹣2,
则f(﹣1)≈0.37+1﹣2<0,
f(0)=1﹣0﹣2=﹣1<0,
f(1)≈2.72﹣1﹣2<0,
f(2)≈7.39﹣2﹣2>0,
f(3)≈20.09﹣3﹣2>0.
故f(1)f(2)<0,
故选:C.
二.填空题(共4小题)
6.(2013•闵行区二模)用二分法研究方程x3+3x﹣1=0的近似解x=x0
若精确到0.1,至少运算n次,则n+x0的值为 5.3.
【解答】解:根据运算得下表:
因为f(0.3125)<0,且f(0.34375>0,
满足f(0.3125)×f(0.34375)<0,
且区间长度:0.34375﹣0.3125=0.03125<0.1,
∴n=5,x0=0.3,n+x0=5.3.
故答案为:5.3.
7.某同学求“方程x3=﹣x+1的根x0所在区间D”时,设函数f(x)=x3+x﹣1,算得f(﹣1)<0,f(1)>0;在以下的过程中,他用“二分法”又取3个值,分别是x1,x2,x3,就能确定区间D,则区间D是(0.5,0.75).
【解答】解:设f(x)=x3+x﹣1,算得f(﹣1)<0,f(1)>0,由f(0)=﹣1<0,f(1)=1>0,可知方程必有一根在区间(0,1)内;再由f(0.5)=﹣0.375<0,可知方程必有一根在区间(0.5,1)内;f(0.75)>0,可知方程必有一根在区间(0.5,0.75)内.
故答案为:(0.5,0.75).
8.(2016秋•亭湖区校级月考)若函数f(x)=x3+3x﹣1在区间[n,n+1)(n∈Z)上有零点,则n=0.
【解答】解:由f(0)=0+0﹣1=﹣1<0,f(1)=1+3﹣1=3>0及零点定理知,f(x)的零点在区间(0,1)上,两端点为连续整数
∴零点所在的一个区间[n,n+1)(k∈Z)是(0,1)
∴n=0,
故答案为:0.
9.函数f(x)=x2+ax+b有零点,但不能用二分法求出,则a,b的关系是a2﹣4b=0.
【解答】解:函数f(x)=x2+ax+b有零点,但不能用二分法求出,
说明函数是二次函数,函数的图象与x轴有一个交点,
即△=a2﹣4b=0
故答案为:a2﹣4b=0.
三.解答题(共3小题)
10.关于x的方程2x2﹣3x﹣2k=0在(﹣1,1)内有一个实根,求实数k的取值范围.
【解答】解:设f(x)=2x2﹣3x﹣2k,则
∵关于x的方程2x2﹣3x﹣2k=0在(﹣1,1)内有一个实根,
∴f(﹣1)f(1)<0或f(1)=0或△=0,
即(2+3﹣2k)(2﹣3﹣2k)<0或k=﹣或k=﹣.
∴(5﹣2k)(﹣1﹣2k)<0
∴﹣≤k<或k=﹣.
11.某市A地到B地的电话线路发生故障,这是一条10km长的线路,每隔50m 有一根电线杆,如何迅速查出故障所在?
【解答】解:由于10km=10 000m,
故有200根电线杆.从中间开始取如果是好的向右去,如果是坏的向左取,以、
等为间断点,也就是运用“二分法”的原理进行快速判断.
12.设计二分法算法,求方程x3﹣x﹣1=0在区间[1,1.5]内的解(精度为0.01).【解答】解:函数f(x)=x3﹣x﹣1=0在区间[1,1.5]上连续,
且f(1)=1﹣1﹣1<0,f(1.5)=0.875>0;
故函数f(x)=x3﹣x﹣1在区间[1,1.5]内内必有零点;
列表如下,如下:
这个零点的近似值为1.32.。
