北京工业大学-材料力学-应力应变状态典型习题解析
第十三章北航 材料力学 全部课件 习题答案
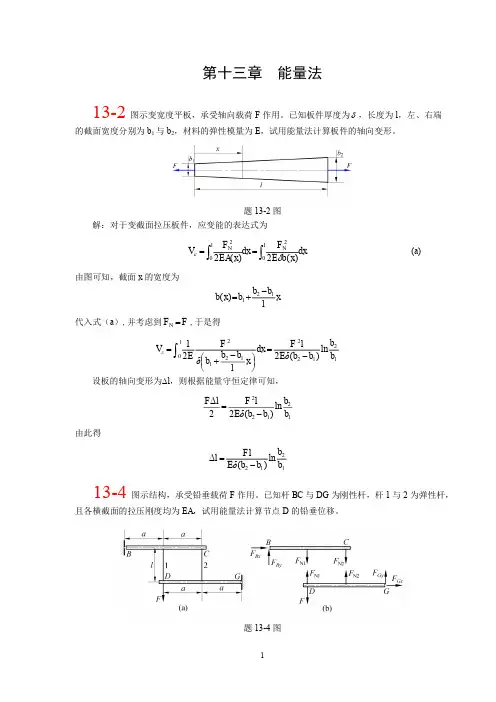
M ( x2 ) Fx2 M C ,
图 13-9 根据卡氏定理，得
C
1 [ EI
a 0
( Fx1 )(
x1 )dx1 a
a 0
( Fx2 )(1)dx2 ]
5Fa 2 （） 6EI
A A
13-10 图示各梁，弯曲刚度 EI 均为常数，试用卡氏定理计算横截面 A 的挠度 与转角 。
3 3
3 3
–F
F 2
3 Fa 3 3 Fa 12
3 Fa 12
3
a
3 6
9
故有
ΔB
求 AB 的运算过程列表如下： i 1 2 3
i 1
3
F Ni FNi li 3Fa （←） EA 12EA
li
a a a
F Ni
2 3a 1
FNi
F
F Ni FNi l i
2 3 F 3
3a 1
–F
3 F 3
3 F 6
3a
F 2
故有
5 3 F 6
AB
F Ni FNi li 5 3F （） EA 6 EA i1
3
(b) 解：求Δ B 和 AB 的单位状态分别示如图 13-17b（1）和 b（2） 。
图 13-17b 求 Δ B 的运算过程列表如下：
i 1 2 3 4
转角。
图示刚架，承受载荷 F 作用。设弯曲刚度 EI 为常数，试用卡氏定理计算截面 C 的
题 13-9 图 解：在截面 C 处假想附加一矩为 M C 的力偶（见图 13-9） ，由图可得
M x1 ( F
第八章 北航 材料力学 全部课件 习题答案
8-18 构件表层一点处的应力如图 a 所示，为了测量应力，在该点沿 0°，45°与 90°
粘贴三个应变片，幷测得相应正应变依次为 0 , 45 与 90 （图 b） 。已知材料的弹性模量为 E， 泊松比为，试根据上述测试应变值，确定该点处的正应力x，y 与切应力x。
题 8-18 图 解：当45°与45°时，相应截面的正应力为 5 x y x y cos90 sin 90 x y 2 2 2 x y x y x y 5 cos(90 ) sin(90 ) 2 2 2 根据广义胡克定律，45°方位的正应变则为
1 ( y x ) E 联立求解式（a） ， （b）与（c） ，于是得
σ (
30 10 20sin 90 )MPa 40.0MPa 2 30 10 τ ( sin 90 )MPa 10.0MPa 2
(b)解：由题图所示应力状态可知，
σ x 30MPa，σ y 10MPa，τ x 20MPa，α 22.5
由此可得指定斜截面上的正应力和切应力分别为
Fs F 20kN， | M | Fa 201kN m 20kN m
微体 A，B 和 C 的应力状态依次如图 8-9 a,b 和 c 所示。
图 8-9 对于图 a 所示应力状态，其正应力为
3
σA
|M | 6 20 103 N 6.00 107 Pa 60.0MPa 2 2 Wz 0.050 0.200 m
7
100 80 100 80 cos(120 ) 50sin(120 )( MPa) 128.3 MPa 2 2 根据广义胡克定律，得 30° 的正应变为
北京工业大学考研材料力学真题09-13
北京工业大学2012年硕士研究生入学考试试题A B C注：所有答案必须做在答题纸上，做在试题纸上无效！第页(共6 页)注：所有答案必须做在答题纸上，做在试题纸上无效！第页(共6 页)注：所有答案必须做在答题纸上，做在试题纸上无效！第页(共6 页)注：所有答案必须做在答题纸上，做在试题纸上无效！第页(共6 页)注：所有答案必须做在答题纸上，做在试题纸上无效！第页(共6 页)e23PlPl已知：2-7. 一刚性杆AB ，A 端铰支，B 端作用一集中力P ，C 、D 处与两根抗弯刚度均为EI 的细长杆铰接，4l AC CD ==,2l DB =，CE H DF ==，如图所示。
试求当结构由细长杆的失稳而毁坏时，载荷P 的临界值。
（10分）题2-7图注：所有答案必须做在答题纸上，做在试题纸上无效！第 页 (共6 页)1-5. ~OO7gIMllt%I¥J3f1J (o~O) fof:flIJ7lJ~;ff1lfl¥Jm.OO~OOOFJT7j\, iXW3ffJtff;f§[r'1JI¥J~~*~~~~, ~-~ (~ (, 4*)A.m 1fl: 5lliN;ffi , m m 5lli!t /F [r'1J ;B. m1.iL5lliNT-RJ, mm5lli!t;ffi ~;c. m1fl, mffi5lli!ttl3if§ RJ; T I50 1500i40i .oili . Ii y50 lorD ~.....--'! 30 Ij 30 4!{}I MPa A BC DR911-6 002-6. B~Q: ff~7}/{f5t\(;1iIf q(x), ;1t-g-j; Jg R, fFffl x ,r2, 0 nn ~iIDJ:.~U1~ aBC TIl]) DY.5t~: &a=O.6xlO·3 , b ,r2, C4''tiFzD DY.1f.Jg &b=1.2xlO·4 , tjf45i1!'lim. E=200GPa, rst~b~ ,lFO.3, l,J.\:sjt: 1) 7}/{f5j;-g-j; R *+, 2) 7}~j;1Ij; R fFfflOO1ft~ x? CI5?t)R60aI_---'-'-'--"-"'--_~:n2-7. ri~mJgJ:[2'j] , P3~£:7v.o, ~Jf-:7vt, (t < ~), tj*4!¥J5E!i'l1fliiJg E, ~t~b~Jg,Lt,)~WJ~*~~rPJtfct) F ~Q7'~j;1~~E Tf'Fffl (:!lQ 00), 1Jt*: ~t~~~Jf-!¥J[;Jl:1t:i: M ~QH t~I¥J [;Jl:1ti: £ill 0 CI5 *F。
材料力学习题解答81
30
40 sin( 60 ) 20 cos( 60 ) 2 20 0.866 20 0.5 7.32 MPa
30
80
习题27(b)图
27.如图所示各平面应力状态，各应力分量的单位为 MPa ，用解析法求指定截面上的正应力和切应力。 (b)
x y x y cos 2 xy sin 2 2 2 x y sin 2 xy cos 2 2
2) y 0, x 0
F
0
45
结论： 横力弯曲梁截面上的 剪力所产生的剪切变形 将使梁的截面产生微小 的翘曲效应。
2.58 45
y
h
b
1m
1m
2m
35．如图所示平面应力状态，各应力分量的单位为 MPa
3 材料的弹性模量 E 200 GPa ，泊松比 0.，求该点的应变分量
28．如图所示平面三角形单元体的斜面为自由表面， 角度 30 ，各应力分量的单位为MPa，求 x 和 xy 解:
x ? y 40 MPa xy ?
x
n
60
x y x y cos 2 xy sin 2 2 2 x y sin 2 xy cos 2 40 2 x 40 x 40 cos120 xy sin 120 0 2 2 x 40 40 sin 120 xy cos 120 0 xy x tan 120 2 2 x 40 x 40 40 cos120 x tan 120 sin 120 0 2 2 2 x 40 ( x 40)(0.5 1.732 0.866) 0
材料力学复习习题解析
B
b
e
A
a
c
d
?
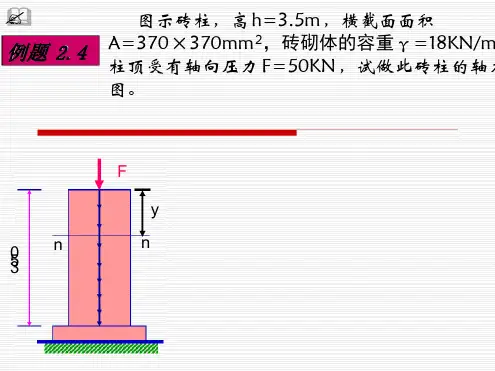
例题
2.12
图示的杆系是由两根圆截面钢杆铰接而成。已知
α＝300，杆长L＝2m，杆的直径 d=25mm，材
料的弹性模量 E＝2.1×105MPa，设在结点 A处悬 挂一重物 F＝100kN ，试求结点 A的位移δ A。
B1
2C
FNAB FNAC
αα
A
A?
F
塑性材料冷作硬化后，材料的力学性能发生了变化。试判断以
（B）屈服极限；
（C）强度极限；
据图示三种材料拉伸时的应力－应变曲线，得出如下四种结论，请判断哪一个是
正确的：
（A）强度极限 σｂ（1）＝σｂ（2）＞ σｂ（3）； 弹性模量 E（1） ＞ E（2） ＞ E（3）；
延伸率 δ（1）＞ δ（2）＞ δ（3） ；
（B）强度极限 σｂ（2） ＞ σｂ（1）＞ σｂ（3）； 弹性模量 E（2） ＞ E（1） ＞ E（3）；
（B）OAB →BD →DOAB ；
（C）OAB →BAO→ODB；
（D）OAB →BD →DB。
正确答案是（
）
关于材料的力学一般性能，有如下结论，请判断哪一个是正确的：
（A）脆性材料的抗拉能力低于其抗压能力；
（B）脆性材料的抗拉能力高于其抗压能力；
（C）塑性材料的抗拉能力高于其抗压能力；
（D）脆性材料的抗拉能力等于其抗压能力。
试判断下列论述是否正确，正确的在括号内打 “√”，错误的打“ ×”
（7）承受斜弯曲的杆件，其中性轴必然通过横截面的形心， 而且中性轴上正应力必为零。（ ）
（8）承受偏心拉伸（压缩）的杆件，其中性轴仍然通过横 截面的形心。 （ ）
材料力学典型例题及解析 13.电测应力分析典型习题解析
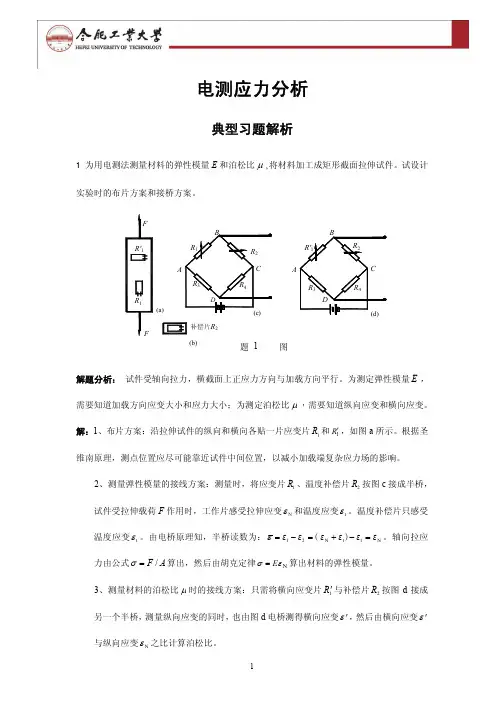
1、测轴向拉力 F
将各个应变片接成图 b 所示的全桥。应变仪读数为：
3
ε = ε1 − ε3 + ε2 − ε4
=（εF
+
εM
+
ε）t −（−
µεF
−
µεM
+
ε）t +（εF
−
εM
+
ε）t −（−
µεF
+
µεM
+
ε
）
t
= 2（1 + µ)εF
于是
εF
=
ε 2（1 +
。
µ）
由胡克定律，得相应的正应力为 σ
力σ1
和σ 3
与母线的夹角分别为－45°和
=
E ⋅ εM
=
1 2
E ⋅ε
。
讨论：图 b 所示的半桥接线法，可以自动补偿温度效应，无需接入温度补偿片。
解 II：也可采用图 c 的布片方案和图 d 的全桥接桥方案，这时，各应变片感受的应变分别为
ε1 = εM + ε t； ε2 = −εM + ε t； ε3 = －µεM + ε t； ε4 = µεM + ε t； 应变仪的读数为 ε = ε1 − ε2 − ε3 + ε4 = 2(1 + µ )εM
2 图 a 所示为受纯弯曲的矩形截面梁。已知，材料的弹性模量 E 、泊松比 µ 。要求测出最
大的弯曲应力。试设计布片和接桥方案。
(a)
(c)
(b)
(d)
题2图
解题分析：梁的上下表面各点处为单向应力状态，且正应力方向平行于梁的轴线。
解 I：在梁的上下表面沿主应力方向各贴一片应变片 R1 、 R2 ，按图 b 接成半桥。梁发生弯
应力状态与应变状态例题
B.（1）不正确、（2）正确；
C.（1）、（2）都正确；
D.（1）、（2）都不正确。
若构件内危险点的应力状态为二向等拉，则除 （ B ）强度理论以外，利用其他三个强度理论得到 的相当应力是相等的。
A.第一； B.第二； C.第三； D.第四；
r1
r2
r3 1 3
第二强度理论
3
＝
1＋
1－（2＋3）
对于铸铁: 0.25
1 3 2
2
（1＋）
0.8
0.5
1
2
1
2 2
2
3 2
3
1 2
3
0.6
基本习题结束
铸铁水管冬天结冰时会因冰膨胀而被胀裂， 而管内的冰却不会破坏。这是因为（ B ）。
第一强度理论
1 ＋
23 11
x 10， y 23， xy 11
max
min
x y
2
x
2
y
2
2 x
10
29.8MPa
3.72MPa
(单位 MPa)
1 29.28MPa，2 3.72MPa，3 0
1 29.28MPa< 30MPa
故满足强度要求。
某结构上危险点处的应力状态如图所示，其中σ＝ 116.7MPa，τ＝46.3MPa。材料为钢，许用应力［σ］＝ 160MPa。试用第三、第四强度理论校核此结构是否安全。
xy
cos 2
0
故所给45度方向是主应力方向。
一受扭圆轴,直径d=20mm,圆轴的材料为 钢,E=200GPa,ν=0.3。现测得圆轴表面上与轴线成450 方向的应变为ε=5.2×10-4,试求圆轴所承受的扭矩。
第四章北航的材料力学全部课件习题答案
第四章 扭 转4-5 一受扭薄壁圆管，外径D = 42mm ，内径d = 40mm ，扭力偶矩M = 500N •m ，切变模量G =75GPa 。
试计算圆管横截面与纵截面上的扭转切应力，并计算管表面纵线的倾斜角。
解：该薄壁圆管的平均半径和壁厚依次为mm 122 mm 5.20)22(210=-==+=d D d D R δ，于是，该圆管横截面上的扭转切应力为189.4MPa Pa 10894.1m001.00.02052πN 500π282220=⨯=⨯⨯==δτR T 依据切应力互等定理，纵截面上的扭转切应力为 MPa 4.189=='ττ 该圆管表面纵线的倾斜角为rad 102.53rad 1075104.189396-⨯=⨯⨯==G τγ 4-7 试证明，在线弹性范围内，且当R 0/δ≥10时，薄壁圆管的扭转切应力公式的最大误差不超过4.53%。
解：薄壁圆管的扭转切应力公式为δR Tτ20π2=设βδR =/0，按上述公式计算的扭转切应力为3220π2π2δβTδR T τ== (a)按照一般空心圆轴考虑，轴的内、外直径分别为 δR D δR d +=-=002 2，极惯性矩为 )4(2π])2()2[(32π)(32π2200404044p δR δR δR δR d D I +=--+=-=由此得)14(π)12()2()4(π)2(23022000p max ++=++=+=ββδβδδδT R R R TδR I T τ (b)比较式(a)与式(b)，得)12(214)12()14(ππ222332max++=++⋅=ββββββδδβT Tττ 当100==δβR 时，9548.0)1102(10211042max=+⨯⨯⨯+⨯=ττ可见，当10/0≥δR 时，按薄壁圆管的扭转切应力公式计算τ的最大误差不超过4.53％。
4-8 图a 所示受扭圆截面轴，材料的γτ-曲线如图b 所示，并可用mC /1γτ=表示，式中的C 与m 为由试验测定的已知常数。