非局域生长方程标度奇异性分析
非线性方程论文:非线性方程分歧多重特征值Lyapunov-Schmidt约化半线性椭圆方程

非线性方程论文:非线性方程分歧多重特征值Lyapunov-Schmidt约化半线性椭圆方程【中文摘要】本文主要讨论一类非线性方程F(λ,u) =λu ? G(u) =θ的分歧问题,这里F : R×X→X为非线性可微映射,X为Banach空间.Krasnoselski的经典分歧定理在G∈C1(X,X)为具有变分结构的紧算子的条件下,利用Morse理论证得了A = G (θ)的p重特征值都是F(λ,u) =θ的分歧点.当A = G (θ)和G为紧算子时,又进一步利用拓扑度理论证得了A的奇(代数)重特征值为F(λ,u) =θ的分歧点.本文将条件减弱为G (θ)为满足紧线性的算子,(?)利用Lyapunov-Schmidt约化和隐函数定理论证了Krasnoselski的分歧定理,又进一步计算了分歧方向.最后,为了使抽象理论更容易理解,本文分别以具体的半线性椭圆方程及方程组作为例子,应用我们得到的抽象定理得到分歧点附近的局部解集结构.【英文摘要】In this paper,we mainly discuss the bifurcation problem of nonlinear equationF(λ,u) =λu-G(u) =θ, where F : R×X→X is a nonlinear di?erential mapping,X is a Banach space.The Krasnoselski’s classical bifurcation proved using Morse theorem which pmultiplicity eigenvalues of A = G (θ) are bifurcation points for F(λ,u) =θwith thecase in which G∈C1(X,X) is a compact variational operator.Moreover,he provedvia topological theorem that the eigenvalue of A with oddalgebraic multiplicityis a bifurcation point of F(λ,u) =θin the case that A = G (θ) and G are com-pact. We weak thecondition for G (θ) is compact,and 0 < dim(N(λ*I - G (θ))=p <∞,N(λ*I - G (θ)) R(λ*I - G (θ)) = {θ}, prove the Krasnoselski’s bifur-cation theorem via Lyapunov-Schmidtreduction and the implicit function theo-rem.Furthermore,wecompute the direction of bifurcation. At last,to understandtheabstract theorem more easily,we applying the main theorem tothe semilinearelliptic equation and systems.We have the local construct of the solution sets nearthe bifurcation points fromthe abstract theorem.【关键词】非线性方程分歧多重特征值 Lyapunov-Schmidt约化半线性椭圆方程【采买全文】1.3.9.9.38.8.4.8 1.3.8.1.13.7.2.1 同时提供论文写作一对一辅导和论文发表服务.保过包发.【说明】本文仅为中国学术文献总库合作提供,无涉版权。
非厄米量子系统的奇异行为:探索非厄米哈密顿量下的奇异点与拓扑相变

非厄米量子系统的奇异行为:探索非厄米哈密顿量下的奇异点与拓扑相变摘要非厄米量子系统,由于其与开放系统的内在联系,近年来在凝聚态物理学、光子学和量子信息科学等领域引起了广泛的研究兴趣。
与传统的厄米系统不同,非厄米系统的哈密顿量不再满足厄米共轭对称性,这导致了一系列奇异的物理现象。
本文将深入探讨非厄米量子系统中的奇异点(Exceptional Points,EPs)和拓扑相变,揭示它们之间的深刻联系,并展望其在未来技术中的潜在应用。
引言在传统的量子力学框架下,封闭系统的哈密顿量必须是厄米的,以保证能量本征值的实数性。
然而,当我们考虑与环境相互作用的开放系统时,非厄米哈密顿量自然而然地出现。
非厄米系统不仅在理论上具有丰富的物理内涵,而且在实验上也具有广泛的可实现性。
奇异点是非厄米系统中的一种特殊点,在这些点上,系统的本征值和本征态发生简并,导致非厄米哈密顿量不再对角化。
拓扑相变则是凝聚态物理学中的一个重要概念,它描述了系统在参数变化时,其拓扑性质发生突变的现象。
近年来,研究者们发现,非厄米系统中的奇异点与拓扑相变之间存在着深刻的联系。
非厄米哈密顿量与奇异点非厄米哈密顿量的本征值一般为复数,其虚部反映了系统与环境的能量交换。
当系统的参数变化时,两个或多个本征值可能会相遇并发生简并,形成奇异点。
在奇异点附近,系统的本征值和本征态表现出高度的敏感性,微小的扰动都可能导致系统性质的剧烈变化。
奇异点的存在为非厄米系统带来了许多独特的物理现象。
例如,在光学系统中,奇异点可以导致单向激光发射、完美吸收和拓扑激光等现象。
在量子信息科学中,奇异点可以用于实现量子态的高效制备和操控。
非厄米系统中的拓扑相变拓扑相变是凝聚态物理学中的一个重要概念,它描述了系统在参数变化时,其拓扑性质发生突变的现象。
传统的拓扑相变主要发生在厄米系统中,例如量子霍尔效应和拓扑绝缘体。
近年来,研究者们发现,非厄米系统中也存在着丰富的拓扑相变现象。
非线性方程组数值解法

非线性方程组数值解法随着科学技术的进步和发展,人们发现非线性方程组在科学研究中起着越来越重要的作用,成为解决复杂科学问题的有力工具。
解决非线性方程组的核心是采用有效的数值解法,它们可以帮助我们快速解决复杂的非线性问题。
一般来说,解决非线性方程组的数值解法可以分为三类:一类是积分方法,一类是有限元方法,另一类是迭代方法。
积分方法包括欧拉法和梯形法等;有限元方法则包括Galerkin方法、Ritz方法、Kirchhoff方法等;而迭代方法有Newton-Raphson方法、拟牛顿投影方法、拟牛顿变量步长方法、McKenna迭代法等。
积分方法按照方程组的方向将时间分解为若干步,并利用各步的积分求解出方程组的解。
它的优点是收敛性强,适用范围广,但缺点是计算量大,实际计算起来比较复杂。
有限元方法将非线性方程组转换成一组有限元方程,然后利用有限元解法求解出解析解。
它的优点是快速计算和分空间,可以解决含有空间变量的非线性问题,但缺点是收敛性一般,容易发散。
迭代方法首先采用初始值作为方程组的解,然后不断迭代求解,该方法的优点是可以用来求解非线性方程组的定点解,但也有缺点,如求解精度较低,耗时较长。
在实际应用中,解决非线性方程组数值解法需要考虑多方面因素,如准确性、可行性、处理效率和使用复杂度等,以选择合适的解法。
此外,还需要考虑非线性方程组的特殊性质,如线性方程组不可约或不可约变系数等,以决定是否可以采用一般的解法。
因此,解决非线性方程组的数值解法是一项复杂的工作,要求工程师必须运用知识和技术,有系统地考虑不同的解法,并在不同情况下进行取舍,才能获得最佳的结果。
总之,解决非线性方程组的数值解法具有复杂的理论和实际应用,为解决复杂科学问题提供了有力的工具,受到了越来越多的关注。
只有深入地研究各类数值解法,推动它们的发展,才能满足现实需求,建立科学有效的解决方案,最终实现理想的结果。
第三章MHD不稳定性

第三章 MHD 不稳定性3.1扭曲模与交换模 不稳定性来自等离子体中的自由能。
一般来说,大尺度不稳定性的自由能主要来自各种物理量的梯度分布。
在等离子体中主要就是等离子体本身温度、密度分布,以及磁场的梯度。
前者就是压强梯度,后者可以产生电流,特别是场向电流。
所以MHD 不稳定性主要包括电流驱动的扭曲模(撕裂模)和压强驱动的交换模(气球模)。
有关这两种MHD 模式,我们在《高等等离子体物理I 》中已经讨论过。
交换模(气球模)主要来自能量原理中的压强驱动项()()()*0p W d p δ⊥⊥∇⎡⎤=-⋅∇⋅⎣⎦⎰x ξξκ。
由0p λ=∇κ,显然有()200p W d p δλ⊥∇⎡⎤=-⋅∇<⎣⎦⎰x ξ,如果0λ>(0||p ∇κ),则平衡是不稳定的;反之,若0λ<(0||p -∇κ),则平衡是稳定的。
我们称0λ>(0||p ∇κ)是坏曲率,而0λ<(0||p -∇κ)是好曲率。
如果磁力线的“根”是固定的,则只有非常局域的短波模式才能增长起来。
这种局域短波模式称为“气球模”(或者“气泡模”)。
扭曲模(撕裂模)主要来自能量原理中的电流驱动项()()()0||**000112011ˆ22J J W d d b c c δ⊥⊥⊥⊥⎡⎤⎡⎤⋅=-⨯⋅=-⨯⋅⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰J B x ξB B x ξB B 。
扭曲模的主要特征是:1) 磁力线具有因为||J 引起的螺旋结构;2) 螺旋结构导致等离子体的整体扭曲;3) 扭曲与长波扰动相同的(共振的)螺旋结构。
这些共振的扰动结构一定发生在环形等离子体的有理面上,因为在有理面上的磁力线才能与螺旋结构的扰动“共振”。
3.2 撕裂模3.2 .1 磁岛、磁重联扭曲模发展起来之后,会在小尺度上形成很强的梯度。
在这样的尺度上,非理想MHD 效应如电阻效应、电子惯性、电子压强梯度、甚至波-粒子相互作用引起的反常(湍性)电阻等可能成为重要的,理想等离子体的磁力线冻结条件被破坏。
Burgers方程的非局域对称的局域化及对称约化

Burgers方程的非局域对称的局域化及对称约化本文以对称方法为基本工具,围绕着对称的基本理论,研究了非线性偏微分方程,并给出了贝克隆变换及其新的群不变解。
第一章简要介绍了对称的发展背景和研究现状,对本文相关的概念做了解释和说明,同时概括了本文的主要研究内容,并给出1+1维Burgers方程的李点对称及其群不变解。
第二章利用了潘勒卫分析法中的WTC方法证明了Burgers方程是潘勒卫可积的。
第三章根据截断潘勒卫展开法得到了Schwarz形式的Burgers方程并构造出Burgers方程的非局域对称,利用非局域对称局域化的思想求出自贝克隆变换及群不变解。
最后我们将上面的方法进行了推广,根据截断潘勒卫展开法得到了Schwarz 形式的Bu-rgers方程并构造出无穷多非局域对称,考虑到复杂性我们先研究n=2的非局域对称的情况,利用非局域对称局域化的思想求出自贝克隆变换及群不变解,特别还给出了孤子与Kummer波以及Airy波的新的相互作用解。
浙江大学理学院第十二期校级srtp学生立项评审汇总表
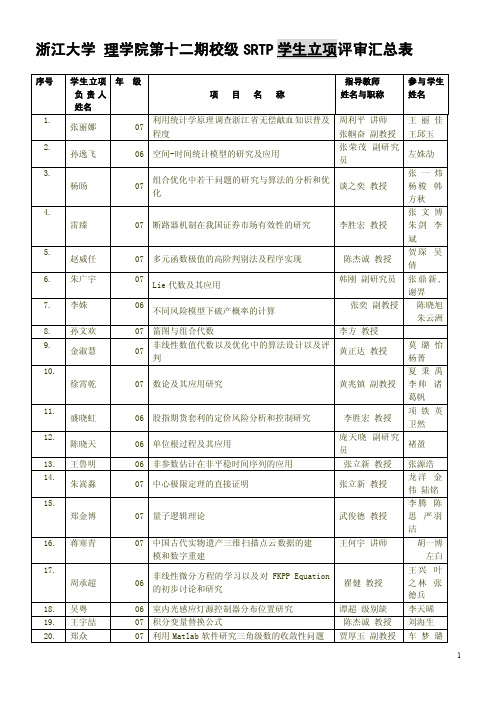
07
程度
张帼奋 副教授 王邱玉
孙逸飞
06 空间-时间统计模型的研究及应用
张荣茂 副研究 左姝劼
员
杨旸
组合优化中若干 问题的研 究与算法的 分析和优
07
谈之奕 教授
化
张一炜 杨梭 韩 方秋
张文博
雷臻
07 断路器机制在我国证券市场有效性的研究
李胜宏 教授 朱 剑 李
斌
赵威任
07 多元函数极值的高阶判别法及程序实现
陈杰诚 教授 刘海生
郑众
07 利用 Matlab 软件研究三角级数的收敛性问题 贾厚玉 副教授 车 梦 璐
1
21. 崔欣 22.
佘晓萌
23. 沈小勇 24.
樊琪
25. 张连云
26. 马宇斌 27. 谭越 28. 叶 兵 29. 宋平越 30. 朱 琼 31.
鲍金科 32. 廖 扬 33. 陈 拓 34.
07 居点变迁
讲师
07 多客体识别的机制研究
徐青
07 以校内网为例的真实虚拟社区用户的心理与行 吴明证 为研究
07 儿童脚印地板的创新设计及其工效学分析
张智君
07 积极情绪对面部表情认知及记忆的影响
许百华
07 后悔体验对不同风险偏好者决策的影响
马剑虹
郑全全 07 焦虑在特定情境(谈判情境下)对决策的影响
张昭教授 周宏伟副教授
朱岩教授
07 浙大紫金港校区三维导览及分析
刘仁义 教授
07 论杭州地铁对其周边商住用房价格的影响
冯友建 副教授
07 基于 GIS 和 RS 的浙大三校区景观格局对比分析 陆丽珍 副教授
07 杭州民间传说与民俗的整理、表达与研究
一类带非局部项的allen-cahn方程解的存在性

一类带非局部项的allen-cahn方程解的存在性带有非局部项的Allen-Cahn方程是一类重要的非线性偏微分方程,研究它的解的存在性具有重要的理论意义和实际应用价值。
本文将介绍关于带非局部项的Allen-Cahn方程解存在性的一些主要研究工作和结果。
Allen-Cahn方程是一个经典的描述相分离现象的模型,它在物理、化学、材料学等领域中具有广泛的应用。
方程的基本形式为:ε²∆u-f(u)+λ∇W*u=0(1)其中,u(x)是未知函数,表示时间和空间变量,ε是小的正数,f(u)是一个给定的非线性函数,λ是常数,∆是拉普拉斯算子,W是一个权重核算子,*表示卷积操作。
带有非局部项的Allen-Cahn方程是在经典Allen-Cahn方程的基础上引入了非局部项的一个扩展。
非局部项代表了系统中物质的非局部相互作用,可以更好地描述物质的长程相互作用和相界面的形成过程。
关于带有非局部项的Allen-Cahn方程解的存在性的研究工作主要集中在两个方面,一个是存在性的充分条件,另一个是存在性的证明方法。
首先,对于存在性的充分条件,很多学者通过构造合适的能量函数,证明了一些条件下带有非局部项的Allen-Cahn方程存在解。
其中一个经典的充分条件是“能量估计”,也称为Ginzburg-Landau能量估计。
根据能量估计,当能量的衰减速度快于等于非局部项的增长速度时,方程存在解。
此外,还有学者通过研究方程的动力学行为,证明了带有非局部项的Allen-Cahn方程的解存在。
其次,关于存在性的证明方法,主要有两类。
一类是基于变分方法的证明方法,另一类是基于解的连续性的证明方法。
变分方法是一种广泛应用的证明方法,它通过构造适当的变分问题,证明了方程的解存在。
而基于解的连续性的证明方法则是先证明该方程的解存在于一定的函数空间中,然后通过限制序列的紧性,得到方程的解存在。
在具体的研究中,学者们从不同的角度出发,针对不同类型的非局部项,展开了许多具体的研究。
非均匀环境中非局部扩散方程的传播动力学

非均匀环境中非局部扩散方程的传播动力学非均匀环境中非局部扩散方程的传播动力学一、引言扩散过程是自然界中常见的现象之一,它广泛应用于物理、化学、生物学等领域。
在传统的扩散理论中,假设扩散过程是以局部的方式进行的,即扩散的速度仅依赖于扩散物质在某一点的浓度梯度。
然而,在非均匀环境中,局部扩散理论往往不能很好地描述实际扩散的行为。
因此,非局部扩散方程的研究越来越受到学者们的关注。
二、非局部扩散方程的建立非局部扩散方程是描述非均匀环境中扩散过程的数学模型。
相对于局部扩散方程,非局部扩散方程引入了非局部扩散项,描述了扩散物质在非局部范围内的传输特性。
非局部扩散方程一般形式如下:∂c/∂t = D(-△)^α c其中,c是扩散物质的浓度,t是时间,D是扩散系数,α是非局部参数,△是Laplace算子。
在非局部扩散方程中,△^α代表了非局部效应,描述了扩散物质在非局部范围内的传输特性。
三、非局部扩散方程的数值模拟为了研究非局部扩散方程的传播动力学,需要进行数值模拟。
一种常用的数值方法是离散化非局部扩散方程,然后采用有限差分或有限元方法进行求解。
另外,还可以利用蒙特卡洛方法进行模拟。
通过数值模拟,可以得到非局部扩散方程在不同环境下的传播特性,如浓度分布的变化规律、传播速度的变化趋势等。
四、非均匀环境对非局部扩散方程的影响在非均匀环境中,非局部扩散方程的传播动力学性质常常会受到影响。
一方面,非均匀环境会引起扩散系数的空间变化,导致扩散速度的非均匀分布。
另一方面,非均匀环境中存在梯度,使得扩散物质在空间上的传播路径发生改变。
因此,非均匀环境对非局部扩散方程的传播行为具有重要的影响。
五、非局部扩散方程的应用非局部扩散方程的研究不仅在理论上具有重要意义,而且在实际应用中也有着广泛的应用价值。
例如,在环境工程中,非局部扩散方程可以用于描述污染物在土壤中的传播过程;在材料科学中,非局部扩散方程可以用于描述材料的弛豫行为;在生物学中,非局部扩散方程可以用于描述生物分子在细胞内的运输过程等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的 F mi — ce a l Visk正常 标度 关 系.对于 奇异 标度 行 为 , 一 1时为 超粗 化奇 异标 度行 为 ,l < 1 y ‰ O t 。 时为 内禀 奇
w(, ~ 丽 1)
f ( )~ Au
~
, பைடு நூலகம்
《
() 2
() 3
其 中 g 1£ (, )一 (h 2+ z£ 一h ,) E( r ,) ( £]>为高度 差涨 落关联 函数 , 异标度 函数 为 奇
1n, 》 . t ls C 1 0
由 ()式 和 ()式 得 2 3
的 定 义 为
W L ) < : ; ) 瓦( (, 一 ∑ [(, ~ f )
,
式中: L表示生长系统的横向尺度;(, 为 f hY£ -) 时刻;处表面的生长高度; f一 ∑ ; (, 表示在 £ 瓦( ) ^芏£ )
时刻 表 面的平 均生长 高度 ;… > ( 表示 对 噪声 的统 计平 均. a l _ F mi y等 4 出当生 长表 面具 有标 准 的 自仿 射结 提
第 2 6卷 第 1期
Vo. 1 26 No.1
徐 州 工 程 学 院 学 报 (自 然 科 学 版 )
J u n l o z o n t u e f Te h o o y ( t r l ce c s o r a f Xu h u I s i t o c n lg t Na u a S in e Ed t n ii ) o
为 正 常标 度行 为 , 而非局 域情况 下 出现奇 异标度 行为.
关 键 词 : 局 域 生 长 方 程 ; 度 奇 异 性 ; 力 学 重 整 化 群 理 论 非 标 动
中图分 类号 : 4 4 2 文献 标 志码 : O 1.2 A
文章编 号 :6 43 8 2 1 ) 10 6 —6 1 7 —5 X(0 1 0 —0 20
・
6 ・ 2
张 丽 萍 , : 局 域 生 长 方 程 标 度 奇 异 性 分 析 等 非
f ,
,
t《 Z , () 4
£》
g( , ~ f
其 中 , 一O tz ‰ 局域 粗糙 度指 数 . a ‰ , 一 //, 为 l o 当 ≠ 时 出现奇 异标 度 , a ‰ ( ) 就恢 复到 自仿 射 当 ≠ 时 4式
型m]化 学气 相沉 积模型 中等. 、 ¨ 当表 面界面粗 化生 长不满 足 F mi - ce a l Vi k自仿射标 度时 , y s 呈现所 谓奇 异 标 度性质 , 即整个表 面 的标 度性 质和局 域标 度 的性质不 相 同. 当出现奇 异标度 时 , 域表面 宽度 w( ,) 由 局 1 要 如 下标 度关 系替代 , 即
( 0B 18 ) CX g 0 Z ;中国 矿 业 大 学青 年 基金 项 目(O 6 4 ) Z 0 A0 3
作 者简 介 : 丽 萍 ( 9 7 ) 女 , 西 西 安人 , 张 17一 , 陕 副教 授 , 士研 究 生 , 要 从 事表 面界 面 生 长 标度 理 论 和 多场耦 合 研 究. 博 主
摘要 : 用 动力 学重 整化群 方 法, 析表 面界 面粗 化 生长 动力 学 的标度 奇 异 性 , 到 非局域 生 采 分 得
长方 程 动力学标度 奇 异指 数的 一般 结果 , 将该 结 果 应用 于 非局 域 K ra- ai— h n ( P ) 并 ad rP r i a g K Z 方 sZ
21 0 1年 3 月
M a . 11 r 2O
非 局 域 生 长 方 程 标 度 奇 异 性 分 析
张 丽 萍l1, a6 张连 英 , , a
( . 国矿 业 大 学 a 深 部 岩 土 力 学 与地 下 工 程 国 家 重 点 实验 室; 1中 .
b 理 学院 , 苏 徐 州 2 1 1 ; . 州 工 程 学 院 ,江 苏 徐 州 2 1 0 ) . 江 2 16 2 徐 2 0 8
近年 来 , 平衡 的表 面界 面粗化 生长 问题 成 为研 究 的 热点口 ] 这是 因为许 多 实 际材 料 的生 长 过程 , 非 . 如
晶体 生 长 、 分子 束外延 生 长 、 气相 沉积 生长 , 都会涉 及到表 面界 面粗化 生长动 力学 问题 . 在表 面界面粗 化生长
动力 学理论 中 , 标度行 为通 常可 以用总 的表 面宽度 ( 有时也 称为粗糙 度 ) ( £ 的标度性 质来表 示. ( £ w L,) W L, )
收 稿 日期 : 0 01 - 2 2 1—21 基 金项 目 : 家 重 点基 础 研 究 发 展 计 划 项 目 ( 0 7 D 0 4 0 江 苏 省 创 新 学者 攀 登 项 目 ( K2 0 0 7 j江 苏 省 研 究 生 培 养 创 新 工 程 项 目 国 2 0C 2 9 0 ) B 080)
构时 , ( £ W L, )具有 渐进行 为 , 即
fp , t W( £ L,)~ { f
L ,
t L, 《
t》 L ,
() 1
这里 a是粗 化指数 , 生长指 数 , — a 是 动力学 指数 , 称为 系统 的特 征时 间. 卢是 L
研究发 现 , 自仿 射标度 性 或奇异 标度性 也广 泛存在 于表 面界面 的粗化生 长过程 中. 非 这一 现象 首次在模 拟理想 分子 束 外 延生 长 。 中发 现. 来 人们 发 现奇 异标 度 行 为存 在 于无 序生 长模 型[-] 电化学 沉积 模 后 11 、 01
程和 非局域 L i a amaVia ( D 方程 , a D sS r - l i L V) — ln 以判 断其标度 奇 异性.研 究结果 表 明: 生长 方程 的 动力 学标度 奇异 性除 了与基底 维数 、 最相 关项有 关 外, 与非 局域 因子 密切相 关 , 还 局域 条 件 下表现
