框架柱正截面压弯承载力计算Nmin
柱子承载力计算
柱子承载力计算 Prepared on 22 November 2020三、框架柱承载力计算（一）正截面偏心受压承载力计算柱正截面偏心受压承载力计算方法与《混凝土基本原理》中相同（混凝土规范）。
如图所示。
即非抗震时：（3-62）（3-63）其中：（3-64）但考虑地震作用后，有两个修正，即：◆正截面承载力抗震调整系数。
◆保证“强柱弱梁”，对柱端弯矩设计值按梁端弯矩来调整。
（混凝土规范11.4.2一、二、三级框架柱端组合的弯矩设计值为：（3-65）一级框架结构及9度各类框架还应满足：（3-66）其中：——为节点上下柱端截面顺时针或反时针方向组合的弯矩设计值之和，如图所示；——为节点左右梁端截面反时或顺时针方向组合的弯矩设计值之和的较大者，一级框架节点左右梁端均为负弯矩时，绝对值较小的弯矩应取0；——为节点左右梁端截面按反时针或顺时针方向采用实配钢筋截面面积和材料标准值，且考虑承载力抗震调整系数计算的正截面抗震受弯承载力所对应的弯矩值之和的较大者。
其可按有关公式计算。
——为柱端弯矩增大系数，一级取，二级取，三级取。
求得节点上下柱端的弯矩设计值之和后，一般情况下可按弹性分析所得的节点上下柱端弯矩比进行分配。
对于顶层柱和轴压比小于的柱，可不调整，直接采用内力组合所得的弯矩设计值。
当反弯点不在柱的层高范围内时，柱端截面组合的弯矩设计值可直接乘以上述柱端弯矩增大系数。
一、二、三级框架底层柱下端截面组合的弯矩设计值，应分别乘以增大系数，，，且底层柱纵筋宜按上下端的不利情况配置。
（二）斜截面受剪承载力计算1、柱剪力设计值（混凝土规范11.4.4为了保证“强剪弱弯”，柱的设计剪力应调整。
一、二、三级的框架柱的剪力设计值按下式调整：（3-67）一级框架和9度各类框架还应满足：（3-68）其中：——柱端截面组合的剪力设计值；——考虑地震作用组合，且经调整后的框架柱上、下端弯矩设计值，分别按顺时针和反时针进行计算，取其中较大者；——分别为柱上、下端截面反时针或顺时针方向按实配钢筋面积、材料强度标准值，且考虑承载力抗震调整系数的正截面抗震受弯承载力所对应的弯矩，且取两个方向的较大者。
柱抗震正截面受弯承载力计算
-3488.5972 39.98805823
609.2055
1850.7355Байду номын сангаас
-803.0672
-48.3372 -132.93377
-125.5781131 -105.6102812 -126.7209682
大偏压 0.518 547.9880582 43.45423439 80 0.121212121 -1350.613917
40 660 164.8302603 0.249742819 不需要 23 187.8302603 5.714285714 ＞5考虑 11.4131496 1 1 1.081954771 203.2238463 198 3996.5772
计算公式 γ 内力 γ
RE|M|/kN·m REN/kN
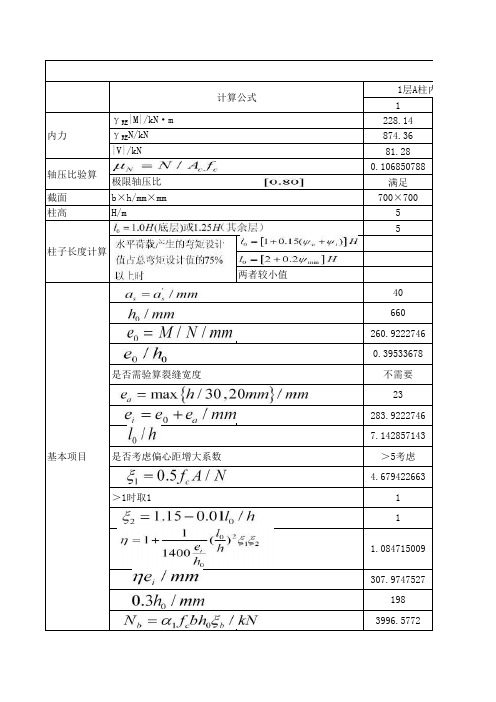
1层A柱内力组合 1 228.14 874.36 81.28 0.106850788 满足 700×700 5 5
|V|/kN 轴压比验算 截面 柱高 极限轴压比 b×h/mm×mm H/m
柱子长度计算 两者较小值 40 660 260.9222746 0.39533678 是否需验算裂缝宽度 不需要 23 283.9222746 7.142857143 基本项目 是否考虑偏心距增大系数 ＞5考虑 4.679422663 ＞1时取1 1 1 1.084715009 307.9747527 198 3996.5772
0.125139332
0.121212121
-1541.883876 -419.6448232 -2006.848275 -1465.770159
980 3920
980 3920
980 3920
980 3920
980 3920
受弯构件正截面受弯承载力计算
受弯构件正截面受弯承载力计算
在进行受弯构件正截面受弯承载力计算时，首先需要了解构件的几何尺寸和材料特性。
几何尺寸包括构件的宽度、高度和长度，材料特性包括材料的抗弯强度和弹性模量等。
在进行受弯构件正截面受弯承载力计算时，一般采用等效应力法。
根据等效应力法，构件的正截面受弯承载力可以通过以下公式计算：M=σ×S
其中，M是受弯构件所受弯矩，σ是构件截面上的应力，S是截面的抵抗矩。
在计算截面上的应力时，可以使用以下公式：
σ=M×y/I
其中，M是受弯构件所受弯矩，y是距离截面中性轴距离，I是截面的惯性矩。
在计算截面的抵抗矩时，可以使用以下公式：
S=y×A×f
其中，y是距离截面中性轴距离，A是截面的面积，f是材料的抗弯强度。
综合以上公式，可以得到受弯构件的正截面受弯承载力公式：
N=σ×S=(M×y/I)×(y×A×f)
根据构件的几何尺寸和材料特性，可以计算出受弯构件的正截面受弯
承载力。
需要注意的是，在实际工程中，受弯构件的应力和截面的抵抗矩常常
不是均匀分布的，需要进行更加详细的计算和分析。
此外，由于材料的塑
性变形和结构的不完美性等因素的存在，实际承载能力可能小于理论计算值。
综上所述，受弯构件正截面受弯承载力计算是结构工程中的重要任务，它通过等效应力法来确定构件在受弯状态下的承载能力。
在实际工程中，
应该考虑到材料和结构的各种因素，进行更加精细的分析和计算。
框架 柱正截面受弯承载力计算
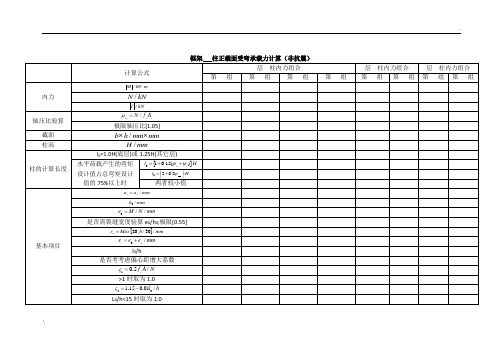
计算公式
层柱内力组合
层柱内力组合
层柱内力组合
第组
第组
第组
第组
第组
第组
第组
第组
内力
轴压比验算
极限轴压比[1.05]
截面
柱高
柱的计算长度
l0=1.0H(底层)或1.25H(其它层)
水平荷载产生的弯矩设计值占总弯矩设计值的75%以上时
两者较小值
基本项目
是否需裂缝宽度验算e0/h0;极限[0.55]
l0/h
是否考考虑偏心距增大系数
>1时取为1.0
L0/h<15时取为1.0
续表
计算公式
层柱内力组合
层柱内力组合
层柱内力组合
第组
第组
第组
第组
第组
第组
第组
第组
基本项目
大小偏心受压的判定
类型
大偏心受压的计算
X<2as’时取为2 as’
小偏心受பைடு நூலகம்的计算
单侧
双侧
实配钢筋/mm2
单侧
单侧
总配筋率
柱子承载力计算
三、框架柱承载力计算（一）正截面偏心受压承载力计算柱正截面偏心受压承载力计算方法与《混凝土基本原理》中相同图所示。
3规范7.）。
如（混凝土即非抗震时：（3-62）（3-63）其中：（3-64）但考虑地震作用后，有两个修正，即：数。
调整系抗正截面承载力震◆◆保证“强柱弱梁”，对柱端弯矩设计值按梁端弯矩来调整。
（混凝土规范11.4.2，抗震规范6.2.2，6.2.3）即：一、二、三级框架柱端组合的弯矩设计值为：（3-65）一级框架结构及9度各类框架还应满足：专业文档供参考，如有帮助请下载。
．）66（3-：其中矩的合弯针方向组截面顺时针或反时下——为节点上柱端示如；图所设计值之和，设弯矩组合的时反时或顺针方向——为节点左右梁端截面值对时，绝弯梁端均为负矩大和的较者，一级框架节点左右计值之；应取0较小的弯矩配实采用顺时针方向针点左右梁端截面按反时或——为节正算的整系数计调，且考虑承载力抗震积钢筋截面面和材料标准值公关可其按有和的较大者。
之力截面抗震受弯承载所对应的弯矩值。
式计算1。
三级取1.1.取1.4，二级取2，级系弯——为柱端矩增大数，一分弹性可情况下按般之矩柱节得点上下端的弯设计值和后，一求。
分比进行配矩端下点的所析得节上柱弯专业文档供参考，如有帮助请下载。
．对于顶层柱和轴压比小于0.15的柱，可不调整，直接采用内力组合所得的弯矩设计值。
当反弯点不在柱的层高范围内时，柱端截面组合的弯矩设计值可直接乘以上述柱端弯矩增大系数。
一、二、三级框架底层柱下端截面组合的弯矩设计值，应分别乘以增大系数1.5，1.25，1.15，且底层柱纵筋宜按上下端的不利情况配置。
（二）斜截面受剪承载力计算1、柱剪力设计值（混凝土规范11.4.4，抗震规范6.2.5）为了保证“强剪弱弯”，柱的设计剪力应调整。
一、二、三级的框架柱的剪力设计值按下式调整：（3-67）一级框架和9度各类框架还应满足：（3-68）其中：——柱端截面组合的剪力设计值；——考虑地震作用组合，且经调整后的框架柱上、下端弯矩设计值，分别按顺时针和反时针进行计算，取其中较大者；专业文档供参考，如有帮助请下载。
框架D柱正截面受弯承载力计算抗震
1.3559913 -6147.4665161 605.000 2420.000 605.000 2420.000
As As
Ne ξ 1 0.5 ξ α 1 f c bh fy h0 as
' '
2 0
单侧 全部
A s, min ρ min bh/mm
2
, ρ min 0.2%
h0/mm e0=M/N/mm
e0/h0;极限[0.55] 是否需裂缝宽度验算
ea=Max[20,h/30]/mm
e i e 0 e a / mm e e i 0.5h a s /mm
N b α 1 f c bh 0 ξ b /kN
大、小偏 心受压 的判定
b
N-Nb
e i 0.3h
0
-1526.772 136.923 大偏压 0.518 0.198 <0.518
类型
N/ α 1 f c b/mm
2a s时取为 2a
'
' s
As As
' '
Ne α 1 f c b h 0 2 fy h0 as
' '
-3.947
ξ
N ξ b α 1 f c bh Ne 0.43 α 1 f c bh
30 520 112.713 0.217 20 132.713 104.663 2474.072 -997.752 -23.287 小偏压 0.518 0.309 <0.518 -7.491
30 520 189.922 0.365 20 209.922 181.872 2474.072 -974.612 53.922 大偏压 0.518 0.314 <0.518 -6.952
钢筋混凝土圆柱正截面受弯承载力计算方法研究
钢筋混凝土圆柱正截面受弯承载力计算方法研究钢筋混凝土圆柱是一种重要的构件之一，其受弯承载力的精确计算对确保施工质量、降低施工成本具有重要的意义。
近年来，建筑工程学科的发展，为钢筋混凝土结构的设计和施工提供了更加专业化和科学化的支撑。
本文以“钢筋混凝土圆柱正截面受弯承载力计算方法研究”为研究内容，结合国内外相关理论，讨论钢筋混凝土圆柱正截面受弯承载力的计算方法。
钢筋混凝土圆柱的受弯承载力可以使用系列受弯计算公式进行测算，主要根据钢筋混凝土圆柱受弯稳定性和受弯承载力分析。
这些受弯计算公式可以根据钢筋混凝土圆柱正截面受弯承载力现场测定、钢筋混凝土材料性能参数和圆柱正截面受弯稳定性计算等环节来确定。
钢筋混凝土圆柱受弯承载力的精确测定，必须从材料与施工内容等方面入手。
钢筋级别的选择、钢筋的配筋比例的控制、混凝土的质量、施工技术的控制等都是决定钢筋混凝土圆柱正截面受弯承载力的重要因素。
同时，在计算钢筋混凝土圆柱正截面受弯承载力时，仍有一些技术细节需要注意，如：钢筋混凝土圆柱截面受弯稳定性分析时，应考虑圆柱截面受荷载时的变形和受弯稳定性扣除面积；混凝土圆柱受弯承载力的计算时，应考虑材料弹性模量、强度等性能参数，以及试验和计算结果；在计算混凝土圆柱受弯承载力时，还要考虑钢筋受拉应力和混凝土受拉应力的分布；同时，还要考虑荷载的作用方向，因为不同的荷载方向可能会导致不同的钢筋混凝土圆柱正截面受弯承载力。
此外，在实际钢筋混凝土圆柱正截面受弯承载力计算中，紧附于混凝土圆柱外部的对象，如预应力钢筋桩等，会导致混凝土圆柱形变及受弯承载力的变化，应当纳入计算中。
此外，在实际的施工中，钢筋混凝土圆柱以及其他承载构件，有可能受到水平载荷的作用，从而影响其受弯承载力，因此，应根据实际情况，计算其水平载荷对受弯承载力的影响。
综上所述，钢筋混凝土圆柱正截面受弯承载力计算是一个非常复杂的工程。
根据钢筋混凝土圆柱正截面受弯稳定性、材料性能参数、施工技术等，确定其受弯承载力，以确保施工质量，降低施工成本。
n=γ αsωn框架柱受轴压力计算
n=γ αsωn框架柱受轴压力计算在建筑设计中，框架柱是承受轴压力的重要结构元素之一。
为了确保工程的安全性和稳定性，对于框架柱的受轴压力计算是必不可少的。
本文将介绍一种常用的计算方法，即n=γ αs ωn法。
1. 引言框架柱是建筑结构中承受垂直荷载的竖向构件，其主要作用是将荷载传递到基础，并保证建筑的稳定性。
在设计框架柱时，必须考虑其受轴压力的大小，以确保结构的安全性。
2. n=γ αs ωn法的原理n=γ αs ωn法是一种常用的框架柱受轴压力计算方法。
其中，n为柱的阻尼系数，γ为柱的材料系数，αs为柱的截面尺寸系数，ωn为柱的固有圆频率。
3. n=γ αs ωn法的计算步骤3.1 确定柱的材料系数γ根据框架柱所使用材料的特性，确定其相应的材料系数γ。
常见的材料系数有混凝土、钢材等。
3.2 确定柱的截面尺寸系数αs根据柱的截面形状和尺寸，查表或计算得到柱的截面尺寸系数αs。
不同形状和尺寸的柱对应不同的αs值，该值反映了柱的几何特性。
3.3 确定柱的固有圆频率ωn柱的固有圆频率ωn与柱的质量和刚度密切相关，可通过有限元分析或经验公式计算得到。
基于质量和刚度的参量，柱的固有圆频率可以反映其自振情况。
3.4 计算柱的轴力根据公式n=γ αs ωn，代入相应的参数，计算柱的轴力。
得到的结果即为柱所受的轴压力。
4. 示例计算为了更好地说明n=γ αs ωn法的应用，下面以一根混凝土框架柱为例进行计算。
假设柱的材料系数γ为1.5，柱的截面尺寸系数αs为0.8，柱的固有圆频率ωn为10 Hz。
根据公式n=γ αs ωn，代入参数计算柱的轴力，得到结果为15 kN。
5. 结论通过n=γ αs ωn框架柱受轴压力计算方法，我们可以得到框架柱所受的轴压力。
这一计算方法考虑了材料、截面尺寸和自振情况等因素，能够较为准确地评估柱的承载能力和稳定性。
需要注意的是，本文介绍的n=γ αs ωn法只是一种常用的计算方法，具体的计算应根据具体情况而定。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ea (mm) 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00
N-Nb (KN) -1438.97 -1438.97 -986.22 -986.22 361.43 361.43 -1381.76 -1381.76 -802.59 -802.59 810.16 810.16 -1369.19 -1369.19 -822.98 -822.98 742.22 742.22 -1471.80 -1471.80 -1028.77 -1028.77 317.43 317.43
柱 类 别
b*h 层次 (mm） 500*500 500*500 500*500 500*500 500*500 500*500 500*500 500*500 500*500 500*500 4.5 4.5 5.2 5.2 4.5 4.5 4.5 4.5 5.2 5.2 4.5 4.5 4.5 4.5 5.2 5.2 4.5 4.5 4.5 4.5 5.2 5.2 l0/h 9.00 9.00 9.00 9.00 10.40 10.40 9.00 9.00 9.00 9.00 10.40 10.40 9.00 9.00 9.00 9.00 10.40 10.40 9.00 9.00 9.00 9.00 10.40 10.40 l0/i 31.18 31.18 31.18 31.18 36.03 36.03 31.18 31.18 31.18 31.18 36.03 36.03 31.18 31.18 31.18 31.18 36.03 36.03 31.18 31.18 31.18 31.18 36.03 36.03
判断 破坏 类型 大偏压 大偏压 大偏压 大偏压 小偏压 小偏压 大偏压 大偏压 大偏压 大偏压 小偏压 小偏压 大偏压 大偏压 大偏压 大偏压 小偏压 小偏压 大偏压 大偏压 大偏压 大偏压 小偏压 小偏压
小偏压 As=As' x=N/fc·b ξ (mm) ·α 1 —— —— —— —— 0.675 0.675 —— —— —— —— 0.759 0.759 —— —— —— —— 0.761 0.761 —— —— —— —— 0.653 0.653 —— —— —— —— 750 750 —— —— —— —— 750 750 —— —— —— —— 750 750 —— —— —— —— 750 750 37.03 37.03 100.35 100.35 288.83 288.83 45.03 45.03 126.03 126.03 351.59 351.59 46.78 46.78 123.18 123.18 342.09 342.09 32.43 32.43 94.40 94.40 282.68 282.68
顶层 A柱 二层 底层 顶层 B柱 二层 底层 顶层 C柱 二层 底层 顶层 D柱 二层 底层
弯承载力计算Nmin（表5-7） 是否考虑附加弯矩 M1 50.05 50.05 40.97 40.97 -0.72 -0.72 -43.57 -43.57 -58.74 -58.74 -78.37 -78.37 25.23 25.23 15.86 15.86 -36.92 -36.92 -54.06 -54.06 -60.00 -60.00 -63.43 -63.43 M2 50.87 50.87 44.14 44.14 -42.96 -42.96 -43.62 -43.62 -58.79 -58.79 -80.30 -80.30 28.52 28.52 56.84 56.84 -59.62 -59.62 -55.12 -55.12 -62.98 -62.98 -74.76 -74.76 N 264.73 264.73 717.49 717.49 2065.13 2065.13 321.94 321.94 901.11 901.11 2513.86 2513.86 334.51 334.51 880.72 880.72 2445.92 2445.92 231.90 231.90 674.93 674.93 2021.13 2021.13 M1/M2 34-12*M1/M2 -0.98 -0.98 -0.93 -0.93 -0.02 -0.02 -1.00 -1.00 -1.00 -1.00 -0.98 -0.98 -0.88 -0.88 -0.28 -0.28 -0.62 -0.62 -0.98 -0.98 -0.95 -0.95 -0.85 -0.85 45.81 45.81 45.14 45.14 34.20 34.20 45.99 45.99 45.99 45.99 45.71 45.71 44.62 44.62 37.35 37.35 41.43 41.43 45.77 45.77 45.43 45.43 44.18 44.18 判 断 不考虑 不考虑 不考虑 不考虑 考虑 考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 不考虑 Cmη ns 1.13 1.13 1.32 1.32 1.37 1.37 1.18 1.18 1.34 1.34 1.72 1.72 1.23 1.23 1.05 1.05 1.65 1.65 1.10 1.10 1.24 1.24 1.60 1.60 M 50.87 50.87 44.14 44.14 58.70 58.70 43.62 43.62 58.79 58.79 80.30 80.30 28.52 28.52 56.84 56.84 59.62 59.62 55.12 55.12 62.98 62.98 74.76 74.76 e0 （mm) 192.16 192.16 61.53 61.53 28.42 28.42 135.49 135.49 65.25 65.25 31.94 31.94 85.26 85.26 64.54 64.54 24.38 24.38 237.69 237.69 93.31 93.31 36.99 36.99
选用钢筋 备注 （mm2) 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 4C18,As=1017 ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ ρ >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2% >0.2%
大偏压
大偏压 As=As' As=As' x-2a' ξ (mm) (mm) (x<2a') (x>2a' 0.08 -42.9748 4 0.08 -42.9748 4 0.22 20.34761 <0 0.22 20.34761 <0 —— —— —— —— 0.10 -34.9734 116 0.10 -34.9734 116 0.27 46.02943 <0 0.27 46.02943 <0 —— —— —— —— 0.10 -33.2154 232 0.10 -33.2154 232 0.27 43.17818 0.27 43.17818 —— —— —— —— 0.07 -47.5664 73 0.07 -47.5664 73 0.21 14.39609 <0 0.21 14.39609 <0 —— —— —— ——
-0.72 2026.13 -42.96 2065.13 11.17 -78.37 2474.86 -80.30 2513.86 34.30 -36.92 2406.92 -59.62 2445.92 22.36 -63.43 1982.13 -74.76 2021.13 29.37
ei (mm) 212.16 212.16 81.53 81.53 48.42 48.42 155.49 155.49 85.25 85.25 51.94 51.94 105.26 105.26 84.54 84.54 44.38 44.38 257.69 257.69 113.31 113.31 56.99 56.99
框架柱正截面压弯承载力计算Nmin（表5-7） 组合内力 柱截面 M N (KN·m) (KN) 上端 下端 上端 下端 上端 下端 上端 下端 上端 下端 上端 下端 上端 下端 上端 下端 上端 下端 上端 下端 上端 下端 上端 下端 50.05 50.87 40.97 44.14 -0.72 -42.96 -43.62 -43.57 -58.79 -58.74 -78.37 -80.30 25.23 28.52 56.84 15.86 -36.92 -59.62 -55.12 -54.06 -62.98 -60.00 -63.43 -74.76 237.73 264.73 690.49 717.49 2026.13 2065.13 321.94 348.94 901.11 904.11 2474.86 2513.86 307.51 334.51 880.72 876.52 2406.92 2445.92 231.90 258.90 674.93 701.93 1982.13 2021.13