理论力学(第三版)第1章第4节质点运动定律
理论力学1234

绪 论
奠基时期牛顿的《自然哲学的数学原理》一书可
看作是理论力学的第一部著作。从牛顿三定律出发可
演绎出力学运动的全部主要性质。另一位理论力学先
驱是瑞士的雅各布· 伯努利,他最早从事变形体力学的
研究,推导出沿长度受任意载荷的弦的平衡方程。通 过实验,他发现弦的伸长和张力并不满足线性的胡克
定律,并且认为线性关系不能作为物性的普遍规律。
二、研究对象
研究物体机械运动普遍遵循的基本规律的一 门学科。
〈一〉矢量力学:主要从力的观点以牛顿三定
律为基础,以力和加速度为基本量,用矢量
法分析问题。
〈二〉分析力学:
从能量的观点,以功和能作为基本 量,用广义坐标作为运动的独立变量, 应用比较系统的数学分析方法,得到了 很多有用的表达式,建立起力学系统所 服从的规律。
加速度
2 ar r r _____ 径向加速度 1 d 2 a r 2r (r ) __ 横向加速度 r dt
ar : 是因径向速度大小和横向速度方向改变引起 a : 是因横向速度大小和径向速度方向改变引起
注意: 在极坐标系中,虽然加速度的表达式较直 角坐标系复杂,但对某些问题的处理较直角坐 标系更为方便!
(横向加速度)
(2)方法二
0 0 在平面极坐标系中,r 径向单位矢, 横向单位 0 矢(指向 增加方向),均非恒矢量 r rr d 0 0 0 r v r ( r r ) r r r 质点速度 dt 0 0 sin i cosj r cosi sin j 0 0 sin i cosj ( sin i cosj ) r 0 0 r 0 0 0 0 r r vr r v v r vr r ( r 大小变化引起的)径向速度 v r(r方向变化引起的)横向速度
理论力学第三版(周衍柏)习题答案
⎧x = r cosϕ + a cosψ
⎨ ⎩
y
=
a
sinψ
又由于在
∆
r AOB 中,有
sinψ
=
2a sin ϕ
(正弦定理)所以
2a sinψ 2 y
sin ϕ =
=
r
r
联立以上各式运用
sin 2 ϕ + cos 2 ϕ = 1
由此可得
cosϕ = x − a cosψ = x − a 2 − y 2
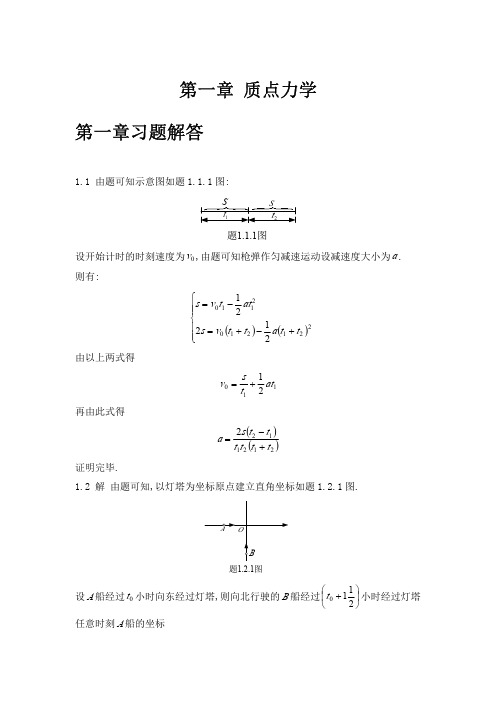
1.8 解 以焦点 F 为坐标原点,运动如题 1.8.1 图所示]
-7-
y
M
•
θ
OF
x
题 1. 8. 1图
则 M 点坐标
对 x, y 两式分别求导
⎧x = r cosθ
⎨ ⎩
y
=
r
sinθ
⎪⎧ẋ = ṙ cosθ − rθ̇ sinθ
⎨ ⎪⎩
ẏ
=
ṙ
sinθ
+
rθ̇
cosθ
故
( ) ( ) v2
即 沿位矢方向加速度
( ) a = ̇ṙ − rθ̇2
垂直位矢方向加速度 对③求导
( ) a⊥ = rθ̇̇ + 2ṙθ̇
ṙ̇ = λṙ = λ2r
对④求导
θ̇̇ =
−
µθ r2
ṙ
+
µ r
θ̇
=
µθ
⎛ ⎜
⎝
µ r
+
λ
⎞ ⎟
⎠
把③④⑦⑧代入⑤⑥式中可得
a//
=
λ2r
−
µ 2θ 2 r
理论力学第一章质点力学

F1 F2
分别作用在两个物体上
重点加深理解的几个问题
(1)牛顿定律是经典力学的基础,核心是牛顿 第二定律; (2)三个定律相互独立;牛顿第一定律是牛顿 第二定律的前提. 牛顿第一定律定义了惯性系,对力给出了定性 定义(力是改变运动状态的原因). 牛顿第三定律与参考系选择无关. (但第三定律只对接触力严格成立). (3) 质量 引力质量=惯性质量
二、经典力学的相对性原理
(1)惯性系与非惯性系 地球系可近似视为惯性系
x x vt y y (2)伽利略变换式 (不同惯性系之间的变换) z z t t
(3)相对性原理 (不同惯性系之间)
a a
相对性原理的实质:物理定律在不同惯性系是相同的 (物理规律是绝对的)
约束反作用力不作功.
例如 曲面约束的物理意义则表现为曲面的支撑力.
*关于力的属性的说明(3)
保守力、非保守力与耗散力
(线积分)
力的功 W
B
A
B F dr Fx dx Fy dy Fz dz 一般与路径有关.
A
若力的功(线积分)与实际路径无关,仅与始末位置有关, 这种力称为保守力(保守力场). (1)保守力必然存在势能函数
(转动参考系的牵连加速度为 a [ r ( r )] )
(平动参照系的平移加速度为 a0
ma0
)
(3).柯里奥利惯性力 Fc0 2m v
(转动参考系的柯里奥利加速度为aco 2 v
速度矢量方向沿轨道切线方向(运动方向)。
加速度矢量
a lim
t 0
理论力学(周衍柏)第一章质点力学

(1)矢量形式的运动学方程
rr(t)
理论力学:Theoretical mechanics 当质点运动时r是时间t的单值连续函数。此方程常用来 进行理论推导。它的特点是概念清晰,是矢量法分析质点 运动的基础。
(2)直角坐标形式的运动学方程
x x(t)
y
y (t)
z z ( t )
这是常用的运动学方程,尤其当质点的轨迹未知时。它是 代数方程,虽然依赖于坐标系,但是运算容易。
说明: ① 参照物不同,对同一个物体运动的描述结果可能不同;
② 观察者是站在参照系的观察点上; ③ 不特别说明都以地球为参照系。
2. 坐标系
理论力学:Theoretical mechanics 为了定量研究的空间位置,就必须在参考系上建立坐标 系。参照系确定后,在参照系上选择适宜的坐标系,便于 用教学方式描述质点在空间的相对位置(方法)。
ji
解: 确定动系和静系 静系:河岸 动系:河流 研究对象:小船
理论力学:Theoretical mechanics
:0 牵连速度, : 绝对速度, :相 对 速度
ji
由:
0
0
c2i
r d
dt
j
c1 cosi c1 sin
j
i
选取极坐标, 得
理论力学:Theoretical mechanics
0:人行走速度, : 风速(相对于地), :风 相对于人的速
度 由:
得: 理论力学:Theoretical mechanics
得: 解得:
y
2
2
理论力学:Theoretical mechanics
因此:x 4,y 4
风速: x2y2 4 2km/h
理论力学知识总结

学生整理,时间有限,水平有限,仅供参考,如有纰漏,请以老师、课本为主。
第一章质点力学(1)笛卡尔坐标系 位置:k z j y i x ++=r速度:k z j y i x dtr d ...v ++== 加速度:k z j y i x dtv d ......a ++== (2)极坐标系坐标:j i e r θθsin cos += j i e θθθcos sin +-= r e r =r 速度:r r .v = .v θθr =加速度:2...θr r a r -= .....2θθθr r a += (3)自然坐标系(0>θd ) 坐标:ds r d e t =θd e d e t n = θρd ds = 速度:t e v v = 加速度:n t e v e v ρ2.a +=(4)相对运动(5)牛顿运动定律 牛顿第一定律:惯性定律 牛顿第二定律:)(a m v m P dtP d dt v d m F ==== 牛顿第三定律:2112F F -= (6)功、能量vF dt rd F dt dW P rFd dA ⋅=⋅=== (7)(7)有心力第二章 质点动力学的基本定理知识点总结: 质点动力学的基本方程质点动力学可分为两类基本问题:. (1) .已知质点的运动,求作用于质点的力; (2) 己知作用于质点的力,求质点的运动。
动量定理 动量:符号动量定理微分形式动量守恒定律:如果作用在质点系上的外力主失恒等于零,质点系的动量保持不变。
即:质心运动定理:质点对点O 的动量矩是矢量mv r J i ⨯= 质点系对点0的动量矩是矢量i ni nii i i v m r J J ∑∑=⨯==1若z 轴通过点0,则质点系对于z 轴的动量矩为∑==ni z z z J M J ][若C 为质点系的质心,对任一点O 有 c c c J mv r J +⨯=02. 动量矩定理∑∑=⨯=⨯=nie i i n i i i i M F r v m r dt d dt dJ )()( 动量矩守恒:合外力矢量和为零,则动量矩为常矢量。
物理学教程第三版第一章质点运动学

第一章 质点运动学 1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( )(A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r(C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s(D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s(2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v (C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故ts t ΔΔΔΔ≠r ,即|v |≠v . 但由于|d r |=d s ,故ts t d d d d =r ,即|v |=v .由此可见,应选(C). 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ; (2)t d d r ; (3)t s d d ; (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x . 下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;t d d r 表示速度矢量;在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D). 1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a t表示切向加速度.对下列表达式,即(1)d v /d t =a ;(2)d r /d t =v ;(3)d s /d t =v ;(4)d v /d t |=a t.下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的(C) 只有(2)是对的 (D) 只有(3)是对的分析与解td d v 表示切向加速度a t,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用;t r d d 在极坐标系中表示径向速率v r (如题1 -2 所述);t s d d 在自然坐标系中表示质点的速率v ;而t d d v 表示加速度的大小而不是切向加速度a t.因此只有(3) 式表达是正确的.故选(D).1 -4 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -7 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s .求:(1) 质点在运动开始后4.0 s 内的位移的大小;(2) 质点在该时间内所通过的路程;(3) t =4 s 时质点的速度和加速度.分析 位移和路程是两个完全不同的概念.只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等.质点在t 时间内的位移Δx 的大小可直接由运动方程得到:0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据0d d =t x 来确定其运动方向改变的时刻t p ,求出0~t p 和t p ~t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t =4.0 s 时质点速度和加速度可用tx d d 和22d d t x 两式计算.题 1-5 图解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x(2) 由 0d d =tx 得知质点的换向时刻为s 2=p t (t =0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t =4.0 s 时1s0.4s m 48d d -=⋅-==t t x v 2s0.422m.s 36d d -=-==t t x a 1 -8 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求:(1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;分析 质点的轨迹方程为y =f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,(详见题1-1分析).解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为 2412x y -=这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置.(3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x 其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r题 1-6 图 1 -9 质点的运动方程为23010t t x +-=22015t t y -=式中x ,y 的单位为m,t 的单位为s.试求:(1) 初速度的大小和方向;(2) 加速度的大小和方向.分析 由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向.解 (1) 速度的分量式为t tx x 6010d d +-==v t ty y 4015d d -==v 当t =0 时, v 0x =-10 m·s-1 , v 0y =15 m·s-1 ,则初速度大小为 120200s m 0.18-⋅=+=y x v v v设v 0与x 轴的夹角为α,则23tan 00-==x yαv v α=123°41′(2) 加速度的分量式为2s m 60d d -⋅==ta x x v , 2s m 40d d -⋅-==t a y y v 则加速度的大小为 222s m 1.72-⋅=+=y x a a a设a 与x 轴的夹角为β,则 32tan -==x y a a β β=-33°41′(或326°19′)1 -11 质点沿直线运动,加速度a =4 -t2 ,式中a 的单位为m·s-2 ,t 的单位为s.如果当t =3s时,x =9 m,v =2 m·s-1 ,求质点的运动方程.分析 本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决.由t a d d v =和tx d d =v 可得t a d d =v 和t x d d v =.如a =a (t )或v =v (t ),则可两边直接积分.如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分.解 由分析知,应有⎰⎰=t t a 0d d 0v v v 得 03314v v +-=t t (1)由 ⎰⎰=t x x t x 0d d 0v 得 00421212x t t t x ++-=v (2) 将t =3s时,x =9 m,v =2 m·s-1代入(1)、(2)得 v 0=-1 m·s-1, x 0=0.75 m于是可得质点运动方程为75.0121242+-=t t x 1 -20 一半径为0.50 m 的飞轮在启动时的短时间内,其角速度与时间的平方成正比.在t =2.0s 时测得轮缘一点的速度值为4.0 m·s-1.求:(1) 该轮在t′=0.5s的角速度,轮缘一点的切向加速度和总加速度;(2)该点在2.0s内所转过的角度.分析 首先应该确定角速度的函数关系ω=kt 2.依据角量与线量的关系由特定时刻的速度值可得相应的角速度,从而求出式中的比例系数k ,ω=ω(t )确定后,注意到运动的角量描述与线量描述的相应关系,由运动学中两类问题求解的方法(微分法和积分法),即可得到特定时刻的角加速度、切向加速度和角位移.解 因ωR =v ,由题意ω∝t 2 得比例系数322s rad 2-⋅===Rtt ωk v 所以 22)(t t ωω== 则t ′=0.5s 时的角速度、角加速度和切向加速度分别为12s rad 5.02-⋅='=t ω2s rad 0.24d d -⋅='==t tωα 2s m 0.1-⋅==R αa t总加速度n t t n R ωR αe e a a a 2+=+= ()()2222s m 01.1-⋅=+=R ωR αa在2.0s内该点所转过的角度 rad 33.532d 2d 203202200====-⎰⎰t t t t ωθθ 1 -21 一质点在半径为0.10 m 的圆周上运动,其角位置为342t θ+=,式中θ 的单位为rad,t 的单位为s.(1) 求在t =2.0s时质点的法向加速度和切向加速度.(2) 当切向加速度的大小恰等于总加速度大小的一半时,θ 值为多少?(3) t 为多少时,法向加速度和切向加速度的值相等?分析 掌握角量与线量、角位移方程与位矢方程的对应关系,应用运动学求解的方法即可得到.解 (1) 由于342t θ+=,则角速度212d d t tθω==.在t =2 s 时,法向加速度和切向加速度的数值分别为 22s 2s m 30.2-=⋅==ωr a t n2s 2s m 80.4d d -=⋅==t ωr a t t (2) 当22212/t n t a a a a +==时,有223n t a a =,即 ()()422212243t r rt = 得 3213=t此时刻的角位置为 rad 15.3423=+=t θ(3) 要使t n a a =,则有()()422212243t r rt =t =0.55s。
大学_理论力学教程第三版(周衍柏著)课后答案下载

理论力学教程第三版(周衍柏著)课后答案下载理论力学教程第三版内容简介绪论第一章质点力学1.1 运动的描述方法1.2 速度、加速度的分量表示式1.3 平动参考系1.4 质点运动定律1.5 质点运动微分方程1.6 非惯性系动力学(一)1.7 功与能1.8 质点动力学的基本定理与基本守恒定律1.9 有心力小结补充例题思考题习题第二章质点组力学2.1 质点组2.2 动量定理与动量守恒定律2.3 动量矩定理与动量矩守恒定律 2.4 动能定理与机械能守恒定律2.5 两体问题2.6 质心坐标系与实验室坐标系2.7 变质量物体的运动2.8 位力定理小结补充例题思考题习题第三章刚体力学3.1 刚体运动的分析3.2 角速度矢量3.3 欧拉角3.4 刚体运动方程与平衡方程3.5 转动惯量3.6 刚体的平动与绕固定轴的.转动3.7 刚体的平面平行运动3.8 刚体绕固定点的转动__3.9 重刚体绕固定点转动的解 __3.10 拉莫尔进动小结补充例题思考题习题第四章转动参考系4.1 平面转动参考系4.2 空间转动参考系4.3 非惯性系动力学(二)__4.5 傅科摆小结补充例题思考题习题第五章分析力学5.1 约束与广义坐标5.2 虚功原理5.3 拉格朗日方程5.4 小振动5.5 哈密顿正则方程5.6 泊松括号与泊松定理5.7 哈密顿原理5.8 正则变换__5.9 哈密顿-雅可比理论__5.10 相积分与角变数__5.11 刘维尔定理小结补充例题思考题习题附录主要参考书目理论力学教程第三版目录本书是在第二版的基础上修订而成的,适用于高等学校物理类专业的理论力学课程。
本书与第二版相比内容保持不变,仅将科学名词、物理量符号等按照国家标准和规范作了更新。
本书内容包括质点力学、质点组力学、刚体力学、转动参考系及分析力学等,每章附有小结、补充例题、思考题及习题。
理论力学习题

第一章 质点运动学填空1. 在平面极坐标系中,单位向量的微分为: , ,速度的两个分量为 , ,加速度的两个分量为 。
2. 在自然坐标系下,单位向量的微分为: , 速度表示为: ,切向加速度为: ,法向加速度为: 。
3. 点M 沿螺旋线自外向内运动,如图所示。
它走过的弧长与时间的一次方成正比,则点的加速度越来越 (填:大、小、不变),点M 越跑越 (填:快、慢、不变)。
选择题1. 在直角坐标系下,某质点速度随时间的变化为:2234 (m/s)t i t j - ,则在1s 时,质点轨迹的曲率半径ρ= ( ) A. 0 m B. m ∞ C. 1 m D. 5 m计算和证明题:1. 有一作平面曲线运动的质点,其速度在y 轴上的投影于任何时刻均为常数c .试证:任何情况下,加速度的值可用下式表示3v a c ρ= ,其中v 为速率,ρ为轨道曲率半径.M·3. 质点作平面运动,其速率保持为常数.试证此质点速度矢量与加速度矢量相互垂直。
4. 一质点沿抛物线22y px =运动. 其切向加速度的量值为法向加速度量值的2k -倍.如此质点从弦的一端(,)2pp 以速率u 出发,试求其达到正焦弦另一端时的速率.)p )p5,质点沿着半径为r 的圆周运动,其加速度矢量与速度矢量间的夹角α保持不变。
求:(1),质点的速率随时间而变化的规律,(2),质点速率关于速度与x 之间夹角θ之间的函数关系。
已知初始时,速率为0v ,速度与x 轴夹角为0θ。
6,如图所示,细长杆A 端沿半径为R 的半圆槽底滑动,杆紧靠槽边以角速度ω倒下。
求:当杆与x 轴的夹角为ϕ时,杆的端点A 和杆上与槽边的接触点C 的速度。
开始时A 点在半圆槽底端A 0处。
x第二章 质点动力学填空题1.如果运动质点所受的力的作用线始终通过某一定点,我们称此力为有心力,而这个定点叫 。
2. 在直角坐标系下,某质点的动量为:32cos te i t j -- ,则作用在质点上的力F= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上举力(与空气阻力一样的公式)为: f CSv2
式中C为比例常数, S为翅膀的面积,飞翔的条件
f mg ,即 v mg CS
我们作简单的几何相似性假设,设鸟的几何线度为l,质
量m ~ l3, S ~l2,于是起飞的临界速度 vc l
燕子最小滑翔速度大约20km/h,鸵鸟体长是燕子的大约 25倍,显然它要飞翔的速度最少是燕子的5倍, 这是飞机 的起飞速度, 鸵鸟奔跑的速度实际上只有40km/h.
P
tt0,坐标原点重合 vx
z z
x x vt
y y
y y
z z
正变换
t t
z z t t
逆变换
伽利略变换中默认了绝对时空
速度变换: dxd(xv)td(xv)t
dt dt
dt
x轴方向有相 对匀速运动
u x u x v u y u y u z u z
对于描述力学规律而言,一切惯性系都是平权 的、等价的.
在一个惯性系中所做的任何力学实验,都不能 判断该惯性系相对于其他惯性系的运动.
舟行不觉
《关于托勒密和哥白尼两大世界体系的对话》伽利略 1632
(ii) 牛顿的绝对时空观
绝对的空间,就其本性而言,是与任何外界 事物无关而永远相同和不动的. 绝对的、真正的和数学的时间自身在流逝着, 而且由于其本性而均匀地与任何外界事物无 关地流逝着.
牛顿第三定律
FabFba
注意:二力同性质,共存亡, 分于两物,处于同一直线.
力学相对性原理 力学定律的数学形式在一切惯性系中不变。
伽利略变换
x x vt y y z z t t
正变换
x x vt y y z z t t
逆变换
y y
S S' vt
O O'
z z
P x x
u u v
i
注意:质点 惯性系 瞬时性 矢量性
牛顿第三定律
FabFba
注意:作用力和反作用力施加在两个不同的物体上,它们属同一 性质的力,并互以对方的存在为自己存在的前提.它们同时产生, 同时消灭,相互依存,形成对立的局面.
例 鸵鸟是当今世界上最大的鸟,有人说它不会飞是翅 膀的退化. 但是如果它长一副和身体成比例的翅膀,它 能飞起来吗?
第一章 质点力学
动力学的主要内容
研究物体的机械运动与作用力之间的关系
动力学所涉及的研究内容包括:
1. 动力学第一类问题——已知系统的运动, 求作用在系统上的力. 2. 动力学第二类问题——已知作用在系统上 的力,求系统的运动.
1 牛顿运动定律
牛顿第一定律 任何物体如果没有受到其他物体的作用时,都将保 持静止状态或匀速直线运动状态. ——惯性定律
惯性: 物体保持其运动状态不变的性质 力: 物体间相互作用
它不仅说明了物体具有惯性的性质,还为整个力学 体系选定了一类特殊的参考系——惯性参考系
惯性系与非惯性系
y´
a
T
x´
F
mg
惯性系 牛顿定律成立的参考系
非惯性系 相对于惯性系作加速运动的参考系
牛顿第二定律
F
dp
dt
动量: pmv
F Fi
思考问题:
•拔河比赛胜负的关键是什么?
摩擦力的大小,大者赢
•马德堡半球是用两队各8匹马向相反方向 拉开的,如果一端拴在固定物上,另一端 需要几匹马,才能拉开半球? 还是8匹 •大人国是否能够存在, 利用几何相似性分析之. 不可能, 重力就会压坏他.
2 力学相对性原理和伽利略变换
(i) 力学相对性原理 力学定律的数学形式在一切惯性系中不变.
空间有相对 匀速运动
uuv
加速度变换: aa
经典力学规律具有伽利略变换不变性:
S 系 : F m a S 系 : F m a
小结
牛顿第一定律
任何物体如果没有受到其他物体的作用,都将保持
静止状态或匀速直线运动状态. 惯性定律
牛顿第二定律
F
dp
dt
动量: pmv
F Fi
i
注意:质点 惯性系 瞬时性 矢量性
aa
—— 牛顿
长度的量度和时间的量度都与参考系无关 !?
(iii) 伽利略变换
在两个惯性系中考察 同一物理事件
y y
S S' vt
O O'
z z
两个惯性系: s s
P x x
一物理事件: 质点到达 P 点 两个惯性系的描述分别为:
(x, y,z,t) (x,y,z,t)
两个描述的关系称为变换
y y
S S'
