新观察八年级数学(下册)第十七章反比例函数(附答案)
华师大版八年级下册数学第17章 函数及其图象含答案
华师大版八年级下册数学第17章函数及其图象含答案一、单选题(共15题，共计45分)1、如图，直线与x轴、y轴分别相交于点A、B，过点B作，使，将绕点O顺时针旋转，每次旋转，则第2021次旋转结束时，点C的对应点落在反比例函数的图象上，则k 的值为（）A.-4B.4C.-6D.62、函数y=的图象经过（1，-1），则函数y=kx-2的图象是（）A. B. C. D.3、如图，CB=1，且OA=OB，BC⊥OC，则点A在数轴上表示的实数是（）A. B.﹣ C. D.﹣4、动点P从（0，3）出发，沿所示的方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，当点P第2014次碰到长方形的边时，点P的坐标为（）A.（1，4）B.（5，0）C.（6，4）D.（8，3）5、若式子有意义，则点P（a，b）在（）A.第一象限B.第二象限C.第三象限D.第四象限6、对于一次函数y=kx+b(k，b为常数)，下表中给出5组自变量及其对应的函数值，其中恰好有一个函数值计算有误，则这个错误的函数值是（）x -1 0 1 2 3y 2 5 8 12 14A.5B.8C.12D.147、一个反比例函数与一个一次函数在同一坐标平面内的图像如图示，如果其中的反比例函数解析式为，那么该一次函数可能的解析式是（）A. B. C. D.8、不论m取何实数，抛物线y=2（x+m）2+m的顶点一定在下列哪个函数图象上（）A.y=2x 2B.y=-xC.y=-2xD.y=x9、圆的周长公式为C=2πr，下列说法正确的是（）A.π是自变量B.π和r都是自变量C.C是π的自变量D.C是r的自变量10、在平面直角坐标系中，点P的坐标为（﹣2，a2+1），则点P所在的象限是（）A.第一象限B.第二象限C.第三象限D.第四象限11、函数的图象经过点(2，8)，则下列各点不在图象上的是( )A.(4，4)B.(-4，-4)C.(8，2)D.(-2，8)12、如图，在平面直角坐标系中，Rt△ABC的顶点A，B分别在y轴、x轴上，OA=2，OB=1，斜边AC∥x轴，若反比例函数y= (k>0，x>0)的图象经过AC的中点D，则k的值为（）A.4B.5C.6D.813、下列函数中，是一次函数的有（）个．①y=x；②y=；③y=+6；④y=3﹣2x；⑤y=3x2．A.1B.2C.3D.414、矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（）A.（3，1）B.（3，）C.（3，）D.（3，2）15、如图反映的过程是小明从家去食堂吃早餐，接着去图书馆读报，然后回家．其中x表示时间，y表示小明离家的距离，小明家、食堂、图书馆在同一直线上．根据图中提供的信息，有下列说法：（1）食堂离小明家0.4km；（2）小明从食堂到图书馆用了3min；（3）图书馆在小明家和食堂之间；（4）小明从图书馆回家的平均速度是0.04km/min．其中正确的有（）A.4个B.3个C.2个D.1个二、填空题(共10题，共计30分)16、在平面直角坐标系xOy中，对于不在坐标轴上的任意一点P(x，y)，我们把点P′称为点P的“倒影点”．直线y＝－x＋1上有两点A，B，它们的“倒影点”A′，B′均在反比例函数y＝的图象上．若AB＝2 ，则k＝________．17、如图，和都是等腰直角三角形，,反比例函数在第一象限的图象经过点B，若，则的值为________.18、一次函数y=-2x+b中，当x=1时，y<1；当x=-1时，y>0，则b的取值范围是________。
初二数学反比例函数试题答案及解析
初二数学反比例函数试题答案及解析1. 如图，矩形AOBC 中，顶点C 的坐标（4，2），又反比例函数y ＝的图像经过矩形的对角线的交点P ，则该反比例函数关系式是（ ）A ．y ＝（x ＞0）B ．y ＝（x ＞0）C ．y ＝（x ＞0）D ．y ＝（x ＞0）【答案】B【解析】过P 点作PE ⊥x 轴于E ，PF ⊥y 轴于F ，如图， ∵四边形OACB 为矩形，点P 为对角线的交点， ∴S 矩形OEPF =S 矩形OACB =×8=2． ∴k=2．∴反比例函数关系式为y=（x ＞0）， 故选：B ．【考点】反比例函数图象上点的坐标特征2. 已知反比例函数y=的图象上有三个点（2，）,(3,),(,),则，，的大小关系是（ ） A ．＞＞ B ．＞＞ C ．＞＞D ．＞＞【答案】A.【解析】试题解析：∵-k 2-1＜0 ∴反比例函数y=的图象在第二、四象限∴＞＞ 故选A.【考点】反比例函数图象上点的坐标特征．3. 已知长方形的面积为10，则它的长y 与宽x 之间的关系用图象大致可表示为图中的（ ）A ．B ．C ．D ．【答案】A【解析】由长方形的面积公式得y=，且x ＞0，y ＞0，而B 中有x ＜0，y ＜0的情况，C ，D 中有x=0或y=0的情况，据此即可得出结果． 解：∵xy=10∴y=，（x＞0，y＞0）故选A．点评：现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用实际意义确定其所在的象限．4.下列函数中，y是x的反比例函数的是（）A．y=﹣B．y=﹣C．y=D．y=【答案】B【解析】此题应根据反比例函数的定义，解析式符合y=（k≠0）的形式为反比例函数．解：A、是正比例函数，故错误；B、是反比例函数，故正确；C、不符合反比例函数的定义，故错误；D、不符合反比例函数的定义，故错误．故选B．点评：本题考查反比例函数的定义，熟记反比例函数解析式的一般式（k≠0）是解决此类问题的关键．5.已知一次函数y=x+2与反比例函数y=（x≠﹣1）的图象在第一象限内的交点为P（x，3）．（1）求x的值；（2）求反比例函数的解析式．【答案】（1）x=1 （2）y=【解析】（1）先把P点坐标代入一次函数解析式得到得x0+2=3，然后解一次方程可得到x的值；（2）先写出P点坐标，然后把P点坐标代入反比例解析式求出m即可．解：（1）把P（x0，3）代入y=x+2得x+2=3，解得x=1；（2）P点坐标为（1，3），把P（1，3）代入y=得m+1=1×3=3，解得m=2，故反比例函数的解析式为y=．点评：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了待定系数法求函数解析式．6.如图是我们学过的反比例函数图象，它的函数解析式可能是（）A．B．C．D．【答案】B【解析】反比例函数的性质：当时，图象在第一、三象限，在每一象限内，y随x的增大而减小；当时，图象在第二、四象限，在每一象限内，y随x的增大而增大.由图可得它的函数解析式可能是故选B.【考点】反比例函数的性质点评：反比例函数的性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.7.如果函数的图象是双曲线，且在第二、四象限内，求k的值.【答案】-2【解析】反比例函数的性质：当时，图象在第一、三象限，在每一象限内，y随x的增大而减小；当时，图象在第二、四象限，在每一象限内，y随x的增大而增大.∵该函数的图象是双曲线且在第二、四象限∴，解得∴.【考点】反比例函数的性质点评：反比例函数的性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.8.如图，平行于y轴的直尺（一部分）与双曲线（）交于点、，与轴交于点、，连结,, ，点、的刻度分别为5、2（单位：），直尺的宽度为，．（1）试求反比例函数的解析式和点的坐标；（2）试求的面积．【答案】（1），；（2）【解析】（1）由题意得AB=5－2＝3，即可求得点A纵坐标为3，再结合OB=2cm可求得点A 的坐标，从而可以求得反比例函数的解析式，再根据点C的横坐标即可求得C点的坐标；（2）由根据三角形、梯形的面积公式求解即可.（1）由题意得AB=5－2＝3，∴点A纵坐标为3又∵OB=2cm∴点A的坐标是（2，3）．∴k＝6∴反比例函数的解析式为∵点C的横坐标是4，把x＝4代入得，，∴C点坐标为；（2）∴.【考点】反比例函数的性质点评：反比例函数的性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.9.已知y与x+2成反比例，且当x=5时，y=-6，求：（1）y与x的关系式；（2）当y=2时x的值。
八年级下册数学第十七章反比例函数单元测试二(附答案)c
八年级下册数学第十七章反比例函数单元测试二（附答案）学校:___________姓名：___________班级：___________考号：___________一、选择题1．如图1，已知函数x k y 11=与函数xk y 22=的图象交于A 、B 两点，过点A 作 AC ⊥y 轴于C ，过点B 作BD ⊥y 轴于D ，连接AD 、BC ．若四边形ACBD 的面积是4，则2k 的值是 （ ）A ．8B ．4C ．2D ．12．反比例函数xk y 1-=的图像经过点（-2，3)则k 的值是（ ） A. -5 B. -6 C. -7 D.上述答案都不对3．若A （x 1，y 1），B （x 2，y 2），C （x 3，y 3）是反比例函数y=图象上的点，且x 1＜x 2＜0＜x 3，则y 1、y 2、y 3的大小关系正确的是（ ） A 、y 3＞y 1＞y 2 B 、y 1＞y 2＞y 3 C 、y 2＞y 1＞y 3D 、y 3＞y 2＞y 14．如图，反比例函数的图象经过点A （﹣1，﹣2）．则当x ＞1时，函数值y 的取值范围是（ ）A 、y ＞1B 、0＜y ＜lC 、y ＞2D 、0＜y ＜25．如图，正方形ABOC 的边长为2，反比例函数ky x =图像过点A ，则k 的值是xy ABO 图1C DA 、2B 、2-C 、4D 、4-6．已知：点()m m A ,在反比例函数x y 4=的图象上，点B 与点A 关于坐标轴对称，以AB为边作正方形，则满足条件的正方形的个数是A ． 4B ． 5C ． 3D ．87．如图，反比例函数()0ky x x=>的图象经过矩形OABC 对角线的交点M ，分别与AB BC 、相交于点.D E 、若四边形ODBE 的面积为6，则k 的值为A ．1 B. 2 C. 3 D. 48．在边长为1的4×4方格上建立直角坐标系（如图甲），在第一象限内画出反比例函数x y 16=、x y 6=、xy 4=的图象，它们分别经过方格中的一个格点、二个格点、三个格点；在边长为1的10×10方格上建立直角坐标系（如图乙），在第一象限内画出反比例函数的图象，使它们经过方格中的三个或四个格点，则最多可画出几条 ( )A ． 12B ． 13 C．25 D ． 509．下列函数表达式中，属于反比例函数的是（ ） A ．1-=x y B ．x y 1=C ．122+-=x y D ．2y x =甲乙x y C OA B10．如果双曲线xky =经过点（2-，3），那么此双曲线也经过点（ ） （A ）)3,2(-- （B ）)2,3( （C ）)2,3(- （D ）)2,3(-- 二、填空题11．在函数x y 3-= 的图象上有两个点（－2，1y ），(－1，2y ),则函数值1y ，2y ，的大小为 .12．如图，已知矩形OABC的面积是3100，它的对角线OB 与双曲线)0(＞x xky =交于点D ，且OB:OD ＝5:3，则=k ．13．函数的图象如图所示，则结论：①两函数图象的交点A 的坐标为（3,3)；②当；④当x 逐渐增大时,随着x 的增大而减小．其中正确结论的序号是____ _.yy 1＝xy 2＝9xx14．如图，已知矩形OABC 的面积为3100，它的对角线OB 与双曲线x k y =相交于点D ，且OB ∶OD ＝5∶3，则k ＝____________．15．如图，已知双曲线(0)ky x x=>经过矩形OABC 过AB 的中点F ，交BC 于点E ，且四边形OEBF 的面积为2，则k =________．16．已知正比例函数kx y =与反比例函数()0>=k xky 的一个交点是（2，3），则另一个交点是 . 三、计算题17．（8分）函数xy 6=的图象如图所示．（1）),(y x P n （12n =，，）是第一象限内图象上的点，且x y ，都是整数．求出所有的点()n P x y ，；（2）若P （m ，y 1），Q(-3，y 2)是函数xy 6=图象上的两点，且y 1> y 2，求实数m 的取值范围．18．如图，已知反比例函数（m 是常数，m≠0），一次函数y=ax+b （a 、b 为常数，a≠0），其中一次函数与x 轴，y 轴的交点分别是A （﹣4，0），B （0，2）． （1）求一次函数的关系式；（2）反比例函数图象上有一点P 满足：①PA ⊥x 轴；②PO=（O 为坐标原点），求反比例函数的关系式；（3）求点P 关于原点的对称点Q 的坐标，判断点Q 是否在该反比例函数的图象上．四、解答题19．(10分)如图，已知一次函数y ＝kx ＋b 的图象交反比例函数42(0)my x x-=>的 图象于点A 、B ，交x 轴于点C ． (1)求m 的取值范围；(2)若点A 的坐标是(2，－4)，且 ，求m 的值和一次函数的解析式．20．右图中曲线是反比例函数xn y 7+=的图象的一支． （1）这个反比例函数图象的另一支位于哪个象限？常数n 的取值范围是什么？（2）若一次函数3432+-=x y 的图象与反比例函数的图象交于点A ，与x 轴交于点B ，△AOB 的面积为2，求n 的值．21．某小学为每个班级配备了一种可以加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热，每分钟水温上升10ºC ，待加热到100ºC ，饮水机自动切断电源，水温开始下降，水温和时间成反比例关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温为20ºC ，接通电源后，水温和时间的关系下图所示，回答下列问题； （1）分别求出0≤x ≤8和8＜x ≤a 时，y 和x 之间的关系式； （2）求出图中a 的值．（3）下表是该小学的作息时间，若同学们希望在上午第一节下课8：20时能喝到不超过 40ºC 的开水，已知第一节下课前无人接水，请直接写出生活委员应该在什么时间或时间段接通饮水机电源（不可以用上课时间）．22．已知反比例函数ky x =的图象经过点A （1，3）．（1）试确定此反比例函数的解析式； （2）当x =2时, 求y 的值；（3）当自变量x 从5增大到8时，函数值y 是怎样变化的？23．（本题满分5分） 如图，反比例函数8y x=的图象过矩形OABC 的顶点B ，OA 、OC 分别在x 轴、 y 轴的正半轴上，OA ：OC=2：1．（1）设矩形OABC 的对角线交于点E ，求出E 点的坐标； （2）若直线2y x m =+平分矩形OABC 面积，求m 的值．时间 节次 上午[来源:21世纪教育网] 7：20 到校21世纪教育网 7：45~8：20 第一节 8：30~9：05 第二节 …… …… 8 a x /miny /ºC100 20O24．据媒体报道，近期“手足口病”可能进入发病高峰期，某校根据《学校卫生工作条例》，为预防“手足口病”，对教室进行“薰药消毒”．已知药物在燃烧机释放过程中，室内空气中每立方米含药量y （毫克）与燃烧时间x （分钟）之间的关系如图所示（即图中线段OA 和双曲线在A 点及其右侧的部分），根据图象所示信息，解答下列问题： （1）写出从药物释放开始，y 与x 之间的函数关系式级自变量的取值范围；（2）据测定，当空气中每立方米的含药量低于2毫克时，对人体无毒害作用，那么从消毒开始，至少在多长时间内，师生不能进入教室？25．（6分）给出下列命题：命题1：直线x y =与双曲线x y 1=有一个交点是（1，1）； 命题2：直线x y 8=与双曲线xy 2=有一个交点是（21，4）；命题3：直线x y 27=与双曲线xy 3=有一个交点是（31，9）；命题4：直线x y 64=与双曲线xy 4=有一个交点是（41，16）；……………………………………………………（1）请你阅读、观察上面命题，猜想出命题n （n 为正整数）； （2）请验证你猜想的命题n 是真命题．参考答案1．C 2．A 3．A 4．D 5．D 6．B 7．B 8．B 9．B 10．C 11．12y y12．12 13．①③④ 14．12 15．216．（-2，-3）17．解：（1）因为),(y x P n 是第一象限内的图象上点，且x y ，都是整数．所以x 只能取1，2，3，6．………………………………………1分当x=1时，y=6；当x=2时，y=3；当x=3时，y=2；当x=6时，y=1；………3分 所以所有的点分别为P 1（1，6），P 2（2，3），P 3（3，2），P 4（6，1）…4分（2） 当P （m ，y 1）在第一象限时，均有y 1> y 2，此时m>0，…………………… 5分 当P （m ，y 1）在第三象限时，当m<-3时有y 1> y 2， ………………………7分 所以实数m 的取值范围为：m>0或m<-3。
初二数学反比例函数试题答案及解析
初二数学反比例函数试题答案及解析1.如图，在平面直角坐标系中，双曲线经过点B，连结OB．将OB绕点O按顺时针方向旋转90°并延长至A，使OA＝2OB，且点A的坐标为（4，2）．（1）求过点B的双曲线的函数关系式；（2）根据反比例函数的图像，指出当x＜－1时，y的取值范围；（3）连接AB，在该双曲线上是否存在一点P，使得S△ABP ＝S△ABO，若存在，求出点P坐标；若不存在，请说明理由．【答案】（1）双曲线的函数关系式为y=﹣；（2）当x＜﹣1时，0＜y＜2；（3）存在；点P坐标为（﹣，4）．【解析】（1）作AM⊥x轴于点M，BN⊥x轴于点N，由相似三角形的判定定理得出△AOM∽△OBN，OA=2OB，再根据OA=2OB，点A的坐标为（4，2）可得出B点坐标，进而得出反比例函数的关系式；（2）由函数图象可直接得出结论；（3）根据AB两点的坐标可知AB∥x轴，S△ABP =S△ABO=5，再分当点P在AB的下方与当点P在x轴上方两种情况即可得出结论．试题解析：（1）作AM⊥x轴于点M，BN⊥x轴于点N，∵OB⊥OA，∠AMO=∠BNO=90°，∴∠AOM=∠NBO，∴△AOM∽△OBN．∵OA=2OB，∴，∵点A的坐标为（4，2），∴BN=2，ON=1，∴B（﹣1，2）．∴双曲线的函数关系式为y=﹣；（2）由函数图象可知，当x＜﹣1时，0＜y＜2；（3）存在．∵yA =yB，∴AB∥x轴，∴S△ABP =S△ABO=5，∴当点P在AB的下方时，点P恰好在x轴上，不合题意舍去；当点P在x轴上方时，点P在第二象限，得AB•（yP ﹣2）=5，即×5×（yP﹣2）=5，解得yP=4，∴点P坐标为（﹣，4）．【考点】1、相似三角形的判定与性质；2、待定系数法；3、函数大小的比较；4、反比例函数2.如图，直线y=x﹣1与反比例函数y=的图象交于A、B两点，与x轴交于点C，已知点A的坐标为（﹣1，m）．⑴求反比例函数的解析式；⑵若点P（n，-1）是反比例函数图象上一点，过点P作PE⊥x轴于点E，延长EP交直线AB于点F，求△CEF的面积．⑶若B（2,1），当x为何值时，一次函数的值大于反比例函数的值【答案】（1）反比例函数解析式为：y=；=．（2）S△CEF（3）当x＞2或- 1＜x＜0时，一次函数的值大于反比例函数的值．【解析】（1）将点A的坐标代入直线解析式求出m的值，再将点A的坐标代入反比例函数解析式可求出k的值，继而得出反比例函数关系式；（2）将点P的纵坐标代入反比例函数解析式可求出点P的横坐标，将点P的横坐标和点F的横坐标相等，将点F的横坐标代入直线解析式可求出点F的纵坐标，将点的坐标转换为线段的长度后，即可计算△CEF的面积；（3）直接根据图像即可得到．试题解析：（1）将点A的坐标代入y=x﹣1，可得：m=﹣1﹣1=﹣2，将点A（﹣1，﹣2）代入反比例函数y=，可得：k=﹣1×（﹣2）=2，故反比例函数解析式为：y=；（2）将点P的纵坐标y=﹣1，代入反比例函数关系式可得：x=﹣2，将点F的横坐标x=﹣2代入直线解析式可得：y=﹣3，故可得EF=3，CE=OE+OC=2+1=3，=CE×EF=．故可得S△CEF（3）根据图象可知：当x＞2或- 1＜x＜0时，一次函数的值大于反比例函数的值，【考点】反比例函数与一次函数的交点问题．3.某函数具有下列性质：①图像在二、四象限内；②在每个象限内，函数值随自变量的增大而增大．则其函数解析式可以为．【答案】y=．【解析】首先根据题意可得此函数可以是反比例函数，并且k<0，所以函数解析式可以为：y=．故答案是y=．【考点】反比例函数的性质．4.已知，与成反比例，与成正比例，并且当时，，当时，．（1）求关于的函数关系式；（6分）（2）当时，求的值．（4分）【答案】（1）y关于x的函数关系式为y=+4（x﹣2）；（2）y=5．【解析】（1）根据正比例函数和反比例函数的定义，可设y1=，y2=b（x﹣2），则y=﹣b（x﹣2），再把x=3时，y=5，当x=1时，y=﹣1得到关于a和b的方程组，解方程组得到a=3，b=﹣4，所以y=+4（x﹣2）；（2）把x=代入y=+4（x﹣2）中，计算出对应的函数值即可．试题解析：（1）设y1=，y2=b（x﹣2），则y=﹣b（x﹣2），根据题意得，解得，所以y关于x的函数关系式为y=+4（x﹣2）；（2）把x=代入y=+4（x﹣2）得y=12+4×（﹣2）=5．【考点】待定系数法求反比例函数解析式．5.如图，反比例函数（x＞0）的图象经过矩形OABC对角线的交点M，分别于AB、BC交于点D、E，若四边形ODBE的面积为9，则k的值为（）A．1 B．2 C．3 D．4【答案】C.【解析】试题解析：由题意得：E、M、D位于反比例函数图象上，则S△OCE =，S△OAD=，过点M作MG⊥y轴于点G，作MN⊥x轴于点N，则S□ONMG=|k|，又∵M为矩形ABCO对角线的交点，∴S矩形ABCO=4S□ONMG=4|k|，由于函数图象在第一象限，k＞0，则++9=4k，解得：k=3．故选C.【考点】反比例函数系数k的几何意义．6.下列函数中，y是x的反比例函数的是（）A．y=﹣B．y=﹣C．y=D．y=【答案】B【解析】此题应根据反比例函数的定义，解析式符合y=（k≠0）的形式为反比例函数．解：A、是正比例函数，故错误；B、是反比例函数，故正确；C、不符合反比例函数的定义，故错误；D、不符合反比例函数的定义，故错误．故选B．点评：本题考查反比例函数的定义，熟记反比例函数解析式的一般式（k≠0）是解决此类问题的关键．7.函数yl=x（x≥0），（x＞0）的图象如图所示，则结论：①两函数图象的交点A的坐标为（3，3）；②当x＞3时，y2＞y1；③当x=1时，BC=8；④当x逐渐增大时，yl随着x的增大而增大，y2随着x的增大而减小．其中正确结论的序号是．【答案】①③④【解析】逐项分析求解后利用排除法求解．①可列方程组求出交点A的坐标加以论证．②由图象分析论证．③根据已知先确定B、C点的坐标再求出BC．④由已知和函数图象分析．解：①根据题意列解方程组，解得，；∴这两个函数在第一象限内的交点A的坐标为（3，3），正确；②当x＞3时，y1在y2的上方，故y1＞y2，错误；③当x=1时，y1=1，y2==9，即点C的坐标为（1，1），点B的坐标为（1，9），所以BC=9﹣1=8，正确；④由于y1=x（x≥0）的图象自左向右呈上升趋势，故y1随x的增大而增大，y 2=（x＞0）的图象自左向右呈下降趋势，故y2随x的增大而减小，正确．因此①③④正确，②错误．故答案为：①③④．点评：本题考查了一次函数和反比例函数图象的性质．解决此类问题的关键是由已知和函数图象求出正确答案加以论证．8.如图，一次函数y=2x﹣2的图象与x轴、y轴分别相交于B、A两点，与反比例函数的图象在第一象限内的交点为M（3，m）．（1）求反比例函数的解析式；（2）在x轴上是否存在点P，使AM⊥PM？若存在，求出点P的坐标；若不存在，说明理由．【答案】（1）y=（2）存在．理由见解析【解析】（1）先把M（3，m）代入y=2x﹣2求出m，确定M点的坐标，然后利用待定系数法确定反比例函数解析式；（2）先确定A点坐标为（0，﹣2），B点坐标为（1，0），再根据勾股定理计算出AB=；根据M点坐标得到MC=4，BC=2，则利用勾股定理可计算出BM=2，然后证明Rt△OBA∽Rt△MBP，利用相似比计算出BP，于是可确定P点坐标．解：（1）把M（3，m）代入y=2x﹣2得m=2×3﹣2=4，∴M点坐标为（3，4），把M（3，4）代入y=得k=3×4=12，∴反比例函数的解析式为y=；（2）存在．作MC⊥x轴于C，如图，把x=0代入y=2x﹣2得y=﹣2；把y=0代入y=2x﹣2得2x﹣2=0，解得x=1，∴A点坐标为（0，﹣2），B点坐标为（1，0），∴OA=2，OB=1，在Rt△OAB中，AB==，∵M点坐标为（3，4），∴MC=4，BC=3﹣1=2，在Rt△MBC中，MB==2，∵MA⊥MB，∴∠BMP=90°，而∠OBA=∠MBP，∴Rt△OBA∽Rt△MBP，∴=，即=，∴BP=10，∴OP=11，∴点P的坐标为（11，0）．点评：本题考查了反比例函数的综合题：掌握反比例函数图象上点的坐标特征和待定系数法确定函数解析式；熟练运用勾股定理和相似比进行几何计算．9.如图，反比例函数的图象与一次函数y=mx+b的图象交于A（1，3），B（n，﹣1）两点．（1）求反比例函数与一次函数的解析式；（2）根据图象回答：当x取何值时，反比例函数的值大于一次函数的值．（3）求△AOB 的面积．【答案】（1）y= y=x+2 （2）x ＜﹣3或0＜x ＜1 （3）4【解析】（1）把A （1，3）代入反比例函数即可得到k=3，然后把B （n ，﹣1）代入y=求出n ，再把A 点和B 点坐标代入y=mx+b 中得到关于m 、b 的方程组，然后解方程组即可；（2）观察图象可得到当x ＜﹣3或0＜x ＜1时，反比例函数的图象都在一次函数的图象的上方； （3）先求出直线AB 与x 轴的交点C 的坐标，则S △OAB =S △OAC +S △OBC ，然后利用三角形的面积公式计算即可．解：（1）把A （1，3）代入反比例函数，∴k=1×3=3，∴反比例函数的解析式为y=， 把B （n ，﹣1）代入y=得，n=﹣3，∴点B 的坐标为（﹣3，﹣1），把A （1，3）、点B （﹣3，﹣1）代入一次函数y=mx+b 得，m+b=3，﹣3m+b=﹣1，解得m=1，b=2，∴一次函数的解析式为y=x+2；（2）当x ＜﹣3或0＜x ＜1时，反比例函数的值大于一次函数的值； （3）连OA 、OB ，直线AB 交x 轴与C 点，如图， 对于y=x+2，令y=0，x=﹣2， ∴C 点坐标为（﹣2，0），∴S △OAB =S △OAC +S △OBC =×2×3+×2×1=4．点评：本题考查了反比例函数与一次函数的交点问题：同时满足反比例函数的解析式和一次函数的解析式的点的坐标为它们图象的交点坐标．也考查了待定系数法求函数的解析式以及坐标轴上点的坐标特点．10. 已知点A(1，2)在反比例函数y=的图象上，则该反比例函数的解析式是( ) A ．y=B ．y=C ．y=D ．y=2x【答案】C【解析】由点A(1，2)在反比例函数y=的图象上根据待定系数法即可求得结果. 解：∵点A(1，2)在反比例函数y=的图象上 ∴∴该反比例函数的解析式是y= 故选C.【考点】待定系数法求函数关系式点评：待定系数法求函数关系式是初中数学的重点，是中考中比较常见的知识点，一般难度不大，需熟练掌握.11.当k＜0，反比例函数和一次函数的图象大致是（）【答案】B【解析】根据反比例函数和一次函数的性质分析即可.解：因为k＜0，所以反比例函数的图象经过第二、四象限，一次函数的图象经过第二、三、四象限，符合条件的只有B选项，故选B.【考点】反比例函数和一次函数的图象点评：解题的关键是熟练掌握一次函数的性质：当时，图象经过第一、二、三象限；当时，图象经过第一、三、四象限；当时，图象经过第一、二、四象限；当时，图象经过第二、三、四象限.12.若y－2与x成反比例且当x＝3时y＝1，则y与x之间函数关系式为。
新人教版初中数学8年级下册17章17.1.2反比例函数的图象和性质同步测控优化训练(含答案)
反比率函数的图象和性质一、课前预习 (5 分钟训练 )1.什么是反比率函数 ?2.判断下边哪些式子表示y 是 x 的反比率函数？为何？(1)xy=1 ； (2)y=5 － x ；(3)y=2 ； (4)y=2a(a 为常数且 a ≠ 0).35xx3.已知反比率函数y= k的图象经过点（ 2,3），则在每一象限内 ,y 随 x 的增大而 __________.x4.画出反比率函数y=6和 y=6 的图象 .xx二、课中加强 (10分钟训练 )1.假如反比率函数y=k的图象经过点 (－3,4),那么 k 的值是 ()x43A.－ 12B.12C.D.342.如图 ,某闭合电路中 ,电源的电压为定值,电流 I(A) 与电阻 R( Ω)成反比率 .右图表示的是该电路中电流 I 与电阻 R 之间关系的图象,则用电阻 R 表示电流 I 的函数关系式为 ()2366A.I=B.I=C.I=D.I=R R R Rk3.函数 y=x(k ≠ 0)的图象如下图,那么函数y=kx － k 的图象大概是 ()4.以下图给出了反比率函数y=2和 y=2的图象，你知道哪一个是y=2的图象吗？3x3x3x____.5.已知反比率函数y=3m 2，当 m_____________ 时，其图象的两个分支在第一、三象限x内；当 m_____________ 时，其图象在每个象限内y 随 x 的增大而增大 .6.直线 y=2x 与双曲线y= k的一个交点坐标为(2，4),则它们的另一个交点坐标是__________. x三、课后稳固 (30分钟训练 )1.若点 (－ 2,y )、 (1,y2 )、 (2,y )都在反比率函数 y=的图象上 ,则有 ()131xA.y ＞ y ＞ yB.y ＞ y ＞ y2C.y ＞ y ＞ yD.y ＞ y ＞ y312313312212.已知一个矩形的面积为 24 cm 2，其长为 y cm ，宽为 x cm ，则 y 与 x 之间的函数关系的图象大概是 ()3.已知函数 y=k的图象过点 A(6, － 1),则以下点中不在该函数图象上的点是()xA.( － 2,3)B.(－ 1,－ 6)C.(1,－ 6)D.(2, － 3)4.已知 k ＞ 0，则函数 y=kx 、 y=k的图象大概是以下图中的 ()xk5.反比率函数 y=x(k ＞ 0)在第一象限的图象如下图，点M 是图象上一点，MP 垂直 x 轴于点 P ，假如△ MOP 的面积为 1，那么 k 的值是 ()A.1B.2C.3D.46.已知反比率函数的图象必定经过点 (－ 3， 4) ，则这个函数分析式是 _____________.7.请你写出一个反比率函数 ,使它的图象在第二、四象限 :_____________.8.已知反比率函数 y= k的图象与直线y=2x 和 y=x+1 的图象过同一点 (1，2) ，则当 x ＞0 时，x这个反比率函数值 y 随 x 的增大而 _____________ (填增大或减小 ).9.已知双曲线 y=3k，在每个象限内，自变量x 渐渐增大， y 的值也跟着渐渐增大，那么xk 的取值范围为 _____________.10.已知正比率函数y=kx 与反比率函数 y=3的图象都过点 A(m ， 1)，求此正比率函数分析x式及另一个交点的坐标 .参照答案一、课前预习(5 分钟训练 )1.什么是反比率函数 ?答案 :一般地，形如 y= k(k 是常数， k ≠ 0)的函数叫做反比率函数 .x2.判断下边哪些式子表示y 是 x 的反比率函数？为何？(1)xy=1 ； (2)y=5 － x ；(3)y=2 ； (4)y=2a(a 为常数且 a ≠ 0).35xkx答案 :(1)(3)(4) 是反比率函数，由于(1)(3)(4) 是形如 y= (k 是常数， k ≠ 0)的函数； (2)不是x反比率函数，由于 (2) 不是形如 y= k(k 是常数， k ≠ 0)的函数 .x3.已知反比率函数y= k的图象经过点（ 2,3），则在每一象限内 ,y 随 x 的增大而 __________.x答案 :减小4.画出反比率函数y=6和 y=6 的图象 .xx分析：（ 1）列表：x－6－5－4－3－2－11 234566－－y=－2 －3 － 6 6321.51.21－ 1x 1.2 1.5y=6 1.21.523 6 － 6 － 3 － 2 － 1.5 － 1.2 － 11x（2）描点 .(3) 连线 ,图象如图 .二、课中加强 (10 分钟训练 )1.假如反比率函数 y= k的图象经过点 (－ 3,4), 那么 k 的值是 ()x4 3 A. － 12 B.12 C.D.34分析： 将 (－ 3,4)的坐标代入 y= k,得 k= －12.x答案： A2.如图 ,某闭合电路中 ,电源的电压为定值 ,电流 I(A) 与电阻 R( Ω)成反比率 .右图表示的是该电路中电流 I 与电阻 R 之间关系的图象 ,则用电阻 R 表示电流 I 的函数关系式为 ()2 3 6 6 A.I=B.I=C.I=D.I=RRRR分析： 设 I=k,将(3,2) 代入即得 k=6.R答案 :Ck3.函数 y=x(k ≠ 0)的图象如下图 ,那么函数 y=kx － k 的图象大概是 ( )解 :y= k在二、四象限 ,因此 k ＜ 0,则 y=kx － k 向左倾斜 ,与 y 轴交于正半轴.x答案 :C4.以下图给出了反比率函数 y=2和 y=2 的图象，你知道哪一个是 y=2 的图象吗？3x3x3x____.分析 :反比率函数 y=2 的图象在第一、三象限，而反比率函数y= 2 的图象在第二、3x3x四象限 .答案 :(2)5.已知反比率函数y=3m 2，当 m_____________ 时，其图象的两个分支在第一、三象限x内；当 m_____________ 时，其图象在每个象限内y 随 x 的增大而增大 .分析 :若使反比率函数y=3m 2的图象的两个分支在第一、三象限内， 需使 3m － 2＞ 0，2x3m 2的图象在每个象限内即 m；若使反比率函数 y=y 随 x 的增大而增大，需使3 2x3m －2＜ 0，即 m.2 2 3答案 :3 36.直线 y=2x 与双曲线 y= k的一个交点坐标为 (2，4),则它们的另一个交点坐标是__________.xy= k 上，因此 4= k，得 k=8，则它与分析 :由于点 (2， 4)在双曲线y=2x 构成方程组x28x 2,x -2,y, 解得(－ 2，－ 4).x y4 或y -4, 因此另一个交点坐标是y 2x,答案 :(－2，－ 4)三、课后稳固 (30 分钟训练 )1.若点 (－ 2,y )、 (1,y 2 )、 (2,y )都在反比率函数 y=的图象上 ,则有 ()131xA.y ＞ y 2＞ yB.y ＞ y ＞ y2C.y ＞ y ＞ yD.y ＞ y ＞ y313 1331221分析 :由于 y=1在第四象限内随 x 的增大 y 增大 ,又知道 1＜ 2,因此 y 2＜ y 3.而(－ 2,y 1) 在x第二象限 ,故 y 1＞ 0,因此 y 1＞ y 3＞ y 2.答案 :B2.已知一个矩形的面积为24 cm 2，其长为 y cm ，宽为 x cm ，则 y 与 x 之间的函数关系的图分析 :依据矩形面积公式得 y=24，此中 k=24 ＞ 0，x ＞ 0，因此函数关系的图象大概是答x案D 的图象.答案 :D3.已知函数 y=k的图象过点 A(6, － 1),则以下点中不在该函数图象上的点是()xA.( － 2,3)B.(－ 1,－ 6)C.(1,－ 6)D.(2, － 3)分析 :将点 A(6, － 1)代入 y= k,得 k= － 6,再将四个选择项点坐标代入分析式考证,两坐标x之积不为－ 6 的即不在图象上 .答案 :Bk 的图象大概是以下图中的 ()4.已知 k ＞ 0，则函数 y=kx 、 y=x分析 :当 k ＞ 0 时正比率函数 y=kx 的图象经过原点和一、三象限，而反比率函数y= －kx的图象在二、四象限，因此选C.选项 A 的正比率函数y=kx 的图象经过原点和二、四象限，则 k ＜0.选项 B 的反比率函数y= － k的图象在一、三象限，则－k ＞ 0,即 k ＜0.选项xD 的错误和选项 A 、 B 的错误同样 .答案 :Ck 5.反比率函数y=(k ＞ 0)在第一象限的图象如下图， 点 M 是图象上一点， MP 垂直 x 轴于x点 P ，假如△ MOP 的面积为 1，那么 k 的值是 ( )A.1B.2C.3D.4分析 :△ MOP 的面积等于1 的坐标为 (x 11OP ×PM=1 ，假如设点 M， y ),由于反比率函数k211因此 OP=|x 1|=x 1，PM=|y 1|=y 1 ，即 y=(k ＞ 0)的图象在第一象限，×OP ×PM=x 1y 1=1.x22因此 k=x 1y 1=2.答案 :B6.已知反比率函数的图象必定经过点(－ 3， 4) ，则这个函数分析式是 _____________.分析 :设反比率函数分析式为y= k，当 x= － 3 时 ,y=k =4，解得 k= －12，因此这个函12 x3数分析式是 y=.答案 :y=12xx7.请你写出一个反比率函数 ,使它的图象在第二、四象限 :_____________.分析 :在二、四象限的反比率函数所拥有的性质是 k ＜0.答案 :y=1(不独一 ,k ＜0 即可 )xy= k的图象与直线8.已知反比率函数 y=2x 和 y=x+1 的图象过同一点 (1，2) ，则当 x ＞0 时，x这个反比率函数值 y 随 x 的增大而 _____________ (填增大或减小 ).分析 :先求直线 y=2x 和 y=x+1 的图象的交点为 (1，2)，把点 (1，2)代入反比率函数y= k中 ,x得 k=2，因此 x ＞ 0 时这个反比率函数值 y 随 x 的增大而减小 .答案 :减小9.已知双曲线 y=3 k，在每个象限内，自变量x 渐渐增大， y 的值也跟着渐渐增大，那么xk 的取值范围为 _____________.分析 :若使双曲线 y=3 k在每个象限内自变量x 渐渐增大， y 的值也跟着渐渐增大， 则x3－ k ＜ 0，得 k ＞ 3. 答案 :k ＞ 310.已知正比率函数 y=kx 与反比率函数 y=3的图象都过点A(m ， 1)，求此正比率函数分析x式及另一个交点的坐标 .解 : ∵y= 3的图象过 A(m ， 1)点，则 1=3 ， xm∴m=3，即 A(3 ， 1).将 A(3 ， 1)代入 y=kx ，得 k= 1，3∴正比率函数分析式为y= 1 x . 3又1x 3 ,∴x=±3. 3x当 x=3 时， y=1 ；当 x= － 3 时， y= － 1.∴另一交点为 (－ 3，－ 1).。
八年级数学下册 第十七章 反比例函数单元综合测试(含解析) 新人教版
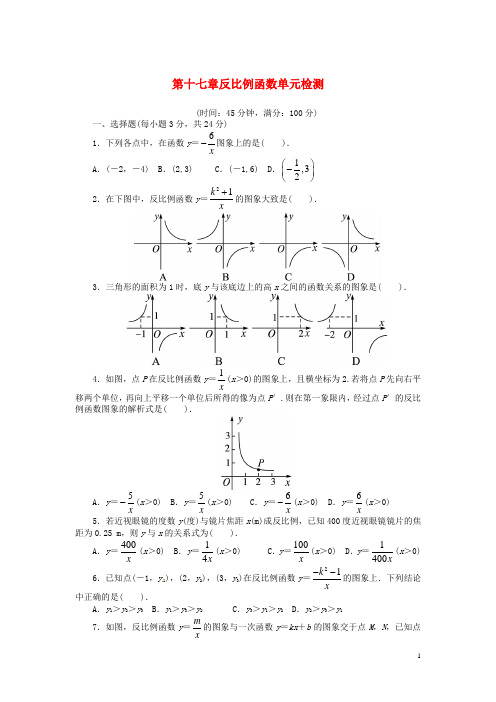
第十七章反比例函数单元检测(时间：45分钟，满分：100分)一、选择题(每小题3分，共24分)1．下列各点中，在函数y ＝6x-图象上的是( )． A ．(－2，－4) B ．(2,3) C ．(－1,6) D ．1,32⎛⎫- ⎪⎝⎭2．在下图中，反比例函数y ＝21k x+的图象大致是( )．3．三角形的面积为1时，底y 与该底边上的高x 之间的函数关系的图象是( )．4．如图，点P 在反比例函数y ＝1x(x ＞0)的图象上，且横坐标为2.若将点P 先向右平移两个单位，再向上平移一个单位后所得的像为点P ′.则在第一象限内，经过点P ′的反比例函数图象的解析式是( )．A ．y ＝5x -(x ＞0) B ．y ＝5x(x ＞0) C ．y ＝6x -(x ＞0) D ．y ＝6x(x ＞0) 5．若近视眼镜的度数y (度)与镜片焦距x (m)成反比例，已知400度近视眼镜镜片的焦距为0.25 m ，则y 与x 的关系式为( )．A ．y ＝400x(x ＞0) B ．y ＝14x (x ＞0)C ．y ＝100x (x ＞0) D ．y ＝1400x (x ＞0) 6．已知点(－1，y 1)，(2，y 2)，(3，y 3)在反比例函数y ＝21k x--的图象上．下列结论中正确的是( )．A ．y 1＞y 2＞y 3B ．y 1＞y 3＞y 2C ．y 3＞y 1＞y 2D ．y 2＞y 3＞y 17．如图，反比例函数y ＝mx的图象与一次函数y ＝kx ＋b 的图象交于点M ，N ，已知点M 的坐标为(1,3)，点N 的纵坐标为－1，根据图象信息可得关于x 的方程mx＝kx ＋b 的解为( )．A ．－3,1B ．－3,3C ．－1,1D ．3，－18．在平面直角坐标系中，直线y ＝6－x 与函数y ＝4x(x ＞0)的图象相交于A ，B 两点，设点A 的坐标为(x 1，y 1)，那么长为x 1，宽为y 1的矩形面积和周长分别为( )．A ．4,12B ．8,12C ．4,6D ．8,6 二、填空题(每小题4分，共20分)9．已知反比例函数y ＝kx 的图象经过点(1，－2)，则k ＝__________. 10．如图是反比例函数y ＝kx(k ≠0)在第二象限内的图象，若图中的矩形OABC 的面积为2，则k ＝__________.11．如图，反比例函数y ＝kx的图象位于第一、三象限，其中第一象限内的图象经过点A (1,2)，请在第三象限内的图象上找一个你喜欢的点P ，你选择的P 点坐标为__________．12．过反比例函数y ＝kx(k ≠0)图象上一点A ，分别作x 轴，y 轴的垂线，垂足分别为B ，C ，如果△ABC 的面积为3，则k 的值为__________．13．双曲线y 1、y 2在第一象限的图象如图所示，y 1＝4x，过y 1上的任意一点A ，作x 轴的平行线交y 2于B ，交y 轴于C ，若S △AOB ＝1，则y 2的解析式是__________．三、解答题(共56分)14．(本小题满分10分)如图所示，在平面直角坐标系中，一次函数y ＝kx ＋1的图象与反比例函数y ＝9x的图象在第一象限相交于点A ，过点A 分别作x 轴、y 轴的垂线，垂足分别为点B ，C ．如果四边形OBAC 是正方形，求一次函数的关系式．15．(本小题满分10分)由物理知识知道，在力F (N)的作用下，物体会在力F 的方向上发生位移s (m)，力F 所做的功W (J)满足：W ＝Fs .当W 为定值时，F 与s 之间的函数图象如图所示．(1)力F 所做的功是多少？(2)试确定F 与s 之间的函数表达式； (3)当F ＝4 N 时，s 是多少？16．(本小题满分12分)已知如图中的曲线是反比例函数y ＝5mx(m 为常数)图象的一支．(1)求常数m 的取值范围；(2)若该函数的图象与正比例函数y ＝2x 的图象在第一象限的交点为A (2，n )，求点A 的坐标及反比例函数的解析式．17．(本小题满分12分)如图所示，一次函数y ＝ax ＋b (a ≠0)的图象与反比例函数y ＝kx(k ≠0)的图象交于M ，N 两点．(1)求反比例函数与一次函数的解析式；(2)根据图象写出使反比例函数的值大于一次函数的值的x的范围．18．(本小题满分12分)给出下列命题：命题1：点(1,1)是直线y＝x与双曲线y＝1x的一个交点；命题2：点(2,4)是直线y＝2x与双曲线y＝8x的一个交点；命题3：点(3,9)是直线y＝3x与双曲线y＝27x的一个交点；…….(1)请观察上面命题，猜想出命题n(n是正整数)；(2)证明你猜想的命题n是正确的．参考答案1. 答案：C2. 答案：D3. 答案：C4. 答案：D5. 答案：C 设y ＝k x ，将(0.25,400)代入y ＝kx，得k ＝100， ∴y ＝100x(x ＞0)． 6. 答案：B 因为－k 2－1＜0，所以反比例函数y ＝21k x--的图象在第二、四象限，(2，y 2)，(3，y 3)在同一象限，y 随x 的增大而增大，即y 2＜y 3＜0，又y 1＞0，所以y 1＞y 3＞y 2.7. 答案：A 由M (1,3)代入y ＝mx得，m ＝3，所以y ＝3x ，将N 点纵坐标－1代入y ＝3x，得x ＝－3. 所以N (－3，－1)，根据图象的意义知，方程mx＝kx ＋b 的解就是它们的交点坐标的横坐标，所以方程的解为－3或1.8. 答案：A 因为y ＝6－x 与函数y ＝4x的图象相交于A ，B ，则有点A (x 1，y 1)的坐标满足两个关系式y 1＝6－x 1，y 1＝14x ，且x 1＞0，y 1＞0. 所以长为x 1，宽为y 1的矩形面积为x 1y 1＝4，矩形周长为2(y 1＋x 1)＝2×6＝12，故选A. 9. 答案：－2 10. 答案：－211. 答案：答案不唯一，如(－1，－2) x ，y 满足xy ＝2且x ＜0，y ＜0即可． 12. 答案：6或－6 根据反比例函数的几何意义可得出S △ABC ＝12|k |，所以|k |＝6，则k ＝±6.13. 答案：y 2＝6x y 1＝4x，过y 1上的任意一点A ，作x 轴的平行线交y 2于B ，交y 轴于C ，S △AOB ＝1.∴△CBO 面积为3，∴y 2的解析式是y 2＝6x. 14. 解：∵S 正方形OBAC ＝OB 2＝9，∴OB ＝AB ＝3， ∴点A 的坐标为(3,3)．∵点A 在一次函数y ＝kx ＋1的图象上， ∴3k ＋1＝3，解得k ＝23. ∴一次函数的关系式是y ＝23x ＋1. 15. 解：(1)W ＝Fs ＝2×7.5＝15(J)．(2)F ＝15s. (3)当F ＝4 N 时，s ＝15154F =＝3.75(m)． 16. 解：(1)∵这个反比例函数的图象分布在第一、三象限，∴5－m ＞0，解得m ＜5.(2)∵点A (2，n )在正比例函数y ＝2x 的图象上， ∴n ＝2×2＝4，则A 点的坐标为(2,4)． 又∵点A 在反比例函数y ＝5mx-的图象上， ∴4＝52m-，即5－m ＝8. ∴反比例函数的解析式为y ＝8x. 17. 分析：(1)利用点N 的坐标可求出反比例函数的表达式，据此求点M 的坐标．由两点M ，N 的坐标可求出一次函数的表达式；(2)反比例函数的值大于一次函数的值表现在图象上，就是双曲线在直线的上方，由此可求出x 的范围．解：(1)把N (－1，－4)代入y ＝k x 中，得－4＝1k -， 所以k ＝4.反比例函数的表达式为y ＝4x. 又点M (2，m )在双曲线上，所以m ＝2，即点M (2,2)．把M (2,2)，N (－1，－4)代入y ＝ax ＋b 中，得22,4.a b m a b +=⎧⎨-+=-⎩解得2,2.a b =⎧⎨=-⎩故一次函数的表达式为y ＝2x －2.(2)由图象可知，当x ＜－1或0＜x ＜2时，反比例函数的值大于一次函数的值．18. 解：(1)命题n ：点(n ，n 2)是直线y ＝nx 与双曲线y ＝3n x的一个交点(n 是正整数)．(2)把2,x n y n=⎧⎨=⎩代入y ＝nx ，左边＝n 2，右边＝n ·n ＝n 2， ∵左边＝右边，∴点(n ，n 2)在直线上．同理可证：点(n ，n 2)在双曲线上，∴点(n ，n 2)是直线y ＝nx 与双曲线y ＝3n x的一个交点，命题正确．。
初二数学反比例函数试题答案及解析
初二数学反比例函数试题答案及解析1.如图，过反比例函数图象上的一点A，作x轴的垂线，垂足为B点，则．【答案】4．【解析】根据反比例函数k的几何意义可得：S=k=4．△AOB故答案是4．【考点】反比例函数系数k的几何意义．2.某函数具有下列性质：①图像在二、四象限内；②在每个象限内，函数值随自变量的增大而增大．则其函数解析式可以为．【答案】y=．【解析】首先根据题意可得此函数可以是反比例函数，并且k<0，所以函数解析式可以为：y=．故答案是y=．【考点】反比例函数的性质．3.如图，一次函数y=2x﹣2的图象与x轴、y轴分别相交于B、A两点，与反比例函数的图象在第一象限内的交点为M（3，m）．（1）求反比例函数的解析式；（2）在x轴上是否存在点P，使AM⊥PM？若存在，求出点P的坐标；若不存在，说明理由．【答案】（1）y=（2）存在．理由见解析【解析】（1）先把M（3，m）代入y=2x﹣2求出m，确定M点的坐标，然后利用待定系数法确定反比例函数解析式；（2）先确定A点坐标为（0，﹣2），B点坐标为（1，0），再根据勾股定理计算出AB=；根据M点坐标得到MC=4，BC=2，则利用勾股定理可计算出BM=2，然后证明Rt△OBA∽Rt△MBP，利用相似比计算出BP，于是可确定P点坐标．解：（1）把M（3，m）代入y=2x﹣2得m=2×3﹣2=4，∴M点坐标为（3，4），把M（3，4）代入y=得k=3×4=12，∴反比例函数的解析式为y=；（2）存在．作MC⊥x轴于C，如图，把x=0代入y=2x﹣2得y=﹣2；把y=0代入y=2x﹣2得2x﹣2=0，解得x=1，∴A点坐标为（0，﹣2），B点坐标为（1，0），∴OA=2，OB=1，在Rt△OAB中，AB==，∵M点坐标为（3，4），∴MC=4，BC=3﹣1=2，在Rt△MBC中，MB==2，∵MA⊥MB，∴∠BMP=90°，而∠OBA=∠MBP，∴Rt△OBA∽Rt△MBP，∴=，即=，∴BP=10，∴OP=11，∴点P的坐标为（11，0）．点评：本题考查了反比例函数的综合题：掌握反比例函数图象上点的坐标特征和待定系数法确定函数解析式；熟练运用勾股定理和相似比进行几何计算．4.如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（）A． 12米B． 13米C．14米D．15米【答案】A【解析】根据梯子、地面、墙正好构成直角三角形，再根据勾股定理解答即可．解：如图所示，AB=13米，BC=5米，根据勾股定理AC===12米．故选A．点评：此题是勾股定理在实际生活中的运用，比较简单．5.若点A（﹣2，a），B（﹣1，b），C（3，c）在双曲线（k＞0）上，则a、b、c的大小关系为（用“＜”将a、b、c连接起来）．【答案】b＜a＜c【解析】根据题意，易得a、b、c的值，比较可得答案．解：根据题意，易得a=﹣，b=﹣k，c=，又由k＞0，易得b＜a＜c．故答案为b＜a＜c．点评：本题考查反比例函数图象上的点的特点，同一反比例函数图象上点的横纵坐标的积为同一常数．6.已知点A(1，2)在反比例函数y=的图象上，则该反比例函数的解析式是( )A．y=B．y=C．y=D．y=2x【答案】C【解析】由点A(1，2)在反比例函数y=的图象上根据待定系数法即可求得结果.解：∵点A(1，2)在反比例函数y=的图象上∴∴该反比例函数的解析式是y=故选C.【考点】待定系数法求函数关系式点评：待定系数法求函数关系式是初中数学的重点，是中考中比较常见的知识点，一般难度不大，需熟练掌握.7.两个反比例函数，在第一象限内的图像如图所示，点，，，…，在函数的图像上，它们的横坐标分别是，，，…，，纵坐标分别是1，3，5，…，共2013个连续奇数，过点，，，…，分别作y轴的平行线，与函数的图像交点依次是（，），（，），（，），…，（，），则 .【答案】【解析】因为点P1，P2，P3，…，P2010在反比例函数图象上，根据P1，P2，P3的纵坐标，推出P2010的纵坐标，再根据和的关系求解即可．解：∵P1，P2，P3的纵坐标为1，3，5，是连续奇数∴Pn 的纵坐标为：2n-1∴P2013的纵坐标为2×2013-1=4025∵与在横坐标相同时，的纵坐标是的纵坐标的2倍∴．【考点】找规律-坐标的变化点评：解题的关键是仔细分析所给图形的特征得到规律，再根据得到的规律解题即可.8.如图，正方形OABC的面积为9，点O为坐标原点B在函数的图象上，点P （m，n）在的图象上任意一点，过P分别作x轴y轴的垂线，垂足分别是E，F，并设长方形OEPF和正方形OABC不重合部分的的面积为S。
初二数学反比例函数试题答案及解析
初二数学反比例函数试题答案及解析1.如图，经过原点的两条直线、分别与双曲线相交于A、B、P、Q四点，其中A、P两点在第一象限，设A点坐标为（3，1）．（1）求值及点坐标；（4分）（2）若P点坐标为（a，3），求a值及四边形APBQ的面积；（4分）（3）若P点坐标为（m，n），且，求P点坐标．（4分）【答案】（1）k=3，B点坐标为（﹣3，﹣1）；（2）a=1，四边形APBQ的面积为16；（3P点坐标为（1，3）．【解析】（1）根据分别莲花山图象上点的坐标特征得到k=3×1=3，再根据正比例函数图象和反比例函数图象的性质得到点A与点B关于原点对称，则B点坐标为（﹣3，﹣1）；（2）根据反比例函数图象上点的坐标特征得到a=1，即P点坐标为（1，3），再根据正比例函数图象和反比例函数图象的性质得到点P与点Q关于原点对称，所以点Q的坐标为（﹣1，﹣3），由于OA=OB，OP=OQ，则根据平行四边形的判定得到四边形APBQ为平行四边形，然后根据两点间的距离公式计算出AB，PQ，可得到即AB=PQ，于是可判断四边形APBQ为矩形，再计算出PA和PB，然后计算矩形APBQ的面积；（3）由于四边形APBQ为平行四边形，加上∠APB=90°，则可判断四边形APBQ为矩形，则OP=OA，根据两点间的距离公式得到m2+n2=10，且mn=3，则利用完全平方公式得到（m+n）2﹣2mn=10，可得到m+n=4，根据根与系数的关系可把m、n看作方程x2﹣4x+3=0的两根，然后解方程可得到满足条件的P点坐标．试题解析：（1）把A（3，1）代入y=得k=3×1=3，∵经过原点的直线l与双曲线y=（k≠0）相交于A、B、1∴点A与点B关于原点对称，∴B点坐标为（﹣3，﹣1）；（2）把P（a，3）代入y=得3a=3，解得a=1，∵P点坐标为（1，3），∵经过原点的直线l与双曲线y=（k≠0）相交于P、Q点，2∴点P与点Q关于原点对称，∴点Q的坐标为（﹣1，﹣3），∵OA=OB，OP=OQ，∴四边形APBQ为平行四边形，∵AB2=（3+3）2+（1+1）2=40，PA2=（1+1）2+（3+3）2=40，∴AB=PQ，∴四边形APBQ为矩形，∵PB 2=（1+3）2+（3+1）2=32，PQ2=（3﹣1）2+（1﹣3）2=8，∴PB=4，PQ=2，∴四边形APBQ的面积=PA•PB=2•4=16；（3）∵四边形APBQ为平行四边形，而∠APB=90°，∴四边形APBQ为矩形，∴OP=OA，∴m2+n2=32+12=10，而mn=3，∵（m+n）2﹣2mn=10，∴（m+n）2=16，解得m+n=4或m+n=﹣4（舍去），把m、n看作方程x2﹣4x+3=0的两根，解得m=1，n=3或m=3，n=1（舍去），∴P点坐标为（1，3）．【考点】反比例函数综合题．2.如图，反比例函数（x＞0）的图象经过矩形OABC对角线的交点M，分别于AB、BC交于点D、E，若四边形ODBE的面积为9，则k的值为（）A．1 B．2 C．3 D．4【答案】C.【解析】试题解析：由题意得：E、M、D位于反比例函数图象上，则S△OCE =，S△OAD=，过点M作MG⊥y轴于点G，作MN⊥x轴于点N，则S□ONMG=|k|，又∵M为矩形ABCO对角线的交点，∴S矩形ABCO=4S□ONMG=4|k|，由于函数图象在第一象限，k＞0，则++9=4k，解得：k=3．故选C.【考点】反比例函数系数k的几何意义．3.如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（）A． 12米B． 13米C．14米D．15米【答案】A【解析】根据梯子、地面、墙正好构成直角三角形，再根据勾股定理解答即可．解：如图所示，AB=13米，BC=5米，根据勾股定理AC===12米．故选A ．点评：此题是勾股定理在实际生活中的运用，比较简单．4. 某厂现有300吨煤，这些煤能烧的天数y 与平均每天烧的吨数x 之间的函数关系是（ ） A ．（x ＞0）B ．（x≥0）C ．y=300x （x≥0）D ．y=300x （x ＞0）【答案】A【解析】这些煤能烧的天数=煤的总吨数÷平均每天烧煤的吨数，把相关数值代入即可． 解：∵煤的总吨数为300，平均每天烧煤的吨数为x ， ∴这些煤能烧的天数为y=（x ＞0），故选：A ．点评：此题主要考查了根据实际问题列反比例函数关系式，得到这些煤能烧的天数的等量关系是解决本题的关键．5. 如图，反比例函数的图象与一次函数y=mx+b 的图象交于A （1，3），B （n ，﹣1）两点．（1）求反比例函数与一次函数的解析式；（2）根据图象回答：当x 取何值时，反比例函数的值大于一次函数的值．（3）求△AOB 的面积．【答案】（1）y= y=x+2 （2）x ＜﹣3或0＜x ＜1 （3）4【解析】（1）把A （1，3）代入反比例函数即可得到k=3，然后把B （n ，﹣1）代入y=求出n ，再把A 点和B 点坐标代入y=mx+b 中得到关于m 、b 的方程组，然后解方程组即可；（2）观察图象可得到当x ＜﹣3或0＜x ＜1时，反比例函数的图象都在一次函数的图象的上方； （3）先求出直线AB 与x 轴的交点C 的坐标，则S △OAB =S △OAC +S △OBC ，然后利用三角形的面积公式计算即可．解：（1）把A （1，3）代入反比例函数，∴k=1×3=3，∴反比例函数的解析式为y=， 把B （n ，﹣1）代入y=得，n=﹣3，∴点B 的坐标为（﹣3，﹣1），把A （1，3）、点B （﹣3，﹣1）代入一次函数y=mx+b 得，m+b=3，﹣3m+b=﹣1，解得m=1，b=2，∴一次函数的解析式为y=x+2；（2）当x ＜﹣3或0＜x ＜1时，反比例函数的值大于一次函数的值； （3）连OA 、OB ，直线AB 交x 轴与C 点，如图， 对于y=x+2，令y=0，x=﹣2，∴C 点坐标为（﹣2，0），∴S △OAB =S △OAC +S △OBC =×2×3+×2×1=4．点评：本题考查了反比例函数与一次函数的交点问题：同时满足反比例函数的解析式和一次函数的解析式的点的坐标为它们图象的交点坐标．也考查了待定系数法求函数的解析式以及坐标轴上点的坐标特点．6. 已知点A(1，2)在反比例函数y=的图象上，则该反比例函数的解析式是( ) A ．y=B ．y=C ．y=D ．y=2x【答案】C【解析】由点A(1，2)在反比例函数y=的图象上根据待定系数法即可求得结果. 解：∵点A(1，2)在反比例函数y=的图象上 ∴∴该反比例函数的解析式是y=故选C.【考点】待定系数法求函数关系式点评：待定系数法求函数关系式是初中数学的重点，是中考中比较常见的知识点，一般难度不大，需熟练掌握.7. 如图，正方形ABOC 的面积为4，反比例函数的图象过点A ，则k ＝ ．【答案】—4 【解析】反比例函数中k 的几何意义，即过双曲线上任意一点引x 轴、y 轴垂线，所得矩形面积为．解：依题意得， 又∵图象位于第二象限， ∴ ∴．【考点】反比例函数中k 的几何意义点评：本题属于基础应用题，只需学生熟练掌握反比例函数中k 的几何意义，即可完成.8. 如图，在平面直角坐标系中，已知点在双曲线上，轴于D ，轴于，点在轴上，且，则图中阴影部分的面积之和为A ．6B ．12C ．18D ．24【答案】B【解析】过A 作AG 垂直于x 轴，交x 轴于点G ，由AO=AF ，利用三线合一得到G 为OF 的中点，根据等底同高得到三角形AOD 的面积等于三角形AFD 的面积，再由A ，B 及C 三点都在反比例函数图象上，根据反比例的性质得到三角形BOD ，三角形COE 及三角形AOG 的面积都相等，都为，由反比例解析式中的k 值代入，求出三个三角形的面积，根据阴影部分的面积等于三角形BOD 的面积+三角形COE 的面积+三角形AOG 的面积+三角形AFG 的面积=4三角形AOD 的面积，即为2|k|，即可得到阴影部分的面积之和．解：过A 作AG ⊥x 轴，交x 轴于点G∵AO=AF ，AG ⊥OF ，∴G 为OF 的中点，即OG=FG ， ∴S △OAG =S △FAG ，又A ，B 及C 点都在反比例函数上，∴S △OAG =S △BOD =S △COE ==3，∴S △OAG =S △BOD =S △COE =S △FAG =3，则S 阴影=S △OAG +S △BOD +S △COE +S △FAG =12， 故选B ．【考点】反比例函数的性质，等腰三角形的性质，三角形的面积公式 点评：反比例函数（k≠0）图象上的点到坐标轴的垂线，此点到原点的连线及坐标轴围成的直角三角形的面积等于，熟练掌握此性质是解本题的关键．9. 如图所示，设A 为反比例函数图象上一点，且矩形ABOC 的面积为3，则这个反比例函数解析式为 .【答案】【解析】由矩形ABOC 的面积为3根据反比例函数系数k 的几何意义可得，再根据图象在第二象限即可求得结果.解： 因为矩形ABOC 的面积为3 所以，解得 因为图象在第二象限， 所以， 所以这个反比例函数解析式为．【考点】反比例函数系数k 的几何意义点评：反比例函数系数k 的几何意义：过双曲线上任意一点引x 轴、y 轴垂线，所得矩形面积为．10.如图，点A（m，m＋1），B（m＋1，2m－3）都在反比例函数的图象上．（1）求m，k的值；（2）如果M为x轴上一点，N为y轴上一点，以点A，B，M，N为顶点的四边形是平行四边形，试求直线MN的函数表达式．【答案】（1）m＝3，k＝12；（2）或【解析】（1）根据反比例函数图象上的点的坐标的特征可得，即可求得结果；（2）存在两种情况，①当M点在x轴的正半轴上，N点在y轴的正半轴上时，②当M点在x轴的负半轴上，N点在y轴的负半轴上时，根据平行四边形的性质求解即可.（1）由题意可知，解得m1＝3，m2＝－1（舍去）∴A（3，4），B（4，3）；∴k＝4×3＝12；（2）存在两种情况，如图：①当M点在x轴的正半轴上，N点在y轴的正半轴上时，设M1点坐标为（x1，0），N1点坐标为（0，y1）．∵四边形AN1M1B为平行四边形，∴线段N1M1可看作由线段AB向左平移3个单位，再向下平移3个单位得到的由（1）知A点坐标为（3，4），B点坐标为（4，3），∴N1点坐标为（0，1），M1点坐标为（1，0）设直线M1N1的函数表达式为，把x＝1，y＝0代入，解得．∴直线M1N1的函数表达式为；②当M点在x轴的负半轴上，N点在y轴的负半轴上时，设M2点坐标为（x2，0），N2点坐标为（0，y2）．∵AB∥N1M1，AB∥M2N2，AB＝N1M1，AB＝M2N2，∴N1M1∥M2N2，N1M1＝M2N2．∴线段M2N2与线段N1M1关于原点O成中心对称．∴M2点坐标为（-1，0），N2点坐标为（0，-1）．设直线M2N2的函数表达式为，把x＝-1，y＝0代入，解得，∴直线M2N2的函数表达式为所以，直线MN的函数表达式为或．【考点】反比例函数的综合题点评：此类问题难度较大，在中考中比较常见，一般在压轴题中出现，需特别注意.11.如图，点A（x1，y1）、B（x2，y2）都在双曲线上，且，；分别过点A、B向x轴、y轴作垂线段，垂足分别为C、D、E、F，AC与BF相交于G点，四边形FOCG的面积为2，五边形AEODB的面积为14，那么双曲线的解析为 ．【答案】【解析】根据S 矩形AEOC =S 矩形OFBD =（S 五边形AEODB -S △AGB -S 四边形FOCG ）+S 四边形FOCG ，先求得S 矩形AEOC 和S 矩形OFBD 的值，利用k=AE•AC=FB•BD 即可求得函数解析式． ∵x 2-x 1=4，y 1-y 2=2 ∴BG=4，AG=2 ∴S △AGB =4∵S 矩形AEOC =S 矩形OFBD ，四边形FOCG 的面积为2即AE•AC=6 ∴.【考点】反比例函数与一次函数的性质点评：此题难度稍大，综合性比较强，注意反比例函数上的点向x 轴y 轴引垂线形成的矩形面积等于反比例函数的k 值．12. 如图，正方形OABC 的面积为9，点O 为坐标原点B 在函数的图象上，点P （m ，n ）在的图象上任意一点，过P 分别作x 轴y 轴的垂线，垂足分别是E ，F ，并设长方形OEPF 和正方形OABC 不重合部分的的面积为S 。