梁坤京理论力学第十二章动量矩定理课后答案
动量矩定理
分离变量
d (Jω) = −M ， M = kω dt
上式积分
J dω = −kdt ω
ωo
∫2
ω0
J
dω ω
=
∫
t 0
−
kdt
解得
t = J 1n2
k
再对式（1）积分，将等式左边积分上限改为ω ，得
ω
∫ ω0 J
dω ω
=
∫
t 0
−
kdt
解得
ω
=
ω
0
e
−k J
t
即
dθ dt
−k t
= ω0e J
∫ θ =
FT1 = FT′1
FT2 = FT′2
以顺时针转向为正，分别应用两轮对其转动轴的转动微分方程有
J1α1 = M − (FT1 − FT2 )R1
J 2α 2
=
( FT1′
−
FT
′
2
)R2
−M′
α1 : α 2 = R2 : R1
（1）
（2） （3）
159
理论力学（第七版）课后题答案 哈工大.高等教育出版社
计算在此 3 种情况下，圆盘对轴 O 的动量矩。
2R
2R
ω0 O
vA R A
ω0 ωr O
vA A ωr
(b1)
(c1)
图 12-2
解 （1）在图 12-2a 中，轮 A 绕 O 定轴转动
JO
=
1 2
mR 2
+
m(2R)2
=
9 2
mR 2
LO
=
J OωO
=
9 2
ω
O
第十二章动能定理习题解答
第十二章动能定理习题解答习题12–1一刚度系数为k的弹簧，放在倾角为的斜面上。
弹簧的上端固定，下端与质量为m的物块A相连，图12-23所示为其平衡位置。
如使重物A从平衡位置向下沿斜面移动了距离，不计摩擦力，试求作用于重物A上所有力的功的总和。
图12-23Wmgink2(t(t)2)2kmginkt22k2212–2如图12-24所示，在半径为r的卷筒上，作用一力偶矩M=a+b2，其中为转角，a和b为常数。
卷筒上的绳索拉动水平面上的重物B。
设重物B的质量为m，它与水平面之间的滑动摩擦因数为不计绳索质量。
当卷筒转过两圈时，试求作用于系统上所有力的功的总和。
图12-244π0WMMd(a+b2)d8aπ2643bπ3WFmg4πr4πmgr644W8aπ2bπ34πmgrπ(6πa16π2b3mgr)3312–3均质杆OA长l，质量为m，绕着球形铰链O的铅垂轴以匀角速度转动，如图12-25所示。
如杆与铅垂轴的夹角为，试求杆的动能。
图12-2511mmdEk(dm)v2(d某)(某in)2(in2)某2d某22l2llm1Ek(2in2)某2d某ml22in202l612–4质量为m1的滑块A沿水平面以速度v移动，质量为m2的物块B沿滑块A以相对速度u滑下，如图12-26所示。
试求系统的动能。
图12-26Ek11m1v2m2[(uco30v)2(uin30)2]22-1-11m1v2m2(u2v22uvco30)2211m1v2m2(u2v23uv)2212–5如图12-27所示，滑块A质量为m1，在滑道内滑动，其上铰接一均质直杆AB，杆AB长为l，质量为m2。
当AB杆与铅垂线的夹角为时，滑块A的速度为vA，杆AB的角速度为试求在该瞬时系统的动能。
图12-27EkEkAEkAB11ll112m1vAm2[(vAco)2(in)2](m2l2)22222212111122m1vAm2(vAl22l vAcol22)2241211122m1vAm2(vAl22lvAco)22312–6椭圆规尺在水平面内由曲柄带动，设曲柄和椭圆规尺都是均质细杆，其质量分别为m1和2m1，且OC=AC=BC=l，如图12-28所示。
理论力学——第12章 动量矩定理
28
maC mg sinq FS
0 mg cosq FN
JC FSR
[1] [2] [3] [4]
由[2]式得 FN mg cosq
[1] ，[3]两式中含有三个未知数aC 、FS、 ，需补充附加条件。
讨论 1．设接触面绝对光滑，即f = f´‘ =0
均为 v 。 2
17
§12-3 刚体绕定轴的转动微分方程
如图示一定轴转动刚体，由质点系对z轴动量矩定理
d
dt
(J z)
n i 1
M z (Fi )
或
d n
Jz
dt
M z (Fi )
i 1
也可为
J z M（z F )
或
d2 n
Jz
dt 2
M z (F )
i 1
以上各式称为刚体绕定轴转动微分方程
dt
rg(PA PB ) r 2PA r 2PB gJO
16
[例4] 已知：猴子A重=猴子B重，猴B以相对绳速度 v
上爬，猴A不动，问当猴B向上爬时，猴A将如何动？ 动的速度多大？（轮重不计）
解：因
MO(F(e)) 0 ,
故系统的动量矩守恒。
0mAvArmB (vvA)r
vA
v 2
猴A与猴B向上的绝对速度是一样的,
R22
1 2
R11
LO
(
J1 R2 2
J2 R2 2
m2
m3 )R2v3
8
§12-2 动量矩定理
1．质点的动量矩定理
对质点动量矩求一次导数，得
d dt
MO
(mv)
d dt
理论力学基础 动量矩定理3
平 面
二、分清各构件的运动情况（平移、转动、平面运动、 静止）
运 动
三、各构件的运动情况之间的关系
微 （平移：速度、加速度）（转动：角速度、角加速度）
分
方 （平面运动：质心速度和加速度、角速度、角加速度）
程
四、根据运动情况运用各类方程
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第十二章 动量矩定理
Fi(e)
F1
D
运 动 微 分 方 程
d
dt
JC
JC
m
d
2
rC
dt 2
F (e)
i
C
M C (Fi(e) )
x′
O
x
刚体平面运动微分方程
JC
d 2
dt 2
M C (Fi(e) )
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第十二章 动量矩定理
例题十五 如图所示，有一轮子，轴的直径为
例题十九 如图所示，板的质量为m1，受水平力
F作用，沿水平面运动，板与平面间的动摩擦因数
第 六 节
为f。在板上放一质量为m2的均质实心圆柱，此圆 柱对板只滚不滑。求板的加速度。（习题12－18）
平
C
面 运
动
微
分
方 程
F2′ FN′ 2
F
C
ar m2g
aC
a
F
FN2 F2
F1
m1g
FN1
鞍山科技大学机械工程与自动化学院工程力学系
mg
鞍山科技大学机械工程与自动化学院工程力学系
梁坤京理论力学第十二章动量矩定理课后答案
动量矩定理12-1 质量为m 的点在平面Oxy 内运动，其运动方程为: x a cos t y bsin2 t 式中a 、b 和 为常量。
求质点对原点 O 的动量矩。
解：由运动方程对时间的一阶导数得原点的速度V xdxsin t dt aV y dy 2b cos2 t 质点对点 O 的动量矩为L O M o (mV x ) M 0(mV y )mv x y mv y x m ( a sin t) bsin2 t m 2b cos2 t acos t 2mab cos 3 t 12-3 如图所示，质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A,质心为C, AC = e ；轮子半径为 R,对轴心A 的转动惯量为J A ； C 、A 、B 三点在同一铅直线上。
（1 ）当轮子只 滚不滑时，若 V A 已知，求轮子的动量和对地面上 B 点的动量矩。
（2）当轮子又滚又滑时， 若V A 、 已知，求轮子的动量和对地面上 B 点的动量矩。
解：（1）当轮子只滚不滑时 B 点为速度瞬心。
轮子角速度V A R质心C 的速度V CBCR e轮子的动量p mv Cmv A (方向水平向右)R对B 点动量矩L B J B2 2 2由于 J B J C m (R e) J A me m (R e) 故 L B J A me 2 m （R e ）2食 （2）当轮子又滚又滑时由基点法求得 C 点速度。
V C V A V CA V A e 轮子动量 p mv C m(v A e) （方向向右） 对B 点动量矩L B mv C BC J Cm(v A 2e) (R e) (J A me) mv A (R e) (J A mRe) 12-13 如图所示，有一轮子，轴的直径为 50 mm 无初速地沿倾角 20的轨道滚下，设 只滚不滑，5秒内轮心滚动的距离为 s =3m 。
试求轮子对轮心的惯性半径。
解：取轮子为研究对象，轮子受力如图（ a ）所示，根据刚体平面运动微分方程有 ma C mgsi n F （ 1） J C = Fr （ 2）因轮子只滚不滑，所以有 a c = r （ 3） ® 12将式（3）代入式（1）、（2）消去F 得到mr sinm?g上式对时间两次积分，并注意到 t = 0时 0, 0,则 mgrt 2 sin mgrt 2s in 2(J C mr 2) 2(m 2 mr 2) 把 r = 0.025 m 及 t = 5 s 时，s 'grt 2sin f gt 2sin-r r「s r 1grt 2sin 2( 2 r 2) r 3 m 代入上式得0.0259.8 52si n202 30.09 m 90 mm12-17 图示均质杆 AB 长为I ，放在铅直平面内，杆的一端 A 靠在光滑铅直墙上，另一端 B 放在光滑的水平地板上，并与水平面成 °角。
同济理论力学 第十二章 动量矩定理
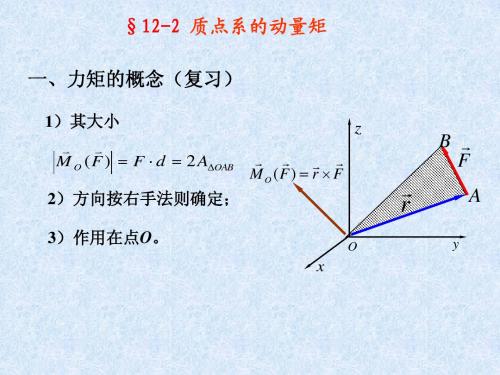
' ri rQ ri
Q为任一动点
dmvi
z
Mi
ri
rQ
O
ri
Q
y
' ' ' dri ( rQ vi )dm ( ri vQ )dm ( ri )dm dt
质点系动量矩守恒
L x 常量
有心力
mv
M
M O (mv ) r mv 常矢量
M O (mv ) 的大小始终不变，为两倍的 2、
A
r
h F O
1、行星运行轨道必为一平面轨迹
Δ OMA面积
M o (mv ) r mv mv h
dω P 2 dω 1 R1 FR1 解: 左轮: J1 dt 2 g dt d P2 2 d J R2 FR2 右轮: 2 dt 2 g dt
1 < 2,
1 < 2,
例12-7: 旋转调速器在外伸刚性臂上悬挂两个重量P的小球,初始 转动时角速度0,求当悬挂小球与垂直线夹角为时的角速度. 解:
P 初始转动时: L1 2 (a0 )a g
P 夹角为时: L2 2 (a l sin ) (a l sin ) g
vQ 0 2、当Q为固定点 ： LQ LO rQ p
rQC vQ 0
r // v Q 时 ： 3、当 QC
LO rQ p LQ
四、刚体的动量矩
１、平动刚体对任一固定点O的动量矩 LO ri mi vi mrc v rc p ２、定轴转动刚体对转轴的动量矩：
理论力学(哈工大版)第十二章动量矩定理(全面版)资料
理论力学(哈工大版)第十二章动量矩定理（全面版）资料第八章 动量矩定理8-1 质点系的动量矩（待强化） 一．动量矩的概念质点对点O 的动量矩：v m r v m m O ⨯=)( 质点对轴 z 的动量矩：)()(xy O z v m m v m m = 对着轴看：顺时针为负 逆时针为正质点对点O 的动量矩与对轴z 的动量矩之间的关系：[])( )(v m m v m m z z O = kg·ｍ2/s 。
二．质点系的动量矩 质系对点O 动量矩：i i i i i OO v m r v m mL ⨯==∑∑)(质系对轴z 动量矩：[]z Oii zz L v m m L)(==∑三．质点系的动量矩的计算c c c mv r L L ⨯+=0质点系对任意定点O 的动量矩，等于质点系对质心的动量矩，与将质点系的动量集中于质心对于O 点动量矩的矢量和。
质点系对质心的绝对运动动量矩，等于质点系对随质心平动的参考系的相对运动动量矩。
结论：在计算质点系对于质心的动量矩时，用质点相对于惯性参考系的绝对速度vi ，或用质点相对于固结在质心上的平动参考系的相对速度vi `，所得结果是一样的。
四、刚体的动量矩 1．平动刚体C C C O O v m r v m m L ⨯==)( )(C z z v m m L =2．定轴转动刚体ωZ z J L =3．平面运动刚体C C C C C O m m L v O C L v r L +⨯=+⨯= ω⋅+=C C z z J v m m L )(平面运动刚体对垂直于质量对称平面的固定轴的动量矩，等于刚体随同质心作平动时质心的动量对该轴的动量矩与绕质心轴作转动时的动量矩之和。
8-2 动量矩定理（待强化） 一．质点的动量矩定理)()]([ , )(F m v m F r v r O O m dtdm dt d =⨯=⨯ 质点对任一固定点的动量矩对时间的导数，等于作用在质点上的力对同一点之矩。
理论力学_12.动量矩定理
故：
d dt
(r m v ) r F ,
d dt
[ m O ( m v )] m O ( F )
质点对任一固定点的动量矩对时间的导数，等于作用在质 点上的力对同一点之矩。这就是质点对固定点的动量矩定理。
例3 单摆 已知m，l，t =0时= 0，从静止 开始释放。 求单摆的运动规律。 解：将小球视为质点。 受力分析；受力图如图示。
r
i
i
m iv
C
ri ) m i v
i
rC m i v i
ri m i v i
i
rC m v C
ri m i v
其中 L C ri m i v i 为质点系相对质心C的动量矩。 （注意：vi为质点的绝对速度。） 即 质点系对任意定点O的动量矩，等于质点系对质心的动量矩， 与将质点系的动量集中于质心对于O点动量矩的矢量和。
L z J z m 2 vr 1 2 ( m1r
2
J ，z
1
m1r ；
2
v r
m 2 vr
1 2
m 1 m 2 ) rv
系统所受外力对转轴z的矩为
M z ( Fi
(e)
) M
(e)
O
Fr M
O
f m 2gr
dL dt
z
M z (Fi
)
d 1 ( m m 2 ) rv M 2 1 dt
例如：试计算圆盘对轴O的 动量矩。质点的质量均为m。
O1 B C
vr vr
vr
L O L O 1 rO 1 m v O 1 3 mv r R l 3 m l 0 3m (vr R l 0 )
十二章动量矩定理
F mv
M0(F)
o
Ｑ
y
x
由牛顿第二定律
m
dv dt
F
d dt
(mv)
F
r
d dt
(mv)
r
F
d (r mv) r d(mv) dr mv
dt
ห้องสมุดไป่ตู้
dt dt
理论力学电子教程
第十二章 动量矩定理
d (r mv) r F dt
M0(mv) m0(F)
理论力学电子教程
第十二章 动量矩定理
C
m2
IOZ M
式中
M
m1
O
IOZ
1 3
m1L2
1 2
m2
r
2
m2L2
理论力学电子教程
第十二章 动量矩定理
代入已知值得：
IOZ
1 10 0.32 3
1 40 0.152 2
40 0.32
4.35kg m2
M 20 4.6rad / s2
IOZ 4.35
理论力学电子教程
第十二章 动量矩定理
dt
M y (mv)]
my (Fe )
d [
dt
M z (mv)]
mz (Fe )
理论力学电子教程
第十二章 动量矩定理
【典型题精解】
例12-1 滑块Ａ，Ｂ质量分别为２Ｋｇ，0.5Ｋｇ，用长１
米的绳连接，在水平光滑滑竿上滑动，绳和竿的质量不计。
竿绕铅垂轴转动，轴的摩擦也不计。当 rA 0.6m 时，滑块 Ａ以速度０.４ｍ／Ｓ沿竿向外运动，竿的角速度 0.5rad / s
求此时竿的角加速度。
1m
B rB
动量矩定理作业参考答案及解答
g (顺时针), 2r
FOx = 0,
1 FOy = mg (↑) 2
6．如题图所示，有一轮子，轴的直径为 50mm，无初速的沿倾角θ=20°的轨道
滚下，设只滚不滑，5s 内轮心滚过的距离为 s=3m。试求轮子对轮心的惯性半径。
s
提示：本题用刚体平面运动微分方程求解。注意到轮心加速度可由式 1 s = at 2 求得，且轮心加速度 a 与轮子角加速度α关系 a = rα ，其中 r 为轮轴的 2 半径。 解：
a mg
Ff × r = mρ α
2
由以上两式消去 Ff 得 ρ 2 =
r ( g sin θ − a )
α
=
r 2 t 2 g sin θ − r 2 = 8113(mm) 2 2s
ρ= & 90mm
r 2 t 2 g sin θ − r 2 = 8113(mm) 2 , ⇒ 2s
答案： ρ 2 =
整个系统对轴 O 的动量矩守恒
p 1 p LO = L1 + L2 = r 2 1 ω + 2 r (ωr − at ) = 0 2 g g
解得
ω=
2aP2 t , r (2 P2 + P1 )
α=
2aP2 dω = dt r (2 P2 + P1 )
答案： ω =
2aP2 t , r (2 P2 + P1 )
vB
A
ωB
B
D
1 1）对杆分析，杆对轴 A 的动量矩 L A1 = m2 R 2ω 3 2）对轮分析
ω B R = ωl
ωB =
齿轮对轮心 B 的动量矩为 齿轮对轴 A 的动量矩为
ωl
理论力学 第六版部分习题答案 第12章
T=
m 2 2 2 ω l sin θ 6
12-5 自动弹射器如图 13-5a 放置，弹簧在未受力时的长度为 200 mm，恰好等于筒长。 欲使弹簧改变 10 mm，需力 2 N。如弹簧被压缩到 100 mm，然后让质量为 30 g 的小球自弹 射器中射出。求小球离开弹射器筒口时的速度。
Fk 30°
12-9 2 个质量均为 m2 的物体用绳连接，此绳跨过滑轮 O，如图 13-10 所示。在左方 物体上放有 1 带孔的薄圆板，而在右方物体上放有 2 个相同的圆板，圆板的质量均为 m1。 此质点系由静止开始运动，当右方物体和圆板落下距离 x1 时，重物通过 1 固定圆环板，而 其上质量为 2m1 的薄板则被搁住。摩擦和滑轮质量不计。如该重物继续下降了距离 x2 时速 度为零，求 x2 与 x1 的比。 解 第 1 阶段：系统由静止运动 x1 距离。由动能定理
12-6 平面机构由 2 匀质杆 AB，BO 组成，2 杆的质量均为 m，长度均为 l，在铅垂平 面内运动。在杆 AB 上作用 1 不变的力偶矩 M，从图 13-7a 所示位置由静止开始运动。不计 摩擦，求当杆端 A 即将碰到铰支座 O 时杆端 A 的速度。
P
P
θ
B vB
ω AB
vB vC vA
(c)
即
1 (2m1 g + m2 g ) x1 − (m1 g + m2 g ) x1 = (3m1 + 2m2 )v 2 2 1 （1） m1 gx1 = (3m1 + 2m2 )v 2 2 m2 gx2 − (m1 g + m2 g ) x2 = 0 − 1 (m1 + 2m2 )v 2 2
（2）
图 13-10
梁坤京理论力学第十二章动量矩定理课后
动量矩定理12-1 质量为m 的点在平面Oxy 内运动，其运动方程为：tb y ta x ωω2sin cos ==式中a 、b 和ω为常量。
求质点对原点O 的动量矩。
解：由运动方程对时间的一阶导数得原点的速度tb t y v t a txv y x ωωωω2cos 2d d sin d d ==-==质点对点O 的动量矩为ta tb m t b t a m xmv y mv m M m M L y x O O ωωωωωωcos 2cos 22sin )sin ()()(0⋅⋅+⋅-⋅-=⋅+⋅-=+=y x v vt mab ωω3cos 2=12-3 如图所示，质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A ，质心为C ，AC = e ；轮子半径为R ，对轴心A 的转动惯量为J A ；C 、A 、B 三点在同一铅直线上。
（1）当轮子只滚不滑时，若v A 已知，求轮子的动量和对地面上B 点的动量矩。
（2）当轮子又滚又滑时，若v A 、ω已知，求轮子的动量和对地面上B 点的动量矩。
解：（1）当轮子只滚不滑时B 点为速度瞬心。
轮子角速度 Rv A=ω质心C 的速度)(e R Rv C B v AC +==ω 轮子的动量A C mv ReR mv p +==（方向水平向右） 对B 点动量矩ω⋅=B B J L 由于222)( )( e R m me J e R m J J A C B ++-=++= 故 []Rv e R m me J L AA B 22)( ++-=（2）当轮子又滚又滑时由基点法求得C 点速度。
e v v v v A CA A C ω+=+=轮子动量 )(e v m mv p A C ω+== （方向向右） 对B 点动量矩)( )()()( )( 2e mR J e R mv me J e R e v m J BC mv L A A A A C C B +++=-+++=+=ωωωω12-13 如图所示，有一轮子，轴的直径为50 mm ，无初速地沿倾角︒=20θ的轨道滚下，设只滚不滑，5秒内轮心滚动的距离为s = 3 m 。
大学本科理论力学课程第12章 动量定理--纯理论
第十二章 动量定理
第十二章 动量定理
1、动量：
(1) 质点的动量： mv
(2) 质点系的动量：
n
mivi 或 mvC
i 1
（3）刚体动量： mvC
2、动量定理：
d (mv) F dt
mv2 mv1
t2 F dt
t1
质点动量守恒
dP
dt
d dt
mv
Fe
P2 P1
t2 t1
（12－8）
理论力学电子教程
第十二章 动量定理
将
dP dt
d dt
mv
Fe
改成
dP Fedt
质点系动量的微分等于质点系所受外力系的元冲量的矢量和。
积分后有：
P2 P1
t2 t1
Fedt
改写为： P2 P1 Ie
（12－9）
上述即为质点系动量定理的积分形式，又称冲量定理。
质点系动量在某时间间隔内的改变量，等于各质点系所受全部
外力在同一时间间隔内冲量的矢量和。
在坐标轴上投影有：
p2 x p1x p2 y p1 y
I ex I ey
p2 z p1z
I ez
（12－10）
上式表明：在某一时间间隔内，质点系动量在 任一固定轴上投影的改变量，等于作用于质点 系的外力冲量在同一轴上投影的代数和。
理论力电子教程
Fedt
Ie
3、质心运动定理：
MaC
d dt
mv
Fe
质心运动守恒
质点系动量守恒
理论力学电子教程
第十二章 动量定理
测验 半径为 r 的圆轮沿着半径为R的圆弧曲面作纯滚动，杆OA以 匀角速度转动，已知： 10rad / s,OA r 10cm, AB l 40cm, R 20cm，
梁坤京理论力学第十二章动量矩定理课后答案
梁坤京理论力学第十二章动量矩定理课后答案案场各岗位服务流程销售大厅服务岗：1、销售大厅服务岗岗位职责：1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点；2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1）自检仪容仪表以饱满的精神面貌进入工作区域2）检查使用工具及销售大厅物资情况，异常情况及时登记并报告上级。
班中工作程序服务流程行为规范迎接指引递阅资料上饮品（糕点）添加茶水工作要求1）眼神关注客人，当客人距3米距离时，应主动跨出自己的位置迎宾，然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候：“您好！欢迎光临！”2）在客人前方1-2米距离领位，指引请客人向休息区，在客人入座后问客人对座位是否满意：“您好！请问坐这儿可以吗？”得到同意后为客人拉椅入座“好的，请入座！”3）若客人无置业顾问陪同，可询问：请问您有专属的置业顾问吗？，为客人取阅项目资料，并礼貌的告知请客人稍等，置业顾问会很快过来介绍，同时请置业顾问关注该客人；4）问候的起始语应为“先生-小姐-女士早上好，这里是XX销售中心，这边请”5）问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6）关注客人物品，如物品较多，则主动询问是否需要帮助（如拾到物品须两名人员在场方能打开，提示客人注意贵重物品）；7）在满座位的情况下，须先向客人致歉，在请其到沙盘区进行观摩稍作等待；阶段工作及服务流程班中工作程序工作要求注意事项饮料（糕点服务）1）在所有饮料（糕点）服务中必须使用托盘；2）所有饮料服务均已“对不起，打扰一下，请问您需要什么饮品”为起始；3）服务方向：从客人的右面服务；4）当客人的饮料杯中只剩三分之一时，必须询问客人是否需要再添一杯，在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触；5）在客人再次需要饮料时必须更换杯子；下班程序1）检查使用的工具及销售案场物资情况，异常情况及时记录并报告上级领导；2）填写物资领用申请表并整理客户意见；3）参加班后总结会；4）积极配合销售人员的接待工作，如果下班时间已经到，必须待客人离开后下班；1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1）为来访的客人提供全程的休息及饮品服务；2）保持吧台区域的整洁；3)饮品使用的器皿必须消毒；4）及时补充吧台物资；5）收集客户意见、建议及问题点；1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1）自检仪容仪表以饱满的精神面貌进入工作区域2）检查使用工具及销售大厅物资情况，异常情况及时登记并报告上级。
理论力学12—2动量矩定理
由运动学关系，得
a1r1 a2r2
注意到 F F ，联立求解以上三式得
a1
Mr22 J1r22 J2r12
M
F′n F′
r2 O2
FO1y F
O1 FO1x
Fn
m1g
FO2y
O2
FO2x
m2g
例题 10 关于突然解除约束问题
FOy
O
FOx
W=mg
解除约束前： FOx=0, FOy=mg/2
FOy
mg
aC aD raB r(a A aB )
aC
4 5
g
例17 均质杆质量为m，长为l，在铅直平面内一端沿着水平地 面，另一端沿着铅垂墙壁，从图示位置无初速地滑下。不计摩 擦，求开始滑动的瞬时，地面和墙壁对杆的约束反力。
解：以杆AB为研究对象，分析受力。
杆作平面运动，设质心C的加速度为
aCx、aCy，角加速度为a。
例动3 量高矩定炉理运送矿石的卷扬机如图。已知鼓轮的半径为R，质量
为m1，绕O轴转动。小车和矿石的总质量为m2。作用在鼓轮上
的力偶矩为M，鼓轮对转轴的转动惯量为J，轨道倾角为a。设
绳质量和各处摩擦不计，求小车的加速度a。
解：以系统为研究对象，受力如图。 以顺时针为正，则
LO J m2vR MO (F (e) ) M m2 g sin a R
3mr2 mr2 A 18mr2
21mr2
O
(c) A 2
LO L杆 L盘 J杆 ( ) LA mO (2mvA ) 3mr2 J A A (2m)(3r)3r
3mr2 mr2 A 18mr2 3mr2 mr2 (2) 18mr2
23mr2
(b)r
哈工大理论力学教研室《理论力学Ⅰ》(第7版)章节题库-动能定理(圣才出品)
十万种考研考证电子书、题库视频学习平台
第 12 章 动量矩定理
一、选择题 1．图 12-1 所示无重刚杆 AB，两端各固连一个小球，其质量分别为 m1、m2。若 m1 ＞m2，不计空气阻力，则当杆 AB 在重力作用下由水平静止位置进入运动后（ ）落地。 A．两端同时 B．A 端先 C．B 端先 D．无法判断
图 12-10
解：系统初始静止，T1 = 0 ，当杆 AB 运动到与铅垂线夹角为 时的动能为
下面建立 与 vC 的关系。
4 / 25
圣才电子书 十万种考研考证电子书、题库视频学习平台
垂线的夹角 为常数，杆长为 l。
（3）图 12-8（c）：均质 L 型刚杆，质量为 m，在铅垂面内以等角速度 ω 绕轴 O 转 动。
（4）图 I4-8（d）：质量为 m1 的滑块，沿水平直线运动，通过铰链 A，用长为 l 质量 为 m2 的刚杆固结一垂球 B，重球质量为 m3。设图示瞬时，滑块的速度为 υ，杆 AB 绕 A 点 转动的角速度为 ω。
履带
段合在一起是一个均质圆环，作平面运动，其动能为
因此，系统的总动能为
（2）图 12-8（b）：杆 0A 作锥形转动，取 dx 微段，其质量为 dm = m dx ，速度 l
v = xsin ，动能为
因此，杆 0A 总的动能为
（3）图 12-8（c）：L 型杆由 OA 和 AB 两部分组成，它们都作定轴转动。 OA 段： AB 段： 则 L 型杆的动能为
D．
【答案】D
图 12-2
3．质量为 m 的均质细圆环半径为 R，其上固结一个质量也为 m 的质点 A（图 12-3）。 细圆环在水平面上作纯滚动，图示瞬时角速度为 ω，则系统的动能为（ ）。
理论力学C12-动量定理
y
xC1 = xC 2
M 1b+m 2 a 3 3 xC1 = M +m
设大三角块的位移为s 设大三角块的位移为 ，则
a
v mg
v Mg
x
v FN
y
b
xC 2
M ( b − s ) + m[ a + (b − a ) − s ] = M +m
1 3 2 3
解得
m(b − a ) s= M +m
s
x
如图所示，电动机外壳固定在水平基础上，定子、 例6 如图所示，电动机外壳固定在水平基础上，定子、转子的质量分别为 m1、m2。设定子质心位于转轴中心 1，由于制造误差，转子质心 2 到O1 设定子质心位于转轴中心O 由于制造误差，转子质心O 的距离为e， 转动。 质心运动方程； 的距离为 ，已知转子以匀角速度ω 转动。求： (1) 质心运动方程；(2) 基 础对电机总的水平和铅垂反力；(3) 若电机没有螺栓固定，各处摩擦不计， 础对电机总的水平和铅垂反力； 若电机没有螺栓固定，各处摩擦不计， 初始时电机静止， 转动时电动机外壳的运动。 初始时电机静止，求转子以匀角速度ω转动时电动机外壳的运动。 建立如图坐标，任一瞬时， 解：(1) 建立如图坐标，任一瞬时，θ＝ω t，即有 ，
质点系动量定理的有限形式 r (e) r r p t r v p − p0 = ∑ I d p = ∑ ∫ F (e) d t 或 ∫
p0 0
在某一时间间隔内，质点系动量的改变量等于在这 段时间内作用于质点系外力冲量的矢量和。 质点系动量定理的有限投影形式
px − p0 x = ∑ I x ( e ) , p y − p0 y = ∑ I y ( e ) , pz − p0 z = ∑ I z ( e )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
动量矩定理1２－１ 质量为m 的点在平面Ｏx ｙ内运动,其运动方程为:tb y ta x ωω2sin cos ==式中a 、b 和ω为常量。
求质点对原点Ｏ的动量矩。
解:由运动方程对时间的一阶导数得原点的速度tb t y v t a txv y x ωωωω2cos 2d d sin d d ==-==质点对点O 的动量矩为ta tb m t b t a m xmv y mv m M m M L y x O O ωωωωωωcos 2cos 22sin )sin ()()(0⋅⋅+⋅-⋅-=⋅+⋅-=+=y x v vﻩ t mab ωω3cos 2=1２-3 如图所示，质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A ,质心为Ｃ，A Ｃ ＝ e ；轮子半径为Ｒ，对轴心A 的转动惯量为ＪA ;C 、Ａ、B 三点在同一铅直线上。
（１)当轮子只滚不滑时，若v Ａ已知，求轮子的动量和对地面上B 点的动量矩。
（２)当轮子又滚又滑时，若v A 、ω已知,求轮子的动量和对地面上Ｂ点的动量矩。
解：(1)当轮子只滚不滑时B 点为速度瞬心。
ﻩ 轮子角速度Rv A=ωﻩ质心C 的速度)(e R Rv C B v AC +==ωﻩ ﻩ轮子的动量(A C mv ReR mv p +==ﻩ方向水平向右） ﻩ对Ｂ点动量矩ω⋅=B B J L ﻩ由于ﻩ 222)( )( e R m me J e R m J J A C B ++-=++=故[]Rv e R m me J L AA B 22)( ++-=ﻩ(２）当轮子又滚又滑时由基点法求得C 点速度。
e v v v v A CA A C ω+=+=轮子动量( )(e v m mv p A C ω+==ﻩ方向向右） 对B 点动量矩)( )()()( )( 2e mR J e R mv me J e R e v m J BC mv L A A A A C C B +++=-+++=+=ωωωω12-13 如图所示，有一轮子，轴的直径为50 m ｍ，无初速地沿倾角︒=20θ的轨道滚下,设只滚不滑，5秒内轮心滚动的距离为s = 3 m 。
试求轮子对轮心的惯性半径。
解:取轮子为研究对象,轮子受力如图(ａ）所示，根据刚体平面运动微分方程有 ﻩ F mg ma C -=θsin ﻩ (1) J Ｃα = Ｆr ﻩ ﻩ（2）因轮子只滚不滑，所以有 a Ｃ ＝αr （3）将式（3）代入式(1)、(２）消去F 得到ﻩg mr J mr C 2sin +==θϕα上式对时间两次积分，并注意到ｔ = 0时0 ,0==ϕϕ ,则 ﻩ)(2sin )(2sin )(2sin 22222222r grt mr m mgrt mr J mgrt C +=+=+=ρθρθθϕ 把 r = ０.0２5 m 及ｔ = 5 ｓ时，m 3==ϕr s 代入上式得mm 90m 09.013220sin 58.9025.012sin 2sin 2222==-⨯︒⨯=-=-=s gt r r grt θϕθρ12-17 图示均质杆AB 长为l ,放在铅直平面内,杆的一端Ａ靠在光滑铅直墙上,另一端B 放在光滑的水平地板上,并与水平面成0ϕ角。
此后，令杆由静止状态倒下。
求（1）杆在任意位置时的角加速度和角速度;（2)当杆脱离墙时，此杆与水平面所夹的角。
解：（1)取均质杆为研究对象,受力分析及建立坐标系Oxy 如图(a),杆AB 作平面运动,质心在Ｃ点。
刚体平面运动微分方程为ﻩﻩ)3( sin 2cos 2)2( )1( N N N N ϕϕαlF l F J mg F y m F x m A B C B C A C ⋅-⋅=-==由于ϕϕsin 2,cos 2ly l x C C ==ﻩﻩ将其对间t 求两次导数,且注意到 αϕωϕ-=-= ,，得到 ﻩ )5( )sin cos (2)4( )cos sin (222ϕωϕαϕωϕα+-=-=l y l x C C将式(4)、（5)代入式(１)、(２)中,得mgml F mlF BA ++-=-=)sin cos (2)cos sin (22N 2N ϕωϕαϕωϕα再将F N A ,F ＮB 的表达式代入式（3）中，得ϕϕωϕαϕϕϕωϕααsin )cos sin (4cos 2cos )sin cos (42222--++-=ml mgl ml J C即ϕααcos 242mglml J C +-=ﻩ 把 122ml J C =代入上式得 ϕαcos 23l g=而td d ωα=ﻩ分离变量并积分得ﻩ ϕϕϕϕωωωd cos 23d 00l g -=⎰⎰ﻩ)sin (sin 30ϕϕω-=lg(２)当杆脱离墙时F N A ＝ 0，设此时1ϕϕ=则0)cos sin (2121N =-=ϕωϕαmlF A ﻩ 将α和ω表达式代入上式解得01sin 32sin ϕϕ=ﻩﻩ )sin 32arcsin(01ϕϕ=12－19 均质实心圆柱体A 和薄铁环Ｂ的质量均为ｍ，半径都等于r ,两者用杆AB 铰接，无滑动地沿斜面滚下,斜面与水平面的夹角为θ，如图所示如杆的质量忽略不计,求杆AB 的加速度和杆的内力。
解:分别取圆柱A 和薄铁环B 为研究对象，其受力分析如图(a ）、（b ）所示，Ａ和B 均作平面运动,杆ＡB 作平动,由题意知T T ,,F F a a a B A B A '=====ααα。
对圆柱A 有 ﻩ)2( )1( sin A 11T αθJ r F F F mg ma =--=对薄铁环B 有 ﻩ)4( )3( sin 22αθB J r F F mg T ma =-+'=联立求解式(1）、（2）、(3）、(4），并将T T 22,,2F F mr J r m J B A '===，以及根据只滚不滑条件得到的ａ = αr 代入,解得(θsin 71TT mg F F ='=ﻩ压力)及 θsin 74g a =1２-２１ 图示均质圆柱体的质量为m ，半径为r ，放在倾角为︒60的斜面上。
一细绳缠绕在圆柱体上，其一端固定于点Ａ,此绳与A 相连部分与斜面平行。
若圆柱体与斜面间的摩擦系数为31=f ，试求其中心沿斜面落下的加速度ａC 。
解：取均质圆柱为研究对象,其受力如图(a)所示，圆柱作平面运动，则其平面运动微分方程为)3( 60sin )2( 60cos 0)1( )(T N T F F mg ma mg F r F F J C --︒=︒-=-=α 而ﻩﻩ F = ｆＦN ﻩﻩ ﻩ (4）圆柱沿斜面向下滑动,可看作沿A Ｄ绳向下滚动，且只滚不滑，所以有ﻩａＣ=αr 把上式及31=f 代入式（3)、（4)解方程(1)至(4)，得 a C ＝ 0.３55g ﻩ (方向沿斜面向下)12-23 均质圆柱体A 和B 的质量均为m ，半径为ｒ，一绳缠在绕固定轴Ｏ转动的圆柱A 上,绳的另一端绕在圆柱B 上，如图所示。
摩擦不计。
求:(1）圆柱体B 下落时质心的加速度;（2）若在圆柱体A 上作用一逆时针转向,矩为Ｍ的力偶,试问在什么条件下圆柱体B 的质心习题9－8图AαAv Aa rCTF gm(a)加速度将向上。
解:(1）分别取轮Ａ和B 研究,其受力如图(ａ）、（b ）所示，轮A 定轴转动,轮Ｂ作平面运动。
对轮Ａ运用刚体绕定轴转动微分方程 ﻩr F J A A T =α （1)对轮B 运用刚体平面运动微分方程有B ma F mg ='-T （2)r F J B B T '=α (３）再以C 为基点分析B 点加速度，有r r a a a B A BC C B ⋅+⋅=+=αα (4) 联立求解式(1）、(２)、(3)、(4)，并将T T F F '=及22r mJ J A B ==代入,解得ﻩ g a B 54=２)若在A 轮上作用一逆时针转矩M ，则轮A 将作逆时针转动，对A 运用刚体绕定轴转动微分方程有r F M J A A T -=α （５） 以C 点为基点分析B 点加速度,根据题意，在临界状态有0tt =+-=+=r r a a a B A BC C B αα （6）联立求解式(5）、(6)和(2)、(３）并将T T '=及22r m J J A B ==代入,得 ﻩmgr M 2=故当转矩mgr M 2>时轮B 的质心将上升。
９－8 图示圆柱体A 的质量为m ，在其中部绕以细绳，绳的一端B 固定。
圆柱体沿绳子解开的而降落,其初速为零。
求当圆柱体的轴降落了高度ｈ时圆柱体中心A 的速度υ和绳子的拉力ＦT 。
解:法1：图（a ）T F mg ma A -=ﻩ（１) r F αJ A T =ﻩ(2） r αa A = （３）221mr J A = 解得 mg F 31T=（拉) g a A 32=(常量） (４)由运动学 gh h a v A A 3322==（↓） 法2:由于动瞬心与轮的质心距离保持不变,故可对瞬心C 用动量矩定理：mgr J C =ϕﻩ（5) 2223mr mr J J A C =+=又 ra A=ϕg a A 32=(同式（4）) 再由 T F mg ma A -=习题9－11图DBrαD NF Fagm MM f(a)得 mg F 31T=（拉) gh h a v A A 3322==(↓) ９－10 图示重物A 的质量为ｍ,当其下降时,借无重且不可伸长的绳使滚子C 沿水平轨道滚动而不滑动。
绳子跨过不计质量的定滑轮D 并绕在滑轮B 上。
滑轮B 与滚子C 固结为一体。
已知滑轮Ｂ的半径为Ｒ，滚子C 的半径为r ，二者总质量为m ′，其对与图面垂直的轴O 的回转半径为ρ。
求：重物Ａ的加速度。
解:法１：对轮: Fr TR J O -=αﻩ（1） T F a m O -='ﻩ(２)对A :T mg ma A -=ﻩ（3）又：tH H A a a a ==绳以O 为基点：tn n t HO HO O H H a a a a a ++=+ααα)(t t r R r R a aa O HO H -=-=-=(→)α)(r R a A -=(↓)(4)由上四式联立，得(注意到2ρm J O '=)1)()()()()(2222222+-+⋅'=-++'-=r R r m m gr R m r m r R mg a A ρρ法2:对瞬心E 用动量矩定理(本题质心瞬心之距离为常数）)(r R T J E -=α T mg ma A -= 又α)(r R a A -=)(222r m r m J J O E +'='+=ρ 可解得：1)()(222+-+⋅'=r R r m m ga A ρ9-１1 图示匀质圆柱体质量为m ，半径为r ,在力偶作用下沿水平面作纯滚动。