有限元查错
有限元计算工程误差的允许误差

有限元计算工程误差的允许误差
有限元计算工程误差的允许误差是指在有限元计算中,由于数值计算的限制和模型假设的简化等原因,计算结果和实际结果之间存在的误差。
这些误差可能对工程决策产生影响,因此必须对其进行允许误差的评估和控制。
允许误差的评估需要考虑多种因素,如数值计算方法的精度、模型的准确性、实际工况的复杂程度等。
其中,数值计算方法的精度是评估计算误差的重要因素之一。
通过对数值计算方法的收敛性和稳定性进行分析,可以确定计算误差的上限。
此外,对模型的准确性进行评估也是允许误差评估的重要步骤。
通过与实际测量数据进行比较,可以确定模型误差的大小和分布情况。
控制允许误差的方法包括加强数值计算方法的精度和稳定性、优化模型的准确性、增加采样点、使用不同的计算方法进行验证等。
其中,加强数值计算方法的精度和稳定性可以通过增加计算精度、减小网格尺寸、使用高阶元等方法实现。
优化模型的准确性则需要考虑模型的复杂程度和实际测量数据的可靠性。
增加采样点可以提高计算结果的精度和可靠性,但也会增加计算成本。
使用不同的计算方法进行验证可以帮助确定计算结果的可靠性。
在工程实践中,允许误差的确定和控制是有限元计算的关键问题之一。
只有在误差可控的情况下,才能保证有限元计算结果的准确性和可靠性,从而为工程决策提供重要的支持。
- 1 -。
有限元方法基础教程勘误

有限元方法基础教程勘误The finite element method (FEM) is a numerical technique used for finding approximate solutions of partial differential equations. 有限元方法是一种用于寻找偏微分方程的近似解的数值技术。
It has a wide range of applications in various fields such as structural analysis, heat transfer, fluid dynamics, and electromagnetic fields. 它在结构分析、热传递、流体力学和电磁场等各个领域有着广泛的应用。
One of the most important aspects of learning FEM is understanding the basic principles and concepts behind it. 学习有限元方法最重要的一个方面是理解它背后的基本原理和概念。
This includes understanding how to discretize the domain into finite elements, formulating the element equations, and assembling the global equations. 这包括理解如何将域离散为有限元素、制定元素方程和装配全局方程。
In the book "有限元方法基础教程," it is important to have an accurate and error-free version in order to effectively learn and apply the concepts taught in the text. 在《有限元方法基础教程》这本书中,具有准确无误的版本对于有效学习和应用所教授的概念非常重要。
有限元误差估计

有限元误差估计
有限元误差估计是在有限元方法中用于评估数值解与真实解之间的差异的技术。
它提供了对数值解的准确性和收敛性的估计,帮助评估数值模拟的可靠性和精度。
常见的有限元误差估计方法包括:
1.后验误差估计(Posteriori Error Estimation):在有限元计算完成后,使用一些后处理技术来估计数值解的误差。
这些技术通常基于残差的计算、解的重构、网格细化等方法。
2.可靠性误差估计(Reliable Error Estimation):这种误差估计方法旨在提供对数值解误差的下界估计,确保数值解的准确性。
常见的方法包括最小割方法、可靠的后验估计等。
3.马尔可夫不等式(Markov's Inequality):这是一种基本的误差估计方法,通过将数值解的误差与其范数进行比较,给出误差的上界估计。
4.差分误差估计(Difference Error Estimation):这种方法通过将有限元离散化的问题与其连续的解进行比较,估计数值解的误差。
常见的方法包括基于差分格式的稳定性分析和收敛性分析。
这些方法的选择和应用取决于具体的数值模拟问题和有限元方法的特点。
通常,有限元误差估计是一个重要的步骤,用于指导网格适应性和误差控制策略,以提高数值解的准确性和效率。
试验和有限元的误差

试验和有限元的误差全文共四篇示例,供您参考第一篇示例:试验和有限元分析是工程领域常用的两种方法,它们常常用于预测和分析结构在不同载荷条件下的响应。
无论是试验还是有限元分析,都存在着误差,因此了解和评估这些误差是非常重要的。
本文将探讨试验和有限元分析中的误差,以及如何有效地管理和减小这些误差。
让我们来看看试验中存在的误差。
试验通常涉及到测量物理量,如应力、应变、位移等。
由于测量设备的精度、环境条件、人为操作等因素,测量结果往往会存在一定的误差。
测量设备的刻度可能不够精确,环境温度和湿度可能会影响到测量结果的准确性,操作人员的技术水平也会对测量结果产生影响。
试验中还可能会出现一些偶然误差,如设备故障、实验样品的缺陷等。
这些偶然误差在一定程度上会影响试验结果的准确性。
对于试验中可能存在的误差,我们需要采取相应的措施来减小这些误差的影响。
比如说,可以通过校准测量设备、控制实验环境、提高操作技术来减小误差,并且在试验结果分析时考虑到可能的误差范围,以便更准确地评估结构的响应。
与试验不同,有限元分析是一种数值计算方法,它通过将结构分割成有限个小单元,利用数学方程对这些小单元进行求解,从而得到结构的响应。
有限元分析中也存在着误差。
有限元分析中的误差可以来自模型的简化。
由于实际结构往往非常复杂,我们在进行有限元建模时往往需要对结构进行简化,例如忽略一些小的细节,这样会导致模型与实际结构存在一定的差异,从而引入误差。
有限元分析中的误差还可能来自数值计算的方法和参数选择。
数值计算方法的选取、边界条件的处理、网格划分的精度等因素都会对有限元分析结果的精度产生影响。
在进行有限元分析时,需要认真选择合适的数值计算方法,合理处理边界条件,以及进行网格收敛性分析,以减小这些误差的影响。
有限元分析中还可能存在由于数值计算误差引起的问题。
使用有限元方法进行求解时,使用的数值积分、迭代收敛条件等都可能会引入数值计算误差,从而影响到结果的准确性。
有限元查错
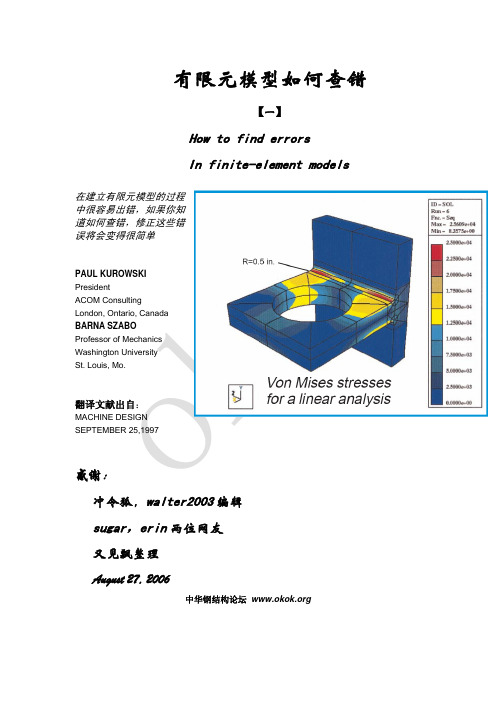
有限元模型如何查错【一】How to find errors In finite-element models在建立有限元模型的过程 中很容易出错,如果你知 道如何查错,修正这些错 误将会变得很简单PAUL KUROWSKI President ACOM Consulting London, Ontario, Canada BARNA SZABO Professor of Mechanics Washington University St. Louis, Mo.翻译文献出自:MACHINE DESIGN SEPTEMBER 25,1997感谢: 冲令狐,walter2003 编辑sugar,erin 两位网友又见飘整理 August 27, 2006中华钢结构论坛 【正文部分】:有限元分析的第一步就是建立被分析对象的数学模型,这要求我们思索建模 的理论基础如弹性理论,板的 Reissner 理论,塑性变形理论等,和考虑问题的其 它信息如几何描述、材料特性,约束和荷载等等。
分析的目的就是由这些条件, 计算得到精确解 u _ EX 并同时得到位移 u _ EX 的应力函数 F ( u _ EX ) 如 Von Mises 应力等。
应力函数 F ( u _ EX ) 仅仅依赖于数学 模型的定义,而与求解该数学问题的数值近似计算方法无关;同时应力函数F ( u _ EX ) 也不依赖于网格划分、网格类型和单元尺寸。
函数 F ( u _ EX ) 与模型实体物理性质之间的差异,被称为“模型错误” 。
下一步就是使用有限元方法去找到精确解 u _ EX 的近似值 u _ FE 。
这个过程 包括选择网格划分和构件类型,如对二维板用八节点(矩形)单元,依此类推。
网格划分&单元定义被称为有限元的离散化。
离散化产生的误差可以被定义为:e=F (u _ EX ) − F (u _ FE ) F (u _ EX )大部分的分析应该把这个误差控制在 10%以内。
有限元误差估计

有限元误差估计引言有限元方法(Finite Element Method,简称FEM)是一种广泛应用于工程和科学领域的数值分析方法。
它通过将一个连续问题离散化为有限个子域,然后在每个子域上构建局部近似函数来求解问题。
有限元误差估计是在使用有限元方法求解问题时评估数值解与真实解之间的误差的重要步骤。
本文将详细介绍有限元误差估计的概念、原理和常用方法,以及其在工程和科学领域中的应用。
1. 有限元误差估计概述在使用有限元方法求解偏微分方程等连续问题时,我们通常需要将问题离散化为一个由节点和单元组成的网格。
然后,在每个单元上构建近似函数,并利用这些近似函数来计算数值解。
然而,由于近似函数只是对真实解的近似,因此数值解必然存在一定的误差。
有限元误差估计就是通过对离散化后得到的数值解进行分析,评估其与真实解之间的误差大小。
它是验证数值解精度和可靠性的重要手段之一。
2. 有限元误差估计原理有限元误差估计的原理基于两个关键概念:局部近似和全局汇总。
局部近似是指在每个单元上构建的近似函数,它能够较好地逼近真实解。
全局汇总是指将每个单元上的近似函数通过加权求和等方式得到整个域上的数值解。
在有限元方法中,我们通常使用残差作为误差的度量。
残差是真实解满足偏微分方程的程度,即方程左侧减去方程右侧得到的差值。
通过对残差进行分析,我们可以推导出数值解与真实解之间的误差估计。
3. 有限元误差估计方法有限元误差估计方法可以分为两大类:直接方法和间接方法。
3.1 直接方法直接方法是通过对离散化后得到的数值解进行分析,直接给出误差估计。
其中一种常用的直接方法是基于残差平方积分技术(Residual Squares Integration Technique)。
该方法通过对残差平方进行积分,并利用一些数学技术来推导出误差估计。
3.2 间接方法间接方法是通过构造辅助问题,利用辅助问题的解与真实解之间的关系来估计误差。
其中一种常用的间接方法是基于重构技术(Recovery Technique)。
有限元计算中的误差来源与处理方法

有限元计算中的误差来源与处理方法在有限元计算中,用户最关心自己计算的结果是否准确与合理,那么今天就和大家谈谈有限元计算的误差来源,按照误差来源类型主要分为两类:1、有限元理论假设引入的误差有限元这种数值计算方法,为了实现对现实问题的计算,引入一些力学假设,即(1)连续介质假设,认为计算模型是理想连续,没有孔洞,即位移具有单值性,但是实际产品在加工中难以避免会引入初始的孔洞缺陷,例如铸造件。
(2)材料均匀性假设,认为模型的材料参数不随空间变化为变化,是均匀的,但是实际产品在工艺处理过程中,例如淬火,都会使得材料的力学性能发生改变,并不能严格满足材料均匀性。
有限元理论与真实物理世界的差别通过一个系数来进行折中,也就是有限元计算得到一个基准结果,再通过实验进行对比,计算得到二者的转换系数。
2.有限元计算过程的误差有限元的计算过程主要包括前处理,求解和后处理三个阶段,有限元计算过程的误差主要发生在前处理和求解阶段。
第一个误差来源,即模型简化,发生在前处理阶段模型简化的是否恰当直接影响的计算结果,一般情况数值计算模型与产品的加工CAD模型还是有区别的,数值计算模型只要求把模型的主要特征反映出来,而舍去一下细致的特征,从而平衡了求解精度与计算效率。
第二个误差来源,即材料参数,就是反映计算模型的材料参数,如弹性模量,泊松比等,但是如前所述,即使找到材料参数也不能完全反应由于工艺造成的材料非均匀性,如果输入了错误的材料参数,则计算得到结果没有价值。
第三个误差来源,即工况对接,所谓工况对接,就是在软件中设置的位移约束和载荷与模型实际工况的对应情况,软件只提供了有限的位移约束和载荷类型,而分析模型可能收到的约束和载荷非常多,如果二者对应不正确,则计算结果也没有价值。
第四个误差来源,即网格划分,这个大家容易理解,也是目前很多文献提到的比较多的一个误差,要想将该误差降到最低,必须通过合理的网格加密得到网格无关解。
3.总结与处理有限元理论假设引入的误差是有限元理论与生俱来的,无法避免只能通过一些实验数据进行修正,这也说明要想有限元对工程设计产生作用,必须有与实验对比的过程。
刚塑性有限元数值模拟中产生误差的原因及改进方法(精)

刚塑性有限元数值模拟中产生误差的原因及改进方法1 引言塑性加工过程的有限元数值模拟,可以获得金属变形的详细规律,如网格变形、速度场、应力和应变场的分布规律,以及载荷-行程曲线。
通过对模拟结果的可视化分析,可以在现有的模具设计上预测金属的流动规律,包括缺陷的产生(如角部充不满、折叠、回流和断裂等)。
利用得到的力边界条件对模具进行结构分析,从而改进模具设计,提高模具设计的合理性和模具的使用寿命,减少模具重新试制的次数。
在制造技术飞速发展、市场竞争日益加剧的今天,塑性加工过程的计算机模拟可在模具虚拟设计、制造阶段就能充分检验模具设计的合理性,减少新产品模具的开发研制时间,对用户需求做出快速响应,提高市场竞争能力。
由此可见,金属成型过程的有限元模拟已是模具计算机集成制造系统中必不可少的模具设计检验环节。
金属成形工艺分体积成形和板料成形两大类,相应地,用于分析其流动规律的有限元法也分为两类,即:刚塑性、刚粘塑性有限元和弹塑性有限元。
体积成形中的挤压成形和锻造成形在实际生产中应用很广,中外学者在这方面进行了很多研究,其中二维模拟技术已相当成熟,三维模拟是目前的世界研究热点。
刚塑性、刚粘塑性有限元模拟能否对模具设计的合理性做出可靠校验,取决于模拟的精度和效率。
作者结合从事二维塑性有限元模拟的经验和当前的三维塑性有限元模拟系统开发的实践,对刚塑性、刚粘塑性有限元模拟过程中产生误差的原因进行了全面的详细分析,并提出相应的解决方法,同时以具体实例说明。
2 刚塑性、刚粘塑性有限元模拟中产生误差的原因及改进方法2.1 刚塑性有限元法求解的数学基础刚塑性有限元法是假设材料具有刚塑性的特点,把实际的加工过程定义为边值问题,从刚塑性材料的变分原理或上界定理出发,接有限元模式把能耗率表示为节点速度的非线性函数,利用数学上的最优化原理,在给定变形体某些表面的力边界条件和速度边界条件的情况下,求满足平衡方程、本构方程和体积不变条件的速度场和应力场。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元模型如何查错【一】How to find errors In finite-element models在建立有限元模型的过程 中很容易出错,如果你知 道如何查错,修正这些错 误将会变得很简单PAUL KUROWSKI President ACOM Consulting London, Ontario, Canada BARNA SZABO Professor of Mechanics Washington University St. Louis, Mo.翻译文献出自:MACHINE DESIGN SEPTEMBER 25,1997感谢: 冲令狐,walter2003 编辑sugar,erin 两位网友又见飘整理 August 27, 2006中华钢结构论坛 【正文部分】:有限元分析的第一步就是建立被分析对象的数学模型,这要求我们思索建模 的理论基础如弹性理论,板的 Reissner 理论,塑性变形理论等,和考虑问题的其 它信息如几何描述、材料特性,约束和荷载等等。
分析的目的就是由这些条件, 计算得到精确解 u _ EX 并同时得到位移 u _ EX 的应力函数 F ( u _ EX ) 如 Von Mises 应力等。
应力函数 F ( u _ EX ) 仅仅依赖于数学 模型的定义,而与求解该数学问题的数值近似计算方法无关;同时应力函数F ( u _ EX ) 也不依赖于网格划分、网格类型和单元尺寸。
函数 F ( u _ EX ) 与模型实体物理性质之间的差异,被称为“模型错误” 。
下一步就是使用有限元方法去找到精确解 u _ EX 的近似值 u _ FE 。
这个过程 包括选择网格划分和构件类型,如对二维板用八节点(矩形)单元,依此类推。
网格划分&单元定义被称为有限元的离散化。
离散化产生的误差可以被定义为:e=F (u _ EX ) − F (u _ FE ) F (u _ EX )大部分的分析应该把这个误差控制在 10%以内。
同时由于建立模型和模型的 离散化一定会产生这个误差, 正确运用有限元分析就包括对这两类误差进行评估 和控制。
有限元分析结果中的名义误差&真实误差是有区别的,最好能够加以区 别:Eapparent = Emodeling + Ediscretization Etrue ≤ Emodeling + Ediscretization名义误差可以比建模误差和离散误差的总和小,二者可能反号而相互抵消。
结果的好坏取决于模型是否反应实际(模型误差的大小)和有限元软件在转化过 程中的精度控制(离散化误差的大小) 。
WHAT IS MODELING ERROR? 何为模型误差?假设要分析一个支架,我们首先考虑到的问题应该包括:我们想得到什么结 果?是最大应力还是最大变形?是固有频率、弯曲刚度、还是温度分布?支架是 否处于弹性变形阶段?极限荷载形式有几种情况?如何模拟支撑条件等等。
有了 一个明确的目标和对我们使用的理论自身局限性的把握, 分析者就可以建立模型中华钢结构论坛 了。
有时这个模型与CAD模型是相似的,但相当多的情况是,为了简化网格的 划分,我们有必要修改模型的拓扑描述。
部分建模的过程包括以下一些问题:用 壳单元模拟薄壁墙体,对对称性、反对称性或两者的运用,是否考虑细部及忽略 不重要的特征等。
比如,选用壳单元而不用实体单元意味着我们考虑到数学模型 和相应的有限元软件的运作方式而作出了一个重要的决定。
当(研究对象的)拓扑描述已经比较理想后, 我们还需要对材料属性(选择线弹 性、弹塑性或其他)、荷载及支撑条件进行理想的简化。
我们认为这些简化精确 反应了所需模型的重要数据, 而建模当中的一些重要决策有时并未过多的考虑这 些(方面)。
简化了的模型经常是概念错误的,一个检验模型是否不合理的方法是 其解析解对应的应变能是否无穷大或趋近于零; 另一个方法是对应于数学模型的 我们感兴趣的数据在结果没有得到体现。
很多分析者认为一个有效的网格生成器 可以生成高质量的网格并降低模型误差,其实不尽然,模型是在网格划分前假定 的,因此,最合理的网格划分也无法修正一个简化不合理的数学模型。
A SYSTEMATIC APPROACH 一个系统的方法确保模型误差较小的唯一方式是把所需研究的数据放在对模型假设不敏感 之处。
类似地, 通过把所需研究的数据放在对离散不敏感之处 (不敏感的表现是: 结果对更细的网格划分或更大的p值并不发生明显的改变) ,以减少离散误差。
举 个例子:比如说我们对一块简支板沿着边缘方向的剪力感兴趣,那么经典的克西 霍夫板模型(Kirchhoff’s plate)是不可用的,可以通过一个Reissner模型或一个全 3D的弹性模型轻而易举地检验出来。
一个关于板弯曲的Reissner模型假设所有平 面内位移沿厚度方向呈线性变化、剪应变沿厚度方向保持不变。
若采用更厚的板 的话会迫使人们去置疑简支的意义、 同时会置疑是否可以给出一个精确的物理描 述。
通过系统化的途径来控制模型误差,你需要有一个分级的观点。
一个定义良 好的数学模型应该被看作是一个一般的数学模型的特殊形式。
举个例子:一个基 于线弹性理论的模型可以看作是一个几何非线性或材料非线性或两者兼而有之 的模型的特殊形式。
同样地,关于板的Reissner理论是全三维的、内有无限多可 能的板模型的特例。
当Mises应力比材料屈服点还大时,采用基于线弹性理论的 模型是不合理的。
对于一个更为庞大的模型,需要用更为复杂精确的理论来模拟 实际结构。
在任何情况下,在解决非线性问题的时候,线性模型只能被看作是该 问题的第一步。
实际上,要控制模型误差非常困难,因为对于很多模型来说,有限元代码与 单元定义及其相应理论相关。
打个比方, 单元库里可能对某单元进行这样的定义: “20节点、triquadratic位移、三线型温度、杂交、线性压力、简化积分”。
改变 模型就意味着要改变这些单元,这样会增加建模的复杂程度。
在很多情况下,由 于分析时间的紧凑以及完全进行所需计算时需要极高的专业技术, 模型误差甚至 都不会得到考虑。
通过系统方式对模型误差进行控制落后于其他有限元的发展。
最近的一个名中华钢结构论坛 为 StressCheck 的代码已经被引入到商业有限元软件中,它能够自动地估计模型 误差和离散误差,能对单元的拓扑描述、多项式次数以及相应的理论进行独立处 理。
比如说,对于可用一个高等模型来模拟弯曲的层状薄板,那么该高等模型的 最低层次应该是 Reissner 模型, 最高到三维情况。
通过高等模型的不断重复计算, 可以逐渐地“简化”模型假设直到结果不再显著改变为止。
MODELING ERRORS FROM CONVERGENCE TESTS 从收敛性检查中获知模型误差遵循 h 准则进行细化网格或者 p 准则来增大单元阶数,通过增大模型中自由 度的数目等手段,收敛性分析能够减小离散化误差。
实际上,任何有限元分析的 结果都应该由一个不断收敛迭代的过程而非单步的求解产生。
类似的认知在基于 使用 p 单元技术对每一步解答进行收敛性分析的有限元程序里将会体现的更为 透彻,例如 Pro/Mechanica, StressCheck,其他的 p 准则代码等等。
一次收敛性检查也可以对某一些经常被离散误差掩盖的特殊模型误差例如 “奇异解”扮演清道夫的角色。
问题是,奇异现象往往是某一个人在自由度数目 增加之后观测敏感性数据如何变化时出现的,此时若这些数据不趋于稳态解,则 ,要么就是模 要么就是离散化太粗糙(太少量的单元数或者太低的 p 单元阶次) 型定义错误,或者二者皆有之。
数值收敛性检查并非万无一失的奇异解探测法宝,当敏感性数据缓慢发散 时,通过数值计算的方式来进行检查将会非常困难,或者完全不可能。
此种情况 类似于计算这样一个求和式:∑ λ=1∞1 1 1 = 1+ + + + λ 2 3 41此求和式的极限是无穷大,但是,假设用一百万取代求和的上限值,计算一 百万次后再继续进行迭代的话对结果产生的影响几可忽略不计。
它似乎是收敛 的,当然,最终应该由分析者决定这些对应于解析解的相关数据是有限的还是无 穷的。
HAZARDS OF COMPARISONS 比较分析的风险试验之间的相关性提供了一个快速高效的方法来校核一系列的建模假定,并 且帮助查找包括奇异性的模型错误。
但无误的关联性也有可能被误读,并不能百 分百的证明模型是正确的,为什么呢,因为有限元方法求解的结果包含两方面误 差的影响:建模误差和离散性误差【注:离散化误差主要是由插值函数带来的,由于用任何一种单元进行离散,它都有自己的位移或者别的插值函数,其导出的 应力,应变值将会受到位移函数的影响,比如说三角形单元,导致单元内的应变 ;此二者可近似抵消而得 值为常数,但精确的应力值是一个平滑过度的应力场】中华钢结构论坛 到接近正确的结果。
假设某人想用两点来模拟很小的滚轴支撑一根梁,得到其转 角值,当此模型基于弹性理论时,用两点来表征滚轴支撑已经发生了概念错误, 在点支撑下的转角位移是无限的, 这样基于多自由度的有限元模型将会得到偏大 的转角位移值。
与此同时,一个粗糙的网格划分将会产生一个较大的离散化误差来掩盖由于 低估了转角值带来的概念性误差。
一个可信的分析结果得到的转角值应当是在滚 轴支撑被正确的模拟之后产生的,偶尔有些情况,模型得到的转角数据也会和某 个人看到的试验数据非常接近。
仅此两个错误就可以导致模型的失真,用此类模型计算应力和响应是不可靠 的。
利用网格划分技术使得计算数据与试验观测值互相匹配的方法被广泛使用, 但这并不是一个好方法。
为了正确的评价和解释某个试验的结果数据,离散化误 差必须比试验观测误差要小,并且,大量的模型离散化误差应该由试验来分别校 核。
【正文部分完】中华钢结构论坛 。
