定积分及其应用练习 带详细答案
不定积分+定积分及其应用习题附带答案
1．设是在上的一个原函数,且为奇函数,则是 ( )()F x ()f x (),-∞+∞()F x ()f x A ．偶函数 B ． 奇函数C ． 非奇非偶函数 D ．不能确定2．已知的一个原函数为,的一个原函数为,则的一个原函数()f x cos x ()g x 2x ()f g x ⎡⎤⎣⎦为 ( )A ．B ． 2x 2cos x C ． D ．2cos x cos x3．设为连续导函数,则下列命题正确的是 ( )()f x A ． ()()1222f x dx f x c '=+⎰B ．()()22f x dx f x c'=+⎰C ． ()()()222f x dx f x ''=⎰D ．()()2f x dx f x c'=+⎰4．设且()22cos sin f x x '= ,则=( )()00f =()f x A ． B ． 212x x -212x -C ． D ．1x -313x x-5．设是的一个原函数,则2xe-()f x ( )()02()limx f x x f x x∆→-∆-=∆A ． B ．22xe -28xe-C ． D ．22xe--24xe-6．设,则=( )()xf x e -=()ln f x dx x'⎰A ．B ． 1x-c +ln x c -+C ．D ． 1c x+ln x c +7．若是的一个原函数,则ln x x ()f x =()f x '8．设的一个原函数为()()tan 2f x k x =,则 2ln cos 23x k =9．若,则()2f x dx x c =+⎰=()231x f x dx -⎰10．()()2cos 2sin 2d θθθ=⎰11．若,则()()f x dx F x c =+⎰()xx ef e dx --=⎰12．若,则()ln cos f x x '=⎡⎤⎣⎦()f x =13．计算()23x xe dx +⎰14．计算()()sin ln cos ln x x dx x⎡⎤⎡⎤⎣⎦⎣⎦⎰15．计算ln(tan )sin cos x dxx x ⎰16．计算21arctan1x dx x +⎰17．计算11sin dx x+⎰18．计算19．计算20．计算21．计算22．计算23. 计算()221tan xex dx+⎰24．已知的一个原函数为,求()f x sin x x()3x f x dx '⎰1、解:可导奇函数的导函数必为偶函数.必为偶函数.选A()()f x F x '∴=2、解:(1),()()cos sin f x x x '==- ()()()22sin 2g x x x f g x x'==∴=-⎡⎤⎣⎦(2)()2cos 2cos (sin )xx x '=- 选B sin 2x =-∴3、解:()()12222f x dx f x d x''=⎰⎰()122f x c =+选A4、解：(1)()22cos 1cos f x x '=- ()1f x x'∴=- (2)()22x f x x c=-+且得()00f =0c =,选A ()22x f x x =-5、解：(1)原式=()()()022limx f x x f x x∆→-∆--⎡⎤⎣⎦-2∆()2f x '=-(2)()2xF x e-= ()()222x xf x e e --'∴==-(3) 原式= 选D222(2)4xx ee ----=6、解：(1)()()ln ln ln f x dx f x d xx''=⎰⎰()ln f x c=+(2)(),xf x e -= ()1lnln 1ln x xf x e ex-∴===(3)原式=选C 1c x+7、解：(1)()ln F x x x= ()()1ln f x F x x'∴==+(2) ()()11ln f x x x''=+=8、解：()2ln cos 23F x x =()()2sin 223cos 2xf x x -∴=-故 ()()4tan 21ln 3x F x x '=-=+43k =-9、解： 原式=()()331113f x d x ---⎰()3113x c =--+10、解：原式=2222cos sin 4sin cos d θθθθθ-⎰221144sin cos d d θθθθ=-⎰⎰11cot tan 44t cθθ=--+或1csc 2c θ⎛⎫=-+ ⎪⎝⎭11、解：原式=()()xxx f edeF e c----=-+⎰12、解：()ln cos f x dx xdx'=⎡⎤⎣⎦⎰⎰()1ln sin f x x c =+()1sin sin c x xf x e c e -==⋅13、解:原式=()22323x xx x e e dx ⎡⎤++⋅⎢⎥⎣⎦⎰()2923xxxe dx dx e dx=++⎰⎰⎰219232ln 91ln 3x x xx e e c ⋅⋅=++++14、解:原式=()()sin ln cos ln ln x x d x⋅⎰()()sin ln sin ln x d x =⎰=()21sin ln 2x c +⎡⎤⎣⎦15、解:原式=()2ln tan tan cosx dxx x⎰()ln tan tan tan x d xx=⎰()()ln tan ln tan x d x =⎰ ()21ln tan 2x c =+⎡⎤⎣⎦16、解:原式=221arctan11x dx x x ⎛⎫+ ⎪⎝⎭⎰21arctan111x d x x ⎛⎫=- ⎪⎝⎭⎛⎫+ ⎪⎝⎭⎰11arctan arctand x x=-⎰211arctan 2cx ⎛⎫=-+ ⎪⎝⎭17、解:原式=21sin 1sin xdx x --⎰21sin cos cos x dx dx x x=-⎰⎰2cos tan cos d xx x =+⎰1tan cos x cx=-+18、解:2,1,2t x t dx tdt==-=原式=()2221211tdt dt tt t=++⎰⎰=2arctan t c+c+回代19、解:令2tan ,sec x t dx tdt==原式=32tan sec sec ttdtt⎰=2tan sec td t⎰()2sec 1sec t d t=-⎰31sec sec 3t t c =-+()()3122221113x x c +-++回代20、解:令2sin ,2cos x t dx tdt ==原式=2cos 2sin cos t dtt t ⎰1csc 2tdt =⎰()1ln csc cot 2t t c -+公式12c 回代21、解:(倒代换)令211,x dx dt t t-==原式==-11arcsin 333t c =-=-+13arcsin 3c x-+回代13arccos 3c x=+(注:(三角代换)令3sec ,x t =,3sec tan dx t tdt =原式=3sec tan 19sec tan 3t t dt t c t t =+⎰)13arccos 3c x+回代22、解:2,1,xt e t ==+ ()222ln 1,1tx tdx dtt=+=+原式=222211211t t t dt dtt t ⋅+-=++⎰⎰=()2arctan t t c-+2c-+回代23、解： 原式=()221tan2tan xex x dx++⎰2tan 2tan x d x e xdx=+⎰⎰2x e 222tan tan 22tan x x x e x x e dx e xdx =-⋅⋅+⎰⎰22tan 2tan x x e x x e dx =-⋅⎰22tan x xe dx +⎰2tan x e x c=+24、解： ()sin x F x x= ()()2cos sin x x xf x F x x -'∴==原式()3x df x =⎰()()323x f x f x x dx=-⋅⎰2222cos sin cos sin 3x x x x x x x x dx x x --=⋅-⎰2cos sin 3sin 3sin x x x x xd x xdx=--+⎰⎰2cos sin 3sin 3sin 3sin x x x x x x xdx xdx =--++⎰⎰2cos 4sin 6cos x x x x x c=--+1．设初等函数在区间有定义，则在上一定 （ ）()f x [],a b ()f x [],a b A ．可导 B ．可微C ．可积D ．不连续2．若连续，下列各式正确的是 （ ）f A ．()()ba d f x dx f x dx =⎰B ．()()df x dx f x dx dx =⎰C ． ()()bx d f t dt f x dx =⎰D ．()()xad f t dt f x dx =⎰3. 下列关系式中正确的是 （ ）A ．B ．21100x x e dx e dx =⎰⎰211x x e dx e dx≥⎰⎰C ．D ．以上都不对211x x e dx e dx ≤⎰⎰4．下列各式中，正确的是 （ ）A ．B ．2101x e dx ≤≤⎰211x e dx e≤≤⎰C ． D ．以上都不对2120x e e dx e ≤≤⎰5．下列函数在区间上可用牛顿——莱布尼兹公式的是 （ ）[]1,1-AB ．C1x 6．设在上，[],a b ()()()0,'0,''0f x f x f x ><>记，，，则有 （ ）()110S f x dx =⎰()()2S f b b a =⋅-()()32b aS f b f a -=+⎡⎤⎣⎦A ． B ．123S S S <<213S S S <<C ． D ．312S S S<<231S S S <<7．xx →=8．设连续，且，则 ()f x ()()xe xF x f t dt -=⎰()'F x =9．设连续，则 ()'f x 1'2x f dx ⎛⎫= ⎪⎝⎭⎰10．设则()()120121f x f x dx x=-+⎰ ()1f x dx =⎰11．设连续，且则 ()f x ()21301,(1)x f t dt x x -=+>⎰()8f =12．设，则y 的极小值为()01xy t dt =-⎰13．方程，确定，求cos 0yx t e dt tdt +=⎰⎰()y y x =0x dydx=14．设在连续，且满足，求 ()f x []0,1()()13243f x x x f x dx =-⎰()f x 15．讨论方程在区间内实根的个数4013101xx dt t --=+⎰()0,116．设在连续，且在单调减少，讨论在区间()f x [],a b (),a b ()()1xa F x f t dt x a=-⎰的单调性(),a b 17．求()22220limx t xx t e dt te dt→⎰⎰18．设其中为连续函数，求()()2xa x F x f t dt x a=-⎰f ()lim x a F x →19．设，且可导，，求()()01122xf t dt f x =-⎰()f x ()0f x ≠()f x20．若为连续的奇函数，判别的奇偶性()f x ()0xf t dt ⎰21．1321sin x x x dx-⎡⎤⎣⎦⎰22．已知，求221x t e dt -⎰()1xf x dx⎰23．1⎰24．设连续，证明()f x 并由此计算()()20sin 2sin f x dx f x dx ππ=⎰⎰0π⎰1、解：初等函数在定义区间内必连续，连续必可积。
定积分练习题参考答案
3
x
4
sin 2
x
dx
解：原式
3
xdctgx
xctgx
3
3
ctgxdx
4
4
4
1 4
3 9
ln
sin
x
3
4
1 4
3 9
ln
3 ln 2
2 2
1 4
3 9
1 2
ln
3 2
3
14．
4 ln x dx
1x
解：原式 2
4
ln xd
x
1
2
4
4
x ln x
1
1
xd ln x
2
sin 2x 0
0
sin
2
x
2
xdx
3 1
6 4 0 xd cos 2x
3 6
1 4
x
cos
2x
0
0
cos 2xdx
3 6
4
18．
e
1
sin
ln
x
dx
解：原式
x sinlnLeabharlann x e 1e1
x cosln
x
1 x
dx
e
sin 1
e
1
cosln
x
dx
e sin 1
x cosln
x e 1
d
3
sin
2
d
sin
4
22 3 3
4． 1 xdx
1 5 4x
解：令 5 4x u ，则 x 5 1 u 2 ， dx 1 udu
44
2
定积分及其应用练习 带详细答案
定积分及其应用题一 题面：求由曲线2(2)y x =+与x 轴,直线4y x =-所围成的平面图形的面积． 答案：323．变式训练一题面：函数f （x )＝错误!的图象与x 轴所围成的封闭图形的面积为( ) A.错误! B ．2 C ．3D ．4答案：D. 详解：画出分段函数的图象，如图所示，则该图象与x 轴所围成的封闭图形的面积为错误!×2×2＋∫错误!02cos x d x ＝2＋2sin x 错误!＝4.变式训练二 题面:由直线y ＝2x 及曲线y ＝3－x 2围成的封闭图形的面积为( ) A ．2错误! B ．9－2错误! C.错误!D 。
错误!答案： 详解：注意到直线y ＝2x 与曲线y ＝3－x 2的交点A ,B 的坐标分别是(－3，－6)，(1，2)，因此结合图形可知,由直线y ＝2x 与曲线y ＝3－x 2围成的封闭图形的面积为错误!（3－x 2－2x ）d x ＝错误!错误!＝3×1－错误!×13－12－错误!错误!＝错误!，选D.题二 题面：如图所示,在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为（ ）．A ．14B ．错误!C ．错误!D ．错误!变式训练一题面：函数f (x ）＝sin(ωx ＋φ)的导函数y ＝f ′(x )的部分图象如图所示，其中，P 为图象与y 轴的交点，A ，C 为图象与x 轴的两个交点,B 为图象的最低点．若在曲线段ABC 与x 轴所围成的区域内随机取一点，则该点在△ABC 内的概率为________．答案：错误!. 详解：设A（x0，0），则ωx0＋φ＝错误!，∴x0＝错误!－错误!.又y＝ωcos(ωx＋φ)的周期为错误!，∴|AC｜＝错误!,C错误!。
依题意曲线段错误!与x轴围成的面积为S＝－∫错误!－错误!＋错误!错误!－错误!ωcos(ωx＋φ）d x＝2。
∵｜AC|＝πω，｜y B|＝ω，∴S△ABC＝错误!.∴满足条件的概率为错误!.变式训练二题面：（2012•福建）如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（）A．B．C．D．答案:C.详解：根据题意，正方形OABC的面积为1×1=1,而阴影部分由函数y=x与y=围成，其面积为∫01（﹣x）dx=（﹣）｜01=，则正方形OABC中任取一点P，点P取自阴影部分的概率为=；故选C．金题精讲题一题面：(识图求积分，二星)已知二次函数y＝f(x)的图象如图所示,则它与x轴所围图形的面积为()．A．错误!B．错误!C．错误!D．错误!答案:变式训练一题面：如图求由两条曲线y ＝－x 2,y ＝－错误!x 2及直线y ＝－1所围成的图形的面积．答案:错误!。
数学必修二：微积分中的定积分习题答案
数学必修二：微积分中的定积分习题答案在微积分学习的过程中，掌握定积分的概念和求解方法是非常重要的。
本文将提供一些关于定积分的习题，并给出详细的解答，帮助读者更好地理解和掌握定积分的应用。
一、基础习题1. 求函数f(x)=2x的定积分∫[1, 3] 2x dx的值。
解答：利用定积分的定义，首先求出原函数F(x) = x^2，在[1, 3]范围内，F(3) - F(1)即为所求的定积分的值。
F(x) = x^2∫[1, 3] 2x dx = [x^2]1^3 = 3^2 - 1^2 = 8。
2. 计算定积分∫[-2, 2] |x| dx。
解答：分段函数|x|的定义为：当x≥0时，|x| = x；当x<0时，|x| = -x。
所以在[-2, 2]范围内，|x|可分为两个部分，负值和正值。
∫[-2, 2] |x| dx = ∫[-2, 0] -x dx + ∫[0, 2] x dx。
根据定积分的性质，负号可以提出定积分符号外，所以上式等于：= -∫[-2, 0] x dx + ∫[0, 2] x dx。
根据定积分的定义，∫[-2, 0] x dx = [x^2/2]_(-2)^0 = (0^2/2) - ((-2)^2/2) = 2。
同样，∫[0, 2] x dx = [x^2/2]_0^2 = 2^2/2 - 0^2/2 = 2。
将上述结果代入原式得：-∫[-2, 0] x dx + ∫[0, 2] x dx = -2 + 2 = 0。
二、综合习题1. 求函数f(x) = x^3 - 2x在[-1, 2]上的定积分。
解答：首先求出原函数F(x)，F(x) = （x^4/4） - (x^2)。
∫[-1, 2] (x^3 - 2x)dx = [（x^4/4） - (x^2)]_(-1)^2。
将x代入方程得：= （2^4/4） - (2^2) - [(-1)^4/4] - [(-1)^2] = 8/4 - 4 - 1/4 - 1。
定积分及其应用习题详解
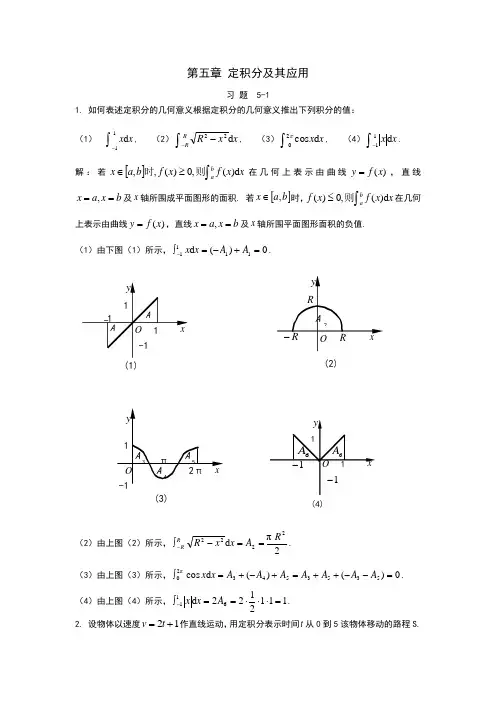
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义根据定积分的几何意义推出下列积分的值： （1）⎰-x x d 11, （2）⎰--x x R R R d 22, （3）⎰x x d cos 02π, （4）⎰-x x d 11.解：若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时，⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围平面图形面积的负值. （1）由下图（1）所示，0)(d 1111=+-=⎰-A A x x .（2）由上图（2）所示，2πd 2222R A x x R R R==-⎰-.（3）由上图（3）所示，0)()(d cos 5353543π20=--++=+-+=⎰AA A A A A A x x .（4）由上图（4）所示，1112122d 611=⋅⋅⋅==⎰-A x x .2. 设物体以速度12+=t v 作直线运动，用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解：=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解：任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =，小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式：∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解：上在]1,0[)(2x x f =连续函数，故可积，因此为方便计算，我们可以对[]0,1 n 等分，分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点，故∑∑∑===∆=∆=∆n i i i n i i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ（即时∞→n ），由定积分的定义得： 120d x x ⎰=31．5. 利用定积分的估值公式，估计定积分⎰-+-1134)524(x x x d 的值.解：先求524)(34+-=x x x f 在[]1,1-上的最值，由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小，知min max 5093,111024f f ==，由定积分的估值公式，得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ，哪个积分值较大解：在[]0,1区间内：22xx x x e e ≥⇒≥ 由性质定理知道：⎰10 d x e x≥⎰10 d 2x e x7. 证明：⎰---<<2121212d 22x e ex 。
定积分应用题附答案(可编辑修改word版)
⎩ y ⎨ ⎩ 2 《定积分的应用》复习题一．填空：1. 曲线 y = ln x , y = ln a , y = ln b (0 < a < b )及y 轴所围成的平面图形的面积为 A =ln be y dy =b-aln a2. 曲线y = x 2和y = x 所围成的平面图形的面积是 1 3二．计算题：1. 求由抛物线 y 2= 2x 与直线 2x + y – 2 = 0 所围成的图形的面积。
解：（1）确定积分变量为 y ，解方程组⎧ y 2 = 2x ⎧x 1 = 1/ 2 ⎧ x 2 = 2 ⎨y = -2x + 2 得 ⎩ y 1 = 11 , ⎨ = -2 即抛物线与直线的交点为（ ，1）和( 2 , - 2 ).故所求图形在直线 y = 1 和 y 2= - 2 之间，即积分区间为［－2，1 ］。
（2）在区间［－2，1］上，任取一小区间为［ y , y + dy ］,对应的窄条面积近 1 1似于高为［(１－ y ）- y 2 ］,底为 dy 的矩形面积，从而得到面积元素22 11dA = [(１－ y)-y 2 ]dy22(3)所求图形面积 A =1[（1- 11 y ）- y2 ]dy = [y - 1 y 2 – 1 y3 ]1 =9⎰ - 22246-242. 求抛物线 y = - x 2+ 4x - 3 及其在点（0，- 3）和（3，0）处的切线所围成的图形的面积。
解：由 y = - x 2 + 4x – 3 得y ' = -2x + 4 , y '(0) = 4, y '(3) = -2 。
抛物线在点（0，- 3）处的切线方程为 y = 4x – 3 ;在点（3，0）处的切线方程为 3 y = - 2x + 6 ; 两切线的交点坐标为 （ ，3 ）。
2故 面积 A =⎰⎰2=⎰2⎪ ⎰ ⎰ ⎰ =3 (1+ 2 c os + )d + 2 (1+ cos 2)d = 3392 [(4x - 3) - (x + 4x - 3)] dx +3 [(-2x + 6) - (x + 4x - 3)] dx = 023. 求由摆线 x = a (t – sint) , y = a( 1- cost) 的一拱（ 0 ≤ t ≤ 2）与横轴所围成的图形的面积。
(完整word版)定积分典型例题20例答案
定积分典型例题20例答案例1 求33322321lim(2)n n n n n →∞+++．分析 将这类问题转化为定积分主要是确定被积函数和积分上下限．若对题目中被积函数难以想到，可采取如下方法：先对区间[0,1]n 等分写出积分和，再与所求极限相比较来找出被积函数与积分上下限．解 将区间[0,1]n 等分，则每个小区间长为1i x n ∆=，然后把2111n n n=⋅的一个因子1n 乘入和式中各项．于是将所求极限转化为求定积分．即33322321lim(2)n n n n n →∞+++=333112lim ()n n n n nn →∞+++=13034xdx =⎰．例2 2202x x dx -⎰=_________．解法1 由定积分的几何意义知，2202x x dx -⎰等于上半圆周22(1)1x y -+= (0y ≥)与x 轴所围成的图形的面积．故2202x x dx -⎰=2π． 解法2 本题也可直接用换元法求解．令1x -=sin t （22t ππ-≤≤），则222x x dx -⎰=2221sin cos t tdt ππ--⎰=2221sin cos t tdt π-⎰=2202cos tdt π⎰=2π 例3 （1）若22()x t xf x e dt -=⎰，则()f x '=___；（2）若0()()xf x xf t dt =⎰，求()f x '=___．分析 这是求变限函数导数的问题，利用下面的公式即可()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ''=-⎰．解 （1）()f x '=422x x xe e ---；（2） 由于在被积函数中x 不是积分变量，故可提到积分号外即0()()xf x x f t dt =⎰，则可得()f x '=0()()xf t dt xf x +⎰．例4 设()f x 连续，且31()x f t dt x -=⎰，则(26)f =_________．解 对等式310()x f t dt x -=⎰两边关于x 求导得32(1)31f x x -⋅=，故321(1)3f x x -=，令3126x -=得3x =，所以1(26)27f =． 例5 函数11()(3)(0)x F x dt x t =->⎰的单调递减开区间为_________．解 1()3F x x'=-，令()0F x '<得13x >，解之得109x <<，即1(0,)9为所求． 例6 求0()(1)arctan xf x t tdt =-⎰的极值点．解 由题意先求驻点．于是()f x '=(1)arctan x x -．令()f x '=0，得1x =，0x =．列表如下：故1x =为()f x 的极大值点，0x =为极小值点．例7 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同，其中2arcsin 0()xt g x e dt -=⎰，[1,1]x ∈-，试求该切线的方程并求极限3lim ()n nf n→∞．分析 两曲线()y f x =与()y g x =在点(0,0)处的切线相同，隐含条件(0)(0)f g =，(0)(0)f g ''=．解 由已知条件得2(0)(0)0t f g e dt -===⎰，且由两曲线在(0,0)处切线斜率相同知2(arcsin )2(0)(0)11x x e f g x -=''===-．故所求切线方程为y x =．而3()(0)3lim ()lim33(0)330n n f f n nf f n n→∞→∞-'=⋅==-． 例8 求 22000sin lim(sin )x x xtdtt t t dt→-⎰⎰；分析 该极限属于型未定式，可用洛必达法则． 解 22000sin lim (sin )x x xtdtt t t dt→-⎰⎰=2202(sin )lim (1)(sin )x x x x x x →-⋅⋅-=220()(2)lim sin x x x x →-⋅-=304(2)lim 1cos x x x→-⋅-x(,0)-∞0 (0,1)1 (1,)+∞()f x '-＋－=2012(2)lim sin x x x→-⋅=0．注 此处利用等价无穷小替换和多次应用洛必达法则．例9 试求正数a 与b ，使等式2201lim1sin x x t dt x b x a t→=-+⎰成立． 分析 易见该极限属于型的未定式，可用洛必达法则． 解 20201lim sin x x t dt x b x a t →-+⎰=220lim 1cos x x a x b x →+-=22001lim lim 1cos x x x b x a x→→⋅-+201lim 11cos x x b x a →==-，由此可知必有0lim(1cos )0x b x →-=，得1b =．又由2012lim 11cos x x x a a→==-， 得4a =．即4a =，1b =为所求． 例10 设sin 20()sin x f x t dt =⎰，34()g x x x =+，则当0x →时，()f x 是()g x 的（ ）．A ．等价无穷小．B ．同阶但非等价的无穷小．C ．高阶无穷小．D ．低阶无穷小．解法1 由于 22300()sin(sin )cos lim lim()34x x f x x xg x x x →→⋅=+ 2200cos sin(sin )lim lim34x x x x x x →→=⋅+ 22011lim 33x x x →==． 故()f x 是()g x 同阶但非等价的无穷小．选B ．解法2 将2sin t 展成t 的幂级数，再逐项积分，得到sin 223370111()[()]sin sin 3!342x f x t t dt x x =-+=-+⎰，则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f x g x x x x→→→-+-+===++． 例11 计算21||x dx -⎰．分析 被积函数含有绝对值符号，应先去掉绝对值符号然后再积分．解 21||x dx -⎰＝0210()x dx xdx --+⎰⎰＝220210[][]22x x --+＝52．注 在使用牛顿－莱布尼兹公式时,应保证被积函数在积分区间上满足可积条件．如 33222111[]6dx x x --=-=⎰，则是错误的．错误的原因则是由于被积函数21x 在0x =处间断且在被积区间内无界.例12 设()f x 是连续函数，且10()3()f x x f t dt =+⎰，则()________f x =．分析 本题只需要注意到定积分()baf x dx ⎰是常数（,a b 为常数）．解 因()f x 连续，()f x 必可积，从而10()f t dt ⎰是常数，记1()f t dt a =⎰，则()3f x x a =+，且11(3)()x a dx f t dt a +==⎰⎰．所以2101[3]2x ax a+=，即132a a +=， 从而14a =-，所以 3()4f x x =-．例13 计算2112211x x dx x-++-⎰．分析 由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性． 解 2112211x x dx x-++-⎰=211112221111x x dx dx x x--++-+-⎰⎰．由于22211x x+-是偶函数，而211x x+-是奇函数，有112011xdx x-=+-⎰, 于是2112211x x dx x -++-⎰=2102411x dx x +-⎰=22120(11)4x x dx x--⎰=11200441dx x dx --⎰⎰ 由定积分的几何意义可知12014x dx π-=⎰, 故211122444411x x dx dx xππ-+=-⋅=-+-⎰⎰．例14 计算220()xd tf x t dt dx -⎰，其中()f x 连续． 分析 要求积分上限函数的导数，但被积函数中含有x ，因此不能直接求导，必须先换元使被积函数中不含x ，然后再求导．解 由于220()xtf x t dt -⎰=2221()2x f x t dt-⎰． 故令22x t u -=，当0t =时2u x =；当t x =时0u =，而2dt du =-，所以220()x tf x t dt -⎰=201()()2x f u du -⎰=201()2x f u du ⎰， 故220()x d tf x t dt dx -⎰=201[()]2x d f u du dx ⎰=21()22f x x⋅=2()xf x ．错误解答220()x d tf x t dt dx -⎰22()(0)xf x x xf =-=． 错解分析 这里错误地使用了变限函数的求导公式，公式()()()xad x f t dt f x dx 'Φ==⎰中要求被积函数()f t 中不含有变限函数的自变量x ，而22()f x t -含有x ，因此不能直接求导，而应先换元．例15 计算30sin x xdx π⎰．分析 被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法．解30s i n x x d x π⎰30(c o s )x d x π=-⎰33[(c o s )](c o s )x x x d x ππ=⋅---⎰ 30cos 6xdx ππ=-+⎰326π=-． 例16 计算120ln(1)(3)x dx x +-⎰．分析 被积函数中出现对数函数的情形，可考虑采用分部积分法．解 120ln(1)(3)x dx x +-⎰=101ln(1)()3x d x +-⎰=1100111[ln(1)]3(3)(1)x dx x x x +-⋅--+⎰ =101111ln 2()2413dx x x-++-⎰11ln 2ln324=-． 例17 计算20sin x e xdx π⎰．分析 被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法．解 由于2sin xe xdx π⎰20sin xxde π=⎰220[sin ]cos xx e x e xdx ππ=-⎰220cos x e e xdx ππ=-⎰， （1）而20cos xe xdx π⎰20cos xxde π=⎰220[cos ](sin )xx e x e x dx ππ=-⋅-⎰20sin 1x e xdx π=-⎰， （2）将（2）式代入（1）式可得20sin xe xdx π⎰220[sin 1]x e e xdx ππ=--⎰,故20sin xe xdx π⎰21(1)2e π=+．例18 计算1arcsin x xdx ⎰．分析 被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．解 10arcsin x xdx ⎰210arcsin ()2x xd =⎰221100[arcsin ](arcsin )22x x x d x =⋅-⎰21021421x dx x π=--⎰． （1） 令sin x t =，则2121x dx x-⎰222sin sin 1sin td t tπ=-⎰220sin cos cos ttdt t π=⋅⎰220sin tdt π=⎰201cos22t dt π-==⎰20sin 2[]24t t π-4π=． （2）将（2）式代入（1）式中得1arcsin x xdx =⎰8π． 例19设()f x [0,]π上具有二阶连续导数，()3f π'=且0[()()]cos 2f x f x xdx π''+=⎰，求(0)f '．分析 被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解． 解 由于0[()()]cos f x f x xdx π''+⎰00()sin cos ()f x d x xdf x ππ'=+⎰⎰[]000{()sin ()sin }{[()cos ]()sin }f x x f x xdx f x x f x xdx ππππ'''=-++⎰⎰()(0)2f f π''=--=．故 (0)f '=2()235f π'--=--=-． 例20 计算243dxx x +∞++⎰． 分析 该积分是无穷限的的反常积分，用定义来计算． 解2043dx x x +∞++⎰=20lim 43t t dx x x →+∞++⎰=0111lim ()213t t dx x x →+∞-++⎰ =011lim [ln ]23t t x x →+∞++=111lim (ln ln )233t t t →+∞+-+ =ln 32．。
(完整版)定积分应用题附答案
《定积分的应用》复习题一．填空：1．曲线ln ,ln ,ln (0)y x y a y b a b y ===<<及轴所围成的平面图形的面积为A =ln ln by ae dy ⎰=b-a______2.2y x y ==曲线和 ____13____二．计算题：1．求由抛物线 y 2 = 2x 与直线 2x + y – 2 = 0 所围成的图形的面积。
解：（1）确定积分变量为y ，解方程组2222y x y x ⎧=⎨=-+⎩ 得12121/22,12x x y y ==⎧⎧⎨⎨==-⎩⎩ 即抛物线与直线的交点为（21，1）和( 2 , - 2 ).故所求图形在直线y = 1和y = - 2 之间，即积分区间为［－2，1 ］。
（2）在区间［－2，1］上，任取一小区间为［ y , y + dy ］,对应的窄条面积近似于高为［(１－21y ）-21y 2 ］,底为dy 的矩形面积，从而得到面积元素 dA = [(１－21y)- 21y 2 ]dy (3)所求图形面积 A =⎰-12[（1- 21y ）-21y 2 ]dy = [y - 41y 2 – 61y 3]12-= 942．求抛物线 y = - x 2 + 4x - 3 及其在点（0，- 3）和（3，0）处的切线所围成的图形的面积。
解：由y = - x 2 + 4x – 3 得 '24,'(0)4,'(3)2y x y y =-+==-。
抛物线在点（0，- 3）处的切线方程为 y = 4x – 3 ;在点（3，0）处的切线方程为 y = - 2x + 6 ; 两切线的交点坐标为 （ 32，3 ）。
故 面积A =332223029[(43)(43)][(26)(43)]4x x x dx x x x dx --+-+-+-+-=⎰⎰3．求由摆线 x = a (t – sint) , y = a( 1- cost) 的一拱（02t π≤≤）与横轴所围成的图形的面积。
第6章定积分的应用习题集及答案
第六章 习题 定积分的应用一．选择题1．曲线x y ln =、a y ln =、b y ln =（b a <<0）和y 轴所围图形的面积为（ C ） （A ）⎰ba xdx ln ln ln ； （B ）⎰be a e xdx e ； （C ）⎰ba ydy e ln ln ； （D ）⎰ae b e xdx ln ．2．曲线x e y =下方与该曲线过原点的切线左方和y 轴右方所围图形的面积为（a ）（A ）⎰-10)(dx ex e x ； （B ）⎰-edy y y y 1)ln (ln ； （C ）⎰-e x x dx x e e 1)(； （D ）⎰-10)ln (ln dy y y y ．3．摆线)sin (t t a x -=、)cos 1(t a y -=（0>a ）的一拱（π20≤≤t ）与x 轴所围图形绕x 轴旋转一周所成旋转体的体积为（ D ）（A ）⎰-ππ2022)cos 1(dt t a ； （B ）⎰--at t a d t a ππ2022)]sin ([)cos 1(； （C ）⎰-a dt t a ππ2022)cos 1(； （D ）⎰--ππ2022)]sin ([)cos 1(t t a d t a ． 4．曲线θρcos 2a =(0>a )所围图形的面积为（ D ）（A ）⎰22)cos 2(21πθθd a ； （B ）⎰-ππθθd a 2)cos 2(21；（C ）⎰πθθ202)cos 2(21d a ； （D ）⎰202)cos 2(212πθθd a ．5．连续曲线)(x f y =与直线a x =、b x =（b a <≤0）及x 轴围成的图形绕y 轴旋转一周生成的旋转体体积为（ B ）（A ）⎰ba dx x xf )(2π；（B ）⎰ba dx x f x )(2π；（C ）⎰ba dx x xf )(22π；（D ）⎰ba dx x f x )(22π． 6．半径为R 的半球形水池已装满水．要将水全部吸出水池，需做功的为 （ C ）（A ）⎰-Rdy y R 022)(π；（B ）⎰Rdy y 02π；（C ）⎰-Rdy y R y 022)(π；（D ）⎰Rdy y 03π．二．计算题1．求曲线221x y =与822=+y x 所围图形（上半平面部分）的面积．解：易知：曲线221x y =与822=+y x 的交点为(2,2)±。
数学选修2-2定积分的简单应用练习题含答案
数学选修2-2定积分的简单应用练习题含答案学校：__________ 班级：__________ 姓名：__________ 考号：__________1. 曲线y=sin x与x轴在区间[0, 2π]上所围成阴影部分的面积为（）A.−4B.−2C.2D.42. 由直线x=0，x=2，y=0和抛物线x=√1−y所围成的平面图形绕x轴旋转所得几何体的体积为（）A.46 15πB.43π C.1615π D.83π3. 由直线x=1，x=2，y=0与抛物线y=x2所围成的曲边梯形的面积为（）A.1 3B.53C.73D.1134. 由曲线y=x2+2与y=3x，x=0，x=1所围成的平面图形的面积为（）A.5 6B.1C.53D.25. 曲线y=x2和y2=x所围成的平面图形绕x轴旋转一周后，所形成的旋转体的体积为（）A.3π10B.π2C.π5D.7π106. 函数y=sin x，y=cos x在区间(π4，5π4)内围成图形的面积为（）A.√2B.2√2C.3√2D.4√27. 一物体在力F(x)=3+e2x(x的单位：m，F的单位：N)的作用下，沿着与力F相同的方向，从x=0处运动到x=1处，力F(x)所做的功为（）A.(3+e2)JB.(3+12e2)J C.(52+12e2)J D.(2+e2)J8. 由曲线y=√x，y=x−2及x轴所围成的封闭图形的面积是()A.4B.103C.163D.1549. 下列表示图中f(x)在区间[a, b]上的图象与x 轴围成的面积总和的式子中，正确的是（ ）A.∫f ba (x)dx B.|∫f ba (x)dx|C.∫f c 1a (x)dx +∫f c 2c 1(x)dx +∫f cc 2(x)dxD.∫f c 1a (x)dx −∫f c 2c 1(x)dx +∫f cc2(x)dx10. 直线y =x 与曲线y =√x 3围成的平面图形的面积是．（ ） A.14 B.2 C.1D.1211. 设函数f(x)=ax 2+c(a ≠0)，若∫f 10(x)dx =f(x 0)，0≤x 0≤1，则x 0的值为________．12. y =cos x 与直线x =0，x =π及x 轴围成平面区域面积为________．13. 由曲线y =|x|，y =−|x|，x =2，x =−2合成的封闭图形绕y 轴旋转一周所得的旋转体的体积为V ，则V =________．14. 两曲线x −y =0，y =x 2−2x 所围成的图形的面积是________．15. 由曲线y =x 2和直线x =0，x =1，以及y =0所围成的图形面积是________． 16.若在平面直角坐标系xOy 中将直线y =x 2与直线x =1及x 轴所围成的图形绕x 轴旋转一周得到一个圆锥，则该圆锥的体积V 圆锥=∫π10(x 2)2dx =π12x 3|10=π12据此类比：将曲线y =x 2与直线y =9所围成的图形绕y 轴旋转一周得到一个旋转体，则该旋转体的体积V =________．17. 在直角坐标平面内，由直线x=1，x=2，y=0和曲线y=1所围成的平面区域的x面积是________．18. 在xOy平面上，将抛物线弧y=1−x2(0≤x≤1)、x轴、y轴围成的封闭图形记为D，如图中曲边三角形OAB及内部．记D绕y轴旋转一周而成的几何体为Ω，过点(0, y)(0≤y≤1)作Ω的水平截面，所得截面面积为(1−y)π，试构造一个平放的直三棱柱，利用祖暅原理得出Ω的体积值为________．19. 函数f(x)=x3−x2+x+1在点(1, 2)处的切线与函数g(x)=x2−x围成的图形的面积等于________．2ax2−a2x)dx，则f(a)的最大值为________．20. 已知f(a)=∫(1x2在第一象限内的交点为P.21. 已知曲线C1：y2=2x与C2：y=12(1)求曲线C2在点P处的切线方程；(2)求两条曲线所围成图形的面积S.22. 求由曲线y=x2+2与y=3x，x=0，x=2所围成的平面图形的面积．23. 已知曲线C:y=x2(x≥0)，直线l为曲线C在点A(1, 1)处的切线．（1）求直线l的方程；（2）求直线l与曲线C以及x轴所围成的图形的面积．24. 如图一是火力发电厂烟囱示意图．它是双曲线绕其一条对称轴旋转一周形成的几何体，烟囱最细处的直径为10m，最下端的直径为12m，最细处离地面6m，烟囱高14m，试求该烟囱占有空间的大小．（精确到0.1m3）25.(1)已知复数z的共轭复数是z¯，且z⋅z¯−3iz=10，求z；1−3ix所围成的平面图形的面积．(2)求曲线y=√x与直线x+y=2，y=−1326.（1）已知(√x +2√x4)n 展开式的前三项系数成等差数列．求n ．（2）如图所示，在一个边长为1的正方形AOBC 内，曲线y =x 2和曲线y =√x 围成一个叶形图（阴影部分），向正方形AOBC 内随机投一点（该点落在正方形AOBC 内任何一点是等可能的），求所投的点落在叶形图内部的概率．27. 求由下列给出的边界所围成的区域的面积： （1）y ＝sin x(π4≤x ≤π)，x =π4，y ＝0；（2）y ＝x 2，y ＝2x 2，x ＝1；（3）y ＝x 2，y =√x ．28. 求由y =4−x 2与直线y =2x −4所围成图形的面积．29. 已知曲线y =sin x 和直线x =0，x =π，及y =0所围成图形的面积为S 0． （1）求S 0．（2）求所围成图形绕ox 轴旋转所成旋转体的体积．30. 已知函数y =f(x)的图形如图所示，给出y =f(x)与x =10和x 轴所围成图形的面积估计值；要想得到误差不超过1的面积估计值，可以怎么做？31. 已知曲线C:y =√x 和直线：x −2y =0由C 与围成封闭图形记为M ． （1）求M 的面积；（2）若M 绕x 轴旋转一周，求由M 围成的体积．32. 已知f(x)为一次函数，且f(x)=x ∫f 20(t)dt +1， （1）求函数f(x)的解析式；（2）若g(x)=x ⋅f(x)，求曲线y =g(x)与x 轴所围成的区域绕x 轴旋转一周所得到的旋转体的体积．33. 已知圆锥的高为ℎ，底半径为r ，用我们计算抛物线下曲边梯形面积的思路，推导圆锥体积的计算公式． [提示：（1）用若干张平行于圆锥底面的平面把它切成n 块厚度相等的薄片；（2）用一系列圆柱的体积近似地代替对应的薄片，圆柱的高为ℎn ，底半径顺次为：rn ，2r n，3r n…，(n−1)r n，r ；（3）问题归结为计算和式V(n)=ℎn ×(12+22+...+n 2)×πr 2n 2，当n 越来越大时所趋向的值．]．34. 求曲线y =√x(0≤x ≤4)上的一条切线，使此切线与直线x =0，x =4以及曲线y =√x 所围成的平面图形的面积最小．35. 过点(0, 1)作曲线L:y =ln x 的切线，切点为A ．又L 与x 轴交于B 点，区城D 由L 、x 轴与直线AB 围成，求区域D 的面积及D 绕x 轴旋转一周所得旋转体的体积．36. 求曲线y =2x −x 2，y =2x 2−4x 所围成图形的面积．37. 已知∫(103ax +1)(x +b)dx =0，a ，b ∈R ，试求ab 的取值范围．38. 求下列曲线所围成图形的面积：曲线y=cos x，x=π2，x=3π2，y=0．39. 求曲线y=sin x与直线x=−π2，x=5π4，y=0所围成的平面图形的面积．40. 如图，直线y＝kx分抛物线y＝x−x2与x轴所围图形为面积相等的两部分，求k的值．参考答案与试题解析数学选修2-2定积分的简单应用练习题含答案一、 选择题 （本题共计 10 小题 ，每题 3 分 ，共计30分 ） 1.【答案】 D【考点】定积分在求面积中的应用 【解析】由积分的几何意义可得，S =2∫sin π0xdx ，即可得出结论． 【解答】解：由积分的几何意义可得，S =2∫sin π0xdx =(−cos x)|0π=4． 故选：D ． 2.【答案】 A【考点】用定积分求简单几何体的体积 【解析】由题意此几何体的体积可以看作是∫π20(1−x 2)2dx ，求出积分即得所求体积． 【解答】解：由题意几何体的体积； ∫π20(1−x 2)2dx=π(x −23x 3+15x 5)|02=π(2−23×23+15×25) =4615π 故选A ． 3. 【答案】 C【考点】定积分在求面积中的应用 【解析】先根据题意画出区域，然后依据图形利用定积分表示出曲边梯形的面积，最后用定积分的定义求出所求即可． 【解答】解：直线x =1，x =2，y =0与抛物线y =x 2所围成的曲边梯形的面积为S =∫x 221dx =13x 3|12=83−13=73，故选：C ．4.【答案】 A【考点】定积分的简单应用 【解析】因为所求区域均为曲边梯形，所以使用定积分方可求解，然后求出曲线y =x 2+2与y =3x 的交点坐标，然后利用定积分表示所围成的平面图形的面积，根据定积分的定义解之即可． 【解答】解：联立{y =x 2+2y =3x，解得x 1=1，x 2=2∴ S =∫(10x 2+2−3x)d x =[13X 3+2X −32X 2]01=56 故选：A 5.【答案】 A【考点】用定积分求简单几何体的体积 【解析】欲求曲线y =x 2和y 2=x 所围成的平面图形绕x 轴旋转一周后所形成的旋转体的体积，可利用定积分计算，即求出被积函数y =π(x −x 4)在0→1上的积分即可． 【解答】解：设旋转体的体积为V ，则v =∫π10(x −x 4)dx =π(12x 2−15x 5)|01=3π10．故旋转体的体积为：3π10． 故选A ． 6. 【答案】 B【考点】定积分在求面积中的应用 【解析】根据定积分的几何意义，所求面积为S =∫(5π4π4sin x −cos x)dx ，然后利用公式求出sin x −cos x 的原函数F(x)，算出F(5π4)−F(π4)的值，即为所求图形的面积． 【解答】解：根据题意，所求面积为S =∫(5π4π4sin x −cos x)dx =(−cos x −sin x +C)|π45π4 （其中C 为常数） ∴ S =(−cos 5π4−sin5π4+C)−(−cos π4−sin π4+C)=(√22+√22+C)−(−√22−√22+C)=2√2 故选B 7.【答案】 C【考点】定积分的简单应用 【解析】先根据题意建立关系式∫(103+e 2x )dx ，然后根据定积分的计算法则求出定积分的值即可． 【解答】解：根据题意可知F(x)所做的功为∫(103+e 2x )dx =(3x +12e 2x )|01=3+12e 2−12=52+12e 2故选C ．8.【答案】 B【考点】定积分在求面积中的应用 【解析】根据定积分的几何意义，先求出积分的上下限，即可求出所围成的图形的面积 【解答】解：联立直线y =x −2，曲线y =√x 构成方程组，解得{x =4,y =2,联立直线y =x −2，y =0构成方程组，解得{x =2,y =0,如图所示：∴曲线y=√x，y=x−2及x轴所围成的封闭图形的面积S=∫√x40dx−∫(42x−2)dx=2x32|04 −(1x2−2x)|24=163−2=103．故选B．9.【答案】D【考点】定积分在求面积中的应用定积分定积分的简单应用【解析】先根据定积分的几何意义可知将区间[a, b]分成三段，然后利用上方曲线方程减下方的曲线方程，求积分即为面积，从而求出所求．【解答】解：根据定积分的几何意义可知将区间[a, b]分成三段利用上方曲线方程减下方的曲线方程，求积分即为面积S=∫fc1a (x)dx−∫fc2c1(x)dx+∫fcc2(x)dx故选：D10.【答案】D【考点】定积分在求面积中的应用【解析】先画出画出直线y=x与曲线y=√x3围成的平面图形，然后求出交点横坐标得到积分上下限，然后利用定积分表示出图形的面积，根据定积分的运算法则进行求解即可．【解答】解：画出直线y=x与曲线y=√x3围成的平面图形图形关于原点对称，交点的横坐标为−1，1∴直线y=x与曲线y=√x3围成的平面图形的面积是∫(1−1√x3−x)dx=2∫(1√x3−x)dx=2(34x43−12x2)|01=2(34−12−0)=12故选D ．二、 填空题 （本题共计 10 小题 ，每题 3 分 ，共计30分 ） 11.【答案】 √33【考点】定积分的简单应用 【解析】求出定积分∫f 10(x)dx ，根据方程ax 02+c =∫f 10(x)dx 即可求解．【解答】解：∵ f(x)=ax 2+c(a ≠0)，∴ f(x 0)=∫f 10(x)dx =[ax 33+cx]01=a3+c ．又∵f(x 0)=ax 02+c ．∴ x 02=13，∵ x 0∈[0, 1]∴ x 0=√33． 12.【答案】2【考点】定积分在求面积中的应用 【解析】本题利用直接法求解，根据三角函数的对称性知，曲线y =cos x 与直线x =0，x =π所围成的平面区域的面积S 为：曲线y =cos x 与直线x =0，x =π2所围成的平面区域的面积的两倍，最后结合定积分计算面积即可． 【解答】解：根据对称性，得：曲线y =cos x 与直线x =0，x =π所围成的平面区域的面积S 为：曲线y =cos x 与直线x =0，x =π2所围成的平面区域的面积的两倍， ∴ S =2∫cos π20xdx =2 故答案为2．13.【答案】323π【考点】旋转体（圆柱、圆锥、圆台）用定积分求简单几何体的体积【解析】作出曲线围成的封闭图象，根据旋转得到旋转体的结构即可得到结论．【解答】解：曲线y=|x|，y=−|x|，x=2，x=−2合成的封闭图形绕y轴旋转一周所得的旋转体为底面半径为2，高为4的圆柱，去掉2个底面半径为2，高为2的圆锥，则对应的体积为π×42−2×13π×22×2=16π−16π3=323π，故答案为：323π14.【答案】92【考点】定积分在求面积中的应用【解析】先根据题意画出区域，然后依据图形得到积分上限为3，积分下限为0，从而利用定积分表示出曲边梯形的面积，最后用定积分的定义求出所求即可．【解答】解：先根据题意画出图形，得到积分上限为3，积分下限为0；两曲线x−y=0，y=x2−2x所围成的图形的面积是∫(33x−x2)dx而∫(303x−x2)dx=(32x2−13x3)|03=272−9=92∴曲边梯形的面积是92故答案为92．15. 【答案】13【考点】定积分在求面积中的应用 【解析】作出两个曲线的图象，求出它们的交点，由此可得所求面积为函数y =x 2在区间[0, 1]上的定积分的值，再用定积分计算公式加以运算即可得到本题答案． 【解答】解：∵ 曲线y =x 2和直线L:x =1的交点为A(1, 1)，∴ 曲线C:y =x 2、直线L:x =1与x 轴所围成的图形面积为 S =∫x 210dx =13x 3|01=13．故答案为：13．16. 【答案】81π2【考点】用定积分求简单几何体的体积 【解析】根据类比推理，结合定积分的应用，即可求出旋转体的体积． 【解答】解：根据类比推理得体积V =∫π90(√y)2dy =∫π90ydy =12πy 2|09=81π2，故答案为：81π2.17.【答案】 ln 2【考点】定积分在求面积中的应用 【解析】先根据所围成图形的面积利用定积分表示出来，然后根据定积分的定义求出面积即可． 【解答】解：由题意，S =∫1x 21dx =ln x|12=ln 2．故答案为：ln 2． 18. 【答案】√34π 【考点】用定积分求简单几何体的体积 【解析】(1−y)π看作是把一个底面边长为1，高为π的直三棱柱平放得到的，根据祖暅原理，每个平行水平面的截面积相等，故它们的体积相等，即可得出结论． 【解答】解：(1−y)π看作是把一个底面边长为1，高为π的直三棱柱平放得到的， 根据祖暅原理，每个平行水平面的截面积相等，故它们的体积相等， 即Ω的体积为π⋅√34=√34π． 故答案为√34π． 19. 【答案】92【考点】定积分在求面积中的应用 【解析】求出函数的切线方程，利用积分的几何意义即可求出区域的面积． 【解答】解：函数的导数为f′(x)=3x 2−2x +1，则在(1, 2)处的切线斜率k =f′(1)=3−2+1=2， 则对应的切线方程为y −2=2(x −1)，即y =2x ， 由{y =x 2−x y =2x，解得x =3或x =0，则由积分的几何意义可得阴影部分的面积S =∫(302x −x 2+x)dx =(32x 2−13x 3)| 30 =92，故答案为：92．20. 【答案】29【考点】定积分的简单应用 【解析】先根据定积分的运算公式求出f(a)的解析式，然后利用二次函数的图象和性质即可求出f(a)的最大值． 【解答】解：f(a)=∫(102ax 2−a 2x)dx =(23ax 3−12a 2x 2)|01=23a −12a 2∴ 当a =23时，f(a)取最大值，最大值为29 故答案为：29三、 解答题 （本题共计 20 小题 ，每题 10 分 ，共计200分 ） 21.【答案】解：(1)∵ 交点为P(2,2),∴ 曲线C 2的导函数为：y ′=x ∴ 切点坐标为(2,2)，故该点的切线方程为：2x −y −2=0. (2)两曲线交点坐标(0,0),(2,2), S ∈∫(√2x −12x 2)20dx =43.【考点】定积分在求面积中的应用利用导数研究曲线上某点切线方程 【解析】 此题暂无解析 【解答】解：(1)∵ 交点为P(2,2),∴ 曲线C 2的导函数为：y ′=x ∴ 切点坐标为(2,2)，故该点的切线方程为：2x −y −2=0. (2)两曲线交点坐标(0,0),(2,2), S ∈∫(√2x −12x 2)20dx =43. 22. 【答案】解：联立{y =x 2+2y =3x，解得x 1=1，x 2=2∴ S =∫(10x 2+2−3x)d x +∫(213x −x 2−2)d x =[13X 3+2X −32X 2]01+[32X 2−13X 3−2X]12=1【考点】定积分的简单应用 【解析】因为所求区域均为曲边梯形，所以使用定积分方可求解． 【解答】解：联立{y =x 2+2y =3x，解得x 1=1，x 2=2∴ S =∫(10x 2+2−3x)d x +∫(213x −x 2−2)d x =[13X 3+2X −32X 2]01+[32X 2−13X 3−2X]12=1 23. 【答案】解：（1）由y′=2x ，则切线l 的斜率k =y′|x=1=2×1=2，切线l 的方程为y −1=2(x −1)即2x −y −1=0；（2）如图，所求的图形的面积s =∫x 2120dx +∫[112x 2−(2x −1)]dx =112．【考点】定积分在求面积中的应用利用导数研究曲线上某点切线方程【解析】（1）根据导数的几何意义即可求出切线方程；（2）根据定积分的几何意义即可求出所围成的图形的面积． 【解答】解：（1）由y′=2x ，则切线l 的斜率k =y′|x=1=2×1=2，切线l 的方程为y −1=2(x −1)即2x −y −1=0；（2）如图，所求的图形的面积s =∫x 2120dx +∫[112x 2−(2x −1)]dx =112．24.【答案】解：由题意，将烟囱横截面按照如图放置，建立坐标系如图，双曲线的短轴长为2A =10，并且过(−6, 6)，所以双曲线方程为y 225−11x 225×36=1，所以V =π∫(8−611x 236+25)dx =1659.2m 3【考点】用定积分求简单几何体的体积 双曲线的特性【解析】由题意建立坐标系，得到如图的双曲线，烟囱最细处的直径为10m 即2a =10，最下端的直径为12m ，最细处离地面6m ，即双曲线经过(−6, 6)，烟囱高14m ，即自变量范围为−6到8，由此利用定积分的值得到体积． 【解答】解：由题意，将烟囱横截面按照如图放置，建立坐标系如图，双曲线的短轴长为2A =10，并且过(−6, 6)， 所以双曲线方程为y 225−11x 225×36=1，所以V =π∫(8−611x 236+25)dx =1659.2m 325.【答案】解：(1)设z =a +bi (a,b ∈R )， 则z ¯=a −bi ，∴ z ⋅z ¯−3iz =a 2+b 2+3b −3ai . 又∵ z ⋅z ¯−3iz =101−3i =1+3i ， ∴ {a 2+b 2+3b =1，−3a =3，解得 {a =−1，b =0，或{a =−1，b =−3，∴ z =−1或z =−1−3i . (2)由{y =√x ，x +y =2，解得{x =1，y =1，即曲线y =√x 与直线x +y =2的交点坐标为(1,1)， 同理可得，曲线y =√x 与直线y =−13x 的交点坐标为(0,0)，直线x +y =2与直线y =−13x 的交点坐标为(3,−1)，所以围成的平面图形的面积为： S =∫(√x +13x)10dx +∫(2−x +13x)31dx=(23x 32+16x 2)|01+(2x −13x 2)|13=136．【考点】 复数的运算 共轭复数复数代数形式的混合运算 定积分在求面积中的应用 【解析】 此题暂无解析 【解答】解：(1)设z =a +bi (a,b ∈R )， 则z ¯=a −bi ，∴ z ⋅z ¯−3iz =a 2+b 2+3b −3ai . 又∵ z ⋅z ¯−3iz =101−3i =1+3i ， ∴ {a 2+b 2+3b =1，−3a =3，解得 {a =−1，b =0，或{a =−1，b =−3，∴ z =−1或z =−1−3i . (2)由{y =√x ，x +y =2，解得{x =1，y =1，即曲线y =√x 与直线x +y =2的交点坐标为(1,1)， 同理可得，曲线y =√x 与直线y =−13x 的交点坐标为(0,0)， 直线x +y =2与直线y =−13x 的交点坐标为(3,−1)，所以围成的平面图形的面积为： S =∫(√x +13x)10dx +∫(2−x +13x)31dx=(23x 32+16x 2)|01+(2x −13x 2)|13=136．26. 【答案】解：（1）∵ (√x 2x4)n 展开式的前三项系数成等差数列，∴ C n 0+C n 2(12)2=2C n 1⋅12…∴ 1+n(n−1)2×14=n ，整理得n 2−9n +8=0，n 1=1（舍） n 2=8…（2）所投的点落在叶形图内记为事件A ，由几何概型的概率公式得： P(A)=叶形图面积AOBC 的面积=∫(10√x−x 2)dx1=(23x 32−13x 3)|01=13…【考点】二项式定理的应用定积分在求面积中的应用 等差数列的性质几何概型计算（与长度、角度、面积、体积有关的几何概型） 【解析】（1）由题意可得，C n 0+C n 2(12)2=2C n 1⋅12，解关于n 的方程即可；（2）由几何概型的概率公式可知，需求叶形图的面积，利用定积分∫(10√x −x 2)dx 可求叶形图的面积，从而使问题解决． 【解答】解：（1）∵ (√x 2√x4)n 展开式的前三项系数成等差数列，∴ C n 0+C n 2(12)2=2C n 1⋅12…∴1+n(n−1)2×14=n，整理得n2−9n+8=0，n1=1（舍）n2=8…（2）所投的点落在叶形图内记为事件A，由几何概型的概率公式得：P(A)=叶形图面积AOBC的面积=∫(1√x−x2)dx1=(23x32−13x3)|01=13…27.【答案】利用S=∫ππ4sin xdx=(−cos x)|π4π=1+√22．利用S=∫10(2x2−x2)dx=23x3|01−13x3|01=13．由于{y=x2y=√x，解得{x=0y=0或{x=1y=1，所以S=∫10(√x−x2)dx=23x32|01−13x3|01=23−13=13．【考点】定积分的简单应用【解析】首先求出被积函数的原函数，进一步利用定积分知识求出结果．【解答】利用S=∫ππ4sin xdx=(−cos x)|π4π=1+√22．利用S=∫10(2x2−x2)dx=23x3|01−13x3|01=13．由于{y=x2y=√x，解得{x=0y=0或{x=1y=1，所以S=∫10(√x−x2)dx=23x32|01−13x3|01=23−13=13．28.【答案】解：由y=4−x2与直线y=2x−4联立，可得交点(−4, −12)，(2, 0)，∴y=4−x2与直线y=2x−4所围成图形的面积S=∫(2−44−x2−2x+4)dx=(−13x3−x2+8x)|−42=36．【考点】定积分在求面积中的应用【解析】先联立方程，组成方程组，求得交点坐标，可得被积区间，再用定积分表示出y=4−x2与直线y=2x−4所围成图形的面积，即可求得结论．【解答】解：由y=4−x2与直线y=2x−4联立，可得交点(−4, −12)，(2, 0)，∴y=4−x2与直线y=2x−4所围成图形的面积S=∫(2−44−x2−2x+4)dx=(−13x 3−x 2+8x)|−42=36．29. 【答案】解：（1）S 0=∫sin π0xdx =[−cos x]0π=(−cos π)−(−cos 0)=1+1=2 （2）V =π∫sin 2π0xdx =π[x2−14sin 2x]0π=π(π2−14×0)=π22【考点】用定积分求简单几何体的体积 定积分在求面积中的应用【解析】（1）根据题意可知曲线y =sin x 和直线x =0，x =π，及y =0所围成图形的面积为S 0=∫sin π0xdx ，解之即可；（2）所围成图形绕ox 轴旋转所成旋转体的体积为V =π∫sin 2π0xdx ，根据定积分的定义解之即可． 【解答】解：（1）S 0=∫sin π0xdx =[−cos x]0π=(−cos π)−(−cos 0)=1+1=2 （2）V =π∫sin 2π0xdx=π[x 2−14sin 2x]0π=π(π2−14×0)=π2230.【答案】解：设f(x)=ax 3+bx 2+cx +d ，则f′(x)=3ax 2+2bx +c ， 由图象可知{ f(0)=0f(1)=1f′(4)=0f′(7)=0，即{ d =0a +b +c =0c 3a =28−2b 3a =11，解得{ a =2137b =−33137c =168137d =0， ∴ f(x)=2137x 3−33137x 2+168137x ． ∴ S =∫f 100(x)dx =(2137×x 44−33137×x 33+168137×x 22)|10≈17.5． 若要想得到误差不超过1的面积估计值，可使用分段函数求出f(x)的解析式，然后使用定积分求出面积． 【考点】定积分在求面积中的应用 【解析】设f(x)=ax 3+bx 2+cx +d ，利用待定系数法确定函数关系式，利用定积分求出面积估计值；若要误差小可分段求出f(x)的解析式，然后使用定积分求出面积． 【解答】解：设f(x)=ax 3+bx 2+cx +d ，则f′(x)=3ax 2+2bx +c ，由图象可知{ f(0)=0f(1)=1f′(4)=0f′(7)=0，即{ d =0a +b +c =0c 3a =28−2b 3a =11，解得{ a =2137b =−33137c =168137d =0， ∴ f(x)=2137x 3−33137x 2+168137x ． ∴ S =∫f 100(x)dx=(2137×x 44−33137×x 33+168137×x 22)|10≈17.5． 若要想得到误差不超过1的面积估计值，可使用分段函数求出f(x)的解析式，然后使用定积分求出面积． 31. 【答案】解：（1）曲线C:y =√x 和直线：x −2y =0联立，可得交点坐标为(4, 2)，则 S =∫(40√x −12x)dx =(23x 32−x 24)|04=43；（2）V =∫[40π(√x)2−π(x2)2]dx =π(x 22−x 312)|04=8π3．【考点】用定积分求简单几何体的体积 旋转体（圆柱、圆锥、圆台）【解析】（1）求得交点坐标，可得积分区间，即可求M 的面积； （2）旋转一周所得旋转体的体积应该用定积分来求．【解答】 解：（1）曲线C:y =√x 和直线：x −2y =0联立，可得交点坐标为(4, 2)，则 S =∫(40√x −12x)dx =(23x 32−x 24)|04=43； （2）V =∫[40π(√x)2−π(x2)2]dx=π(x 22−x 312)|04=8π3．32.【答案】 解：（1）设f(x)=kx +b ， ∵ f(x)=x ∫f 20(t)dt +1， ∴ kx +b =x •(kt 22+bt)|02+1，∴ kx +b =(2k +2b)x +1，∴ k =−2，b =1， ∴ f(x)=−2x +1，；2)g(x)=xf(x)=−2x 2+x ， ∴ V =π∫[120xf(x)]2dx =π240． 【考点】用定积分求简单几何体的体积定积分【解析】（1）利用待定系数法，结合定积分的定义求函数f(x)的解析式；（2）求出g(x)，应用定积分来求旋转体的体积．【解答】解：（1）设f(x)=kx+b，∵f(x)=x∫f2(t)dt+1，∴kx+b=x•(kt22+bt)|02+1，∴kx+b=(2k+2b)x+1，∴k=−2，b=1，∴f(x)=−2x+1，；2)g(x)=xf(x)=−2x2+x，∴V=π∫[120xf(x)]2dx=π240．33.【答案】解：（1）若干张平行于圆锥底面的平面把它切成n块厚度相等的薄片；（2）用一系列圆柱的体积近似地代替对应的薄片，圆柱的高为ℎn ，底半径顺次为：rn，2r n ，3rn…，(n−1)rn，r；（3）问题归结为计算和式V(n)=ℎn ×(12+22+...+n2)×πr2n2，当n越来越大时所趋向的值．（对V求极限V=limn→∞ℎn×(12+22+...+n2)×πr2n2=lim n→∞ℎn⋅16n(n+1)(2n+1)⋅πr2n2=ℎπr26limn→∞2n2+3n+1n2=πr2ℎ3=13S底ℎ故圆锥的体积等于13的圆柱体的体积【考点】用定积分求简单几何体的体积【解析】利用极限的定义进行分割、近似代换和求极限的方法，进行推到【解答】解：（1）若干张平行于圆锥底面的平面把它切成n块厚度相等的薄片；（2）用一系列圆柱的体积近似地代替对应的薄片，圆柱的高为ℎn ，底半径顺次为：rn，2r n ，3rn…，(n−1)rn，r；（3）问题归结为计算和式V(n)=ℎn ×(12+22+...+n2)×πr2n2，当n越来越大时所趋向的值．（对V求极限V=limn→∞ℎn×(12+22+...+n2)×πr2n2=lim n→∞ℎ⋅1n(n+1)(2n+1)⋅πr22=ℎπr26limn→∞2n2+3n+1n2=πr2ℎ3=13S底ℎ故圆锥的体积等于13的圆柱体的体积34.【答案】解：设(x0, y0)为曲线y=√x(0≤x≤4)上任一点，得曲线于该点处的切线方程为：y−y0=2√x −x0)即y=y02+2√x．得其与x=0，x=4的交点分别为(0,y02)，(4,y02+2y0)于是由此切线与直线x=0，x=4以及曲线y=√x所围的平面图形面积为：S=∫(4 0y022x√x)dx=2y0+x−163=2√x0x−163应用均值不等式求得x0=2时，S取得最小值．即所求切线即为：y=22+√22．【考点】定积分在求面积中的应用【解析】先根据导数的几何意义求出曲线y=√x(0≤x≤4)上任一点处的切线方程，再求出积分的上下限，然后利用定积分表示出图形面积，最后利用定积分的定义进行求解即可．【解答】解：设(x0, y0)为曲线y=√x(0≤x≤4)上任一点，得曲线于该点处的切线方程为：y−y0=2x −x0)即y=y02+2x．得其与x=0，x=4的交点分别为(0,y02)，(4,y02+2y0)于是由此切线与直线x=0，x=4以及曲线y=√x所围的平面图形面积为：S=∫(4 0y022√x√x)dx=2y0+√x−163=2√x0√x−163应用均值不等式求得x0=2时，S取得最小值．即所求切线即为：y=2√2+√22．35.【答案】解：设切线方程为y =kx +1，切点坐标为(a, b)， 则{k =1aka +1=b ln a =b ，解得a =e 2，b =2，∴ 切线方程为y =1e 2x +1．将y =0代入y =1e 2x +1得x =−e 2，∴ B(−e 2, 0)． ∴区域D 的面积为∫(e 2−e 21e 2x+1)dx −∫ln e 21xdx=x 22e 2+x|e 2−e 2−x(ln x −1)|e 21=2e 2+e 2=3e 2．区域D 绕x 轴旋转一周所得几何体体积为13⋅π⋅22⋅2e 2−π⋅∫(e 21ln x)2dx =8πe 23−π⋅x[(ln x)2−2ln x +2]|e 21=8πe 23−(2e 2−2)⋅π=2πe 23+2π．【考点】用定积分求简单几何体的体积 【解析】求出A 的坐标和切线方程，则所求面积和体积均可用两个定积分的差来表示． 【解答】解：设切线方程为y =kx +1，切点坐标为(a, b)， 则{k =1aka +1=b ln a =b，解得a =e 2，b =2，∴ 切线方程为y =1e 2x +1．将y =0代入y =1e 2x +1得x =−e 2，∴ B(−e 2, 0)． ∴区域D 的面积为∫(e 2−e 21e 2x+1)dx −∫ln e 21xdx=x 22e 2+x|e 2−e 2−x(ln x −1)|e 21=2e 2+e 2=3e 2．区域D 绕x 轴旋转一周所得几何体体积为13⋅π⋅22⋅2e 2−π⋅∫(e 21ln x)2dx=8πe 23−π⋅x[(ln x)2−2ln x +2]|e 21=8πe 23−(2e 2−2)⋅π=2πe 23+2π．36. 【答案】解：由{y =2x −x 2y =2x 2−4x ，得{x =0y =0或{x =2y =0， ∴ 所求图象的面积为：∫[20(2x −x 2)−(2x 2−4x)]dx =∫(206x −3x 2)dx =(3x 2−x 3)|02=3×22−23=12−8=4． 【考点】定积分在求面积中的应用 【解析】先求出两曲线的交点坐标，利用定积分的应用即可求出对应图形的面积． 【解答】解：由{y =2x −x 2y =2x 2−4x ，得{x =0y =0或{x =2y =0， ∴ 所求图象的面积为：∫[20(2x −x 2)−(2x 2−4x)]dx =∫(206x −3x 2)dx =(3x 2−x 3)|02=3×22−23=12−8=4． 37. 【答案】解：∫(103ax +1)(x +b)dx =∫[103ax 2+(3ab +1)x +b]dx=[ax 3+12(3ab +1)x 2+bx]|01 =a +12(3ab +1)+b =0即3ab +2(a +b)+1=0 设ab =t ∴ a +b =−3t+12则a ，b 为方程x 2+3t+12x +t =0两根△=(3t+1)24−4t ≥0∴ t ≤19或t ≥1∴ a ⋅b ∈(−∞, 19]∪[1, +∞) 【考点】定积分的简单应用 【解析】先根据定积分的运算法则建立a 与b 的等量关系，然后设ab =t 则a +b =−3t+12，再利用构造法构造a ，b 为方程x 2+3t+12x +t =0两根，然后利用判别式可求出a ．b 的取值范围． 【解答】解：∫(103ax +1)(x +b)dx =∫[103ax 2+(3ab +1)x +b]dx=[ax 3+12(3ab +1)x 2+bx]|01 =a +12(3ab +1)+b =0即3ab +2(a +b)+1=0 设ab =t ∴ a +b =−3t+12则a ，b 为方程x 2+3t+12x +t =0两根△=(3t+1)24−4t ≥0∴ t ≤19或t ≥1∴ a ⋅b ∈(−∞, 19]∪[1, +∞) 38.【答案】解：根据对称性，得： 曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的平面区域的面积S 为：曲线y =cos x与直线x =π2，x =π所围成的平面区域的面积的二倍， ∴ S =−2∫cos ππ2xdx =−2sin x =2．故曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的面积为2．【考点】定积分在求面积中的应用 【解析】本题利用直接法求解，根据三角函数的对称性知，曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的平面区域的面积S 为：曲线y =cos x 与直线x =π2，x =π所围成的平面区域的面积的二倍，最后结合定积分计算面积即可． 【解答】解：根据对称性，得： 曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的平面区域的面积S 为：曲线y =cos x与直线x =π2，x =π所围成的平面区域的面积的二倍， ∴ S =−2∫cos ππ2xdx =−2sin x =2．故曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的面积为2．39. 【答案】解：s =∫|5π4−π2sin x|dx =−∫sin 0−π2xdx+∫sin π0xdx−∫sin 5π4πxdx=cos x|−π20−cos x|0π+cos x|π5π4=1+2+(−√22+1)=4−√22． 【考点】定积分在求面积中的应用 【解析】求曲线y =sin x 与直线x =−π2，x =5π4，y =0所围成的平面图形的面积【解答】解：s =∫|5π4−π2sin x|dx =−∫sin 0−π2xdx+∫sin π0xdx−∫sin 5π4πxdx=cos x|−π20−cos x|0π+cos x|π5π4=1+2+(−√22+1)=4−√22． 40.【答案】 由 {y =kx y =x −x2 得 {x =1−k y =k −k 2 (0<k <1)． 由题设得∫10−k[(x −x 2)−kx]dx =12∫(10x −x 2)dx 即∫10−k[(x −x 2)−kx]dx =12( 12x 2−13x 3)|01=112 ∴ (1−k)3=12 ∴ k ＝1−√432∴ 直线方程为y ＝(1−√432)x ． 故k 的值为：k =1−√432．【考点】定积分的简单应用 【解析】先由 {y =kx y =x −x 2 得 {x =1−k y =k −k 2 ，根据直线y ＝kx 分抛物线y ＝x −x 2与x 轴所围成图形为面积相等的两个部分得∫10−k[(x −x 2)−kx]dx =12∫(10x −x 2)dx 下面利用定积分的计算公式即可求得k 值． 【解答】由 {y =kx y =x −x 2得 {x =1−k y =k −k 2 (0<k <1)．由题设得∫10−k[(x −x 2)−kx]dx =12∫(10x −x 2)dx 即∫10−k[(x −x 2)−kx]dx =12( 12x 2−13x 3)|01=112试卷第31页，总31页 ∴ (1−k)3=12 ∴k ＝1−√432∴ 直线方程为y ＝(1−√432)x ． 故k 的值为：k =1−√432．。
（完整版）定积分习题及答案
第五章定积分(A 层次)1．203cos sin xdx x ；2．a dx x ax222；3．31221xxdx ；4．1145x xdx ；5．411xdx ；6．14311xdx ；7．21ln 1e xx dx ；8．02222xxdx ；9．dx x 02cos 1；10．dx x x sin 4；11．dx x 224cos 4；12．55242312sin dx xxx x ；13．342sin dx xx ；14．41ln dx xx ；15．1xarctgxdx ；16．202cosxdx e x ；17．dx x x 02sin ；18．dx x e 1ln sin ；19．243cos cos dx x x ；20．40sin 1sin dx x x ；21．dx xxx 02cos 1sin ；22．2111lndx xx x ；23．dx xx 4211；24．20sin ln xdx ；25．211dx xxdx0。
(B 层次)1．求由0cos 0x y ttdtdte 所决定的隐函数y 对x 的导数dxdy 。
2．当x 为何值时，函数x tdt tex I 02有极值？3．x xdt t dxd cos sin 2cos 。
4．设1,211,12xx x x xf ，求20dx x f 。
5．1lim22xdtarctgt xx 。
6．设其它,00,sin 21xx xf ，求x dt t f x。
7．设时当时当0,110,11xex xxf x，求201dx xf 。
8．2221limnn nnn。
9．求nk nknknnen e 12lim 。
10．设x f 是连续函数，且12dt t f x x f ，求x f 。
11．若2ln 261xtedt ，求x 。
12．证明：212121222dxeex。
13．已知axxx dx ex axa x 224lim，求常数a 。
(完整版)§定积分的应用习题与答案
第六章 定积分的应用（A ）1、求由下列各曲线所围成的图形的面积 1）221x y =与822=+y x （两部分都要计算）2）xy 1=与直线x y =及2=x3）xe y =，xe y -=与直线1=x4）θρcos 2a =5）t a x 3cos =，t a y 3sin =１、求由摆线()t t a x sin -=，()t a y cos 1-=的一拱()π20≤≤t 与横轴所围成的图形的面积２、求对数螺线θρae=()πθπ≤≤-及射线πθ=所围成的图形的面积３、求由曲线x y sin =和它在2π=x 处的切线以及直线π=x 所围成的图形的面积和它绕x 轴旋转而成的旋转体的体积４、由3x y =，2=x ，0=y 所围成的图形，分别绕x 轴及y 轴旋转，计算所得两旋转体的体积５、计算底面是半径为R 的圆，而垂直于底面上一条固定直径的所有截面都是等边三角形的立体体积６、计算曲线()x y -=333上对应于31≤≤x 的一段弧的长度７、计算星形线t a x 3cos =，t a y 3sin =的全长８、由实验知道，弹簧在拉伸过程中，需要的力→F （单位：N ）与伸长量S （单位：cm ）成正比，即：kS =→F （k 是比例常数），如果把弹簧内原长拉伸6cm ， 计算所作的功９、一物体按规律3ct x =作直线运动，介质的阻力与速度的平方成正比，计算物体由0=x 移到a x =时，克服介质阻力所作的功１０、 设一锥形储水池，深15m ，口径20m ，盛满水，将水吸尽，问要作多少功？１１、 有一等腰梯形闸门，它的两条底边各长10cm 和6cm ，高为20cm ，较长的底边与水面相齐，计算闸门的一侧所受的水压力１２、 设有一长度为λ，线密度为u 的均匀的直棒，在与棒的一端垂直距离为a 单位处有一质量为m 的质点M ，试求这细棒对质点M 的引力(B)1、设由抛物线()022>=p px y 与直线p y x 23=+ 所围成的平面图形为D 1） 求D 的面积S ;2）将D 绕y 轴旋转一周所得旋转体的体积2、求由抛物线2x y =及x y =2所围成图形的面积，并求该图形绕x 轴旋转所成旋转体的体积3、求由x y sin =，x y cos =，0=x ，2π=x 所围成的图形的面积，并求该图形绕x 轴旋转所成旋转体的体积4、求抛物线px y 22=及其在点⎪⎭⎫⎝⎛p p ,2处的法线所围成的图形的面积5、求曲线422+-=x x y 在点()4,0M 处的切线MT 与曲线()122-=x y 所围成图形的面积6、求由抛物线ax y 42=与过焦点的弦所围成的图形面积的最小值7、求由下列曲线所围成图形的公共部分的面积 1）θρcos 3=，θρcos 1+=2）θρsin a =，()θθρsin cos +=a ，0>a8、由曲线()16522=-+y x 所围成图形绕x 轴旋转所成旋转体的体积9、求圆心在()b ,0半径为a ，()0>>a b 的圆，绕x 轴旋转而成的环状体的体积10、计算半立方抛物线()32132-=x y 被抛物线32x y =截得的一段弧的长度(C)1、用积分方法证明半径为R 的球的高为H 的球缺的的体积为⎪⎭⎫ ⎝⎛-=32H R H V π2、分别讨论函数x y sin =⎪⎭⎫⎝⎛≤≤20πx 在取何值时，阴影部分的面积1S ，2S 的和21S S S +=取最大值和最小值3、求曲线x y =()40≤≤x 上的一条切线，使此切线与直线0=x ， 4=x 以及曲线x y =所围成的平面图形的面积最小4、半径为r 的球沉入水中，球的上部与水面相切，球的密度与水相同，现将球从水中取出，需作多少功？第六章 定积分应用 习 题 答 案（A ）1、1）342+π，346-π 2）2ln 23- 3）21-+ee 4）2a π 5）283a π2、23a π 3、()ππ2224--e e a 4、12-π，42π 5、7128π，564π 6、3334R 7、3432- 8、a 6 9、kJ 18.0 10、3732727a kc （其中k 为比例常数）11、()kJ 5.57697 12、()kN 14373 13、取y 轴经过细直棒⎪⎪⎭⎫⎝⎛+-=2211t a aGmu F y 22t a a Gmu F x +-=λ(B)1、1）⎰-=⎪⎪⎭⎫ ⎝⎛--=pp p dy p y y p S 322316223 或()⎰⎰=⎪⎭⎫⎝⎛+-++=20229231622322pp p p dx px x p dx px px S2）⎰⎰--=⎪⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛-=pp p p p dy p y dy y p V 33322215272223πππ 2、()⎰=-=10231dx x x A ()()ππ⎰=⎪⎭⎫⎝⎛-=10222103dx x x V3、()()⎰⎰-=-+-=244222cos sin sin cos πππdx x x dx x x A()()()()()()⎰⎰=-+-=24224022cos sin sin cos πππππdx x x dx x x V4、抛物线在点⎪⎭⎫⎝⎛p p ,2处的法线方程为： p y x 23=+，以下解法同第一题2316p A = 5、MT ：x y 24-=，切线MT 与曲线()122-=x y 的交点坐标为⎪⎭⎫⎝⎛1,23，()2,3- ⎰-=⎪⎪⎭⎫ ⎝⎛---=122491224dy y y A 6、提示：设过焦点()0,a 的弦的倾角为α则弦所在直线的方程为()a x y -=αtan由()a x y -=αtan ，ax y 42=得两交点纵坐标为()()21csc 2csc 2y ctg a ctg a y =+<-=αααα所以()()dy a y yctg a A y y ⎰⎥⎦⎤⎢⎣⎡-+=2142αα ()()32222csc 34csc 4csc 4ααααa ctg a a -+=()()3232csc 34csc 4ααa a -=()32csc 38αa =因为πα<<0 当2πα=时 ()3csc α取得最小值为1所以 当2πα=时 过焦点的弦与抛物线ax y 42=所围成的图形面积()32csc 382απa A =⎪⎭⎫ ⎝⎛最小7、1）()()πθθθθπππ45cos 321cos 1212232302=⎥⎦⎤⎢⎣⎡++=⎰⎰d d A2）()()[]⎰⎰-=++=ππππθθθθθ22220241cos sin 21sin 21a d a d a A 8、()()⎰⎰------+=44442222165165dx xdx xV ππ()()⎰-=⎭⎬⎫⎩⎨⎧----+=4422222160165165ππdx xx9、解法同题810、提示：()32132-=x y ，32x y = 联立得交点⎪⎪⎭⎫ ⎝⎛36,2，⎪⎪⎭⎫ ⎝⎛-36,2 所求弧长()⎰+=212'12dx y s由()32132-=x y 得()yx y 2'1-=于是()()()()()1231321134222'-=--=⎪⎪⎭⎫ ⎝⎛-=x x x y x y于是得()⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡-+=⎰12598123122321221dx x S(C)1、证明：此处球缺可看作由如图阴影（图222R y x =+的一部分）绕y 轴旋转而成所以()⎰⎰---==RHR RHR dy y R dy x V 222ππR HR R HR y yR ---=332ππ()[]()[]3323H R R H R R R -----=ππ⎪⎭⎫ ⎝⎛-=32H R H π2、解：()⎰-=tdx x t S 11sin sin ()⎰-=22sin sin πtdx t x S()()⎰-=tdx x t t S 1sin sin +()⎰-2sin sin πtdx t x=⎪⎭⎫ ⎝⎛≤≤-⎪⎭⎫⎝⎛-+201sin 22cos 2ππt t t t ()0cos 22'=⎪⎭⎫⎝⎛-=t t t S π，得驻点2421ππ==t t易知()()002''1''<>t S t S122max -=⎪⎭⎫ ⎝⎛=∴ππS S ，124min -=⎪⎭⎫⎝⎛=πS S3、解：设()00,y x 为曲线x y =()40≤≤x 上任一点，易得曲线于该点处的切线方程为：()00021x x x y y -=- 即0022x x y y +=得其与0=x ， 4=x 的交点分别为⎪⎭⎫ ⎝⎛2,00y ，⎪⎪⎭⎫⎝⎛+0022,4y y 于是由此切线与直线0=x ， 4=x 以及曲线x y =所围的平面图形面积为：3164222004000-+=⎪⎪⎭⎫ ⎝⎛-+=⎰x y dx x x x y S3164200-+=x x 问题即求31642-+=xx S ()40≤≤x 的最小值 令022321=+=--xxS 得唯一驻点2=x 且为唯一极小值所以 当2=x 时，S 最小 即所求切线即为：2222+=x y 4、如图：以水中的球心为原点，上提方向作为坐标轴建立坐标系易知任意[]dx x x +,段薄片在提升过程中在水中行程为r －x ，而在水上的行程为2r －（r －x ）＝r ＋x因为求的密度与水相同，所以在水中提升过程中浮力与重力的合力为零，不做功，而在水面上提升时，做功微元为()()dx x r x r g dW +-=22π()()g r dx x r x r g dW W r r r r 42234ππ⎰⎰--=+-==。
定积分及其应用练习-带详细答案
题一 题面: 求由曲线y (x2)2与x轴，直线y4x所围成的平面图形的面积.
答案：32•
变式训练一
题面：
x+2—2<x<0,
函数f(x)=n的图象与x轴所围成的封闭图形的面积
2cos x0<x<2来自为()5a.2
C.3
答案：D.
详解：
画出分段函数的图象，如图所示，贝够图象与
面积为2 >2 >2+*o2cos xdx=2+2sin
-3
为图象与y轴的交点，A,C为图象与x轴的两个交点，B为图象的最低点.
若在曲线段ABC与x轴所围成的区域内随机取一点，则该点在△ABC
变式训练二
题面：
由直线y=2x及曲线y=3—x2围成的封闭图形的面积为()
A.23
B.9—2 3
肿5
C.亍
答案：
f32
D2
详解:
注意到直线y=2x与曲线y=3-x2的交点A,B的坐标分别是(-3,-
6),(1,2),因此结合图形可知，由直线y=2x与曲线y=3-x2围成的封闭图
形的面积为1(3—x2—2x)dx=3x-3x3-x2
(完整版)高等数学定积分应用习题答案.doc
第六章定积分的应用习题6-2 (A) 1．求下列函数与x 轴所围部分的面积：(1) y x 2 6x 8, [0, 3]( 2) y 2x x2 , [ 0, 3]2．求下列各图中阴影部分的面积：1.图 6-13．求由下列各曲线围成的图形的面积：(1) y e x , y e x与x1;( 2) y ln x 与 x 0, y ln a, y ln b (b a 0) ;(3) y 2x x2与 y x , y 0 ;( 4) y 2 2 x , y 2 (x 1) ;(5) y 2 4(1 x) 与 y 2 x , y 0 ;(6) y x2 与 y x , y 2x ;(7) y 2 sin x , y sin 2x (0 x ) ;(8) y x 2,x 2 y 2 （两部分都要计算）;2 84．求由曲线y ln x 与直线 y 0, x e 1 , x e 所围成的图形的面积。
5．求抛物线y x 2 4 x 3 及其在点 (0, 3) 和 (3, 0) 处的切线所围成的图形的面积。
6．求抛物线y 2 2 px 及其在点 ( p, p) 处的法线所围成的图形的面积。
27．求曲线x y a 与两坐标轴所围成的图形的面积。
x 2 y 21 所围图形的面积。
8．求椭圆2 b 2a9．求由摆线x a(t sin t), y a(1 cost ) 的一拱（0 t 2 ) 与横轴所围图形的面积。
10．求位于曲线y e x下方与由该曲线过原点的切线的左方及x 轴之间的图形的面积。
11．求由下列各方程表示的曲线围成的图形的面积：(1) 2a sin (a 0) ;( 2) 2a (2 cos ) (a 0);(3) 2 2 cos 2 （双纽线） ;12. 把抛物线y2 4ax 及直线 x x( x 0 0) 所围成的图形绕x 轴旋转，计算所得旋转抛物体的体积。
13. 由 y x 3 , x 2 , y 0 所围成的图形，分别绕x 轴及 y 轴旋转，计算所得两个旋转体的体积。
(完整版)高等数学定积分应用习题答案
第六章 定积分的应用习题 6-2 (A)1． 求下列函数与 x 轴所围部分的面积：]3,0[,86)1(2+-=x x y ]3,0[,2)2(2x x y -=2． 求下列各图中阴影部分的面积： 1.图 6-13．求由下列各曲线围成的图形的面积：;1,)1(===-x e y e y x x 与;)0(ln ,ln ,0ln )2(>>====a b b y a y x x y 与;0,2)3(2==-=y x y x x y 与;)1(,2)4(22--==x y x y;0,2)1(4)5(2=-=-=y x y x y 与;2,)6(2x y x y x y ===与;)0(2sin ,sin 2)7(π≤≤==x x y x y;8,2)8(222（两部分都要计算）=+=y x x y4．的图形的面积。
所围成与直线求由曲线e x e x y x y ====-,,0ln 15．的面积。
处的切线所围成的图形和及其在点求抛物线)0,3()3,0(342--+-=x x y6．的面积。
处的法线所围成的图形及其在点求抛物线),2(22p ppx y = 7．形的面积。
与两坐标轴所围成的图求曲线a y x =+8．所围图形的面积。
求椭圆12222=+by a x9．。
与横轴所围图形的面积（的一拱求由摆线)20)cos 1(),sin (π≤≤-=-=t t a y t t a x10．轴之间的图形的面积。
的切线的左方及下方与由该曲线过原点求位于曲线x e y x =11．求由下列各方程表示的曲线围成的图形的面积： ;)0(sin 2)1(>=a a θρ;)0()cos 2(2)2(>+=a a θρ ;2cos 2)3(2（双纽线）θρ=抛物体的体积。
轴旋转，计算所得旋转所围成的图形绕及直线把抛物线x x x x ax y )0(4.12002>==体的体积。
旋转轴旋转，计算所得两个轴及所围成的图形，分别绕由y x y x x y 0,2,.133===14．求下列已知曲线所围成的图形，按指定的轴旋转所产生的旋转体的体积： ;,0,,0)1(轴绕与x y a x x axcha y ====;,2sin )2(轴绕与x xy x y π== ;,)20(cos sin )3(轴绕与x x x y x y π≤≤==;0,2,ln )4(轴绕与y y x x y === ;0,2)5(2轴绕与y y x y x x y ==-=;,16)5()6(22轴绕y y x =+-。
五、定积分及其应用
2
sin
xd sin
x
.
0
0
2
3.【解】
令
1
f
xdx
A ，则由
f
x
1 x2
1 2x4
f xdx ，得
1
A
1
1 x2
dx
A 2
1
1 x4
dx
1
A ，解得 A 6 ，所以
6
7
f x
1 x2
3 7x4
.
4.【解】
1 0
f
xdx
x
1
2 0
f
xd
x 2
x
f
x
1
0
1
2 0
x f xdx
0
20
0
2
x t
x cos x dx
t cost dt
t cost dt
cost dt 2 3 ，
0
0
0
3
x 2 t
x cos xdx
t 2 cost dt
t cost dt 2
cost dt 5 ，
2
0
0
0
则 n x cos x dx 3 2n 1 n2 . 0
arcsin2x
1
1 1
，
1 2 x 1 2
22
2 2
3
2
1
dx
3
2
x2 x 1
d x 1
2 ln x 1
x 1 2 1 2
2
3
x2 x 2 ln 2 1
3，
2 2
原式 ln 2 3 . 2
8.【证明】
定积分应用题附答案
《定积分的应用》复习题一．填空：1．曲线ln ,ln ,ln (0)y x y a y b a b y ===<<及轴所围成的平面图形的面积为A =ln ln by ae dy ⎰=b-a______2.2y x y ==曲线和 ____13____二．计算题：1．求由抛物线 y 2 = 2x 与直线 2x + y – 2 = 0 所围成的图形的面积。
解：（1）确定积分变量为y ，解方程组2222y x y x ⎧=⎨=-+⎩ 得12121/22,12x x y y ==⎧⎧⎨⎨==-⎩⎩ 即抛物线与直线的交点为（21，1）和( 2 , - 2 ).故所求图形在直线y = 1和y = - 2 之间，即积分区间为［－2，1 ］。
（2）在区间［－2，1］上，任取一小区间为［ y , y + dy ］,对应的窄条面积近似于高为［(１－21y ）-21y 2 ］,底为dy 的矩形面积，从而得到面积元素 dA = [(１－21y)- 21y 2 ]dy (3)所求图形面积 A =⎰-12[（1-21y ）-21y 2 ]dy = [y - 41y 2 – 61y 3]12-= 942．求抛物线 y = - x 2 + 4x - 3 及其在点（0，- 3）和（3，0）处的切线所围成的图形的面积。
解：由y = - x 2 + 4x – 3 得 '24,'(0)4,'(3)2y x y y =-+==-。
抛物线在点（0，- 3）处的切线方程为 y = 4x – 3 ;在点（3，0）处的切线方程为 y = - 2x + 6 ; 两切线的交点坐标为 （ 32，3 ）。
故 面积A =332223029[(43)(43)][(26)(43)]4x x x dx x x x dx --+-+-+-+-=⎰⎰3．求由摆线 x = a (t – sint) , y = a( 1- cost) 的一拱（02t π≤≤）与横轴所围成的图形的面积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
定积分及其应用题一 题面：求由曲线2(2)y x =+与x 轴，直线4y x =-所围成的平面图形的面积． 答案：323．变式训练一题面：函数f (x )＝⎩⎪⎨⎪⎧x ＋2－2≤x <0，2cos x ⎝ ⎛⎭⎪⎫0≤x ≤π2的图象与x 轴所围成的封闭图形的面积为( )B ．2 |C ．3D ．4答案：D.详解：画出分段函数的图象，如图所示，则该图象与x 轴所围成的封闭图形的面积为12×2×2＋∫π202cos x d x ＝2＋2sin x |π20＝4.变式训练二 题面：由直线y ＝2x 及曲线y ＝3－x 2围成的封闭图形的面积为( )￥A ．2 3B ．9－23答案： 详解：注意到直线y ＝2x 与曲线y ＝3－x 2的交点A ，B 的坐标分别是(－3，－6)，(1,2)，因此结合图形可知，由直线y ＝2x 与曲线y ＝3－x 2围成的封闭图形的面积为⎠⎛－31(3－x 2－2x )d x ＝⎝ ⎛⎭⎪⎫3x －13x 3－x 2⎪⎪⎪1－3＝3×1－13×13－12－⎣⎢⎡3×－3－13×－33]－－32＝323，选D.题二 ^题面：如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为( )．A ．1B ．1C ．1D ．17变式训练一题面：函数f (x )＝sin(ωx ＋φ)的导函数y ＝f ′(x )的部分图象如图所示，其中，P 为图象与y 轴的交点，A ，C 为图象与x 轴的两个交点，B 为图象的最低点．若在曲线段ABC 与x 轴所围成的区域内随机取一点，则该点在△ABC 内的概率为________．：答案：π4. 详解：设A (x 0,0)，则ωx 0＋φ＝π2，∴x 0＝π2ω－φω. 又y ＝ωcos(ωx ＋φ)的周期为2πω， ∴|AC |＝πω，C ⎝ ⎛⎭⎪⎫π2ω－φω＋πω，0.依题意曲线段ABC 与x 轴围成的面积为 S ＝－∫π2ω－φω＋πωπ2ω－φωωcos(ωx ＋φ)d x ＝2. ∵|AC |＝πω，|y B |＝ω，∴S △ABC ＝π2. ∴满足条件的概率为π4.。
变式训练二 题面：（2012•福建）如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为（ ）A ．B ．·C ．D ．答案：C. 详解：根据题意，正方形OABC 的面积为1×1=1， 而阴影部分由函数y=x 与y=围成，其面积为∫01（﹣x ）dx=（﹣）|01=，则正方形OABC 中任取一点P ，点P 取自阴影部分的概率为=； 故选C ．【金题精讲 题一 题面：（识图求积分，二星）已知二次函数y ＝f (x )的图象如图所示，则它与x 轴所围图形的面积为( )．A ．2π5B ．43C ．32D ．π2答案：变式训练一…题面：如图求由两条曲线y ＝－x 2，y ＝－14x 2及直线y ＝－1所围成的图形的面积．答案：43. 详解：由⎩⎨⎧y ＝－x 2，y ＝－1，得交点 A (－1，－1)，B (1，－1)．由⎩⎪⎨⎪⎧y ＝－14x 2，y ＝－1，得交点C (－2，－1)，D (2，－1)． ∴所求面积S ＝2⎣⎢⎡⎦⎥⎤∫10⎝ ⎛⎭⎪⎫－14x 2＋x 2d x ＋⎠⎛12⎝ ⎛⎭⎪⎫－14x 2＋1d x ＝43. 》变式训练二 题面：例1求在[0,2]π上，由x 轴及正弦曲线sin y x =围成的图形的面积. 答案：4. 详解：作出sin y x =在[0,2]π上的图象如右 sin y x =与x 轴交于0、π、2π，所 求积2200sin |sin |(cos )|(cos )|4s xdx xdx x x ππππππ=+=---=⎰⎰题二 题面：（作图求积分，四星）求曲线36y x x =-与曲线2y x =所围成的图形的面积．#x y-Л2Л交点的横坐标分别为2,0,3-，12112S =．变式训练一题面：求曲线2y x =，y x =及2y x =所围成的平面图形的面积. 答案：76. 详解：作出2y x =，y x =及2y x =的图如右解方程组22y x y x =⎧⎨=⎩ 得24x y =⎧⎨=⎩ 00x y =⎧⎨=⎩ 解方程组2y x y x =⎧⎨=⎩得11x y =⎧⎨=⎩ 00x y =⎧⎨=⎩∴所求面积12201(2)(2)s x x dx x x dx =-+-⎰⎰12201(2)xdx x x dx =+-⎰⎰212320111|()|23x x x =+- 76=答：此平面图形的面积为76变式训练二 题面：%求由抛物线28(0)y x y =>与直线6x y +=及0y =所围成图形的面积.答案：403. 详解：作出28(0)y x y =>及6x y +=的图形如右：y解方程组2860y x x y ⎧=⎨+-=⎩ 得24x y =⎧⎨=⎩解方程组600x y y +-=⎧⎨=⎩ 得60x y =⎧⎨=⎩∴所求图形的面积26028(6)s xdx x dx =+-⎰⎰322620221402|(6)|323x x x ⋅+-= 题三 题面： （1）由曲线y x =，直线2y x =-及y 轴所围成的图形的面积为_______．（2）由曲线2y x =与直线2y x =-所围成的封闭图形的面积为_______．·答案：（1）163；（2）92．变式训练一题面： 设f （x ）=，函数图象与x 轴围成封闭区域的面积为（ ）A ．B ．】C ．D ．答案：C.详解：根据题意作出函数的图象：xO2(66根据定积分，得所围成的封闭区域的面积S=故选C…变式训练二 题面：已知函数的图象与x 轴所围成图形的面积为（ ） A ． 1/2 B ．1 C ． ]2D ．3/2 答案：D. 详解：由题意图象与x 轴所围成图形的面积为102(1)cos x dx xdx π--++⎰⎰210021()|sin |2x x x π-=-++ 112=+ 32=.故选D ．题四 题面：（导数与积分结合，二星）设函数()mf x x ax =+的导函数为()21f x x '=+，则21()f x dx -⎰的值等于______．答案：56．变式训练一题面："设函数f (x )＝x m ＋ax 的导函数f ′(x )＝2x ＋1，则⎠⎛12f (－x )d x 的值等于( )答案：A. 详解：由于f (x )＝x m ＋ax 的导函数f ′(x )＝2x ＋1，所以f (x )＝x 2＋x ，于是∫21f (－x )d x＝∫21(x 2－x )d x ＝⎝ ⎛⎭⎪⎫13x 3－12x 2⎪⎪⎪21＝56.变式训练二 题面： ）设函数f (x )＝x m ＋ax 的导函数f ′(x )＝2x ＋1，则⎠⎛12f (－x )d x 的值等于( )答案：A. 详解：由于f (x )＝x m ＋ax 的导函数为f ′(x )＝2x ＋1，所以f (x )＝x 2＋x ，于是⎠⎛12f (－x )d x ＝⎠⎛12 (x 2－x )d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3－12x 221＝56. 题五 题面： …（化简后求积分，四星）（1）求21sin 2xdx π-20sin cos x x dxπ=-⎰原式4204(cos sin )(sin cos )x x dx x x dx πππ=-+-⎰⎰22 2.=（2）440(sin cos )22x xdx π+⎰变式训练一题面：与定积分∫3π01－cos x d x 相等的是( ) ∫3π0sinx2d x∫3π0⎪⎪⎪⎪⎪⎪sin x 2d x x2d x )))D ．以上结论都不对[答案：B. 详解：∵1－cos x ＝2sin 2x 2，∴∫3π01－cos x d x ＝∫3π02 ⎪⎪⎪⎪⎪⎪sin x 2d x ＝2∫3π0⎪⎪⎪⎪⎪⎪sinx 2d x .变式训练二 题面： 40cos xdx π=⎰________. 答案：22. 《详解： 因为40cos xdx π=⎰sin x ⎪⎪⎪ π40＝sin π4＝22，所以∫π40cos x d x ＝22.题六题面： （定积分的运用，三星）函数f (x )＝sin(ωx ＋φ)的导函数y ＝f ′(x )的部分图象如图所示，其中，P 为图象与y 轴的交点，A ，C 为图象与x 轴的两个交点，B 为图象的最低点．(1)若φ＝π6，点P 的坐标为⎝⎛⎭⎪⎫0，332，则ω＝________； (2)若在曲线段ABC 与x 轴所围成的区域内随机取一点，则该点在△ABC 内的概率为________．[解析] (1)函数f (x )＝sin(ωx ＋φ)求导得，f ′(x )＝ωcos(ωx ＋φ)，把φ＝π6和点⎝⎛⎭⎪⎫0，332代入得ωcos ⎝⎛⎭⎫0＋π6＝332解得ω＝3． … (2)取特殊情况，在(1)的条件下，导函数f ′(x )＝3cos ⎝⎛⎭⎫3x ＋π6，求得A ⎝⎛⎭⎫π9，0， B ⎝⎛⎭⎫5π18，－3，C ⎝⎛⎭⎫4π9，0，故△ABC 的面积为S △ABC ＝12×3π9×3＝π2，曲线段与x 轴所围成的区域的面积S ＝－⎪⎪f x 4π9π9＝－sin ⎝⎛⎭⎫4π3＋π6＋sin ⎝⎛⎭⎫3π9＋π6＝2，所以该点在△ABC 内的概率为P ＝S △ABC S ＝π4.同类题一题面：设y ＝f (x )是二次函数，方程f (x )＝0有两个相等的实根，且f ′(x )＝2x －2.(1)求y ＝f (x )的表达式；(2)求y ＝f (x )的图象与两坐标轴所围成图形的面积．答案：(1) f (x )＝x 2－2x ＋1.… (2) 13. 详解：(1)设f (x )＝ax 2＋bx ＋c (a ≠0)，则f ′(x )＝2ax ＋b .又f ′(x )＝2x －2，所以a ＝1，b ＝－2，即f (x )＝x 2－2x ＋c .又方程f (x )＝0有两个相等实根，所以Δ＝4－4c ＝0，即c ＝1.故f (x )＝x 2－2x ＋1.(2)依题意，所求面积为S ＝⎠⎛01(x 2－2x ＋1)d x ＝(13x 3－x 2＋x )|10＝13. 。
同类题二题面：设y =f （x ）是二次函数,方程f （x ）=0有两个相等的实根，且f ′（x ）=2x +2.（1）求y =f （x ）的表达式；（2）求y =f （x ）的图象与两坐标轴所围成图形的面积.（2）若直线x =－t （0＜t ＜1＝把y =f （x ）的图象与两坐标轴所围成图形的面积二等分，求t 的值.答案：￥（1）f （x ）=x 2+2x +1.（2）13. （3）t =1－321. 详解： （1）设f （x ）=ax 2+bx +c ，则f ′（x ）=2ax +b ，又已知f ′（x ）=2x +2∴a =1，b =2. ∴f （x ）=x 2+2x +c又方程f （x ）=0有两个相等实根，∴判别式Δ=4－4c =0，即c =1.[故f （x ）=x 2+2x +1.（2）依题意，有所求面积=31|)31()12(0123201=++=++--⎰x x x dx x x . （3）依题意，有x x x x x x t t d )12(d )12(2021++=++⎰⎰---， ∴023123|)31(|)31(t t x x x x x x ---++=++，－31t 3+t 2－t +31=31t 3－t 2+t ，2t 3－6t 2+6t －1=0，∴2（t －1）3=－1，于是t =1－321.思维拓展题一题面：（几何法求积分，四星）（1）计算0⎰，121sin x xdx -⎰；（2）求椭圆22221x y a b +=的面积．0044b S a ==⎰⎰，转化为圆的面积．同类题一题面：求定积分11dx -⎰的值. 答案：2π． 详解：11dx -⎰表示圆x 2＋y 2＝1在第一、二象限的上半圆的面积． 因为2S π=半圆，又在x 轴上方．所以11dx -⎰＝2π．同类题二题面：20)ax dx -⎰的值是（ ） A. 143π- B. 143π+ C. 123π- D. 12π- 答案：A.详解：积分所表示的几何意义是以（1，0）为圆心，1为半径第一象限内圆弧与抛物线y=x 2在第一象限的部分坐标轴围成的面积，故只需求出圆的面积乘以四分之一与抛物线在第一象限的部分与x 轴和直线x=1围成的图形的面积之差．即20)ax dx-⎰ 1231001|443x dx x ππ=-=-⎰ 143π=-. 故答案选A。